| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 24 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219016 | |
| Published online | 10 October 2012 | |
Online material
Appendix A: Cosmic-ray interaction model
We consider a model in which low-energy cosmic rays (LECRs) are produced in an unspecified acceleration region and penetrate a nearby cloud of neutral gas at a constant rate (see Fig. A.1). The energetic particles can produce nonthermal X-rays by atomic collisions while they slow down by ionization and radiative energy losses in the dense cloud. We further assume that the LECRs that penetrate the cloud can escape from it after an energy-independent path length Λ, which is a free parameter of the model. The differential equilibrium number of primary CRs of type i (electrons, protons, or α particles) in the cloud is then given by 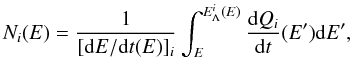 (A.1)where (dQi / dt) is the differential rate of LECRs injected in the cloud, [dE / dt(E)] i is the CR energy loss rate, and the maximum energy
(A.1)where (dQi / dt) is the differential rate of LECRs injected in the cloud, [dE / dt(E)] i is the CR energy loss rate, and the maximum energy 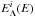 is related to the escape path length Λ (expressed in units of H atoms cm-2) by
is related to the escape path length Λ (expressed in units of H atoms cm-2) by 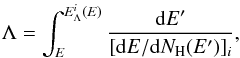 (A.2)where
(A.2)where 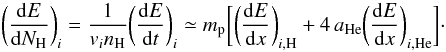 (A.3)Here, vi is the particle velocity, nH the mean number density of H atoms in the cloud, mp the proton mass, aHe = 0.0964 the cosmic abundance of He relative to H (Lodders 2003), and (dE / dx)i,H and (dE / dx)i,He the CR stopping powers (in units of MeV g-1 cm2) in ambient H and He, respectively. We used for electrons the stopping-power tables of Berger & Seltzer (1982) below 1 GeV and the relativistic formulae given by Schlickeiser (2002) above this energy. The stopping powers for protons and α-particles were extracted from the online databases PSTAR and ASTAR, respectively (Berger et al. 2005).
(A.3)Here, vi is the particle velocity, nH the mean number density of H atoms in the cloud, mp the proton mass, aHe = 0.0964 the cosmic abundance of He relative to H (Lodders 2003), and (dE / dx)i,H and (dE / dx)i,He the CR stopping powers (in units of MeV g-1 cm2) in ambient H and He, respectively. We used for electrons the stopping-power tables of Berger & Seltzer (1982) below 1 GeV and the relativistic formulae given by Schlickeiser (2002) above this energy. The stopping powers for protons and α-particles were extracted from the online databases PSTAR and ASTAR, respectively (Berger et al. 2005).
The process of CR transport in the cloud, which does not need to be specified in the above formalism, is nevertheless relevant to estimate the escape path length Λ from the cloud size. It is clear that if the cloud medium is not diffusive, because of, e.g., efficient ion-neutral damping of MHD waves, Λ ~ nHLC, where LC is the characteristic size of the cloud. But otherwise, the escape path length, which can then be estimated as 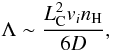 (A.4)can be much greater than the characteristic column density
(A.4)can be much greater than the characteristic column density 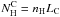 , depending on the diffusion coefficient D. For example, with the typical mean diffusion coefficient for the propagation of Galactic CR nuclei in the local interstellar magnetic field B (Berezinsky et al. 1990),
, depending on the diffusion coefficient D. For example, with the typical mean diffusion coefficient for the propagation of Galactic CR nuclei in the local interstellar magnetic field B (Berezinsky et al. 1990), 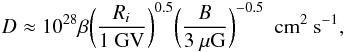 (A.5)where β = vi / c and Ri is the particle rigidity, one gets from Eq. (A.4) for non-relativistic protons:
(A.5)where β = vi / c and Ri is the particle rigidity, one gets from Eq. (A.4) for non-relativistic protons: 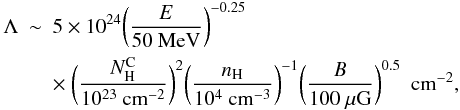 (A.6)where
(A.6)where 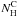 , nH and B are scaled to typical values for massive molecular clouds in the GC region.
, nH and B are scaled to typical values for massive molecular clouds in the GC region.
For nonrelativistic particles diffusing in the cloud with a diffusion coefficient 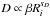 typically with 0.3 < sD < 0.5, the escape path length estimated from Eq. (A.4) depends only mildly on energy as Λ ∝ E − sD / 2. However, we have adopted here a simple slab model with an energy-independent escape path length in order to limit the number of free parameters as much as possible.
typically with 0.3 < sD < 0.5, the escape path length estimated from Eq. (A.4) depends only mildly on energy as Λ ∝ E − sD / 2. However, we have adopted here a simple slab model with an energy-independent escape path length in order to limit the number of free parameters as much as possible.
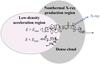 |
Fig. A.1
Schematic illustration of the cosmic-ray interaction model: fast particles produced in a low-density acceleration region can diffusively penetrate a denser cloud (if their kinetic energy is higher than a threshold energy Emin) and then produce nonthermal X-rays by atomic collisions. |
| Open with DEXTER | |
The process of CR penetration into molecular clouds is not well known (see, e.g., Gabici et al. 2007, and references therein). The theoretical predictions range from almost-free penetration (e.g. Cesarsky & Völk 1978) to exclusion of CRs of kinetic energies up to tens of GeV (e.g. Skilling & Strong 1976). Here, for simplicity, we assume that CRs can freely penetrate the clouds if their kinetic energy is higher than a threshold energy Emin, which is another free parameter of the model. We further consider the differential rate of primary CRs that penetrate the nonthermal X-ray production region to be a power law in kinetic energy above Emin: 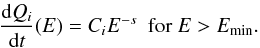 (A.7)The model finally has four free parameters that can be studied from spectral fitting of X-ray data (see Sect. 5): Λ, Emin, the power-law spectral index s, and the metallicity of the X-ray emitting cloud, Z. The X-ray spectral analysis also provides the CR spectrum normalization Ci, which allows one to estimate the power injected by the primary LECRs into the nonthermal X-ray production region:
(A.7)The model finally has four free parameters that can be studied from spectral fitting of X-ray data (see Sect. 5): Λ, Emin, the power-law spectral index s, and the metallicity of the X-ray emitting cloud, Z. The X-ray spectral analysis also provides the CR spectrum normalization Ci, which allows one to estimate the power injected by the primary LECRs into the nonthermal X-ray production region: 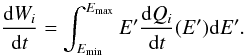 (A.8)In the following, the integration in the above equation is limited to Emax = 1 GeV. Due to CR escape, the power continuously deposited by the fast particles inside the cloud should generally be lower than dWi / dt.
(A.8)In the following, the integration in the above equation is limited to Emax = 1 GeV. Due to CR escape, the power continuously deposited by the fast particles inside the cloud should generally be lower than dWi / dt.
Appendix B: X-rays from accelerated electron interactions
In the framework of the adopted steady-state, slab interaction model, the differential X-ray production rate from collisions of accelerated electrons with the cloud constituents can be written as 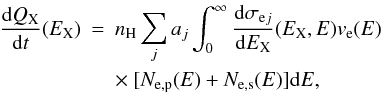 (B.1)where aj is the abundance of element j relative to H in the X-ray emitting cloud, (dσej / dEX) is the differential X-ray production cross section for electron interaction with atoms j, and Ne,p and Ne,s are the differential equilibrium numbers of primary and secondary LECR electrons in the ambient medium, respectively.
(B.1)where aj is the abundance of element j relative to H in the X-ray emitting cloud, (dσej / dEX) is the differential X-ray production cross section for electron interaction with atoms j, and Ne,p and Ne,s are the differential equilibrium numbers of primary and secondary LECR electrons in the ambient medium, respectively.
B.1. Secondary electron production
Primary LECR electrons injected into an interstellar molecular cloud produce secondary electrons mainly from ionization of ambient H2 molecules and He atoms. The corresponding differential production rate of knock-on electrons is given by 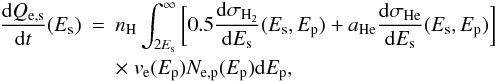 (B.2)where (dσH2 / dEs) and (dσHe / dEs) are the H2 and He differential ionization cross sections for the production of a secondary electron of energy Es by impact of a primary electron of energy Ep. The lower limit of the integral is 2Es, because the primary electron is by convention the faster of the two electrons emerging from the collision. The maximum possible energy transfer is therefore Es = 0.5(Ep − Bj) ≃ 0.5Ep, where BH2 = 15.43 eV and BHe = 24.59 eV are the electron binding energies of H2 and He, respectively. This convention is consistent with the definition of the stopping powers used throughout this paper (see Eq. (A.3)), which also pertain to the outgoing electron of higher energy.
(B.2)where (dσH2 / dEs) and (dσHe / dEs) are the H2 and He differential ionization cross sections for the production of a secondary electron of energy Es by impact of a primary electron of energy Ep. The lower limit of the integral is 2Es, because the primary electron is by convention the faster of the two electrons emerging from the collision. The maximum possible energy transfer is therefore Es = 0.5(Ep − Bj) ≃ 0.5Ep, where BH2 = 15.43 eV and BHe = 24.59 eV are the electron binding energies of H2 and He, respectively. This convention is consistent with the definition of the stopping powers used throughout this paper (see Eq. (A.3)), which also pertain to the outgoing electron of higher energy.
The differential ionization cross sections are calculated from the relativistic binary encounter dipole (RBED) theory (Kim et al. 1994; 2000b). This successful model combines the binary-encounter theory for hard collisions with the dipole interaction of the Bethe theory for fast incident electrons. For the differential oscillator strengths, we use the analytic fits provided by Kim et al. (1994) for H2 and Kim et al. (2000a) for He. For the average orbital kinetic energy of the target electrons, we take UH2 = 15.98 eV and UHe = 39.51 eV.
By inserting Eq. (A.1) into Eq. (B.2) and using for the electron energy loss rate the expression given in Eq. (A.3), we see that the secondary electron production rate does not depend on the absolute density of H atoms in the ambient medium (nH). This comment also applies to the X-ray production rate, which only depends on the relative abundances aj (see Eq. (B.1)). This important property of the adopted steady-state, slab model will allow us to estimate unambiguously the cosmic-ray power dWi / dt (Eq. (A.8)) from the measured X-ray flux.
 |
Fig. B.1
Calculated differential equilibrium electron numbers (Ne; solid lines) for two differential injection rates of primary electrons (dQe,p / dt; dotted lines): a) s = 3, Emin = 10 keV; b) s = 2, Emin = 1 MeV. Also shown are the differential production rates of secondary, knock-on electrons (dQe,s / dt; dashed lines). The H density in the nonthermal X-ray production region, which intervenes in the calculation of Ne,p and Ne,s, is nH = 104 cm-3 and the path length of the primary electrons in this region is Λ = 1024 cm-2. The calculations are normalized to a total power of 1 erg s-1 injected by the primary LECR electrons in the X-ray production region. |
| Open with DEXTER | |
Calculated differential production rates of primary and knock-on electrons are shown in Fig. B.1. Also shown is the corresponding steady-state differential number of secondary electrons in the ambient medium, Ne,s. We calculated the latter from Eqs. (A.1) and (A.2), assuming the characteristic escape path length of the secondary particles to be Λ/2. Although this assumption is uncertain, it has no significant effect on the total X-ray production.
We see in Fig. B.1 that the effect of H2 and He ionization on the electron energy distribution is to redistribute the total kinetic energy of the injected particles to a larger number of lower-energy electrons. Thus, for hard enough primary electron spectrum (i.e. low s and high Emin, see Fig. B.1b), secondary electrons of energies Es ≳ 10 keV could potentially make a significant contribution to the total nonthermal X-ray emission. On the other hand, one can easily check that the successive production of knock-on electrons by the secondary electrons themselves can be safely neglected for the X-ray emission.
B.2. X-ray continuum emission
The X-ray continuum emission is due to the bremsstrahlung of both primary and secondary electrons. We take electron bremsstrahlung into account only in ambient H and He and calculate the differential cross sections from the work of Strong et al. (2000, Appendix A), which is largely based on Koch & Motz (1959). We use the scattering functions from Blumenthal & Gould (1970) to take into account the arbitrary screening of the H and He nuclei by the bound electrons.
B.3. X-ray line emission
 |
Fig. B.2
Calculated X-ray emission produced by LECR electrons with the source spectra shown in Fig. B.1 interacting in a gas cloud of solar metallicity. PEB: primary electron bremsstrahlung; SEB: secondary electron bremsstrahlung. Photoelectric absorption is taken into account with a H column density of 1022 cm-2. |
| Open with DEXTER | |
The X-ray line emission results from the filling of inner-shell vacancies produced by fast electrons in ambient atoms. We consider the Kα and Kβ lines (2p → 1s and 3p → 1s transitions in the Siegbahn notation) from ambient C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni. The corresponding cross sections can be written as 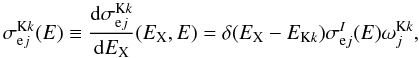 (B.3)where EKk is the energy of line Kk (Kα or Kβ), δ(EX − EKk) is Dirac’s delta function,
(B.3)where EKk is the energy of line Kk (Kα or Kβ), δ(EX − EKk) is Dirac’s delta function, 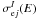 the total cross section for the K-shell ionization of atom j by an electron of energy E, and
the total cross section for the K-shell ionization of atom j by an electron of energy E, and 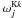 the Kk fluorescence yield for atom j (Kaastra & Mewe 1993). Note that
the Kk fluorescence yield for atom j (Kaastra & Mewe 1993). Note that 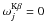 for element j with atomic number ≤ 12 (i.e. Mg), since these atoms do not have 3p electrons in their ground level.
for element j with atomic number ≤ 12 (i.e. Mg), since these atoms do not have 3p electrons in their ground level.
For the K-shell ionization cross sections, we adopted the semi-empirical formula of Quarles (1976), which agrees well with the RBED cross sections for Ni and lighter elements (see Kim et al. 2000b) and is simpler to use. We checked that the Quarles’s formula correctly reproduces the data compiled in Long et al. (1990), in particular at relativistic energies.
The width of the X-ray lines produced by electron impact can be estimated from the sum of the natural widths of the atomic levels involved in the transition. Indeed, broadening effects caused by multiple simultaneous ionizations can be safely neglected for LECR electrons. Thus, the Kα1 and Kα2 components of the Fe Kα line have experimental full widths at half-maximum (FWHM) of only 2.5 and 3.2 eV, respectively (Salem & Lee 1976). However, the energy separation of the two fine-structure components is 13 eV, which is much less than the energy resolution at 6.4 keV of the X-ray cameras aboard XMM-Newton and Chandra, but larger than the expected resolution of the ASTRO-H X-ray Calorimeter Spectrometer (7 eV FWHM; Takahashi et al. 2010). Here, we neglect the fine-structure splitting of the K lines and for simplicity adopt the same width for all the lines: ΔEX = 10 eV.
Figure B.2 shows calculated nonthermal X-ray spectra (LX = EX × dQX / dt) produced by LECR electrons injected with the differential rates shown in Fig. B.1 into a cloud of solar metallicity. We took the photoelectric absorption of X-rays into account using a H column density NH = 1022 cm-2 and the cross sections of Morrison & McCammon (1983). We see in Fig. B.2 that the most prominent line is that of Fe at 6.40 keV. This is because this element has the highest product of Kα fluorescence yield (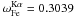 , Kaastra & Mewe 1993) and cosmic abundance. The EW of the Fe Kα line is equal to 293 and 394 eV in the spectra shown in panels a and b, respectively. The second strongest line in these spectra is the Si Kα line at 1.74 keV; its EW is equal to 80 and 90 eV in panels a and b, respectively. We also see in this figure that (i) the shape of the continuum emission reflects the hardness of the primary electron injection spectrum; and (ii) the total X-ray emission is dominated by the contribution of the primary electrons. The emission from the secondary electrons is negligible in panel a and accounts for 10–20% of the total emission below 10 keV in panel b.
, Kaastra & Mewe 1993) and cosmic abundance. The EW of the Fe Kα line is equal to 293 and 394 eV in the spectra shown in panels a and b, respectively. The second strongest line in these spectra is the Si Kα line at 1.74 keV; its EW is equal to 80 and 90 eV in panels a and b, respectively. We also see in this figure that (i) the shape of the continuum emission reflects the hardness of the primary electron injection spectrum; and (ii) the total X-ray emission is dominated by the contribution of the primary electrons. The emission from the secondary electrons is negligible in panel a and accounts for 10–20% of the total emission below 10 keV in panel b.
Appendix C: X-rays from accelerated ion interactions
The differential X-ray production rate from accelerated ion interactions can be written with a slight modification of Eq. (B.1), as follows:  (C.1)where the index i runs over the constituents of the nonthermal ion population. The first term in the integral represents the X-ray production by the primary LECR ions and the second term the contribution of the secondary electrons. As a starting point, we assume in the present work that the LECR ion population is mainly composed of protons and α particles and that the contributions of accelerated metals to the total X-ray emission can be neglected. We therefore do not consider the broad X-ray line emission that can arise from atomic transitions in fast C and heavier species following electron captures and excitations (Tatischeff et al. 1998), except in Sect. 7.2. However, for typical compositions of accelerated cosmic particles, the fast metals significantly contribute neither to the production of the X-ray lines from the ambient atoms nor to the bremsstrahlung continuum radiation (see Tatischeff et al. 1998). We further assume that the accelerated protons and α particles are in solar proportion, that is, Cα / Cp = aHe (see Eq. (A.7)).
(C.1)where the index i runs over the constituents of the nonthermal ion population. The first term in the integral represents the X-ray production by the primary LECR ions and the second term the contribution of the secondary electrons. As a starting point, we assume in the present work that the LECR ion population is mainly composed of protons and α particles and that the contributions of accelerated metals to the total X-ray emission can be neglected. We therefore do not consider the broad X-ray line emission that can arise from atomic transitions in fast C and heavier species following electron captures and excitations (Tatischeff et al. 1998), except in Sect. 7.2. However, for typical compositions of accelerated cosmic particles, the fast metals significantly contribute neither to the production of the X-ray lines from the ambient atoms nor to the bremsstrahlung continuum radiation (see Tatischeff et al. 1998). We further assume that the accelerated protons and α particles are in solar proportion, that is, Cα / Cp = aHe (see Eq. (A.7)).
In the calculations of the equilibrium spectra (Np and Nα), we neglect the nuclear destruction and catastrophic energy loss (e.g. interaction involving pion production) of the fast ions in the cloud. Indeed these processes are not important in comparison with the ionization losses below ~300 MeV nucleon-1 kinetic energy (see, e.g., Schlickeiser 2002) and most of the X-ray emission below 10 keV, which is the prime focus of the present work, is produced by ions in this low energy range (see Fig. 5b).
C.1. Secondary electron production
 |
Fig. C.1
Calculated differential equilibrium numbers of fast particles (Ni; solid lines) for the differential injection rate of primary protons given by s = 2 and Emin = 100 keV (dQp / dt; dotted lines). Also shown are the differential production rates of secondary knock-on electrons (dQe,s / dt; dashed lines). a) Λ = 1021 cm-2; b) Λ = 1024 cm-2. The H density in the nonthermal X-ray production region is nH = 104 cm-3. The calculations are normalized to a total power of 1 erg s-1 injected by the primary LECR protons in this region. |
| Open with DEXTER | |
We calculate the production of secondary electrons associated to the ionization of ambient H2 molecules and He atoms. The corresponding differential ionization cross sections are obtained as in Tatischeff et al. (1998) from the work of Chu et al. (1981). We neglect the production of secondary electrons and positrons that follows the production of charged pions in hadronic collisions. In fact, the corresponding electron and positron source functions can dominate the one of knock-on electrons only at energies >10 MeV (Schlickeiser 2002), and these high-energy leptons are not important for the production of X-rays <10 keV (see Fig. 5a).
Differential production rates of knock-on electrons are shown in Fig. C.1, together with the corresponding equilibrium spectra of primary protons and secondary electrons. This figure illustrates the effects of changing the CR escape path length from Λ = 1021 cm-2 (panel a) to 1024 cm-2 (panel b). In the first case, protons of energies up to 1.4 MeV are stopped in the cloud, whereas in the second case the transition energy between proton stopping and escape is at 71 MeV. We see that above this transition energy the equilibrium spectrum has a similar slope than the source spectrum, whereas at lower energies the equilibrium proton distribution is harder due to the ionization losses. We can anticipate that the total X-ray production rate will be much higher for the case Λ = 1024 cm-2, as a result of the higher proton number at equilibrium above a few MeV.
C.2. X-ray continuum emission
The X-ray continuum emission is due to inverse bremsstrahlung from the fast ions (the radiation of a single photon in the collision of a high-speed ion with an electron effectively at rest) and classical bremsstrahlung from the secondary knock-on electrons. In the nonrelativistic domain, the bremsstrahlung produced by a proton of kinetic energy E in a collision with a H atom at rest has the same cross section as that of an electron of kinetic energy (me / mp)E in a collision with a stationary proton (me and mp are the electron and proton masses, respectively). We calculate this cross section as in Sect. 3.2, but without taking the screening of the H nucleus by the bound electron into account. The cross section for interaction of a proton with a H atom is then multiplied by (1 + 2aHe) to take the ambient He into account. For α particles, we replace the proton energy E by the energy per nucleon of the projectile and multiply the proton cross section by 4 to account for the nuclear charge dependence of the bremsstrahlung cross section.
In the relativistic case, the cross section for proton inverse bremsstrahlung is different from the one for classical electron bremsstrahlung, owing to the appearance of angular and energy abberations in the transformation between the two rest frames of the interacting particles (Haug 2003). We checked that these effects can be neglected in good approximation in the present work.
In Fig. C.2 we show two X-ray spectra corresponding to the particle equilibrium spectra presented in Fig. C.1. We see that the continuum emission is dominated by inverse bremsstrahlung, which is a general rule independent of the model parameters (see Tatischeff et al. 1998). We also see that, as expected, the X-ray production rate is much higher for Λ = 1024 cm-2 than for Λ = 1021 cm-2, the difference being a factor of 22, 337 and 1054 at 1, 10, and 100 keV, respectively.
 |
Fig. C.2
Calculated X-ray emission produced by LECR protons and α-particles interacting in a gas cloud of solar metallicity, for the differential injection rate of primary protons shown in Fig. 9. The contribution of accelerated α-particles is included as explained in the text, assuming in particular the solar abundance Cα / Cp = 0.0964. a) Λ = 1021 cm-2; b) Λ = 1024 cm-2. IB: inverse bremsstrahlung; SEB: secondary electron bremsstrahlung. Photoelectric absorption is taken into account with a H column density of 1022 cm-2. |
| Open with DEXTER | |
C.3. X-ray line emission
For producing X-ray lines from the ambient atoms, we take both the contribution from secondary electrons (see Eq. (B.3)) and that from primary ions into account. The cross sections for K-shell ionization by proton and α-particle impacts are extracted from the data library implemented by Pia et al. (2009) in the Geant4 toolkit for the simulation of particle induced X-ray emission (PIXE). We use the cross sections calculated in the ECPSSR theory with high-velocity corrections (Lapicki et al. 2008). These cross sections are more accurate for mildly relativistic projectiles than those previously employed by Tatischeff et al (1998).
Proton and α-particle collisions with target atoms do not lead to significant line broadening effects caused by multiple simultaneous ionizations. We thus adopt as before a width of 10 eV for all the lines (see Sect. 3.3). We note, however, that the X-ray lines produced by collisions of ions heavier than 4He can be
shifted by several tens of eV, significantly broadened and split up into several components (Garcia et al. 1973). For example, the Fe Kα line produced by impacts of O ions of 1.9 MeV nucleon-1 is blueshifted by ~50 eV in comparison with the one produced by 5-MeV proton impacts, and has a FWHM of ~100 eV (see Garcia et al. 1973, Fig. 3.55).
The most intense line produced by LECR protons and α-particles is also the neutral Fe Kα line at 6.40 keV (Fig. C.2). This line has an EW of 2.31 and 0.80 keV in the spectra shown in Figs. C.2a and b, respectively. The second strongest line in these spectra is the Si Kα line at 1.74 keV; its EW is equal to 309 eV in panel a and 152 eV in panel b.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


