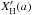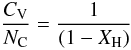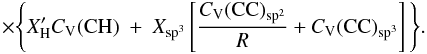| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118483 | |
| Published online | 15 June 2012 | |
Online material
Appendix A: Size-dependent structural properties and surface hydrogenation effects
For an amorphous hydrocarbon material the mean atomic mass, 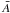 , is given by
, is given by 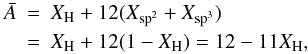 (A.1)where Xsp2 and Xsp3 are the atomic fractions of sp2 and sp3 carbon atoms, respectively. For a bulk material density ρ and a grain radius a the total number of atoms per particle, Natom, is then
(A.1)where Xsp2 and Xsp3 are the atomic fractions of sp2 and sp3 carbon atoms, respectively. For a bulk material density ρ and a grain radius a the total number of atoms per particle, Natom, is then 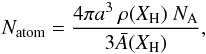 (A.2)where NA is Avogadro’s number. The total number of atoms (C+H) in the bulk of the particle can then be estimated from the simplified expression
(A.2)where NA is Avogadro’s number. The total number of atoms (C+H) in the bulk of the particle can then be estimated from the simplified expression 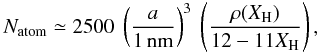 (A.3)which indicates that a 1 nm radius a-C:H particle with XH ≃ 0.5 contains approximately 600 atoms, half of them being hydrogen atoms [NH = XH Natom] and half carbon atoms [NC = (1 − XH) Natom], i.e.,
(A.3)which indicates that a 1 nm radius a-C:H particle with XH ≃ 0.5 contains approximately 600 atoms, half of them being hydrogen atoms [NH = XH Natom] and half carbon atoms [NC = (1 − XH) Natom], i.e., 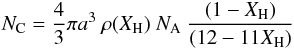 (A.4)or
(A.4)or 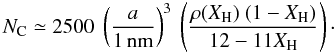 (A.5)Figure A.1 shows NC as a function of radius for typical nano-particle sizes, and also indicates the effect of adopting a lower effective density for the smallest particles with
(A.5)Figure A.1 shows NC as a function of radius for typical nano-particle sizes, and also indicates the effect of adopting a lower effective density for the smallest particles with 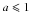 nm (dashed lines).
nm (dashed lines).
 |
Fig. A.1
The number of carbon atoms in a particle, NC, as a function of the particle radius for XH = 0.17 (thin), 0.3, 0.4, 0.5 and 0.62 (thick). The dashed lines show NC for effective radii aeff = a0.8, which simulate lower effective densities for sub-nm particles, i.e., larger effective radii for a given number of carbon atoms. |
| Open with DEXTER | |
The effective volume of a constituent atom within such a particle is 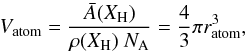 (A.6)and the effective radius of an atom within the solid is then
(A.6)and the effective radius of an atom within the solid is then 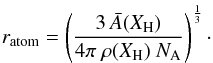 (A.7)The number of surface atoms per particle is given by the volume of the surface layer one atom deep divided by the atomic volume, i.e.,
(A.7)The number of surface atoms per particle is given by the volume of the surface layer one atom deep divided by the atomic volume, i.e., 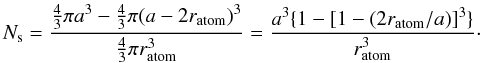 (A.8)The number of atoms per particle
(A.8)The number of atoms per particle 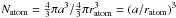 and the fraction of the atoms that are “in” the surface, Fs, is then given by Ns/Natom, i.e.,
and the fraction of the atoms that are “in” the surface, Fs, is then given by Ns/Natom, i.e., 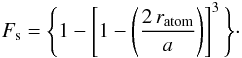 (A.9)Figure A.2 shows Fs as a function of a for various values of XH and indicates that Fs is not particularly sensitive to XH but that the surface contribution is important for sizes less than 10 nm and is dominant for particles as small as 0.5 nm in radius. For particles with a ≳ 30 nm surface effects can be safely ignored.
(A.9)Figure A.2 shows Fs as a function of a for various values of XH and indicates that Fs is not particularly sensitive to XH but that the surface contribution is important for sizes less than 10 nm and is dominant for particles as small as 0.5 nm in radius. For particles with a ≳ 30 nm surface effects can be safely ignored.
 |
Fig. A.2
The fraction of atoms in the surface, Fs, as a function of the particle radius for XH = 0.17 (thin), 0.3, 0.4, 0.5 and 0.62 (thick). |
| Open with DEXTER | |
The average number of hydrogen atoms associated with a carbon atom, based on the bulk composition, is 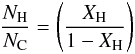 (A.10)and this must also be the minimum hydrogenation at the surface. The coordination of carbon atoms at the particle surface will be incomplete and result in “dangling” C(–)n bonds (n ≤ 3), which are assumed to hydrogenate to form additional C–H bonds at the particle surface. Assuming homogeneous mixing of the atoms, within the particle and at the surface, the number of carbon atoms in the particle is
(A.10)and this must also be the minimum hydrogenation at the surface. The coordination of carbon atoms at the particle surface will be incomplete and result in “dangling” C(–)n bonds (n ≤ 3), which are assumed to hydrogenate to form additional C–H bonds at the particle surface. Assuming homogeneous mixing of the atoms, within the particle and at the surface, the number of carbon atoms in the particle is 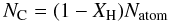 (A.11)and the number carbon atoms at the surface is
(A.11)and the number carbon atoms at the surface is 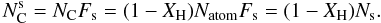 (A.12)The fraction of carbon atoms at the surface is then
(A.12)The fraction of carbon atoms at the surface is then 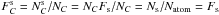 because the same bulk and surface composition are assumed. The possibility that the surface may reconstruct in some way without the addition of hydrogen is ignored here. Such a re-construction would alter the bulk properties, which are assumed to be fixed here, and is not allowed in the model because this would lead to structural inconsistencies.
because the same bulk and surface composition are assumed. The possibility that the surface may reconstruct in some way without the addition of hydrogen is ignored here. Such a re-construction would alter the bulk properties, which are assumed to be fixed here, and is not allowed in the model because this would lead to structural inconsistencies.
A key question here is: How many extra hydrogen atoms are needed to bond with, or equivalently to “passivate”, all of the “dangling” C(–)n bonds at the particle surface? In a statistical sense, for a particle large compared to the mean inter-atomic bond length, the particle surface presents a semi-infinite, planar cut through the network/bulk structure. Thus, a surface carbon atom can only “use” approximately half of its normal bulk coordination and so each hydrogen-passivated, surface carbon atom can have an extra 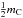 hydrogen atoms attached, where mC is the mean bulk carbon atom coordination number (see Paper I). The number of extra surface-passivating hydrogen atoms, attached to the surface carbon atoms, is then
hydrogen atoms attached, where mC is the mean bulk carbon atom coordination number (see Paper I). The number of extra surface-passivating hydrogen atoms, attached to the surface carbon atoms, is then 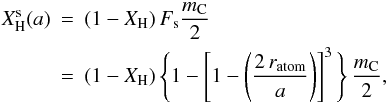 (A.13)where the factor (1 − XH) = XC allows for the fact that only that fraction of the surface atoms are carbon. Substituting into Eq. (2), the particle size-dependent total (surface+bulk) hydrogen atom fraction is given by
(A.13)where the factor (1 − XH) = XC allows for the fact that only that fraction of the surface atoms are carbon. Substituting into Eq. (2), the particle size-dependent total (surface+bulk) hydrogen atom fraction is given by 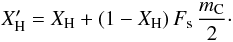 (A.14)In effect, and for small particles, this expression leads to total atomic fractions for the particles
(A.14)In effect, and for small particles, this expression leads to total atomic fractions for the particles 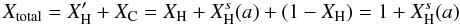 (A.15)that are greater than unity because the surface H atoms are counted as an “extra” atomic fraction, which seems a reasonable approach given that the surface H atoms do not affect the bulk structure. Figure A.3 shows the surface and bulk hydrogen atom fractions as a function of the particle size for values of XH typical of the eRCN model (dashed lines) and the DG model (solid lines).
(A.15)that are greater than unity because the surface H atoms are counted as an “extra” atomic fraction, which seems a reasonable approach given that the surface H atoms do not affect the bulk structure. Figure A.3 shows the surface and bulk hydrogen atom fractions as a function of the particle size for values of XH typical of the eRCN model (dashed lines) and the DG model (solid lines).
 |
Fig. A.3
The total hydrogen atom “fraction”, |
| Open with DEXTER | |
The surface passivation of the particles, by the addition of extra H atoms, occurs for all types of CHn groups (n ≤ 3) and thus their fractional concentration, XCHn, must be augmented in the same way as for the hydrogen atom fraction XH. However, specific surface CH groups, CH(n−1), need to be considered in terms of how they transform to CHn groups by the addition of extra H atoms at the particle surface, i.e., 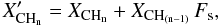 (A.16)which can, as explained above, lead to total atomic fractions greater that unity because of the “extra” surface H atom convention adopted here.
(A.16)which can, as explained above, lead to total atomic fractions greater that unity because of the “extra” surface H atom convention adopted here.
The bulk composition eRCN and DG models therefore turn out to be good representations for particles with radii ≳ 100 nm. Only for smaller particles need surface passivation and particle size effects be of concern. Thus, small, stochastically-heated, amorphous hydrocarbon grains in the ISM are likely to show important size and surface effects, in addition to their properties that will be very strongly dependent on annealing (thermal processing) to more aromatic structures (in the absence of an opposing re-hydrogenation process).
Appendix B: The size-dependent visible-UV electronic properties of a-C(:H)
This Appendix considers, in detail, the necessary solid-state physics at the heart of the derivation of the size-dependent, EUV-cm wavelength, complex refractive indices of a-C(:H) materials.
B.1. The π–π⋆, C6, σ–σ⋆ bands and the a-C(:H) band gap
In order to aid the reader to negotiate the “maze” of the relevant solid-state physics, in the following paragraph the salient points relating to the band gap properties of a-C:H and a-C as, principally, reviewed in the seminal paper by Robertson (1986) are briefly summarised here. The interested is encouraged to delve into the Robertson (1986) review for a deeper understanding of these complex materials.
Within the energy gap, between the valence and conduction bands, of a-C(:H) materials there exist states that control the electronic properties, conductivities, luminescence and doping in these amorphous, semi-conducting materials. The gap in an amorphous, semi-conductor is strictly a pseudo-gap or mobility gap, resulting from a localisation of the contributing states. The mobility edge in such a system is the energy separating these localised states from the extended states (states well within the valence and conduction bands), where increasing disorder leads to the localisation of the contributing states (e.g., the segregation of aromatic clusters). In a-C the valence band and conduction band edges are due to π states, which can support extended states. However, in a-C:H, with decreasing sp2 content, the π density of states decreases and the π–π ⋆ bands will be localised, i.e., isolated from one another. The optical absorption edges of a-C are consistent with broad valence and conduction band tails (pseudo gap 0.4–0.7 eV), which overlap at the gap centre. The tail states in a-C are therefore expected to be the π states of larger than average aromatic clusters. Wider gap a-C:Hs likely belong to the class of materials where deep gap states can be distinguished, i.e., states that are more localised than the tail states and that are associated with “defect” sites where the bonding is different from that of the bulk. These defect states are rather complex and likely associated with a breaking of the weaker π bonds (rather than the σ bonds), which is aided by the fact that π defects can delocalise into conjugated, olefinic, π electron systems (see also the postulate in Sect. B.1.2 below). The defect density in a-C:H correlates inversely with the optical gap and the effect of increasing the hydrogen content in a-C:H materials is to lower the defect density by reducing (aromatic) cluster sizes. This leads to an increase in the defect energy and thereby a decrease in the probability for the occurrence of these defect states within the structure. The creation energy for “dangling bond” sites is ~ 1.8 eV and their character, analogous to that of the planar methyl radical (:CH3), will be π-like in character, as for the olefinic sp2 and aromatic clusters. [End of the band gap physics summary taken from Robertson (1986).]
The wide-band optical spectra of a-C:H materials show two clear, separated bands: a π − π∗ peak at ~4 eV and a σ − σ∗ peak at ~ 13 eV (Robertson 1986). The energy positions of these π − π∗ and σ − σ∗ bands are practically independent of the hydrogen atom content (Kassavetis et al. 2007). Another band at ~ 6.5 eV has been attributed to small, aromatic, “benzene-like” clusters in the structure (e.g., Robertson 1986). Such small aromatic clusters are an intrinsic part of the covalent network and are not fully-hydrogenated like benzene. Here the ~ 6.5 eV band is, nevertheless, designated C6. However, it is much broader than the width predicted for a single, six-fold, aromatic ring and so, as hypothesised below (see Sect. B.1.2), clusters other than simple six-fold, aromatic rings probably contribute to the broadening of the C6 band. With thermal annealing or photo-darkening the π − π∗ peak strengthens with respect to both the σ − σ∗ and C6 bands; trends that result from an increase in aromaticity with annealing. In this work the following characteristic band energies have been used: 4.0 eV for the π − π∗, 6.5 eV for the C6 and 13.0 eV for the σ − σ∗ bands.
B.1.1. The π–π ⋆ band
Figure B.1 shows the aromatic component, i.e., the sum of the π–π ⋆ and C6 bands, contribution to the imaginary part of the index of refraction (upper figure; π–π ⋆ + C6) and in a Tauc plot (lower figure; π–π ⋆ + C6 with the low-energy addition given by Eqs. (21) and (22) in Paper II). Also indicated by the vertical grey lines are the band gap positions for aromatic clusters as a function of NR (=1,2,3,4,5,... from right to left) as predicted by Eq. (3). The position of the UV extinction bump at 217.5 nm (the vertical, dashed, grey line) is also indicated, which lies very close to the predicted “band gap” for NR = 1, i.e., a C6 or benzene-like aromatic cluster.
 |
Fig. B.1
Upper figure: the aromatic component contribution to the imaginary part of the refractive index, k, for the optEC(s) model materials with Eg = 0,0.5,1.0,1.5,2.0 and 2.5 eV (dark grey, pink, brown, yellow, blue and purple lines, from top to bottom, respectively). The dark grey long-dashed curve indicates the adopted C6 band profile peaking at 6.5 eV, as indicated. Lower figure: the same data presented as (αE)0.5 but with the low energy extrapolation now included. See text for details. |
| Open with DEXTER | |
The π–π ⋆ band has been modelled as arising from a power-law distribution of aromatic ring systems. The maximum possible size for the aromatic clusters, NR(max), is determined using the values expected for a bulk material (e.g., Eq. (2) in Paper II and/or Fig. 23 from Robertson 1986) or their size-limited values, NR(a), which can be obtained by solving for NR in Eqs. (3) and (4) given in Paper II. For Eg < 0.5 eV and for the smallest considered particles, i.e., for a = 0.33 nm with ≈ 40 C atoms, NR(max) = 6. Steric considerations imply that the aromatic clusters should principally consist of “isolated” two- and three-ring systems containing about three quarters of the carbon atoms. The remaining carbon atoms must be in olefinic and aliphatic bridging structures such as –CH=CH– and –CH2–, and these must be mostly in the form of short aliphatic chains with paired carbon atoms, i.e., –CH2–CH2–. Indeed, the spectra of sub-nm, H-poor a-C(:H) particles (with Eg = 0.1−0.5 eV) in Figs. 16 to 17 (see Sect. 5.1) clearly reveal only aromatic CH and aliphatic CHn bands, which seem to be consistent with this hypothesis.
The optEC(s)(a) material band gap, Eg, fraction of sp2 C atoms in aromatic clusters, farom., maximum number of rings per aromatic cluster, NR(max), aromatic cluster power-law, p, scaling factor, Sπ − π ⋆ , hydrogen atom fraction, XH, and colour coding scheme.
Paper II gives the derivation of the imaginary part of the complex index of refraction, k, using: 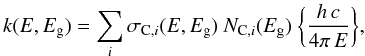 (B.1)where σC,i(E,Eg) is the specific carbon atom cross-section and NC,i(Eg) is the number of carbon atoms per unit volume. In fitting the size-dependent π − π ⋆ contribution to k the material band gap needs to be taken into account and it is therefore convenient to fit the k data in the Tauc form, i.e.,
(B.1)where σC,i(E,Eg) is the specific carbon atom cross-section and NC,i(Eg) is the number of carbon atoms per unit volume. In fitting the size-dependent π − π ⋆ contribution to k the material band gap needs to be taken into account and it is therefore convenient to fit the k data in the Tauc form, i.e., 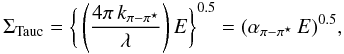 (B.2)and then derive k from,
(B.2)and then derive k from, 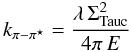 (B.3)The π − π ⋆ band contribution to the cross-section, σC,π − π ⋆ , is given by
(B.3)The π − π ⋆ band contribution to the cross-section, σC,π − π ⋆ , is given by 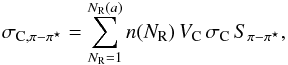 (B.4)where n(NR) is the relative abundance of aromatic ring systems with NR rings, VC = 1023 farom.(Eg) is the number of carbon atoms per unit volume, farom.(Eg) is the fraction of sp2 carbon atoms in aromatic clusters, σC is the assumed aromatic carbon atom cross-section ( ≃ 10-18 cm2) and Sπ − π ⋆ is a scaling factor (see Table B.1). The aromatic cluster size distribution has been modelled using the following power law description,
(B.4)where n(NR) is the relative abundance of aromatic ring systems with NR rings, VC = 1023 farom.(Eg) is the number of carbon atoms per unit volume, farom.(Eg) is the fraction of sp2 carbon atoms in aromatic clusters, σC is the assumed aromatic carbon atom cross-section ( ≃ 10-18 cm2) and Sπ − π ⋆ is a scaling factor (see Table B.1). The aromatic cluster size distribution has been modelled using the following power law description, 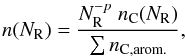 (B.5)where the power law exponent, p, varies from 2.5 to 3.55 for the highest to lowest band gap materials, respectively, and nC(NR) is the number of carbon atoms in an aromatic cluster with NR rings (see Eq. (3) in Paper II). Note that the cluster abundance is normalised by ∑ nC,arom., the total number of carbon atoms in aromatic clusters per unit volume. For the smallest aromatic cluster, NR = 1, a benzene-like ring, a smaller relative abundance, before normalisation, of 0.08 (rather than unity) is assumed because the contribution of this structure is already included, in part, within the C6 band.
(B.5)where the power law exponent, p, varies from 2.5 to 3.55 for the highest to lowest band gap materials, respectively, and nC(NR) is the number of carbon atoms in an aromatic cluster with NR rings (see Eq. (3) in Paper II). Note that the cluster abundance is normalised by ∑ nC,arom., the total number of carbon atoms in aromatic clusters per unit volume. For the smallest aromatic cluster, NR = 1, a benzene-like ring, a smaller relative abundance, before normalisation, of 0.08 (rather than unity) is assumed because the contribution of this structure is already included, in part, within the C6 band.
 |
Fig. B.2
Upper figure: the π − π ⋆ and low energy adjustment (L + π − π ⋆ , orange), C6 (green) and σ − σ∗ (purple) component contributions to the imaginary part of the refractive index, k (blue line), for the optEC(s)(a) model material with Eg(bulk) = 0.25 eV and particle radius of 3 nm (The red line shows the summed L + π − π ⋆ , C6 and σ − σ∗ contributions). Lower figure: the same data as in the upper figure presented as (αE)0.5 (the blue and red lines, where the solid lines show only the summed aromatic, L + π − π ⋆ and C6 components) but where the aromatic cluster band profiles are shown for NR = 2,3,4, ...(thin orange line profiles right to left), the extrapolations to band gap (black lines with the band gap-determining extrapolation data points indicated by the open diamond symbols), the band gap values (thin grey vertical lines), the limiting Eg(NR) value and the bulk material band gap or Tauc gap, Eg,Tauc. See text for details. |
| Open with DEXTER | |
 |
Fig. B.3
Upper figure: the L + π − π ⋆ , C6 and σ − σ∗ component contributions to the imaginary part of the refractive index, k, for Eg(bulk) = 0.25 eV and radius 0.5 nm. Lower figure: the same data presented as (αE)0.5. See text and previous figure for details.The black lines show the aromatic cluster profile extrapolations (determined by the open diamond data points) to the band gap values (thin grey vertical lines). |
| Open with DEXTER | |
For the time being, and until laboratory data give better constraints, “reasonable” Gaussian profiles have been assumed for the aromatic cluster band profiles because the exact form of the bands is unknown. Lorentz and Drude band profiles give wings that are too strong and do not allow a fit to the low-energy behaviour.
The derived Gaussian band peak energy for each given aromatic cluster is given by 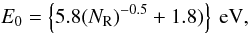 (B.6)and for the width, σG, a band width for a cluster of given NR is assumed so as to yield the correct band gap for that cluster, i.e.,
(B.6)and for the width, σG, a band width for a cluster of given NR is assumed so as to yield the correct band gap for that cluster, i.e., 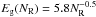 (as per Eq. (4)). With this imposition, a fit was obtained using
(as per Eq. (4)). With this imposition, a fit was obtained using 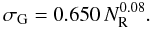 (B.7)The band gap for the given NR cluster is obtained by extrapolation of the band profile at energies (E0 − 0.6) eV and (E0 − 1.2) eV (indicated by the diamonds in Figs. B.2 and B.3), using the above-described width expression, so as to be consistent with the required value. The resulting aromatic cluster band gaps (vertical grey lines), band shapes (orange gaussian profiles) and the band gap extrapolations (sloping black lines) are shown in the lower panels of Figs. B.2 and B.3.
(B.7)The band gap for the given NR cluster is obtained by extrapolation of the band profile at energies (E0 − 0.6) eV and (E0 − 1.2) eV (indicated by the diamonds in Figs. B.2 and B.3), using the above-described width expression, so as to be consistent with the required value. The resulting aromatic cluster band gaps (vertical grey lines), band shapes (orange gaussian profiles) and the band gap extrapolations (sloping black lines) are shown in the lower panels of Figs. B.2 and B.3.
Table B.1 shows the parameters used in the aromatic cluster size distribution fitting and the Eg-XH colour coding scheme. The fraction of sp2 C atoms in aromatic clusters, farom., is taken from Paper I, the maximum number of rings per aromatic cluster, NR(max), is estimated from (Robertson 1986, Fig. 23).
For particle radii larger than 3 nm (for 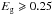 eV), where there is no need to take into account particle size limitations on NR(max), this limiting size depends only on the band gap of the material under consideration. Empirically, the π − π ⋆ -NR(max) size-limitations on the particle optical properties are only of concern for
eV), where there is no need to take into account particle size limitations on NR(max), this limiting size depends only on the band gap of the material under consideration. Empirically, the π − π ⋆ -NR(max) size-limitations on the particle optical properties are only of concern for 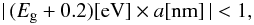 (B.8)i.e., principally for low band gap, small particles (see Figs. 2 and B.4). The aromatic cluster power-law, p, and the scaling factor, Sπ − π ⋆ , can be rather well fit by the following analytical expressions,
(B.8)i.e., principally for low band gap, small particles (see Figs. 2 and B.4). The aromatic cluster power-law, p, and the scaling factor, Sπ − π ⋆ , can be rather well fit by the following analytical expressions, 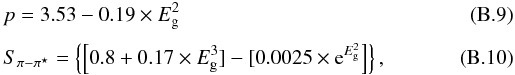 where Sπ − π ⋆ (Eg = 0) = 0.8. However, in the fitting and derivation of the Eg- and size-dependent values of k the values given in Table B.1 were used, these give a more exact representation of the bulk material data.
where Sπ − π ⋆ (Eg = 0) = 0.8. However, in the fitting and derivation of the Eg- and size-dependent values of k the values given in Table B.1 were used, these give a more exact representation of the bulk material data.
 |
Fig. B.4
The size-dependent or effective band gap, Eg(eff) ≡ Eg { a,NR(max) } , vs. the expected bulk material band gap, Eg(bulk), for 0.33, 0.5, 1 amd 3 nm radius particles. The sloping red line shows the behaviour for infinite particle size. |
| Open with DEXTER | |
Figures B.2 and B.3 show the results of modelling the π–π ⋆ band as a power-law distribution of aromatic ring systems for the Eg = 0.25 eV and for two particle radii, a = 3 nm and a = 0.5 nm, where small particle effects are not and are important, respectively. Clearly, the aromatic cluster size-distribution approach (red line) allows a very satisfactory fit to the derived k data (blue line) when cluster size-limiting effects are unimportant (Fig. B.2). The principal effect to note here, as the particle size is reduced (cf., Figs. B.2 and B.3), is a decrease in k at low energies (E < 4 eV, 1/λ < 3 μm-1) and an increase in k in the UV (E ~ 4–9 eV, 1/λ ~ 3–9 μm) resulting in a bump in the ~ 4 μm-1 (~6 eV) region. At higher energies (E > 9 eV), where the σ − σ ⋆ band dominates, the behaviour of k is size independent in this model. For small particle sizes, large aromatic ring systems are not allowed and so that the optical activity associated with these small band gap entities is not present. The aromatic clusters being shifted towards lower NR systems, with higher band gaps, leads to a shift in the optical activity to higher energies.
In order to complete the fitting of the long-wavelength behaviour of the bulk material π − π ⋆ band, with the aromatic cluster size-distribution approach, a linear portion to k is added at energies below 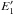 , as per Paper II (Sect. 4.1.2), with a size-dependent behaviour of
, as per Paper II (Sect. 4.1.2), with a size-dependent behaviour of 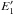 given by
given by 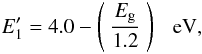 (B.11)which is a slightly modified from of Eq. (21) in Paper II (the constant 4.0 replaces the value of 4.5 used in Paper II). Then, for the size-dependent behaviour the band gap predicted by the largest-possible aromatic cluster, Eg { a,NR(max) } , is used rather than the expected band gap for the bulk material, Eg(bulk), in determining the appropriate size-dependent value of
(B.11)which is a slightly modified from of Eq. (21) in Paper II (the constant 4.0 replaces the value of 4.5 used in Paper II). Then, for the size-dependent behaviour the band gap predicted by the largest-possible aromatic cluster, Eg { a,NR(max) } , is used rather than the expected band gap for the bulk material, Eg(bulk), in determining the appropriate size-dependent value of 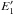 . The relationship between the effective and bulk material band gaps is shown in Fig. B.4.
. The relationship between the effective and bulk material band gaps is shown in Fig. B.4.
For the power-law index at long wavelengths, γ, that given by Eq. (22) in Paper II is used, except for the the two lowest values of Eg, i.e., − 0.1 and 0.0 eV, where setting γ = −0.35 and − 0.14, respectively, gives a better to fit the bulk material data.
The particle size-dependent adjustment of the summed π–π ⋆ and C6 aromatic structure contributions to the determination of k imposes an effective scaling down because of the reduced effects at long-wavelengths. Therefore the π–π ⋆ and C6 contributions are scaled-up to ensure the conservation of neff, i.e., their total integrated contribution to k is taken to be constant. The required π–π ⋆ + C6 enhancement factor, i.e., neff(a)/neff(bulk), is found to be at most ≃ 1.9, 2.5 and 3.1 for 1, 0.5 and 0.33 nm radius particles, with Eg = −0.1 eV, respectively.
B.1.2. The C6 band
The C6 band contribution to the wide-gap optical properties, as derived in Paper II, is shown by the dark grey dashed line in the upper part of Fig. B.1. Given that the adopted C6 band is apparently larger than would be predicted by the Eg relation (Eq. (4)), it is likely, for low-symmetry a-C(:H) materials, that there could be an important contribution from the normally weak π − σ ⋆ transitions involving the promotion of electrons from bonding π orbitals to anti-bonding σ ⋆ orbitals. Here it is hypothesised that the C6 band also contains an important contribution from olefinic sp2-rich clusters as well. In this respect, note that the lowest-lying triplet (singlet) transitions lie at 4.2 eV (7.6 eV) for ethylene, > C = C < , and at 3.9 eV (4.9 eV) for benzene (Robertson 1986). These triplet and singlet band positions are indicated in the upper plot of Fig. B.1. In particular, it is postulated that conjugated olefinic chains and cyclic precursor-aromatic configurations, which upon aromatisation can transform into the aromatic cluster states with NR = 0 to 3 (i.e., benzene-, naphthalene- and anthracene-like structures) contribute to the C6 band. This effect will become weaker as NR increases and hence this is why the C6 band is likely to be particularly broadened by the presence of linked, conjugated olefinic cycles. In support of this Ferrari & Robertson (2004) point out that the clustering of the sp2 phase into chains or even cage-like structures plays a key role in the determination of the properties of amorphous (hydro)carbon materials.
B.1.3. The σ–σ ⋆ band
The σ–σ ⋆ band might also exhibit some size-dependence effects, which might perhaps manifest as a narrowing of the band as the particle size decreases. This could result from a reduction in the range of sp3 C atom structural configurations that would then lead to a profile more characteristic of polyethylene, (CH2)n, or even diamond. This work does not consider this effect but it would be interesting to see if any such a change is seen in laboratory data. However, in order to explain this, the experimental conditions would require the isolation of a-C(:H) nano-particles (a < 3 nm) with a range of H atom concentrations.
Appendix C: The size-dependent optical properties of a-C(:H) materials
Figures C.1 to C.5 show the the imaginary parts (k: upper panels) and the real parts (n: lower panels) of the complex indices of refraction for a-C(:H) materials as a function of wavelength, from EUV to mm wavelengths. Each coloured line represents one of the 14 different band gap materials (Eg = −0.1 to 2.67 eV: see Table B.1 for the full colour code).These figures show the data for particles with radii of 30, 10, 3, 1 and 0.33 nm, respectively, and complement Figs. 3 and 4 given in Sect. 4. Note that in all of the figures the same x- and y-axis ranges are used in order to allow a direct comparison of the various data.
It is found that for particles with radii ≳ 10 nm (i.e., Figs. 3 and C.1 to C.2) that k and n are rather invariant but that they vary significantly for smaller particles, where the most obvious effect is a dramatic decrease in the “continua” at wavelengths longward of ≈ 0.5 μm. However, the underlying spectral bands remain but vary in form as indicated in the figures in Appendix E. This is a direct result of the decreasing maximum aromatic cluster size as particle size decreases.
Note that, as the particles become smaller, there is a “piling-up” or “convergence” effect, in that the optical properties for all band gap materials start to look the same. This is, in major part, a result of the restrictions placed on the largest possible aromatic clusters by the particle size, which leads to an opening-up of the gap with decreasing particle radius. It also indicates a transition towards more molecular properties with prominent bands and weak continua.
 |
Fig. C.1
The real part, n (upper), and imaginary part, k (lower), of the complex index of refraction, m = n(a,Eg,λ) + ik(a,Eg,λ), for 30 nm radius a-C(:H) particles as a function of Eg, as predicted by the optEC(s)(a) model presented in this paper (see Table B.1 for the line colour-coding). |
| Open with DEXTER | |
 |
Fig. C.2
As per Fig. C.1 but for particles of radius 10 nm. |
| Open with DEXTER | |
 |
Fig. C.3
As per Fig. C.1 but for particles of radius 3 nm. |
| Open with DEXTER | |
 |
Fig. C.4
As per Fig. C.1 but for particles of radius 1 nm. |
| Open with DEXTER | |
 |
Fig. C.5
As per Fig. C.1 but for particles of radius 0.33 nm. |
| Open with DEXTER | |
Appendix D: Size-dependent optical-UV properties
Figures D.1 to D.5 present Qext (thick solid), Qsca (dotted), Qabs (dashed) and Qsca/Qext (thin solid), as a function of inverse wavelength, for particle radii of 30, 10, 3, 0.5 and 0.33 nm, and for all considered band gaps. See Tables 1 and B.1 for the line colour-coding; from large gap, purple (2.67 eV), to low band gap, black. These figures complement Figs. 6 and 7 for 100 and 1 nm radii particles. The thin horizontal black lines in each figure show the maximum albedo, i.e., the limit where Qsca/Qext = 1 and the extinction would be due to pure scattering. The vertical, dark grey band shows the observed variation in the central position of the 217 nm UV bump and the vertical, light grey bands on either side indicate observed variation in its observed full width at half maximum (e.g., Fitzpatrick 2004; Fitzpatrick & Massa 2007).
As can clearly be seen in Figs. 6 and D.1, the extinction of hydrogen-rich a-C:H particles (XH ≳ 0.5 or equivalently Eg ≳ 2 eV), with radii greater than 30 nm, will be increasingly dominated by scattering over a wider wavelength region as the particle size increases. In particular, it can be seen that 100 nm radius particles have albedos ≥ 0.5 for XH ≳ 0.2 ( ≡ Eg ≥ 1 eV) over a wavelength range of at least ≈ 0.3–1 μm ( ≈ 1–3 μm-1). For larger hydrogen contents even higher albedos are to be found and over a much wider wavelength range.
 |
Fig. D.1
Qext (thick solid lines), Qsca (dotted lines), Qabs (dashed lines) and Qsca/Qext (thin solid lines) vs. λ-1 for 30 nm radius particles as a function of band gap.The vertical grey line shows the central position of the UV bump at 217 nm and the vertical, lighter grey bands on either side indicate the full width of the observed UV bump (Fitzpatrick 2004; Fitzpatrick & Massa 2007). The thin horizontal black line shows the limit where Qsca/Qext = 1. |
| Open with DEXTER | |
 |
Fig. D.2
Same as for Fig. D.1 but for 10 nm radius particles. The grey squares show the diffuse ISM extinction curve for RV = 3.1 (dark) and 5.1 (light) from (Savage & Mathis 1979, large squares) and (Mathis 1990, small squares). The grey curves indicate the average galactic extinction, and its variation (upper and lower grey curves), as derived by Fitzpatrick & Massa (2007). |
| Open with DEXTER | |
 |
Fig. D.3
Same as for Fig. D.1 but for 3 nm radius particles. |
| Open with DEXTER | |
 |
Fig. D.4
Same as for Fig. D.1 but for 0.5 nm radius particles. |
| Open with DEXTER | |
 |
Fig. D.5
Same as for Fig. D.1 but for 0.33 nm radius particles. |
| Open with DEXTER | |
Appendix E: The size-dependent spectra of optEC(s)(a)-modelled particles
Figures E.1 to E.5 present the predicted spectra, based on the eRCN and DG models, for optEC(s)(a)-modelled particles of radii 30,10,3,1, and 0.33 nm, presented as wavelength times absorption coefficient per carbon atom, λα/NC, in the 2–14 μm region, as a function of wavelength and Eg. The complementary spectra for 100 and 0.5 nm radius particles are given in Figs. 8 and 99. The adopted colour-coding for this plot is from large band gap (2.67 eV, purple) to low band gap ( − 0.1 eV, black) with intermediate values in steps of 0.25 eV from 2.5 (violet) to 0 eV (grey) with the addition of the Eg = 0.1 and − 0.1 eV cases (light grey and black, respectively), i.e., as per Table B.1.
The spectra presented here show a systematic evolution with both the band gap, Eg, as already highlighted in Papers I and II, and perhaps more importantly with particle size. With decreasing band gap, Eg, and as described in Paper I, the intrinsic CC and CHn modes responsible for the modelled absorption features show a clear transformation from sp3-dominated CHn bands to sp2-dominated CHn bands as aromatisation proceeds. Note that the spectra for low band gap materials (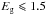 eV) derived from the DG model now include the expected aromatic CH bands, which are due to the passivation/hydrogenation of the aromatic surface.
eV) derived from the DG model now include the expected aromatic CH bands, which are due to the passivation/hydrogenation of the aromatic surface.
The spectra for particle radii down to ≃ 3 nm really do not change substantially. However, descending in radius from 3 to 0.33 nm the following evolutionary sequence(s) is found:
-
a general increase in CH modes with respect to CC modes assurface hydrogenation becomes more important;
-
a significant change in the spectra in the 7–9 μm region for particle radii smaller than 1 nm as the aliphatic CC component contribution declines; and
-
a surprisingly “resilient” aliphatic CH2 band at 6.9 μm, accompanied by an olefinic CH2 band at 7.1 μm, is seen in the spectra of materials with
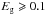 eV.
eV.
Note that bands with central positions long-ward of the vertical grey line (λ > 7.3 μm) are not yet well-determined by laboratory measurements and should therefore be treated with some caution. It is also likely that the bands in the 6.5–7.5 μm region could be too strong in this model and may require re-calibration using better laboratory data when they becomes available.
 |
Fig. E.1
The predicted spectra of optEC(s)(a)-modelled particles of radius 30 nm, presented as the wavelength times absorption coefficient per carbon atom, λα/NC, in the 2–14 μm region (1 Mb = 10-18 cm2). N.B. The bands with central positions long-ward of the vertical grey line (λ(ν0) > 7.3 μm) are not yet well-determined by laboratory measurements. |
| Open with DEXTER | |
 |
Fig. E.2
As per Fig. E.1 but for particles of radius 10 nm. |
| Open with DEXTER | |
 |
Fig. E.3
As per Fig. E.1 but for particles of radius 3 nm. |
| Open with DEXTER | |
 |
Fig. E.4
As per Fig. E.1 but for particles of radius 1 nm. |
| Open with DEXTER | |
 |
Fig. E.5
As per Fig. E.1 but for particles of radius 0.33 nm. |
| Open with DEXTER | |
Appendix F: a-C:H heat capacities
To zero order it can be assumed that the heat capacity of bulk a-C:H/a-C materials is the linear sum of the abundance-weighted heat capacities for the given atom in the given bonding configuration, 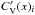 , of the constituent components or chemical groups as per Dwek et al. (1997), i.e.,
, of the constituent components or chemical groups as per Dwek et al. (1997), i.e., 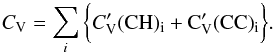 (F.1)Assuming a single heat capacity for the CH component and decomposing the CC component into its sp2 and sp3 constituents and normalising by the number of C atoms per unit volume, NC, gives
(F.1)Assuming a single heat capacity for the CH component and decomposing the CC component into its sp2 and sp3 constituents and normalising by the number of C atoms per unit volume, NC, gives 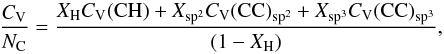 (F.2)which with the substitution R = Xsp3/Xsp2, and recalling that [H] / [C] = XH/(1 − XH), the above equation can be re-written as
(F.2)which with the substitution R = Xsp3/Xsp2, and recalling that [H] / [C] = XH/(1 − XH), the above equation can be re-written as
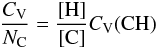
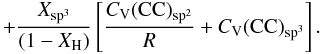 (F.3)The key question is then: what heat capacities should be used for the different components? For CV(CH) the values from Dwek et al. (1997), which were used to determine the heat capacities of PAHs in the ISM, would seem to provide a reasonable approach. For the heat capacity of the sp2 CC component, CV(CC)sp2, a value appropriate for graphite, basically as per Dwek et al. (1997), could be used for the aromatic component or a material typical of an olefinic structure, however, the former approach is rather well-established and is probably to be preferred. For sp3 component heat capacity, CV(CC)sp3, values for diamond or polyethylene could be used; the latter is probably to be preferred.
(F.3)The key question is then: what heat capacities should be used for the different components? For CV(CH) the values from Dwek et al. (1997), which were used to determine the heat capacities of PAHs in the ISM, would seem to provide a reasonable approach. For the heat capacity of the sp2 CC component, CV(CC)sp2, a value appropriate for graphite, basically as per Dwek et al. (1997), could be used for the aromatic component or a material typical of an olefinic structure, however, the former approach is rather well-established and is probably to be preferred. For sp3 component heat capacity, CV(CC)sp3, values for diamond or polyethylene could be used; the latter is probably to be preferred.
For finite-sized hydrocarbon particles the above expressions need to be modified to include the contribution from the surface-bond terminating, or surface passivating, H atoms. In this case the [H]/[C] term in Eq. (F.2) has to be replaced by 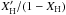 from Eq. (A.14) to give
from Eq. (A.14) to give
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.