| Issue |
A&A
Volume 542, June 2012
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 14 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201117247 | |
| Published online | 05 June 2012 | |
Online material
Appendix A: Hubble archival data
We make use of HST images that were retrieved through the Hubble Legacy Archive web service. The images came from a collection proposals and programs. A table is provided below to summarise the different data and their properties which are important for this paper.
Details of the HST data used in this paper.
Appendix B: Probability test for chance alignment of runaway stars with filaments
Currently, there are no high-resolution, continuous, large field-of-view maps of the 30 Doradus region that show where the star forming filamentary gas and dust are. In the coming year this deficiency will be resolved as the Herschel Space Observatory survey maps of the LMC, HERschel Inventory of The Agents of Galaxy Evolution (HERITAGE) (Meixner et al. 2010), will be publicly released. By combining the HERITAGE maps with the data presented in this paper one could reject the likelihood of O-stars being runaways based on probability. We propose that the definition of a filament from Herschel observations is best defined by the 2nd differential maps Molinari et al. (2010) introduced, where a physically relevant radius from the peaks of the filaments can bear association to the stars.
To do this, we take O-stars similar to the ones discussed in this paper and assume that they are runaways. Using the radial velocity measurements from the Tarantula Survey, we
approximate that there are roughly N number of runaways in total. Then we place a circular boundary around R136 at distance R, where R = Rboundary − Rcluster, and has area Aboundary. Within R distance, let’s assume that gas/dust filaments covers an area Afilament, such that Afilament ≤ Aboundary. Refer to Fig. B.1 for a visual context of the scenario we have now discussed.
With the above conditions, what is the probability that n of N runaway O-stars line up with filamentary structures in the line-of-sight? For simplicity, assume that the N O-stars are randomly distributed within the boundary such that the probability of an O-star lining up with a filament can be expressed as ρ. 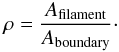 (B.1)To see what probability n of N (n ≤ N) O-stars is in the line-of-sight with filaments we invoke the binomial probability equation as shown below, where we assume that each line-of-sight event is independent of one another.
(B.1)To see what probability n of N (n ≤ N) O-stars is in the line-of-sight with filaments we invoke the binomial probability equation as shown below, where we assume that each line-of-sight event is independent of one another. 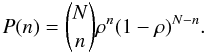 (B.2)
(B.2)
 |
Fig. B.1
A diagram showing how the probabilistic method should be conceptualised. The radius R = Rboundary − Rcluster. All the stars outside of the cluster are initially assumed to be runaways for the binomial probability problem to calculate the likelihood of multiple alignment events between the runaways and the filaments (grey clouds). The filaments at these scales, >5 pc, will not be affected by a single O-star such that nothing remains. |
| Open with DEXTER | |
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


