| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118013 | |
| Published online | 10 February 2012 | |
Online material
Appendix A: An explanation of the spike-like features in the evolution curves
In Fig. 1 we note that at a time of ~ 5 × 104 yr a spike-like feature appears in the evolution curves of some species (e.g. gas phase H2O2 and CH3OH), while the abundances of some other species (e.g. H2O2 and O2 on the grain) change very rapidly at the same time. These features might appear to be caused by faults in the program for solving the set of differential equations. However, after solving the same problem with the Monte Carlo method, which is immune to such numerical instabilities, we find that these features are still present, indicating that they are genuine. How could a smooth ordinary differential equation system generate such an almost-singular feature? In Fig. A.1 we make a zoom-in of Fig. 1 (with several species added and several species removed). It can be seen that, although the time scale of the spike-like feature is relatively short, the evolution is always smooth (except the discreteness caused by the finite sampling of the curve). Then what determines the appearance of such a feature?
 |
Fig. A.1
A zoom-in plot of Fig. 1 (with several species removed and several added), focusing on the spike-like feature (though nothing looks like a spike anymore). The abundance of gH has been multiplied by a factor of 1012 (to make the plot look more compact). |
| Open with DEXTER | |
Because atomic hydrogen is central to the surface chemistry, we first look at the most important reactions governing its abundance on the grain. The main reactions consuming atomic hydrogen on the grains are (in the following a species name preceded by a “g” means a species on the grain, otherwise it is in the gas phase), 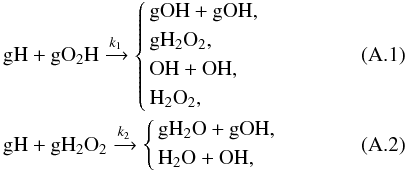 while others such as the reactions with gO3 and gCH2OH are relatively unimportant in the early times. It is mainly produced by
while others such as the reactions with gO3 and gCH2OH are relatively unimportant in the early times. It is mainly produced by 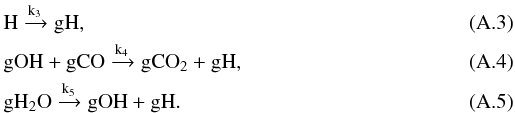 As the abundance of atomic H in the gas phase and the abundance of gCO and gH2O change relatively smoothly, they can be viewed as constant on a short time scale. The main reactions for the consumption and production of gOH are
As the abundance of atomic H in the gas phase and the abundance of gCO and gH2O change relatively smoothly, they can be viewed as constant on a short time scale. The main reactions for the consumption and production of gOH are 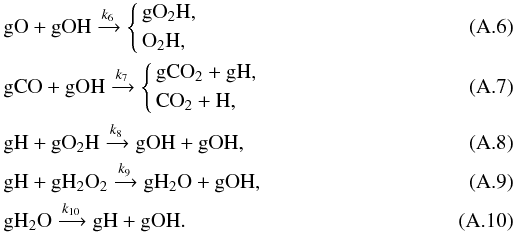 From the above reaction list we may write the evolution equation of gH and gOH as4
From the above reaction list we may write the evolution equation of gH and gOH as4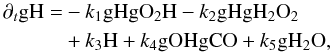 (A.11)
(A.11)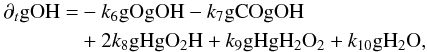 (A.12)or in a more succinct form
(A.12)or in a more succinct form 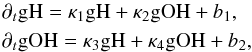 (A.13)where
(A.13)where 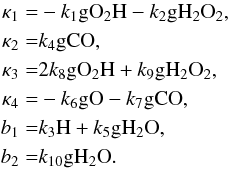 If we view κ1–κ4, as well as b1 and b2, as constants (of course they are not), then Eq. (A.13) can be solved exactly; the solution contains an exponential part and a constant part. The amplitude of the exponential part will be inversely proportional to the determinant of the coefficient matrix
If we view κ1–κ4, as well as b1 and b2, as constants (of course they are not), then Eq. (A.13) can be solved exactly; the solution contains an exponential part and a constant part. The amplitude of the exponential part will be inversely proportional to the determinant of the coefficient matrix 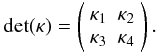 Since κ1–κ4 are not really constant in our problem, we expect that when they become such that det(κ) is close to zero, a spike-like or jump-like behavior would appear. Namely, we require
Since κ1–κ4 are not really constant in our problem, we expect that when they become such that det(κ) is close to zero, a spike-like or jump-like behavior would appear. Namely, we require 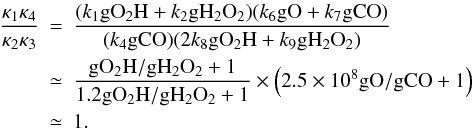 (A.14)The actual value of the parameters have been inserted in the second line of the above equation. These parameters depend on the physical conditions.
(A.14)The actual value of the parameters have been inserted in the second line of the above equation. These parameters depend on the physical conditions.
To satisfy this condition (at least approximately), gO/gCO should be very small. In Fig. A.2 the ratio (κ1κ4)/(κ2κ3) and the value of 2.5 × 108 gO/gCO are plotted as a function of time. The abundances of O, gO, gO2, gH, and gOH are also plotted for reference (not to scale). It can be seen that the (κ1κ4)/(κ2κ3) ratio does decrease, and it approaches a value of unity before the time of the spike/jump feature, and the gO/gCO ratio drops to a very low value monotonically.
 |
Fig. A.2
The ratio (κ1κ4)/(κ2κ3) and the value of 2.5 × 108 × gO/gCO as a function of time. They are to scale. The abundances of several other species are plotted only for reference (not to scale). |
| Open with DEXTER | |
The above mathematical argument can also be understood intuitively. When the gO abundance is so low that reaction (A.6) can be neglected, gOH is only destroyed by reaction (A.7). Each time a gOH radical is consumed, one gH is created (if we neglect the desorption process), and this gH will quickly react with gH2O2 or gO2H to create one or two gOHs. There will then be a net gain in the gOH abundance, leading to its fast growth, and the gH abundance will increase accordingly. Thus we see that reaction (A.8) is crucial in that it produced two gOH radicals by consuming only one gH.
Therefore for such a spike-like feature to occur, the abundance of gO must decrease to a low value such that the reaction between gOH and gO becomes unimportant for consuming
gOH. Namely, we require [ gO ] ≲ [ gCO ] k7/k6 ≃ 5 × 10-13. The abundances of atomic oxygen in the gas phase and on the grain surface are related by O/gO ≃ kevap(gO)/kad(O) ≃ 3 × 106, so equivalently we require [ O ] < 1.5 × 10-6 (i.e., about a factor of 200 less than the initial O abundance) at the time of the spike-like feature. Atomic oxygen is mainly consumed on the grain surface by reacting with another gO to form gO2 (for t ≲ 103 yr) or by reacting with gOH to form gO2H. Only the latter is relevant here. As the abundance of gOH does not change much before the spike-like feature, the time scale for the consumption of atomic oxygen can be estimated to be ln200 × (O/gO)/(k6gOH) ≃ 105 yr, which is on the same order of magnitude as the time of occurrence of the spike-like feature.
The time scale for the endurance of the spike-like feature itself can be estimated to be the time scale for the exhaustion of gO2H or gH2O2 (so that Eqs. (A.11) and (A.12) do not hold anymore) by reacting with gH, which is 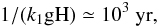 where the gH population (the average number of atomic H on a single grain) is taken to be a median value (10-14) during the rapidly varying period. That equation (A.14) seems to hold after this period (see Fig. A.2) does not mean that gH will keep increasing rapidly, simply because the premise of our argument, namely Eqs. (A.11) and (A.12) are not a good description of the evolution of gH and gOH anymore.
where the gH population (the average number of atomic H on a single grain) is taken to be a median value (10-14) during the rapidly varying period. That equation (A.14) seems to hold after this period (see Fig. A.2) does not mean that gH will keep increasing rapidly, simply because the premise of our argument, namely Eqs. (A.11) and (A.12) are not a good description of the evolution of gH and gOH anymore.
As the abundance of H on the grain increases, almost all the O3 on the grain are converted into O2 and OH. O2 molecules on the grain are then consumed by the slower reaction gH + gO2 → gO2H, with a time scale ~ 105 yr. This explains the prominent peak in the evolution curve of gO2 (see Fig. 1).
Would the spike-like feature have any practical significance (especially observationally)? Ideally, such a short-time feature may be used to constrain the age of a dense cloud, by distinguishing the abundances of certain species between their early-time values (before the spike-like feature) and late-time values (after the spike-like feature). However, due to its dependence on the reaction network being used, which usually contains a lot of uncertainties and is subject to change when new experiments are carried out, the question whether this feature is really relevant for the study of interstellar medium can only be answered by future investigations.
Appendix B: The surface reaction network used in this work
Surface network used in this work.
Appendix C: The enthalpies of the surface species
Enthalpies of the surface species considered in this work that are used to calculate the exoergicities of the surface reactions.
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


