| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/200913282 | |
| Published online | 28 October 2010 | |
Online material
Appendix A: 3D non-LTE treatment of lithium
The calculation of synthetic non-LTE Li I λ 670.8 nm line
profiles from 3D hydrodynamical model atmospheres proceeds in two basic steps. In the
first step, the code NLTE3D provides the departure coefficients 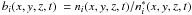 , the ratio of non-LTE to LTE population
number densities for each level i of the Li i model atom as a
function of the geometrical position (x,y,z) in the 3D model atmosphere,
and time (t) as sampled by a number of snapshots (≈ 20) selected to
represent the characteristic temporal variation of the simulation. The departure
coefficient of Li ii is assumed to be 1, since lithium is essentially fully
ionized in the stellar atmospheres of interest.
, the ratio of non-LTE to LTE population
number densities for each level i of the Li i model atom as a
function of the geometrical position (x,y,z) in the 3D model atmosphere,
and time (t) as sampled by a number of snapshots (≈ 20) selected to
represent the characteristic temporal variation of the simulation. The departure
coefficient of Li ii is assumed to be 1, since lithium is essentially fully
ionized in the stellar atmospheres of interest.
In the second step, the departure coefficients are fed into the completely independent spectrum synthesis code Linfor3D9, where they are used to compute the non-LTE line opacity and source function, and in turn the emergent intensity profiles as a function of (x,y,θ,φ,t), where the angles θ and φ specify the orientation of the line-of-sight in polar spherical coordinates. Finally, the emergent mean flux profile is obtained by horizontal, angular, and temporal averaging of the individual intensity profiles.
For this paper, we used an 8-level model atom of Li i to solve the statistical equilibrium equations, considering a total of 11 bound-bound transitions. Details about the energy levels and line transitions are given in Tables A.1 and A.2. The Einstein coefficients Aji provided by the NIST database are related to the Einstein coefficients Bij by
 (A.1)
(A.1)
The corresponding oscillator strength fij is obtained from the relation
 (A.2)
(A.2)
The computationally most expensive part of solving the non-LTE problem is the calculation of the line-blanketed radiation field Jν(x,y,z,t) at each grid point of the selected 3D models, which is needed to determine the photoionization rates for all atomic levels. This is done with a modified version of the radiation transport routines that are used in the CO5BOLD hydrodynamical simulations for computing the radiative energy exchange term ∇Frad(x,y,z). The solution of the radiative transfer equation is based on a Feautrier scheme applied to a set of long characteristics. The continuous opacities used in this context are computed with the routines IONDIS & OPALAM from the Kiel stellar atmosphere package10. Line blanketing is taken into account by adding to the continuous opacity the opacity distribution functions (ODFs, “big division”, vturb = 2 km s-1) of Castelli & Kurucz (2003), including the H i - H + and H i-H i quasi-molecular absorption near 1400 and 1600 Å, respectively. There is a slight inconsistency in the chemical composition adopted for the calculation of the opacities: the continuous opacities are based on the solar abundances of Asplund et al. (2005), while the ODFs rely on the solar composition of Grevesse & Sauval (1998). To obtain the opacities for different metallicities, the solar abundances were scaled by a global factor corresponding to the desired [M/H], with an enhancement of the α-elements by 0.4 dex below [M/H] = −0.5. A total of 600 frequency points were used to obtain the Jν between λ 925 and 19800 Å. We checked that treating continuous scattering as true absorption does not introduce any significant changes in the resulting departure coefficients.
Energy levels of the Li i model atom.
Bound-bound transitions of the Li i model atom.
Given the line-blanketed radiation field Jν(x,y,z,t), the photoionization rate Piκ from level i to the continuum κ is computed as
 (A.3)
(A.3)
where νi is the threshold photoionization frequency for level i, and the photoionization cross-sections αi(ν) for all considered atomic levels are taken from the TOPBASE Opacity Project on-line atomic database at the “Centre de données astronomiques de Strasbourg”11. The photo-recombination rates Pκi from the continuum κ to level i are then given by
 (A.4)
(A.4)
Bν(T) denoting the Kirchhoff-Planck function at local temperature T and frequency ν.
Cross-sections for the collisional ionization and excitation by electrons are computed according to the prescriptions of Seaton (1962) and Van Regemorter (1962), respectively, as given by Allen (1976) and Cox (2000). The oscillator strengths fij from Table A.2 are needed to calculate the collisional excitation cross-sections. Collisional ionization by neutral hydrogen via the charge transfer reaction H(1s) + Li(nl) → Li+(1s2) + H−, and the reverse process H− + Li+(1s2) → H(1s) + Li(nl), are treated according to Barklem et al. (2003) for the first 7 levels. Collisional excitation by neutral hydrogen is ignored, as it was found to be unimportant for thermalizing Li i by Barklem et al. (2003).
The departure coefficients
bi(x,y,z) are finally
obtained by solving the statistical equilibrium equations locally at each grid point
(x,y,z). The profile-averaged radiation field at the line transitions,
 , determines the radiative excitation rates
, determines the radiative excitation rates
 (A.5)
(A.5)
and the radiative de-excitation rates
 (A.6)
(A.6)
where the statistical
weights of lower and upper level, gi and
gj, and the Einstein coefficients
Bij are taken from Table A.2. For the line profile
φν we assume a purely Gaussian
distribution (identical for absorption and emission) with a line width that corresponds to
the local thermal Doppler velocity plus a microturbulence of 1.5 km s-1. The
Doppler shift caused by the line-of-sight component of the hydrodynamical velocity field
is ignored in the present computation. For all transitions except for the resonance line,
 was replaced by the mean continuum intensity
Jν. For the resonance line (transition #1),
the line opacity was taken into account for the computation of
was replaced by the mean continuum intensity
Jν. For the resonance line (transition #1),
the line opacity was taken into account for the computation of  , assuming an f-value of 0.48975
(about 2/3 of the value given in Table A.2 to
represent only the main component of the doublet), together with a typical lithium
abundance of A(Li) = 2.2.
, assuming an f-value of 0.48975
(about 2/3 of the value given in Table A.2 to
represent only the main component of the doublet), together with a typical lithium
abundance of A(Li) = 2.2.
Since  is a non-local quantity that depends in turn on
the bi, a Λ-iteration is employed to obtain a
consistent solution. Fortunately, the Λ iteration converges very rapidly, because even the
Li i resonance line affects the radiation field only marginally, while all the
other lines are very weak. Typically, three iterations are sufficient to achieve
convergence.
is a non-local quantity that depends in turn on
the bi, a Λ-iteration is employed to obtain a
consistent solution. Fortunately, the Λ iteration converges very rapidly, because even the
Li i resonance line affects the radiation field only marginally, while all the
other lines are very weak. Typically, three iterations are sufficient to achieve
convergence.
Finally, the departure coefficients bi are used in the line formation code Linfor3D to compute the non-LTE line opacity
 (A.7)
(A.7)
and the line source function
 (A.8)
(A.8)
where blow and bup are the departure coefficients of lower and upper level, respectively, and Bν is again the Kirchhoff-Planck function.
Appendix B: Analytical fit to 3D NLTE Li abundance as a function of stellar parameters and EW
B.1. Introduction
It is often convenient to have tabular data on an irregular grid y = y(x) condensed into a single function (even with many fit parameters), instead of having to interpolate between the original data points. Choosing a fitting function that is linear in all parameters (e.g., a sum of polynomials as A + Bx + Cx2 or sine/cosine functions) results in a comparatively simple linear problem for finding these parameters, usually with one unique solution. However, the result might not have the desired extrapolation behavior, might be “too wiggly” between the data points, or produce no good fit at all.
A more effective approach might then be to start with a properly crafted function, possibly non-linear, and having fitting parameters “within” the terms as in Aexp(B + Cx). In this case, an iterative process is necessary to determine these parameters. This iteration requires starting values, which will affect the convergence of the process and also the solution if one is found: in this case, the scheme might diverge or converge to different local minima, depending on the starting point. However, this last issue is hardly a problem for our application – we are content with a good fit, and do not necessarily need to achieve the closest one. We continue, however, to have the problem of constructing the fitting function and choosing the initial values for the parameters.
B.2. Method
We used a scheme for recursive term substitution, written in IDL, that attempted not only to find optimum fitting parameters for a given function, but also to automatically determine the optimum functional form itself. The latter was chosen from a set of candidates given by a list of terms and some construction rules. The usual starting point was a constant “function” with one parameter, say A, the best “fit” for which is the mean of y. In each recursion step, all parameters were successively substituted with all of the terms from a list (with possible restrictions), for instance

or

The initial values of (A0, A1, A2) were derived from A by e.g., assuming A0 = A,A1 = 0.1 × A,A2 = 0. Applying a modified version of the IDL function curvefit (requiring also partial derivatives) provided the optimum parameter set for the given function and start values.
This process was repeated with a number of random variations to approach an optimum solution for the given function. The final solution was the globally best fit among all candidate functions and parameters.
The main control parameters are the list of candidate terms and the recursion depth. For the current application, we search a 4D function

where (x0,x1,x2,x3) = (log (EW), log Teff, log g, [Fe/H]), or, for the inverse problem, (A(Li), log Teff, log g, [Fe/H]). We start with

to determine the equivalent width as a function of abundance, based on a simple absorption model for a box-shaped line profile. In the following recursion steps, we replace the parameters with linear terms

which finally results in higher-order polynomials instead of the initial coefficients. In this step, the variation in the COG with the stellar parameters is taken into account. In the process of applying the term substitution, we scanned through several hundred possible functional forms. We decided the most suitable one on the basis of simplicity, and its ability to represent the numerical data with sufficient accuracy.
As described in Sect. 6.1, synthetic grids were computed for three cases, 3D NLTE, 1D LHD NLTE, and 1D LHD LTE. This in principle leads to 6 fitting functions being computed, when both the EW → A(Li) and A(Li) → EW forms are required. We decided to force all three functions in either sense to have the same form, differing only by their parameters. We thus first searched an optimum function for one case (A(Li) → 1D LHD NLTE turned out to be the optimum choice) and then varied only the parameters (and not the functional form) for the other two cases. The final inversion of the function was performed by hand.
B.3. Best-fitting functions
Best-fitting functional forms were produced both to derive A(Li) from EW and to derive EW from A(Li), the latter being useful, e.g., for the preparation of observations. Analytical fit formulae for both cases are presented in Eq. (B.1); fitting coefficients are listed in Table B.1. Three sets of coefficients are listed. The 3D NLTE set is used to fit computations where CO5BOLD 3D hydrodynamical models are used in association with a 3D NLTE time-dependent spectrosynthesis. The 1D NLTE and LTE cases refer instead to computations performed by using LHD one-dimensional models, with spectrosynthesis performed with or
without the inclusion of NLTE effects, based on the same physics and model atoms as for the 3D NLTE case:
 (B.1)
(B.1)
Units are expected to be K for temperature, cm s-2 for log g, and mÅ for EW. As for any fit, extrapolation reliability is difficult to assess. Owing to the high computational cost of 3D-atmosphere model calculations, we limited our grid to the currently available models, which obliged us to extrapolate towards high gravities by 0.4 dex and towards low metallicities by about 0.6 dex. Both extrapolations should be quite safe, since the 670.8 nm Li doublet should be quite insensitive to both parameters. Because of the vanishing line opacity, atmosphere models are scarcely sensitive to metallicity variations below [Fe/H] = −3. Those who might wish to employ the presented formulae to derive Li abundances are nevertheless advised to use caution when extrapolating, especially in Teff and EW. In particular, the saturation part of the COG is almost unsampled, and one cannot expect the present fit to reproduce it properly. Fitting to EW significantly above 100 pm is therefore not advisable.
Coefficients for the analytical fit of EW → A(Li) and A(Li) → EW.
© ESO, 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


