EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 521 (October 2010) A&A, 521 (2010) A70 Online Material
Free Access
Issue
A&A
Volume 521, October 2010
Article Number A70
Number of page(s) 14
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201014067
Published online 21 October 2010

Online Material

Appendix A: Expressions for loop properties

Expressions for some key quantities ( $\langle\tilde{\varphi}\rangle$, K and W) are given here. For compactness, these are given only for $\alpha_{1}\neq0$ and $\alpha_{2}\neq 0$, while special cases (e.g., $\alpha_1=0$) must be dealt with separately. Expressions for constant-$\alpha $ fields can be recovered by setting $\alpha_1=\alpha_2$, which gives more familiar formulae. The superscripts and subscripts that accompany each quantity term denote the upper and lower radial bounds over which the quantity is calculated.

A.1 Average magnetic twist

                                   $\displaystyle \langle\tilde{\varphi}\rangle_0^{R_1}$ = $\displaystyle \frac{\sigma_1 L\Big[1-J_0(\vert\alpha_1\vert R_1)\Big]}{R_1 J_1(\vert\alpha_1\vert R_1)}$ (A.1)
       
$\displaystyle \langle\tilde{\varphi}\rangle_{R_1}^{R_2}$ = $\displaystyle \frac{\sigma_2 L\Big[F_0(\vert\alpha_2\vert R_1)-F_0(\vert\alpha_... ...ig]}{\Big[R_2 F_1(\vert\alpha_2\vert R_2)-R_1 F_1(\vert\alpha_2\vert R_1)\Big]}$ (A.2)
       
$\displaystyle \langle\tilde{\varphi}\rangle_{R_2}^{R_3}$ = $\displaystyle \frac{2\sigma_2 L R_2\Big[B_2 J_1(\vert\alpha_2\vert R_2) + C_2 Y... ...{R_2}\Big)}{B_2 F_0(\vert\alpha_2\vert R_2)\Big[R_3^{~2} - R_2^{~2}\Big]} \cdot$ (A.3)

A.2 Magnetic helicity

                                  K0R1 = 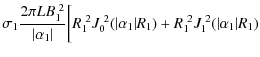$\displaystyle \sigma_1\frac{2\pi L B_1^{~2}}{\vert\alpha_1\vert}\bigg[R_1^{~2} J_0^{~2}(\vert\alpha_1\vert R_1)+R_1^{~2} J_1^{~2}(\vert\alpha_1\vert R_1)$  
    $\displaystyle -2\frac{R_1}{\vert\alpha_1\vert}J_0(\vert\alpha_1\vert R_1)J_1(\vert\alpha_1\vert R_{1})\bigg]$ (A.4)
       
KR1R2 = 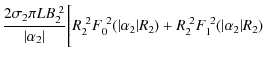$\displaystyle \frac{2\sigma_2\pi LB_2^{~2}}{\vert\alpha_2\vert}\Bigg[R_2^{~2}F_0^{~2}(\vert\alpha_2\vert R_2)+R_2^{~2} F_1^{~2}(\vert\alpha_2\vert R_2)$  
       
    $\displaystyle -2\frac{R_2}{\vert\alpha_2\vert}F_0(\vert\alpha_2\vert R_2)F_1(\vert\alpha_2\vert R_2)$  
       
    $\displaystyle -R_1^{~2} F_0^{~2}(\vert\alpha_2\vert R_1)~-~R_1^{~2} F_1^{~2}(\vert\alpha_2\vert R_1)$  
       
    $\displaystyle +2\frac{R_1}{\vert\alpha_2\vert}F_0(\vert\alpha_2\vert R_1)F_1(\vert\alpha_2\vert R_1)$  
       
    $\displaystyle +\frac{2 B_1 R_1 J_1(\vert\alpha_1\vert R_1)}{B_2}\Big[F_0(\vert\alpha_2\vert R_1)-F_0(\vert\alpha_2\vert R_2)\Big]$  
    $\displaystyle \times\Bigg(\frac{1}{\vert\alpha_1\vert}-\frac{\sigma_{1,2}}{\vert\alpha_2\vert}\Bigg)\Bigg]$ (A.5)

\begin{displaymath}K_{R_2}^{R_3} \!= \! 2\sigma_2 L C_3 R_2\Bigg[\Big(\psi_{R_2}... ... \!\frac{\pi B_3}{2}\Big(R_3^{2} \!-\! R_2^{2}\Big)\Bigg]\cdot \end{displaymath} (A.6)

A.3 Magnetic energy

                               W0 R1 = 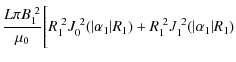$\displaystyle \frac{L\pi B_1^{~2}}{\mu_0}\Bigg[R_1^{~2} J_0^{~2}(\vert\alpha_1\vert R_1)+R_1^{~2} J_1^{~2}(\vert\alpha_1\vert R_1)$  
       
    $\displaystyle -\frac{R_1}{\vert\alpha_1\vert}J_0(\vert\alpha_1\vert R_1)J_1(\vert\alpha_1\vert R_1)\Bigg]$ (A.7)
       
       
WR1 R2 = 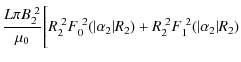$\displaystyle \frac{L\pi B_2^{~2}}{\mu_0}\Bigg[R_2^{~2} F_0^{~2}(\vert\alpha_2\vert R_2)+R_2^{~2} F_1^{~2}(\vert\alpha_2\vert R_2)$  
       
    $\displaystyle -\frac{R_2}{\vert\alpha_2\vert}F_0(\vert\alpha_2\vert R_2)F_1(\vert\alpha_2\vert R_2)$  
       
    $\displaystyle -R_1^{~2} F_0^{~2}(\vert\alpha_2\vert R_1)-R_1^{~2} F_1^{~2}(\vert\alpha_2\vert R_1)$  
       
    $\displaystyle +\frac{R_1}{\vert\alpha_2\vert}F_0(\vert\alpha_2\vert R_1)F_1(\vert\alpha_2\vert R_1)\Bigg]$ (A.8)
       
       
WR2 R3 = $\displaystyle ~\frac{L\pi}{\mu_0}\Bigg[\frac{B_3^{~2}}{2}\bigg(R_3^{~2} - R_2^{~2}\bigg) + C_3^{~2} R_2^{~2}\log\Bigg(\frac{R_3}{R_2}\Bigg)\Bigg]\cdot$ (A.9)

Appendix B: Magnetic field profiles for a selection of 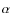$\alpha $-space points

\begin{figure} \par\includegraphics[width=9cm,clip]{14067-figb1.eps} \end{figure} Figure B.1:

The magnetic field profiles, Bz (solid) and B$_\theta $ (dashed), for the six $\alpha $-space points identified in the top left panel of Fig. 4.

Open with DEXTER

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.