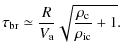Disk formation during collapse of magnetized protostellar cores

P. Hennebelle; A. Ciardi

doi:10.1051/0004-6361/200913008

Free Access

Issue		A&A Volume 506, Number 2, November I 2009


Page(s)		L29 - L32
Section		Letters
DOI		https://doi.org/10.1051/0004-6361/200913008
Published online		24 September 2009

Online Material

Appendix A: Classical analysis of the magnetic braking: cloud embedded into an external medium

In the context of interstellar clouds, the classical analysis of magnetic braking (e.g.; Mouschovias 1991; Shu et al. 1987), considers a rigid and dense axisymmetric cloud. We define $\rho_{\rm c}$ to be its density, R its radius and Z its height. The cloud is surrounded by a diffuse inter cloud medium of density $\rho_{\rm ic}$ . The typical timescale for magnetic braking $\tau_{\rm br}$ , corresponds to the time necessary for torsional Alfvén waves induced by the twisting of the magnetic field line, to propagate over a distance l, such that the mass of gas swept by the waves is comparable to the mass of the cloud itself. At this point, a significant fraction of the cloud angular momentum has been transferred to the intercloud medium.

Two cases can be considered. First, when the magnetic field and the rotation axis are aligned, the waves propagate along the magnetic field at the Alfvén speed $V_{\rm a}$ , and $l \rho_{\rm ic} \simeq Z \rho_{\rm c}$ , leading to

$\displaystyle \tau_{\rm br} \simeq \frac{Z}{V_a} ~ \frac{\rho_{c}}{\rho_{ic}}\cdot$

(A.1)

The second case corresponds to the magnetic field and the rotation axis being perpendicular to each other, and the waves propagating in the equatorial plane of the cloud. The intercloud medium, which at time $t=\tau_{\rm br}$ is reached by the torsional Alfvén waves, is located in a cylinder of radius l and height Z. In this case, $((\tau_{\rm br} V_{\rm a})^2 - R^2) \rho_{\rm ic} \simeq R^2 \rho_{\rm c}$ , which gives

$\displaystyle \tau_{\rm br} \simeq \frac{R}{V_{\rm a}} \sqrt{\frac{\rho_{\rm c}}{\rho_{\rm ic}} + 1}.$

(A.2)

Since in typical astrophysical circumstances the intercloud medium has a density that is low with respect to the cloud density, Eqs. (A.1) and (A.2) show that the braking is usually more efficient when the magnetic field is perpendicular to the rotation axis than when it is parallel. However, this conclusion is obviously correct only when $R \simeq Z$ , i.e., if the cloud aspect ratio is not too different from 1. In particular, from Eqs. (A.1)-(A.2) we see that if $Z/R \ll 1/\sqrt{\rho_{\rm c}/\rho_{\rm ic}}$ , the braking time is shorter in the aligned case than for the perpendicular configuration.

Previous studies have demonstrated that magnetized clouds are usually very flat because of the magnetic compression exerted by the radial component of the magnetic field (see e.g.; Li & Shu 1996, HF08). These magnetized sheets, which are called pseudo-disks, are perpendicular to the average magnetic field. In the same way, centrifugally supported disks are also very flat objects that are perpendicular to the rotation axis. For these extreme configurations, the magnetic braking time can obviously be longer when the magnetic field and the rotation axis are perpendicular than when they are parallel (depending on the respective values of R, Z and $\rho_{\rm c}/\rho_{\rm ic}$ ). Note that strictly speaking, if the magnetic field and the rotation axis are not aligned with each other, the resulting structure is fully tridimensional rather than axisymmetric.

It is interesting to compare Eqs. (A.1)-(A.2) with Eq. (2). Even though the latter is identical to the first for $\rho_{\rm c} = \rho_{\rm ic}$ , there are two major differences. First, even when $R \simeq Z$ , the magnetic braking is not significantly more efficient in the perpendicular configuration than in the aligned one. The relative efficiency of the magnetic braking in the two configurations is, instead, directly proportional to the cloud aspect ratio. Second, as the cloud is compressed along the field lines, the quantity $Z / \sqrt{\rho_{\rm c}}$ is simply proportional to Z^1/2, implying that the magnetic braking time in the aligned configuration decreases. Again this is unlike the case of a rigid cloud embedded in a diffuse intercloud medium.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.