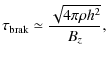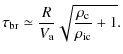| Issue |
A&A
Volume 506, Number 2, November I 2009
|
|
|---|---|---|
| Page(s) | L29 - L32 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200913008 | |
| Published online | 24 September 2009 | |
A&A 506, L29-L32 (2009)
LETTER TO THE EDITOR
Disk formation during collapse of magnetized protostellar cores![[*]](/icons/foot_motif.png)
P. Hennebelle1 - A. Ciardi1,2
1 - Laboratoire de radioastronomie, UMR 8112 du
CNRS, École normale supérieure et Observatoire de Paris, 24 rue
Lhomond, 75231 Paris Cedex 05, France
2 - Laboratoire de Physique des Plasmas, UMR 7648 du CNRS, 10-12 Avenue de l'Europe, 78140 Velizy, France
Received 29 July 2009 / Accepted 14 September 2009
Abstract
Context. In the context of star and planet formation, understanding the formation of disks is of fundamental importance.
Aims. Previous studies found that the magnetic field has a very
strong impact on the collapse of a prestellar cloud, by possibly
suppressing the formation of a disk even for relatively modest values
of the magnetic intensity. Since observations infer that cores have a
substantial level of magnetization, this raises the question of how
disks form. However, most studies have been restricted to the case in
which the initial angle, ![]() ,
between the magnetic field and the rotation axis equals 0
,
between the magnetic field and the rotation axis equals 0![]() .
Here we explore and analyse the influence of non aligned configurations on disk formation.
.
Here we explore and analyse the influence of non aligned configurations on disk formation.
Methods. We perform 3D ideal MHD, AMR numerical simulations for various values of ![]() ,
the ratio of the mass-to-flux to the critical mass-to-flux, and various values of
,
the ratio of the mass-to-flux to the critical mass-to-flux, and various values of ![]() .
.
Results. We find that disks form more easily as ![]() increases from 0 to 90
increases from 0 to 90![]() .
We propose that as the magnetized pseudo-disks become thicker with increasing
.
We propose that as the magnetized pseudo-disks become thicker with increasing ![]() ,
the magnetic braking efficiency is lowered. We also find that even small values of
,
the magnetic braking efficiency is lowered. We also find that even small values of ![]() (
(![]() 10-20
10-20![]() )
show significant differences with the aligned case.
)
show significant differences with the aligned case.
Conclusions. Within the framework of ideal MHD, and for our
choice of initial conditions, centrifugally supported disks cannot form
for values of ![]() smaller than
smaller than ![]() 3 when the magnetic field and the rotation axis are perpendicular, and smaller than about
3 when the magnetic field and the rotation axis are perpendicular, and smaller than about ![]() 5-10 when they are perfectly aligned.
5-10 when they are perfectly aligned.
Key words: magnetohydrodynamics (MHD) - instabilities - ISM: kinematics and dynamics - ISM: clouds - ISM: structure - star: formation
1 Introduction
Understanding the formation of protostellar disks is an important issue in the context of star and planet formation. The presence of circumstellar disks is well established around T-Tauri stars (Watson et al. 2007), as well as around younger class I and II protostars. However, because of difficulties in disentangling the emission of the disk and envelope, the existence of disks around class 0 objects remains a matter of debate (Mundy et al. 2000; Belloche et al. 2002; Jorgensen et al. 2007).
Starting with a level of rotation consistent with observations, hydrodynamical numerical simulations discovered that centrifugally supported disks form with characteristic diameters of the order of a few hundred AU (Matsumoto & Hanawa 2003; Hennebelle et al. 2004; Goodwin et al. 2007; Commerçon et al. 2008). These structures are the unavoidable consequence of angular momentum conservation during the collapse phase. In addition, since these disks are massive and strongly self-gravitating, they are prone to gravitational instability and have often been found to fragment, leading to the formation of a small cluster of stars.
However, magnetic fields appear to have an important impact. Magnetohydrodynamic (MHD) simulations (e.g., Machida et al. 2005; Banerjee & Pudritz 2006) find that even for modest values of the magnetic intensity, disk formation can be suppressed by magnetic braking (Shu et al. 1987; Mouschovias 1991; Basu & Mouschovias 1995; Galli et al. 2006) which transports angular momentum from the inner parts of the cloud towards its outer regions (Allen et al. 2003; Fromang et al. 2006; Price & Bate 2007; Hennebelle & Fromang 2008, hereafter HF08; Mellon & Li 2008, 2009).
The typical values of ![]() ,
the ratio of the mass-to-flux to the critical mass-to-flux ratio, at
which the formation of a rotationally supported disk is suppressed,
vary from one study to another; probably because of different choices
of initial conditions. For example, while Mellon & Li (2008) estimate that the value of
,
the ratio of the mass-to-flux to the critical mass-to-flux ratio, at
which the formation of a rotationally supported disk is suppressed,
vary from one study to another; probably because of different choices
of initial conditions. For example, while Mellon & Li (2008) estimate that the value of ![]() ,
below which disks do
not form, is larger than 10, Price & Bate (2007) and HF08 find that this occurs when
,
below which disks do
not form, is larger than 10, Price & Bate (2007) and HF08 find that this occurs when
![]() .
A broad distribution
of
.
A broad distribution
of ![]() has been inferred from observations, but most cores have magnetic fields corresponding to values of
has been inferred from observations, but most cores have magnetic fields corresponding to values of ![]() typically smaller than 5 (Crutcher 1999). This raises a fundamental question about how disks can form in spite of the relatively high degree of magnetization.
typically smaller than 5 (Crutcher 1999). This raises a fundamental question about how disks can form in spite of the relatively high degree of magnetization.
Most theoretical studies have been performed by assuming a simple initial configuration in which the magnetic field and the rotation axis are parallel. Notable exceptions are the works of Machida et al. (2006), who explored the influence of a non zero angle between the magnetic field axis and the rotation axis, and Price & Bate (2007) who considered the case where the two axes are perpendicular. However, none of these works focused on the problem of disk formation and magnetic braking in great details, which are the topics of the present work.
The paper is organised as follows: in Sect. 2, we analyse
the magnetic braking emphasizing the importance of the initial angle, ![]() ;
in Sect. 3 numerical simulations of collapsing cores for various values of
;
in Sect. 3 numerical simulations of collapsing cores for various values of ![]() and
and ![]() are presented; Sect. 4 concludes the paper.
are presented; Sect. 4 concludes the paper.
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{13008fg1.ps}\includegraph...
...th=5.5cm]{13008fg4.ps}\includegraphics[width=6.2cm]{13008fg6.ps} }\end{figure}](/articles/aa/full_html/2009/41/aa13008-09/Timg18.png) |
Figure 1:
Density and velocity profiles. First column is for |
| Open with DEXTER | |
2 Magnetic braking: physical analysis
The classical analysis of magnetic braking, presented in Appendix,
assumes that there is a clear distinction between the cloud and the
intercloud medium. However, inside a collapsing core the situation
differs a priori. Density gradients (typically
![]() )
throughout the cloud make it difficult to discriminate between its
dense inner parts and the diffuse external medium. It is therefore not
entirely clear to what extent the classical analysis may be applied to
understand the magnetic braking operating inside a collapsing dense
core. Indeed various studies have already demonstrated that internal
magnetic braking is more complex
(e.g., Galli et al. 2006; HF08).
)
throughout the cloud make it difficult to discriminate between its
dense inner parts and the diffuse external medium. It is therefore not
entirely clear to what extent the classical analysis may be applied to
understand the magnetic braking operating inside a collapsing dense
core. Indeed various studies have already demonstrated that internal
magnetic braking is more complex
(e.g., Galli et al. 2006; HF08).
A simple analysis of the terms responsible for
angular momentum transport through the cloud is elucidating.
We consider a collapsing cloud permeated by a uniform magnetic field, Bz.
Rotation with respect to the z-axis generates a toroidal field, ![]() (r,
(r, ![]() and z are cylindrical coordinates) and we have
and z are cylindrical coordinates) and we have
where
which clearly shows that the braking time is shorter as, h, decreases. Assuming that the column density remains roughly constant, we find that
As discussed
in Galli & Shu (1993), Li & Shu (1996)
and HF08, a magnetized cloud flattens along the field lines producing a
thin magnetic pseudo-disk, which unlike centrifugally supported disks,
is dynamically collapsing. We can relate the scale-height of the
pseudo-disk, h, to the angle ![]() .
For an aligned system, assuming mechanical equilibrium along the z-axis, one can infer the relation (see HF08 for details)
.
For an aligned system, assuming mechanical equilibrium along the z-axis, one can infer the relation (see HF08 for details)
which reflects that the gravity and magnetic pressure compress the gas along the z-axis while the thermal pressure resists the compression. In this equation
where
3 Numerical simulations
3.1 Numerical setup
To carry out our numerical simulations, we used the AMR code Ramses
(Teyssier 2002; Fromang et al. 2006). Throughout the simulations,
the Jeans length is resolved with at least 10 cells. An HLLD
solver is employed. The initial conditions consist of a 1 solar
mass spherical cloud whose profile, given by
![]() ,
resembles the observed cores. We impose a density contrast of 10 between the central density
,
resembles the observed cores. We impose a density contrast of 10 between the central density
![]() cm-3 and the edge density,
cm-3 and the edge density,
![]() .
Outside the cloud, the gas has a density of
.
Outside the cloud, the gas has a density of
![]() and it is in pressure equilibrium with the cloud edge.
As in HF08, we use a barotropic equation of state.
The cloud is initially in solid body rotation and threaded by a
magnetic field, along the z-axis, whose intensity is proportional to the total column density through the cloud. The rotation axis is in the x-z plane and at an angle
and it is in pressure equilibrium with the cloud edge.
As in HF08, we use a barotropic equation of state.
The cloud is initially in solid body rotation and threaded by a
magnetic field, along the z-axis, whose intensity is proportional to the total column density through the cloud. The rotation axis is in the x-z plane and at an angle ![]() with respect to the magnetic field. The ratio of rotation to gravitational energy is equal to
with respect to the magnetic field. The ratio of rotation to gravitational energy is equal to
![]() ,
while the degree of magnetization is determined by the parameter
,
while the degree of magnetization is determined by the parameter ![]() .
The initial thermal to gravitational energy ratio is
.
The initial thermal to gravitational energy ratio is ![]() 0.25.
0.25.
3.2 Results
For various values of ![]() and
and ![]() ,
Fig. 1 shows
the density and velocity distribution in the x-y plane
(first row) and y-z
plane (second row). These correspond to the initial direction of the
magnetic field being respectively
perpendicular and parallel to the plane of the snapshot. Note that the
rotation axis is also either perpendicular or parallel, except in the
case of
,
Fig. 1 shows
the density and velocity distribution in the x-y plane
(first row) and y-z
plane (second row). These correspond to the initial direction of the
magnetic field being respectively
perpendicular and parallel to the plane of the snapshot. Note that the
rotation axis is also either perpendicular or parallel, except in the
case of
![]() for which it is slightly tilted.
At the time of the snapshots, the mass of the gas denser than 1010 cm-3 (the density at which the gas becomes adiabatic) is
for which it is slightly tilted.
At the time of the snapshots, the mass of the gas denser than 1010 cm-3 (the density at which the gas becomes adiabatic) is ![]() 0.15
0.15 ![]() ,
while the mass of the gas denser than 1013 cm-3 is
,
while the mass of the gas denser than 1013 cm-3 is ![]() 0.1
0.1 ![]() .
.
The first two columns show results for the cases ![]() and
and ![]() ,
respectively, with
,
respectively, with
![]() .
In the
.
In the ![]() case, a dense disk whose diameter is
case, a dense disk whose diameter is ![]() 200 AU
forms around the central object. The size of the disk is estimated by
determining the position at which the velocity is roughly perpendicular
to the disk radius, so that the rotation velocity dominates over the
infall motions.
The cut across the y-z plane also shows an outflow being launched perpendicularly to the disk.
In the
200 AU
forms around the central object. The size of the disk is estimated by
determining the position at which the velocity is roughly perpendicular
to the disk radius, so that the rotation velocity dominates over the
infall motions.
The cut across the y-z plane also shows an outflow being launched perpendicularly to the disk.
In the ![]() case, no disk of significant size forms.
The gas instead falls directly towards the central thermally supported core.
The entire configuration is unstable leading to significant departures from the axisymmetric configuration.
The cut across the y-z plane also shows the thin pseudo-disk (
case, no disk of significant size forms.
The gas instead falls directly towards the central thermally supported core.
The entire configuration is unstable leading to significant departures from the axisymmetric configuration.
The cut across the y-z plane also shows the thin pseudo-disk (
![]() AU,
AU,
![]() AU for
AU for ![]() cm-3),
which is compressed by the magnetic pressure exerted by the curved field lines.
The top panel of the third column (
cm-3),
which is compressed by the magnetic pressure exerted by the curved field lines.
The top panel of the third column (![]() ,
,
![]() )
shows that a
disk-like structure of
)
shows that a
disk-like structure of ![]() 150 AU
forms around the
central object (as shown by the velocity field, rotation dominates over
infall in this structure). We note that the structure appears to be
non-axisymmetric and that the entire velocity field is more complex
than in the first case (
150 AU
forms around the
central object (as shown by the velocity field, rotation dominates over
infall in this structure). We note that the structure appears to be
non-axisymmetric and that the entire velocity field is more complex
than in the first case (![]() ,
,
![]() ).
For
).
For ![]() with
with
![]() (bottom panel of third column) the pseudo disk, visible at
(bottom panel of third column) the pseudo disk, visible at
![]() AU, is twisted and overall thicker by a factor of
AU, is twisted and overall thicker by a factor of ![]() 2-3 than the case
2-3 than the case ![]() ,
,
![]() (bottom panel of the second column). Additionally, we have performed simulations of the case
(bottom panel of the second column). Additionally, we have performed simulations of the case
![]() for which we also find a disk. According to the analysis presented in
Sect. 2, we believe that the thickness of the pseudo-disk is at
the origin of the formation of a rotationally dominated disk-like
structure, since it reduces the magnetic braking efficiency as shown by
Eq. (1). To confirm that the different behaviours are indeed related to differences in the
magnetic braking efficiency, we plot in Fig. 2 the quantity
for which we also find a disk. According to the analysis presented in
Sect. 2, we believe that the thickness of the pseudo-disk is at
the origin of the formation of a rotationally dominated disk-like
structure, since it reduces the magnetic braking efficiency as shown by
Eq. (1). To confirm that the different behaviours are indeed related to differences in the
magnetic braking efficiency, we plot in Fig. 2 the quantity
![]() which appears in Eq. (2). The cases
which appears in Eq. (2). The cases
![]() (solid line),
(solid line),
![]() (dotted line) and
(dotted line) and
![]() (dashed line) are shown. As can be seen, the quantity
(dashed line) are shown. As can be seen, the quantity
![]() is higher, and the two peaks are closer (equivalently the gradients
between the peaks are stiffer), for the aligned case; implying that the
quantity
is higher, and the two peaks are closer (equivalently the gradients
between the peaks are stiffer), for the aligned case; implying that the
quantity
![]() is higher by at least
is higher by at least ![]() 50-100% than for the two misaligned configurations (
50-100% than for the two misaligned configurations (
![]() at z=0, for symmetry reasons). This sudden change of behaviour as
at z=0, for symmetry reasons). This sudden change of behaviour as ![]() increases, indicates, as suggested by Eqs. (3-4), that the
aligned configuration is probably too restrictive for studying disk formation in collapsing magnetized cores.
increases, indicates, as suggested by Eqs. (3-4), that the
aligned configuration is probably too restrictive for studying disk formation in collapsing magnetized cores.
| Figure 2:
|
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{13008fg8.ps}\includegraph...
...h=5.5cm]{13008fg9.ps}\includegraphics[width=6.2cm]{13008fg10.ps} }\end{figure}](/articles/aa/full_html/2009/41/aa13008-09/Timg54.png) |
Figure 3:
Density and velocity cut through the y-z plane. The centrifugally supported disk, when it exists, is seen nearly face on.
First panel is for |
| Open with DEXTER | |
Figure 3 shows the density and velocity distributions in the y-z plane for larger values of
![]() .
The first panel illustrates the
.
The first panel illustrates the ![]() and
and
![]() case, while the second panel shows results for
case, while the second panel shows results for
![]() .
In both cases a disk of
.
In both cases a disk of ![]() 150-200 AU forms. We note that the densities in these disks are significantly lower than those observed in the
150-200 AU forms. We note that the densities in these disks are significantly lower than those observed in the ![]() and
and
![]() case (first row of Fig. 1);
their structure is clearly more complex, and we note the presence of
extended spiral arms, which are almost one order of magnitude denser
than in the rest of the disk.
Finally, the third panel of Fig. 3 shows results for
a highly magnetized cloud rotating perpendicularly to the magnetic field (
case (first row of Fig. 1);
their structure is clearly more complex, and we note the presence of
extended spiral arms, which are almost one order of magnitude denser
than in the rest of the disk.
Finally, the third panel of Fig. 3 shows results for
a highly magnetized cloud rotating perpendicularly to the magnetic field (![]() ,
,
![]() ). In this case, even though the magnetic braking is less efficient than in the
aligned configuration, the magnetic field is so strong thatno disk forms.
Interestingly, we also see that a relatively strong outflow is launched.
For completeness, we also considered the case (
). In this case, even though the magnetic braking is less efficient than in the
aligned configuration, the magnetic field is so strong thatno disk forms.
Interestingly, we also see that a relatively strong outflow is launched.
For completeness, we also considered the case (![]() ,
,
![]() )
for which we find that a small disk-like object of size 50-100 AU
forms. Thus, we conclude that in the perpendicular case and within the
framework of ideal MHD, disks can form for values of
)
for which we find that a small disk-like object of size 50-100 AU
forms. Thus, we conclude that in the perpendicular case and within the
framework of ideal MHD, disks can form for values of ![]() higher than
higher than ![]() 3.
It seems probable to us that, given the complex field geometry induced
in these non aligned configurations, ambipolar diffusion as well as
ohmic dissipation may play a role in the formation of small disks.
3.
It seems probable to us that, given the complex field geometry induced
in these non aligned configurations, ambipolar diffusion as well as
ohmic dissipation may play a role in the formation of small disks.
4 Conclusion
To study the formation of circumstellar disks, we have performed
numerical simulations of the gravitational collapse of magnetized dense
prestellar cores for a range of values of ![]() and
and ![]() (the initial angle between magnetic field and the rotation axis). Our main conclusions are the following. In the aligned case (
(the initial angle between magnetic field and the rotation axis). Our main conclusions are the following. In the aligned case (
![]() )
disk formation is prevented for values of
)
disk formation is prevented for values of ![]() as high as
as high as ![]() 5-10. In the non aligned cases, and even for relatively small values of
5-10. In the non aligned cases, and even for relatively small values of
![]() ,
disks can form for smaller values of
,
disks can form for smaller values of
![]() ,
corresponding to larger magnetic field intensities.
The main reason for this change of behaviour is a decrease, for increasing
,
corresponding to larger magnetic field intensities.
The main reason for this change of behaviour is a decrease, for increasing ![]() ,
of the magnetic braking efficiency, which is linked to an increase in the thickness of the magnetized pseudo-disk.
This is caused by the magnetic field lines being twisted by the
rotation about an axis parallel to the plane of the pseudo-disk.
When
,
of the magnetic braking efficiency, which is linked to an increase in the thickness of the magnetized pseudo-disk.
This is caused by the magnetic field lines being twisted by the
rotation about an axis parallel to the plane of the pseudo-disk.
When
![]() ,
we find that disks may form for smaller values of
,
we find that disks may form for smaller values of ![]() ,
as long as
,
as long as
![]() ,
and for even lower values of
,
and for even lower values of ![]() ,
disk formation does not seem to be possible.
Nevertheless, for these highly magnetized configurations,
the question of whether a disk may form at later times,
or because of non-ideal MHD effects (Hosking & Whitworth 2004; Machida et al. 2008; Mellon & Li 2009), remains unanswered.
We recall that although Belloche et al. (2002)
observe a significant amount of rotation in the envelope of IRAM04191,
they exclude a disk of size larger than 20 AU. This result is very
difficult to explain without a magnetic field, but agrees at least
qualitatively with our conclusion if the source is sufficiently
magnetized (Troland & Crutcher 2008).
,
disk formation does not seem to be possible.
Nevertheless, for these highly magnetized configurations,
the question of whether a disk may form at later times,
or because of non-ideal MHD effects (Hosking & Whitworth 2004; Machida et al. 2008; Mellon & Li 2009), remains unanswered.
We recall that although Belloche et al. (2002)
observe a significant amount of rotation in the envelope of IRAM04191,
they exclude a disk of size larger than 20 AU. This result is very
difficult to explain without a magnetic field, but agrees at least
qualitatively with our conclusion if the source is sufficiently
magnetized (Troland & Crutcher 2008).
Another important point is that while in the purely hydrodynamical case, and for the cloud parameters used, fragmentation occurs; we do not identify fragmentation in any of themagnetized cases explored. It is however possible that with a better treatment of the thermal processes, the magnetized disks which form in the low magnetized configurations, may also fragment.
AcknowledgementsThis work was performed using HPC resources from GENCI-cines (2009-042036) and cemag. A.C. is supported by the ANR grant MAGNET and by the Marie Curie Reintegration Grant MAGPLUS. We thank Shantanu Basu as well as an anonymous referee for comments which have improved the paper significantly.
References
- Allen, A., Li, Z.-Y., & Shu, F. 2003, ApJ, 599, 363 [NASA ADS] [CrossRef]
- Banerjee, R., & Pudritz, R. 2006, ApJ, 641, 949 [NASA ADS] [CrossRef]
- Basu, S., & Mouschovias, T. 1995, ApJ, 452, 386 [NASA ADS] [CrossRef]
- Belloche, A., André, P., Despois, D., et al. 2002, A&A, 393, 927 [NASA ADS] [CrossRef] [EDP Sciences]
- Commerçon, B., Hennebelle, P., Audit, E., Chabrier, G., & Teyssier, R. 2008, A&A, 482, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Crutcher, R. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences]
- Galli, D., & Shu, F. 1993, ApJ, 417, 243 [NASA ADS] [CrossRef]
- Galli, D., Lizano, S., Shu, F., et al. 2006, ApJ, 647, 374 [NASA ADS] [CrossRef]
- Goodwin, S., Whitworth, A., & Ward-Thompson, D. 2004, A&A, 423, 169 [NASA ADS] [CrossRef] [EDP Sciences]
- Hennebelle, P., Whitworth, A., Cha, S.-H., et al. 2004, MNRAS, 340, 870 [NASA ADS] [CrossRef]
- Hennebelle, P., & Fromang, S. 2008, A&A, 477, 9 [NASA ADS] [CrossRef] [EDP Sciences] (HF08)
- Hennebelle, P., & Teyssier, R. 2008, A&A, 477, 25 [NASA ADS] [CrossRef] [EDP Sciences]
- Hosking, G., & Whitworth, A. 2004, MNRAS, 347, 994 [NASA ADS] [CrossRef]
- Jorgensen, J., Bourke, T., Myers, P., et al. 2007, ApJ, 659, 479 [NASA ADS] [CrossRef]
- Li, Z-Y., & Shu, F. 1996, ApJ, 472, 211 [NASA ADS] [CrossRef]
- Machida, M., Matsumoto, T., Tomisaka, K., et al. 2005, MNRAS, 362, 369 [NASA ADS] [CrossRef]
- Machida, M., Matsumoto, T., Hanawa, T., et al. 2006, ApJ, 645, 1227 [NASA ADS] [CrossRef]
- Machida, M., Tomisaka, K., Matsumoto, T., et al. 2008, ApJ, 677, 327 [NASA ADS] [CrossRef]
- Matsumoto, T., & Hanawa, T. 2003, ApJ, 595, 913 [NASA ADS] [CrossRef]
- Mellon, R., & Li, Z.-Y. 2008, ApJ, 681, 1356 [NASA ADS] [CrossRef]
- Mellon, R., & Li, Z.-Y. 2009, ApJ, 698, 922 [NASA ADS] [CrossRef]
- Mouschovias, T. 1991, ApJ, 373, 169 [NASA ADS] [CrossRef]
- Mundy L., Looney, L., & Welch, W. 2000, in Protostars and Planets IV (Book - Tucson: University of Arisona Press, eds. Manning, V., Boss, A. P. & Russell, S. S., 355
- Price, D., & Bate, M. 2007, MNRAS, 377, 77 [NASA ADS] [CrossRef]
- Shu, F., Adams, F., & Lizano, S., 1987, ARA&A, 25, 23 [NASA ADS] [CrossRef]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences]
- Troland, T., & Crutcher, R. 2008, ApJ, 680, 457 [NASA ADS] [CrossRef]
- Watson, A., Stapelfeldt, K., Wood, K., et al. 2007, prpl, 523
Online Material
Appendix A: Classical analysis of the magnetic braking: cloud embedded into an external medium
In the context of interstellar clouds, the classical analysis of magnetic braking (e.g.; Mouschovias 1991; Shu et al. 1987), considers a rigid and dense axisymmetric cloud. We define
![]() to be its density, R its radius and Z its height.
The cloud is surrounded by a diffuse inter cloud medium of density
to be its density, R its radius and Z its height.
The cloud is surrounded by a diffuse inter cloud medium of density
![]() .
The typical timescale for magnetic braking
.
The typical timescale for magnetic braking
![]() ,
corresponds to the time necessary for torsional Alfvén waves
induced by the twisting of the magnetic field line, to propagate over a distance l,
such that the mass of gas swept by the waves is comparable to the mass
of the cloud itself. At this point, a significant fraction of the cloud
angular momentum has been transferred to the intercloud medium.
,
corresponds to the time necessary for torsional Alfvén waves
induced by the twisting of the magnetic field line, to propagate over a distance l,
such that the mass of gas swept by the waves is comparable to the mass
of the cloud itself. At this point, a significant fraction of the cloud
angular momentum has been transferred to the intercloud medium.
Two cases can be considered. First, when the magnetic field and
the rotation axis are aligned, the waves propagate along the magnetic
field at the Alfvén speed ![]() ,
and
,
and
![]() ,
leading to
,
leading to
The second case corresponds to the magnetic field and the rotation axis being perpendicular to each other, and the waves propagating in the equatorial plane of the cloud. The intercloud medium, which at time
Since in typical astrophysical circumstances the intercloud medium has a density that is low with respect to the cloud density, Eqs. (A.1) and (A.2) show that the braking is usually more efficient when the magnetic field is perpendicular to the rotation axis than when it is parallel. However, this conclusion is obviously correct only when
Previous studies have demonstrated that magnetized clouds are
usually very flat because of the magnetic compression exerted by the radial
component of the magnetic field (see e.g.; Li & Shu 1996,
HF08).
These magnetized sheets, which are called pseudo-disks, are
perpendicular to the average magnetic field. In the same way,
centrifugally supported disks are also very flat objects that are
perpendicular to the rotation axis. For these extreme configurations,
the magnetic braking time can obviously be longer
when the magnetic field and the rotation axis are perpendicular than
when they are parallel (depending on the respective values of R, Z and
![]() ).
Note that strictly speaking, if the magnetic field and the rotation
axis are not aligned with each other, the resulting structure is fully
tridimensional rather than axisymmetric.
).
Note that strictly speaking, if the magnetic field and the rotation
axis are not aligned with each other, the resulting structure is fully
tridimensional rather than axisymmetric.
It is interesting to compare Eqs. (A.1)-(A.2) with
Eq. (2). Even though the latter is identical to the first for
![]() ,
there are two major differences. First, even when
,
there are two major differences. First, even when
![]() ,
the magnetic braking is not significantly more efficient in the
perpendicular configuration than in the aligned one. The relative
efficiency of the magnetic braking in the two configurations is,
instead, directly proportional to the cloud aspect ratio. Second, as
the cloud is compressed along the field lines, the quantity
,
the magnetic braking is not significantly more efficient in the
perpendicular configuration than in the aligned one. The relative
efficiency of the magnetic braking in the two configurations is,
instead, directly proportional to the cloud aspect ratio. Second, as
the cloud is compressed along the field lines, the quantity
![]() is simply proportional to Z1/2, implying that the magnetic braking time in the aligned configuration decreases. Again this is unlike the case of a rigid cloud
embedded in a diffuse intercloud medium.
is simply proportional to Z1/2, implying that the magnetic braking time in the aligned configuration decreases. Again this is unlike the case of a rigid cloud
embedded in a diffuse intercloud medium.
Footnotes
- ... cores
![[*]](/icons/foot_motif.png)
- Appendix A is only available in electronic form at http://www.aanda.org
All Figures
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{13008fg1.ps}\includegraph...
...th=5.5cm]{13008fg4.ps}\includegraphics[width=6.2cm]{13008fg6.ps} }\end{figure}](/articles/aa/full_html/2009/41/aa13008-09/Timg18.png) |
Figure 1:
Density and velocity profiles. First column is for |
| Open with DEXTER | |
| In the text | |
| |
Figure 2:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\mbox{\includegraphics[width=5.5cm]{13008fg8.ps}\includegraph...
...h=5.5cm]{13008fg9.ps}\includegraphics[width=6.2cm]{13008fg10.ps} }\end{figure}](/articles/aa/full_html/2009/41/aa13008-09/Timg54.png) |
Figure 3:
Density and velocity cut through the y-z plane. The centrifugally supported disk, when it exists, is seen nearly face on.
First panel is for |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.