| Issue |
A&A
Volume 502, Number 2, August I 2009
|
|
|---|---|---|
| Page(s) | L1 - L4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/200911997 | |
| Published online | 02 July 2009 | |
Online Material
Appendix A: Graphical representation of the 3D temperature correction, 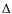 T,
the quality of the fit, QF, and the sensitivity of the fit,
T,
the quality of the fit, QF, and the sensitivity of the fit,
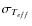
![\begin{figure}
\par\includegraphics[width=18cm,clip]{11997fg2.ps}
\end{figure}](/articles/aa/olm/2009/29/aa11997-09/Timg52.png) |
Figure A.1:
The temperature differences (3D - 1D) using 1D models with |
Appendix B: 3D-1D temperature correction and the lithium abundance in metal-poor F-type dwarfs
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{11997fg3.ps}
\end{figure}](/articles/aa/olm/2009/29/aa11997-09/Timg53.png) |
Figure B.1: 3D-1D abundance correction versus effective temperature difference for the test case of a metal-poor F-type dwarf. For details see text. |
Here we present an example where it is advantageous to use a 1D model corrected for the 3D-1D temperature difference when deriving the chemical abundance from spectral line analysis: the abundance of lithium in a metal-poor F-type dwarf obtained from the 670.7 nm resonance line. We
performed a 3D-NLTE spectrum synthesis calculation for the line on the 3D model with
![]() = 6280 K,
= 6280 K,
![]() = 4.0, [M/H] = -2.0 (cf. Table 1). We considered the resulting spectrum as representing an observation. Unlike a real observation, however, the underlying lithium abundance and stellar parameters are exactly known. According to Table 3 the temperature correction from H
= 4.0, [M/H] = -2.0 (cf. Table 1). We considered the resulting spectrum as representing an observation. Unlike a real observation, however, the underlying lithium abundance and stellar parameters are exactly known. According to Table 3 the temperature correction from H![]() fitting amounts to 74 K in this case, i.e. the 1D model that fits the 3D H
fitting amounts to 74 K in this case, i.e. the 1D model that fits the 3D H![]() profile best is 74 K cooler than the 3D model. We then calculated for a series of thirteen 1D (LHD) models of different effective temperatures 1D lithium line profiles in LTE and NLTE. In the 1D spectrum synthesis, we assumed a microturbulence velocity of 1 km s-1; however, the actual value is not important since the line was chosen to be very weak. We derived for each model the lithium abundance matching the line strength obtained in 3D. Figure B.1 depicts the resulting abundance differences between the underlying lithium abundance assumed in the 3D model and the derived 1D abundance, versus the effective temperature differences between 1D models and the 3D model. As evident from the plot, one reduces the abundance error resulting from the erroneous effective temperature of the 1D model when applying the 3D-1D temperature correction. This holds irrespective of whether the 1D abundance analysis is performed in LTE or NLTE. Not surprisingly, the figure also shows that the correction of the effective temperature does not result in a perfect match of the lithium abundances in a 1D analysis.
profile best is 74 K cooler than the 3D model. We then calculated for a series of thirteen 1D (LHD) models of different effective temperatures 1D lithium line profiles in LTE and NLTE. In the 1D spectrum synthesis, we assumed a microturbulence velocity of 1 km s-1; however, the actual value is not important since the line was chosen to be very weak. We derived for each model the lithium abundance matching the line strength obtained in 3D. Figure B.1 depicts the resulting abundance differences between the underlying lithium abundance assumed in the 3D model and the derived 1D abundance, versus the effective temperature differences between 1D models and the 3D model. As evident from the plot, one reduces the abundance error resulting from the erroneous effective temperature of the 1D model when applying the 3D-1D temperature correction. This holds irrespective of whether the 1D abundance analysis is performed in LTE or NLTE. Not surprisingly, the figure also shows that the correction of the effective temperature does not result in a perfect match of the lithium abundances in a 1D analysis.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


