| Issue |
A&A
Volume 502, Number 2, August I 2009
|
|
|---|---|---|
| Page(s) | 515 - 528 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200811263 | |
| Published online | 04 June 2009 | |
Online Material
Appendix A: Modeling dust evolution
Interstellar dust plays a major role in the evolution of the postshock gas because its survival is required for ![]() formation. For a constant dust-to-gas mass ratio, the dust dominates the cooling efficiency of the gas at high (T> 106 K) temperatures (Dwek 1987), but for such high temperatures, the timescale for dust destruction is shorter than the gas cooling time (Smith et al. 1996). This Appendix details how the evolution of the dust-to-gas mass ratio in the postshock gas is calculated. This calculation is coupled to that of the gas cooling, detailed in Appendix B.
formation. For a constant dust-to-gas mass ratio, the dust dominates the cooling efficiency of the gas at high (T> 106 K) temperatures (Dwek 1987), but for such high temperatures, the timescale for dust destruction is shorter than the gas cooling time (Smith et al. 1996). This Appendix details how the evolution of the dust-to-gas mass ratio in the postshock gas is calculated. This calculation is coupled to that of the gas cooling, detailed in Appendix B.
The dominant dust destruction process depends on the shock velocity. In this study, we consider the effect of thermal and inertial sputtering by grain-ion collisions. This is the dominant mode of destruction in a hot (
![]() K) plasma, resulting from fast (
100-1000 km s-1) intergalactic shocks (e.g. Dwek et al. 1996; Draine & Salpeter 1979).
K) plasma, resulting from fast (
100-1000 km s-1) intergalactic shocks (e.g. Dwek et al. 1996; Draine & Salpeter 1979).
It is assumed that dust grains have an initial radius equal to the effective (mean) radius of
![]() m. This radius is calculated from the MRN dust size distribution (Sect. B.1). At each time step, the fraction of dust remaining in the gas
m. This radius is calculated from the MRN dust size distribution (Sect. B.1). At each time step, the fraction of dust remaining in the gas
![]() ,
is computed in parallel to the postshock gas cooling:
,
is computed in parallel to the postshock gas cooling:
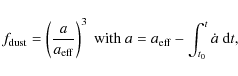 |
(A.1) |
where
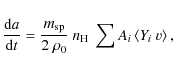 |
(A.2) |
where
For
![]() km s-1, we integrate the equation of deceleration of the dust grains with respect to the gas
km s-1, we integrate the equation of deceleration of the dust grains with respect to the gas
where
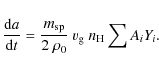 |
(A.4) |
By integrating these differential equations, the radius of the dust grains as a function of their velocity has been deduced (see Borkowski & Dwek 1995, for a complete parametrization of
Figure A.1 shows the dust mass fraction remaining in the gas after isobaric cooling from the postshock temperature
![]() to 104 K as a function of the shock velocity. The dotted line includes both thermal and inertial sputtering. For comparison, the dashed line only includes dust destruction by thermal sputtering. Our calculation for thermal sputtering with a single grain size (
to 104 K as a function of the shock velocity. The dotted line includes both thermal and inertial sputtering. For comparison, the dashed line only includes dust destruction by thermal sputtering. Our calculation for thermal sputtering with a single grain size (
![]() m) is in very good agreement with the study by Smith et al. (1996) who used a grain size distribution. For
m) is in very good agreement with the study by Smith et al. (1996) who used a grain size distribution. For
![]()
![]() 106 K, i.e.
106 K, i.e.
![]() km s-1, most of the dust is destroyed before the gas has cooled to 104 K. The gas that is heated to less than
km s-1, most of the dust is destroyed before the gas has cooled to 104 K. The gas that is heated to less than
![]() K keeps a major part of its dust content and may therefore form
K keeps a major part of its dust content and may therefore form ![]() .
.
Appendix B: Modeling the cooling of hot gas
This Appendix details how we model the cooling of the hot gas. The cooling functions used in the calculations are presented in Sect. B.1. The results are discussed in Sect. B.2.
The time dependence of both the gas temperature and the dust-to-gas mass ratio has been calculated. We start from gas at an initial postshock temperature
![]() with a galactic dust-to-gas ratio, a solar metallicity and assume equilibrium ionization. From a range of postshock temperatures up to 104 K, the isobaric gas cooling is calculated by integrating the energy balance equation which gives the rate of decrease of the gas temperature:
with a galactic dust-to-gas ratio, a solar metallicity and assume equilibrium ionization. From a range of postshock temperatures up to 104 K, the isobaric gas cooling is calculated by integrating the energy balance equation which gives the rate of decrease of the gas temperature:
where
The time-dependent total cooling function is the sum of the dust cooling (weighted by the remaining fraction of dust mass, see Appendix A) and the gas cooling contributions.
We neglect the effect of the magnetic field on the compression of the gas. This assumption is in agreement with observations and numerical simulations, provided that the gas is not gravitationally bound (see Sect. 3.1 for details and references). The thermal gas pressure
![]() is constant in the calculations.
is constant in the calculations.
B.1 Physical processes and cooling functions
B.1.1 Cooling by atomic processes in the gas phase
The calculations of the non-equilibrium (time-dependent) ionization states and isobaric cooling rates of a hot, dust-free gas for the cooling efficiency by atomic processes has been taken from Gnat & Sternberg (2007). The electronic cooling efficiency,
![]() ,
includes the removal of electron kinetic energy via recombination with ions, collisional ionization, collisional excitation followed by line emission, and thermal bremsstrahlung.
,
includes the removal of electron kinetic energy via recombination with ions, collisional ionization, collisional excitation followed by line emission, and thermal bremsstrahlung.
![]() is shown in Fig. B.1 (black solid line
is shown in Fig. B.1 (black solid line![]() ) and reproduces the standard ``cosmic cooling curve'' presented in many papers in the literature (e.g. Sutherland & Dopita 1993). Note that most of the distinct features that appear for the ionization equilibrium case are smeared out in the nonequilibrium cooling functions and that the nonequilibrium abundances reduce the cooling efficiencies by factors of 2 to 4 (Sutherland & Dopita 1993; Gnat & Sternberg 2007). The chemical species that dominate the gas cooling are indicated in Fig. B.1 near the
) and reproduces the standard ``cosmic cooling curve'' presented in many papers in the literature (e.g. Sutherland & Dopita 1993). Note that most of the distinct features that appear for the ionization equilibrium case are smeared out in the nonequilibrium cooling functions and that the nonequilibrium abundances reduce the cooling efficiencies by factors of 2 to 4 (Sutherland & Dopita 1993; Gnat & Sternberg 2007). The chemical species that dominate the gas cooling are indicated in Fig. B.1 near the
![]() cooling curve. Over most of the temperature range, the radiative energy losses are dominated by electron-impact excitation of resonant line transitions in metal ions. At
cooling curve. Over most of the temperature range, the radiative energy losses are dominated by electron-impact excitation of resonant line transitions in metal ions. At
![]()
![]() 104 K, the cooling is mainly due to the collisional excitation of hydrogen Ly
104 K, the cooling is mainly due to the collisional excitation of hydrogen Ly![]() lines. For
lines. For
![]() K, the bremsstrahlung (free-free) radiation becomes dominant.
K, the bremsstrahlung (free-free) radiation becomes dominant.
B.1.2 Cooling by dust grains
Following the method of Dwek (1987), the cooling function of the gas by the dust via electron-grain collisions has been calculated. We adopt an MRN (Mathis et al. 1977) size distribution of dust particles, between 0.01 to ![]() m in grain radius. All the details can be found in Dwek (1987,1986), and we briefly recall here the principles of this calculation. For temperatures lower than 108 K, electron - dust grain collisions cool the gas with a cooling efficiency,
m in grain radius. All the details can be found in Dwek (1987,1986), and we briefly recall here the principles of this calculation. For temperatures lower than 108 K, electron - dust grain collisions cool the gas with a cooling efficiency,
![]()
![]() ,
given by:
,
given by:
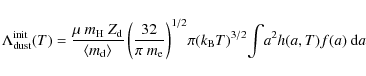 |
(B.2) |
where
The comparison in Fig. B.1 of the initial cooling efficiency by the dust,
![]() ,
and by atomic processes,
,
and by atomic processes,
![]() ,
shows that, for a dust-to-gas mass ratio of
,
shows that, for a dust-to-gas mass ratio of
![]()
![]() 10-3, the dust is initially the dominant coolant of the hot postshock gas for
10-3, the dust is initially the dominant coolant of the hot postshock gas for
![]() K. During the gas cooling, we calculate how much the grains are eroded and deduce the mass fraction of dust that remains in the cooling gas as a function of the temperature. The total cooling function (red curves in Fig. B.1) is deduced by summing the gas and dust cooling rates. We show different cooling efficiencies for different initial temperatures, corresponding to different shock velocities.
K. During the gas cooling, we calculate how much the grains are eroded and deduce the mass fraction of dust that remains in the cooling gas as a function of the temperature. The total cooling function (red curves in Fig. B.1) is deduced by summing the gas and dust cooling rates. We show different cooling efficiencies for different initial temperatures, corresponding to different shock velocities.
B.2 Results: evolution of the hot gas temperature and dust survival
The temperature profiles are shown in Fig. B.2 for different shock velocities (100 to 1000 km s-1), which corresponds to a range of preshock densities of ![]() to 2
to 2 ![]() 10-3 cm-3 for a postshock pressure of 2
10-3 cm-3 for a postshock pressure of 2 ![]() 105 K cm -3.
105 K cm -3.
Figure B.3 shows the remaining fraction of dust mass as a function of the gas temperature. In this plot, the thermal gas pressure is constant and equals the measured average thermal gas pressure of the Stephan's Quintet hot gas
![]()
![]()
![]() .
This plot illustrates a dichotomy in the evolution of the dust to gas mass ratio. On the top right side, a significant fraction of the dust survives in the gas, whereas on the left side, almost all the dust is destroyed on timescales shorter than the collision age (5
.
This plot illustrates a dichotomy in the evolution of the dust to gas mass ratio. On the top right side, a significant fraction of the dust survives in the gas, whereas on the left side, almost all the dust is destroyed on timescales shorter than the collision age (5 ![]() 106 yr). In the intercloud gas shocked at high velocities (
106 yr). In the intercloud gas shocked at high velocities (
![]() km s-1), the dust mass fraction drops rapidly. In clouds where the gas is shocked at
km s-1), the dust mass fraction drops rapidly. In clouds where the gas is shocked at
![]() km s-1, the gas retains a large fraction of its dust content (>20%).
For the gas that is heated to temperatures
T > 106 K, the dust lifetime is shorter than the gas cooling time and most of the dust is destroyed. At lower temperatures (
T < 106 K), the dust cooling rate is lower than the gas cooling rate. Then, the dust never contributes significantly to the cooling of the postshock gas. This last result is in agreement with the earlier study by Smith et al. (1996).
km s-1, the gas retains a large fraction of its dust content (>20%).
For the gas that is heated to temperatures
T > 106 K, the dust lifetime is shorter than the gas cooling time and most of the dust is destroyed. At lower temperatures (
T < 106 K), the dust cooling rate is lower than the gas cooling rate. Then, the dust never contributes significantly to the cooling of the postshock gas. This last result is in agreement with the earlier study by Smith et al. (1996).
Appendix C: Modeling H2 formation
C.1 Cooling function for T < 104 K
This section describes the cooling of clouds below 104 K and H2 formation. We use the chemistry, and the atomic and molecular cooling functions described in Flower et al. (2003) and references therein. The principal coolants are O, ![]() ,
,
![]() and OH (see Fig. 3 in Flower et al. 2003). The time evolution of the gas temperature and composition is computed at a fixed thermal gas pressure equal to that of the intercloud gas (2
and OH (see Fig. 3 in Flower et al. 2003). The time evolution of the gas temperature and composition is computed at a fixed thermal gas pressure equal to that of the intercloud gas (2 ![]() 105 K cm-3). The metallicity and the gas-to-dust mass ratio are assumed to be the solar neighbourhood values. The initial ionization state of the gas is the out-of-equilibrium value resulting from cooling from higher temperatures (Gnat & Sternberg 2007). We assume a standard value for the cosmic ray ionization rate of
105 K cm-3). The metallicity and the gas-to-dust mass ratio are assumed to be the solar neighbourhood values. The initial ionization state of the gas is the out-of-equilibrium value resulting from cooling from higher temperatures (Gnat & Sternberg 2007). We assume a standard value for the cosmic ray ionization rate of ![]()
![]() 10-17 s-1 and the UV radiation field is not considered here (see Sect. 2.2). The initial temperature is 104 K and density
10-17 s-1 and the UV radiation field is not considered here (see Sect. 2.2). The initial temperature is 104 K and density
![]() cm-3. Hydrogen is initially highly ionized. During the postshock gas cooling, hydrogen recombination occurs, the neutral gas cools,
cm-3. Hydrogen is initially highly ionized. During the postshock gas cooling, hydrogen recombination occurs, the neutral gas cools, ![]() starts to form and further cools and condenses the gas.
starts to form and further cools and condenses the gas.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{11263fC2.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg228.png) |
Figure C.2:
Isobaric cooling of the postshock gas and |
Figure C.1 presents the contribution of ![]() line emission to the total cooling function as a function of the gas temperature. It shows the cooling functions of (i) all the
line emission to the total cooling function as a function of the gas temperature. It shows the cooling functions of (i) all the ![]() lines (thick red line); (ii) the
lines (thick red line); (ii) the ![]() rotational lines S(0) to S(5) detected by Spitzer(thin red line); (iii) the total cooling efficiency in which all elements are included (green dashed line). The cooling efficiencies of some other major coolants (O in blue,
rotational lines S(0) to S(5) detected by Spitzer(thin red line); (iii) the total cooling efficiency in which all elements are included (green dashed line). The cooling efficiencies of some other major coolants (O in blue,
![]() in purple, and OH in orange) are also indicated. H2 excitation at low temperatures (
in purple, and OH in orange) are also indicated. H2 excitation at low temperatures (![]() K) is dominated by the contribution associated with
K) is dominated by the contribution associated with ![]() formation.
formation.
C.2 H2 formation
The chemical abundance profiles in the postshock gas are illustrated in Fig. C.2 as a function of time, for the same model as in Fig. C.1
From the time when the gas attains 104 K, it takes ![]()
![]() 105 yrs to form
105 yrs to form ![]() .
This time scales inversely with the dust-to-gas mass ratio. The
.
This time scales inversely with the dust-to-gas mass ratio. The ![]() formation gives rise to a shoulder in the temperature profile around 200 K. At this point, the energy released by
formation gives rise to a shoulder in the temperature profile around 200 K. At this point, the energy released by ![]() formation is roughly balanced by the cooling due to atomic oxygen (see Fig. 3 in Flower et al. 2003).
formation is roughly balanced by the cooling due to atomic oxygen (see Fig. 3 in Flower et al. 2003).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



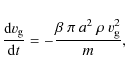
![\begin{figure}
\par\includegraphics[angle=90,width=8cm,clip]{11263fA1.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg197.png)
![\begin{figure}
\par\includegraphics[angle=90,width=15.7cm,clip]{11263fB1.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg201.png)
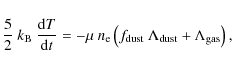
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{11263fB2.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg222.png)
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{11263fB3.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg224.png)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{11263fC1.eps}
\end{figure}](/articles/aa/olm/2009/29/aa11263-08/Timg226.png)