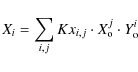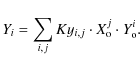EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 502 / No 1 (July IV 2009) A&A, 502 1 (2009) 91-111 Online Material
Free Access
Issue
A&A
Volume 502, Number 1, July IV 2009
Page(s) 91 - 111
Section Galactic structure, stellar clusters, and populations
DOI https://doi.org/10.1051/0004-6361/200810922
Published online 05 March 2009

Online Material

    Appendix A: Alignment of stellar positions to a common reference frame

A.1 Reference frame

We chose to base the reference frame on stellar positions obtained from imaging observations on 1 June 2006. The data are characterized by (a) the largest FOV of all observations used in this work due to large dither offsets and (b) a very low number of saturated stars because of the short integration time used. The data set consists of 80 randomly dithered frames, which allows, in addition, a thorough determination of average stellar positions and their uncertainties via multiple measurements.

In a first step, the lists of point sources identified in the individual exposures (see Sect. 3) were registered relative to the first exposure in the series (which is centered on Sgr A*) by identifying stars common to the frames and determining the relative offsets between the exposures via a least squares fit (uncertainty of the offsets: <0.01 pixel). The individual lists of stars were subsequently merged to a preliminary common list with average positions and corresponding standard deviations. In order for a star to be included in the common list, it had to be detected in at least 8 independent exposures, so that its positional uncertainty could be reliably estimated and in order to eliminate spurious detections.

A.2 Selection of reference stars

In a second step, transformation reference stars were selected from the preliminary common list of stars. Reference stars were identified by a four-step process: (a) brightness selection ( $10.0 < {\rm mag}_{K{\rm s}} < 17.0$); (b) selection of stars with positional uncertainty <0.15 pixel; (c) isolation of the stars: the magnitude difference between a potential reference star and any other star within 8 pixels (0.216'', corresponding to $\sim$3.5 times the FWHM of the PSF) must be at least 3 mag; (d) uniform distribution: final selection of reference stars on a 50 $\times $ 50 pixel (1.35'' $\times $ 1.35'') grid (in case there are several potential reference stars per grid field, the star with the smallest positional uncertainty was selected). We thus obtained 932 reference stars for a combined FOV of $\sim$40'' $\times $ 40''. The brightness selection excludes the brightest stars because they are saturated in some of the frames. The cut-off at the faint end was chosen because of the limited sensitivity of the frames of some observing epochs. The faintest stars may also be frequently affected by systematic offsets due to confusion with nearby resolved and unresolved sources in the dense GC field (see Ghez et al. 2008).

The last two steps in the selection process are important in order to avoid being biased by fields of increased stellar density. In the case of the GC, for example, the density of stars increases toward Sgr A* (see Schödel et al. 2007). It is reasonable to assume that the camera distortion can be described by a well-behaved function. We believe that uniform sampling helps to avoid possible systematic errors. Non-uniform sampling of reference stars would for example lead to a significantly larger number of reference stars detected near Sgr A*. In the central arcseconds there exists a population of early-type stars with known rotation in the plane of the sky (e.g., Paumard et al. 2006). Also, stars in the central arcseconds are subject to larger systematic uncertainties of their positions because of the high stellar density and the presence of numerous bright stars in this region. Ghez et al. (2008) have demonstrated clearly the problem of astrometric errors due to the influence of the unresolved stellar population. The sampling of the reference sources selected by the above described process is highly uniform, with an average density of 0.5 reference sources per arcsec2 (see Fig. A.1).

 \begin{figure} \par\includegraphics[width=9cm,clip]{0922figA1.eps} \end{figure} Figure A.1:

Transformation stars selected from the 1 June 2006 observations are marked by crosses on the FOV obtained after combining the dithered exposures. The average density of transformation stars is indicated by the gray shading. Contour lines are drawn at $0.1\ldots 0.6$ stars per arcsec2.
Open with DEXTER

Due to possible camera distortions, which have at this point not yet been taken into account, the positions of the reference stars can still be biased and have increased uncertainties. For example, the pixel scale may increase or decrease systematically toward the edges and corners of the detector FOV. Therefore, two effects can be expected: (a) systematic deviations of the relative stellar positions measured on different dithered exposures from the positions as they would be measured with a distortion-free camera; and, as a consequence; (b) increased uncertainty of the positions after combining the source lists.

 \begin{figure} \par\includegraphics[width=18cm,clip]{0922figA2.eps} \end{figure} Figure A.2:

Smooth maps of the positional uncertainty of the stars detected in the reference frame from 1 June 2006. After assigning the positional uncertainty of each star to its position, the map was smoothed by applying a Gaussian filter with a FWHM of 2.7''. The left panel shows the uncertainty of the stellar positions in the FOV after combining the astrometric lists from the individual exposures by applying just shifts in x and y coordinates (preliminary combined list, simple mosaicing). The right hand panel shows the uncertainties after aligning the stellar positions via a 3rd order polynomial fit (final combined list). Contour lines are drawn from 0 to 0.16 pixel at intervals of 0.02 pixel. The transformation reduces the overall uncertainty of the positions and eliminates systematic changes of the positional uncertainty due to camera distortions. The average combined uncertainty of all positions is 0.081 pixel before and 0.045 pixel after the polynomial fit. After applying a polynomial transformation to the stellar positions, the uncertainties correlate with the light density in the field. Light density variations arise from the combined effect of stellar density and the presence of bright stars. This can affect the astrometry via the photometric noise in the halos of the bright stars, especially since the used PSF was truncated (see Sect. 3). The unresolved stellar population will contribute as well to increased photometric noise. This can be seen when comparing the uncertainty map with the mosaic image shown in Fig. 1. One can, for example, see that the areas around IRS 7, IRS 1, or the IRS 16 cluster are clearly visible in the uncertainty map. The uncertainty of the stellar positions decreases with distance from Sgr A*, in correlation with the decreasing stellar density (see Schödel et al. 2007).
Open with DEXTER

The systematic deviations of the stellar positions are difficult to correct without precise knowledge of the camera distortions. However, fortunately, if we relax the constraints on absolute astrometry, we can still get accurate measurements of the proper motions. If we accept that there may be some residual distortion present in the reference frame, all we have to do is to apply this distortion consistently to all epochs. We chose a 3rd order polynomial transform for this purpose (see the following section).

The positional accuracy of the reference stars can be improved by aligning the stellar positions from the 80 exposures of the reference epochs via a 3rd order polynomial transform, instead of a simple shift as done to obtain the preliminary combined list. Hence, the astrometric lists for each exposure were aligned with the first exposure in the series via such a transform. The parameters of the transform were established via a least squares fit, using the reference stars common between the given frames. Finally, all astrometric lists of the individual exposures were combined again to a common list.

Note that the last step does not necessarily eliminate camera distortions. The final reference frame may therefore still have residual astrometric distortions. However the last step increases the precision of the stellar positions in the reference frame significantly. We created smooth maps of the positional uncertainties of the stars in the preliminary and final combined lists. As we show in Fig. A.2, the map of the uncertainty of the stellar positions in the final combined list reflects closely the two-dimensional stellar light density. This is exactly what one would expect after possible systematic offsets due to camera distortions have been eliminated successfully and the astrometry of the sources is almost exclusively affected by the structure of the stellar cluster itself. This provides and important cross-check for the validity of our determination of stellar positions in the reference frame.

A.3 Transformation of positions into reference frame

Having established a reference frame with a list of transformation stars, the next step is to transform the stellar positions of the stars detected in each exposure of each epoch to the reference frame. About 400 (the FOV of individual exposures being smaller than the combined FOV of the reference frame) reference stars could be identified in each exposure of our data set. The positions of those stars were then compared with the positions of the corresponding stars in the reference frame in order to determine the parameters (via a least squares algorithm) of a polynomial transformation into the reference frame.

 \begin{figure} \par\includegraphics[width=18cm,clip]{0922figA3.eps} \end{figure} Figure A.3:

Smooth maps of the positional uncertainty of the stars detected in the reference frame from 12 June 2004. The maps were created in the same way as the maps shown in Fig. A.2. The left panel shows the uncertainty of the stellar positions in the FOV after combining the lists of detected stars by applying just shifts in x and y coordinates (simple mosaicing). The right hand panel shows the uncertainties after aligning the stellar positions with the reference frame via a polynomial fit. The transformation reduces the overall uncertainty of the positions and eliminates systematic changes of the positional uncertainty due to camera distortions. The average combined uncertainty of all positions is 0.073 pixel before and 0.027 pixel after the polynomial fit. The overall uncertainty is lower than for the stars in the reference frame because the quality of the AO correction was much better in the observing run on 12 June 2004. Therefore, the correlation of the uncertainty after the polynomial transform with the density of stars and the presence of bright stars is less obvious than in the 2006 data. However, areas of increased positional uncertainty are clearly associated with the IRS 7, IRS 16, and IRS 1. Please note that the different scaling of the maps in the left and right panels. The vertical strip of low uncertainties at the right edge of the FOV is an artifact due to the smoothing and the lack of sources in this area in the data from 12 June 2004.
Open with DEXTER

The IDL routine POLYWARP was used to calculate the transformation parameters between the stellar positions. The POLYWARP procedure is based on a least squares algorithm to solve the coefficients of the following polynomial functions:

\begin{displaymath}% X_{i} = \sum_{i,j}Kx_{i,j}\cdot X_{\rm o}^{j}\cdot Y_{\rm o}^{i} \end{displaymath} (A.1)

and

\begin{displaymath}% Y_{i} = \sum_{i,j}Ky_{i,j}\cdot X_{\rm o}^{j}\cdot Y_{\rm o}^{i}. \end{displaymath} (A.2)

In these equations Xi and Yi correspond to the positions of the reference stars in the June 2006 reference frame, and $X_{\rm o}$ and $Y_{\rm o}$ are the corresponding positions in the given exposure. We chose a maximum value of 3 for the parameters i and j. The result of the transform is not satisfying for $i,j\leq1$, with strong systematic effects visible in the error maps (corresponding to the one shown in Fig. A.2 ). The values $i,j\leq3$ adopted here produce slightly more accurate results than $i,j\leq2$ (a reduction of the average positional uncertainties by $5{-}10\%$). However, this choice does not alter any of the results of this work in a significant way. Choosing an even higher order for the transform is therefore unnecessary and would reduce the precision with which the transformation parameters can be computed.

After transformation of the lists of point sources for each individual frame, the lists corresponding to a given observing epoch were combined. Average fluxes and positions as well as the corresponding uncertainties (the errors on the mean values) could be directly derived from the multiple measurements for each star. Sources that were not detected in multiple exposures were rejected as spurious detections.

Similar to Figs. A.2, A.3 shows the astrometric uncertainties of the sources detected in the 12 June 2004 epoch after (a) just applying shifts in x and y to combine the lists; and (b) after a full third order transformation into the reference frame. Again, it can be seen how the full polynomial transformation reduces the overall positional uncertainties and their systematic changes across the field considerably.

  Appendix B: Offset field

B.1 Proper motions

The methodology applied to extract proper motions from the offset data set was identical to the one for the central field, except that no astrometric positions for the stars were derived. The analysis of the offset proper motions is based on three epochs only (August 2004, July 2005, and May 2008). Stars that were not detected in all three epochs were rejected from the sample. The stellar positions were just transferred roughly into the radio reference frame by applying appropriate offsets. We estimate that the uncertainties of the stellar positions in the offset field may reach up to several 0.1''. Therefore the proper motions for the offset field are not included in the list in Table B.1. The distances of the stars from Sgr A* were measured by using the NaCo pixel scale.

Table B.1:   List of stars with measured proper motion in the GC.

The number stars with proper motions measured in the offset field, after applying the selection criteria, is 4308. In the left panel of Fig. B.1 we show a plot of reduced $\chi ^{2}$ vs. Ks-band magnitude for the proper motion fits of the offset field data. There is not such a clear correlation between $\chi ^{2}_{\rm red}$ and magnitude as in case of the center field data. We believe that this is mainly caused by (a) the low number statistics of the offset field data (only 3 data points per fit) and (b) by the a factor $\sim$2 (see Schödel et al. 2007) lower stellar surface number density in the offset field. The middle and right panels of Fig. B.1 show plots of the distribution of  $\chi ^{2}_{\rm red}$ and velocity uncertainty for the offset field data.

Figure B.2 shows an image of the offset field with measured stellar velocities indicated by arrows, after rejecting the stars with the 5% highest reduced $\chi ^{2}$-values in order to avoid outliers due to the small number of measured positions and thus rather noisy statistics.

 \begin{figure} \par\includegraphics[width=18cm,clip]{0922figB1.eps} \end{figure} Figure B.1:

Error analysis for offset field data. Left: plot of log($\chi ^{2}$) vs. Ks-band magnitude. The straight line is a least square linear fit. Middle: distribution of the velocity uncertainties, black for right ascension and blue for declination. Right: distribution of the reduced $\chi ^{2}$ values for the linear fits of the data of position vs. time. The black histogram is for the fits in right ascension, the blue histogram for the fits in declination.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=17cm,clip]{0922figB2.eps} \end{figure} Figure B.2:

Map of stars and measured proper motions of stars in the GC offset field. North is up and east is to the left. Arrows indicate magnitude and direction of the proper motion velocities. The black arrow in the lower left corner indicates the length of a 1000 km s-1 arrow. Please note that the map is not strictly astrometric.
Open with DEXTER

B.2 Velocity dispersion

We analysed the proper motion data for the offset field in the same way as the data for the central field. The mean projected radial and tangential velocities and the corresponding velocity dispersions are shown in Fig. B.3. The offset data set covers only a small angular section of the NSC and is highly incomplete at small R. Also, there are only three epochs available for the offset field. Therefore the quality of the offset data does not match the quality of the data on the central field. They have not been used for the further analysis in this work. The mean velocities show a larger scatter than in case of the center field data.

However, we believe that it is important to include the offset data in this work for two reasons. (a) They are centered on a different region of the cluster and can thus serve to detect systematic errors related to the alignment of the astrometric data with the reference epoch. We find that the proper motions for all stars common to the center and offset data agree within their $1\sigma $ uncertainties. (b) The offset data sample slightly larger distances from Sgr A*. They support the image of a close to isotropic cluster with a constant velocity dispersion out to projected distances of R=30'' (1.14 pc).

 \begin{figure} \par\includegraphics[width=15cm,clip]{0922figB3.eps} \end{figure} Figure B.3:

Left: projected radial (green) and tangential (blue) velocity dispersions in the GC nuclear star cluster for the offset field (see Fig. 2). Right: mean projected radial and tangential velocities vs. projected distance from Sgr A* for the offset field.
Open with DEXTER


Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.