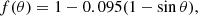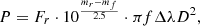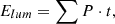| Issue |
A&A
Volume 699, July 2025
|
|
|---|---|---|
| Article Number | L3 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202555481 | |
| Published online | 25 June 2025 | |
Letter to the Editor
Detection of small fresh craters on the Moon
Linking fresh craters to their lunar impact flash events
1
Université Paris Cité, Institut de Physique du Globe de Paris, CNRS, Paris, France
2
Abersytwyth University, Department of Physics, Aberystwyth SY23 3FL, UK
3
Université Côte d’Azur, CNRS–Lagrange, Observatoire de la Côte d’Azur, CS 34229, F 06304 NICE Cedex 4, France
4
University of Leicester, School of Physics and Astronomy, University Road, LE1 7RH Leicester, UK
⋆ Corresponding author: ds869@leicester.ac.uk
Received:
12
May
2025
Accepted:
8
June
2025
The luminous efficiency, η, is the fraction of an impactor’s kinetic energy that is released as light. For lunar impact flashes (LIFs), this value is currently poorly constrained, with values within the literature spanning several orders of magnitude. This is in part due to a lack of ground truth data for observed LIFs where the resultant crater has been identified. We aim to form a database of LIF-linked impact craters in order to refine parameters such as η, and to validate crater scaling laws for small (D < 100 m) regimes. Using PyNAPLE, a lunar surface change-detection pipeline, we performed a systematic search to attempt to locate the resultant craters from a selection of the most energetic LIFs. These LIF-linked craters were used to compare the validity of the frequently used crater scaling laws, and formed the basis for Monte Carlo simulations to identify a more accurate value for the luminous efficiency. We found that the most accurate crater scaling laws tested were the ones of Holsapple, Öpik, and Shoemaker & Wolfe. The Monte Carlo simulations of the predicted crater size from these three scaling laws produces a value for the luminous efficiency of η = 6.0 ± 1.2 × 10−3.
Key words: meteorites / meteors / meteoroids / Moon / planets and satellites: surfaces
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Impact craters are ubiquitous across most types of Solar System bodies, and form some of the most significant features of bodies that lack surface renewal processes. While the majority of impacts come from smaller sub-meter impactors, the larger impactors can cause significant destruction. By studying craters and the flashes of light caused by the impact events, known as lunar impact flashes (LIFs), we are able to better understand the population of impactors (Suggs et al. 2014), allowing for better predictions of when impacts are more likely to occur. The study of these impact craters can also reveal the chronology of the impacted surfaces (Neukum et al. 2001; Hartmann 2005).
While meteoroids fall on the Earth frequently, the majority completely ablate within the atmosphere. In the atmosphereless environment of the Moon, this same population of meteoroids can reach the surface unimpeded. Due to the orbital velocities of these meteoroids (8–72 km s−1), even smaller (< 1 m) meteoroids produce highly energetic impacts, excavate a crater, and can temporarily heat the surface to over 5000 K (Avdellidou et al. 2021), producing incandescence. These impacts have also been shown to produce seismic signals detectable by lunar seismometers (Lognonné et al. 2009).
When this occurs on the dark hemisphere of the Moon, the LIF is observable from the Earth through even moderate (> 0.2 m) telescopes. The ratio of the light produced to the kinetic energy of the impactor is known as the luminous efficiency, η, and is a key parameter for subsequent calculations. Despite this criticality, η is currently not well constrained, with typically used values ranging between 2 × 10−3 and 5 × 10−4 (Bellot Rubio et al. 2000; Ortiz et al. 2006; Swift et al. 2011; Moser et al. 2011; Suggs et al. 2014; Madiedo et al. 2015; Liakos et al. 2019).
The sporadic nature of LIFs, which impact the Moon at around 8 h−1 (Liakos et al. 2024), means that observing even a few events can require many hours of observation. Several observation campaigns, such as ESA’s NELIOTA and NASA’s Meteoroid Environment Office (MEO), as well as amateurs, observe and study these sporadic events, and within the literature and online databases over 650 LIFs have been documented and made publicly available to some extent (Ortiz et al. 2000; Suggs et al. 2008; Madiedo et al. 2014, 2015; Ait Moulay Larbi et al. 2015; Bonanos et al. 2018; Liakos et al. 2019; Zuluaga et al. 2020; Avdellidou et al. 2021; Sheward et al. 2023).
Several scaling laws exist that approximate the relationship between the rim-to-rim diameter of an impact crater and the parameters of the impact that formed it (Gault 1974; Dence et al. 1977; Shoemaker & Wolfe 1982; Öpik 1969; Holsapple 1993; Melosh 1989; Horedt & Neukum 1984); however, they are typically derived using Earth-based explosive or laboratory tests that have then been adapted for use on the lunar surface, and give varying results for the same event. For these scaling laws to be properly tested for accuracy on lunar craters, a significant dataset of impact craters for which the formation event has been recorded is required. Despite the wealth of LIF observations, within the literature only three lunar craters have been identified that also have recorded observations of the corresponding LIF. The first of these craters was a serendipitous discovery (Moser et al. 2014; Robinson et al. 2015). In the second case, targeted Lunar Reconnaissance Orbiter (LRO) observations were utilised to locate the crater (Madiedo et al. 2014; Robinson et al. 2014). With the development of the lunar surface change detection pipeline, PyNAPLE, it was shown that crater detection could be performed in a systematic way on publicly available LRO imagery, and the third of these craters was located (Sheward et al. 2022).
Using these methods, we aim to increase the number of known LIF-linked impact craters, providing ground truth data to enable an investigation into the crater scaling laws for the Moon at a scale of < 100 m, and allow us to further constrain the luminous efficiency.
2. Search for fresh impact craters
Using publicly available observations (Ortiz et al. 2000; Suggs et al. 2008; Madiedo et al. 2014, 2015; Ait Moulay Larbi et al. 2015; Bonanos et al. 2018; Liakos et al. 2019; Zuluaga et al. 2020; Avdellidou et al. 2021; Sheward et al. 2023), we compiled a dataset of LIFs containing their epoch, duration, and estimated selenographic co-ordinates. The majority of publicly available LIFs have been confirmed, either by dual-camera observations or because they have appeared in multiple consecutive frames of a single camera. These observations can be at the same wavelengths (e.g. R band) or, more typically, at two different wavelengths (e.g. R and I bands). Within these databases there are also single-camera, single-frame LIF observations. Without a second observation, these LIFs cannot be verified. In the case of dual-camera dual-band observations, LIFs can be detected in the I band but do not appear to be detectable in the R band, as they are relatively cold events and therefore produce less light in the R band than is detectable. Therefore, in the absence of independent observations that confirm these events, they were excluded from our dataset.
Due to the processing time involved – the processing of a single LIF takes days - and therefore cumulatively would take over three years. This is not feasible, and the prioritisation of more easily detectable events is vital. In order to select the most suitable candidates, we applied a series of filters that select for the optimal occurrence window, time, selenographic location, and energy.
The detection of the resultant craters from these LIFs was achieved using PyNAPLE (Sheward et al. 2022), which employs Lunar Reconnaissance Orbiter Narrow Angle Camera (LRO NAC) images (Robinson et al. 2010) to perform a search in a given radius around the LIF’s approximate location. PyNAPLE is change detection software designed specifically for LRO NAC images and works by forming each ‘before’ and ‘after’ image pair for a given epoch within an area around a given location. Due to the constraints on which images can form these pairs, there are typically not enough images to obtain complete coverage of the search area. Consequently, there can be insufficient image coverage to locate the crater for a given event. Because the LRO is the only source of images used by PyNAPLE, LIFs observed before the start of the LRO mission (September 15 2009) were therefore excluded from the dataset, as no ‘before’ images would exist. Similarly, as LRO NAC images are released on a monthly release schedule three months after acquisition, LIFs observed within three months of the present were also excluded.
Due to the non-continuous LRO imaging, it is not guaranteed that a given area will have been imaged – even if the LRO imaging swath passed over the desired location. This means that realistically more than three months after a LIF are needed to increase the probability of ‘after’ image coverage. Similarly, LIFs that occurred close to the start of LRO operations will have few ‘before’ images. Thus, the LIFs that have the greatest chance of having sufficient before and after images are the ones observed near the midpoint of the LRO operations.
Due to the stray light from the illuminated hemisphere of the Moon, LIF observers typically observe the unilluminated lunar limb, avoiding the polar regions. Errors have been known to exist in the reported co-ordinates of the LIFs, which can report the latitude and longitude as switched around, placing the estimated LIF at or near the lunar poles. The technique used for change detection in the LRO NAC images requires nadir pointing, and the inclination of the LRO’s polar orbit only allows nadir pointing images to be taken between –85°to 85°latitudes. LIFs with reported latitudes outside this range are therefore discarded.
Another consideration is the resolution of LRO NAC images, which varies between 0.5–1.5 m px−1, depending on the altitude of the spacecraft. Craters with a rim-to-rim diameter of a few metres will span only a few pixels, and therefore diameter measurements will be more negatively affected by the uncertainty in the craters’ true location within the pixel. The detection of craters that occupy only a few pixels is also more difficult, as feature identification at such a resolution quickly becomes impossible. Furthermore, higher-energy impacts throw ejecta further away, which can allow the triangulation of the primary crater. In the case of ray ejecta, the ray can simply be traced back towards its source. This allows for a much more targeted detection to occur and leads to the simplification of the crater location process. In order to maximise the probability of locating the fresh crater for a given LIF, these higher-energy LIFs were therefore prioritised by excluding events with a duration shorter than 0.2 s. From the dataset of > 650 LIFs, the 22 most suitable events for detection within LRO NAC imagery were left to be used as the input for PyNAPLE.
3. Crater detection and analysis
3.1. Detection
From the dataset of 22 LIFs passed to PyNAPLE, 12 fresh craters were detected. Of these 12 craters, six were fresh impact craters that both were newly discovered and could be linked to their corresponding parent LIFs. A further three of the located craters are the LIF-linked craters already identified within the literature (Moser et al. 2014; Suggs et al. 2014; Madiedo et al. 2014; Robinson et al. 2014; Sheward et al. 2022). It was confirmed that the three remaining craters were not associated with the LIF on which the search was performed, as they either appeared in images from before the LIF, or were absent from images taken after the LIF. The full > 650 LIF database was searched for any LIFs that both shared a selenographic proximity to these craters and occurred in the same time window to the crater; however, no such LIFs were identified.
The rim-to-rim diameter of the craters was measured using ISIS3’s qview. They were measured from the centre of the selected pixel using best estimates of the crater rim location. In cases in which the high albedo of the freshly exposed regolith caused pixel saturation, we estimated the crater edge by fitting an ellipsoid to the crater for each available after image, and then taking the average measurement. Each LIF-linked crater has been given a unique identifier of the form
Table A.1 provides an overview of the nine events for which a LIF-linked crater was identified, and Fig. 1 shows the ratio images (after divided by before) of a selection of craters.
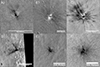 |
Fig. 1. Ratio images for six of the located craters: (A)C110211N16.1W087.8 (4.3 m), (B)C130317N20.7W024.3 (17.6 m), (C)C130911S17.2W020.4 (30.2 m), (D)C170927N08.0W076.5 (23.8 m), (E)C190121S28.3W067.1 (3.5 m), and (F)C190121S28.2W067.2 (12.0 m). |
3.2. Stream identification
To analyse the relationship between the LIF and the size of the resultant crater, we first need to characterise the impact parameters. Meteoroidal impactors either originate from one of many parent streams, or the sporadic background population. For a given stream, each meteoroid can be assumed to have a similar velocity, density, and trajectory. The identification of a sporadic background impact does not enable the parameters to be known with the same level of accuracy as a parent stream; however, there are common values for velocity and density that can be used, and the median impacting angle of 45°can be assumed.
Several methods have been developed to establish the link between impactors and their sources (Suggs et al. 2014; Madiedo et al. 2015; Avdellidou et al. 2021). Five of the LIF events we used have already had their stream identified (see references in Table A.1). For the remaining four LIFs, we followed the methods described in Avdellidou et al. (2021). We found that C091113N17.3E043.7 is likely due to a sporadic meteoroid, C110211N16.1W087.8 likely results from a η-Virginid meteoroid, C110511S16.3W047.1 is likely due to an η-Lyrid meteoroid, and C140504S00.6W019.6 is likely from a Southern μ-Sagittariid meteoroid.
3.3. Scaling laws and luminous efficiency
The luminous energy, Elum, is the energy released as light during an impact, determined by η. Due to this relationship, the estimate of the impacting meteoroids mass is greatly affected by the assumption for η. Due to the orders-of-magnitude range for η, any further calculations performed using them are consequently also uncertain.
Typically, when a LIF is observed, energy calculations are performed using the observed Elum, and a value for η, to derive a pre-impact kinetic energy. From this, crater scaling laws can be utilised to estimate the rim-to-rim diameter of the resultant crater. For our events, we have independent observations of both the formation event and measurements of the craters diameter. This allows us to calculate the estimated crater size from the observed luminous energy, and perform the inverse calculation using the observed crater size to predict the kinetic energy. The comparison of these values allows us to recompute the luminous efficiency to produce a value that can be used to predict the true crater diameter from the observed luminous energy. As different values for the crater diameter are obtained depending on the scaling law used, it is important to select the scaling law that produces results closest to the observed ground truth data. For our tests, we chose to use the scaling laws of Gault (1974), Dence et al. (1977), Shoemaker & Wolfe (1982), Öpik (1969), Holsapple (1993), and Melosh (1989). A further discussion of these scaling laws can be found in Appendix D.
Since the crater scaling laws have several degrees of freedom, it is not practical to obtain enough LIF-linked craters to span the range of possible values. This would require significantly more LIF-linked craters than have currently been obtained. With the values we have, only two craters, C110211N16.1W087.8 and C130317N20.7W024.3, are able to be directly compared, both having been identified as likely originating in the η-Virginids (VIR). This allows for a rudimentary test of the predicted diameters against the observed ground truth. The results of this test are shown in Fig. 2, where it can be seen that the scaling laws of Holsapple, Öpik, and Shoemaker & Wolfe closely match the observed data.
 |
Fig. 2. Comparison of the predicted crater diameters from six scaling laws to two observed craters from the same parent source. The mass of the impactor is given as a range determined by the typically used value for η, 2 × 10−3 and 5 × 10−4. The bold lines is the value calculated using the group velocity of the Virginid meteoroid stream, and the narrow lines are 1σ errors. |
While this gives us an initial insight, the above method considers only two craters and it would be more worthwhile to utilise all the available data. We therefore devised a second method based on a series of Monte Carlo simulations, for which the scaling laws were used to predict the crater diameter given the kinetic energy, luminous efficiency, projectile velocity, density, and impact angle from the stream identification (or non-identification). We performed 105 iterations for each scaling law, for which at every iteration a luminous efficiency was randomly selected from a uniform distribution between 10−5 and 1. We opted for this larger-than-typical range for the luminous efficiency to ensure the completeness of the test. A full breakdown of the used distributions is given in Table B.1. In each iteration, for each LIF-linked crater the known luminous energy was divided by the selected luminous efficiency to produce a kinetic energy. Appendix E describes how the luminous energy for each crater was obtained.
As stream identification only gives the most likely source, it does not rule out a sporadic origin, and so for each impact we randomly selected stream or sporadic origin (unless no candidate parent stream was identified). From this, the velocity and projectile density were taken from a normal distribution of the parent source parameters (for the velocity, σ is the velocity dispersion of the meteoroid stream, and for the projectile density σ is the uncertainty in the density, taken from Jenniskens et al. 2024). Likewise, the impacting angle was selected from a uniform distribution of possible angles for the observed crater morphology (i.e. craters with an ejecta blanket asymmetry have an impact angle of 20–45°).
Using the observed, Do, and predicted, Dp, crater diameters, we obtained 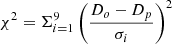 , where σi is the error in Do. By plotting χ2 against η, as in Fig. B.1, we see optimal η for each scaling law by calculating the median for the points with χ2 ≤ 10.7 (
, where σi is the error in Do. By plotting χ2 against η, as in Fig. B.1, we see optimal η for each scaling law by calculating the median for the points with χ2 ≤ 10.7 (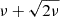 , where degrees of freedom, ν = N − M = 9 − 2 Press et al. 1986), are denoted by dotted lines. As for the initial test, Shoemaker & Wolfe, Holsapple, and Öpik are all somewhat in agreement on a value for η, which produces an average of 6.0 ± 1.2 × 10−3.
, where degrees of freedom, ν = N − M = 9 − 2 Press et al. 1986), are denoted by dotted lines. As for the initial test, Shoemaker & Wolfe, Holsapple, and Öpik are all somewhat in agreement on a value for η, which produces an average of 6.0 ± 1.2 × 10−3.
4. Discussion and conclusion
We have presented here the results from the first 22 LIFs searched for with PyNAPLE. Of these 22 LIFs, 12 craters were identified within LROC imagery, nine of which are believed to be linked to the observed LIFs. The parent streams for these events were subsequently identified and, using two events from the same parent stream, an evaluation of crater scaling laws revealed the most accurate scaling law for the < 100 m size range. Using these craters as ground truth, a rudimentary comparison could be performed on the six most common scaling laws, revealing that Holsapple, Öpik, and to a lesser extent Shoemaker & Wolfe devised the best-fitting scaling laws.
We then performed Monte Carlo simulations for each of the scaling laws, comparing the predicted diameter to the observed diameters, finding that while the populations of scaling laws give luminous efficiency predictions of between 10−1 and 10−4, when only considering the scaling laws that we found previously to be the most accurate we find a value of 6.0 ± 1.2 × 10−3. While this value is larger than the typically used range of 2 × 10−3 − 5 × 10−4, this underestimation of η in previous works could somewhat explain the overestimation of the predicted crater diameters in them, along with the use of inaccurate scaling laws.
While this work takes first steps towards the refinement of the luminous efficiency, the number of LIF-linked craters is still limited. By expanding this dataset further, we aim to further increase the accuracy of η. With the continued utilisation of PyNAPLE, and the expansion of the LIF-linked crater dataset, we can not only work towards a dataset that can be analysed for the luminous efficiency, but also towards the development of scaling laws that are more accurate for the sub-100 m regime.
In aid of this dataset expansion, new techniques to observe LIFs in the short-wave infrared allow for observations to be performed during the daytime, increasing the overall number of high-energy impact flashes that can be observed, and thereby increasing the likelihood that more craters will be located.
Similarly, the LUMIO mission, scheduled to be launched in 2028 to the Earth-Moon L2, will look for LIFs on the lunar far-side (Cervone et al. 2022; Topputo et al. 2023; Merisio & Topputo 2023). This will further bolster the number of LIF observations by extending the LIF observational coverage of the Moon from the near-side hemisphere to nearly the entire lunar surface.
Acknowledgments
CA and DS acknowledge support from STFC grant “Study the impact process on the terrestrial planet moons” (ST/Y006062/1). CA and DS also acknowledge support from UKRI grant “Study Of The Meteoroid Impacts On The Moon” (UKRI1377). This work was supported by the Programme National de Planetologie (PNP) of CNRS/INSU, co-funded by CNES and by the programme “Flash!”. DS, MD and CA also acknowledge support from ANR “ORIGINS” (ANR-18-CE31-0014) and CNES. This work has made use of data from the European Space Agency (ESA) NELIOTA project, obtained with the 1.2-m Kryoneri telescope.
References
- Ait Moulay Larbi, M., Daassou, A., Baratoux, D., et al. 2015, Earth Moon Planets, 115, 1 [Google Scholar]
- Avdellidou, C., Munaibari, E., Larson, R., et al. 2021, Planet. Space Sci., 200, 105201 [NASA ADS] [CrossRef] [Google Scholar]
- Babadzhanov, P. B. 2002, A&A, 384, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babadzhanov, P. B., & Kokhirova, G. I. 2009, A&A, 495, 353 [Google Scholar]
- Bellot Rubio, L. R., Ortiz, J. L., & Sada, P. V. 2000, Earth Moon Planets, 82, 575 [NASA ADS] [Google Scholar]
- Bonanos, A. Z., Avdellidou, C., Liakos, A., et al. 2018, A&A, 612, 76 [Google Scholar]
- Cervone, A., Topputo, F., Speretta, S., et al. 2022, Acta Astron., 195, 309 [Google Scholar]
- Consolmagno, G., Britt, D., & Macke, R. 2008, Chemie der Erde /Geochemistry, 68, 1 [Google Scholar]
- Dence, M. R., Grieve, R. A. F., & Robertson, P. B. 1977, in Impact and Explosion Cratering: Planetary and Terrestrial Implications, eds. D. J. Roddy, R. O. Pepin, & R. B. Merrill, 247 [Google Scholar]
- Drolshagen, E., Ott, T., Koschny, D., et al. 2020, Planet. Space Sci., 184, 104869 [Google Scholar]
- Gault, D. E. 1974, in A Primer in Lunar Geology, eds. R. Greeley, & P. H. Schultz, 137 [Google Scholar]
- Hartmann, W. K. 2005, Icarus, 174, 294 [Google Scholar]
- Holsapple, K. A. 1993, Ann. Rev. Earth Planet. Sci., 21, 333 [CrossRef] [Google Scholar]
- Horedt, G. P., & Neukum, G. 1984, Earth Moon Planets, 31, 265 [Google Scholar]
- Jenniskens, P. 2006, Meteor Showers and their Parent Comets (Cambridge University Press) [CrossRef] [Google Scholar]
- Jenniskens, P., Nénon, Q., Gural, P. S., et al. 2016, Icarus, 266, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P., Estrada, P. R., Pilorz, S., et al. 2024, Icarus, 423, 116229 [Google Scholar]
- Liakos, A., Bonanos, A., Xilouris, E., et al. 2019, ArXiv e-prints [arXiv:1901.11414] [Google Scholar]
- Liakos, A., Bonanos, A. Z., Xilouris, E. M., et al. 2024, A&A, 687, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lognonné, P., Le Feuvre, M., Johnson, C. L., & Weber, R. 2009, J. Geophys. Res., 114, E12 [Google Scholar]
- Luo, X.-Z., Zhu, M.-H., & Ding, M. 2022, J. Geophys. Res., 127, e2022JE007333 [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Morales, N., & Cabrera-Caño, J. 2014, MNRAS, 439, 2364 [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Organero, F., et al. 2015, A&A, 577, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Morales, N., & Santos-Sanz, P. 2019, MNRAS, 486, 3380 [Google Scholar]
- Melosh, H. J. 1989, Impact cratering : a geologic process (Oxford Monographs on Geology and Geophysics) [Google Scholar]
- Merisio, G., & Topputo, F. 2023, Icarus, 389, 115180 [Google Scholar]
- Moser, D. E., Suggs, R. M., Swift, W. R., et al. 2011, in Meteoroids: The Smallest Solar System Bodies, eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, 365 [Google Scholar]
- Moser, D., Suggs, R., Suggs, R. J., et al. 2014, in Asteroids Comets Meteors 2014, eds. K. Muinonen, A. Penttilä, M. Granvik, et al., 365 [Google Scholar]
- Neukum, G., Ivanov, B. A., & Hartmann, W. K. 2001, Space Sci. Rev., 96, 55 [Google Scholar]
- Öpik, E. J. 1969, ARA&A, 7, 473 [Google Scholar]
- Ortiz, J. L., Sada, P. V., Bellot Rubio, L. R., et al. 2000, Nature, 405, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Aceituno, F. J., Quesada, J. A., et al. 2006, Icarus, 184, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., & Teukolsky, S. A. 1986, Numerical recipes. The art of scientific computing (Cambridge: University Press) [Google Scholar]
- Robinson, M. S., Brylow, S. M., Tschimmel, M., et al. 2010, Space Sci. Rev., 150, 81 [CrossRef] [Google Scholar]
- Robinson, M. S., Boyd, A. K., Denevi, B. W., et al. 2014, Lunar Planetary Sci. Conf., 2164 [Google Scholar]
- Robinson, M. S., Boyd, A. K., Denevi, B. W., et al. 2015, Icarus, 252, 229 [Google Scholar]
- Sheward, D., Avdellidou, C., Cook, A., et al. 2022, MNRAS, 514, 4320 [Google Scholar]
- Sheward, D., Delbo, M., Avdellidou, C., et al. 2023, MNRAS, 529, 3828 [Google Scholar]
- Shoemaker, E. M., & Wolfe, R. F. 1982, Satellites Jupiter, A83, 277 [Google Scholar]
- Suggs, R. M., Cooke, W. J., Suggs, R. J., Swift, W. R., & Hollon, N. 2008, Earth Moon Planets, 102, 293 [Google Scholar]
- Suggs, R. M., Moser, D. E., Cooke, W. J., & Suggs, R. J. 2014, Icarus, 238, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Swift, W. R., Moser, D. E., Suggs, R. M., & Cooke, W. J. 2011, Meteoroids The Smallest Solar System Bodies, 125 [Google Scholar]
- Topputo, F., Merisio, G., Franzese, V., et al. 2023, Icarus, 389, 115213 [NASA ADS] [CrossRef] [Google Scholar]
- Zuluaga, J. I., Tangmatitham, M., Cuartas-Restrepo, P., et al. 2020, MNRAS, 492, 1432 [Google Scholar]
Appendix A: Crater table
Summary of the detected craters with their linked LIFs events. Crater IDs beginning with ‘U’ are not linked to a known LIF.
Appendix B: Monte-Carlo parameters and results
Overview of the parameters used in the Monte Carlo and their sources.
 |
Fig. B.1. Results from each of the Monte Carlo simulations for each of the six selected crater scaling laws. The dotted green line represents the median value of the points where χ2≤10.7. Underlaid is the histogram of the number of points where χ2≤10.7. |
Appendix C: Unlinked craters
During the search for LIF-linked craters using PyNAPLE, several features were discovered that were unable to be linked to any known LIF. While searching for the resultant crater from the 2009-Nov-12 LIF, an approximately 4.2 m diameter crater was found at latitude, ϕ = 15.0210, longitude, λ = 76.1805. It was found that this crater could not be linked to the searched event, due to the crater absence from images taken after the epoch of the LIF, instead being formed some time between 2014-Jan-14, and 2018-Aug-15. The LIF database was checked for any events, confirmed or unconfirmed, which could coincide with this formation window, however no candidates with suitable proximity were found to exist.
Similarly, while searching for the resultant crater from the 2009-Dec-21 LIF, an approximately 5.8 m diameter crater was found at ϕ = 28.8236, λ=-35.125. The verification process found that this crater was absent from images taken after the LIF epoch, and therefore was formed some time between 2016-Apr-19 and 2018-May-07, when the first image of the crater was taken. The LIF database was again checked for possible formation events, however no candidates were found.
During the search for the 2019-Jan-21, two impact craters were located within the processed images. The verification process was unable to discount either of these craters as being unlinked, as both craters were present in each image after the event, and absent in images before. As these craters cannot have their sources distinguished, we elected to perform the analysis on both craters as though they are the formed impact crater. By rearranging the crater scaling law of Shoemaker & Wolfe, a value for the luminous efficiency, can be calculated for each of these two craters using the parameters of the flash, and talking an incidence angle of 45° for both impacts, we can compare the resultant η to that calculated by the Monte Carlo simulation. We find that C190121S28.3W067.1 produces η = 2.5 × 10−3, and C190121S28.2W067.2 produces η = 3.7 × 10−5. This would indicate that C190121S28.3W067.1 is most likely the resultant crater from the 2019-Jan-21 impact flash, and C190121S28.2W067.2 was produced by an unknown impact flash some time between the last image of the site without the crater, taken in 2014-Sept-13, and the first image taken with the crater in 2019-Jun-22. No candidate LIF for this crater has been identified within publicly available databases.
This lack of candidate LIFs for these craters is not unexpected, however, as the Moon is constantly bombarded with impactors, however typical Earth-based LIF observing sessions can only occur for approximately 5% of a given month, and will generally only observe on a portion of the Moon. It is therefore unsurprising that the majority of LIFs would go unobserved.
Appendix D: Crater scaling laws
For our tests, we selected the six crater scaling laws of Gault (1974) (taken in the form given in Horedt & Neukum (1984) equation 11), Dence et al. (1977) taken in the form given in Horedt & Neukum (1984) equation 2, Shoemaker & Wolfe (1982), taken in the form given in Horedt & Neukum (1984) equation 3, Öpik (1969), taken in the form given in Horedt & Neukum (1984) equations 7&8, Holsapple (1993) equation 18, and Melosh (1989), taken in the form given in Madiedo et al. (2014). These were chosen as they are the most commonly used scaling laws for lunar impact cratering. While these scaling laws all typically use some combination of the kinetic energy (KE), projectile velocity (V), projectile mass (M), projectile density (ρp), target density (ρt), impact angle (θ), and gravity (g), often they omit some of the parameters. Table D.1 gives a comparison of which parameters are used by each of the scaling laws.
Overview of the scaling law by their parameters.
These scaling laws are derived from laboratory impacts and explosive tests, where the crater diameter is measured after a controlled impact or detonation. The scaling laws are then derived though linear regression of the data. Consequently, while the scaling laws can be accurate for the crater sizes on which they were based, they are generally only valid over these ranges, and tend to deviate outside this range.
As the scaling laws of both Shoemaker & Wolfe and Dence do not factor in the impact angle, and would consequently overestimate D when θ≠ 90°, an additional scaling factor taken as the form given in Horedt & Neukum (1984), of
is implemented, where θ is the impact angle, measured from the horizontal.
Appendix E: Obtaining the luminous energy
The luminous energy, the amount of light released by the flash, is required for subsequent calculations. For the three craters which had been already been identified within literature, C130317N20.7W024.3 (Suggs et al. 2014; Robinson et al. 2014), C130911S17.2W020.4 (Madiedo et al. 2014), and C170927N08.0W076.5 (Sheward et al. 2022), the values for the luminous energy can taken as the published values from these works. While no crater had been previously identified for C180905N08.7E052.5, the luminous energy of the LIF has previously been calculated through aperture photometry, using a calibration star, in Avdellidou et al. (2021).
Similarly, the 2019-Jan-21 LIF, from which the search resulted in the discovery of C190121S28.3W067.1 and C190121S28.2W067.2, had been previously analysed within literature (Madiedo et al. 2019), and therefore the luminous energy could be obtained.
While the location and epoch of LIFs are made publicly available by the Meteoroid Environment Office, the images or analysis of LIFs are only available for some events. Consequently, values for the luminous energy for events C091113N17.3E043.7, C110511S16.3W047.1, and C140504S00.6W019.6 were unable to be obtained.
While the LIF image frames were not obtainable for event C110211N16.1W087.8, the peak V-band magnitude for the flash, mv = 8.1, was made available. From other multi-frame LIF observations, it was determined that an approximation of +1.5 magnitudes per frame would be appropriate to obtain a luminous efficiency of the same approximate order of magnitude as the correct value. Using Eq. E.1 & E.2, taking the value for V band, Δλ = 88 nm, an approximate value, Elum = 84900 J, was obtained.
The power released by the flash for each frame can be calculated with the equation
where Fr is the flux density of a reference star of magnitude, mr, where mf is the magnitude of the flash in the same photometric band, f is the isotropy of the flash, taken as f = 2 for a flash on the lunar surface, Δλ is the bandwidth of the observation, and D is the Earth-Moon distance at the epoch of the flash. The luminous energy can then simply be calculated:
where t is the frame period of the LIF observation.
All Tables
Summary of the detected craters with their linked LIFs events. Crater IDs beginning with ‘U’ are not linked to a known LIF.
All Figures
 |
Fig. 1. Ratio images for six of the located craters: (A)C110211N16.1W087.8 (4.3 m), (B)C130317N20.7W024.3 (17.6 m), (C)C130911S17.2W020.4 (30.2 m), (D)C170927N08.0W076.5 (23.8 m), (E)C190121S28.3W067.1 (3.5 m), and (F)C190121S28.2W067.2 (12.0 m). |
| In the text | |
 |
Fig. 2. Comparison of the predicted crater diameters from six scaling laws to two observed craters from the same parent source. The mass of the impactor is given as a range determined by the typically used value for η, 2 × 10−3 and 5 × 10−4. The bold lines is the value calculated using the group velocity of the Virginid meteoroid stream, and the narrow lines are 1σ errors. |
| In the text | |
 |
Fig. B.1. Results from each of the Monte Carlo simulations for each of the six selected crater scaling laws. The dotted green line represents the median value of the points where χ2≤10.7. Underlaid is the histogram of the number of points where χ2≤10.7. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.