EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) A32 Full HTML
Open Access

Table B.1.

List of reactions included in our chemical model.

Tag Reaction Rate coefficient (cm3 s−1, cm6 s−1, s−1) Ref.
H01H_01 H+ + e− → H + γ krec = CH ⋅ αH; 1
αH = F ⋅ a1 ⋅ 10−19ta2/(1.0 + a3ta4),
F = 1.14,  a1 = 4.309,  a2 = −0.6166,
a3 = 0.6703,  a4 = 0.5300,  t = T/104
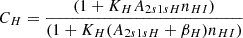C H = ( 1 + K H A 2 s 1 s H n HI ) ( 1 + K H ( A 2 s 1 s H + β H ) n HI ) $ C_H = {(1+K_HA_{2s1sH}n_{HI}) \over (1+K_H(A_{2s1sH} + {\beta}_{H})n_{HI})} $
βH = αH ⋅ (2πmekBTR/h2)3/2exp(−E2s/kTR)
KH ≡ λLyα3/(8πH(z)),  λLyα = 121.5682 nm
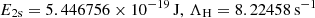E 2 s = 5.446756 × 10 − 19 J , Λ H = 8.22458 s − 1 $ E_\mathrm{{2s}} = 5.446756\times 10^{-19}\,{\mathrm{J}}, \, \Lambda_\mathrm{{H}} = 8.22458\,\mathrm{{s}}^{-1} $
H02H_02 H + γ → H+ + e− kion = CH ⋅ βH ⋅ exp(−E2s1s/kTM); 1
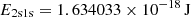E 2 s 1 s = 1.634033 × 10 − 18 J $ \phantom{k_{rec} = } E_{\mathrm{2s1s}} = 1.634033\times 10^{-18}\,\mathrm{J} $
H03H_03 H + e− → H− + γ dex[−17.845 + 0.762logT T ≤ 6000 K 2
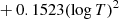+ 0.1523 ( log T ) 2 $ \phantom{ \mathrm{dex}[}+ 0.1523 (\log{T})^{2} $
− 0.03274 ( log T ) 3 ] $ \phantom{ \mathrm{dex}[}- 0.03274 (\log{T})^{3}] $
dex[−16.4199 + 0.1998(logT)2 T >  6000 K
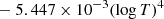− 5.447 × 10 − 3 ( log T ) 4 $ \phantom{ \mathrm{dex}[} -5.447 \times 10^{-3} (\log{T})^{4} $
+ 4.0415 × 10 − 5 ( log T ) 6 ] $ \phantom{ \mathrm{dex}[} + 4.0415 \times 10^{-5} (\log{T})^{6}] $
H04H_04 H− + γ → H + e− 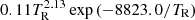0.11 T R 2.13 exp ( − 8823.0 / T R ) $ 0.11T_{\mathrm{R}}^{2.13}\exp\left(-8823.0/T_{\mathrm{R}}\right) $ 3
H05H_05 H− + H → H2 + e− 1.5 × 10−9 T <  300.0 3
4.0 × 10−9T−0.17 T ≥ 300.0
H06H_06 H− + H+ → H + H 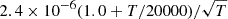2.4 × 10 − 6 ( 1.0 + T / 20000 ) / T $ 2.4\times 10^{-6}(1.0+T/20000)/\sqrt{T} $ 4
H07H_07 H + H+ → H2+ + γ dex[−19.38 − 1.523logT 5
+ 1.118 ( log T ) 2 − 0.1269 ( log T ) 3 ] $ \phantom{\mathrm{dex}[} + 1.118 (\log{T})^{2} - 0.1269 (\log{T})^{3}] $
H08H_08 H2+ + γ → H + H+ 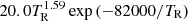20.0 T R 1.59 exp ( − 82000 / T R ) $ 20.0T_{\mathrm{R}}^{1.59}\exp\left(-82000/T_{\mathrm{R}}\right) $ v = 0 3
1.63 × 107exp(−32400.0/TR) LTE
H09H_09 H + H2+ → H2 + H+ 6.4 × 10−10 6
H10H_10 H2 + H+ → H2+ + H [ − 3.3232183 × 10−7 7
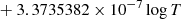+ 3.3735382 × 10 − 7 log T $ \phantom{[} + 3.3735382 \times 10^{-7} \log{T} $
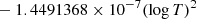− 1.4491368 × 10 − 7 ( log T ) 2 $ \phantom{[} - 1.4491368 \times 10^{-7} (\log{T})^2 $
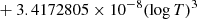+ 3.4172805 × 10 − 8 ( log T ) 3 $ \phantom{[} + 3.4172805 \times 10^{-8} (\log{T})^3 $
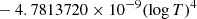− 4.7813720 × 10 − 9 ( log T ) 4 $ \phantom{[} - 4.7813720 \times 10^{-9} (\log{T})^4 $
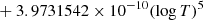+ 3.9731542 × 10 − 10 ( log T ) 5 $ \phantom{[} + 3.9731542 \times 10^{-10} (\log{T})^5 $
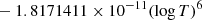− 1.8171411 × 10 − 11 ( log T ) 6 $ \phantom{[} - 1.8171411 \times 10^{-11} (\log{T})^6 $
+ 3.5311932 × 10 − 13 ( log T ) 7 ] $ \phantom{[} + 3.5311932 \times 10^{-13} (\log{T})^7 ] $
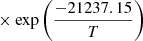× exp ( − 21237.15 T ) $ \phantom{[} \times \exp \left(\frac{-21237.15}{T} \right) $
H11H_11 H+ + H− → H2+ + e− 6.9 × 10−9T−0.35 T ≤ 8000 K 8
9.6 × 10−7T−0.90 T >  8000 K
H12H_12 H2+ + e− → H + H 4.2278 × 10−14 − 2.3088 × 10−17T + 7.3428 × 10−21T2
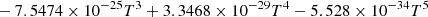− 7.5474 × 10 − 25 T 3 + 3.3468 × 10 − 29 T 4 − 5.528 × 10 − 34 T 5 $ \phantom{[} - 7.5474\times 10^{-25} T^3 + 3.3468\times 10^{-29} T^4 - 5.528\times 10^{-34} T^5 $ 9
H13H_13 H2+ + H2 → H3+ + H 2.0 × 10−9 10
H14H_14 H2 + γ → H2+ + e− 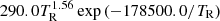290.0 T R 1.56 exp ( − 178500.0 / T R ) $ 290.0T_{\mathrm{R}}^{1.56}\exp\left(-178500.0/T_{\mathrm{R}}\right ) $ 3
H15H_15 H2 + γ → H + H 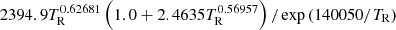2394.9 T R 0.62681 ( 1.0 + 2.4635 T R 0.56957 ) / exp ( 140050 / T R ) $ 2394.9T_{\mathrm{R}}^{0.62681}\left(1.0+2.4635T_{\mathrm{R}}^{0.56957}\right)/\exp\left(140050/T_{\mathrm{R}}\right) $ TR <  15000 11
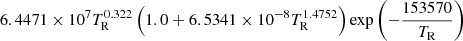6.4471 × 10 7 T R 0.322 ( 1.0 + 6.5341 × 10 − 8 T R 1.4752 ) exp ( − 153570 T R ) $ 6.4471\times 10^7 T_{\mathrm{R}}^{0.322}\left(1.0+6.5341\times 10^{-8}T_{\mathrm{R}}^{1.4752}\right)\exp\left(-\frac{153570}{T_{\mathrm{R}}}\right) $ TR ≥ 15000
H16H_16 H3+ + H → H2+ + H2 7.7 × 10−9exp(−17560.0/TM) 3
H17H_17 H3+ + e− → H2 + H 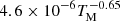4.6 × 10 − 6 T M − 0.65 $ 4.6\times 10^{-6}T_{\mathrm{M}}^{-0.65} $ 3
H18H_18 H2 + H+ → H3+ + γ 10−16 3
H19H_19 H2 + H → H + H + H 6.67 × 10 − 12 T 0.5 exp [ − ( 1 + 63593 T ) ] $ 6.67 \times 10^{-12} T^{0.5} \exp \left[-(1+ \frac{63593}{T}) \right] $ v=0 12
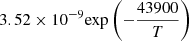3.52 × 10 − 9 exp ( − 43900 T ) $ 3.52 \times 10^{-9} {\exp \left(-\frac{43900}{T}\right)} $ LTE 13
H20H_20 H + e− → H+ + e− + e− exp[−3.271396786 × 101 14
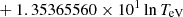+ 1.35365560 × 10 1 ln T eV $ \phantom{\exp[} + 1.35365560 \times 10^{1} \ln T_{\mathrm{eV}} $
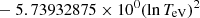− 5.73932875 × 10 0 ( ln T eV ) 2 $ \phantom{\exp[} - 5.73932875 \times 10^{0} (\ln T_{\mathrm{eV}})^{2} $
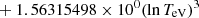+ 1.56315498 × 10 0 ( ln T eV ) 3 $ \phantom{\exp[} + 1.56315498 \times 10^{0} (\ln T_{\mathrm{eV}})^{3} $
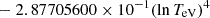− 2.87705600 × 10 − 1 ( ln T eV ) 4 $ \phantom{\exp[} - 2.87705600 \times 10^{-1} (\ln T_{\mathrm{eV}})^{4} $
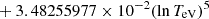+ 3.48255977 × 10 − 2 ( ln T eV ) 5 $ \phantom{\exp[} + 3.48255977 \times 10^{-2} (\ln T_{\mathrm{eV}})^{5} $
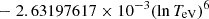− 2.63197617 × 10 − 3 ( ln T eV ) 6 $ \phantom{\exp[} - 2.63197617 \times 10^{-3} (\ln T_{\mathrm{eV}})^{6} $
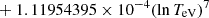+ 1.11954395 × 10 − 4 ( ln T eV ) 7 $ \phantom{\exp[} + 1.11954395 \times 10^{-4} (\ln T_{\mathrm{eV}})^{7} $
− 2.03914985 × 10 − 6 ( ln T eV ) 8 ] $ \phantom{\exp[} - 2.03914985 \times 10^{-6} (\ln T_{\mathrm{eV}})^{8}] $
H21H_21 H3+ + γ → H2 + H+ 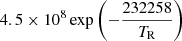4.5 × 10 8 exp ( − 232258 T R ) $ 4.5\times 10^{8}\exp\left(-\frac{232258}{T_{\mathrm{R}}}\right) $ 15
H22H_22 H3+ + e− → 3 H the same as for blueH_17
H23H_23 H + e− → H+ + 2e− 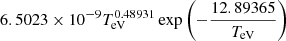6.5023 × 10 − 9 T eV 0.48931 exp ( − 12.89365 T eV ) $ 6.5023\times 10^{-9}T_{\mathrm{eV}}^{0.48931}\exp\left(-\frac{12.89365}{T_{\mathrm{eV}}}\right) $ 16
H24H_24 H+ + H + H → H+ + H2 1.145 × 10−29T−1.12 17
H25H_25 H + H + H → H2 + H 1.14 × 10−31T−0.38 T <  300 K 18
3.9 × 10−30T−1 T ≥ 300 K
H26H_26 H2+ + γ → 2H+ + e− 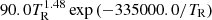90.0 T R 1.48 exp ( − 335000.0 / T R ) $ 90.0 T_{\mathrm{R}}^{1.48}\exp\left(-335000.0/T_{\mathrm{R}}\right) $ 3
H27H_27 H2 + e− → H− + H 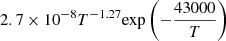2.7 × 10 − 8 T − 1.27 exp ( − 43000 T ) $ 2.7 \times 10^{-8} T^{-1.27} {\exp \left(-\frac{43000}{T}\right)} $ 19
H28H_28 H2 + e− → H + H + e− 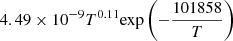4.49 × 10 − 9 T 0.11 exp ( − 101858 T ) $ 4.49 \times 10^{-9} T^{0.11} {\exp \left(-\frac{101858}{T}\right)} $ v = 0 20
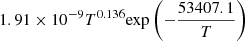1.91 × 10 − 9 T 0.136 exp ( − 53407.1 T ) $ 1.91 \times 10^{-9} T^{0.136} {\exp \left(-\frac{53407.1}{T}\right)} $ LTE 20
H29H_29 H2 + H2 → H2 + H + H 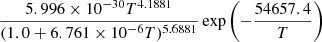5.996 × 10 − 30 T 4.1881 ( 1.0 + 6.761 × 10 − 6 T ) 5.6881 exp ( − 54657.4 T ) $ \frac{5.996 \times 10^{-30} T^{4.1881}}{(1.0 + 6.761 \times 10^{-6} T)^{5.6881}} \exp \left(-\frac{54657.4}{T} \right) $ v = 0 21
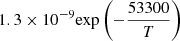1.3 × 10 − 9 exp ( − 53300 T ) $ 1.3 \times 10^{-9} {\exp \left(-\frac{53300}{T}\right)} $ LTE 22
H30H_30 H2 + He → H + H + He dex [ − 27.029 + 3.801 log T − 29487 T ] $ \mathrm{dex} \left[ -27.029 + 3.801 \log{T} - \frac{29487}{T} \right] $ v = 0 23
dex [ − 2.729 − 1.75 log T − 23474 T ] $ \mathrm{dex} \left[ -2.729 -1.75 \log{T} - \frac{23474}{T} \right] $ LTE 23
H31H_31 H− + e− → H + e− + e− exp[−1.801849334 × 101 14
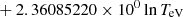+ 2.36085220 × 10 0 ln T eV $ \phantom{\exp [} + 2.36085220 \times 10^{0} \ln T_{\mathrm{eV}} $
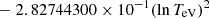− 2.82744300 × 10 − 1 ( ln T eV ) 2 $ \phantom{\exp [} - 2.82744300 \times 10^{-1} (\ln T_{\mathrm{eV}})^{2} $
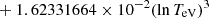+ 1.62331664 × 10 − 2 ( ln T eV ) 3 $ \phantom{\exp [} + 1.62331664\times 10^{-2} (\ln T_{\mathrm{eV}})^{3} $
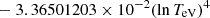− 3.36501203 × 10 − 2 ( ln T eV ) 4 $ \phantom{\exp [} - 3.36501203 \times 10^{-2} (\ln T_{\mathrm{eV}})^{4} $
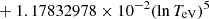+ 1.17832978 × 10 − 2 ( ln T eV ) 5 $ \phantom{\exp [} + 1.17832978\times 10^{-2} (\ln T_{\mathrm{eV}})^{5} $
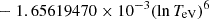− 1.65619470 × 10 − 3 ( ln T eV ) 6 $ \phantom{\exp [} - 1.65619470\times 10^{-3} (\ln T_{\mathrm{eV}})^{6} $
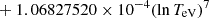+ 1.06827520 × 10 − 4 ( ln T eV ) 7 $ \phantom{\exp [} + 1.06827520\times 10^{-4} (\ln T_{\mathrm{eV}})^{7} $
− 2.63128581 × 10 − 6 ( ln T eV ) 8 ] $ \phantom{\exp [} - 2.63128581\times 10^{-6} (\ln T_{\mathrm{eV}})^{8} ] $
H32H_32 H− + H → H + H + e− 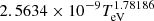2.5634 × 10 − 9 T eV 1.78186 $ 2.5634 \times 10^{-9} T_{\mathrm{eV}}^{1.78186} $ TeV ≤ 0.1 eV 14
exp[−2.0372609 × 101 TeV >  0.1 eV
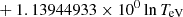+ 1.13944933 × 10 0 ln T eV $ \phantom{\exp [} +1.13944933 \times 10^{0} \ln T_{\mathrm{eV}} $
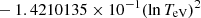− 1.4210135 × 10 − 1 ( ln T eV ) 2 $ \phantom{\exp [} -1.4210135 \times 10^{-1} (\ln T_{\mathrm{eV}})^{2} $
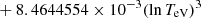+ 8.4644554 × 10 − 3 ( ln T eV ) 3 $ \phantom{\exp [} +8.4644554 \times 10^{-3} (\ln T_{\mathrm{eV}})^{3} $
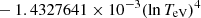− 1.4327641 × 10 − 3 ( ln T eV ) 4 $ \phantom{\exp [} -1.4327641 \times 10^{-3} (\ln T_{\mathrm{eV}})^{4} $
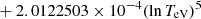+ 2.0122503 × 10 − 4 ( ln T eV ) 5 $ \phantom{\exp [} +2.0122503 \times 10^{-4} (\ln T_{\mathrm{eV}})^{5} $
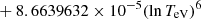+ 8.6639632 × 10 − 5 ( ln T eV ) 6 $ \phantom{\exp [} +8.6639632 \times 10^{-5} (\ln T_{\mathrm{eV}})^{6} $
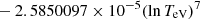− 2.5850097 × 10 − 5 ( ln T eV ) 7 $ \phantom{\exp [} -2.5850097 \times 10^{-5} (\ln T_{\mathrm{eV}})^{7} $
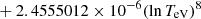+ 2.4555012 × 10 − 6 ( ln T eV ) 8 $ \phantom{\exp [} +2.4555012\times 10^{-6} (\ln T_{\mathrm{eV}})^{8} $
− 8.0683825 × 10 − 8 ( ln T eV ) 9 ] $ \phantom{\exp [} -8.0683825\times 10^{-8} (\ln T_{\mathrm{eV}})^{9}] $
H33H_33 H− + H2+ → H2 + H 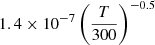1.4 × 10 − 7 ( T 300 ) − 0.5 $ 1.4 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 24
H34H_34 H− + H2+ → H + H + H 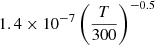1.4 × 10 − 7 ( T 300 ) − 0.5 $ 1.4 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 24
H35H_35 H + H + H2 → H2 + H2 0.143 × 10−31T−0.38 T <  300 K 18
0.486 × 10−30T−1 T ≥ 300 K 18
H36H_36 H + H + He → H2 + He 6.9 × 10−32T−0.4 25
H37H_37 H2+ + H → 2H + H+ exp(−32.912+6.9498×10−5T−3.3248×104/T 9
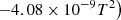− 4.08 × 10 − 9 T 2 ) $ \phantom{\exp(}\left. - 4.08\times 10^{-9}T^2\right) $
H38H_38 H2 + H+ → 2H + H+ exp(−33.404+2.0148×10−4T−5.2674×104/T 9
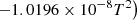− 1.0196 × 10 − 8 T 2 ) $ \phantom{\exp(}\left. - 1.0196\times 10^{-8}T^2\right) $
H39H_39 H3+ + H2 → H3+ + 2H 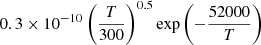0.3 × 10 − 10 ( T 300 ) 0.5 exp ( − 52000 T ) $ 0.3\times 10^{-10}\left(\frac{T}{300}\right)^{0.5}\exp\left(-\frac{52000}{T}\right) $ 26
H40H_40 H3+ + e− → H2+ + H + e− 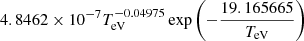4.8462 × 10 − 7 T eV − 0.04975 exp ( − 19.165665 T eV ) $ 4.8462\times 10^{-7}T_{\mathrm{eV}}^{-0.04975}\exp\left(-\frac{19.165665}{T_{\mathrm{eV}}}\right) $ 16
H41H_41 H2+ + e− → H+ + H + e− 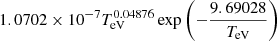1.0702 × 10 − 7 T eV 0.04876 exp ( − 9.69028 T eV ) $ 1.0702\times 10^{-7}T_{\mathrm{eV}}^{0.04876}\exp\left(-\frac{9.69028}{T_{\mathrm{eV}}}\right) $ 16
H42H_42 H + H → H + H+ + e− 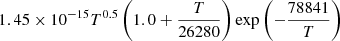1.45 × 10 − 15 T 0.5 ( 1.0 + T 26280 ) exp ( − 78841 T ) $ 1.45\times 10^{-15}T^{0.5}\left(1.0+\frac{T}{26280}\right)\exp\left(-\frac{78841}{T}\right) $ 27
H43H_43 H+ + H + H → H3+ + H 1.238 × 10−29T−1.046 17
H44H_44 H3+ + H− → H2 + H2 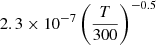2.3 × 10 − 7 ( T 300 ) − 0.5 $ 2.3\times 10^{-7}\left(\frac{T}{300}\right)^{-0.5} $ 28
He01He_01 He+ + e− → He + γ krec = CHeI ⋅ αHeI; 1
α HeI = q [ T M T 2 ( 1 + T M T 2 ) 1 − p ( 1 + T M T 1 ) 1 + p ] − 1 m 3 s − 1 , $ \phantom{k_{1} = } \alpha_{\mathrm{HeI}} =q\left[\sqrt{T_{\mathrm{M}}\over T_2}\left(1+\sqrt{T_{\mathrm{M}}\over T_2}\right)^{1-p} \left(1+\sqrt{T_{\mathrm{M}}\over T_1}\right)^{1+p}\right]^{-1}\! \mathrm{m^{3}s^{-1}}, $
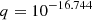q = 10 − 16.744 $ \phantom{k_{1} = } q=10^{-16.744} $, p = 0.711, T1 = 105.114 K, T2 = 3 K.
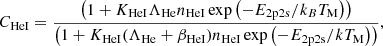C HeI = ( 1 + K HeI Λ He n HeI exp ( − E 2 p 2 s / k B T M ) ) ( 1 + K HeI ( Λ He + β HeI ) n HeI exp ( − E 2 p 2 s / k T M ) ) , $ \phantom{k_{1} = } C_{\mathrm{HeI}} = {\left(1 + K_{\mathrm{HeI}} \Lambda_{\mathrm{He}} n_{\mathrm{HeI}} \exp\left(-E_{\mathrm{2p2s}}/k_BT_{\mathrm{M}}\right)\right) \over \left(1+K_{\mathrm{HeI}} (\Lambda_{\mathrm{He}} + \beta_{\mathrm{HeI}}) n_{\mathrm{HeI}} \exp\left(-E_{\mathrm{2p2s}}/kT_{\mathrm{M}}\right)\right)}, $
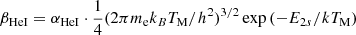β HeI = α HeI · 1 4 ( 2 π m e k B T M / h 2 ) 3 / 2 exp ( − E 2 s / k T M ) $ \phantom{k_{1} = } \beta_{\mathrm{HeI}} = \alpha_{\mathrm{HeI}}\cdot \frac14(2\pi m_{\mathrm{e}} k_B T_{\mathrm{M}}/h^2)^{3/2} \exp\left(-E_{2s}/kT_{\mathrm{M}}\right) $
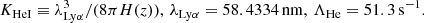K HeI ≡ λ Ly α 3 / ( 8 π H ( z ) ) , λ Ly α = 58.4334 nm , Λ He = 51.3 s − 1 . $ \phantom{k_{1} = } K_{\mathrm{HeI}} \equiv\lambda_{\mathrm{Ly\alpha}}^3/(8\pi H(z)),\, \lambda_{\mathrm{Ly\alpha}} = 58.4334\,\mathrm{nm},\, \Lambda_{\mathrm{He}} = 51.3\,\mathrm{s}^{-1}. $
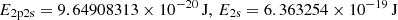E 2 p 2 s = 9.64908313 × 10 − 20 J , E 2 s = 6.363254 × 10 − 19 J $ \phantom{k_{1} = } E_{\mathrm{2p2s}} = 9.64908313\times 10^{-20}\,\mathrm{J},\, E_{\mathrm{2s}} = 6.363254\times 10^{-19}\,\mathrm{J} $
He02He_02 He + γ → He+ + e− kion = CHeI ⋅ βHeIexp(−E2s1s/kBTM); 1
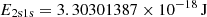E 2 s 1 s = 3.30301387 × 10 − 18 J $ \phantom{k_{1} = } E_{\mathrm{2s1s}} = 3.30301387\times 10^{-18}\,\mathrm{J} $
He03He_03 He + H+ → HeH+ + γ 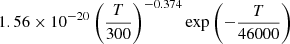1.56 × 10 − 20 ( T 300 ) − 0.374 exp ( − T 46000 ) $ 1.56\times10^{-20} \left(\frac{T}{300}\right)^{-0.374}\exp\left(-\frac{T}{46000}\right) $ 29
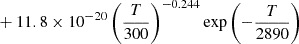+ 11.8 × 10 − 20 ( T 300 ) − 0.244 exp ( − T 2890 ) $ \phantom{ = } + 11.8\times10^{-20}\left(\frac{T}{300}\right)^{-0.244}\exp\left(-\frac{T}{2890}\right) $
He04He_04 HeH+ + H → He + H2+ 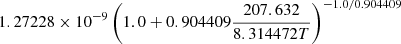1.27228 × 10 − 9 ( 1.0 + 0.904409 207.632 8.314472 T ) − 1.0 / 0.904409 $ 1.27228\times 10^{-9}\left(1.0+0.904409\frac{207.632}{8.314472T}\right)^{-1.0/0.904409} $ 30
He05He_05 HeH+ + γ → He + H+ 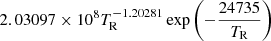2.03097 × 10 8 T R − 1.20281 exp ( − 24735 T R ) $ 2.03097\times 10^8T_{\mathrm{R}}^{-1.20281}\exp\left(-\frac{24735}{T_{\mathrm{R}}}\right) $ 31
He06He_06 He+ + +e− → He+ + γ 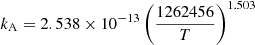k A = 2.538 × 10 − 13 ( 1262456 T ) 1.503 $ k_{\mathrm{A}} = 2.538 \times 10^{-13} \left(\frac{1262456}{T}\right)^{1.503} $ Case A 32
× [ 1.0 + ( 2418500 T ) 0.470 ] − 1.923 $ \phantom{k_{\mathrm{B}} = } \times [1.0+ \left(\frac{2418500}{T}\right)^{0.470}]^{-1.923} $
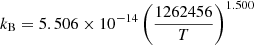k B = 5.506 × 10 − 14 ( 1262456 T ) 1.500 $ k_{\mathrm{B}} = 5.506 \times 10^{-14} \left(\frac{1262456}{T}\right)^{1.500} $ Case B 32
× [ 1.0 + ( 460752 T ) 0.407 ] − 2.242 $ \phantom{k_{\mathrm{B}} = } \times \left[1.0+ \left(\frac{460752}{T}\right)^{0.407}\right]^{-2.242} $
He07He_07 He+ + γ → He+ + +e− 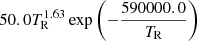50.0 T R 1.63 exp ( − 590000.0 T R ) $ 50.0T_{\mathrm{R}}^{1.63}\exp\left(-\frac{590000.0}{T_{\mathrm{R}}}\right) $ 3
He08He_08 He + H+ → He+ + H 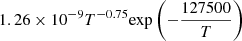1.26 × 10 − 9 T − 0.75 exp ( − 127500 T ) $ 1.26 \times 10^{-9} T^{-0.75} {\exp \left(-\frac{127500}{T}\right)} $ T ≤ 10000 K 33
4.0 × 10−37T4.74 T >  10000 K
He09He_09 He+ + H → He + H+ 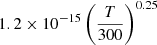1.2 × 10 − 15 ( T 300 ) 0.25 $ 1.2 \times 10^{-15} \left(\frac{T}{300}\right)^{0.25} $ 34
He10He_10 He + H2+ → HeH+ + H 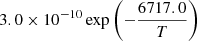3.0 × 10 − 10 exp ( − 6717.0 T ) $ 3.0\times 10^{-10}\exp\left(-\frac{6717.0}{T}\right) $ 35
He11He_11 He+ + H → HeH+ + γ 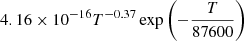4.16 × 10 − 16 T − 0.37 exp ( − T 87600 ) $ 4.16\times 10^{-16}T^{-0.37}\exp\left(-\frac{T}{87600}\right) $ 59
He12He_12 HeH+ + e− → He + H 3.0 × 10−8T−0.5 28
He13He_13 HeH+ + H2 → H3+ + He 1.80 × 10−9 28
He14He_14 HeH+ + γ → He+ + H 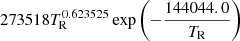273518 T R 0.623525 exp ( − 144044.0 T R ) $ 273518T_{\mathrm{R}}^{0.623525}\exp\left(-\frac{144044.0}{T_{\mathrm{R}}}\right) $ 31
He15He_15 He + e− → He+ + 2e− exp[−4.409864886 × 101 14
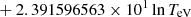+ 2.391596563 × 10 1 ln T eV $ \phantom{\exp[} + 2.391596563 \times 10^{1} \ln T_{\mathrm{eV}} $
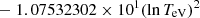− 1.07532302 × 10 1 ( ln T eV ) 2 $ \phantom{\exp[} - 1.07532302 \times 10^{1} (\ln T_{\mathrm{eV}})^{2} $
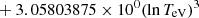+ 3.05803875 × 10 0 ( ln T eV ) 3 $ \phantom{\exp[} +3.05803875 \times 10^{0} (\ln T_{\mathrm{eV}})^{3} $
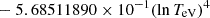− 5.68511890 × 10 − 1 ( ln T eV ) 4 $ \phantom{\exp[} - 5.68511890 \times 10^{-1} (\ln T_{\mathrm{eV}})^{4} $
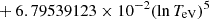+ 6.79539123 × 10 − 2 ( ln T eV ) 5 $ \phantom{\exp[} +6.79539123 \times 10^{-2} (\ln T_{\mathrm{eV}})^{5} $
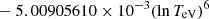− 5.00905610 × 10 − 3 ( ln T eV ) 6 $ \phantom{\exp[} -5.00905610 \times 10^{-3} (\ln T_{\mathrm{eV}})^{6} $
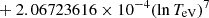+ 2.06723616 × 10 − 4 ( ln T eV ) 7 $ \phantom{\exp[} + 2.06723616\times 10^{-4} (\ln T_{\mathrm{eV}})^{7} $
− 3.64916141 × 10 − 6 ( ln T eV ) 8 ] $ \phantom{\exp[} - 3.64916141 \times 10^{-6} (\ln T_{\mathrm{eV}})^{8}] $
He16He_16 He+ + e− → He+ + +2e− exp[−6.87104099 × 101 14
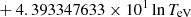+ 4.393347633 × 10 1 ln T eV $ \phantom{\exp[} + 4.393347633 \times 10^{1} \ln T_{\mathrm{eV}} $
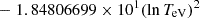− 1.84806699 × 10 1 ( ln T eV ) 2 $ \phantom{\exp[} - 1.84806699 \times 10^{1} (\ln T_{\mathrm{eV}})^{2} $
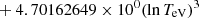+ 4.70162649 × 10 0 ( ln T eV ) 3 $ \phantom{\exp[} + 4.70162649 \times 10^{0} (\ln T_{\mathrm{eV}})^{3} $
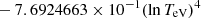− 7.6924663 × 10 − 1 ( ln T eV ) 4 $ \phantom{\exp[} - 7.6924663 \times 10^{-1} (\ln T_{\mathrm{eV}})^{4} $
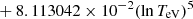+ 8.113042 × 10 − 2 ( ln T eV ) 5 $ \phantom{\exp[} + 8.113042 \times 10^{-2} (\ln T_{\mathrm{eV}})^{5} $
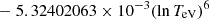− 5.32402063 × 10 − 3 ( ln T eV ) 6 $ \phantom{\exp[} - 5.32402063 \times 10^{-3} (\ln T_{\mathrm{eV}})^{6} $
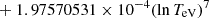+ 1.97570531 × 10 − 4 ( ln T eV ) 7 $ \phantom{\exp[} + 1.97570531\times 10^{-4} (\ln T_{\mathrm{eV}})^{7} $
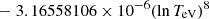− 3.16558106 × 10 − 6 ( ln T eV ) 8 $ \phantom{\exp[} - 3.16558106\times 10^{-6} (\ln T_{\mathrm{eV}})^{8} $
He17He_17 He+ + H− → He + H 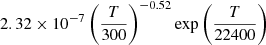2.32 × 10 − 7 ( T 300 ) − 0.52 exp ( T 22400 ) $ 2.32 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.52} {\exp \left(\frac{T}{22400}\right)} $ 36
He18He_18 He + H+ + γ → HeH+ + 2γ 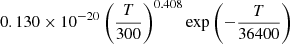0.130 × 10 − 20 ( T 300 ) 0.408 exp ( − T 36400 ) $ 0.130\times10^{-20} \left(\frac{T}{300}\right)^{0.408}\exp\left(-\frac{T}{36400}\right) $ 35
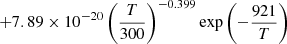+ 7.89 × 10 − 20 ( T 300 ) − 0.399 exp ( − 921 T ) $ + 7.89\times10^{-20}\left(\frac{T}{300}\right)^{-0.399}\exp\left(-\frac{921}{T}\right) $
He19He_19 H2 + He+ → He + H + H+ 10−13 ⋅ (−0.4732142857+0.0369047619⋅T T <  78 K 37
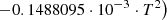− 0.1488095 · 10 − 3 · T 2 ) $ \phantom{10^{-13}\cdot(} \left.-0.1488095\cdot 10^{-3}\cdot T^2\right) $
10−13 ⋅ (1.623809524−0.1587301587⋅10−2⋅T) 78 K ≤ T <  330 K
10−13 ⋅ (0.111111524+0.1555555413⋅10−2⋅T T ≥ 330 K
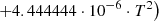+ 4.444444 · 10 − 6 · T 2 ) $ \phantom{10^{-13}\cdot(} \left.+4.444444\cdot 10^{-6}\cdot T^2\right) $
He20He_20 H2 + He+ → H2+ + He 7.2 × 10−15 38
He21He_21 He + H− → He + H + e− 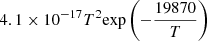4.1 × 10 − 17 T 2 exp ( − 19870 T ) $ 4.1 \times 10^{-17} T^{2} {\exp \left(-\frac{19870}{T}\right)} $ 39
He22He_22 He+ + H2 → He+ + 2H 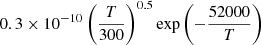0.3 × 10 − 10 ( T 300 ) 0.5 exp ( − 52000 T ) $ 0.3\times 10^{-10}\left(\frac{T}{300}\right)^{0.5}\exp\left(-\frac{52000}{T}\right) $ 26
D01D_01 D+ + e− → D + γ the same as for blueH_01
D02D_02 D + γ → D+ + e− the same as for blueH_02
D03D_03 D + H+ → H + D+ 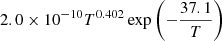2.0 × 10 − 10 T 0.402 exp ( − 37.1 T ) $ 2.0 \times 10^{-10} T^{0.402} \exp \left(-\frac{37.1}{T} \right) $ T ≤ 2 ⋅ 105 K 40
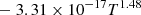− 3.31 × 10 − 17 T 1.48 $ \phantom{=} - 3.31 \times 10^{-17} T^{1.48} $
3.44 × 10−10T0.35 T >  2 ⋅ 105 K
D04D_04 H + D+ → D + H+ 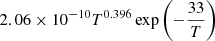2.06 × 10 − 10 T 0.396 exp ( − 33 T ) $ 2.06 \times 10^{-10} T^{0.396} \exp \left(-\frac{33}{T} \right) $ 40
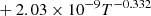+ 2.03 × 10 − 9 T − 0.332 $ \phantom{ =}+ 2.03 \times 10^{-9} T^{-0.332} $
D05D_05 H2 + D+ → HD + H+ [0.417+0.846logT−0.137(logT)2] × 10−9 41
D06D_06 HD + H+ → H2 + D+ 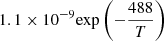1.1 × 10 − 9 exp ( − 488 T ) $ 1.1 \times 10^{-9} {\exp \left(-\frac{488}{T}\right)} $ 41
D07D_07 H + D → HD + γ 10−25[2.80202 − 6.63697lnT T ≤ 200 K 42
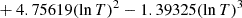+ 4.75619 ( ln T ) 2 − 1.39325 ( ln T ) 3 $ \phantom{10^{-25} [} + 4.75619 (\ln T)^{2} -1.39325 (\ln T)^{3} $
+ 0.178259 ( ln T ) 4 − 0.00817097 ( ln T ) 5 ] $ \phantom{10^{-25} [} + 0.178259 (\ln T)^{4} - 0.00817097 (\ln T)^{5} ] $
10−25exp[507.207 − 370.889lnT T >  200 K
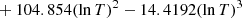+ 104.854 ( ln T ) 2 − 14.4192 ( ln T ) 3 $ \phantom{10^{-25} \exp } + 104.854 (\ln T)^2 - 14.4192 (\ln T)^{3} $
+ 0.971469 ( ln T ) 4 − 0.0258076 ( ln T ) 5 ] $ \phantom{10^{-25} \exp } + 0.971469 (\ln T)^{4} - 0.0258076 (\ln T)^{5} ] $
D08D_08 H2 + D → HD + H dex[−56.4737+5.88886logT T ≤ 2000 K 43
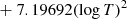+ 7.19692 ( log T ) 2 $ \phantom{\mathrm{dex}[} + 7.19692 (\log{T})^{2} $
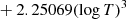+ 2.25069 ( log T ) 3 $ \phantom{\mathrm{dex}[} + 2.25069 (\log{T})^{3} $
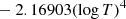− 2.16903 ( log T ) 4 $ \phantom{\mathrm{dex}[} - 2.16903 (\log{T})^{4} $
+ 0.317887 ( log T ) 5 ] $ \left. \phantom{\mathrm{dex}[} + 0.317887 (\log{T})^{5} \right] $
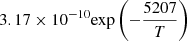3.17 × 10 − 10 exp ( − 5207 T ) $ 3.17 \times 10^{-10} {\exp \left(-\frac{5207}{T}\right)} $ T >  2000 K
D09D_09 HD+ + H → HD + H+ the same as for blueH_09
D10D_10 HD + H → H2 + D 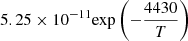5.25 × 10 − 11 exp ( − 4430 T ) $ 5.25 \times 10^{-11} {\exp \left(-\frac{4430}{T}\right)} $ T ≤ 200 K 44
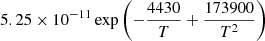5.25 × 10 − 11 exp ( − 4430 T + 173900 T 2 ) $ \phantom{=} 5.25 \times 10^{-11} \exp \left(-\frac{4430}{T} + \frac{173900}{T^{2}}\right) $ T >  200 K
D11D_11 D + H+ → HD+ + γ 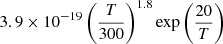3.9 × 10 − 19 ( T 300 ) 1.8 exp ( 20 T ) $ 3.9 \times 10^{-19} \left(\frac{T}{300}\right)^{1.8} {\exp \left(\frac{20}{T}\right)} $ 45
D12D_12 H + D+ → HD+ + γ 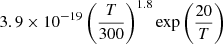3.9 × 10 − 19 ( T 300 ) 1.8 exp ( 20 T ) $ 3.9 \times 10^{-19} \left(\frac{T}{300}\right)^{1.8} {\exp \left(\frac{20}{T}\right)} $ 45
D13D_13 HD+ + γ → H + D+ the same as for blueH_08
D14D_14 HD+ + e− → H + D 7.2 × 10−8T−0.5 46
D15D_15 HD+ + H2 → H2D+ + H the same as for blueH_13
D16D_16 D + H3+ → H2D+ + H 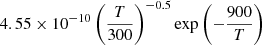4.55 × 10 − 10 ( T 300 ) − 0.5 exp ( − 900 T ) $ 4.55\times 10^{-10} \left(\frac{T}{300}\right)^{-0.5} {\exp \left(-\frac{900}{T}\right)} $ 28
D17D_17 H2D+ + e− → 2H + D 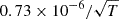0.73 × 10 − 6 / T $ 0.73\times 10^{-6}/\sqrt{T} $ 47
D18D_18 H2D+ + e− → H2 + D 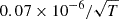0.07 × 10 − 6 / T $ 0.07\times 10^{-6}/\sqrt{T} $ 47
D19D_19 H2D+ + e− → HD + H 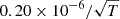0.20 × 10 − 6 / T $ 0.20\times 10^{-6}/\sqrt{T} $ 47
D20D_20 H2D+ + H → H3+ + D 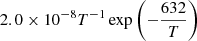2.0 × 10 − 8 T − 1 exp ( − 632 T ) $ 2.0\times 10^{-8}T^{-1}\exp\left(-\frac{632}{T}\right) $ 58
D21D_21 HD+ + H → H2+ + D 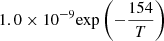1.0 × 10 − 9 exp ( − 154 T ) $ 1.0 \times 10^{-9} {\exp \left(-\frac{154}{T}\right)} $ 48
D22D_22 D + H− → HD + e− 7.5 × 10−10 T <  300 49
2.0 × 10−9T−0.17 T ≥ 300 49
D23D_23 H + D− → HD + e− 7.5 × 10−10 T <  300 49
2.0 × 10−9T−0.17 T ≥ 300 49
D24D_24 HD + H+ → H2+ + D 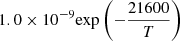1.0 × 10 − 9 exp ( − 21600 T ) $ 1.0 \times 10^{-9} {\exp \left(-\frac{21600}{T}\right)} $ 50
D25D_25 HD+ + H → H2 + D+ 1.0 × 10−9 50
D26D_26 HD+ + γ → H+ + D the same as for blueH_08
D27D_27 H2+ + D → HD+ + H 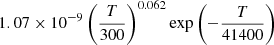1.07 × 10 − 9 ( T 300 ) 0.062 exp ( − T 41400 ) $ 1.07 \times 10^{-9} \left(\frac{T}{300}\right)^{0.062} {\exp \left(-\frac{T}{41400}\right)} $ 51
D28D_28 D + e− → D− + γ dex[−17.845 + 0.762logT T ≤ 6000 K 2
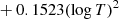+ 0.1523 ( log T ) 2 $ \phantom{ \mathrm{dex}[} + 0.1523 (\log{T})^{2} $
− 0.03274 ( log T ) 3 ] $ \phantom{ \mathrm{dex}[} - 0.03274 (\log{T})^{3}] $
dex[−16.4199 + 0.1998(logT)2 T >  6000 K
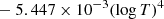− 5.447 × 10 − 3 ( log T ) 4 $ \phantom{ \mathrm{dex}[} -5.447 \times 10^{-3} (\log{T})^{4} $
+ 4.0415 × 10 − 5 ( log T ) 6 ] $ \phantom{ \mathrm{dex}[} + 4.0415 \times 10^{-5} (\log{T})^{6}] $
D29D_29 H + D− → D + H− 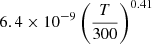6.4 × 10 − 9 ( T 300 ) 0.41 $ 6.4 \times 10^{-9} \left(\frac{T}{300}\right)^{0.41} $ 48
D30D_30 D + H− → H + D− 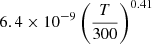6.4 × 10 − 9 ( T 300 ) 0.41 $ 6.4 \times 10^{-9} \left(\frac{T}{300}\right)^{0.41} $ 48
D31D_31 D + D− → D2 + e− the same as for blueH_05
D32D_32 H+ + D− → HD+ + e− 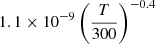1.1 × 10 − 9 ( T 300 ) − 0.4 $ 1.1 \times 10^{-9} \left(\frac{T}{300}\right)^{-0.4} $ 45
D33D_33 D+ + H− → HD+ + e− 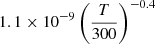1.1 × 10 − 9 ( T 300 ) − 0.4 $ 1.1 \times 10^{-9} \left(\frac{T}{300}\right)^{-0.4} $ 45
D34D_34 D+ + D− → D2+ + e− 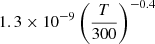1.3 × 10 − 9 ( T 300 ) − 0.4 $ 1.3 \times 10^{-9} \left(\frac{T}{300}\right)^{-0.4} $ 45
D35D_35 H+ + D− → D + H 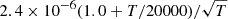2.4 × 10 − 6 ( 1.0 + T / 20000 ) / T $ 2.4\times 10^{-6}(1.0+T/20000)/\sqrt{T} $ 52
D36D_36 D + D+ → D2+ + γ 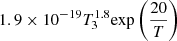1.9 × 10 − 19 T 3 1.8 exp ( 20 T ) $ 1.9 \times 10^{-19} T_{3}^{1.8} {\exp \left(\frac{20}{T}\right)} $ 45
D37D_37 D + H2+ → H2 + D+ the same as for blueH_09
D38D_38 H2+ + D → HD + H+ 1.0 × 10−9 50
D39D_39 HD+ + D → D2+ + H 1.0 × 10−9 53
D40D_40 HD+ + D → D2 + H+ 1.0 × 10−9 50
D41D_41 H + D2+ → D2 + H+ the same as for blueH_09
D42D_42 D2+ + H → HD+ + D 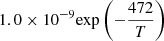1.0 × 10 − 9 exp ( − 472 T ) $ 1.0 \times 10^{-9} {\exp \left(-\frac{472}{T}\right)} $ 53
D43D_43 D2+ + H → HD + D+ 1.0 × 10−9 50
D44D_44 HD + D+ → D2 + H+ 1.0 × 10−9 53
D45D_45 D2 + H+ → HD+ + D 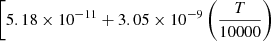[ 5.18 × 10 − 11 + 3.05 × 10 − 9 ( T 10000 ) $ \left[ 5.18 \times 10^{-11} + 3.05 \times 10^{-9} \left(\frac{T}{10000}\right) \right. $ 54
− 5.42 × 10 − 10 ( T 10000 ) 2 ] exp ( − 20100 T ) $ \phantom{[} \left. -5.42 \times 10^{-10} \left(\frac{T}{10000}\right)^{2} \right]{\exp \left(-\frac{20100}{T}\right)} $
D46D_46 D2 + H+ → D2+ + H the same as for blueH_10 52
D47D_47 HD + D → D2 + H 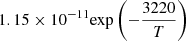1.15 × 10 − 11 exp ( − 3220 T ) $ 1.15 \times 10^{-11} {\exp \left(-\frac{3220}{T}\right)} $ 44
D48D_48 D2 + H → HD + D dex[−86.1558+4.53978logT T ≤ 2200 K 43
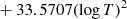+ 33.5707 ( log T ) 2 $ \phantom{\mathrm{dex}[} + 33.5707 (\log{T})^{2} $
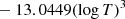− 13.0449 ( log T ) 3 $ \phantom{\mathrm{dex}[} - 13.0449 (\log{T})^{3} $
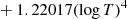+ 1.22017 ( log T ) 4 $ \phantom{\mathrm{dex}[} + 1.22017 (\log{T})^{4} $
+ 0.0482453 ( log T ) 5 ] $ \left. \phantom{\mathrm{dex}[} + 0.0482453 (\log{T})^{5} \right] $
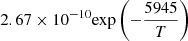2.67 × 10 − 10 exp ( − 5945 T ) $ 2.67 \times 10^{-10} {\exp \left(-\frac{5945}{T}\right)} $ T >  2200 K
D49D_49 HD + γ → H + D 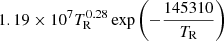1.19 × 10 7 T R 0.28 exp ( − 145310 T R ) $ 1.19\times 10^7 T_{\mathrm{R}}^{0.28}\exp\left(-\frac{145310}{T_{\mathrm{R}}}\right) $ 55
D50D_50 D2+ + γ → D + D+ the same as for blueH_08
D51D_51 D2 + γ → D2+ + e− the same as for blueH_14
D52D_52 D2 + γ → D + D the same as for blueH_15
D53D_53 D− + γ → D + e− the same as for blueH_04
D54D_54 HD + H3+ → H2 + H2D+ 1.0 × 10−9(2.1−0.4⋅log(T)) 3
D55D_55 D2 + e− → D + D + e− 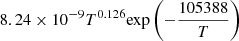8.24 × 10 − 9 T 0.126 exp ( − 105388 T ) $ 8.24 \times 10^{-9} T^{0.126} {\exp \left(-\frac{105388}{T}\right)} $ v = 0 20
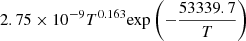2.75 × 10 − 9 T 0.163 exp ( − 53339.7 T ) $ 2.75 \times 10^{-9} T^{0.163} {\exp \left(-\frac{53339.7}{T}\right)} $ LTE
D56D_56 HD+ + H2 → H3+ + D the same as for blueH_13
D57D_57 H2D+ + H2 → H3+ + HD 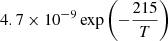4.7 × 10 − 9 exp ( − 215 T ) $ 4.7\times 10^{-9}\exp\left(-\frac{215}{T}\right) $ T <  100 K 3
5.5 × 10−10 T ≥ 100 K
D58D_58 D + e− → D+ + e− + e− the same as for blueH_20 52
D59D_59 HD + e− → D + H− 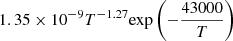1.35 × 10 − 9 T − 1.27 exp ( − 43000 T ) $ 1.35 \times 10^{-9} T^{-1.27} {\exp \left(-\frac{43000}{T}\right)} $ 56
D60D_60 HD + e− → H + D− 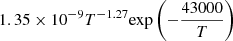1.35 × 10 − 9 T − 1.27 exp ( − 43000 T ) $ 1.35 \times 10^{-9} T^{-1.27} {\exp \left(-\frac{43000}{T}\right)} $ 56
D61D_61 HD + e− → H + D + e− 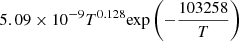5.09 × 10 − 9 T 0.128 exp ( − 103258 T ) $ 5.09 \times 10^{-9} T^{0.128} {\exp \left(-\frac{103258}{T}\right)} $ v = 0 57
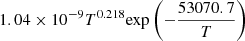1.04 × 10 − 9 T 0.218 exp ( − 53070.7 T ) $ 1.04 \times 10^{-9} T^{0.218} {\exp \left(-\frac{53070.7}{T}\right)} $ LTE
D62D_62 H2 + D+ → H2+ + D the same as for blueH_10 52
D63D_63 H2 + D+ → HD+ + H 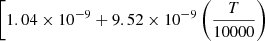[ 1.04 × 10 − 9 + 9.52 × 10 − 9 ( T 10000 ) $ \left[ 1.04 \times 10^{-9} + 9.52 \times 10^{-9} \left(\frac{T}{10000}\right) \right. $ 54
− 1.81 × 10 − 9 ( T 10000 ) 2 ] exp ( − 21000 T ) $ \left. \;-1.81 \times 10^{-9} \left(\frac{T}{10000}\right)^{2} \right]{\exp \left(-\frac{21000}{T}\right)} $
D64D_64 HD + H+ → HD+ + H the same as for blueH_10 52
D65D_65 HD + H → H + D + H the same as for blueH_19 18
D66D_66 HD + He → H + D + He the same as for blueH_30 18
D67D_67 HD + He+ → HD+ + He the same as for blueHe_20 52
D68D_68 HD + He+ → He + H+ + D 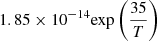1.85 × 10 − 14 exp ( 35 T ) $ 1.85 \times 10^{-14} {\exp \left(\frac{35}{T}\right)} $ 49
D69D_69 HD + He+ → He + H + D+ 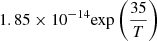1.85 × 10 − 14 exp ( 35 T ) $ 1.85 \times 10^{-14} {\exp \left(\frac{35}{T}\right)} $ 49
D70D_70 HD+ + D → HD + D+ the same as for blueH_09 52
D71D_71 D2 + e− → D + D− 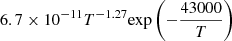6.7 × 10 − 11 T − 1.27 exp ( − 43000 T ) $ 6.7 \times 10^{-11} T^{-1.27} {\exp \left(-\frac{43000}{T}\right)} $ 56
D72D_72 D− + e− → D + e− + e− the same as for blueH_31 52
D73D_73 D− + H → D + H + e− the same as for blueH_32 52
D74D_74 D+ + H− → D + H the same as for blueH_06 52
D75D_75 D+ + D− → D + D the same as for blueH_06 52
D76D_76 H2+ + D− → H2 + D 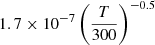1.7 × 10 − 7 ( T 300 ) − 0.5 $ 1.7 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D77D_77 H2+ + D− → H + H + D 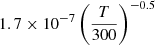1.7 × 10 − 7 ( T 300 ) − 0.5 $ 1.7 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D78D_78 HD+ + H− → HD + H 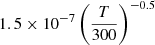1.5 × 10 − 7 ( T 300 ) − 0.5 $ 1.5 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D79D_79 HD+ + H− → D + H + H 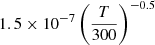1.5 × 10 − 7 ( T 300 ) − 0.5 $ 1.5 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D80D_80 HD+ + D− → HD + D 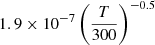1.9 × 10 − 7 ( T 300 ) − 0.5 $ 1.9 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D81D_81 HD+ + D− → D + H + D 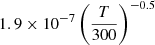1.9 × 10 − 7 ( T 300 ) − 0.5 $ 1.9 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D82D_82 D2+ + H− → D2 + H 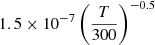1.5 × 10 − 7 ( T 300 ) − 0.5 $ 1.5 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D83D_83 D2+ + H− → D + D + H 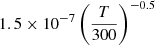1.5 × 10 − 7 ( T 300 ) − 0.5 $ 1.5 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D84D_84 D2+ + D− → D2 + D 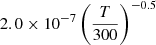2.0 × 10 − 7 ( T 300 ) − 0.5 $ 2.0 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D85D_85 D2+ + D− → D + D + D 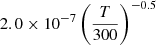2.0 × 10 − 7 ( T 300 ) − 0.5 $ 2.0 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.5} $ 45
D86D_86 D + D2+ → D2 + D+ the same as for blueH_09 52
D87D_87 HD + D+ → HD+ + D the same as for blueH_10 52
D88D_88 HD + D+ → D2+ + H 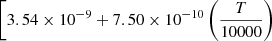[ 3.54 × 10 − 9 + 7.50 × 10 − 10 ( T 10000 ) $ \left[ 3.54 \times 10^{-9} + 7.50 \times 10^{-10} \left(\frac{T}{10000}\right) \right. $ 54
− 2.92 × 10 − 10 ( T 10000 ) 2 ] exp ( − 21100 T ) $ \left. \;-2.92 \times 10^{-10} \left(\frac{T}{10000}\right)^{2} \right]{\exp \left(-\frac{21100}{T}\right)} $
D89D_89 D2 + H+ → HD + D+ 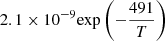2.1 × 10 − 9 exp ( − 491 T ) $ 2.1 \times 10^{-9} {\exp \left(-\frac{491}{T}\right)} $ 53
D90D_90 D2 + D+ → D2+ + D the same as for blueH_10 52
D91D_91 HD + H2 → H + D + H2 the same as for blueH_29 but with ncr → 100ncr 18
D92D_92 D2 + H → D + D + H the same as for blueH_19 52
D93D_93 D2 + H2 → D + D + H2 the same as for blueH_29 52
D94D_94 He + D+ → D + He+ 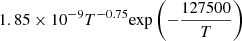1.85 × 10 − 9 T − 0.75 exp ( − 127500 T ) $ 1.85 \times 10^{-9} T^{-0.75} {\exp \left(-\frac{127500}{T}\right)} $ T ≤ 10000 K 45
5.9 × 10−37T4.74 T >  10000 K
D95D_95 He+ + D → D+ + He 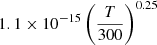1.1 × 10 − 15 ( T 300 ) 0.25 $ 1.1 \times 10^{-15} \left(\frac{T}{300}\right)^{0.25} $ 45
D96D_96 D− + He → D + He + e− 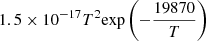1.5 × 10 − 17 T 2 exp ( − 19870 T ) $ 1.5 \times 10^{-17} T^{2} {\exp \left(-\frac{19870}{T}\right)} $ 45
D97D_97 He+ + D− → He + D 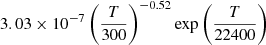3.03 × 10 − 7 ( T 300 ) − 0.52 exp ( T 22400 ) $ 3.03 \times 10^{-7} \left(\frac{T}{300}\right)^{-0.52} {\exp \left(\frac{T}{22400}\right)} $ 45
D98D_98 D2 + He+ → D2+ + He 2.5 × 10−14 53
D99D_99 D2 + He+ → He + D+ + D 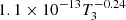1.1 × 10 − 13 T 3 − 0.24 $ 1.1 \times 10^{-13} T_{3}^{-0.24} $ 53
D100D_100 D2 + He → D + D + He the same as for blueH_30 52

Notes. T and TeV are the gas temperature in units of K and eV respectively. References are to the primary source of data for each reaction. Reactions with a peak contribution to the synthesis or destruction of any reactant exceeding 0.1 % are bolded.References. 1: Seager et al. (1999), 2: Wishart (1979), 3: Galli & Palla (1998), 4: Croft et al. (1999), 5: Ramaker & Peek (1976), 6: Karpas et al. (1979), 7: Savin et al. (2004), 8: Poulaert et al. (1978), 9: Coppola et al. (2011a), 10: Theard & Huntress (1974), 11: Novosyadlyj et al. (2022), 12: Mac Low & Shull (1986), 13: Lepp & Shull (1983), 14: Janev et al. (1987), 15: this paper: Fit based on cross-section from https://home.strw.leidenuniv.nl/ ewine/photo/, 16: Méndez et al. (2006), 17: Janev et al. (2003), 18: Glover & Abel (2008), 19: Schulz & Asundi (1967), 20: Trevisan & Tennyson (2002a), 21: Martin et al. (1998), 22: Shapiro & Kang (1987), 23: Dove et al. (1987), 24: Dalgarno & Lepp (1987), 25: Walkauskas & Kaufman (1975), 26: Albertsson et al. (2014), 27: Soon (1992), 28: Database of kinetic data of interest for astrochemical (KIDA, kida.astrochem-tools.org), 29: Courtney et al. (2021), 30: De Fazio (2014), 31: Coppola et al. (2017), 32: Ferland et al. (1992), 33: Kimura et al. (1993), 34: Zygelman et al. (1989), 35: Black (1978), 36: Peart & Hayton (1994), 37: this paper: Fit to data from Schauer et al. (1989); Johnsen et al. (1980) 38: Glover & Abel (2008): Barlow S. G., 1984, PhD thesis, Univ. Colorado 39: Huq et al. (1982), 40: Savin (2002), 41: Lindinger et al. (1982), 42: Dickinson (2005), 43: Fit of Glover & Abel (2008) to data from Mielke et al. (2003), 44: Shavitt (1959), 45: Same as corresponding H reaction, but scaled by D reduced mass (see Glover & Abel (2008)), 46: Strömholm et al. (1995), 47: Datz et al. (1995); Larsson et al. (1996), 48: Dalgarno & McDowell (1956), scaled by D reduced mass (see Glover & Abel (2008)), 49: Same as corresponding H reaction, with branching ratio assumed uniform (see Glover & Abel (2008)), 50: estimate from Glover & Abel (2008), 51: Linder et al. (1995), 52: Same as corresponding H reaction (see Glover & Abel (2008)), 53: Walmsley et al. (2004), 54: Fit of Glover & Abel (2008) based on cross-section from Wang & Stancil (2002) 55: Coppola et al. (2011b), 56: Xu & Fabrikant (2001), 57: Trevisan & Tennyson (2002b), 58: Adams & Smith (1985), 59: Stancil et al. (1998).

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.