| Issue |
A&A
Volume 695, March 2025
|
|
|---|---|---|
| Article Number | L20 | |
| Number of page(s) | 7 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202553692 | |
| Published online | 21 March 2025 | |
Letter to the Editor
The highly magnetic Wolf-Rayet binary HD 45166 resolved with VLTI/GRAVITY⋆
1
Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
2
Leuven Gravity Institute, KU Leuven, Celestijnenlaan 200D, box 2415 3001 Leuven, Belgium
3
The School of Physics and Astronomy, Tel Aviv University, Tel Aviv 6997801, Israel
4
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
5
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9, B-9000 Gent, Belgium
6
Department of Physics and Space Science, Royal Military College of Canada, Kingston, ON, Canada
7
University of Amsterdam, Anton Pannekoek Institute for Astronomy, Amsterdam 1098 XH, The Netherlands
8
NSF NOIRLab, 670 N. A‘ohoku Place, Hilo, HI 96720, USA
9
European Southern Observatory, Santiago, Chile
10
Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
11
Argelander Institut für Astronomie, Auf dem Hügel 71, DE-53121 Bonn, Germany
12
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, DE-53121 Bonn, Germany
13
Institute for Physics and Astronomy, Universität Potsdam, 14476 Potsdam, Germany
⋆⋆ Corresponding author; kunalprashant.deshmukh@kuleuven.be
Received:
7
January
2025
Accepted:
2
March
2025
HD 45166 was recently reported to be a long-period binary comprising a B7 V star and a highly magnetic (⟨B⟩=43.0 ± 0.5 kG) hot Wolf-Rayet-like component, dubbed a quasi Wolf-Rayet (qWR) star in the literature. While originally proposed to be a short-period binary, long-term spectroscopic monitoring suggested a 22.5 yr orbital period. With a derived dynamical mass of 2.03 ± 0.44 M⊙, the qWR component is the most strongly magnetized non-degenerate object ever detected and a potential magnetar progenitor. However, the long period renders the spectroscopic orbital solution and dynamical mass estimates uncertain, casting doubts on whether the qWR component is massive enough to undergo core collapse. Here, we spatially resolve the HD 45166 binary using newly acquired interferometric data obtained with the GRAVITY instrument of the Very Large Telescope Interferometer. Due to the calibrator star being a binary as well, we implemented a new approach for visibility calibration and tested it thoroughly using archival GRAVITY data. The newly calibrated HD 45166 data revealed the unmistakable presence of a companion to the qWR component with an angular separation of 10.9 ± 0.1 mas (which translates to a projected physical separation of 10.8 ± 0.4 au), consistent with the long-period orbit. We obtained a model-independent qWR mass MqWR = 1.96−0.54+0.74 M⊙ using interferometric and spectroscopic data together. This observation robustly confirms that HD 45166 is truly a long-period binary and provides an anchor point for accurate mass determination of the qWR component with further observations.
Key words: techniques: interferometric / binaries: general / stars: evolution / stars: massive / stars: Wolf-Rayet
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
HD 45166 is a binary system comprising a B7 V star and a hot helium star with a Wolf-Rayet (WR)-like spectral appearance (van Blerkom 1978; Willis et al. 1989). The nature of the WR component has been debated for close to a century, having been interpreted as a WR star, a Be star, and a subdwarf star (Anger 1933; Neubauer & Aller 1948; Morgan et al. 1955; Willis & Stickland 1983). Due to its relatively narrow spectral lines, peculiar abundance pattern, and spectral variability, the WR component has been dubbed a “quasi WR star” (qWR) since the 1970s (van Blerkom 1978). Recently, Shenar et al. (2023) detected an extremely strong magnetic field of ⟨B⟩qWR = 43.0 ± 0.5 kG in the qWR component of the system using spectropolarimetric observations secured with the ESPaDOnS spectropolarimeter of the Canada-France-Hawaii Telescope (CFHT). This detection marked the discovery of the first magnetic WR-like object. If massive enough to undergo core collapse, it could also be a promising progenitor of a magnetar – a highly magnetic neutron star (see Kaspi & Beloborodov 2017, and references therein).
One of the most crucial uncertainties regarding HD 45166 is the mass of the qWR component. Steiner & Oliveira (2005) reported a mass of 4.2 M⊙ for the qWR component via dynamical mass measurements and adopting a 1.6 d orbital period. However, Shenar et al. (2023) showed that the 1.6 d period is in fact the pulsational period of the B7 V component. Relying on spectroscopic data spanning over 20 yr, Shenar et al. (2023) instead found a long orbital period of P = 22.5 ± 0.5 yr. From a derived evolutionary mass of MB = 3.40 ± 0.06 M⊙ for the B7 V component and a mass ratio of q = MqWR/MB = 0.60 ± 0.13 derived from the orbit, the authors reported MqWR = 2.03 ± 0.44 M⊙ for the qWR component.
It is uncertain whether helium stars of this mass are core-collapse progenitors (Woosley 2019). The evolution models presented by Shenar et al. (2023), which involve a merger event in what was originally a triple system, predict that the qWR component is massive enough to undergo core collapse. This, however, cannot be claimed with certainty given the large uncertainty on its mass. Moreover, the radial-velocity amplitudes (KqWR = 9.9 ± 1.6 km s−1 and KB = 5.8 ± 1.3 km s−1 for the qWR and B7 V components respectively) are comparable to intrinsic variability amplitudes of both components, making the spectroscopic orbital solution, and therefore the mass ratio, uncertain and challenging.
A robust confirmation that HD 45166 is truly a long-period binary can be attained using long-baseline interferometry. Assuming the orbital solution derived by Shenar et al. (2023) from spectroscopy is correct and using their derived orbital inclination of i = 49 ± 11° from the mass calibration of the B7 V component, the projected orbital separation of the two components should be a sin i = 10.5 ± 1.8 au. At a distance of 991 ± 37 pc measured from the Gaia parallax (Bailer-Jones et al. 2021), this translates to an angular separation of α = 11 ± 2 milliarcseconds (mas). This makes HD 45166 an excellent target for the GRAVITY instrument (GRAVITY Collaboration 2017) of the Very Large Telescope Interferometer (VLTI), which operates in the K-band. The light ratio between the two components in the visual band is close to unity, implying that both components should also be easily visible in the K-band. The K-band magnitude of HD 45166 (K = 9.57) is close to the limiting magnitude of the instrument and requires usage of all four unit telescopes (UTs) of the VLTI.
In this Letter, we present the results acquired from the first interferometric observations of HD 45166 obtained with VLTI/GRAVITY. We report the detection of a companion with characteristics in agreement with the results from Shenar et al. (2023). We demonstrate beyond doubt that HD 45166 is truly a long-period binary, establishing a first interferometric data point and subsequently a first model-independent mass estimate for the qWR component that can be refined with future monitoring. The Letter is structured as follows: Section 2 details the GRAVITY observations, subsequent data reduction, and calibration strategies implemented for HD 45166. In Section 3, we describe our binary search results and updated orbital parameters, and this is followed by a discussion and conclusions in Section 4.
2. Observations, data reduction, and calibration
GRAVITY is a K-band spectro-interferometric instrument sensitive to binary separations of ∼1–100 mas and flux contrasts of ΔK ∼ 5. HD 45166 was observed with VLTI/GRAVITY in snapshot mode on 26 November 2023 (MJD 60274.33) in medium resolution mode (spectral resolving power λ/Δλ = 500) for a total integration time of 18 min. The observation used the four UTs to form the interferometric baselines given the relative faintness of the target. To ensure the target would be observable, we required the seeing to be smaller than 0.7″, and a DIMM seeing of ≈0.4″ was indeed achieved during the exposure.
We included a single calibrator in the observing chain (CAL-SCI). The calibrator star was TYC 732-806-1, which has a comparable K-band magnitude to the science target (K = 9.49). For data reduction and visibility calibration, we used version v1.6.0 of the standard GRAVITY pipeline (Lapeyrere et al. 2014). The observables extracted were the squared visibility (V2), closure phase (T3PHI), differential phase (DPHI), and the K-band spectrum (FLUX).
Unfortunately, the calibrator star TYC 732-806-1 turned out to be a binary, which became obvious from its very large closure phase signal of the order of 35 degrees. We therefore simultaneously fit a binary model (two unresolved stars) and the transfer function to the calibrator’s data (CAL-FREE approach). The transfer function consists of four closure phase offsets for the four triangles and six affine (as a function of wavelength) corrections to the squared visibility for each of the six baselines. Thankfully, this approach leads to a unique solution but with a high correlation between the flux ratio of the binary and the squared visibility. To solve this, we used 32 single-star calibrators taken with the same setup on the VLTI-UTs and used the results to constrain the transfer function for TYC 732-806-1 within typical ranges (CAL-PRIOR approach). Alternatively, we also applied the same self-calibration method to HD 45166 itself without (SCI-FREE approach) and with prior ranges (SCI-PRIOR approach). All analyses were performed with PMOIRED1 (Mérand 2022) version 1.2.10, which introduced the transfer function fitting. More details about this calibration method are included in Appendix A. We also applied a telluric correction to the spectrum using PMOIRED, which implements molecfit (Smette et al. 2015) to produce the continuum normalized spectrum (NFLUX) appropriate for further analysis.
3. Results
We modeled HD 45166 using a parametric model in the PMOIRED software. To do so, we employed the interferometric observables V2 and T3PHI. Similar to Deshmukh et al. (2024), we first qualitatively assessed the data to decide on a binary composed of unresolved stars (i.e., angular diameters less than approximately 0.1 mas). We decided on using V2, T3PHI, and NFLUX for the modeling. Following a preliminary evaluation, we performed a binary grid search (based on Gallenne et al. 2015) consisting of two components: (i) an unresolved star with a fixed position at origin, a flux f1 as a free parameter, and emission lines seen in the spectrum and (ii) an unresolved star with its position (ΔE,ΔN) varied across a grid, a flux f2 = 1 − f1 to ensure a total continuum normalized flux of one, and no spectral lines included. We used a grid ranging from ΔE = –20 to +20 mas and ΔN = –20 to +20 mas. The best-fit solution was obtained based on reduced chi-squared (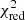 ) minimization. This method was applied for all four approaches mentioned in Section 2. For the final evaluation of the spectra, we used the decimated wavelets approach to fit the spectra of the two components (see Frost et al. 2024).
) minimization. This method was applied for all four approaches mentioned in Section 2. For the final evaluation of the spectra, we used the decimated wavelets approach to fit the spectra of the two components (see Frost et al. 2024).
The parameters affected by the calibration are the continuum flux ratio and separation vector of the binary components. In our fits, these parameters had very small statistical uncertainties, much smaller than the systematics introduced by the uncertainties on the calibration. However, all four calibration strategies led to unique and very consistent binary parameters, as listed in Table 1. As an example, Figure 1 shows GRAVITY data along with the best-fit binary model for the SCI-FREE calibration strategy. Figure 2 shows the corresponding derived spectra for the two components, with only the qWR component possessing emission lines as expected.
HD 45166 best-fit binary parameters for different calibration strategies.
 |
Fig. 1. HD 45166 model of un-calibrated GRAVITY data using the SCI-FREE calibration strategy (see text). The top-left panel shows the UV coverage of the observation. The bottom-left, middle, and right panels show the normalized flux (NFLUX), closure phase (T3PHI), and squared visibilities (V2), respectively, with the data in black and best-fit binary model in red. |
 |
Fig. 2. Derived normalized spectra in the K-band from the GRAVITY data using the SCI-FREE calibration approach. The orange spectrum represents the qWR primary, the green one represents the B7 V secondary, and the gray one represents their sum. Expected emission lines for the qWR are listed based on the GRAVITY NFLUX data shown in Figure 1. |
We adopted the mean values of the best-fit parameters across the four calibration strategies, resulting in a K-band flux ratio of the B7 V component to the qWR component of f2/f1 = 0.83 ± 0.02. Following the method described in Section 5.2 of Deshmukh et al. (2024), we obtained the absolute K-band magnitudes for the two components as 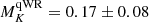 and
and 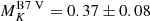 . The latter is consistent with a late-type B dwarf (B8 V), as per Pecaut & Mamajek (2013).
. The latter is consistent with a late-type B dwarf (B8 V), as per Pecaut & Mamajek (2013).
The position of the B7 V component relative to the qWR component was found to be ΔE = 4.83 ± 0.07 mas and ΔN = 9.75 ± 0.12 mas to the east and north, respectively. All errors mentioned are 68% confidence intervals (1σ). Figure 3 illustrates the relative positions of the two components in the binary. Combining the distance to HD 45166 (991 ± 37 pc) with the measured angular binary separation (10.9 ± 0.1 mas), we obtained a projected physical separation of 10.8 ± 0.4 au.
 |
Fig. 3. Relative angular positions of the two components in HD 45166 with the primary fixed at origin. |
We further computed the first 3D orbital solution for HD 45166, combining the radial velocity data from Shenar et al. (2023) and the two interferometric observables from this work (ΔN, ΔE; see Fig. 3). Adopting the distance to HD 45166, the new interferometric observables are sufficient to constrain the two remaining independent unknown quantities in the 3D orbital solution: the orientation in the plane of the sky (Ω) and the total mass (M1 + M2), or (equivalently) the semi-major axis of the relative orbit (a). To evaluate the uncertainties while taking into account the correlations between orbital parameters, we used a bootstrapping approach in which the initial data set of radial velocities and angular ΔE, ΔN positions are replaced by artificial data drawn from normal distributions centered on the observed values and with 1σ dispersion given by the observational uncertainties. The uncertainty on the distance is also included in a similar way. We repeated the process 10 000 times and obtained the distributions of parameters shown in Figures B.1 and B.2.
As expected, the updated orbital parameters are largely consistent with Shenar et al. (2023), Ω being a newly constrained parameter. Thanks to interferometry, we were also able to obtain model-independent component masses, which are also consistent, although with large error bars. Some relevant derived quantities include the following:
-
qWR primary mass:
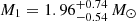
-
B7 V secondary mass:
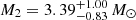
-
Periastron distance:
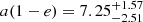 au
au -
MJD for the next periastron passage:
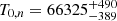 , which in Besselian year is
, which in Besselian year is 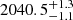 yr.
yr.
Further interferometric and spectroscopic observations will constrain these quantities to a much higher precision. A more detailed description of the various orbital and derived parameters, along with figures, can be found in Appendix B.
4. Discussion and conclusions
We have presented the first interferometric observation of HD 45166 using VLTI/GRAVITY, firmly establishing it as a wide binary consisting of the qWR and the B7 V components separated by 10.9 ± 0.1 mas on the sky. This detection is a robust confirmation of HD 45166 as a long-period binary system. We also obtained the first dynamical mass measurement for the qWR, validating assumptions made in Shenar et al. (2023) and therefore their conclusions.
The measured distance at periastron of ∼7 ± 2 au provides strong evidence that the system is not a product of a previous mass transfer phase from the qWR to its B7 V companion. In that case, the qWR would have been the product of binary stripping rather than a merger, as suggested by Shenar et al. (2023). Producing a 2 M⊙ helium core requires a ∼8 M⊙ progenitor, which would not fill its own Roche lobe before core-helium depletion at a periastron distance of 7 au. Although the current separation would be different from that at the onset of mass transfer, this does not impact our conclusion. Given our derived mass ratio q = 1.7 ± 0.2 and the one at the onset of the hypothetical mass transfer phase, qi ∼ 3.39 M⊙/8 M⊙ = 0.42 (assuming non-conservative mass transfer), the pre-interaction semi-major axis would have been similar to the one that is currently observed. This would exclude binary stripping and instead favor the merger scenario of Shenar et al. (2023). Further observations are critical to completely exclude solutions with a much smaller periastron distance (see Fig. B.1).
Within the uncertainties on the mass of the qWR star, the resulting outcome could either be the formation of an ONeMg white dwarf or undergoing an explosion, possibly through an electron-capture supernova (Chanlaridis et al. 2022). Additionally, in binary systems, stripped stars can undergo an additional phase of mass transfer after core-helium depletion, which at short orbital periods (≲1 day) is expected to remove most of the helium rich layers and produce ultra-stripped supernovae (Tauris et al. 2015). Such a scenario was recently suggested for the formation of the neutron star in the high mass X-ray binary CPD-29 2176 (Richardson et al. 2023). For the case of the qWR star, however, the newly confirmed wide orbit implies a separation too large for future binary interaction, and its final fate will be determined by its own evolution. Placing further constraints on its mass will be critical to determining the actual outcome.
As part of our analysis, we adopted a modified calibration strategy for GRAVITY data, motivated by a bad calibrator star. The calibrator star, TYC 732-806-1, also turned out to be a binary, rendering it unsuitable for visibility calibration using traditional methods. We implemented a novel method to bypass the issue as described in Section 2, which can also be applied to other GRAVITY data affected by bad calibrator stars.
In addition to confirming the binary status of HD 45166, our GRAVITY observation serves as the first relative astrometric measurement of the binary. Given its estimated orbital period of 22.5 yr, follow-up GRAVITY observations over the coming years will provide more astrometric measurements, eventually enabling the determination of a visual orbit for the binary. Combining the orbit with spectroscopic observations will enable much more precise model-independent masses for both components of the binary to be determined. This work therefore represents a crucial step toward determining the mass of the qWR component in HD 45166 and subsequently its true nature as a potential magnetar progenitor.
5. Data availability
All GRAVITY data used in this Letter are available on the ESO Archive. Reduced data may be made available upon request to the authors.
Acknowledgments
Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 112.25RX.001. Based on data obtained from the ESO Science Archive Facility under request number 936605. This research has used measurements obtained at the Mercator Observatory which receives funding from the Research Foundation - Flanders (FWO) (grant agreement I000325N and I000521N). KD and HS acknowledge funding from grant METH/24/012 at KU Leuven. TS acknowledges support from the Israel Science Foundation (ISF) under grant number 0603225041. GAW acknowledges the Discovery Grant support from the Natural Sciences and Engineering Research Council (NSERC) of Canada. PM acknowledges support from the FWO senior fellowship number 12ZY523N.
References
- Anger, C. J. 1933, Harvard College Obs. Bull., 891, 8 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bourges, L., Mella, G., Lafrasse, S., et al. 2017, VizieR On-line Data Catalog: II/346 [Google Scholar]
- Chanlaridis, S., Antoniadis, J., Aguilera-Dena, D. R., et al. 2022, A&A, 668, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deshmukh, K., Sana, H., Mérand, A., et al. 2024, A&A, 692, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frost, A. J., Sana, H., Mahy, L., et al. 2024, Science, 384, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gallenne, A., Mérand, A., Kervella, P., et al. 2015, A&A, 579, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2017, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. M. 2017, ARA&A, 55, 261 [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, in Optical and Infrared Interferometry IV, eds. J. K. Rajagopal, M. J. Creech-Eakman, & F. Malbet, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 9146, 91462D [NASA ADS] [Google Scholar]
- Mérand, A. 2022, in Optical and Infrared Interferometry and Imaging VIII, eds. A. Mérand, S. Sallum, & J. Sanchez-Bermudez, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 12183, 121831N [Google Scholar]
- Mérand, A., Bordé, P., & Coudé du Foresto, V. 2005, A&A, 433, 1155 [Google Scholar]
- Morgan, W. W., Code, A. D., & Whitford, A. E. 1955, ApJS, 2, 41 [Google Scholar]
- Neubauer, F. J., & Aller, L. H. 1948, ApJ, 107, 281 [NASA ADS] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Richardson, N. D., Pavao, C. M., Eldridge, J. J., et al. 2023, Nature, 614, 45 [Google Scholar]
- Shenar, T., Wade, G. A., Marchant, P., et al. 2023, Science, 381, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steiner, J. E., & Oliveira, A. S. 2005, A&A, 444, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauris, T. M., Langer, N., & Podsiadlowski, P. 2015, MNRAS, 451, 2123 [NASA ADS] [CrossRef] [Google Scholar]
- van Blerkom, D. 1978, ApJ, 225, 175 [NASA ADS] [Google Scholar]
- Willis, A. J., & Stickland, D. J. 1983, MNRAS, 203, 619 [Google Scholar]
- Willis, A. J., Howarth, I. D., Stickland, D. J., & Heap, S. R. 1989, ApJ, 347, 413 [NASA ADS] [Google Scholar]
- Woosley, S. E. 2019, ApJ, 878, 49 [Google Scholar]
Appendix A: Calibration of the GRAVITY data
Interferometric data suffer from instrumental and atmospheric effects which result in a multiplicative bias for the visibility amplitude, and additive biases for the phase closure. The usual procedure to account for these effects consists of observing a partially resolved star as an on-sky calibrator to limit the uncertainty introduced in the process (see for example Mérand et al. (2005)). This calibrator needs to be taken close in time (less than 1 hour) within the science target observation, and close-by on sky with the same observing model.
In the case of the observations presented in this work, the calibrator unfortunately turned out to be a binary with a strong signal in both closure phase and visibility. Before deciding to use valuable telescope time and redo the observations with a different calibrator, we tested the idea that the binary signal could be disentangled from the transfer function (TF) signal. This turned out to work remarkably well as we describe in this appendix.
A.1. Validation on archival single-star calibrators
The first step is to check what are the historical values and scatter of the TF for data taken with the same mode and with the same telescopes. For the closure phase, we chose a TF in the form of an additive bias (dominated by birefringence effect in the beam combiner): T3PHItrue = T3PHIobs + bias. For the visibility squared amplitude, we chose a multiplicative factor a with a slope b in wavelength (dominated by atmospheric turbulence, which has a strong chromatic dependency): Vtrue2 = aVobs2[1 + b(λ − 2.2 μm)]. The binarity, on the other hand, manifests as a strong chromatic signal that we verified a posteriori can be disentangled from the TF signal.
We requested from the ESO archive all the proper calibrator observations taken the year prior to our observation in the same mode (medium spectral resolution, combined polarizations) and with the same telescopes (VLTI-UTs), resulting in 32 individual observations2. We applied our calibration strategy by fitting the transfer function and assuming the angular diameters from the JMMC Stellar Diameters Catalog (Bourges et al. 2017). The historical calibrators turned out to have tight scatter of the transfer function parameters. For the closure phase, the bias is typically close to 0, and less than 1 degree in absolute value (see Fig. A.1). For the squared visibilities, 90% of the data have a multiplicative factor a between 0.75 and 0.99, and a chromatic slope b between −0.03 and 0.6.
 |
Fig. A.1. Histograms of calibration parameters fitted to historical good calibrators (partially resolved stars) taken with the same mode and telescopes in the year prior to our data. The three panels cover the 3 types of parameters. Left: Closure phase bias in degrees. Center: V2 multiplicative factor. Right: V2 chromatic slope. |
A.2. Coping with a binary as a calibrator
We first perform a binary grid search using as starting point the most probable TF values of bias=0 for all triangles and (a, b) = (0.95, 0.2) for all baselines as initial values. In this process, 19 parameters are fitted: all except the sizes of the stars in the binary which are set to 0.05 mas based on surface brightness relations.
The binary solution with free TF parameters has a χred2=1.56 (with 1839 degrees of freedom) and the following transfer function values: closure phase biases are all between 0.7 and 8.8 degrees, a between 0.61 and 0.95, and b between 0.11 and 0.62, relatively close to historical values, especially for the V2 parameters (Fig. A.1).
In the fitting process, we can add priors to the transfer function parameters based on our analysis of the historical transfer function values:
-
the closure phase transfer function biases are set to 0±1 degrees
-
the multiplicative transfer function a of the squared visibilities are assumed to be 0.9±0.3
-
the chromatic slope b of the squared visibilities are assumed to be 0.3±0.4
With priors, the binary solution has a χred2=2.32 and very reasonable transfer function values: closure phase biases are all between −0.04 and +0.06 degrees, a between 0.82 and 0.90, and b between 0.25 and 0.42, very much in line with historical values (Fig. A.1).
As a check, using a single-star model and no priors on TF values results in a χred2=7.4 and transfer function values widely incompatible with the historical values, by dozens of sigmas. If we force a prior on the TF, we get χred2=326, which for degrees of freedom (d.o.f.) close to 2000 is a clear indication the single-star model is incompatible with the data. All results are summarized in table A.1.
A.3. Calibration of HD 45166
Based on the convincing binary fit of the calibrator, we applied the same strategy to HD 45166 by fitting a binary model and the transfer function parameters. CAL-FREE corresponds to fix the TF parameters to the ones computed from the calibrator (first line from Table A.1); CAL-PRIOR uses the TF parameters determined on the calibrator, but using priors based on historical values (second line from Table A.1). Conversely, SCI-FREE and SCI-PRIOR are self-calibration approaches where the TF parameters are fitted simultaneously to the binary parameters, with or without priors. The fact that all of these four calibration approaches lead to similar solutions is a strong indication that this calibration method is appropriate in this case.
We cannot guarantee that this approach would work for any observation of any object. In the case of our HD 45166 observations, our calibration seems to work primarily because the TF and astrophysical signals from our model (unresolved binary stars with free spectra) are very distinct, which can hence be determined independently from the minimization algorithm. For example, the closure phase TF is assumed to be a small (of the order of 1 degree or less) bias, where the astrophysical signal has a large amplitude (up to 150 degrees) and strong chromatic variations. Regarding the visibility squared amplitudes, we can note that baselines U3U3 and U3U1 reach maxima (nearly 1), whereas baseline U4U1 reaches minimum (nearly 0) which again is very distinct from the TF signal (see Fig. 1).
Various models applied to the calibrator TYC 732-806-1.
Appendix B: Additional plots
Using the method described in Section 3, we derived six important parameters for HD 45166: total mass of the binary (Mtot), mass of the qWR primary (M1), mass of the B7 V secondary (M2), periastron distance (a(1 − e)), orbital period (P), and mass ratio of the secondary to primary (q). Figure B.1 shows the corner plot for all six parameters. We also show the usual orbital parameters along with the total mass of the binary from our bootstrapping run in Figure B.2 for completeness. The next (‘n’) periastron passage (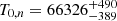 ) is expected in about 15 years from now. We also calculated the next times when true anomaly (ϑ) equals ϑ1 = −ω or ϑ2 = π − ω representing orbital phases in which the projected separation equals actual separation (
) is expected in about 15 years from now. We also calculated the next times when true anomaly (ϑ) equals ϑ1 = −ω or ϑ2 = π − ω representing orbital phases in which the projected separation equals actual separation ( ). Nevertheless, the interferometric orbit can be refined significantly with follow-up observations in the next few years.
). Nevertheless, the interferometric orbit can be refined significantly with follow-up observations in the next few years.
In contrast to Shenar et al. (2023), the component masses derived here are model-independent. However, they have significant uncertainties introduced by the combination of uncertainties on the total mass and the mass ratio. While further epochs will ensure much higher precision on the total mass as well as other orbital parameters, the precision on component masses will still be limited by the precision on mass ratio, or equivalently, on radial velocity semi-amplitudes. This also motivates continued spectroscopic follow-up of HD 45166.
 |
Fig. B.1. Corner plot showing key parameters for HD 45166 and their 1σ confidence intervals obtained from the bootstrapping analysis. Namely, the parameters shown are total mass of the binary (Mtot), mass of the qWR primary (M1), mass of the B7 V secondary (M2), periastron distance (a(1 − e)), orbital period (P), and mass ratio of the secondary to primary (q). |
 |
Fig. B.2. Corner plot showing updated orbital parameters for HD 45166 and their 1σ confidence intervals obtained from the bootstrapping analysis. Namely, we show the total mass of the binary (Mtot), orbital period (P), eccentricity (e), argument of periapsis (ω), longitude of ascending node (Ω), inclination (i), and MJD for the next periastron passage (T0, n). |
All Tables
All Figures
 |
Fig. 1. HD 45166 model of un-calibrated GRAVITY data using the SCI-FREE calibration strategy (see text). The top-left panel shows the UV coverage of the observation. The bottom-left, middle, and right panels show the normalized flux (NFLUX), closure phase (T3PHI), and squared visibilities (V2), respectively, with the data in black and best-fit binary model in red. |
| In the text | |
 |
Fig. 2. Derived normalized spectra in the K-band from the GRAVITY data using the SCI-FREE calibration approach. The orange spectrum represents the qWR primary, the green one represents the B7 V secondary, and the gray one represents their sum. Expected emission lines for the qWR are listed based on the GRAVITY NFLUX data shown in Figure 1. |
| In the text | |
 |
Fig. 3. Relative angular positions of the two components in HD 45166 with the primary fixed at origin. |
| In the text | |
 |
Fig. A.1. Histograms of calibration parameters fitted to historical good calibrators (partially resolved stars) taken with the same mode and telescopes in the year prior to our data. The three panels cover the 3 types of parameters. Left: Closure phase bias in degrees. Center: V2 multiplicative factor. Right: V2 chromatic slope. |
| In the text | |
 |
Fig. B.1. Corner plot showing key parameters for HD 45166 and their 1σ confidence intervals obtained from the bootstrapping analysis. Namely, the parameters shown are total mass of the binary (Mtot), mass of the qWR primary (M1), mass of the B7 V secondary (M2), periastron distance (a(1 − e)), orbital period (P), and mass ratio of the secondary to primary (q). |
| In the text | |
 |
Fig. B.2. Corner plot showing updated orbital parameters for HD 45166 and their 1σ confidence intervals obtained from the bootstrapping analysis. Namely, we show the total mass of the binary (Mtot), orbital period (P), eccentricity (e), argument of periapsis (ω), longitude of ascending node (Ω), inclination (i), and MJD for the next periastron passage (T0, n). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


