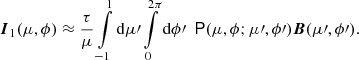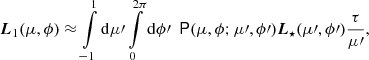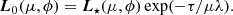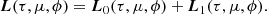| Issue |
A&A
Volume 694, February 2025
|
|
|---|---|---|
| Article Number | A230 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202453188 | |
| Published online | 18 February 2025 | |
X-ray polarization from accretion disk winds
1
Department of Physics and Astronomy, FI-20014 University of Turku, Finland
2
Nordita, Stockholm University and KTH Royal Institute of Technology, Hannes Alfvéns väg 12, SE-10691 Stockholm, Sweden
⋆ Corresponding author; anaghapradeep.a.nitindala@utu.fi
Received:
27
November
2024
Accepted:
16
January
2025
X-ray polarimetry is a fine tool for probing the accretion geometry and physical processes operating in the proximity of compact objects, such as black holes and neutron stars. Recent discoveries made by the Imaging X-ray Polarimetry Explorer question our understanding of the accretion picture. The observed high levels of X-ray polarization in X-ray binaries and active galactic nuclei are challenging to achieve within the conventional scenarios. We investigate the possibility that a fraction (or even all) of the observed polarized signal arises from scattering in the equatorial accretion disk winds, the slow and extended outflows, which are often detected in these systems via spectroscopic means. We find that wind scattering can reproduce the levels of polarization that are observed in these sources.
Key words: accretion / accretion disks / polarization / stars: black holes / stars: neutron / galaxies: Seyfert
© The Authors 2025
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Accretion onto compact objects, such as neutron stars (NSs) and black holes (BHs), fuels some of the brightest X-ray sources: X-ray binaries (XRBs) and active galactic nuclei (AGN). In XRBs, mass is accreted onto the compact object from a close companion. They are found in different spectral states: hard and soft states in XRBs hosting BHs, and banana and island states in NS XRBs (Zdziarski & Gierliński 2004; Remillard & McClintock 2006; Done et al. 2007), and these states are thought to be associated with different accretion geometries. The spectral changes are linked to the changes in the dominant radiative mechanism that is responsible for the broadband spectral production.
The hard-state spectra of BH XRBs are dominated by the Comptonization of soft seed photons by hot electrons in an optically thin inner flow or corona (Sunyaev & Titarchuk 1980; Poutanen & Svensson 1996; Poutanen et al. 1997; Esin et al. 1997). The soft state is dominated by a blackbody-like emission produced by a geometrically thin, optically thick accretion disk (Shakura & Sunyaev 1973; Novikov & Thorne 1973; Page & Thorne 1974). Hard- and soft-intermediate states are also identified at the transitions between these two main states (Homan & Belloni 2005). Similar to XRBs, the X-ray spectra of accreting supermassive BHs in AGN (in particular, of the Seyfert galaxies considered here) are dominated by a power-law-like component (due to Compton upscattering of soft photons) with a high-energy cutoff, and a multitemperature disk blackbody that peaks in the ultraviolet wavelengths (Nandra & Pounds 1994; Pounds et al. 1995; Zdziarski et al. 2000). The current understanding of the accretion geometry and its underlying physical mechanisms in XRBs and AGN is still incomplete. The location of the hot Comptonizing medium (Poutanen et al. 2018; Bambi et al. 2021) and the structure and stability of the optically thick accretion disk (Dexter & Quataert 2012; Jiang et al. 2013) remain debated.
X-ray polarimetry is a novel tool that can provide independent estimates of the accretion geometry, of the parameters of compact object, and of the radiation mechanisms. The polarization angle (PA) is related to the global axis in the system, such as the accretion disk, the jet, or the BH or NS spin: Intrinsic polarization is expected to be either aligned or orthogonal to this axis. Effects of general and special relativity may lead to deviations of PA from this axis (or from the direction orthogonal to that; Connors & Stark 1977; Stark & Connors 1977; Pineault 1977; Pineault & Roeder 1977; Dovčiak et al. 2008; Schnittman & Krolik 2009, 2010; Loktev et al. 2022, 2024). The polarization degree (PD) generally depends on the mechanism producing the broadband spectra. Pure electron-scattering optically thick disk atmospheres that can be relevant to soft-state spectra result in a PD = 11.7% at most for the edge-on systems (Chandrasekhar 1960; Sobolev 1963). For the case of Comptonization, the highest PD ≈ 20% can be achieved in the slab geometry (Poutanen & Svensson 1996, somewhat higher PD of the scattered component can be achieved for the case of Thomson scattering in a slab, Sunyaev & Titarchuk 1985). The PD tends to zero as the corona geometry becomes spherical, but a nonzero net polarization is expected in this case when the reflection from the disk is taken into account (Matt 1993; Poutanen et al. 1996; Dovčiak et al. 2004). The PD is generally expected to depend on the observer inclination: Its highest value is achieved when the source is viewed edge-on. The PD decreases to zero for face-on systems.
General expectations for PD in hard-state systems were low, typically below 2%, due to uncertainties in accretion geometry and BH spin, as well as potential variability in the central source causing depolarization. Together with the typically low inclinations of many sources in the sample, general expectations for PD in the hard-state systems were low and typically lay below 2% (Krawczynski & Beheshtipour 2022; Zhang et al. 2022). Nevertheless, the X-ray PA, when compared to the jet direction, can distinguish between different alternative geometries. The soft-state data in turn were thought to be able to probe the BH spin via the depolarization rate that arises from the PA rotation across the energy band (Stark & Connors 1977; Connors et al. 1980; Dovčiak et al. 2008; Loktev et al. 2022, 2024).
The first X-ray polarimetric observations of XRBs by the Imaging X-ray Polarimetry Explorer (IXPE; Weisskopf et al. 2022) have led to puzzling results (see Dovčiak et al. 2024; Poutanen et al. 2024a; Ursini et al. 2024, for reviews). Low-inclination BH binaries in the hard (or hard-intermediate) state were found to be highly polarized (PD ≈ 4% in Cyg X-1 and Swift J1727.8–1613; Krawczynski et al. 2022; Veledina et al. 2023; Ingram et al. 2024; Podgorný et al. 2024). This is similar to the constraints on PD obtained for AGN (Gianolli et al. 2023; Ingram et al. 2023). In some sources, the PD reached exceptionally high values of ≈10 − 20% (Ursini et al. 2023a; Veledina et al. 2024a). Soft- or soft-intermediate state sources showed no signs of PA rotation (Svoboda et al. 2024a; Marra et al. 2024; Ratheesh et al. 2024; Steiner et al. 2024; Veledina et al. 2024b) and often a high PD that exceeded the standard expectations for the known inclinations. In a number of NS XRBs, a misalignment of the PA with the jet axis or PA rotation was detected (Doroshenko et al. 2023; Rankin et al. 2024; La Monaca et al. 2024; Bobrikova et al. 2024a,b).
These observational properties are challenging to address within the conventional framework that describes the emission of polarized radiation from these sources. Several adjustments of the original models and geometries were considered to align their predictions better with the data. A misalignment between the orbital axis and the spin of the compact object was invoked to enhance the PD and to alter the polarization axis (Krawczynski et al. 2022; Bobrikova et al. 2024a; Rankin et al. 2024). A higher X-ray PD was obtained for the cases of an outflowing material because of the aberration effect (Poutanen et al. 2023; Ratheesh et al. 2024; Dexter & Begelman 2024; Sridhar et al. 2024). In many cases, however, the observed properties can only be explained by stretching or fine-tuning the parameters. It also remains unclear why the soft-state sources show no signs of PA rotation.
An alternative approach to the problem is to assume that polarization originates (partially, entirely, or occasionally) far from the central source, where it remains unaffected by the influences of strong gravity and the fast motions of matter. A natural site for polarization production is scattering of emission from the central source by accretion disk winds.
Observational signatures of accretion disk winds and outflows such as P-Cyg line profiles, blueshifted lines, absorption troughs, and broad emission-line wings were ubiquitously found in XRB spectra (Neilsen & Lee 2009; Ponti et al. 2012, 2016; Muñoz-Darias et al. 2016, 2020; Díaz Trigo & Boirin 2016; Mata Sánchez et al. 2018). These signatures were detected throughout the entire outbursts of XRBs in various wavelengths from the near-infrared to X-rays (Sánchez-Sierras & Muñoz-Darias 2020; Muñoz-Darias & Ponti 2022; Castro Segura et al. 2022; Parra et al. 2024), suggesting that outflows might be common and always present in X-ray binaries. Furthermore, nonzero optical linear polarization of XRBs is known to accompany the wind detections and may originate from the scattering in an optically thin wind (Kosenkov et al. 2017, 2020; Veledina et al. 2019; Kravtsov et al. 2023). This leads to the suggestion that accretion disk winds might play a role in contributing to the X-ray polarization in XRBs. Previous study nevertheless gave negative results (Tomaru et al. 2024).
In the case of broad absorption-line quasars and radio-quiet AGN, wind signatures were found through absorption troughs and blueshifted lines in UV and X-ray wavelengths (Gibson et al. 2009; Tombesi et al. 2010). Narrow blueshifted absorption lines indicating outflows were observed in various ionization states (Crenshaw et al. 2003; Costantini 2010). Equatorial accretion disk winds were also assumed to explain the wings of broad absorption-line quasars (Emmering et al. 1992; Murray et al. 1995). Winds in AGN have been a popular model to unify the different types of AGN (low-luminosity AGN, Seyferts, and broad absorption-line quasars) (Elvis 2000; Giustini & Proga 2019). Thus, it is likely that accretion disk winds are a common feature in AGN as well, similar to XRBs.
We present a broad study of the effects of accretion disk winds on the X-ray polarimetric properties of XRBs and AGN. We consider various properties of the accretion disk wind, such as the opening angle and optical depth, and the angular properties and nature of the illuminating central source. The paper is organized as follows. The model and our solution method are described in Sect. 2. We present the results in Sect. 3. We then discuss our findings and compare the results to the data obtained with IXPE on NS and BH XRBs and Seyfert 1 galaxies in Sect. 4. We summarize our findings in Sect. 5.
2. Model setup and method
We considered the problem of the scattering of X-rays that are produced by the central source in an extended accretion disk wind (see Fig. 1). For our application, we assumed that the central X-ray source is point-like. This is a valid assumption because the size of the X-ray source, a few Schwarzschild radii, is much smaller than the characteristic size of the wind. The radiation from the central source is described by the luminosity (Stokes vector) per unit solid angle L⋆(μ, ϕ) and energy, and in a general case, it depends on the (cosine) angle relative to the disk axis μ and on the azimuthal angle ϕ, and it can be polarized as well. The polarization vector is not necessary aligned with the projection of the symmetry axis on the sky or is perpendicular to that.
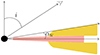 |
Fig. 1. Geometry of the system. The central point-like illuminating source is described by the black circle, the wind is shown in yellow, and the disk is drawn in red. The observer is at an inclination angle i. The opening angle of the wind is given by αw. |
2.1. Scattering in a wind
General expressions for the radiative transfer of polarized radiation in a slab geometry accounting for Thomson scattering are given in Appendix A, where we present the escaping luminosity of the unscattered and single-scattered components. The scattering geometry of the wind is obviously not a slab. However, the expressions for the escaping luminosity hold with a simple substitution of τ/μ′ in Eq. (A.17) by the probability for a photon emitted by the central source at angle μ′ to be scattered within the wind, which depends on the scattering optical depth through the wind in a given direction. In the following, we consider the central illuminating source and the scattering medium to be independent of the azimuthal angle. For the radiation source, we assumed that linear polarization is either parallel to the symmetry axis or is perpendicular to it, and thus, the Stokes U = 0. This means that even though the phase matrix for the four Stokes parameters in Eq. (A.8) depends on the azimuthal angles of the incoming (ϕ′) and scattered (ϕ) radiation, its integration over the azimuthal angle from 0 to 2π yields Stokes U = 0 for the scattered radiation as well. Moreover, below we only consider a linearly polarized source, so that the Stokes V = 0 as well. We also assumed pure scattering (i.e., taking the albedo for a single scattering λ = 1). The Stokes vector thus contains only two components (I, Q).
The unscattered radiation is given by an equation similar to Eq. (A.18),
and the single-scattered radiation is
where the 2 × 2 phase matrix (Chandrasekhar 1960)
now only depends on μ and μ′. For a small optical depth through the wind, the scattering probability is just 1 − exp[−τ(μ′)]≈τ(μ′). We ignored multiple scatterings. We also note that the integration limits in Eq. (2) imply that only radiation emitted to the upper hemisphere and scattered in the wind reaches the observer. In reality, when the wind extends distances that exceed the outer radius of the disk (see Fig. 1), photons emitted to the lower hemisphere might contribute. This additional source would increase the strength of the scattered polarized signal.
2.2. Source of illuminating radiation
An important physical aspect of the system is the property of the central illuminating source luminosity, which we represent as
where L⋆ (without arguments) is the total source luminosity, the angular distribution normalized to unity is ∫01ainc(μ)dμ = 1, and Pinc(μ) is the polarization of the incident radiation. We considered four cases that describe different possible distributions. First, we considered the simplest case of an isotropic unpolarized source,
The second case we considered corresponds to the blackbody radiation from a flat disk. While the intensity does not depend on the viewing angle, the angular distribution of incident luminosity is proportional to the cosine of the inclination,
These two cases can be considered as the first approximation to the incident X-ray emission of accreting BHs in the hard and soft state (Eqs. 5 and 6 respectively). Similarly, the NS spreading layer and the boundary layer or accretion disk can also be approximated by the isotropic spherical and flat sources, respectively.
However, the sources of incident X-ray emission in binaries do not need to be unpolarized or isotropic. The third case we considered is a model that may be applicable to the hard state of accreting BH X-ray binaries, in which X-ray radiation is thought to be produced by thermal Comptonization. In this case, we took the angular distribution of the radiation and polarization degree at 4 keV (in the middle of the IXPE energy range) produced by Comptonization in a static slab (model B in Poutanen et al. 2023) of a Thomson optical depth τT = 1 and an electron temperature of kTe = 100 keV. The angular dependences in this case can be approximated with
The positive P means that polarization vector lies in the meridional plane formed by the normal to the slab and the photon momentum.
The last considered model is the purely electron-scattering-dominated atmosphere that describes the properties of the accretion disk in the soft state of BH X-ray binaries. The angular distribution and polarization can then be approximated by simple formulae (Chandrasekhar 1960; Sobolev 1963; Viironen & Poutanen 2004; Suleimanov et al. 2020),
where the minus sign implies that the polarization is perpendicular to the disk normal. The four cases of the angular distributions of ainc(μ) and Pinc(μ) are shown in Fig. 2.
 |
Fig. 2. Angular distribution (a) and polarization (b) of the incident radiation. The solid red, dotted blue, dashed orange, and dot–dashed black lines correspond to the isotropic (iso), blackbody (bb), Comptonization in a slab (comp), and electron-scattering-dominated disk (es) cases, respectively. |
2.3. Properties of the scattering medium
It is evident that the choice of the optical depth profile is critical. As an example, we chose a Gaussian profile that is given by
where the parameter μw can be interpreted as a sine of the characteristic disk opening angle αw for geometrically thin winds, but it can be even larger than unity in general. The parameter τ0 is the optical depth along the disk midplane. Although the profile Eq. (9) describes the optical depth of the wind and is equal to the scattering probability of a photon emitted at a given angle for small τ0, it does not reflect the angular distribution of the radiation from the central source. The effective optical depth is defined as a product of the angular emission pattern and the actual optical depth,
For small τ0, this is proportional to the probability density dp/dμ for photons to be scattered as a function of inclination, and it is shown in Fig. 3.
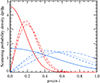 |
Fig. 3. Probability density for photons to be scattered in a wind for different emission models. The solid, dotted, dashed, and dot–dashed lines correspond to the cases of an isotropic, blackbody, Comptonization, and electron-scattering-dominated disk, respectively. The red and blue lines correspond to wind opening angles of αw = 10° and 30°, respectively. |
For an isotropic source, the effective optical depth is simply the same Gaussian as τ(μ). The scattered fraction in this case increases with inclination because more scattering material lies close to the disk. For the flat blackbody-like disk, the dependence of the effective optical depth and scattered fraction on μ is drastically different. The effective optical depth is proportional to μ (since ainc(μ)∝μ), which implies that viewing the system edge-on (μ = cos i ≈ 0) would only result in the observation of scattered radiation. The peak of the effective optical depth is shifted to a higher value of μ ≈ μw = sin αw than in the isotropic case and then again decreases at lower inclinations where the wind optical depth decreases. A similar dependence of the effective optical depth is seen for the electron-scattering-dominated disk. Here, the effective optical depth peaks at a slightly higher μ because the incident emission is more beamed along the disk normal. The radiation pattern produced by Comptonization in a slab falls between the considered cases of isotropic and blackbody emission. This results in a peak of τeff(μ) that appears at intermediate values of μ.
The effective optical depth defines the mean cosine of the interaction angle,
It describes the typical direction of the emission of photons that are scattered in the wind for a given type of illuminating source, optical depth profile, and the wind opening angle. The variation in 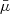 with respect to αw is shown in Fig. 4 for our four emission models. For the three models, the analytical solutions for the integral in Eq. (11) are
with respect to αw is shown in Fig. 4 for our four emission models. For the three models, the analytical solutions for the integral in Eq. (11) are
 |
Fig. 4. Mean interaction angle as a function of the wind opening angle for the four emission patterns isotropic (solid red line), Comptonization (dashed orange), blackbody disk (dotted blue), and electron-scattering-dominated disk (dot-dashed black). |
where 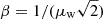 , b = 2.06, and the integrals In = ∫0βxnexp(−x2)dx are
, b = 2.06, and the integrals In = ∫0βxnexp(−x2)dx are
and erf is the error function. All 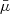 initially increase linearly with αw because scattering material appears at higher latitudes,
initially increase linearly with αw because scattering material appears at higher latitudes, 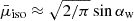 , and others behave as
, and others behave as 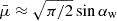 . However, for αw > 30°, they saturate at constant values because the wind material becomes more isotropic and the typical interaction angle is mostly defined by the emission pattern. For example, for the isotropic wind (i.e., for μw → ∞ and β → 0),
. However, for αw > 30°, they saturate at constant values because the wind material becomes more isotropic and the typical interaction angle is mostly defined by the emission pattern. For example, for the isotropic wind (i.e., for μw → ∞ and β → 0), 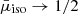 ,
, 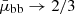 , and
, and 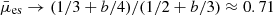 .
. 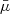 is largest for radiation that is beamed perpendicularly to the disk (electron-scattering-dominated disk) and lowest for an isotropic source, which produces more radiation along the disk where the optical depth of the wind is largest.
is largest for radiation that is beamed perpendicularly to the disk (electron-scattering-dominated disk) and lowest for an isotropic source, which produces more radiation along the disk where the optical depth of the wind is largest.
3. Results
3.1. Dependence on the wind opening angle
We studied the polarization properties of radiation scattered by the wind depending on the parameters for the four emission models. We first considered an isotropic unpolarized source of incident radiation. The dependence of the PD of the scattered component and total emission on the inclination of the observer for different opening angles of the wind and fixed τ0 = 1 is shown in Fig. 5. The PD is reduced at lower inclinations because the perceived symmetry of the system is higher. The PD of scattered emission at low αw and high i reaches values of 30%, in accordance with single scattering in a plane-parallel optically thin slab. Substituting L*(μ′) = L*δ(μ′) to Eq. (3), we obtain (see Eq. (18) of Sunyaev & Titarchuk 1985)
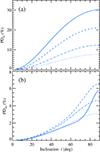 |
Fig. 5. PD of (a) scattered component and (b) total emission as a function of inclination for an isotropic unpolarized incident source. The solid, dashed, dot-dashed, and dotted lines correspond to different opening angles of the wind, αw = 10°, 20°, 30°, and 40°, respectively. The equatorial wind optical depth is τ0 = 1. |
where Pinc is the polarization of the incident emission at μ′ = 0. For an unpolarized central source with Pinc = 0, the maximum PD of the scattered radiation reaches 33% for an edge-on observer. It decreases with increasing wind opening angle because at low αw, the incident radiation is scattered in a plane perpendicular to the disk normal. This produces positive polarization. For high αw, on the other hand, the mean interaction angle 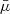 grows, scattering also occurs at high latitudes (high μ′), and negative polarization is produced and the scattered PD is reduced.
grows, scattering also occurs at high latitudes (high μ′), and negative polarization is produced and the scattered PD is reduced.
The total PD depends on the scattered PD and the fraction of scattered radiation. The highest possible PD can be reached at a certain value of αw ≈ 20°. For lower αw, there is less material to scatter, while for higher αw, the scattering medium becomes more isotropic and thereby reduces the polarization.
The scattered and total PD for the case of the blackbody disk illumination is shown in Fig. 6. Similar to the isotropic case, PDsc is positive for low αw as 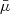 is small. However, as the angular distribution of the blackbody disk radiation is beamed upward from the disk plane, the values of PDsc are lower than that of the isotropic case. The vertical beaming of the illuminating radiation and the high
is small. However, as the angular distribution of the blackbody disk radiation is beamed upward from the disk plane, the values of PDsc are lower than that of the isotropic case. The vertical beaming of the illuminating radiation and the high 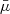 values at high αw eventually results in negative (direction perpendicular to disk normal) PDsc. The total PD is the product of scattered PD and the scattered fraction of radiation. The fraction of scattered light is negligible at low inclinations as the source is vertically beamed, and almost all of the emission that reaches the observer remains unscattered. Thus, PDtot is close to zero at low inclinations. On the other hand, at very high inclinations, most of the radiation that reaches the observer is scattered radiation. The scattered fraction reaches unity for an edge-on observer, and PDtot then equals PDsc.
values at high αw eventually results in negative (direction perpendicular to disk normal) PDsc. The total PD is the product of scattered PD and the scattered fraction of radiation. The fraction of scattered light is negligible at low inclinations as the source is vertically beamed, and almost all of the emission that reaches the observer remains unscattered. Thus, PDtot is close to zero at low inclinations. On the other hand, at very high inclinations, most of the radiation that reaches the observer is scattered radiation. The scattered fraction reaches unity for an edge-on observer, and PDtot then equals PDsc.
For a Comptonizing slab illuminating source, Fig. 7 shows that for a low αw, PDsc is greater than in the isotropic case. This can be explained by the fact that incident radiation is already polarized in the vertical direction. For Pinc = Pcomp of about 7% (Fig. 2), the numerator in Eq. (19) increases by about 20% compared to the case of unpolarized incident radiation, while the denominator for μ = 0 increases by just ≈2%. The PD of the total radiation in this case depends not only on PDsc and the scattered fraction, but also on the intrinsic polarization of the slab. Because the latter is along the same direction as the polarization due to scattering in the wind, the two contributions add up. At low inclinations, PDtot is low because the scattered and intrinsic PD are both small. PDtot very closely follows the intrinsic polarization of the slab as the fraction of scattered light is very small, thereby reducing the contribution of PDsc. At very high inclinations, however, only the scattered component is visible, and hence PDtot reaches PDsc. PDtot exceeds the PD of the incident radiation (shown with the solid black line) when αw ≲ 20°. For thicker winds, radiation scattered at high latitudes reduces the polarization and can even lead to a sign change.
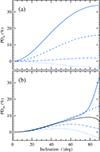 |
Fig. 7. Same as Fig. 5, but for the Comptonization in a slab. The intrinsic PD of the slab is shown by the solid black line. |
The last example is the case of an electron-scattering-dominated disk source. The radiation in this case is beamed more strongly in the vertical direction than in the blackbody disk case, resulting in a greater 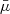 . For small αw < 20°, the PD of the scattered component is positive (Fig. 8) and the PD of the incident radiation is negative. This reduces the overall PD. On the other hand, for αw > 20°, the PD of the scattered radiation has the same sign as that of the incident one, and for αw ≳ 25°, this increases the overall PD.
. For small αw < 20°, the PD of the scattered component is positive (Fig. 8) and the PD of the incident radiation is negative. This reduces the overall PD. On the other hand, for αw > 20°, the PD of the scattered radiation has the same sign as that of the incident one, and for αw ≳ 25°, this increases the overall PD.
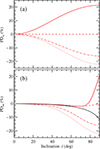 |
Fig. 8. Same as Fig. 5, but for the electron-scattering-dominated disk. The intrinsic PD due to electron scattering in the disk is shown by the solid black line. |
3.2. Dependence on the wind optical depth
The variation in the total PD with inclination for different optical depths for fixed αw is shown in Fig. 9. While the highest considered values of τ0 disagree with the assumption of a low optical depth made in our model, it is important to note that τ0 represents the optical depth value at the disk midplane. At higher inclinations, the optical depth value is much lower and thus satisfies the assumption. The case of an isotropic illuminating source is shown in panel a. As the value of τ0 increases from 0.5 to 1.5, PDtot increases because the greater optical depth implies a larger contribution of the scattered polarized radiation. The behavior of PDtot through the varying optical depth and wind opening angle is shown in Fig. 10a for two inclinations i = 40° and 70°. The highest PD can be obtained for the highest τ0 values and for αw ≈ 20°.
 |
Fig. 9. Total PD as a function of inclination for varying optical depths: τ0 = 0.5 (solid), 0.75 (dashed), 1 (dotted-dashed), 1.25 (dotted), and 1.5 (triple-dot-dashed). The illuminating source is taken to be (a) isotropic, (b) a blackbody unpolarized disk, (c) Comptonization in a slab, and (d) an electron-scattering-dominated disk. The wind opening angle αw is fixed at 20° in cases (a) and (c) and at 40° in cases (b) and (d). In panels (c) and (d), the solid black line shows the PD of the incident radiation. |
 |
Fig. 10. Contours of the constant total PD (in %) on the plane τ0 − αw. The red and blue lines correspond to inclinations of i = 40° and 70°, respectively. The positive PD is shown with the solid lines and the negative PD with the dotted lines. The illuminating source is taken to be (a) isotropic, (b) a blackbody unpolarized disk, (c) Comptonization in a slab, and (d) an electron-scattering dominated disk. The intrinsic PD is zero in cases (a) and (b). In case (c), the intrinsic PD is 4.24% and 8.64% for the two inclinations 40° and 70°, and in case (d), it is −0.73% and −3.46%, respectively. |
For the case of blackbody emission, the optical depth dependence of the PD is shown in Fig. 9b. A change in the optical depth does not affect the maximum attained value of PDtot much because only the scattered radiation is observed at high inclinations. Variation in τ0, however, leads to changes in the scattering fraction at different inclinations, thereby changing the PDtot(i) profile. The overall PD on the plane τ0 − αw is shown in Fig. 10b. Because the incident radiation here is unpolarized, the sign of the PD is determined by the sign of the PD of scattered radiation, which has a monotonic behavior with inclination (Fig. 6). For wind opening angles αw ≲ 25°, PDtot is positive (vertical), and for larger opening angles, PDtot is negative (horizontal). This highlights the importance of the angular distribution of the illuminating source (Fig. 2) and the mean interaction angle (Fig. 4) to the observed polarization.
The role of the optical depth in the polarization of radiation emanating from a Comptonizing slab in the winds is demonstrated in Fig. 9c. The effect of the optical depth variation is only important at high inclinations where the contribution of scattered radiation dominates. Figs. 7 and 10c also show that at low inclinations, PDtot has similar values even when αw varies strongly, whereas PDtot varies more strongly with respect to αw at higher inclinations. Similarly to the blackbody emission, the PD of the scattered component is positive for αw ≲ 30° and negative for thicker winds. Because the intrinsic PD is positive in this model, the total PD increases when the PD of the scattered component exceeds the PD of the incident radiation, that is, for αw ≲ 25°, and it decreases at larger αw. In particular, the PD of the incident emission at i = 70° is 8.64%, and the PD of the total emission may reach values in excess of 10% for τ0 ≳ 0.8 and αw ≈ 10 ° −20°. At i = 40°, the total PD does not reach 5% regardless of τ0 and αw.
For the electron-scattering-dominated disk, the variations in the PDtot due to changes in τ0 for fixed αw = 40° is shown in Fig. 9d. Similarly to the blackbody disk case, the polarization is negative and grows (in absolute value) with increasing τ0. Because the incident radiation here is more beamed perpendicularly to the disk than the blackbody, the typical interaction angle is closer to the disk normal. This produces a higher polarization, which now reaches values −20% for an edge-on observer. The contours of a constant PDtot on the plane τ0 − αw are shown in Fig. 10d. For αw ≲ 20°, the scattered radiation is polarized parallel to the normal, which reduces the total PD. On the other hand, for thicker winds, the situation is reversed and PDtot exceeds the PD of the incident radiation. The highest polarization is produced by scattering in a geometrically and optically thick wind.
4. Discussion
4.1. BH X-ray binaries
4.1.1. Hard state
The low- or hard-state in BH XRBs is seen via spectra that peak at ≈100 keV with a low-temperature disk component (Done et al. 2007). The dominant emitting region is associated with a Comptonizing medium (Sunyaev & Titarchuk 1985; Poutanen & Svensson 1996) of high electron temperatures (Gierlinski et al. 1997; Ibragimov et al. 2005). IXPE observations of the BH binary Cyg X-1 in the hard state measured a PD of ≈4% (Krawczynski et al. 2022), which is much higher than expected for an inclination of ≲30° (Miller-Jones et al. 2021). This has been explained either with a more strongly inclined inner disk compared to the outer disk (Krawczynski et al. 2022) or through Comptonization in a relativistically outflowing corona (Poutanen et al. 2023). The PA was found to align with the position angle of the radio jet (Miller-Jones et al. 2021).
Another BH XRB that was observed by IXPE in the hard-intermediate state was Swift J1727.8−1613. It also showed a PD of ≈4% and an X-ray PA (Veledina et al. 2023) that was aligned with the PA in submillimeter and optical wavelengths (Vrtilek et al. 2023; Kravtsov et al. 2023) as well as the jet direction (Wood et al. 2024). Both sources showed an increasing PD with energy and a constant PA through 2−8 keV range. Moreover, the PA in both cases suggests that the hot emission region is likely extended in a plane perpendicular to the disk axis (Krawczynski et al. 2022; Veledina et al. 2023). This disfavors theoretical models that assume the coronal geometry to be spherical or lamppost-like (Dovčiak et al. 2004; Schnittman & Krolik 2010). Instead, models of polarization based on Comptonization of disk or internal synchrotron photons in an accretion disk corona or hot flow are favored (Sunyaev & Titarchuk 1985; Poutanen & Svensson 1996; Schnittman & Krolik 2010; Poutanen & Veledina 2014), where the hot plasma is extended along the disk plane. However, the high observed PD in these moderate-inclination sources still remain unexplained through these models. This raises the question whether the inclination of the inner accretion disk is higher than that of the outer accretion disk. This can be tested through optical polarization measurements, for example, in the case of MAXI J1820+070 (Poutanen et al. 2022), where a misalignment between the jet axis (BH spin axis) and the orbital axis was discovered. Another possibility is a different source that produces the polarization, such as accretion disk winds.
The isotropic source (Fig. 5) and the Comptonization source (Fig. 7) can produce 4% polarization at inclinations as low as 35°. Moreover, in Swift J1727.8−1613, the PD decreased by 1% as it moved from the hard to the soft state at high luminosity (Ingram et al. 2024), but it recovered its hard-state polarization as it traversed back at low luminosity (Podgorný et al. 2024). The complete recovery of the polarization properties despite the difference of two orders of magnitude in luminosity can be described by a varying optical depth and the wind opening angle (Fig. 10).
Confirmation that the polarization is produced in the winds can be provided by the future eXTP mission, which offers high temporal resolution X-ray polarimetry (Zhang et al. 2019). For example, many X-ray transients show QPOs at subsecond frequencies (van der Klis 2005), and if the X-ray polarization is produced close to the central X-ray source, then this variability should also be reproduced in the polarimetric data. On the other hand, if polarization is produced at much larger distances away from the X-ray source, such as the winds, any variability in the X-ray emission is expected to be smeared out in its polarimetric measurements (see Fig. 4 of Veledina & Poutanen 2015 for a similar analysis of multiwavelength QPOs). Thus, the different components that contribute to the X-ray polarization in different sources can be distinguished.
4.1.2. Soft state
The high- or soft-state in XRBs shows a dominant component peaking at ≈10 keV and has a nonthermal high-energy emission component beyond ≈500 keV (Zdziarski & Gierliński 2004). The soft component is understood to be thermal emission from an optically thick accretion disk (Shakura & Sunyaev 1973; Novikov & Thorne 1973). Both Cyg X-1 and Swift J1727.8−1613 were also observed with IXPE in their soft state (Steiner et al. 2024; Svoboda et al. 2024b), where they showed a much lower PD (≈1%; Dovčiak et al. 2024) than in the hard state. The energy dependence of the polarization (i.e., the increase in PD with energy and constant PA with energy) as seen in the hard state was maintained in the soft state as well for Cyg X-1 (Steiner et al. 2024) and was also seen in the soft-state observations of other sources such as LMC X-3 (Svoboda et al. 2024a) and 4U 1957+11 (Marra et al. 2024). The PD of the latter two sources, even in the highest-energy bins, was lower than ≈6% (see Fig. 7 in Svoboda et al. 2024a). In contrast, IXPE observations of 4U 1630−472 in the soft state (Ratheesh et al. 2024) showed an average PD of 8.3%, and it rose from ≈6% at 2 keV to ≈10% at 8 keV.
Pure electron scattering in the disk atmosphere (Chandrasekhar 1960; Sobolev 1963) can explain the PD seen in moderately inclined sources such as LMC X-3. However, because this is a Thomson scattering process, the PD is constant with energy, unlike what is observed. Moreover, low-inclination sources such as Cyg X-1 and LMC X-1 require the incorporation of absorption effects to the accretion disk emission to produce the observed PD. Even in this case, the PD tends to decrease with energy (rather than increase, as suggested by the observations) in the 2−8 keV band, and any spin of the BH can further decrease the PD (Taverna et al. 2021). Furthermore, when special and general relativistic effects are accounted for (Stark & Connors 1977; Loktev et al. 2022, 2024), the PD is ≈6% at most for high inclinations alone. For inclinations < 30°, the theoretically expected PD is < 0.5%. Thus, the general expectations of polarization values fail to explain the observed PD and its energy dependence in multiple sources that were observed in the soft state, and even more so for the exceptional case of 4U 1630−472.
In our models, the blackbody disk source (Fig. 6) and the disk source with electron scattering (Fig. 8) characterize the soft state. First, sources with inclinations > 30° have a PD of about a few percent, as observed by IXPE. Cyg X-1 seems to have a dominant Comptonized component even in the soft state (Gierliński et al. 1999), and the results presented in Fig. 7 may characterize this source better. Second, the PD increases rapidly for higher inclinations, and the ≈8% PD seen in 4U 1630−472 is realized at an inclination of > 60°. The estimated inclination of 4U 1630−472 is 65 ° < i < 75° (Kuulkers et al. 1998; Tomsick et al. 1998). A polarization of 10% perpendicular to the disk normal can be achieved at i = 70° for αw = 40°. Moreover, the X-ray polarization for this source was again measured in its steep power-law (very high) state. This usually occurs during a transition from hard to soft states. From the ≈8.3% in the soft state, the source PD decreased to ≈7.5% and then ≈6.5% through the steep power-law state (Rodriguez Cavero et al. 2023). This transition can be described by a reduced wind opening angle, αw. As αw decreases from 40° to 30° (corresponding to a decrease in the effective optical depth from 0.63 to 0.55 at i = 65°), Fig. 8 shows that for the given inclination, the PD magnitude decreases from 8% to 5%. Thus, a gradual decrease in the wind opening angle can automatically describe the change in the PD during the state transition period. Our models suggest that the polarization observed in 4U 1630−472 in its soft and steep power-law state is directed perpendicular to the disk normal.
Many of the sources, including 4U 1630−472, showed a dependence of the PD that increased with increasing energy (Ratheesh et al. 2024; Svoboda et al. 2024a; Steiner et al. 2024; Marra et al. 2024). While a detailed analysis of the energy dependence of PD is left to future work, we discuss the potential origins of this trend. The first origin might be the influence of local absorption. While Thomson scattering is independent of energy, true absorption depends on energy. Thus, the albedo, λE = σes/(σes + κab) (where σes is the scattering coefficient and κab is the true absorption coefficient) depends on energy and directly influences the scattered fraction. Alternatively, an inherent energy dependence of the central illuminating source might also lead to an energy dependence of the resulting polarization. Loktev et al. (2022, 2024) described the accretion disk properties, including the Stokes I and Q (and U) parameters, for each inclination and energy band after accounting for special and general relativistic effects in the Schwarzschild and the Kerr metrics, respectively. Doppler effects due to rotation of the accretion disk can also influence the observed energy dependence of the PD. The velocity of the accretion disk increases as the radius decreases, resulting in a stronger Doppler boosting: The higher-energy photons tend to be beamed more strongly along the disk plane, and they therefore have a higher chance to be scattered by equatorial wind. This effect leads to a PD that grows with energy.
The absence of an energy dependence of PA in the sources listed above can be explained by scattering in disk winds that occur far away from the compact object. They are thereby only very little affected by the gravitational effects that tend to rotate the PA (Stark & Connors 1977; Loktev et al. 2022, 2024).
4.2. Weakly magnetized NS binaries
In case of NS XRBs, soft emission can arise from the NS surface or the accretion disk (Shakura & Sunyaev 1973, 1988). These can be approximately modeled as isotropic or blackbody disk-like emission of the central illuminating source, respectively. In principle, the NS surface and the disk can be modeled as a set of blackbodies with different PDs and PAs, and the total polarized flux can be computed from the sum of the corresponding Stokes parameters. On the other hand, the harder Comptonized X-rays are emitted either by a hot corona, by the boundary layer (BL) between the NS and the accretion disk, or by the spreading layer (SL) at the NS surface (Shakura & Sunyaev 1988; Inogamov & Sunyaev 1999; Popham & Sunyaev 2001; Suleimanov & Poutanen 2006).
Observations obtained with IXPE of weakly magnetized NS-LMXBs have measured significant polarization from these sources (Ursini et al. 2024). The PD and PA measurements of sources such as GS 1826−238 (Capitanio et al. 2023) and Cyg X-2 (Farinelli et al. 2023) favor a spherically or vertically extended geometry for the optically thick medium rather than one that is radially extended along the disk plane. Atolls observed in the soft state, such as GX 9+9 (Ursini et al. 2023b), 4U 1820−303 (Di Marco et al. 2023), and 4U 1624−49 (Saade et al. 2024), show an increasing trend of the PD with energy, similar to what was seen in many BH XRBs. While most atoll sources showed a PD lower than ≈2% in the 2−8 keV band, 4U 1820−303 and 4U 1624−49 showed a much higher PD in the higher-energy bands (reaching ≈10% and ≈6%, respectively; Di Marco et al. 2023; Saade et al. 2024). In the case of Z sources, observations of XTE J1701−462 and GX 5−1 have revealed a pattern of the PD that is based on its position on the Z track (Ursini et al. 2024). A higher PD of ≈4−5% was observed at the horizontal branch and a lower PD of ≈1−2% at the normal and flaring branch (Cocchi et al. 2023; Fabiani et al. 2024).
Expected PDs from the disk and the BL were described, for example, by Dovčiak et al. (2008) and Loktev et al. (2022). About ≈6−8% of the PD is achieved in these models at the highest inclinations, zero spin, and at low energies (well below the IXPE range). The contribution to the polarization from the SL was modeled by Farinelli et al. (2024) and Bobrikova et al. (2024c) with a maximum PD of ≈2% at the highest inclinations and high energies. The polarization of a few percent in these sources can be explained by these models. However, the high PD seen in 4U 1820−303 and 4U 1624−49 is still only poorly understood, and scattering in a wind might need to be invoked. In the case of 4U 1624−49 (Saade et al. 2024), at the source inclination of > 60° (Frank et al. 1987), a PD of 6% can be achieved in both cases: whether the central illuminating X-ray source is taken to be the inner accretion disk (Fig. 8) or isotropic (e.g., mimicking the SL; see Fig. 9a). The direction of the PA with respect to the disk normal discerns between the two possibilities. 4U 1820−303 is a moderate-inclination source, and the polarization of the hard and soft components is orthogonal to each other (Di Marco et al. 2023). The latter property is readily explained by the choice of illuminating source in our wind-scattering models. Cooler radiation from a disk-type source (Figs. 6 and 8) shows a polarization perpendicular to the disk normal, while the hotter radiation from the SL (isotropic) or inner hot flow (Comptonization) (Figs. 5 and 7) is polarized along the disk normal. We only considered the contribution to the polarization from scattering in the winds above the accretion disk midplane so far. However, an additional contribution can also be provided by the winds at the opposite side of the disk, that is, below the disk midplane (see Fig. 1). Because the polarization from both parts will be aligned, greater PD values can be obtained that explain the high observed polarization values in sources such as 4U 1820−303.
In addition to the atoll and Z sources mentioned above, IXPE also measured the polarization of some peculiar sources, such as Cir X-1 (Rankin et al. 2024) and GX 13+1 (Bobrikova et al. 2024a,b). While the PD of Cir X-1 was ≈1% throughout, the PA seemed to vary across different orbital phases (≈50° rotation) and different hardness ratios (Rankin et al. 2024). This was explained by the presence of two components that cause the observed polarization (BL and SL), depending on the accretion rate. A misalignment between the NS rotation axis and the orbital disk axis might explain the varying PA. Unless the source is highly inclined, the SL cannot produce a polarization of ≈1.5% (Bobrikova et al. 2024c) but if the emission from the SL is scattered in the accretion disk wind, the observed PD can be reached for inclinations as low as 25° (Fig. 9a). The absence of strong gravitational effects in wind scattering can explain the difference in PA with respect to polarization produced in the BL.
GX 13+1 is an X-ray burster that shows variable polarization with respect to time and energy (Bobrikova et al. 2024a). The PA slowly increased with time and varied up to 70°, while the PD first decreased and then increased after an observed dip in the light curve. A constant polarization component, such as scattering in the wind, along with a variable component that depends on the BL and SL were used to explain the observed behavior of polarization. The constant component needs to have a PD of ≈2% for a source with a high inclination, 60°–85° (see Fig. 12 in Bobrikova et al. 2024a). This is easily reached in our models, and the direction of the PA will help us further to identify the nature of the central illuminating X-ray source in the case. On the other hand, when we assume that the BL or SL contributes to the constant component and the winds dictate the variable component, we need to explain a PD variation from ≈5% to ≈3.5%. This can be understood by the varying optical depth of the wind material. Figure 9a shows that by varying the optical depth, τ0, and hence the optical depth profile over all inclinations, the total PD produced can be altered. Fixing the inclination at 60°, for example, we can obtain a polarization of 3% for τ0 = 0.75 and 5% for τ0 = 1.25.
Another crucial point is the changing PA with time. This can be interpreted by invoking the misaligned BL and the changing optical depth in the winds. Optically thin winds allow more polarized light from the BL or SL to pass through, while optically thicker winds will reduce the light from the central source. The PA of the observed radiation, which depends on the source of the polarization and its geometry, therefore varies. The further observation and analysis of this source by Bobrikova et al. (2024b) suggested a disk component with a PD of ≈6.5% (see their Fig. 5). This is difficult to reach in the IXPE range (Loktev et al. 2022), but scattering in the winds provides an alternate solution for reaching high PD values like this.
4.3. X-ray pulsars
During the first two and a half years of operation, IXPE has observed a dozen X-ray pulsars (see Poutanen et al. 2024a, for a review). In most of them, polarization was significantly detected, and the variations in the PA with the pulse phase followed the rotating vector model (RVM; Meszaros et al. 1988; Poutanen 2020). However, two bright transients LS V+44 17 (Doroshenko et al. 2023) and Swift J0243.6+6124 (Poutanen et al. 2024b) showed a peculiar behavior. Two observations of LS V+44 17 in 2023 about two weeks apart showed a dramatically different dependence of the PA with pulse phase, with the PA profiles in the two observations being in antiphase. The data might be explained by a two-component model in which one pulse-phase-dependent component produced by the pulsar follows the RVM, while another polarized component does not vary with phase. The polarized flux of the constant component was estimated to be about 3−4% of the average flux, which might be produced if that component had a PD of 30% and contributed one-tenth of the mean flux, for example. The suggestion put forward by Doroshenko et al. (2023) was that scattering in the equatorial disk wind could be the origin of the constant polarized component. For a high-inclination source such as LS V+44 17, our wind-scattering model (see Figs. 5 and 9a) can easily reproduce the data. The value of PD and direction of PA of the constant component not only sheds light on the relevant central X-ray source, but also constrains the inclination of the source. The disk inclination needs to be ≳50° for a PD of 4% in the total emission (Fig. 9a).
A similar analysis was also reported for Swift J0243.6+6124 (Poutanen et al. 2024b). IXPE observed the source three times during its 2023 outburst. In two observations, the pulse-phase dependence of the PA followed a double sine wave, which is inconsistent with the RVM. Using the two-component model, the authors showed that the pulse-phase variation in the PA can be reconciled with the RVM. In this source, the polarized flux of the constant component varied between 1.5% and 3% of the mean flux, which can also easily be explained by the wind scattering.
We again recall that our models only present polarization produced in winds that are on the near side of the disk for the observer (above the disk midplane in Fig. 1). Contribution from winds on the far side of the disk (below the disk midplane) would increase the observed PD. Because radiation from X-ray pulsars depends on the azimuthal angle (i.e., on the pulsar phase), polarization produced by wind scattering is also expected to vary with pulsar phase, but a smaller amplitude than that of the pulsar radiation itself. This would be an interesting problem to solve in the future.
4.4. Seyfert 1 galaxies
IXPE has measured the X-ray polarization of three Seyfert 1 galaxies, namely, IC 4329A (Ingram et al. 2023), NGC 4151 (Gianolli et al. 2023, 2024), and MCG-5-23-16 (Marinucci et al. 2022; Tagliacozzo et al. 2023). The latter showed a marginally significant polarization of 1.6 ± 0.7% (corresponding to an upper limit of 3.2% at the 99% confidence level). At a possible inclination of 30°, this small PD can be produced by thermal Comptonization in a slab geometry, or it can be produced by Thomson scattering of this radiation in a wind with a wide range of wind opening angles and optical depths (Fig. 7). Alternatively, scattering in a wind of αw ≈ 40° of an intrinsically unpolarized isotropic source can produce this PD (Fig. 5).
The measured polarization of IC 4329A was 3.3 ± 1.1%, and it was aligned with the jet (Ingram et al. 2023). Based on our models (Fig. 7), this implies that the inclination of the source is between ≈20°–35°, which is consistent with the inclination expected for a Seyfert 1.2 galaxy.
NGC 4151 shows an X-ray PD of 4.5 ± 0.9%. The measured PA = 81 ° ±6° in the 2−8 keV band aligns well with the extended radio emission, which is presumably perpendicular to the accretion disk plane. Scattering in the winds can reproduce this polarization for inclinations over 40° (Fig. 7) which is the expected inclination of the central part of a Seyfert 1.5 galaxy. Bentz et al. (2022) modeled the emission-line variations by constraining the broad-line region opening angle of ≈57° (i.e., 33° if measured from the disk plane) and the observer inclination of 58°. The observed X-ray PD can then be reproduced by Comptonization in a slab geometry (see the dashed lines in Fig. 2), or by scattering of this radiation in a wedge (wind or broad-line region) with an opening angle of 30° (Fig. 7), or even by scattering of an isotropic unpolarized source in a wind (Fig. 9a).
5. Summary
Models of XRBs and AGN are well described by a multitemperature blackbody disk and a Comptonizing corona. However, recent IXPE observations of these objects did not only show that the X-ray PD is larger than previously understood, but also discovered variations in the polarization that have invoked advanced models. Additionally, XRBs and AGN have shown the ubiquitous presence of accretion disk winds, which led to the speculation that scattering in the winds might contribute to the observed polarization in these sources. We have developed a model for the X-ray polarization that is produced in XRBs and AGN by single Thomson scattering in the accretion disk winds, with variable wind opening angles and optical depths. We showed that our model can explain the high levels of polarization observed in these sources. For 4U 1630−472, a high PD of ≈8% was observed in the soft state, which can be achieved by our models for high inclinations. Moreover, the source showed a constant PA with respect to energy, which is expected because scattering in the winds occurs much farther away from the central BH and the general relativistic rotation of the PA is negligible. In the case of GX 13+1, a slow rotation of the PA of up to 70° was observed. This can be explained by scattering in winds that are produced in the outer regions of the accretion disk, which is misaligned with the BL or SL of the NS. A slow variation in the optical depth of the winds naturally results in a slow rotation of the observed PA. Finally, for LS V +44 17, the standard RVM model was unable to explain the dramatic change in the observed PA over a short period of time. Instead, the observed data can be explained by assuming that two components contribute to polarization: a pulse-phase-dependent component that follows the RVM model, and a constant component described by scattering in the winds. Thus, we showed that scattering in accretion disk winds is important for understanding the polarization properties, and hence, the geometry of the accretion regimes in XRBs and AGN. We leave a more detailed modeling of a source that is not axially symmetric for future work, together with the study of the energy dependence of the polarization in our models.
Acknowledgments
This research has been supported by the Academy of Finland grant 355672 (AV) and the Ministry of Science and Higher Education grant 075-15-2024-647. Nordita is supported in part by NordForsk.
References
- Bambi, C., Brenneman, L. W., Dauser, T., et al. 2021, Space Sci. Rev., 217, 65 [CrossRef] [Google Scholar]
- Bentz, M. C., Williams, P. R., & Treu, T. 2022, ApJ, 934, 168 [CrossRef] [Google Scholar]
- Bobrikova, A., Forsblom, S. V., Di Marco, A., et al. 2024a, A&A, 688, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobrikova, A., Di Marco, A., La Monaca, F., et al. 2024b, A&A, 688, A217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bobrikova, A., Poutanen, J., & Loktev, V. 2024c, A&A, submitted, [arXiv:2409.16023] [Google Scholar]
- Capitanio, F., Fabiani, S., Gnarini, A., et al. 2023, ApJ, 943, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Castro Segura, N., Knigge, C., Long, K. S., et al. 2022, Nature, 603, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative Transfer (New York: Dover) [Google Scholar]
- Cocchi, M., Gnarini, A., Fabiani, S., et al. 2023, A&A, 674, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Connors, P. A., & Stark, R. F. 1977, Nature, 269, 128 [Google Scholar]
- Connors, P. A., Piran, T., & Stark, R. F. 1980, ApJ, 235, 224 [Google Scholar]
- Costantini, E. 2010, Space Sci. Rev., 157, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., & George, I. M. 2003, ARA&A, 41, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., & Begelman, M. C. 2024, MNRAS, 528, L157 [Google Scholar]
- Dexter, J., & Quataert, E. 2012, MNRAS, 426, L71 [CrossRef] [Google Scholar]
- Díaz Trigo, M., & Boirin, L. 2016, Astron. Nachr., 337, 368 [Google Scholar]
- Di Marco, A., La Monaca, F., Poutanen, J., et al. 2023, ApJ, 953, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [Google Scholar]
- Doroshenko, V., Poutanen, J., Heyl, J., et al. 2023, A&A, 677, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dovčiak, M., Karas, V., & Matt, G. 2004, MNRAS, 355, 1005 [CrossRef] [Google Scholar]
- Dovčiak, M., Muleri, F., Goosmann, R. W., Karas, V., & Matt, G. 2008, MNRAS, 391, 32 [CrossRef] [Google Scholar]
- Dovčiak, M., Podgorný, J., Svoboda, J., et al. 2024, Galaxies, 12, 54 [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Emmering, R. T., Blandford, R. D., & Shlosman, I. 1992, ApJ, 385, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Esin, A. A., McClintock, J. E., & Narayan, R. 1997, ApJ, 489, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Fabiani, S., Capitanio, F., Iaria, R., et al. 2024, A&A, 684, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Fabiani, S., Poutanen, J., et al. 2023, MNRAS, 519, 3681 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., Waghmare, A., Ducci, L., & Santangelo, A. 2024, A&A, 684, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A. R., & Lasota, J.-P. 1987, A&A, 178, 137 [Google Scholar]
- Gianolli, V. E., Kim, D. E., Bianchi, S., et al. 2023, MNRAS, 523, 4468 [NASA ADS] [CrossRef] [Google Scholar]
- Gianolli, V. E., Bianchi, S., Kammoun, E., et al. 2024, A&A, 691, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, R. R., Jiang, L., Brandt, W. N., et al. 2009, ApJ, 692, 758 [Google Scholar]
- Gierlinski, M., Zdziarski, A. A., Done, C., et al. 1997, MNRAS, 288, 958 [CrossRef] [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [CrossRef] [Google Scholar]
- Giustini, M., & Proga, D. 2019, A&A, 630, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Homan, J., & Belloni, T. 2005, Ap&SS, 300, 107 [Google Scholar]
- Ibragimov, A., Poutanen, J., Gilfanov, M., Zdziarski, A. A., & Shrader, C. R. 2005, MNRAS, 362, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., Ewing, M., Marinucci, A., et al. 2023, MNRAS, 525, 5437 [CrossRef] [Google Scholar]
- Ingram, A., Bollemeijer, N., Veledina, A., et al. 2024, ApJ, 968, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 1999, Astron. Lett., 25, 269 [NASA ADS] [Google Scholar]
- Jiang, Y.-F., Stone, J. M., & Davis, S. W. 2013, ApJ, 778, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenkov, I. A., Berdyugin, A. V., Piirola, V., et al. 2017, MNRAS, 468, 4362 [NASA ADS] [CrossRef] [Google Scholar]
- Kosenkov, I. A., Veledina, A., Berdyugin, A. V., et al. 2020, MNRAS, 496, L96 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, V., Nitindala, A. P., Veledina, A., et al. 2023, ATel, 16245, 1 [NASA ADS] [Google Scholar]
- Krawczynski, H., & Beheshtipour, B. 2022, ApJ, 934, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczynski, H., Muleri, F., Dovčiak, M., et al. 2022, Science, 378, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Kuulkers, E., Wijnands, R., Belloni, T., et al. 1998, ApJ, 494, 753 [NASA ADS] [CrossRef] [Google Scholar]
- La Monaca, F., Di Marco, A., Poutanen, J., et al. 2024, ApJ, 960, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Loktev, V., Veledina, A., & Poutanen, J. 2022, A&A, 660, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loktev, V., Veledina, A., Poutanen, J., Nättilä, J., & Suleimanov, V. F. 2024, A&A, 685, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinucci, A., Muleri, F., Dovciak, M., et al. 2022, MNRAS, 516, 5907 [NASA ADS] [CrossRef] [Google Scholar]
- Marra, L., Brigitte, M., Rodriguez Cavero, N., et al. 2024, A&A, 684, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mata Sánchez, D., Muñoz-Darias, T., Casares, J., et al. 2018, MNRAS, 481, 2646 [Google Scholar]
- Matt, G. 1993, MNRAS, 260, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Meszaros, P., Novick, R., Szentgyorgyi, A., Chanan, G. A., & Weisskopf, M. C. 1988, ApJ, 324, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
- Muñoz-Darias, T., & Ponti, G. 2022, A&A, 664, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz-Darias, T., Casares, J., Mata Sánchez, D., et al. 2016, Nature, 534, 75 [Google Scholar]
- Muñoz-Darias, T., Armas Padilla, M., Jiménez-Ibarra, F., et al. 2020, ApJ, 893, L19 [CrossRef] [Google Scholar]
- Murray, N., Chiang, J., Grossman, S. A., & Voit, G. M. 1995, ApJ, 451, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405 [Google Scholar]
- Neilsen, J., & Lee, J. C. 2009, Nature, 458, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, Black Holes (Les Astres Occlus) (New York: Gordon& Breach), 343 [Google Scholar]
- Page, D. N., & Thorne, K. S. 1974, ApJ, 191, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parra, M., Petrucci, P. O., Bianchi, S., et al. 2024, A&A, 681, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pineault, S. 1977, MNRAS, 179, 691 [Google Scholar]
- Pineault, S., & Roeder, R. C. 1977, ApJ, 213, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Podgorný, J., Svoboda, J., Dovčiak, M., et al. 2024, A&A, 686, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponti, G., Fender, R. P., Begelman, M. C., et al. 2012, MNRAS, 422, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Bianchi, S., Muñoz-Darias, T., et al. 2016, Astron. Nachr., 337, 512 [Google Scholar]
- Popham, R., & Sunyaev, R. 2001, ApJ, 547, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Done, C., & Osborne, J. P. 1995, MNRAS, 277, L5 [NASA ADS] [Google Scholar]
- Poutanen, J. 2020, A&A, 641, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [CrossRef] [Google Scholar]
- Poutanen, J., & Veledina, A. 2014, Space Sci. Rev., 183, 61 [CrossRef] [Google Scholar]
- Poutanen, J., Nagendra, K. N., & Svensson, R. 1996, MNRAS, 283, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Krolik, J. H., & Ryde, F. 1997, MNRAS, 292, L21 [NASA ADS] [Google Scholar]
- Poutanen, J., Veledina, A., & Zdziarski, A. A. 2018, A&A, 614, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., Veledina, A., Berdyugin, A. V., et al. 2022, Science, 375, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Veledina, A., & Beloborodov, A. M. 2023, ApJ, 949, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Tsygankov, S. S., & Forsblom, S. V. 2024a, Galaxies, 12, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., Tsygankov, S. S., Doroshenko, V., et al. 2024b, A&A, 691, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rankin, J., La Monaca, F., Di Marco, A., et al. 2024, ApJ, 961, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Ratheesh, A., Dovčiak, M., Krawczynski, H., et al. 2024, ApJ, 964, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [Google Scholar]
- Rodriguez Cavero, N., Marra, L., Krawczynski, H., et al. 2023, ApJ, 958, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Saade, M. L., Kaaret, P., Gnarini, A., et al. 2024, ApJ, 963, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Sierras, J., & Muñoz-Darias, T. 2020, A&A, 640, L3 [EDP Sciences] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2009, ApJ, 701, 1175 [CrossRef] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2010, ApJ, 712, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1988, Adv. Space Res., 8, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolev, V. V. 1963, A Treatise on Radiative Transfer (Princeton: Van Nostrand) [Google Scholar]
- Sridhar, N., Ripperda, B., Sironi, L., Davelaar, J., & Beloborodov, A. M. 2024, ApJ, submitted [arXiv:2411.10662] [Google Scholar]
- Stark, R. F., & Connors, P. A. 1977, Nature, 266, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, J. F., Nathan, E., Hu, K., et al. 2024, ApJ, 969, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Stokes, G. G. 1851, Trans. Camb. Philos. Soc., 9, 399 [NASA ADS] [Google Scholar]
- Suleimanov, V., & Poutanen, J. 2006, MNRAS, 369, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Suleimanov, V. F., Poutanen, J., & Werner, K. 2020, A&A, 639, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1985, A&A, 143, 374 [NASA ADS] [Google Scholar]
- Svoboda, J., Dovčiak, M., Steiner, J. F., et al. 2024a, ApJ, 960, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Svoboda, J., Dovčiak, M., Steiner, J. F., et al. 2024b, ApJ, 966, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Tagliacozzo, D., Marinucci, A., Ursini, F., et al. 2023, MNRAS, 525, 4735 [CrossRef] [Google Scholar]
- Taverna, R., Marra, L., Bianchi, S., et al. 2021, MNRAS, 501, 3393 [NASA ADS] [Google Scholar]
- Tomaru, R., Done, C., & Odaka, H. 2024, MNRAS, 527, 7047 [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomsick, J. A., Lapshov, I., & Kaaret, P. 1998, ApJ, 494, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Ursini, F., Marinucci, A., Matt, G., et al. 2023a, MNRAS, 519, 50 [Google Scholar]
- Ursini, F., Farinelli, R., Gnarini, A., et al. 2023b, A&A, 676, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ursini, F., Gnarini, A., Capitanio, F., et al. 2024, Galaxies, 12, 43 [NASA ADS] [CrossRef] [Google Scholar]
- van der Klis, M. 2005, Astron. Nachr., 326, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Veledina, A., & Poutanen, J. 2015, MNRAS, 448, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Veledina, A., Berdyugin, A. V., Kosenkov, I. A., et al. 2019, A&A, 623, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veledina, A., Muleri, F., Dovčiak, M., et al. 2023, ApJ, 958, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Veledina, A., Muleri, F., Poutanen, J., et al. 2024a, Nat. Astron., 8, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Veledina, A., Poutanen, J., Bocharova, A., et al. 2024b, A&A, 688, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viironen, K., & Poutanen, J. 2004, A&A, 426, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vrtilek, S. D., Gurwell, M., McCollough, M., & Rao, R. 2023, ATel, 16230, 1 [NASA ADS] [Google Scholar]
- Weisskopf, M. C., Soffitta, P., Baldini, L., et al. 2022, JATIS, 8, 026002 [NASA ADS] [Google Scholar]
- Wood, C. M., Miller-Jones, J. C. A., Bahramian, A., et al. 2024, ApJ, 971, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., & Gierliński, M. 2004, Prog. Theor. Phys. Suppl., 155, 99 [CrossRef] [Google Scholar]
- Zdziarski, A. A., Poutanen, J., & Johnson, W. N. 2000, ApJ, 542, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Santangelo, A., Feroci, M., et al. 2019, Sci. China Phys. Mech. Astron., 62, 29502 [Google Scholar]
- Zhang, W., Dovčiak, M., Bursa, M., et al. 2022, MNRAS, 515, 2882 [CrossRef] [Google Scholar]
Appendix A: Polarized radiative transfer in a slab
The radiation field is fully described by the Stokes vector (Stokes 1851) I = (I, Q, U, V)T. We introduce the spherical coordinate system with the z-axis along the disk axis 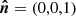 . We choose the external polarization basis defined by the vector
. We choose the external polarization basis defined by the vector 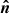 and the unit vector along the photon momentum
and the unit vector along the photon momentum 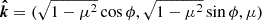 , with μ being the cosine of the polar angle and ϕ is the azimuthal angle. The basis for the scattered photon is given by
, with μ being the cosine of the polar angle and ϕ is the azimuthal angle. The basis for the scattered photon is given by
Similar expressions can be written for the external basis for the incoming photon before scattering 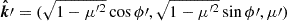 with changing ϕ by ϕ′ and μ by μ′.
with changing ϕ by ϕ′ and μ by μ′.
Scattering of radiation is best described using the internal bases formed by the two photon momenta. The internal basis for the scattered photon is
where 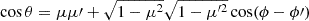 is the cosine of the scattering angle. Similarly, the internal basis for the incoming photon can be obtained by replacing
is the cosine of the scattering angle. Similarly, the internal basis for the incoming photon can be obtained by replacing 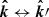 .
.
Transformation of the Stokes vector between the external and internal bases is described by the rotation matrix
where for scattered photon  we have
we have
Similar expressions can be written for an incoming photon  .
.
A rather general form of the radiative transfer equation (RTE) describing Thomson scattering (and true absorption) in the plane-parallel atmosphere that allows us to consider arbitrary polarized source of radiation as well as nonaxisymmetric scattering medium can be written as (Chandrasekhar 1960):
where dτ = σTnedz is the Thomson scattering optical depth, λ is the albedo for single scattering (i.e. the ratio of the scattering to the total opacity). The source Stokes vector S can be expressed through the integral over the solid angle of the Stokes vector of the incoming radiation and the phase matrix:
where the phase matrix is given by the product of two rotation matrices and the scattering matrix:
The Thomson scattering matrix is
and the elements of the phase matrix are
where 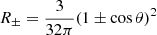 and other matrix elements are zeros. Cosines and sines of the difference and sum of χ and χ1 can be computed using relations
and other matrix elements are zeros. Cosines and sines of the difference and sum of χ and χ1 can be computed using relations
Let us consider a slab of finite vertical (scattering) optical depth τ0 with the boundary condition at the bottom I(τ = 0, μ, ϕ) = B(μ, ϕ). For small τ0, we can solve the RTE in the single-scattering approximation by representing the solution as a sum of unscattered radiation and radiation that is scattered once. The unscattered radiation is:
The single-scattered radiation is then given by the Stokes vector
where S1 is given by Eq. (A.8) with I0 instead of I. In the case of small optical depth (when single-scattering approximation can be used), I1 can be approximated
The same expression can be rewritten in terms of the luminosity per unit solid angle emitted in a given direction L ∝ μI as
where the incident luminosity at the boundary is L⋆(μ, ϕ)∝μB(μ, ϕ) and the unscattered escaping luminosity
The total escaping luminosity (Stokes vector) is
All Figures
 |
Fig. 1. Geometry of the system. The central point-like illuminating source is described by the black circle, the wind is shown in yellow, and the disk is drawn in red. The observer is at an inclination angle i. The opening angle of the wind is given by αw. |
| In the text | |
 |
Fig. 2. Angular distribution (a) and polarization (b) of the incident radiation. The solid red, dotted blue, dashed orange, and dot–dashed black lines correspond to the isotropic (iso), blackbody (bb), Comptonization in a slab (comp), and electron-scattering-dominated disk (es) cases, respectively. |
| In the text | |
 |
Fig. 3. Probability density for photons to be scattered in a wind for different emission models. The solid, dotted, dashed, and dot–dashed lines correspond to the cases of an isotropic, blackbody, Comptonization, and electron-scattering-dominated disk, respectively. The red and blue lines correspond to wind opening angles of αw = 10° and 30°, respectively. |
| In the text | |
 |
Fig. 4. Mean interaction angle as a function of the wind opening angle for the four emission patterns isotropic (solid red line), Comptonization (dashed orange), blackbody disk (dotted blue), and electron-scattering-dominated disk (dot-dashed black). |
| In the text | |
 |
Fig. 5. PD of (a) scattered component and (b) total emission as a function of inclination for an isotropic unpolarized incident source. The solid, dashed, dot-dashed, and dotted lines correspond to different opening angles of the wind, αw = 10°, 20°, 30°, and 40°, respectively. The equatorial wind optical depth is τ0 = 1. |
| In the text | |
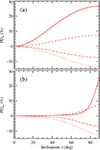 |
Fig. 6. Same as Fig. 5, but for the blackbody unpolarized disk. |
| In the text | |
 |
Fig. 7. Same as Fig. 5, but for the Comptonization in a slab. The intrinsic PD of the slab is shown by the solid black line. |
| In the text | |
 |
Fig. 8. Same as Fig. 5, but for the electron-scattering-dominated disk. The intrinsic PD due to electron scattering in the disk is shown by the solid black line. |
| In the text | |
 |
Fig. 9. Total PD as a function of inclination for varying optical depths: τ0 = 0.5 (solid), 0.75 (dashed), 1 (dotted-dashed), 1.25 (dotted), and 1.5 (triple-dot-dashed). The illuminating source is taken to be (a) isotropic, (b) a blackbody unpolarized disk, (c) Comptonization in a slab, and (d) an electron-scattering-dominated disk. The wind opening angle αw is fixed at 20° in cases (a) and (c) and at 40° in cases (b) and (d). In panels (c) and (d), the solid black line shows the PD of the incident radiation. |
| In the text | |
 |
Fig. 10. Contours of the constant total PD (in %) on the plane τ0 − αw. The red and blue lines correspond to inclinations of i = 40° and 70°, respectively. The positive PD is shown with the solid lines and the negative PD with the dotted lines. The illuminating source is taken to be (a) isotropic, (b) a blackbody unpolarized disk, (c) Comptonization in a slab, and (d) an electron-scattering dominated disk. The intrinsic PD is zero in cases (a) and (b). In case (c), the intrinsic PD is 4.24% and 8.64% for the two inclinations 40° and 70°, and in case (d), it is −0.73% and −3.46%, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \boldsymbol{L}_0(\mu )=\boldsymbol{L}_{\star } (\mu )\, \exp [-\tau (\mu )], \end{aligned} $$](/articles/aa/full_html/2025/02/aa53188-24/aa53188-24-eq1.gif)
![$$ \begin{aligned} \boldsymbol{L}_1 (\mu ) = \int \limits _{0}^{1} \mathrm{d}\mu \prime \; \mathsf P (\mu ;\mu \prime ) \boldsymbol{L}_{\star } (\mu \prime )\, \{1-\exp [-\tau (\mu \prime )]\}, \end{aligned} $$](/articles/aa/full_html/2025/02/aa53188-24/aa53188-24-eq2.gif)
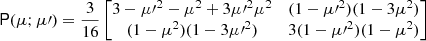
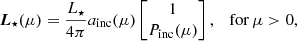

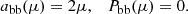
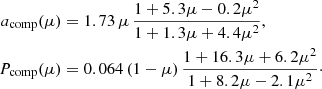
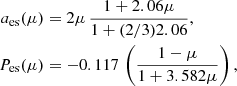
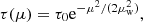
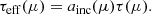
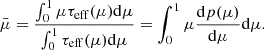
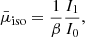
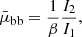
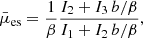
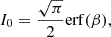
![$$ \begin{aligned} I_1&= \frac{1}{2} \left[1-\exp (-\beta ^2)\right], \end{aligned} $$](/articles/aa/full_html/2025/02/aa53188-24/aa53188-24-eq18.gif)
![$$ \begin{aligned} I_2&= \frac{1}{2} \left[-\beta \exp (-\beta ^2)+I_0\right], \end{aligned} $$](/articles/aa/full_html/2025/02/aa53188-24/aa53188-24-eq19.gif)
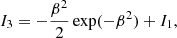
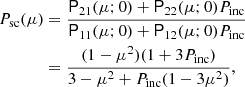
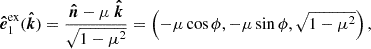
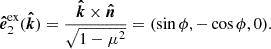
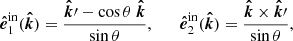
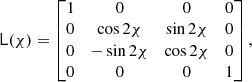
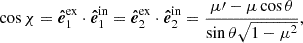
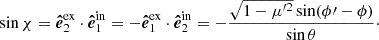
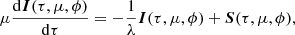
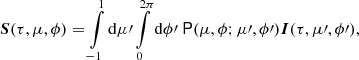
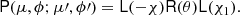
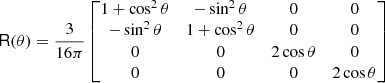
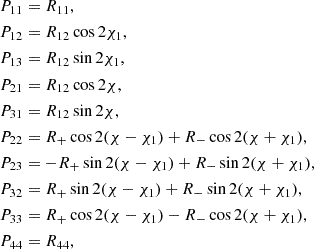
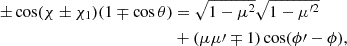
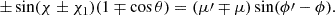
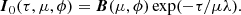
![$$ \begin{aligned} \boldsymbol{I}_1 (\tau , \mu , \phi ) = \int \limits _0^{\tau } \frac{\mathrm{d}\tau \prime }{\mu } \boldsymbol{S}_1 (\tau \prime ,\mu ,\phi ) \exp [-(\tau -\tau \prime )/\lambda \mu ], \end{aligned} $$](/articles/aa/full_html/2025/02/aa53188-24/aa53188-24-eq56.gif)