| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | L19 | |
| Number of page(s) | 9 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202452335 | |
| Published online | 21 November 2024 | |
Letter to the Editor
Origin of the black hole spin in lower-mass-gap black hole-neutron star binaries
1
Department of Physics, Anhui Normal University, Wuhu, Anhui 241002, China
2
Guangxi Key Laboratory for Relativistic Astrophysics, School of Physical Science and Technology, Guangxi University, Nanning 530004, China
3
Département d’Astronomie, Université de Genève, Chemin Pegasi 51, 1290 Versoix, Switzerland
4
Gravitational Wave Science Center (GWSC), Université de Genève, 24 quai E. Ansermet, 1211 Geneva, Switzerland
5
Nevada Center for Astrophysics, University of Nevada, Las Vegas, NV 89154, USA
6
Department of Physics and Astronomy, University of Nevada, Las Vegas, NV 89154, USA
7
School of Physics and Physical Engineering, Qufu Normal University, Qufu, Shandong 273165, China
8
Department of Physics, School of Physics and Materials Science, Nanchang University, Nanchang 330031, China
9
College of Physics, Guizhou University, Guiyang, Guizhou 550025, PR China
⋆ Corresponding author; yingqin2013@hotmail.com
Received:
21
September
2024
Accepted:
9
November
2024
During the fourth observing run, the LIGO-Virgo-KAGRA Collaboration reported the detection of a coalescing compact binary (GW230529−181500) with component masses estimated at 2.5 − 4.5 M⊙ and 1.2 − 2.0 M⊙ with 90% credibility. Given the current constraints on the maximum neutron star (NS) mass, this event is most likely a lower-mass-gap (LMG) black hole-neutron star (BHNS) binary. The spin magnitude of the BH, especially when aligned with the orbital angular momentum, is critical in determining whether the NS is tidally disrupted. An LMG BHNS merger with a rapidly spinning BH is an ideal candidate for producing electromagnetic counterparts. However, no such signals have been detected. In this study, we employ a detailed binary evolution model that incorporates new dynamical tide implementations to explore the origin of BH spin in an LMG BHNS binary. If the NS forms first, the BH progenitor (He-rich star) must begin in orbit shorter than 0.35 days to spin up efficiently, potentially achieving a spin magnitude of χBH > 0.3. Alternatively, if a nonspinning BH (e.g., MBH = 3.6 M⊙) forms first, it can accrete up to ≈0.2 M⊙ via case BA mass transfer (MT), reaching a spin magnitude of χBH ≈ 0.18 under Eddington-limited accretion. With a higher Eddington accretion limit (i.e., 10.0 ̇MEdd), the BH can attain a significantly higher spin magnitude of χBH ≈ 0.65 by accreting approximately 1.0 M⊙ during case BA MT phase.
Key words: binaries: close / stars: black holes / stars: neutron
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Mergers of black hole–neutron star (BHNS) systems are prime targets for gravitational-wave (GW) detection by the Advanced LIGO (Aasi et al. 2015), Advanced Virgo (Acernese et al. 2015), and KAGRA (Somiya 2012; Aso et al. 2013) observatories. The LIGO-Virgo-KAGRA (LVK) Collaboration first detected two high-confidence GWs from BHNS mergers, GW200105 and GW200115 (Abbott et al. 2021; Nitz et al. 2023), at the end of the third observing run (O3). On May 29, 2023, during the fourth observing run (O4), GW230529−181500 (abbreviated as GW230529) was detected at 18:15:00 UTC with high significance by the LIGO Livingston observatory, while the other observatories were offline or lacked the sensitivity to detect this signal (Abac et al. 2024). The LVK reported the two component masses of GW230529 to be 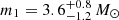 and
and 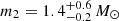 (90% confidence intervals) by adopting a high-spin secondary prior.
(90% confidence intervals) by adopting a high-spin secondary prior.
Dynamical mass measurements of low-mass BH X-ray binary population have constrained the lower edge of stellar mass BHs to be around 5 M⊙ (Bailyn et al. 1998; Özel et al. 2010; Farr et al. 2011). On the other hand, the maximum mass for nonrotating NSs has been inferred to be 2 − 3 M⊙ (Rhoades & Ruffini 1974; Kalogera & Baym 1996; Müller & Serot 1996; Özel & Freire 2016; Margalit & Metzger 2017; Ai et al. 2020; Shao et al. 2020; Fan et al. 2024). The combination of the highest-mass NSs and the lowest-mass BHs suggests an absence of BHs within the mass range of 2.5 − 5 M⊙. This is commonly referred to as the lower-mass gap (LMG, see a recent review paper from Shao 2022). Therefore, considering current constraints on the maximum NS, the most probable interpretation of GW230529 is an LMG BHNS merger1. For BHNS mergers, the effective inspiral spin χeff that can be directly constrained by the GW signal is defined as
where mBH and mNS are the BH and NS masses, χBH and χNS are their corresponding dimensionless spins, and 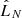 is the unit vector of the orbital angular momentum. Given the measurement of
is the unit vector of the orbital angular momentum. Given the measurement of 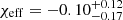 for GW230529, its primary was inferred to have a spin component
for GW230529, its primary was inferred to have a spin component 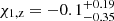 , which is typically low.
, which is typically low.
Instead of directly plunging into the BH, the NS in a BHNS merger can, under certain circumstances, be tidally disrupted by the strong gravitational field of the BH. This tidal disruption generates remnant baryonic material outside the BH, which might power a range of electromagnetic (EM) counterparts, including a short gamma-ray burst (e.g., Paczynski 1991; Narayan et al. 1992; Zhang 2018) and kilonova emission (e.g., Li & Paczyński 1998; Metzger et al. 2010; Zhu et al. 2020). The intrinsic brightness of the EM emission in BHNS mergers is significantly influenced by the amount of mass that is ejected during the tidal disruption process. This mass ejection is determined by the system properties, including the BH mass, the NS mass, the NS equation-of-state (EoS), and the magnitude and orientation of the spins of both objects (e.g., Kyutoku et al. 2015; Foucart et al. 2018; Zhu et al. 2021a,b). Recent investigations suggested a probability of approximately 2% to 41% for kilonova emission from GW230529, depending on the EoS of the NS (Kunnumkai et al. 2024). In particular, an NS is more likely to be tidally disrupted by a low-mass BH with a high spin (Hu et al. 2022). Consequently, an LMG BHNS binary with a high BH spin is a promising candidate for producing significant tidal disruption.
Binary population synthesis models using delayed supernova (SN) prescription (Fryer et al. 2012) can produce BHNS binaries with the primary BH in the LMG (Belczynski et al. 2012; Zevin et al. 2020; Broekgaarden et al. 2021; Chattopadhyay et al. 2021; Olejak et al. 2022; Zhu et al. 2024a). If the first-born compact object is an NS, it may accrete enough mass from its companion to trigger an accretion-induced collapse, potentially forming BHNS mergers like the source of GW230529 (Zhu et al. 2024b). In the context of the field binary evolution, a BH can obtain a high spin either through tidal spin-up on its progenitor (e.g., Detmers et al. 2008; Qin et al. 2018, 2019; Bavera et al. 2020; Hu et al. 2022, 2023; Qin et al. 2023) or through super-Eddington accretion from its companion star (e.g., Bavera et al. 2021; Qin et al. 2022; Shao & Li 2022; Wang et al. 2024b).
In this Letter, we study the origin of BH spin in an LMG BH and an NS binary. To this end, we first study an NS + He-rich star that interact through tides, as well as a BH + He-rich star that interact through tides and mass transfer. Second, we identify the models that may be reasonable scenarios for the system GW230529. The structure of this paper is as follows. We briefly describe in Section 2 the method we used in our study. Subsequently, we present in Section 3 the main results of our findings. Finally, the conclusions with some discussion are summarized in Section 4.
2. Methods
We adopted the released version r15140 of the MESA stellar evolution code (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023) to conduct the detailed binary modeling. Following the method of recent studies (e.g., Fragos et al. 2023; Lyu et al. 2023; Wang et al. 2024b; Zhu et al. 2024a), we created single He-rich stars at the zero-age helium main sequence and then relaxed them to reach thermal equilibrium (defined as when the ratio of He-burning luminosity to total luminosity exceeds 99%). Convection was modeled using the mixing-length theory (Böhm-Vitense 1958), with a mixing-length of αmlt = 1.93, while semiconvection was treated with an efficiency parameter of α = 1.0 (Langer et al. 1983). The Ledoux criterion was adopted to determine convective zone boundaries, and step overshooting was modeled as an extension with αp = 0.1Hp, where Hp represents the pressure scale height at the Ledoux boundary. To calculate nucleosynthesis, we used the approx21.net network.
Rotational mixing and angular momentum transport were treated as diffusive processes (Heger & Langer 2000), incorporating the effects of the Goldreich-Schubert-Fricke instability, Eddington-Sweet circulations, and both secular and dynamical shear mixing. We applied diffusive element mixing from these processes using an efficiency parameter of fc = 1/30 (Chaboyer & Zahn 1992; Heger & Langer 2000). Given the sensitivity of the μ-gradient to rotationally induced mixing, we mitigated it by applying a reduction factor of fμ = 0.05, as recommended in Heger & Langer (2000). In our simulations, we evolved He-rich stars with initial metallicity of Z = Z⊙, where Z⊙ was set to 0.0142 (Asplund et al. 2009).
We modeled the wind mass-loss of He-rich stars following Hu et al. (2022) and accounted for the rotation-enhanced mass loss using the formulation from (Heger & Langer 1998; Langer 1998),
where ω and ωcrit are the angular and critical angular velocities at the stellar surface, respectively. The critical angular velocity is defined as ωcrit2 = (1 − L/LEdd)GM/R3, with L, M, R representing the stellar total luminosity, mass, and radius, respectively; LEdd is the Eddington luminosity, and G is the gravitational constant. The exponent ξ = 0.43 was adopted from Langer (1998). It is important to note that we did not account for gravity-darkening effects, as discussed in Maeder & Meynet (2000).
Stars have extended atmospheres that allow mass transfer (MT) to occur through the first Lagrangian point (L1) even when the star remains within its Roche lobe (i.e., R1 < RRL, as described by the Ritter scheme, Ritter 1988). Kolb & Ritter (1990) further extended the Ritter scheme to cases where R1 > RRL. In this work, we modeled MT using the Kolb scheme (Kolb & Ritter 1990) and adopted the implicit MT method (Paxton et al. 2015). For simplicity, we assumed conservative mass transfer through L1 between a He-rich star and its companion.
For tidal interactions, we applied dynamical tides to He-rich stars with radiative envelopes (Zahn 1977). The synchronization timescale was calculated using the prescriptions from Zahn (1977), Hut (1981), Hurley et al. (2002), and the tidal torque coefficient E2 was adopted from the updated fitting formula in Qin et al. (2018). Recent studies by Sciarini et al. (2024) have highlighted inconsistencies in implementing dynamic tides compared to Zahn (1977). We used the correction proposed by Sciarini et al. (2024) and provide detailed explanations in the appendix.
Given the negligible natal spin of the first-born BH in binaries (e.g., Fragos & McClintock 2015; Qin et al. 2018; Fuller & Ma 2019; Belczynski et al. 2020), we assumed that the BH was initially nonrotating. As the BH accretes material through a disk at a rate Ṁacc, its mass increases according to the following growth rate:
where η is the radiation efficiency determined by the innermost stable circular orbit. As the BH mass increases, its spin evolves according to (Bardeen 1970; Bardeen et al. 1972; Podsiadlowski et al. 2003; Marchant et al. 2017)
for 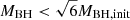 , where
, where 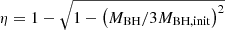 .
.
The standard Eddington accretion rate, which represents the critical rate at which the outward force from radiation pressure balances the inward gravitational pull, is defined as
where c is the speed of light, G is the gravitational constant, and κ is the opacity, primarily determined by pure electron scattering. The opacity is given by κ = 0.2(1 + X), cm2, g−1, where X is the hydrogen mass fraction (e.g., Kippenhahn & Weigert 1990).
We evolved He-rich stars until central carbon exhaustion was achieved. To calculate the baryonic remnant mass (Mbar), we used the delayed SN prescription (Fryer et al. 2012). The gravitational mass (Mrem) for NSs was then determined using the following relation (Lattimer & Yahil 1989; Timmes et al. 1996):
while for BHs, we followed the method of Fryer et al. (2012) to approximate the Mrem using
Additionally, we accounted for the neutrino loss mechanism described by Zevin et al. (2020). We assumed a maximum NS mass of 2.5,M⊙.
3. Results
3.1. Tidal spin-up
In the scenario of tidal spin-up, we focused on systems composed of an NS and a He-rich star in a close binary. As investigated previously by Detmers et al. (2008), Qin et al. (2018), Hu et al. (2022), a He-rich star in a close binary system can be efficiently spun up by tidal interactions with its companion. This process can potentially lead to the formation of a fast-spinning NS or BH, with the outcome primarily dependent on the initial mass of the He-rich star and its metallicity (see Figure 3 in Lyu et al. 2023). Figure 1 illustrates the remnant mass as a function of the initial He-rich star mass for different metallicities (1.0 Z⊙, 0.1 Z⊙, and 0.01 Z⊙). At lower metallicities (0.1 Z⊙ and 0.01 Z⊙), He-rich stars are expected to retain more mass due to the reduced strength of metallicity-dependent winds (Vink et al. 2001). For BHs that formed at solar metallicity within the LMG (2.5 − 5.0 M⊙), the initial mass of He-rich stars needs to range from approximately 8.0 M⊙ to ≈11.5 M⊙ (from ≈7.0 M⊙ to ≈10.0 M⊙ at 0.1 Z⊙ and from ≈7.0 M⊙ to ≈9.5 M⊙ at 0.01 Z⊙).
 |
Fig. 1. Remnant mass as a function of the initial mass of nonrotating He-rich stars at three distinct metallicities, represented by different line styles: a dash-dotted line for 1.0 Z⊙, a dashed line for 0.1 Z⊙, and a dotted line for 0.01 Z⊙. The LMG is indicated by the gray shaded region. |
We carried out a detailed binary modeling of He-rich stars to track the evolution of their angular momentum, which ultimately determines the spin of the resulting BHs. The initial mass range of He-rich stars was selected to ensure the formation of BHs within the LMG. We modeled the NS as a point mass with MNS = 1.4 M⊙ and evolved the He-rich star with an initial masses (MZamHe) linearly ranging from 7.0 M⊙ to 12.0 M⊙ at a step of 1.0 M⊙. The initial orbital period spanned from approximately 0.06 days (the point at which He-rich stars begin to overflow their Roche lobes) to 2.2 days (beyond which tidal interactions become negligible; see detailed testing in Qin et al. 2018), with a logarithmic spacing of Δlog(P/days)≈0.16 dex. We evolved He-rich stars with different initial metallicities (1.0 Z⊙, 0.1 Z⊙, and 0.01 Z⊙) until central carbon depletion. In all binary modeling, the initial angular velocities of He-rich stars were synchronized with the orbital motion.
Figure 2 displays the spin of BHs that formed from the direct collapse of He-rich stars under various conditions. The left panel shows the results for He-rich stars with an initial metallicity of 1.0 Z⊙. For systems in wider orbits (log(P/days)≳ − 0.25), the tidal forces are too weak to significantly spin up He-rich stars, resulting in BHs with low spin (χBH < 0.2). To achieve a moderate BH spin (i.e., χBH > 0.3), the initial orbital period must be shorter than approximately 0.35 days (log P ≈ −0.46). Stellar winds from He-rich stars typically reduce their mass, leading to a widening of the binary system. However, He-rich stars with lower initial metallicities can form double compact objects in closer orbits due to weaker winds. These low-metallicity stars (see the middle and right panels) can retain more angular momentum, forming fast-spinning BHs when they are sufficiently massive. Additionally, NSBH systems (where the NS forms first, as opposed to BHNS systems, where the BH forms first) formed at low metallicities are expected to merge more quickly due to GW emission (Peters 1964). We note that the parameter space (see the plus symbol) that leads to the formation of GW230529 is very limited when considering its low BH spin.
 |
Fig. 2. Black hole dimensionless spin χBH as a function of the He-rich star mass and the orbital period. The black symbols represent the initial parameters (He-rich star mass and orbital period), and the colored symbols indicate the final parameters. The color gradient along the line traces the evolution of χBH, assuming that the He-rich star collapses directly into a BH without losing mass or angular momentum. The triangles represent BNS systems, circles denote NSBH systems, stars indicate dynamical delayed instability (DDI), and crosses mark initial overflow cases. The three columns correspond to different metallicities (left: 1.0 Z⊙; middle: 0.1 Z⊙; and right: 0.01 Z⊙). The plus symbol refers to the systems that might be representative of the progenitors of GW230529. |
3.2. Accretion-induced spin-up
In the scenario of accretion-induced spin-up, we considered a close binary system consisting of a BH and a He-rich star. As an example, Figure 3 illustrates the increase in the spin of the BH as it accretes material. Previous studies have shown that super-Eddington accretion can well explain the high spin of a BH in high-mass X-ray binaries (Qin et al. 2022) and in double BH systems (e.g., Bavera et al. 2021; Shao & Li 2022; Zevin & Bavera 2022; Briel et al. 2023). Observational evidence for super-Eddington accretion was identified in several BH X-ray binaries, including examples such as V404 Cygni (Motta et al. 2017) and GRO J1655-40 (Neilsen et al. 2016). In our binary modeling, we allowed the accretion rate to exceed the standard Eddington limit by up to ten times, that is, 10 ṀEdd.
 |
Fig. 3. Black hole dimensionless spin χBH as a function of the ratio of accreted mass to its initial mass. |
Before we report the results of the grid study, we first present our findings on the evolution of a specific binary sequence, as shown in Figure 4. This close binary system consists of a 3.6 M⊙ BH and a 6.0 M⊙ He-rich star, with an initial orbital period of 0.08 days. The upper panel illustrates that the system undergoes case BA, BB, and BC MT phases. During the case BA MT phase, the MT rate initially rises above 10−5 M⊙/yr before it gradually decreases to the Eddington-limited accretion rate. Under the assumption of standard Eddington accretion, we considered any excess material to be lost from the vicinity of the accretor as an isotropic wind that carried the specific orbital angular momentum of the accretor. Notably, the BH spin increased to χBH ≈ 0.17. The system then became detached as the He-rich star temporarily contracted at the end of the core-helium burning phase. The He-rich star subsequently expanded, initiating the case BB and Case BC MT phases, during which the BH spin increased more slowly due to the limited duration of the accretion period.
 |
Fig. 4. Mass-transfer rate (upper panel) and BH spin χBH (lower panel) as functions of the model number. The dashed line indicates the standard Eddington accretion rate (1.0 ̇MEdd). In the binary sequence shown, the initial masses of the BH and He-rich star are 3.6 M⊙ and 6.0 M⊙, respectively, with an initial orbital period of 0.08 days. Different MT phases are highlighted in various colors: Case BA (green), case BB (blue), and case BC (gray). |
As illustrated in Figure 1, we focus edon He-rich stars with solar metallicity and masses ranging from 3.0 to 8.0 M⊙, at which NSs are expected to form. The BH was modeled as a point mass with MBH = 3.6 M⊙. The upper limit for the initial orbital period was set to 10 days, below which no MT occurs through the L1 point (see recent studies on similar MT phases in Zhang et al. 2023). Conversely, the lower limit corresponded to systems for which Roche-lobe overflow begins in the initial model. In the left panel of Figure A.1, we show the evolution of the BH mass as a function of the He-rich star mass and the orbital period. When we assume Eddington-limited accretion, the BH can accrete up to approximately 0.2 M⊙ during the case BA MT phase, reaching a maximum mass of MBH ≈ 3.8 M⊙. This accretion adds specific angular momentum, spinning up the BH to a dimensionless spin parameter χBH ≈ 0.18. When the BH accretes material beyond the standard Eddington limit, it can significantly increase both its mass and spin (see also Figure 3). The right panels of Figures A.1 and A.2 display the evolution of the BH mass and spin within the given parameter space, allowing for up to 10 ṀEdd in our binary modeling. In all the binary sequences, the BH can increase its mass by up to approximately 1.0 M⊙ through the case BA MT phase, resulting in an efficient spin-up to χBH ≈ 0.65. In both cases, the parameter space (see the plus symbol) that potentially produces GW230529 is much larger than in the scenario of tidal spin-up.
4. Conclusions and discussion
We used detailed binary evolution tools to investigate the origins of BH spin in lower-mass-gap (LMG) BH and NS binary systems. We explored two primary formation scenarios: tidal spin-up of the BH progenitor, and accretion-induced spin-up. To address this, we conducted a parameter space study across two grids of He-rich stars in binary systems and analyzed various conditions.
First, we evolved single He-rich stars to determine the mass range in which BHs are expected to form within the LMG across three different metallicities. With the new implementation of the dynamical tides as suggested in Sciarini et al. (2024), we find that He-rich stars must be in closer orbits to achieve significant spin-up. In the tidal spin-up scenario, we performed a grid of detailed binary models involving a He-rich star and an NS in close orbits. At solar metallicity, in systems with wider orbits (log(P/days)≳ − 0.25), tidal forces are insufficient to spin up He-rich stars, resulting in low-spin BHs (χBH < 0.2). To achieve moderate BH spin (χBH > 0.3), the initial orbital period needs to be shorter than approximately 0.35 days (log(P/days)≈ − 0.46). At lower metallicities, weaker mass-loss winds cause the systems to become more compact, resulting in the formation of faster BH binaries. In this scenario, it is noted that the spin of the BH formed in the LMG can span the entire range from zero to maximally spinning. Recent findings by Ma & Fuller (2023) showed that tidal interactions are predominantly driven by standing gravity modes, as opposed to traveling waves, which were previously suggested by Zahn (1977). As a result, earlier estimates of tidal spin-up may have been overestimated.
In the accretion-induced spin-up scenario, we explored a grid of models involving a BH with MBH = 3.6 M⊙ and He-rich stars within the mass range of 3.0 to 8.0 M⊙. When we assumed Eddington-limited accretion, the BH can accrete up to approximately 0.2 M⊙ during the case BA MT phase, resulting in a spin magnitude of χBH ≈ 0.18. However, under a higher accretion limit of 10.0 ̇MEdd, the BH can achieve a significantly higher spin magnitude of χBH ≈ 0.65 by accreting about 1.0 M⊙ during the same MT phase. In this scenario, the spin of the BH that formed in the LMG is typically low even with a moderate Eddington accretion limit when compared with the case of tidal spin-up. Only in a few systems can BHs attain a high spin magnitude. Notably, the spin of a BH can decrease due to the launching of a Blandford-Znajek jet (Blandford & Znajek 1977) during periods of hyperaccretion (Lei et al. 2017; Wang & Zhang 2024). For merging binary BHs that formed through isolated binary evolution channels, Gallegos-Garcia et al. (2021) found that stable MT, rather than the classical common-envelope channel, may play a dominant role. In contrast, they found that binary neutron star mergers are primarily formed through the common-envelope channel and not through stable MT (Gallegos-Garcia et al. 2023).
The formation channels explored in this study could be relevant to the origin of GW230529 (Abac et al. 2024). Using the population synthesis code COMPAS Stevenson et al. (2017), Vigna-Gómez et al. (2018), Neijssel et al. (2019), Team COMPAS (2022), Zhu et al. (2024a) suggested that GW230529 likely originated from the isolated massive binary evolution channel. In support of this, Chandra et al. (2024) found that the first-born BH in GW230529 is consistent with the classical isolated binary evolution scenario. This aligns with earlier studies indicating that BHs typically form first (Xing et al. 2024), largely due to rotation-dependent accretion efficiency onto nondegenerate stars (de Mink et al. 2013). Although the possibility that GW230529 formed through dynamical assembly cannot be entirely ruled out, current estimates suggest that the merger rate through this channel is particularly low (e.g., ≲1 Gpc−3 yr−1, see Ye et al. 2024). As more data are gathered by the LVK Collaboration, additional BH and NS mergers involving BH within the LMG are likely to be reported.
It is worth noting that Wang et al. (2024a) recently reported a potential mass-gap BH in a wide binary with a circular orbit.
Acknowledgments
We thank the referee for constructive comments that helped improve the manuscript. We also thank Bing Zhang and Jin-Ping Zhu for their helpful comments. Y.Q. acknowledges support from the Anhui Provincial Natural Science Foundation (grant No. 2308085MA29) and the National Natural Science Foundation of China (grant No. 12473036). G.M. has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No 833925, project STAREX). C.J.F is supported by the National Natural Science Foundation of China Grant No. 12305057. Q.W.T acknowledges support from Jiangxi Provincial Natural Science Foundation (grant Nos. 20242BAB26012 and 20224ACB211001). This work was partially supported by the National Natural Science Foundation of China (grant Nos. 12065017, 12192220, 12192221, 12133003, 12203101, U2038106, 12103003). All figures are made with the free Python module Matplotlib (Hunter 2007).
References
- Aasi, J., Abbott, B. P., Abbott, R., et al. 2015, CQG, 32, 074001 [Google Scholar]
- Abac, A. G., Abbott, R., Abouelfettouh, I., et al. 2024, ApJ, 970, L34 [CrossRef] [Google Scholar]
- Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, ApJ, 915, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Acernese, F., Agathos, M., Agatsuma, K., et al. 2015, CQG, 32, 024001 [NASA ADS] [CrossRef] [Google Scholar]
- Ai, S., Gao, H., & Zhang, B. 2020, ApJ, 893, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Aso, Y., Michimura, Y., Somiya, K., et al. 2013, Phys. Rev. D, 88, 043007 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bailyn, C. D., Jain, R. K., Coppi, P., & Orosz, J. A. 1998, ApJ, 499, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M. 1970, Nature, 226, 64 [Google Scholar]
- Bardeen, J. M., Press, W. H., & Teukolsky, S. A. 1972, ApJ, 178, 347 [Google Scholar]
- Bavera, S. S., Fragos, T., Qin, Y., et al. 2020, A&A, 635, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belczynski, K., Wiktorowicz, G., Fryer, C. L., Holz, D. E., & Kalogera, V. 2012, ApJ, 757, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
- Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, 520, 5724 [Google Scholar]
- Broekgaarden, F. S., Berger, E., Neijssel, C. J., et al. 2021, MNRAS, 508, 5028 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., & Zahn, J. P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
- Chandra, K., Gupta, I., Gamba, R., et al. 2024, ArXiv e-prints [arXiv:2405.03841] [Google Scholar]
- Chattopadhyay, D., Stevenson, S., Hurley, J. R., Bailes, M., & Broekgaarden, F. 2021, MNRAS, 504, 3682 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
- Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, Y.-Z., Han, M.-Z., Jiang, J.-L., Shao, D.-S., & Tang, S.-P. 2024, Phys. Rev. D, 109, 043052 [NASA ADS] [CrossRef] [Google Scholar]
- Farr, W. M., Sravan, N., Cantrell, A., et al. 2011, ApJ, 741, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Foucart, F., Hinderer, T., & Nissanke, S. 2018, Phys. Rev. D, 98, 081501 [NASA ADS] [CrossRef] [Google Scholar]
- Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [Google Scholar]
- Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Fryer, C. L., Belczynski, K., Wiktorowicz, G., et al. 2012, ApJ, 749, 91 [Google Scholar]
- Fuller, J., & Ma, L. 2019, ApJ, 881, L1 [Google Scholar]
- Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Gallegos-Garcia, M., Berry, C. P. L., & Kalogera, V. 2023, ApJ, 955, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., & Langer, N. 1998, A&A, 334, 210 [NASA ADS] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [CrossRef] [Google Scholar]
- Hu, R.-C., Zhu, J.-P., Qin, Y., et al. 2022, ApJ, 928, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, R. C., Zhu, J. P., Qin, Y., et al. 2023, ArXiv e-prints [arXiv:2301.06402] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kalogera, V., & Baym, G. 1996, ApJ, 470, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer Berlin, Heidelberg) [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kunnumkai, K., Palmese, A., Bulla, M., et al. 2024, ArXiv e-prints [arXiv:2409.10651] [Google Scholar]
- Kyutoku, K., Ioka, K., Okawa, H., Shibata, M., & Taniguchi, K. 2015, Phys. Rev. D, 92, 044028 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
- Lattimer, J. M., & Yahil, A. 1989, ApJ, 340, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Lei, W.-H., Zhang, B., Wu, X.-F., & Liang, E.-W. 2017, ApJ, 849, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Lyu, F., Yuan, L., Wu, D. H., et al. 2023, MNRAS, 525, 4321 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, L., & Fuller, J. 2023, ApJ, 952, 53 [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, A&A, 361, 159 [NASA ADS] [Google Scholar]
- Marchant, P., Langer, N., Podsiadlowski, P., et al. 2017, A&A, 604, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margalit, B., & Metzger, B. D. 2017, ApJ, 850, L19 [Google Scholar]
- Metzger, B. D., Martínez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S. E., Kajava, J. J. E., Sánchez-Fernández, C., et al. 2017, MNRAS, 471, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H., & Serot, B. D. 1996, Nucl. Phys. A, 606, 508 [CrossRef] [Google Scholar]
- Narayan, R., Paczynski, B., & Piran, T. 1992, ApJ, 395, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Neijssel, C. J., Vigna-Gómez, A., Stevenson, S., et al. 2019, MNRAS, 490, 3740 [Google Scholar]
- Neilsen, J., Rahoui, F., Homan, J., & Buxton, M. 2016, ApJ, 822, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Nitz, A. H., Kumar, S., Wang, Y.-F., et al. 2023, ApJ, 946, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Olejak, A., Fryer, C. L., Belczynski, K., & Baibhav, V. 2022, MNRAS, 516, 2252 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., & Freire, P. 2016, ARA&A, 54, 401 [Google Scholar]
- Özel, F., Psaltis, D., Narayan, R., & McClintock, J. E. 2010, ApJ, 725, 1918 [CrossRef] [Google Scholar]
- Paczynski, B. 1991, Acta Astron., 41, 257 [NASA ADS] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
- Peters, P. C. 1964, Phys. Rev., 136, 1224 [Google Scholar]
- Podsiadlowski, P., Rappaport, S., & Han, Z. 2003, MNRAS, 341, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, Y., Fragos, T., Meynet, G., et al. 2018, A&A, 616, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [Google Scholar]
- Qin, Y., Shu, X., Yi, S., & Wang, Y.-Z. 2022, Res. Astron. Astrophys., 22, 035023 [Google Scholar]
- Qin, Y., Hu, R. C., Meynet, G., et al. 2023, A&A, 671, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rhoades, C. E., & Ruffini, R. 1974, Phys. Rev. Lett., 32, 324 [CrossRef] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Sciarini, L., Ekström, S., Eggenberger, P., et al. 2024, A&A, 681, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shao, Y. 2022, Res. Astron. Astrophys., 22, 122002 [CrossRef] [Google Scholar]
- Shao, Y., & Li, X.-D. 2022, ApJ, 930, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, D.-S., Tang, S.-P., Jiang, J.-L., & Fan, Y.-Z. 2020, Phys. Rev. D, 102, 063006 [CrossRef] [Google Scholar]
- Somiya, K. 2012, CQG, 29, 124007 [NASA ADS] [CrossRef] [Google Scholar]
- Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [Google Scholar]
- Team COMPAS (Riley, J., et al.) 2022, ApJS, 258, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., & Weaver, T. A. 1996, ApJ, 457, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Vigna-Gómez, A., Neijssel, C. J., Stevenson, S., et al. 2018, MNRAS, 481, 4009 [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, Y., & Zhang, B. 2024, Nat. Astron., submitted [arXiv:2403.06416] [Google Scholar]
- Wang, S., Zhao, X., Feng, F., et al. 2024a, Nat. Astron., submitted [arXiv:2409.06352] [Google Scholar]
- Wang, Z.-H.-T., Hu, R.-C., Qin, Y., et al. 2024b, ApJ, 965, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Xing, Z., Bavera, S. S., Fragos, T., et al. 2024, A&A, 683, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ye, C. S., Kremer, K., Ransom, S. M., & Rasio, F. A. 2024, ApJ, 975, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1977, A&A, 57, 383 [Google Scholar]
- Zevin, M., & Bavera, S. S. 2022, ApJ, 933, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Zevin, M., Spera, M., Berry, C. P. L., & Kalogera, V. 2020, ApJ, 899, L1 [Google Scholar]
- Zhang, B. 2018, The Physics of Gamma-Ray Bursts (Cambridge Univeristy Press) [Google Scholar]
- Zhang, W. T., Wang, Z. H. T., Zhu, J. P., et al. 2023, MNRAS, 526, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Yang, Y.-P., Liu, L.-D., et al. 2020, ApJ, 897, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Wu, S., Yang, Y.-P., et al. 2021a, ApJ, 917, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Wu, S., Yang, Y.-P., et al. 2021b, ApJ, 921, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Hu, R.-C., Kang, Y., et al. 2024a, ApJ, 974, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, J.-P., Qin, Y., Wang, Z.-H.-T., et al. 2024b, MNRAS, 529, 4554 [NASA ADS] [CrossRef] [Google Scholar]
Appendix
The synchronization timescale (τsync) for dynamical tides proposed by Sciarini et al. (2024) is given as:
where q = M2/M is the mass ratio, I the moment of inertia, R the stellar radius, a the semimajor axis, E2 tidal torque coefficient. Assuming constant value for Ωorb and τsync, Sciarini et al. (2024) provided the analytical solution as follows.
where Ω0 = Ωspin(t = 0). Assuming that τsync and Ωorb are constant through a step (Detmers et al. 2008; Paxton et al. 2015), thus we obtain
where j = 1, 2 is the index of each star, Ωi.j is the angular frequency at the face of cell i toward the surface, and Ωi, j, 0 = Ωi.j(t = 0). After implementing the above equation in the MESA binary module, we computed several models using different definitions of τsync. In these tests, we evolved a binary system consisting of a BH and a He-rich star with identical initial masses but varying initial orbital periods (0.2, 0.5, and 1.0 days). We assumed that the He-rich star was initially synchronized with its orbit.
In Figure A.3, we distinguish the models computed with the newly proposed τsync as S24 and those using the default τsync as H02 (see Equation (8) in Sciarini et al. (2024)). The left panel illustrates the spin-up of the He-rich star following central helium depletion, with varying τsync values. Comparatively, the tidal effects using the newly proposed τsync (Sciarini et al. 2024) are weaker than those with the default one (Hurley et al. 2002). The right panel shows the resulting BH spin, assuming the He-rich star undergoes direct collapse to form a BH. In scenarios with weaker tides, the BH spin magnitude is reduced in close binaries (e.g., with orbital periods shorter than 1.0 days).
 |
Fig. A.1. BH mass acquired through Roche-lobe accretion from a He-rich star, plotted against the star’s mass and the orbital period. Black and colored symbols represent the initial and final values for the He-rich star mass and orbital period. The color gradient along the lines indicates the evolving mass of the BH as a function of the He-rich star mass and orbital period. Symbols denote different scenarios: circles for BHNS systems, stars for dynamical delayed instability (DDI), and crosses for initial overflow cases. The two panels correspond to different accretion rates: 1.0 ṀEdd in the left panel and 10.0 ṀEdd in the right panel. The plus symbol refers to the systems that might be representative of the progenitors of GW230529. |
 |
Fig. A.3. The ratio of the He-rich star’s rotational period to the orbital period (P1/Porb, left panel) and the resulting BH spin (χBH, right panel) are plotted as functions of model number for different initial orbital periods (red: 0.2 days; green: 0.5 days; blue: 1.0 days). Two synchronization timescales are compared: the solid line represents τsync from Sciarini et al. (2024), while the dashed line corresponds to τsync from Hurley et al. (2002). Vertical lines indicate the point at which the He-rich star reaches central helium depletion. |
All Figures
 |
Fig. 1. Remnant mass as a function of the initial mass of nonrotating He-rich stars at three distinct metallicities, represented by different line styles: a dash-dotted line for 1.0 Z⊙, a dashed line for 0.1 Z⊙, and a dotted line for 0.01 Z⊙. The LMG is indicated by the gray shaded region. |
| In the text | |
 |
Fig. 2. Black hole dimensionless spin χBH as a function of the He-rich star mass and the orbital period. The black symbols represent the initial parameters (He-rich star mass and orbital period), and the colored symbols indicate the final parameters. The color gradient along the line traces the evolution of χBH, assuming that the He-rich star collapses directly into a BH without losing mass or angular momentum. The triangles represent BNS systems, circles denote NSBH systems, stars indicate dynamical delayed instability (DDI), and crosses mark initial overflow cases. The three columns correspond to different metallicities (left: 1.0 Z⊙; middle: 0.1 Z⊙; and right: 0.01 Z⊙). The plus symbol refers to the systems that might be representative of the progenitors of GW230529. |
| In the text | |
 |
Fig. 3. Black hole dimensionless spin χBH as a function of the ratio of accreted mass to its initial mass. |
| In the text | |
 |
Fig. 4. Mass-transfer rate (upper panel) and BH spin χBH (lower panel) as functions of the model number. The dashed line indicates the standard Eddington accretion rate (1.0 ̇MEdd). In the binary sequence shown, the initial masses of the BH and He-rich star are 3.6 M⊙ and 6.0 M⊙, respectively, with an initial orbital period of 0.08 days. Different MT phases are highlighted in various colors: Case BA (green), case BB (blue), and case BC (gray). |
| In the text | |
 |
Fig. A.1. BH mass acquired through Roche-lobe accretion from a He-rich star, plotted against the star’s mass and the orbital period. Black and colored symbols represent the initial and final values for the He-rich star mass and orbital period. The color gradient along the lines indicates the evolving mass of the BH as a function of the He-rich star mass and orbital period. Symbols denote different scenarios: circles for BHNS systems, stars for dynamical delayed instability (DDI), and crosses for initial overflow cases. The two panels correspond to different accretion rates: 1.0 ṀEdd in the left panel and 10.0 ṀEdd in the right panel. The plus symbol refers to the systems that might be representative of the progenitors of GW230529. |
| In the text | |
 |
Fig. A.2. Similar to Figure A.1, but the color representing the BH spin χBH. |
| In the text | |
 |
Fig. A.3. The ratio of the He-rich star’s rotational period to the orbital period (P1/Porb, left panel) and the resulting BH spin (χBH, right panel) are plotted as functions of model number for different initial orbital periods (red: 0.2 days; green: 0.5 days; blue: 1.0 days). Two synchronization timescales are compared: the solid line represents τsync from Sciarini et al. (2024), while the dashed line corresponds to τsync from Hurley et al. (2002). Vertical lines indicate the point at which the He-rich star reaches central helium depletion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



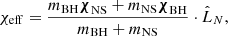
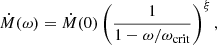
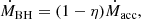
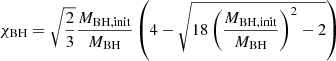
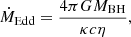
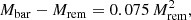
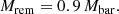
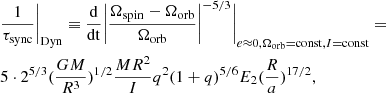
![$$ \begin{aligned} \frac{\Omega _{\rm spin}(t)-\Omega _{\rm orb}}{\Omega _{\rm orb}} = [(\frac{\Omega _{\rm 0}-\Omega _{\rm orb}}{\Omega _{\rm orb}})^{-5/3}+\mathrm{sgn}(\Omega _{\rm 0}-\Omega _{\rm orb})\frac{t}{\tau _{\rm sync}}]^{-3/5}, \end{aligned} $$](/articles/aa/full_html/2024/11/aa52335-24/aa52335-24-eq16.gif)
![$$ \begin{aligned} \Delta \Omega _{i.j}&=\Omega _{\rm orb}\{[(\frac{\Omega _{i.j}-\Omega _{\rm orb}}{\Omega _{\rm orb}})^{-5/3}+\mathrm{sgn}(\Omega _{i,j,\mathrm{0}}-\Omega _{\rm orb})\frac{\delta t}{\tau _{\mathrm{sync},j}}]^{-3/5}\nonumber \\&-\frac{\Omega _{i.j}-\Omega _{\rm orb}}{\Omega _{\rm orb}}\}, \end{aligned} $$](/articles/aa/full_html/2024/11/aa52335-24/aa52335-24-eq17.gif)