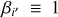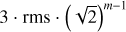| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 13 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202451492 | |
| Published online | 30 October 2024 | |
A millisecond pulsar position determined to 0.2 mas precision with VLBI
1
Mizusawa VLBI Observatory, National Astronomical Observatory of Japan,
2-12 Hoshigaoka-cho, Mizusawa, Oshu,
Iwate
023-0861,
Japan
2
Centre for Astrophysics & Supercomputing, Swinburne University of Technology,
PO Box 218,
Hawthorn,
Victoria
3122,
Australia
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
4
NASA Goddard Space Flight Center Code 61A,
8800 Greenbelt Rd,
Greenbelt,
20771
MD,
USA
★★ Corresponding author; hdingastro@hotmail.com
Received:
13
July
2024
Accepted:
23
September
2024
Context. Precise millisecond pulsar (MSP) positions determined with very long baseline interferometry (VLBI) hold the key to building the connection between the kinematic and dynamic reference frames respectively used for VLBI and pulsar timing. A frame connection would provide an important pathway to examining the planetary ephemerides used in pulsar timing, and would potentially enhance the sensitivities of the pulsar timing arrays used to detect stochastic gravitational-wave background in the nano-Hz regime.
Aims. We aim to significantly improve the precision of the VLBI-based MSP position (from >1 mas at present) by reducing the two dominant components in the positional uncertainty – the propagation-related uncertainty and the uncertainty resulting from the frequency-dependent core shifts of the reference sources.
Methods. We introduce a new differential astrometry strategy called PINPT (Phase-screen Interpolation plus frequeNcy-dePendent core shifT correction; pronounced “pinpoint”), which entails the use of multiple calibrators observed at several widely separated frequencies. The strategy allows determination of the core shift and mitigates the impact of residual delay in the atmosphere. We implemented the strategy on PSR J2222-0137, an MSP that is well constrained astrometrically with VLBI and pulsar timing.
Results. Using the PINPT strategy, we determined core shifts for four AGNs around PSR J2222-0137, and derived a VLBI-based pulsar position with uncertainties of 0.17 mas and 0.32 mas in Right Ascension and Declination, respectively, approaching the uncertainty level of the best-determined timing-based MSP positions. Additionally, incorporating the new observations into historical ones, we refined the pulsar proper motion and the parallax-based distance to the <10 µas yr-1 level and the subparsec level, respectively.
Conclusions. The realization of the PINPT strategy promises a factor-of-five positional precision enhancement (over conventional VLBI astrometry) for all kinds of compact radio sources observed at <2 GHz, including most fast radio bursts.
Key words: techniques: interferometric / astrometry / reference systems / quasars: general / radio continuum: stars
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Millisecond pulsars (MSPs) refer to recycled fast-spinning neutron stars, which exhibit unparalleled spin stability compared to other pulsars (Hobbs et al. 2010). Using the pulsar timing technique (e.g., Detweiler 1979), which records and models the pulse arrival times, astronomers have used MSPs to deliver the most stringent tests of gravitational theories (e.g., Freire & Wex 2024). Collectively, an array of MSPs scattered across the sky, known as a pulsar timing array (PTA), can be used to directly probe the stochastic gravitational-wave background (GWB) in the nanohertz (nHz) regime (Sazhin 1978).
Recent years have seen the major PTA consortia get closer than ever before to achieving high-significance detections of a homogeneous GWB (Agazie et al. 2023; Reardon et al. 2023; Antoniadis et al. 2023; Xu et al. 2023). Despite the breakthrough, deepening our understanding of the sources of the GWB still requires continuous improvement of the PTA sensitivities. The optimal strategy to sustain PTA sensitivity enhancement is to regularly add new MSPs to the PTAs (Siemens et al. 2013), as carried out by the MeerKAT Pulsar Timing Array (MPTA; Miles et al. 2023). However, it is generally difficult to quantify the red timing “noises” (in which the GWB signal resides) for a relatively shortly timed (≲3000 days) MSP; one way to overcome this difficulty is to incorporate independent astrometric measurements (i.e., sky position, proper motion, and parallax) into the inference of timing parameters (Madison et al. 2013).
The very long baseline interferometry (VLBI) technique can provide precise, robust, and model-independent astrometric measurements for MSPs, and can achieve a certain astrometric precision in much shorter time span compared to using pulsar timing (e.g., Brisken et al. 2002; Chatterjee et al. 2009; Deller et al. 2019). Therefore, the incorporation of precise VLBI astrometric measurements into the timing analysis of MSPs is essential for testing gravitational theories (e.g., Deller et al. 2008; Kramer et al. 2021), and may substantially enhance the PTA sensitivities (Madison et al. 2013).
However, this incorporation is technically challenging. First, incorporating precise VLBI proper motion and parallax into a timing analysis can be limited by the potential temporal structure evolution of the reference sources used in VLBI astrometry. Second, incorporating a VLBI pulsar position into a timing analysis necessitates a good understanding of the transformation between the two distinct kinds of reference systems used by VLBI astrometry and pulsar timing. Though both VLBI astrometry and pulsar timing are usually presented with respect to the barycenter of the Solar System, VLBI astrometry is conducted in the kinematic reference frame established with remote AGNs that are quasi-static on the sky (making them robust to inaccurate planetary ephemerides), while pulsar timing studies are carried out in the dynamic reference frame, which requires reliable planetary ephemerides to convert Earth-based pulse arrival times to the barycenter of the Solar System. The dynamic coordinate is floated to a kinematic coordinate system through observations of common objects, such as differential observations of asteroids with respect to stars. VLBI observations of MSPs with respect to AGNs will allow us to determine a rotation of the dynamic coordinate system defined by planetary ephemerides with respect to the inertial coordinate system (based on VLBI observations of AGNs) (Madison et al. 2013; Wang et al. 2017; Liu et al. 2023a).
The residuals in pulsar positions from VLBI and timing observations after a subtraction of the rotation will allow us to provide an independent assessment of pulsar timing errors and validate the PTA error model. We consider this question as a matter of great importance because any claim that a PTA has detected GWB is based upon a model of pulsar timing errors.
So far, planetary-ephemeris-dependent frame rotation remains poorly constrained. This is mainly because of the relatively large (≳1 mas) VLBI position uncertainties of MSPs (e.g., Liu et al. 2023a) as compared to the ≲0.2 mas timing position uncertainties for the best-timed MSPs (e.g., Perera et al. 2019). According to Liu et al. (2023b), 50 VLBI-based MSP positions with the current precision level would constrain the frame rotation to the 0.3 mas level; this constraint would be improved to the 0.1 mas level if VLBI could determine MSP positions to 0.3 mas precision. Therefore, reducing the VLBI position uncertainties of MSPs is key to building the planetary-ephemeris-dependent frame tie, examining the quality of planetary ephemerides, and hence facilitating the quantification of the timing noises resulting from inaccurate planetary ephemerides.
In this paper, we introduce and test a novel method that allows us to significantly improve the precision of pulsar VLBI positions. Throughout the paper, uncertainties are provided at 68% confidence, unless otherwise stated; the mathematical expressions (including the subscripts and superscripts) defined throughout this paper are universally valid.
2 A novel observing strategy and test observations
2.1 The PINPT strategy
As radio pulsars are generally faint (∼1 mJy at 1.4 GHz, and with steep spectra), the standard approach for directly determining positions in the quasi-inertial VLBI frame involving the measurement of group delays is not feasible. Instead, the absolute positions of pulsars have been determined using differential astrometry with respect to relatively bright reference sources, which are normally AGNs that are not point-like. As the position of a suitable nearby AGN can be determined using standard absolute astrometry techniques, such relative position measurements allow a connection between the pulsar position and the quasi-inertial frame. However, standard absolute astrometry techniques do not account for any structure in the AGN, and so the position extracted for any one of these sources is effectively that of the peak brightness in the image. The brightest spot in the 2D brightness distribution (or simply image) of an AGN also serves as the reference point for differential astrometry, which is usually the optically thick jet core (as long as the AGN is not flaring). As the AGN images normally vary with observing frequency ν, the reference point (or the jet core) evolves with ν as well; additionally, frequency-dependent image models of the reference sources are required for pulsar astrometry.
Three main error sources contribute to the error budget of the absolute pulsar position (see Sect. 3.2 of Ding et al. 2020a), namely (i) the uncertainty in the absolute position of the primary phase calibrator (derived and registered in the Radio Fundamental Catalogue1, or the ICRF3 catalog; Charlot et al. 2020), (ii) the unknown frequency-dependent core shifts (hereafter simply referred to as core shifts; e.g., Bartel et al. 1986; Lobanov 1998) of the reference sources (or more generally, the frequency evolution of reference source structures), and (iii) differences in the line-of-sight propagation delay between the direction of the calibrator source (where it has been solved) and the direction of the target. At L band, core shifts amounting to ∼1.2 mas (Sokolovsky et al. 2011) usually dominate the error budget; second to that, the propagation-related systematic error of the absolute pulsar position is also prominent, given the relatively large (≳1 deg) separation between the pulsar and its primary phase calibrator.
To suppress the aforementioned positional uncertainties, we designed a special observing strategy of differential astrometry, which extends the core-shift-determining method pioneered by Voitsik et al. (2018), and combines the method with the multiview (referring specifically to 2D interpolation throughout this paper) strategy (e.g., Rioja et al. 2017; Hyland et al. 2023). The proposed observing strategy, referred to as the PINPT (Phasescreen Interpolation plus frequeNcy-dePendent core shifT correction; read as “pinpoint”) strategy, requires a group of less than or approximately equal to 6 observations for absolute position determination: ≲3 L-band Multi-View observations of the pulsar (pulsar sessions), and ≲3 core-shift-determining observations on nearby AGNs (which must include the three calibrators used in the L-band Multi-View sessions), each at different observing frequency ν. Where suitable L-band in-beam calibrators are identified, the pulsar sessions can also be used as the L- band core-shift-determining session, hence reducing the required observing time.
Our observing strategy of multifrequency observations with multiple phase calibrators has three advantages. First, with the multifrequency observations of AGNs, the core shifts of the AGNs will be well determined, which will significantly reduce the core-shift-related errors of the absolute pulsar position. Second, using the Multi-View strategy will remove propagation- related systematic errors to at least the first order (e.g., Ding et al. 2020b). Finally, with the three phase calibrators of the MultiView setup, the pulsar position uncertainties due to uncertain reference source positions will drop by a factor of ≤ √3 (see Sect. 4.4 of Ding et al. 2020b) compared to using only one phase calibrator.
2.2 Observations
To test the PINPT strategy, we ran four observing sessions in December 2021 and January 2022 using the Very Long Baseline Array (VLBA) on PSR J2222-0137, a millisecond pulsar that has been well determined astrometrically by previous campaigns (Deller et al. 2013; Guo et al. 2021, hereafter referred to as D13 and G21). The observations, carried out under the project code BD244, include two 2 h L-band Multi-View observations and two 2hr core-shift-determining observations at S/X band and Ku (∼15 GHz) band, respectively. The first L-band observation was scheduled within 2 days of the S/X- and Ku-band observations (in order to minimize structure evolution of the phase calibrators), and served as both pulsar session and core-shift-determining session; whereas the second L-band observation was solely a pulsar session.
More specifically, in the L-band observations, a “target pointing” covers PSR J2222-0137 and two in-beam (at L band) calibrators identified by D13, namely FIRST J222112-012806 (J2221) and FIRST J222201-013236 (J2222); scans on this field were interleaved with scans on three brighter but off-beam AGNs (hereafter referred to as off-beam calibrators), namely ICRF J221852.0-033536 (J2218), ICRF J221947.2-005132 (J2219), and ICRF J222646.5+005211 (J2226), with a cycle time of 5 minutes. In the S/X- and Ku-band observations, J2221 and the three off-beam calibrators (hereafter referred to as the core-shift-probing AGNs) were observed alternately (with 5min and 2min cycles, respectively). All of the four core-shiftprobing AGNs are selected to have displayed resolved jet-core radio features in VLBI data, which eases the core-shift determination (see Sect. 4.2.2). Being fainter at higher observing frequencies, PSR J2222-0137 was skipped in the S/X- and Ku- band observations. The calibrator plans of the observations are displayed in Fig. A.1. In addition to the phase calibrators relatively close to PSR J2222-0137 on the sky, the bright blazar ICRF J214805.4+065738, further away from the sky region of interest, was used as the fringe finder to correct instrumental delays and filter bandpass. The unresolved flux densities and the angular separations of the aforementioned sources can be found in Table A.1.
To precisely determine the core shifts, a wide variety of observing frequencies are required. The S/X-band observation simultaneously covers two frequency bands, at around ∼2.3 and ∼8.4 GHz. Additionally, the L-band observations were designed to cover two separate frequency ranges centered around 1.44 and 1.76 GHz, respectively. Altogether, we sampled five distinct frequency ranges for the purpose of core-shift determination. The observing configurations, the phase calibration strategies (see Sect. 3), and the purposes of the four BD244 sessions are summarized in Table 1. The VLBA data prior to data reduction can be accessed with the project code BD244 at the NRAO Archive Interface2.
3 Data reduction and direct results
All data reduction was performed with the psrvlbireduce3 pipeline, which runs functions of AIPS (Greisen 2003) through ParselTongue (Kettenis et al. 2006), and images sources with DIFMAP (Shepherd et al. 1994). The data reduction follows the standard workflow described in Ding et al. (2020a), except for the phase calibration. Despite the total observing time of only 8 hours, the phase calibration of this work is sophisticated. There are two different procedures of phase calibration, and which is used depends on the purpose of the session, and more precisely on whether it is a target session or a core-shift-determining session. As noted in Sect. 2.2, the first L-band observation serves as both a target session and a core-shift-determining session, and is therefore reduced twice in two distinct procedures. The phase calibration strategies applied to the four observing sessions are summarized in Table 1 and described as follows.
Observing setups, phase calibration strategies, and the purposes of the four BD244 sessions.
3.1 Target sessions
For the data reduction of target sessions, we did not split the data into two by observing frequency (one at around 1.44 GHz and the other at around 1.76 GHz). By doing so, the average central frequency 1.6 GHz agrees with previous astrometric campaigns of PSR J2222-0137 (D13, G21), and the acquired image S/N (and hence the positional precision) is not lowered. As mentioned in Sect. 2.2, the two L-band observations involve five phase calibrators, including off-beam calibrators and two in-beam calibrators (also see Fig. A.1 and Table A.1). We implemented the phase calibration of PSR J2222-0137 in two different ways, depending on the astrometric goal.
3.1.1 In-beam astrometry
A previous astrometric campaign targeting PSR J2222-0137 was carried out between October 2010 and June 2012, spanning 1.7 yr (D13, G21). The two new target sessions extend the astrometric time baseline by a factor of 6.6 to 11.3 yr, promising higher astrometric precision (especially for proper motion). To capitalize on the long time baseline, we phase-referenced PSR J2222-0137 to the same reference source (i.e., J2222) used in the previous campaign following the data reduction procedure of D13 (including using the same image model of J2222). The updated results of in-beam astrometry are reported in Sect. 4.1.
3.1.2 Multi-View (2D interpolation)
As one form of the Multi-View strategy, 2D interpolation uses ≥3 reference sources to derive the phase solution at the sky position of the target (e.g., Rioja et al. 2017), which can at least remove propagation-related systematic errors to first order. In order to determine the precise absolute position of PSR J2222-0137, we applied Multi-View (as part of the PINPT strategy) with the off-beam calibrators, all of which have well-determined absolute positions1. We reiterate that realizing the PINPT strategy requires a combination of Multi-View session(s) and core-shiftdetermining session(s); these two kinds of sessions need to be arranged close to each other to minimize the effects of structure evolution. The second L-band observation is ≈40 days apart from the core-shift-determining sessions. Therefore, MultiView was applied to the first L-band observation, but not the second one.
In practice, we realized the Multi-View in two different approaches, as described in Appendix B. Both approaches consistently render the position 22h22m05s99997 ± 0.1 mas, –01°37′15.″7825±0.2 mas for PSR J2222-0137 at MJD 59554.0, and 22h22m01s.373131 ±0.03 mas, –01°32′36.″797654 ±0.06mas for J2222. For further examination, we also applied the two approaches of Multi-View to the X-band data (where the chance of phase wrap errors is much smaller than at L band), and confirmed with J2221 that the two approaches give almost identical positions. The availability of the J2222 position, as well as the J2221 position 22h21m12s680887 ± 0.01 mas, –01°28′06.″730985 ± 0.02 mas, offers a distinct pathway to the absolute position of PSR J2222-0137 (see Sect. 5). We note that the three positions presented above can only be considered relative positions with respect to the off-beam calibrators; and the positional uncertainties only include the statistical component related to random (thermal) noise in the VLBI image of PSR J2222-0137.
3.2 Core-shift-determining sessions
The determination of AGN core shifts requires a wide coverage of observing frequencies. As mentioned in Sect. 2.2, the core-shift-determining sessions cover five frequency ranges. We first split the S/X-band data into S-band data and X-band data, and likewise split the wide-L-band data into two datasets – one at ~l.44GHz and the other at ~1.76 GHz. Thus, we acquired five datasets altogether, each taken at a different observing wavelength: λ – 2, 4, 13, 17, and 21 cm.
From each of the five datasets, we measured the J2221 position with respect to each off-beam calibrator by (1) phasereferencing J2221 to each off-beam calibrator, and (2) dividing the phase-referenced J2221 data by its final image model obtained at λ, and (3) fitting the J2221 position. In phase referencing, the final image model of an off-beam calibrator at λ was applied to the phase calibration of the off-beam calibrator; subsequently, the acquired phase solution was applied to both the off-beam calibrator and J2221. To make the final image models of the off-beam calibrators and J2221, we first applied 13 cm models to the datasets of respective sources at all λ during phase calibration (or self-calibration for J2221). In this way, we aligned the reference points of each core-shift-probing AGN across λ. Thereafter, we singled out the aligned datasets, and remade the models of J2221 and off-beam calibrators at each λ. The final image models of in-beam and off-beam calibrators at all λ have been made publicly available4 to allow the reproduction of our results.
Enhanced astrometric results of PSR J2222-0137.
4 Astrometric parameters and core shifts
The data reduction described in Sect. 3 produced (a) two pulsar positions measured with respect to J2222, (b) Multi-View positions of the pulsar, J2221, and J2222, and (c) 5 × 3 = 15 J2221 positions from the core-shift-determining sessions. The products (a) and (c) can provide stringent constraints on astrometric parameters and core shifts, respectively.
4.1 Astrometric inference
We added the two new pulsar positions measured with respect to J2222 to previous pulsar positions (measured with respect to J2222), and remade the Bayesian inference as described in G21. The resultant astrometric parameters are provided in Table 2. For comparison, the previous VLBI results reported by G21 are also listed in Table 2. Unsurprisingly, the proper motion improves substantially, namely by a factor of approximately 7, while the parallax is also enhanced by ≈14%, corresponding to a refined trigonometric distance of 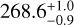 pc for PSR J2222-0137. On the other hand, the 3σ discrepancy in µδ reveals an underestimated systematic uncertainty in Declination reported by previous works, which is likely due to the vertical J2222 structure evolution that has a much greater impact on astrometric results determined over short (≲2 yr) time span.
pc for PSR J2222-0137. On the other hand, the 3σ discrepancy in µδ reveals an underestimated systematic uncertainty in Declination reported by previous works, which is likely due to the vertical J2222 structure evolution that has a much greater impact on astrometric results determined over short (≲2 yr) time span.
4.2 Core-shift determination
Following the pioneering work of Voitsik et al. (2018), we developed new packages to infer the core shifts of the four coreshift-probing AGNs from the 15 J2221 positions (with respect to three off-beam calibrators at five λ) in a Bayesian style. The core-shift inference requires three ingredients – (1) a prescription of the systematic errors of the 15 J2221 positions, (2) a mathematical description of the core shifts, and (3) an underlying mathematical relation between core shift and λ (or observing frequency ν). These three ingredients are addressed below.
4.2.1 Systematic errors on measured J2221 positions
Along with the 15 J2221 positions, their random errors due to noise in the J2221 images were also obtained with data reduction (described in Sect. 3.2). Additionally, atmospheric propagation effects will introduce systematic errors, which change with ν and the angular separation between J2221 and the reference source.
We quantified the systematic errors by
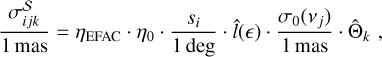 (1)
(1)
where 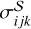 denotes systematic errors; the subscript i = J2218, J2219, J2226 specifies the reference source; the second subscript j = 1–5 corresponds to one of the five observing frequencies (see Sect. 3.2); the last subscript k = α, δ refers to Right Ascension (RA) or Declination (Dec); ηEFAC is a scaling factor (for the estimated systematic uncertainty) to be determined with Bayesian analysis; η0 is the initial scaling factor that brings
denotes systematic errors; the subscript i = J2218, J2219, J2226 specifies the reference source; the second subscript j = 1–5 corresponds to one of the five observing frequencies (see Sect. 3.2); the last subscript k = α, δ refers to Right Ascension (RA) or Declination (Dec); ηEFAC is a scaling factor (for the estimated systematic uncertainty) to be determined with Bayesian analysis; η0 is the initial scaling factor that brings 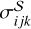 to a reasonable value (∼1 mas) before inferring ηEFAC, which eases the inference of ηEFAC at a later stage; si represents the angular separation between J2221 and the reference source;
to a reasonable value (∼1 mas) before inferring ηEFAC, which eases the inference of ηEFAC at a later stage; si represents the angular separation between J2221 and the reference source; 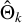 denotes the fractional synthesized beam size (projected to RA or Dec); and
denotes the fractional synthesized beam size (projected to RA or Dec); and 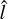 and σ0 stand for the two terms changing with antenna elevations ϵ and ν, respectively. In this work, we set η0 ≡ 1, and the adopted
and σ0 stand for the two terms changing with antenna elevations ϵ and ν, respectively. In this work, we set η0 ≡ 1, and the adopted 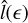 and σ0(ν) are described in Appendix C.
and σ0(ν) are described in Appendix C.
4.2.2 The directions of core shifts
Regarding the ingredient (2), we describe the core shift of the i′- th (i′ = J2218, J2219, J2221, J2226) AGN with two parameters – the core-shift magnitude 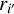 , and the direction of core shift
, and the direction of core shift 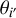 . As noted in Voitsik et al. (2018), it is difficult to infer both
. As noted in Voitsik et al. (2018), it is difficult to infer both 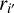 and
and 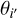 for each of the four core-shift-probing AGNs from the 15 J2221 positions without prior constraints, which has been taken into account in the design of the observations. As mentioned in Sect. 2.2, all of the core-shift-probing AGNs are selected to have displayed a clear jet-core radio feature on VLBI scales. Following Voitsik et al. (2018), we assumed that core-shift directions are aligned with the respective AGN jet directions, thereby gaining prior knowledge of the core-shift directions with analysis of VLBI images of the AGNs. The determination of AGN jet directions is detailed in Appendix D.
for each of the four core-shift-probing AGNs from the 15 J2221 positions without prior constraints, which has been taken into account in the design of the observations. As mentioned in Sect. 2.2, all of the core-shift-probing AGNs are selected to have displayed a clear jet-core radio feature on VLBI scales. Following Voitsik et al. (2018), we assumed that core-shift directions are aligned with the respective AGN jet directions, thereby gaining prior knowledge of the core-shift directions with analysis of VLBI images of the AGNs. The determination of AGN jet directions is detailed in Appendix D.
4.2.3 The relation between core shift and observing frequency
The relation between core shift and observing frequency is given by Konigl (1981) as 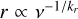 , where the index kr is equal to 1 when synchrotron self-absorption (that leads to the jet core radio emissions) is in equipartition (Blandford & Königl 1979). For the i′ -th AGN, we initially adopted an equivalent formalism,
, where the index kr is equal to 1 when synchrotron self-absorption (that leads to the jet core radio emissions) is in equipartition (Blandford & Königl 1979). For the i′ -th AGN, we initially adopted an equivalent formalism,
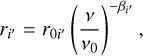 (2)
(2)
as the relation between 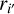 and ν, where
and ν, where 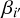 is a power index to be determined in Bayesian analysis; and v0 and
is a power index to be determined in Bayesian analysis; and v0 and 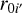 refer to the reference frequency and the core-shift magnitude at the reference frequency, respectively.
refer to the reference frequency and the core-shift magnitude at the reference frequency, respectively.
Using the Bayesian inference described in Appendix E, we derive 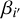 along with other model parameters, which are provided in Table E.1. For the derivation, we choose v0 = 2.27 GHz, the median of the five central frequencies (see Sect. 3.2 and Fig. 1). The
along with other model parameters, which are provided in Table E.1. For the derivation, we choose v0 = 2.27 GHz, the median of the five central frequencies (see Sect. 3.2 and Fig. 1). The 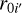 at a different v0 can be calculated using Eq. (2). When
at a different v0 can be calculated using Eq. (2). When 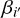 are included in the inference, the reduced chi-square
are included in the inference, the reduced chi-square 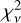 of inference is 1.9. Although
of inference is 1.9. Although 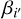 is significantly (≳3 σ) determined for 2 of the 4 AGNs, it is consistent with 1 in all cases. In comparison, when performing the inference with all
is significantly (≳3 σ) determined for 2 of the 4 AGNs, it is consistent with 1 in all cases. In comparison, when performing the inference with all 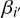 fixed to 1, we acquired consistent results with generally higher precision. Moreover, the
fixed to 1, we acquired consistent results with generally higher precision. Moreover, the 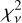 decreases to 1.2, suggesting
decreases to 1.2, suggesting 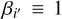 as an appropriate assumption for this work. We adopt the results derived assuming
as an appropriate assumption for this work. We adopt the results derived assuming 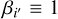 for further analysis. The adopted core-shift model is illustrated in Fig. 1.
for further analysis. The adopted core-shift model is illustrated in Fig. 1.
 |
Fig. 1 Jet core relative positions of FIRST J222112-012806 measured with respect to the jet cores of three reference sources (i.e., ICRF J221852.0-033536, ICRF J221947.2-005132, and ICRF J222646.5+005211) at five observing wavelengths. Systematic uncertainties calculated with Eq. (1) have been included in the positional uncertainties. Models of the combined core shifts are derived assuming |
5 An ultraprecise MSP position obtained with VLBI
With 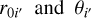 determined for the three off-beam calibrators and J2221, we calculated the core shifts of the four AGNs at 1.6 GHz, and proceeded to derive the absolute position of PSR J2222-0137. The derivation was realized with three different approaches. In the first approach, the pulsar position obtained with Multi-View (presented in Sect. 3.1.2) was corrected for the core-shift refinements in the assumed positions of the off- beam calibrators (as described by Eq. (F.3) in Appendix F). We obtained the pulsar position
determined for the three off-beam calibrators and J2221, we calculated the core shifts of the four AGNs at 1.6 GHz, and proceeded to derive the absolute position of PSR J2222-0137. The derivation was realized with three different approaches. In the first approach, the pulsar position obtained with Multi-View (presented in Sect. 3.1.2) was corrected for the core-shift refinements in the assumed positions of the off- beam calibrators (as described by Eq. (F.3) in Appendix F). We obtained the pulsar position 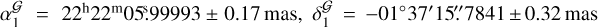 in the geocentric reference frame at the reference epoch tref of MJD 59554.0, which corresponds to
in the geocentric reference frame at the reference epoch tref of MJD 59554.0, which corresponds to 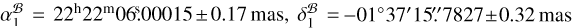 with respect to the barycenter of the Solar System after removing the parallax effects. Here, the positional uncertainty is the addition in quadrature of the statistical uncertainty (provided in Sect. 3.1.2) and the ∆xtarget uncertainty described in Appendix F.
with respect to the barycenter of the Solar System after removing the parallax effects. Here, the positional uncertainty is the addition in quadrature of the statistical uncertainty (provided in Sect. 3.1.2) and the ∆xtarget uncertainty described in Appendix F.
In the second approach, we first acquired the J2221 position xJ2221 at 1.6 GHz by correcting the X-band J2221 position (obtained with Multi-View, see Sect. 3.1.2) using the same process employed in the previous approach for the target source PSR J2222-0137. Subsequently, we reprocessed all VLBA data (including the two new pulsar sessions and the historical ones) of PSR J2222-0137, phase-referencing PSR J2222-0137 to J2221. With the position series obtained from the data reduction, we inferred the reference pulsar position 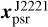 (measured with respect to J2221) and its uncertainty at tref = MJD 59554.0 (along with other astrometric parameters) using the Bayesian analysis described in Ding et al. (2023). Combining xJ2221, the image model position
(measured with respect to J2221) and its uncertainty at tref = MJD 59554.0 (along with other astrometric parameters) using the Bayesian analysis described in Ding et al. (2023). Combining xJ2221, the image model position 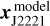 of J2221, and
of J2221, and 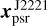 , the absolute position of PSR J2222-0137 was determined with Eq. (F.6) to be
, the absolute position of PSR J2222-0137 was determined with Eq. (F.6) to be 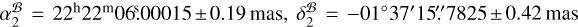 , where the error budget of the position is detailed in Appendix F.1 and Table F.2.
, where the error budget of the position is detailed in Appendix F.1 and Table F.2.
The last approach is essentially the same as the second one, except that J2222 is used instead of J2221. Accordingly, the absolute pulsar position was calculated with the J2222 position xJ2222 at 1.6 GHz, the image model position 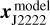 of J2222, and the reference pulsar position
of J2222, and the reference pulsar position 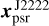 measured with respect to J2222. We obtained
measured with respect to J2222. We obtained 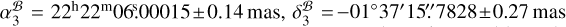 .
.
The pulsar positions derived with the three approaches are summarized in the upper part of Table 3. The intermediate results leading to the three pulsar positions are provided in Table F.2. Though all three approaches render highly consistent absolute pulsar positions, the first approach offers a snapshot (on the timescale of AGN structure evolution) localization (of PSR J2222-0137) that is independent of the previous astrometric observations of PSR J2222-0137, as opposed to the two other approaches (which use the multifrequency multi-source observations to perfect the position and structure of one of the in-beam calibrators – rather than the pulsar – at that snapshot in time, before standard differential astrometry is performed using the frozen model of the astrometric reference source). Therefore, we report 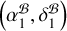 at tref = MJD 59554.0 as the primary absolute position of PSR J2222–0137.
at tref = MJD 59554.0 as the primary absolute position of PSR J2222–0137.
Absolute pulsar positions with respect to the barycenter of the Solar System, derived with the PINPT strategy.
6 Comparison to timing positions
A priori, we expect the position difference between the VLBI PINPT measurement and that made by pulsar timing to be consistent. With a sample size of 1, it is difficult to ascribe any discrepancy to one or the other of the measurement techniques, or to a systematic difference between dynamic and kinematic frames – but we can use the level of agreement to set a probabilistic upper limit on the error contribution from any of these three potential sources. The most precise published timing-based position of PSR J2222-0137 is reported in G21. In Table 3 of G21, three positions are provided for tref = MJD 55743, which include one position derived assuming a proper motion determined with VLBI, and two positions derived without using any VLBI prior (hereafter referred to as timing-only positions).
To test the PINPT strategy with pulsar timing, we re-derived 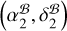 and
and 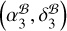 at tref = MJD 55743 (same as that of G21) following the method described above in Sect. 5, under the assumption that the structures of J2221 and J2222 do not evolve with time. The results are displayed in Table 3. Intermediate results for the calculations are provided in Table F.2. Compared to the absolute pulsar position determined for MJD 59554 using either the J2221 or the J2222 approach, the pulsar position derived for MJD 55743 with the same approach is reported with smaller uncertainty. This is because the reference pulsar position
at tref = MJD 55743 (same as that of G21) following the method described above in Sect. 5, under the assumption that the structures of J2221 and J2222 do not evolve with time. The results are displayed in Table 3. Intermediate results for the calculations are provided in Table F.2. Compared to the absolute pulsar position determined for MJD 59554 using either the J2221 or the J2222 approach, the pulsar position derived for MJD 55743 with the same approach is reported with smaller uncertainty. This is because the reference pulsar position 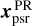 is better constrained at MJD 55743 (see Appendix F.1 and Table F.2), around which the pulsar was observed more densely with VLBI.
is better constrained at MJD 55743 (see Appendix F.1 and Table F.2), around which the pulsar was observed more densely with VLBI.
To minimize the correlation between the timing and VLBI positions, we only compare the VLBI positions to the two timing-only positions (of G21), which are listed in Table 3 as the “DMX” and “non-DMX” positions. Here, “DMX”, named by G21, refers to the pulsar timing model that describes DM with a piecewise constant function (Demorest et al. 2013; G21), while “non-DMX” refers to the timing model that approximates DM variations with a cubic function (G21). The DMX and non-DMX timing positions are marginally consistent to within 2σ (here and hereafter, σ refers to the addition in quadrature of the uncertainties of the two compared sides), with the uncertainty of the DMX position being more conservative than the non-DMX one.
On the other side of the comparison, 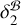 and
and 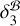 are consistent with each other. However,
are consistent with each other. However, 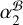 is smaller than
is smaller than 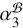 at 3 σ significance, which is associated with a ~3 σ discrepancy between the two µα measured with respect to J2221 (
at 3 σ significance, which is associated with a ~3 σ discrepancy between the two µα measured with respect to J2221 (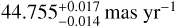 ) and J2222 (44.707 ± 0.005 mas yr–1, as reported in Table 2), respectively. The discrepancy between
) and J2222 (44.707 ± 0.005 mas yr–1, as reported in Table 2), respectively. The discrepancy between 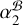 and
and 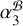 likely indicates the violation of the assumption that the structures of J2221 and J2222 do not evolve with time. The jet direction of J2221 is almost aligned with the RA direction (see Fig. D.1). As noted in D13, the relatively severe structure evolution of J2221 is believed to result in (1) a less precise parallax derived with respect to J2221 (as the parallax magnitude in the RA direction is ≈2.4 times larger than in the Dec. direction), and (2) a biased µα determination. Specifically, the discrepancy between
likely indicates the violation of the assumption that the structures of J2221 and J2222 do not evolve with time. The jet direction of J2221 is almost aligned with the RA direction (see Fig. D.1). As noted in D13, the relatively severe structure evolution of J2221 is believed to result in (1) a less precise parallax derived with respect to J2221 (as the parallax magnitude in the RA direction is ≈2.4 times larger than in the Dec. direction), and (2) a biased µα determination. Specifically, the discrepancy between 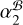 and
and 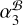 (or the µα discrepancy) can be explained by a 0.56 mas larger (or fractionally 18% higher according to Table E.1) rJ2221 (1.6 GHz) at MJD 55743 compared to at MJD 59554. On the other hand, thanks to the horizontal jet of J2221,
(or the µα discrepancy) can be explained by a 0.56 mas larger (or fractionally 18% higher according to Table E.1) rJ2221 (1.6 GHz) at MJD 55743 compared to at MJD 59554. On the other hand, thanks to the horizontal jet of J2221, 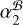 is almost free from the impact of structure evolution (of J2221), and is therefore more favorable than
is almost free from the impact of structure evolution (of J2221), and is therefore more favorable than 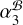 . The favorability is further strengthened by the indication of vertical structure evolution of J2222 mentioned in Sect. 4.1. Therefore, we adopt
. The favorability is further strengthened by the indication of vertical structure evolution of J2222 mentioned in Sect. 4.1. Therefore, we adopt 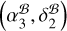 as the absolute pulsar position at MJD 55743. A more sophisticated treatment in the future could incorporate positions in both axes from both sources, weighting them by some measure of expected reliability and taking into account the covariance between the two measurements.
as the absolute pulsar position at MJD 55743. A more sophisticated treatment in the future could incorporate positions in both axes from both sources, weighting them by some measure of expected reliability and taking into account the covariance between the two measurements.
When comparing 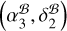 to the two timing-only positions, we first find good consistency between
to the two timing-only positions, we first find good consistency between 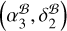 and the DMX position, with
and the DMX position, with 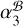 and the DMX RA being consistent to within 0.3 σ, and
and the DMX RA being consistent to within 0.3 σ, and 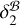 and the DMX Dec consistent to within 1.1σ. On the other hand, despite the 1.5σ consistency between
and the DMX Dec consistent to within 1.1σ. On the other hand, despite the 1.5σ consistency between 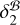 and the non-DMX Dec.,
and the non-DMX Dec., 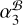 is smaller than the non-DMX RA at >3σ significance. It is not impossible that the >3σ RA discrepancy is caused by the use of different kinds of reference systems. Therefore, we cannot yet conclude that the new PINPT results favor the DMX timing model over the non-DMX model with just one MSP.
is smaller than the non-DMX RA at >3σ significance. It is not impossible that the >3σ RA discrepancy is caused by the use of different kinds of reference systems. Therefore, we cannot yet conclude that the new PINPT results favor the DMX timing model over the non-DMX model with just one MSP.
Moreover, we reiterate that 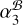 is subject to additional errors induced by the potential horizontal structure evolution of J2222. A more robust test of the PINPT strategy with pulsar timing can be achieved by comparing
is subject to additional errors induced by the potential horizontal structure evolution of J2222. A more robust test of the PINPT strategy with pulsar timing can be achieved by comparing 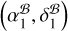 to timing positions (based on different timing models) derived at MJD 59554. A preliminary timing analysis, incorporating a large number of new datasets, shows reasonably good consistency with
to timing positions (based on different timing models) derived at MJD 59554. A preliminary timing analysis, incorporating a large number of new datasets, shows reasonably good consistency with 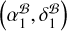 . Detailed results will be reported as part of an upcoming timing paper. Additionally, applying the PINPT strategy to just a few well-timed MSPs will allow a much more stringent test of the new strategy.
. Detailed results will be reported as part of an upcoming timing paper. Additionally, applying the PINPT strategy to just a few well-timed MSPs will allow a much more stringent test of the new strategy.
7 Summary
Using the PINPT strategy, we determined an MSP position with a precision of ~0.2 mas using VLBI, which improves on the previous precision level by a factor of approximately 5 (e.g., Ding et al. 2020a; Liu et al. 2023a), and is comparable with the precision level of the timing positions of the best-timed MSPs (e.g., Perera et al. 2019). According to Liu et al. (2023a), applying the PINPT strategy to 50 MSPs promises <0.1 mas precision for the connection between the kinematic and dynamic reference frames, which is more than three times more precise than the previous expectation. Considering that systematic errors of calibrator source positions are in the range of 0.05–0.2 mas1 and are unlikely to be improved within several decades, our strategy provides a position accuracy that approaches the practical limit.
In general, the PINPT strategy can be used in a broader context: it can sharpen the VLBI localization of any compact steep-spectrum radio source, which could facilitate studies of, for example, fast radio bursts (e.g., Bhandari et al. 2023) or mergers of two neutron stars (e.g., Mooley et al. 2022). Furthermore, it is important to stress that the PINPT strategy is not only meant to enhance the precision of absolute positions, but could have a fundamental impact on differential astrometry as well. Due to the temporal structure evolution of the reference source(s) (which includes core-shift variations; Plavin et al. 2019), proper motions and parallaxes measured with respect to AGNs could be potentially biased (e.g., D13, also see Sect. 6), which is believed to have driven the occasional inconsistencies between VLBI and timing proper motions for the longest timed MSPs (Ding et al. 2023). However, traditional differential astrometry with one calibrator is incapable of quantifying the positional variations due to structure evolution, and is therefore subject to extra systematic errors. In the scenario of precise in-beam astrometry, the variability in the core shifts of the reference sources is a leading source of systematic error. Multi-epoch PINPT observations, on the other hand, can constrain the coreshift variabilities, thus minimizing their detrimental influence on astrometric results. As pulsar astrometry is considered, joining the core-shift-determining sessions to in-beam or Multi-View astrometry can provide accurate pulsar proper motions and parallaxes that remain unbiased by core-shift variabilities, which can then be safely incorporated into pulsar timing analysis.
Acknowledgements
H.D. appreciates the EACOA Fellowship awarded by the East Asia Core Observatories Association. H.D. thanks Wei Zhao for the discussion about jet direction determination. This work is mainly based on observations with the Very Long Baseline Array (VLBA), which is operated by the National Radio Astronomy Observatory (NRAO). The NRAO is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. Pulse ephemerides of PSR J2222–0137 were made for the purpose of pulsar gating, using data from the Effelsberg 100-meter telescope of the Max-Planck-Institut für Radioastronomie. This work made use of the Swinburne University of Technology software correlator, developed as part of the Australian Major National Research Facilities Programme and operated under license (Deller et al. 2011).
Appendix A Supporting materials for Sect. 2.2
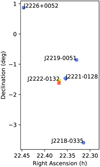 |
Fig. A.1 The calibrator plans for the PINPT observations of this work, which involve two in-beam phase calibrators and three out-of-beam calibrators of PSR J2222–0137 (shown in red). More source information can be found in Table A.1. Among the two in-beam calibrators, FIRST J222201–013236, marked by golden circle, was used in previous astrometric campaigns (Deller et al. 2013; Guo et al. 2021); FIRST J222112–012806, marked by blue diamond, is used for core-shift determinations (see Sect. 4.2.2). The adopted phase calibration strategies are described in Sect. 2.2 and summarized in Table 1. |
Appendix B Two approaches of Multi-View (2D interpolation)
As mentioned in Sect. 3.1.2, Multi-View was realized in two approaches. In both approaches, J2219 — the closest to PSR J2222–0137 among the off-beam calibrators, was used as the main phase calibrator. In the first approach, we made a phase calibration with J2219, then interpolated the phase solution to the approximate sky position of PSR J2222–0137 by performing two 1D interpolation operations (e.g., Ding et al. 2020b) one after another. Specifically, the phase solution was first extrapolated along the J2219-to-J2226 line to the intersection with the straight line connecting J2218 and PSR J2222–0137. The derived phase solution was then extrapolated again along the J2218-to-pulsar line, to the position of PSR J2222–0137.
In the second approach, the phase solution acquired with J2219 was passed to J2218 and J2226. Subsequently, selfcalibration was performed with both J2218 and J2226. The acquired incremental phase solutions ϕJ2218 and ϕJ2226 were then linearly added together as cJ2218⋅ϕJ2218 + cJ2226⋅ϕJ2226 (here, cJ2218 and cJ2226 are constants described in Appendix F), which essentially moves the virtual calibrator (explained in Ding et al. 2020b) to the approximate sky position of the target (i.e., PSR J2222–0137, J2221, or J2222).
Appendix C î(є) and σ0(v)
In Eq. 1, there are two functions — î(є) and σ0(v). The former describes the fractional atmospheric path length as a function of the antenna elevation є, while the latter characterizes the evolution of the systematic error with respect to the observing frequency v. We define î(є) as l/RE, where l and RE are, respectively, the atmospheric path length and the radius of the Earth (not including the atmosphere). It is easy to calculate that
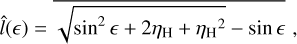 (C.1)
(C.1)
where the overline commands averaging over the observation; ηH = hatmo/RE is the atmosphere thickness divided by RE. We adopted ηΗ = 0.15 calculated with the upper height of the ionosphere (≈ 965 km) and the average Earth radius of 6371 km.
Using simulations, the relation between propagation-related positional error and v has been studied by Martí-Vidal et al. (2010), and is provided in Fig. 6 of Martí-Vidal et al. (2010). As the simulations of Martí-Vidal et al. (2010) assume a 5° angular separation between the target and the reference source, we divided the results of Martí-Vidal et al. (2010) by a factor of 5 (to reach the systematics per degree separation), and adopted the divided results as σ0(v). In Eq. 1, we assume 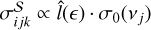 , while having little knowledge about the coefficient. Therefore, the nuisance parameter ηEFAC (to be determined in Bayesian inference) is essential for completing Eq. 1, and recovering the true magnitude of
, while having little knowledge about the coefficient. Therefore, the nuisance parameter ηEFAC (to be determined in Bayesian inference) is essential for completing Eq. 1, and recovering the true magnitude of 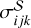 .
.
Appendix D The determination of AGN jet directions
AGN jet directions ϕjet and their uncertainties have been directly estimated from their VLBI images (e.g., Kovalev et al. 2017). Likewise, we determined ϕjet of the 4 core-shift-probing AGNs from the final image models4 of the 4 sources using the newly developed package arcfits5. For the ϕjet determination, we prioritized the use of image models obtained at 15 GHz because, compared to at lower frequencies, 1) the jet core is closer to the central engine, and 2) the spatial resolution is higher. In case extended jet features were not identified by arcfits, we moved on to the image model of the next highest frequency. The obtained ϕjet results are illustrated alongside the AGN images in Fig. D.1, and provided in Table D.1. arcfits derives ϕjet and their uncertainties in an automatic way described as follows.
D.1 The noise level of the residual map
After reading a VLBI image, a 2D array of flux densities can be obtained. From this 2D map, the noise level rms of the residual map (i.e., the image after removing all detected source components) can be derived, which is a preparation for measuring ϕjet. We established the residual map and estimated the rms in the following way. We first marginalized the 2D array of flux densities into a 1D array, and calculated the standard deviation of the flux densities. All flux densities higher than 7 times the standard deviation were considered “detected”, and were removed from the 1D array. We repeated this standard deviation calculation and removal of detected points until we reached the residual map, in which no more detection can be identified. The standard deviation of this residual map was adopted as the residual map noise level rms.
Unresolved flux densities & angular separations from PSR J2222–0137.
AGN jet position angles ϕjet determined with arcfits.
D.2 Elliptical cuts on the inner regions of VLBI images
The hitherto most advanced method of measuring the position angles of radio features outside the compact radio core is by 1) converting the positions in a VLBI image from Cartesian coordinate to a polar coordinate centered around the brightest spot of the image, and 2) applying circular cuts to the VLBI image (e.g., Cui et al. 2023). As far as core-shift studies are concerned, a ϕjet determined close to the compact radio core is expected to better approximate the core-shift direction, as compared to a ϕjet determined afar (e.g., Konigl 1981). Due to intrinsic structure and/or scatter broadening, the compact radio core is usually larger than the synthesized beam, while normally resembling the beam (e.g., Fig. D.1). In other words, there is no prior information about the size of the compact radio core. As a result, when the synthesized beam is non-circular, circular cuts applied in close proximity to the compact radio core might lead to the misidentification of the compact radio core (stretching along the major axis) as radio features outside the compact core. Although this anomaly can be corrected by human intervention, other systematic errors might be introduced during the human intervention.
As a novel method that is i) largely free of human intervention, and ii) dedicated to ϕjet determination in close proximity to the compact radio core, we cut an image model with a number of increasingly large ellipses that a) have the same axis ratio and position angle as the synthetic beam, and b) are centered at the image pixel of the highest flux density. Given that the position angle and axis ratio are both constant, the n-th (n = 1,2,3,…) ellipse can be characterized by its semi-major axis an ; a position on this ellipse can be defined with one additional parameter — the position angle (east of north) ϕ. In this work, we universally adopted
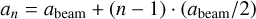 (D.1)
(D.1)
for the ellipses, where abeam refers to the semi-major axis of the synthesized beam.
Among the ellipses ascertained by Eq. D.1, the innermost ellipse outside the compact radio core was used to derive ϕjet; the position angle corresponding to the maximum flux density on the ellipse was adopted as the ϕjet. An ellipse is considered outside the compact radio core, when it meets the following criteria:
- (i)
the maximum flux density on the ellipse is > 7 rms (see Appendix D.1 for the meaning and calculation of rms), and
- (ii)
the median flux density on the ellipse is < 3 rms, and
- (iii)
ϕjet uncertainty can be calculated with the method detailed in Appendix D.3.
If no ellipse meets the criteria, the AGN is considered a compact source without extended radio features.
D.3 The uncertainty on the AGN jet direction
In Appendix D.2, we adopted the position angle of the maximum flux density 𝒮max on the innermost elliptical cut outside the compact radio core as the ϕjet. Random noises in the image might distort the flux density distribution, and deviate the position of the maximum flux density on the ellipse. The degree of flux density change due to random noises is limited: the chance of large flux density changes due to random noises is lower than smaller flux density changes. Given a flux density drop δ𝒮 induced by random noises, one can estimate the chance of the drop by counting flux densities 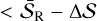 in the residual map (see Appendix D.1 for explanation of the residual map), where
in the residual map (see Appendix D.1 for explanation of the residual map), where 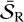 stands for the mean flux density of the residual map. Reversely, provided a confidence level where the flux densities in the residual map is
stands for the mean flux density of the residual map. Reversely, provided a confidence level where the flux densities in the residual map is 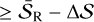 , we can derive the δ𝒮 corresponding to the confidence level. In this way, we estimated Δ𝒮 corresponding to 68% confidence level from the residual map. At 68% confidence, we expect
, we can derive the δ𝒮 corresponding to the confidence level. In this way, we estimated Δ𝒮 corresponding to 68% confidence level from the residual map. At 68% confidence, we expect 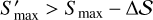 , where
, where 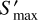 isthe maximum flux density changed by random noises.
isthe maximum flux density changed by random noises.
On the ellipse (where ϕjet is determined), we identify all position angles ϕ where the flux densities equal to Smax − δ𝒮. When exactly two ϕ are acquired, the two ϕ are adopted as the 1σ uncertainty interval of ϕjet. Otherwise (which is rare), we consider the ellipse likely still intersects the compact radio core, and move onto the next ellipse further afield.
 |
Fig. D.1 AGN contour plots obtained from the core-shift-determining sessions, and the AGN jet directions determined with arcfits. For the jet direction determinations, image models obtained at higher observing frequencies are preferred, unless extended jet features are not identified by arcfits. The flux density on the m-th (m = 1,2,3,…) contour equals to |
Appendix E The Bayesian inference of core shifts
We derived the core-shift model with quartet6, a newly developed package dedicated to inferring core-shift-related parameters in a Bayesian manner, which is explained as follows.
E.1 Mathematical formalism
Apart from the aforementioned parameters ri, θi, βi and ηEFAC, the reference positions 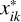 are also required in the model of core shifts. For the Bayesian inference, the likelihood function is
are also required in the model of core shifts. For the Bayesian inference, the likelihood function is
![${P_{CS}} \propto {\left( {\mathop {\mathop \prod \nolimits^ }\limits_i \mathop {\mathop \prod \nolimits^ }\limits_j \mathop {\mathop \prod \nolimits^ }\limits_k {\sigma _{ijk}}} \right)^{ - 1}}\exp \left[ { - {1 \over 2}\mathop {\mathop \sum \nolimits^ }\limits_i \mathop {\mathop \sum \nolimits^ }\limits_j \mathop {\mathop \sum \nolimits^ }\limits_k {{\left( {{{{x_{ijk}} - {{\mathop x\limits^ }_{ijk}}} \over {{\sigma _{ijk}}}}} \right)}^2}} \right],$](/articles/aa/full_html/2024/11/aa51492-24/aa51492-24-eq79.png) (E.1)
(E.1)
where xijk and 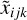 refer to, respectively, the observed and the modeled J2221 positions with respect to the i-th reference source at observing frequency νj; the total positional uncertainty σijk is the addition-in-quadrature of random and systematic errors. In Eq. E.1, the modeled J2221 positions
refer to, respectively, the observed and the modeled J2221 positions with respect to the i-th reference source at observing frequency νj; the total positional uncertainty σijk is the addition-in-quadrature of random and systematic errors. In Eq. E.1, the modeled J2221 positions 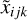 follow the relation
follow the relation
![$\matrix{ {} & {{{\mathop x\limits^ }_{ij\alpha }} = \left[ {{r_{{\rm{J}}2221}}\left( {{v_j}} \right)\cos {\theta _{{\rm{J}}2221}} - {r_i}\left( {{v_j}} \right)\cos {\theta _i}} \right] + x_{i\alpha }^ * } \cr {} & {{{\mathop x\limits^ }_{ij\delta }} = \left[ {{r_{{\rm{J}}2221}}\left( {{v_j}} \right)\sin {\theta _{{\rm{J}}2221}} - {r_i}\left( {{v_j}} \right)\sin {\theta _i}} \right] + x_{i\delta }^ * ,} \cr } $](/articles/aa/full_html/2024/11/aa51492-24/aa51492-24-eq82.png) (E.2)
(E.2)
where the formalism of ri′ (vj) is given by Eq. 2.
E.2 Priors
For the Bayesian inference, we adopted the following prior information:
- (i)
When the inference of βi′ is requested, the prior constraints of βi′ follow a uniform distribution between 0.3 and 3, which is denoted as βi′ ~ 𝓤 (0.3,3).
- (ii)
r0i′ ~ 𝓤 (0,5), where the unit is mas.
- (iii)
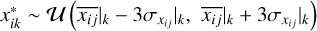 , where
, where 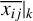 and σxij|k stand for the average and standard deviation of xijk over all observing frequencies j; one lower limit and one upper limit are universally used for all observing frequencies.
and σxij|k stand for the average and standard deviation of xijk over all observing frequencies j; one lower limit and one upper limit are universally used for all observing frequencies. - (iv)
ηEFAC ~𝓤 (0, 20).
- (v)
The prior constraints on θi′ follow Gaussian distributions characterized by the AGN jet directions ϕjet in Table D.1. Namely, θi′ ~ 𝒢 (ϕjet|i′ ,σϕjet|i′). In the case of asymmetric ϕjet uncertainty, the larger side of the uncertainty is used as the σϕjet|i′.
Appendix F The calculation of an absolute pulsar position and its uncertainty
The determination of the absolute position of PSR J2222–0137 through the PINPT strategy relies on well determined absolute positions of the off-beam calibrators. This work is based on the off-beam calibrator positions 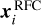 reported in the 2024A release of the Radio Fundamental Catalogue1 (RFC). Generally speaking, for Multi-View carried out with 3 off-beam calibrators, the relation between the target position xtarget and the off-beam calibrator positions xq (q = 1,2, 3) is
reported in the 2024A release of the Radio Fundamental Catalogue1 (RFC). Generally speaking, for Multi-View carried out with 3 off-beam calibrators, the relation between the target position xtarget and the off-beam calibrator positions xq (q = 1,2, 3) is
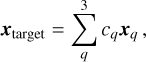 (F.1)
(F.1)
where xtarget is known to a precision good enough to guide the Multi-View; cq are coefficients that can be solved with the additional condition
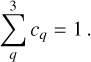 (F.2)
(F.2)
Therefore, in Multi-View, offsets in the off-beam calibrator positions would lead to offset in the target position (refined with Multi-View), as
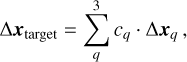 (F.3)
(F.3)
where Δxq result from 1) core shifts of the off-beam calibrators, and 2) inaccurate positions of the off-beam calibrator image models, and are calculated by
![${\rm{\Delta }}{x_q} = \left( {x_q^{{\rm{model}}} - x_q^{{\rm{RFC}}}} \right) + \left[ {{r_q}\left( {{v_{psr}}} \right) - r_q^{{\rm{RFC}}}} \right].$](/articles/aa/full_html/2024/11/aa51492-24/aa51492-24-eq89.png) (F.4)
(F.4)
Here, 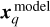 refers to the image model position of the q-th off- beam calibrator; rq (vpsr) denotes the core shift of the q-th off- beam calibrator at the observing frequency of interest (which is 1.6 GHz, the observing frequency of the pulsar sessions, for this work);
refers to the image model position of the q-th off- beam calibrator; rq (vpsr) denotes the core shift of the q-th off- beam calibrator at the observing frequency of interest (which is 1.6 GHz, the observing frequency of the pulsar sessions, for this work); 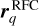 is the residual core shift of the RFC position.
is the residual core shift of the RFC position.
Specific to this work, q = i = J2212, J2219, J2226. ci for various targets are provided in Table F.1. According to Porcas (2009), 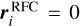 , when 1)
, when 1)  is derived with group-delay astrometry (that removes the ionosphere-induced group delay with dual-band or multi-band geodetic observations), and 2) βi = 1. Both conditions are met for this work:
is derived with group-delay astrometry (that removes the ionosphere-induced group delay with dual-band or multi-band geodetic observations), and 2) βi = 1. Both conditions are met for this work: 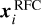 are estimated with group-delay astrometry; and we already assume that βi ≡ 1 in the Bayesian analysis (see Sect. 4.2.3). Therefore, we adopt
are estimated with group-delay astrometry; and we already assume that βi ≡ 1 in the Bayesian analysis (see Sect. 4.2.3). Therefore, we adopt 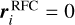 in this work.
in this work.
The uncertainty on Δxtarget is calculated by the addition-in- quadrature of the uncertainties on the components ciΔxi, where the uncertainty of Δxi is further derived by the addition-in- quadrature of the uncertainties on 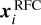 and ri.
and ri.
F.1 Deriving an absolute pulsar position via a nearby AGN
When the target itself is an AGN (e.g., J2221, J2222), Eq. F.3 needs to be generalized to
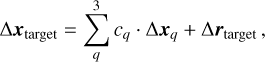 (F.5)
(F.5)
where Δrtarget is the core-shift difference between vpsr and the observing frequency vIBC of the AGN target. Accordingly, the uncertainty on Δxtarget is further added in quadrature by the uncertainty of Δrtarget.
The availability of a nearby AGN (hereafter referred to as IBC) around a pulsar (or other targets of interest) provides an alternative pathway to the absolute position of the pulsar. After applying the position correction Δxtarget calculated with Eq. F.5, the absolute position xIBC of the IBC at vpsr can be derived. Provided i) the image model position 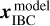 of the IBC, and ii) the pulsar position
of the IBC, and ii) the pulsar position 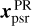 determined with phase referencing with respect to the IBC, the absolute pulsar position can be calculated as
determined with phase referencing with respect to the IBC, the absolute pulsar position can be calculated as
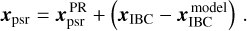 (F.6)
(F.6)
This pathway of deriving the absolute position may become the only option in cases where Multi-View of the target of interest cannot be arranged (e.g., when the target is an unpredictable radio transient). The uncertainty of xpsr derived via the IBC is the addition-in-quadrature of the Δxtarget uncertainty, the 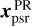 uncertainty (estimated with Bayesian inference in this work), and the statistical uncertainty of the IBC position obtained with Multi-View at vIBC.
uncertainty (estimated with Bayesian inference in this work), and the statistical uncertainty of the IBC position obtained with Multi-View at vIBC.
Core-shift models derived at the reference frequency of 2.27 GHz with Bayesian inference.
References
- Agazie, G., Anumarlapudi, A., Archibald, A. M., et al. 2023, ApJ, 951, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniadis, J., Arumugam, P., Arumugam, S., et al. 2023, A&A, 678, A50 [CrossRef] [EDP Sciences] [Google Scholar]
- Bartel, N., Herring, T. A., Ratner, M. I., Shapiro, I. I., & Corey, B. E. 1986, Nature, 319, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Bhandari, S., Marcote, B., Sridhar, N., et al. 2023, ApJ, 958, L19 [CrossRef] [Google Scholar]
- Blandford, R. D., & Königl, A. 1979, ApJ, 232, 34 [Google Scholar]
- Brisken, W. F., Benson, J. M., Goss, W., & Thorsett, S. 2002, ApJ, 571, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, P., Jacobs, C., Gordon, D., et al. 2020, A&A, 644, A159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chatterjee, S., Brisken, W. F., Vlemmings, W. H. T., et al. 2009, ApJ, 698, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, Y., Hada, K., Kawashima, T., et al. 2023, Nature, 621, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A., Verbiest, J., Tingay, S., & Bailes, M. 2008, ApJ, 685, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Brisken, W. F., Phillips, C. J., et al. 2011, PASP, 123, 275 [Google Scholar]
- Deller, A., Boyles, J., Lorimer, D., et al. 2013, ApJ, 770, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Deller, A. T., Goss, W. M., Brisken, W. F., et al. 2019, ApJ, 875, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., Ferdman, R. D., Gonzalez, M., et al. 2013, ApJ, 762, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Detweiler, S. 1979, ApJ, 234, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, H., Deller, A. T., Freire, P., et al. 2020a, ApJ, 896, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, H., Deller, A. T., Lower, M. E., et al. 2020b, MNRAS, 498, 3736 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, H., Deller, A. T., Stappers, B. W., et al. 2023, MNRAS, 519, 4982 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., & Wex, N. 2024, Liv. Rev. Relativ., 27, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Greisen, E. W. 2003, Astrophys. Space Sci. Lib., 285, 109 [NASA ADS] [Google Scholar]
- Guo, Y., Freire, P., Guillemot, L., et al. 2021, A&A, 654, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hobbs, G., Lyne, A., & Kramer, M. 2010, MNRAS, 402, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Hyland, L. J., Reid, M. J., Orosz, G., et al. 2023, ApJ, 953, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Kettenis, M., van Langevelde, H. J., Reynolds, C., & Cotton, B. 2006, ASP Conf. Ser., 351, 497 [NASA ADS] [Google Scholar]
- Konigl, A. 1981, ApJ, 243, 700 [Google Scholar]
- Kovalev, Y., Petrov, L., & Plavin, A. 2017, A&A, 598, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, M., Stairs, I., Manchester, R., et al. 2021, Phys. Rev. X, 11, 041050 [NASA ADS] [Google Scholar]
- Liu, N., Zhu, Z., Antoniadis, J., et al. 2023a, A&A, 670, A173 [Google Scholar]
- Liu, Y., Cao, S., Biesiada, M., et al. 2023b, ApJ 949 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Madison, D. R., Chatterjee, S., & Cordes, J. M. 2013, ApJ, 777, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Martí-Vidal, I., Guirado, J., Jiménez-Monferrer, S., & Marcaide, J. 2010, A&A, 517, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miles, M. T., Shannon, R. M., Bailes, M., et al. 2023, MNRAS, 519, 3976 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Anderson, J., & Lu, W. 2022, Nature, 610, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Perera, B., DeCesar, M., Demorest, P., et al. 2019, MNRAS, 490, 4666 [NASA ADS] [CrossRef] [Google Scholar]
- Plavin, A., Kovalev, Y., Pushkarev, A., & Lobanov, A. 2019, MNRAS, 485, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Porcas, R. 2009, A&A, 505, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reardon, D. J., Zic, A., Shannon, R. M., et al. 2023, ApJ, 951, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Rioja, M. J., Dodson, R., Orosz, G., Imai, H., & Frey, S. 2017, AJ, 153, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Sazhin, M. 1978, Sov. Astron, 22, 36 [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987 [NASA ADS] [Google Scholar]
- Siemens, X., Ellis, J., Jenet, F., & Romano, J. D. 2013, Class. Quantum Gravity, 30, 224015 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolovsky, K. V., Kovalev, Y. Y., Pushkarev, A. B., & Lobanov, A. P. 2011, A&A, 532, A38 [CrossRef] [EDP Sciences] [Google Scholar]
- Voitsik, P., Pushkarev, A., Kovalev, Y. Y., et al. 2018, Astron. Rep., 62, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. B., Coles, W. A., Hobbs, G., et al. 2017, MNRAS, 469, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Chen, S., Guo, Y., et al. 2023, RAA, 23, 075024 [NASA ADS] [Google Scholar]
Available at https://github.com/dingswin/arcfits. The writing of the package has benefited from the discussion with Dr. Wei Zhao, who already has a preliminary script to derive directions along the jet ridge line using circular slicing (see https://github.com/AXXE251/AGN-JET-RL).
All Tables
Observing setups, phase calibration strategies, and the purposes of the four BD244 sessions.
Absolute pulsar positions with respect to the barycenter of the Solar System, derived with the PINPT strategy.
Core-shift models derived at the reference frequency of 2.27 GHz with Bayesian inference.
All Figures
 |
Fig. 1 Jet core relative positions of FIRST J222112-012806 measured with respect to the jet cores of three reference sources (i.e., ICRF J221852.0-033536, ICRF J221947.2-005132, and ICRF J222646.5+005211) at five observing wavelengths. Systematic uncertainties calculated with Eq. (1) have been included in the positional uncertainties. Models of the combined core shifts are derived assuming |
| In the text | |
 |
Fig. A.1 The calibrator plans for the PINPT observations of this work, which involve two in-beam phase calibrators and three out-of-beam calibrators of PSR J2222–0137 (shown in red). More source information can be found in Table A.1. Among the two in-beam calibrators, FIRST J222201–013236, marked by golden circle, was used in previous astrometric campaigns (Deller et al. 2013; Guo et al. 2021); FIRST J222112–012806, marked by blue diamond, is used for core-shift determinations (see Sect. 4.2.2). The adopted phase calibration strategies are described in Sect. 2.2 and summarized in Table 1. |
| In the text | |
 |
Fig. D.1 AGN contour plots obtained from the core-shift-determining sessions, and the AGN jet directions determined with arcfits. For the jet direction determinations, image models obtained at higher observing frequencies are preferred, unless extended jet features are not identified by arcfits. The flux density on the m-th (m = 1,2,3,…) contour equals to |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.