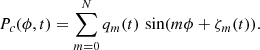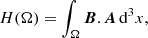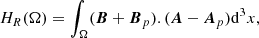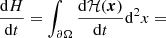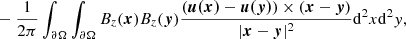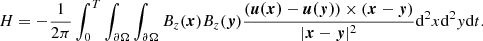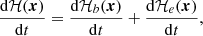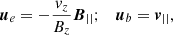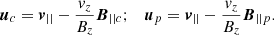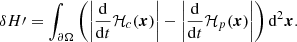| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 14 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202451428 | |
| Published online | 25 October 2024 | |
Global and local dynamics of X-flare-producing active regions during solar cycle 25 peak phase
1
High Altitude Observatory, NSF-NCAR, 3080 Center Green Dr, Boulder, CO 80301, USA
2
Department of Atmospheric Sciences, University of Sao Paulo, R. do Matão, 1226, Sao Paulo, 05508-090 SP, Brazil
3
National Solar Observatory, 3665 Discovery Dr, Boulder, CO 80303, USA
4
Hansen Experimental Physics Laboratory, 452 Lomita Mall, Stanford, CA 94305-4085, USA
5
Lynker Space, Lynker 5445 Conestoga Ct Ste 100, Boulder, CO 80301, USA
⋆ Corresponding author; brenorfs@gmail.com
Received:
9
July
2024
Accepted:
21
August
2024
Context. The configuration of the longitudinally elongated region that active regions (ARs) cluster around, known as a toroid belt, has been shown to be an indicator of intense activity. In particular, complex ARs at locations in the north and/or south toroids tend to appear “tipped-away” with respect to each other. On the other hand, magnetic helicity has been used as an indicator of flare activity in ARs.
Aims. As solar cycle (SC) 25 approaches its peak, a number of significant (X-class) flares have been produced. Here, we investigate the circumstances surrounding two of the most flare-prolific ARs of solar cycle 25, namely, ARs 13590 and 13514. Two aspects of the evolution of these ARs are investigated in this work: the global-scale magnetic toroid configuration and small-scale magnetic field morphology and topology – before, during, and after the onset of major flares.
Methods. We studied the global morphology of the solar magnetic fields near intense flares in terms of the spatial distribution of ARs on magnetic fields synoptic maps. On AR scales, we analyzed the magnetic helicity accumulation, as well as its current-carrying and potential components.
Results. Our results are consistent with major flare-prolific ARs from solar cycles 23 and 24. In particular, we observe a consistent dominance of current-carrying magnetic helicity at the time of major flares. The evolution of global magnetic toroids, indicating the occurrence of flare-prolific ARs in the tipped-away portion of the toroid, together with the local dynamics of complex ARs, could offer a few weeks of lead time to prepare for upcoming space weather hazards.
Key words: Sun: activity / Sun: flares / Sun: magnetic fields / sunspots
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Storms associated with intense solar flares and coronal mass ejection events are the cause of numerous hazardous effects, ranging from the disruption of power grids (Omatola & Okeme 2012) and impairment of satellites (Afraimovich et al. 2009) to ecological and environmental effects (Tinsley et al. 1989; Bianco et al. 2019). For this reason, there is a vested interest in understanding the conditions that lead to intense flares and, ultimately, to improve the prediction of these events. Much of this effort is based on the analysis of the morphology of the magnetic field in active regions (ARs) leading up to intense flares, including the magnetic flux, magnetic helicity, magnetic winding, current helicity, and other parameters. Recently, however, the evolutionary patterns of observed global configuration of the ARs’ latitude-longitude distribution has been demonstrated to provide useful information for understanding pre-storm conditions; thereby allowing for a useful lead time for predicting possible upcoming solar storms by days to weeks (instead of hours).
The Sun’s global scale axisymmetric magnetic field is known to follow established spatio-temporal patterns such as the butterfly diagram, under which the distribution of sunspots at the beginning of a given cycle emerge first at mid-latitudes (i.e., 30–35° latitude) and migrates towards the equator as the cycle progresses (Afraimovich et al. 2009). This pattern repeats itself following the ∼11-year Schwabe-cycle. The physical origin of the butterfly diagram is understood in terms of the dynamo cycle (Charbonneau 2020). Although the overall trend of flare events is correlated with the butterfly diagram and the 11-year cycle, this association is negligible in terms of the prediction of intense flare events and mitigation of its effects.
More important in terms of the understanding and prediction of solar storms are the intermediate periodicities of the Sun, also known as solar seasons, which include Rieger-type periodicities and quasi biennial oscillations (Dikpati et al. 2023; Gurgenashvili et al. 2017; Silva & Lopes 2017; Badalyan & Obridko 2011). These are oscillations with characteristic timescales ranging from several months to three years that modulate the flare activity and are strongly associated with the non-axissymmetric component of the Sun’s magnetic field (Dikpati et al. 2023). Recent research indicates that the origin of these intermediate periodicities of the solar magnetic activity lies in the dynamics of Rossby waves in the Sun’s interior, most likely in the tachocline regions (Dikpati et al. 2017; Zaqarashvili et al. 2010a,b). Rossby waves are oscillations that arise in rotating fluids (and plasmas) due to the action of the Coriolis force and are one of the fundamental building blocks in the understanding of atmospheric dynamics (Pedlosky 2013). Rossby waves in the Sun’s interior differ from those in planetary atmospheres, since they are believed to be strongly affected by and to interact with the underlying magnetic fields in this region (Zaqarashvili et al. 2007; Teruya et al. 2022).
It has long known that meandering patterns created by the propagation of Rossby waves and associated low- and high-pressure (troughs and ridges) regions determine the formation of clouds and subsequent rainfall by inducing small scale convective motions (Bluestein 1992; Teruya et al. 2024; Teubler & Riemer 2021). Since knowledge of the dynamics of Rossby waves and their proper representation in numerical atmospheric models have been one of the central points in advancing weather prediction, this raises the question of whether the dynamics of Rossby waves could leave imprints on the global-scale morphology of the solar magnetic field that would be useful for indicating that an intense storm is about to happen. This idea motivated recent studies to search for such patterns from global synoptic magnetic field charts. Dikpati et al. (2021) suggested that prior to intense Sun storms, there is a particular signature in the spatial organization of ARs as observed at the photosphere, that magnetic activity toroids become locally warped at certain longitudes as the storm approaches, with a higher likelihood of intense storms occurring at longitudes where north and south activity toroids tip away from each other. This hypothesis is based on the nonlinear interactions among Rossby waves, dynamo-generated magnetic fields, and tachocline differential rotation. Due to this interaction, the system dynamically evolves to produce large-scale nonaxisymmetry on the initially purely zonal large-scale field, leading to a wavy-like large-scale fields pattern (Dikpati et al. 2018). Since this mechanism occurs separately in the northern and southern hemispheres, in regions where the perturbed northern and southern hemisphere toroids approach each other latitudinally, some flux cancellation is expected to occur through magnetic reconnection, leading to diminished magnetic field available for emergence. Dikpati et al. (2021) analyzed in detail the circumstances that led to the 2003 Halloween storm, one of the largest storms to be directly observed, including a flare estimated to be of class X-42 (Thomson et al. 2004), showing the “tipping away” effect of the toroids that preceded the storm.
The global-scale toroid features were indeed shown to successfully explain a peak-phase storm, as in the case of the Halloween storms of 2003, however, Raphaldini et al. (2023) later showed that the minima-phase storms cannot be interpreted based on the global dynamics of warped toroids. Raphaldini et al. (2023) combined the toroid analysis on a global spatial scale and the analysis of topological properties of the magnetic fields on ARs and demonstrated that a combination of both approaches provides a good assessment of the likelihood of an upcoming storm.
The question at hand now considers whether we can reliably predict the peak-phase storms well ahead of time from global toroid analysis. To answer this question, we delve deeper into the analysis of cycle 25 peak-phase storms by adapting the approaches proposed by Dikpati et al. (2021) and Raphaldini et al. (2023). We selected two X-class flare producing ARs during the peak phase of solar cycle 25: AR 13514, which appeared and erupted in December 2023, and AR 13590, which appeared and erupted in February 2024, leading to multiple flares and associated coronal mass ejections (CMEs).
2. Data and methods
Here, we outline the two main methods used in this article, namely, a toroid fitting for analyzing the global scale activity belt, as well as a magnetic field helicity calculation for analyzing the magnetic field topology at the AR scale. Details on both these methods can be found in Dikpati et al. (2021) and Raphaldini et al. (2022).
2.1. Data and selection criteria
Magnetogram datasets, both on the global and AR scales, were obtained from Solar Dynamics Observatory (SDO) Helioseismic and Magnetic Imager (HMI). We used global magnetic field synoptic maps with daily cadence to derive magnetic toroids, in contrast to our approach in previous works (Dikpati et al. 2021; Raphaldini et al. 2023) where the analysis was performed based on one synoptic map for each Carrington rotation. The current study has allowed us to investigate the evolution of features on a faster timescale than that of a Carrington rotation. The analysis of the magnetic field morphology and topology on the AR scale was performed using Spaceweather HMI Active Region Patch (SHARP) vector magnetogram datasets with a 12 minute cadence for both selected AR regions Bobra et al. (2014). The ARs analyzed here, AR 13514 (December 2013) and AR AR13590 (February 2024) were selected on the basis of the following criteria: (i) they produced large X-class flares, (ii) the flare activity occurred mainly on the central part of the disk to avoid errors from near to limp data, and (iii) they occurred in the peak phase of the cycle, that is, the time of peak activity of the cycle ( ± 1.5 years).
2.2. Derivation of global toroid patterns
The spatial distribution of ARs, although complex, is not random. Overall, it is characterized by a clustering of ARs around a certain latitude that drifts towards the equator from the beginning to the end of a given cycle as it progresses following the butterfly diagram. This suggests the existence of an activity belt that exists due to the dynamo generated toroidal magnetic field (Guerrero et al. 2017), most likely at the tachocline region. It is perturbed by waves excited by instabilities at that region (Dikpati & Gilman 1999). The idea to link the observational signature of this toroidal belt located and the tachocline and the distribution of AR observed at the photospheric level can be traced back to Norton & Gilman (2005). More recently, these ideas were explored by Dikpati et al. (2021) by employing a sophisticated trust region reflective (TRR) algorithm (Branch et al. 1999), where the spatial distribution of ARs is fitted by a superposition of Fourier modes. The outcomes from this technique have been used to analyze the 2003 Halloween storm, which produced the largest flare in this century to this date (Thomson et al. 2004). It was suggested that ARs producing the largest flares tended to occur in regions where the northern hemisphere toroid tips away from the southern hemisphere toroid; namely, at longitudes with a greater latitudinal distance between the toroids.
Raphaldini et al. (2023) analyzed other X-class flaring ARs from solar cycle 24, concluding that this idea applies much better around the maximum phase of the cycle, when there are enough ARs at the photosphere for the fitting procedure to work. During the late declining phase, such as that seen for the biggest X-flare of cycle 24 occurring in September 2017, global toroid patterns containing flare-producing ARs evolved too fast to allow a sustained locally tipped away longitude to survive; thus, it was no help in hindcasting an upcoming storm. Instead, the September 2017 storm occurred primarily due to an inactive AR12673 suddenly becoming most active through the complex interaction of a recurrent emergence in that location. Nonetheless, during peak-phase, the toroids evolve slowly, allowing for a sustained longitude location where the north and south toroids are tipped away from each other.
Here, we briefly describe the procedure to derive globally warped toroid patterns for our selected ARs 13590 and 13514. Given a line-of-sight (LoS) magnetic field Blos(θ, ϕ) synoptic chart at time t in Carrington rotation (CR) number, where θ is latitude and ϕ is longitude, the global toroid patterns Pc(ϕ, t), are determined by fitting the distribution of centroids of unsigned flux of Blos in the form of a superposition of Fourier modes:
Here, Pc(ϕ, t) represents the latitudinal position of the center of the toroidal activity band, qm(t) is the amplitude of the m-th mode, and ζm(t) is the respective Fourier phase. The joint parameter estimation includes the objective determination of the number of modes N that best fit the data. This is performed iteratively by the TRR method, following Dikpati et al. (2021) and Branch et al. (1999).
2.3. Helicity flux calculations
Magnetic helicity, being a conserved quantity in the ideal case (Biskamp 2003), is an important quantity in magnetohydrodynamics. Furthermore, the helicity has an important topological interpretation in terms of the linking number, which represents the number of crossings between pairs of magnetic field lines, weighted by the intensity of the magnetic fluxes (Arnold & Khesin 2009). The magnetic helicity associated with a magnetic field B in a bounded volume Ω is defined as:
where A is the vector potential associated with the magnetic field B, defined via B = ∇ × A. The practical application of Eq. (2) to the study of solar magnetic fields based on photospheric measurements is problematic for two reasons. First, Eq. (2) is gauge-dependent, that is, the vector potential is chosen up to a choice of a potential field B = ∇ × (A + ∇ϕ), where ψ is any given smooth scalar field. Second, magnetic field measurements are typically given at the photospheric surface, rather than at volume. To make the concept of helicity more readily applicable for photospheric measurements Berger & Field (1984) introduced the concept of relative helicity defined as:
where Bp is a potential magnetic field (∇ × Bp = 0) defined as Bp.n = B.n, where n is the unit normal vector to the surface ∂Ω and Ap is the respective vector potential. As a result, ℋR can be shown to be gauge-invariant. To compute ℋR(Ω) from data sampled at a surface, we can compute the helicity fluxes through it via the expression:
where u(x) is the velocity of the foot-point associated with the magnetic field line at a point x in the photosphere, ∂Ω is a surface enclosing a magnetic flux tube seating at the photosphere. Then, dℋ(x)/dt is the helicity density flux which allows the evaluation of which areas within the AR are most relevant for the helicity density flux (Prior & MacTaggart 2020; Raphaldini et al. 2022). Integrating Eq. (4) between times t = 0 and t = T, we can obtain the accumulated helicity in the [0, T] interval:
Early examples of estimation of various forms of magnetic helicity budgets in ARs can be found in Chae (2001, 2004), Kusano et al. (2002, 2004), while the association between magnetic helicity calculated from photospheric data and flare activity was presented in Moon et al. (2002). More recently, it was suggested that the relative importance of the helicity associated with the current carrying part of the helicity played an important role in the likelihood of strong flare occurrence (Pariat et al. 2017; Green et al. 2022; Zuccarello et al. 2018), leading to the concept of a “flare index” that measures the relative contribution of the current-carrying helicity. To address this notion, we introduce the following components of the magnetic helicity flux densities:
where dℋe(x)/dt represents the emergence term of the helicity density flux, that is, the component of the helicity due to vertical plasma velocities ue (i.e., emergence/submergence); dℋb(x)/dt, on the other hand, represents the respective component due to horizontal (surface) plasma velocities, ub, where the respective velocity components are obtained by:
where the field line velocities denoted by u are now expressed in terms of plasma velocities denoted by v. On the other hand, we can obtain the plasma velocity components contributing to the current-carrying helicity and to the potential helicity as:
The current-carrying (dℋc(x)/dt) and potential (dℋc(x)/dt) components of the helicity density flux are obtained upon the following substitutions in Eq. (4): u → uc for the current-carrying component and u → up for the potential component.
We can now introduce a measure of imbalance between the current-carrying and potential helicity fluxes:
The interpretation of the helicity flux imbalance is as follows: when δH′> 0 indicates a dominance of the current-carrying component of the helicity density flux, while δH′< 0 indicates a dominance of the potential component of the helicity density flux. In previous studies (Raphaldini et al. 2022, 2023), this notion was applied to several ARs during solar cycle 24 with varying levels of activity, from non-flaring to very flare-prolific (e.g., AR-12673) proving to be a good indicator of flare activity. Here, we used the open software ARTop (Alielden et al. 2023), which calculates magnetic helicity and its related quantities from SHARP magnetograms. As an intermediate step, it utilizes DAVE4VM method (Schuck 2008) to estimate the plasma velocities.
3. Results
Solar cycle 24 was exceptionally weak (Svalgaard et al. 2005) and presented a remarkable hemispheric asymmetry (Li et al. 2019). Despite its low sunspot activity, SC-24 still produced a number of flare-prolific ARs (Sun & Norton 2017; Raphaldini et al. 2022, 2023; Moraitis et al. 2019). Intriguingly, the most flare prolific AR of SC-24 was AR 12673 (Sun & Norton 2017), which occurred in the descending phase of the cycle, approaching its minimum. Numerous studies have explored topological aspects of major SC-24 ARs. In particular, in the case of AR 12673, it was shown that a combination of a pre-existing decaying AR with a new emergence at the same location produced a remarkably complex structure with strong magnetic fluxes, which led to 4 X-class flares (of which a X-13.37 and a X-11.88 were the two strongest of the cycle) and 27 M-class flares. The fact that its strong flare activity resulted from recurrent emergences at the same location suggests that some deep-rooted mechanism lies behind it. This mechanism could be due to a combination of dynamo generated magnetic fields, tachocline instabilities, and waves (Dikpati & Gilman 1999). These wavy-patterns, resulting from tachocline instabilities, can leave signatures on the global magnetic field configuration as observed from magnetic field synoptic maps, a feature that was investigated in Dikpati et al. (2021), Raphaldini et al. (2023) for SC-23/24).
Currently, we are likely in the first half of the peak period (defined here as the peak time ±1.5 years, with current data as well as projections (Upton & Hathaway 2023) pointing out to a slightly stronger as well as more symmetric cycle, with a dominant northern hemisphere throughout most of 2023. Up to this point, a handful of X-flare producing ARs emerged during SC-25. Therefore, we would like to compare the properties that led to strong flare activity in these ARs, with the properties already observed in past cycles. Thus, we selected two ARs presenting significant flare activity and where the bulk of this activity occurred in the central part of the disk: AR 13590 and AR 13514.
3.1. AR 13590
AR 13590 appeared on the disk on February 18, 2024. At first, near the limb, it manifested itself as a α-type spot and soon after (within one day) a secondary polarity appeared and the AR 13590 evolved into a β structure. The negative polarity on the left side of the AR started becoming less coherent, resulting in a β − γ structure within just two days of its emergence, namely, by February 20. We discuss this in greater detail in Sect. 3.1.2, where we also describe how we estimated its helicity evolution. Subsequently, in the vicinity of the positive polarity (on the right side of the AR) a secondary structure with negative polarity gained strength, ultimately leading to a β − γ − δ structure by the third day of its appearance, on February 21. As soon as the β − γ − δ structure was established, still on February 21, a first X-class (X-1.9) flare was produced. On the subsequent day, additional two X-class flares were produced, the first one of class X-1.3 and the second one of class X-6.3. Between February 22 and February 25, seven more M-class flares were produced. The AR remained as a β − γ − δ until it reached the left side of the disk, on February 29, subsequently decaying away as a β and then a α structure until it disappeared on the limb. None of the X-class flares, however, resulted in significant impacts on Earth, since none of them resulted in coronal mass ejection (CME) events. In the following, we analyze how the topological properties of AR 13590 in terms of magnetic helicity, combined with Global magnetic field morphology derived from synoptic magnetograms, can help detect properties that distinguish the phase that occurs just before a major flare.
3.1.1. Global analysis
By implementing the algorithm described in Sect. 2.2, we employed the SDO/HMI daily magnetogram fits files to derive the toroidal band, within which the ARs are tightly stringed. These are daily updated magnetic field synoptic maps that were constructed by averaging over four hours values within 60° of the central meridian, which is when a given Carrington longitude leaves this central region of the disk the magnetic field values are kept fixed until it re-appears in the central part of the disk, resulting in a 3600 × 1440 pixel image. Four panels from the top to the bottom in Fig. 1 display the weekly evolution of the global distribution of ARs in such toroids before, during, and after the intense solar storms occurring from the eruption of AR 13590 on February 21. The top two panels display the global configurations on February 7 and 14, when AR 13590 did not emerge yet. In the third panel, we see AR 13590 at the heliographic longitude of ∼224°. Between February 21 and 22, it produced three X-class and associated CMEs, as well as several M-class and C-class flares. The bottom-most panel displays how the toroids (north toroid containing AR 13590) are evolving.
 |
Fig. 1. Evolution of global patterns of AR distributions in tight-fit toroids in the interval of a week from the top to the bottom panels. AR13590 appears at an absolute heliographic longitude of 224 degree in the north toroidal band, and erupted to produce X-flare on February 21. Here, the solid blue line represents the fit for the AR centroids in the northern toroid band, while the solid red line represents that for the AR centroids in the southern toroid, respective dashed lines represent the spreads in the respective “trust-region” derived optimized fits. |
Multiple properties are immediately revealed from Fig. 1. First, in all panels, both the north and south toroids have very similar warped patterns in the form of combinations of three dominant large-scale longitudinal modes with wavenumbers m = 1, 2, 3. They show a predominantly antisymmetric tipping, being tipped away from each other in most of the longitudes (see ∼60–160° and ∼200–300°) and consequently producing a flare-prone locations in the toroidal band. Previously Dikpati et al. (2021) showed that such configurations are indicative of upcoming big flares, such as that produced the Halloween storms of 2003. In the February 21 case, X-flares and associated CMEs were caused by the eruption of the AR 13590. We see in the third panel that AR 13590, located at absolute heliographic longitude of 224-degree, is at the largest tipped-away portion in the north toroid. Most importantly, we find in the top two panels (see the green ellipse) that the tipped-away longitude-range has been formed even two weeks before AR 13590 actually emerged there. Thus, the global toroid patterns offers hints on the pre-solar-storm surface locations, from where the eruptions could occur and produce big flares if ARs, particularly the complex ones having δ configurations, indeed emerge there.
Second, all the panels reveal that the toroids are tipped towards each other, producing a near-overlapping locations around 140–180°, where they are prone to weakening themselves through reconnection and annihilation (Guerrero et al. 2016). However, at certain longitudes, a slight symmetric tipping is also visible, around 35–40° longitude, where the north toroid is moving away from the equator, while the south toroid is toward the equator, making them bend symmetrically. These locations may not be very favorable for big flares and solar storms from the global point of view, but they are still an extremely complex local dynamics with respect to one or more ARs emerging there leading to a big storm. The least favorable location is the longitude range, approximately between 140–180°, where the north and south toroids tip towards each other; due to containing oppositely directed magnetic fields, they end up becoming weak.
Third, a careful look at the bottom-most panel reveals that the pronounced tip between the north and south toroids is slowly going away. Both toroids relax to a pattern that is much less warped, compared to the top three panels.
Apart from the largest tipped-away portion of the toroid in the longitude range of 200–300°, in which the AR 13590 emerged and caused several X-flares, the north and south global toroid patterns reveal the occurrence of the second largest tipped-away portion; namely, in the longitude range of 60–160°. Another big and complex AR 13576 emerged in that tipped-away part of the south toroid (see around 60°). All ARs for this storm-period are marked in Fig. A.1. AR 13576 existed in a less pronounced tipped-away region than AR 13590. Nonetheless, its existence in a sustained, globally tipped-away south toroid pattern, in addition to the absence of opposite-hemisphere counterpart at that longitude-location, and its complex structure (β − γ − δ during most of its passage through the disk) led AR 13576 to erupt to produce one X-2.5 flare on February 16, along with 23 M-flares, 101 C-flares, and associated CMEs. Thus, we find that ARs emerging in the largest as well as the second largest tipped-away parts of the north and/or south toroids are prone to erupt in the form of biggest flares and often with associated CMEs.
3.1.2. Magnetic field morphology and helicity analysis
To gain insights into the specific magnetic field topology, in particular, the magnetic helicity, and what it can tell us about the flare activity in AR 13590, we analyzed not only the time series derived from various forms of magnetic helicity (introduced in Sect. 2.3), but also the spatial distributions derived from the magnetic helicity flux densities (also introduced in Sect. 2.3).
First, we describe the time series of the helicity-related quantities integrated throughout the entire domain. The accumulated helicity time series is portrayed in Fig. 2a, shown as the total helicity, the current helicity and potential helicity. Up until t ∼ 90 hours, we see a dominance of positive helicity (note the flipped axis), which is initially predominantly potential and then becomes predominantly current-carrying, leading to the first X- class flare at t∼ 90. After that, the curve reverses its slope with more positive helicity being injected, with a consistent pattern of dominant current-carrying helicity. Figure 2b shows the helicity imbalance, representing how much the injection of helicity is dominated by potential (negative values) or current-carrying (positive) injection. We see that the injection is predominantly positive from the beginning, suggesting a dominance in terms of the current-carrying helicity. As noted in previous works (Raphaldini et al. 2022, 2023), large flares, particularly X-class flares, are accompanied by peaks in the helicity imbalance, indicating a fast injection of complex current-carrying field. This pattern is observed here, although not all peaks in the imbalance correspond to large flares.
 |
Fig. 2. Evolution of Helicity parameters for AR 13590. (a) Magnetic helicity accumulation for AR 13590 together with its potential and current-carrying components, (b) Helicity imbalance for AR 13590. Purple vertical lines indicate X-class flares, while yellow vertical lines indicate M-class flares. Accumulated helicity time series is normalized by cadence time unit t = 720 s. |
Figure 3 compares the evolution of the radial magnetic field, Bz, with the magnetic helicity density flux, dℋ(x)/dt. As noted in previous works (Raphaldini et al. 2022; MacTaggart et al. 2021), the helicity density flux is similar in shape to the magnetic flux and, in particular, footpoints tend to concentrate much of the helicity input. Since the early stages of its appearance, AR 13590 presented a strong magnetic helicity flux, suggesting that reasonable about of helicity had already been injected before reliable observations were possible (i.e., at the easternmost region of the disk near the limb). At t = 36 h (Fig. 3b) from the appearance of the AR on the disk, we can observe a fairly complex distribution of the helicity flux with both negative and positive helicities being injected throughout a large portion of the domain. As time evolves, near the largest flare, at t = 107 hours (Fig. 3d), the distribution of helicity injection is more concentrated in space and dominated by a negative helicity injection. This pattern remains until the time when the last M-class flare occurs at around t = 174 hours (Fig. 3f), after which the AR starts decaying away.
 |
Fig. 3. Evolution of the magnetic flux (left) and magnetic helicity density flux (right) for AR 13590. |
3.1.3. Comparison with other ARs on the disk
It is useful to compare the helicity parameters derived from AR 13590 with other ARs present on the disk during the same period to illustrate these results. To do so, we selected an additional six ARs that were on the disk on February 22, the day when AR 13590 produced its largest flare. We have selected other six ARs according to the SHARP classification, occupying different latitudes in both the northern and southern hemispheres. We attempted to pick pairs of ARs in similar longitudes with one to the north of the equator and one to the south, along with one example of an AR with no counterpart in the opposite hemisphere (AR 13584), which include:
-
AR 13585/13586: this AR pair was grouped into a single SHARP, constituting a giant patch that occupied roughly 40° of longitudinal extent and 20° in the meridional direction in the northern hemisphere. While AR13585 was situated closer to the equator, at around 13°N and to the west compared with AR 13586, AR 13586 was located northward at around 13°N. AR 13585 did not produce any flares, while AR 13586 produced two flares, a C-6.1 flare and a C-5.0 flare. Both were characterized by simple structures that alternated between α and β classes throughout their passage on the disk.
-
AR 13587: mostly characterized by a β structure and produced a single C-class flare (C-4.0). Located in the southern hemisphere at around 21°S, its longitude evolution followed roughly the evolution of AR 13585, however, in the opposite hemisphere.
-
SHARP 10825: a diffuse bipolar structure located slightly towards the north of AR 13587, still in the southern hemisphere at around 10°S.
-
AR 13584: this AR was located in the southern hemisphere at around 15°S approximately 30° to the west of AR 13587, it alternated between α and β classes throughout its passage on the disk and presented a moderate level of activity, producing six C-class flares, the largest being a C-7.9 flare. No ARs in the northern hemisphere were present on the disk in similar longitudes.
-
SHARP 10852: a small unipolar patch that followed roughly the longitude evolution of AR 13586, albeit in the southern hemisphere, leading to no flares.
-
SHARP 10861: This patch followed roughly the longitude evolution of AR 13590, albeit in the southern hemisphere at around 25°S, leading to no flares.
Below, we present a table summarizing various helicity parameters addressed in this study: total helicity, current helicity, potential helicity, and helicity imbalance. The following findings can be listed from this comparison:
-
AR 13590 presents by far the highest values of the helicity parameters, with total helicity on the order of 1021 G2 km4. This represents one order of magnitude larger than the second-largest values found in the ARs with moderate level of activity. Furthermore, the integrated current-helicity in that AR was on the order of 30% larger than the potential-helicity. See Fig. 4 for a comparison of the evolution of the total helicity in these ARs.
-
An overall tendency of decrease in the helicity parameters as the level of activity is decreased with, roughly speaking, the parameters change by one order of magnitude from high level of activity (AR 13590) to moderate level of activity (ARs 13585/13586/AR 13584 and AR 13587), except for the maximum value of the helicity imbalance in AR 13584, which has comparable values with two of the non-flaring regions.
-
In the AR 13585/AR 13586 patch, the one presenting activity was AR 13586, which was farthest away from its southern hemisphere counterpart (AR 13587). While the latitudinal distance between AR 13585 and AR13587 was ∼30°, the distance between AR 13586 and SHARP 13586.
-
In the AR 13585/AR 13586 patch, the one to present activity was AR 13586, which was farthest away from its southern hemisphere counterpart (AR 13587). While the latitudinal distance between AR 13585 and AR13587 was ∼30°, the longitudinal distance between AR 13586 and SHARP 10852 was ∼50°.
-
The longitudinal distance between AR 13590 and its southern hemisphere counterpart, SHARP 10861, was ∼43°.
-
AR 13584 had no counterpart in the northern hemisphere and resulted in a moderate level of activity.
 |
Fig. 4. Comparison of the evolution of the total accumulated helicity of the ARs in Table 1. Time series are normalized by cadence time unit t = 720 s. |
Comparison of helicity (in G2 Km2 s−1, accumulated helicity normalized by cadence time unit = 720 s) parameters of ARs present on the disk on February 22, 2024.
Summarizing, the analysis of the ARs that were present on the disk on the day of the largest flare produced by AR 13590, is consistent with the idea that the level of activity, and associated level of complexity produced by an AR follows a trend of being more pronounced when it is farther from counterparts in the opposite hemisphere.
3.2. AR 13514
AR 13514 appeared on the eastern side of the disk on December 6, 2023, in close proximity to AR 13513. Since AR 13513 and AR 13514 are assigned to the same SHARP, we analyzed them together here. AR 13514 was first manifested as a β spot, remaining this way for several days, and generating the first C-class flares still as a β structure, already on the western side of the disk on December 12. On December 14, the bipolar the initial bipolar structure morphed into a β − γ spot with the emergence of a secondary elongated negative polarity to the south of the initially dominant positive polarity, resulting in a X-class flare (X-2.87) as well as two M-class flares. On December 15, the spot further gained complexity, leading up to a β − γ − δ structure generating two more M-class flares. Thereafter, as the AR approached the limb on the western side of the disk, it started decaying away, however, still producing another M-class flare on December 17. Several of the M and X class flares generated by AR 13514 resulted in CMEs, leading to moderate geomagnetic storms.
AR 13513 was initially situated to the north and slightly to the west of AR 13514, initially as a β spot on December 5 when it produced three M-class flares, followed by two more X-class flares on December 6, since these flares occurred still near to the limb where magnetogram datasets are not reliable, they are not displayed here. Subsequently, AR 13513 developed into a β − γ structure, which remained as such until December 11. AR 13513 also produced 50 C-class flares.
3.2.1. Global analysis
As detailed in Sect. 3.1.1, we first show the evolution of global toroid patterns in the north and south here, with the north toroid containing AR 13514, which erupted on December 14 to produce big flares. The four panels of Fig. 6 display the evolution a week before the occurrence of big storms, as well during and after the storm.
 |
Fig. 5. Evolution of global patterns of AR distributions in tight-fit toroids in the interval of a week from the top to the bottom panels. AR13514 appears at the absolute heliographic longitude of 137 degree in the north toroidal band, and erupted to produce X-flare on December 14. |
 |
Fig. 6. Evolution of hemispheric sunspot number in the northern and southern hemispheres. Here, the time series are smoothed with a one Carrington-rotation smoothing window. The two shaded gray regions denote the periods of the two storms addressed here. |
Right away, we can spot several distinctive features in Figure 5. First, as in Fig. 1, the global toroids unveil pretty sustained, slowly evolving patterns for three weeks. This is a typical feature of the peak-phase global toroids and has already been illustrated in Dikpati et al. (2021) and Raphaldini et al. (2023) for the peak-phase storms of cycles 23 and 24, respectively. One small difference in the north and south toroids (compared to what we see in Fig. 1) is that the north toroid is represented as a combination of only two longitudinal modes, m = 1 and 2, but the south toroid contains a combination of m = 1, 2, 3 modes, indicating the existence of north-south asymmetry, which is small but quantifiable by our toroid derivation method.
Second, we find that the tip between the north and south toroids is not most pronounced in the longitude-range of 80–170°, within which the AR 13514 is located (i.e., at 137-degree); instead, the tip is at its maximum in the range of 250–350 degrees in longitude. Despite the antisymmetric tip at 137-degree longitude-location being not the largest, but the second largest (with the largest being at 250–350 degrees in longitude), it is nonetheless a significant antisymmetric tip; furthermore, it is certainly not the location where the north and south toroids come closest to each other (e.g., 190°). Due to the absence of any southern hemisphere counterpart for this AR, the AR 13514 at 137-degree longitude continued to grow strong.
Third, the toroid patterns in both hemispheres relax to more flattened structure than sufficient warping they had before and during (see, e.g., top two panels in Fig. 5) the X-flare. This feature is very similar to that in the case of the February 21 storm (see, e.g., Fig. 1). Despite being neither in the most tipped-away part of the toroid belt, nor in the closest or overlapping part with the opposite-hemisphere counterpart, the biggest storms occurred from AR 13514 in December 14. This is due to two reasons: (i) the absence of any ARs at that longitude in the south toroid helped AR 13514 remain strong, despite not being located at the maximum tipped-away part of the toroid and (ii) the presence of multiple ARs in the proximity of 137-degree caused complex interactions among them through local dynamics. While we describe the latter in detail in the next subsection, we elucidate the former through the use of Fig. 1, which displays the daily sunspot data in the north and south, both smoothed by one Carrington Rotation averaging.
Despite the north and south progressing in sync during the most of cycle 25 rising phase, occasionally, we see some significant north-south asymmetry. Figure 6 reveals that the activity in the northern hemisphere was stronger than the south in December 2023. No significantly strong ARs emerged at or near the vicinity of 137-degree longitude in the south. Consequently, the oppositely directed flux from the south could not reconnect and thereby annihilate the AR 13514 substantially.
One intriguing question arises, however, regarding what we can predict from Fig. 7 regarding the most pronounced tipped away longitudes (250–350°), which contain several ARs in both toroids in the north and south. These ARs (13491, 13492, 13502, and 13503 in the north and 13494, 13501, and 13504 in the south; see, e.g., Fig. A.2) did not produce the biggest class flares; nevertheless, the hypothesis of tipped-away locations of the toroids containing ARs being flare-prone remains valid because they produced multiple M- and C-class flares during that time.
 |
Fig. 7. Post-storm toroid-patterns’ evolution containing AR 13514, which continued to produce big flares until December 31 and January 1. |
An interesting turn was taken by AR 13514 when it went to the back side after producing X-flare on December 14 and came to the front side in two weeks. We display in Fig. 7, the evolution of toroids containing AR 13514 for four successive days, from December 29, 2023 to January 1, 2024. Even though the toroid pattern relaxed to some extent, a careful examination of the panels from the top to the bottom in Fig. 7 reveals that the antisymmetric tip at longitude 137-degree is growing again at the expense of the north and south toroids’ coming closer to each at 180–200°. Over the course of three days, from December 30, 2023 to January 1, 2024, the longitudinal distance between northern and southern toroids grew from 35°–37° at 137° longitude, while at 180°–200°it decreased from 34°–29°. The sustaining AR 13514 was renamed as AR 13536, according to NOAA convention, when it reappeared on the front side. Figure A.3 displays all ARs tagged with NOAA numbers. Eventually, this AR (13536), surviving even after one rotation, erupted again on December 31 and January 1, producing an even bigger X-flare (X5) and multiple other M- and C-class flares. The sustained tipped away longitude-location of AR 13536 (which was AR 13514 in the previous rotation), longevity of its highly complex structure and complex interactions with other ARs in close proximity have been the crucial factors for producing more storms when it reappeared in the front again.
3.2.2. Magnetic field morphology and helicity analysis
First, we describe the time series of the helicity-related quantities displayed in Fig. 8. The accumulated helicity, Fig. 8a, shows an initial small dominance of positive helicity, which is predominantly potential. After t ∼ 80 hours, the slope of the curve changes with negative helicity being injected, now with a predominance of current-carrying helicity until the first M-class flare occurs at After t ∼ 140 hours, followed by a steep increase in the accumulated helicity starting at t ∼ 150 hours, predominantly current-carrying, leading up to a sequence of M-class and one X-class flare between t ∼ 180 and t ∼ 200 hours, with the accumulated helicity rate going from −0.2 × 1020 to 2 × 1020 G2 Km2 s−1 within 30 hours. The tendency of the accumulated helicity continues, leading to another pair of M-class flares at t ∼ 210 hours. The helicity imbalance, shown in Fig. 8b shows that initially the imbalance fluctuates around zero until a steep increase occurs at around t ∼ 180 hours, jumping from near 0–2 × 1017 G2 Km2 s−1 in less than 10 hours, with the two major peaks roughly corresponding to the X-class flare at t ∼ 190 hours and the second major peak corresponding to a pair of M-class flares at t ∼ 210 hours.
 |
Fig. 8. Evolution of the helicity parameter for AR 13514. (a) Magnetic helicity accumulation for AR 13514 together with its potential and current-carrying components and (b) helicity imbalance for AR 13514. Purple vertical lines indicate X-class flares, while yellow vertical lines indicate M-class flares. Accumulated helicity time series is normalized by cadence time unit t = 720 s. |
Figure 9 shows the evolution of the magnetic flux and the helicity density flux. As suggested by the time series shown in Fig. 8, in the early stages of the appearance of AR 13514, very little helicity injection is observed throughout the domain (see Fig. 9a). Significant helicity density injection can be observed only after t ∼ 160 hours (see Fig. 9d) with a spacial pattern largely dominated by negative helicity density only. The area where the helicity injection is concentrated expands leading up to the time when the major flare occurs at t ∼ 192 hours (see Fig. 9f), still dominated by negative helicity injection, with minor spots of positive helicity injection.
 |
Fig. 9. Evolution of the magnetic flux (left) and magnetic helicity density flux (right) for AR 13514. |
Throughout the whole passage through the disk, the helicity injection density is dominated by the AR 13514 portion of the SHARP, with AR 13513 having a much weaker input. Since AR 13513 presented significant flares on December 5 and 6 (five M-class flares overall), it is likely that a significant amount of helicity had already been injected during its passage through the limb.
4. Conclusions
Solar cycle 25 is close to or progressing towards its peak, allowing us to draw comparisons with solar cycle 24. One of the main differences seen for cycle 25, compared to cycles 23 and 24, is that solar activity in the north and south hemispheres is progressing in sync. Here, we have selected two of the major X-flare producing ARs during peak-phase of cycle 25 to study the circumstances that has led to their intense activity. The selected ARs were AR 13514, which occurred in December 2023, and AR 13590, which occurred in February 2024. The approach taken here combines analysis of the properties of magnetic fields at the spatial scale of the ARs, as well as the global magnetic field configuration in terms of the spatial distribution of ARs on the sphere. In particular, the global configurations are analyzed by fitting ARs’ centroids in toroids, which appear in the form of warped, narrow bands.
AR 13514 appeared on disk on December 6, 2023, in close proximity, and one day later than AR 13513. While AR 13513 produced a few M-class flares in the first two days, suggesting that it had developed a few days earlier on the back side, AR 13514 slowly evolved, only producing significant flare activity near the central part of the disk. This feature can be observed in the evolution of the accumulated magnetic helicity, which remained stable for about five days after its appearance. Then it went through a steep increase that led to four M-class flares and one X-class flare (X-2.87). AR 13514 further produced 43 C-class flares. In accordance with previous studies (Pariat et al. 2017; Raphaldini et al. 2022) we also find that the current-carrying part of the magnetic helicity dominated the trigger of intense flare. The magnetic helicity imbalance on the order of ∼1017 G2 km2 s−1 is comparable with previous case studies (Raphaldini et al. 2022).
In terms of the global magnetic field configuration, AR 13514 developed in a region to the east of the portion where south and north magnetic toroids came close to each other. However, in closer inspection, the evolution of the magnetic toroids in time showed that this portion of the magnetic toroids was increasingly tipping away from each other, leading to an even larger storm, an X-5 produced by AR 13536 as soon as it appeared on the disk on December 31, 2023. This is essentially the reappearance of AR 13514 on the front side after AR 13514 completed its far-side transit. The long-lived pattern of AR 13514 suggests that it could have resulted from the location responsible for recurrent emergence (see, e.g., a detailed discussion in van Driel-Gesztelyi & Green 2015). Theoretical works suggest that recurrent storms at the same location could result from sustained bulges (local high-pressure regions) that create favorable conditions for magnetic flux emergence (Dikpati et al. 2021). These bulges are the consequences of global nonlinear interactions among differential rotation, dynamo-generated magnetic fields and Rossby waves.
AR 13590 appeared on the disk on December 18, 2023; however, unlike AR 13514, it appeared with already substantial magnetic flux and magnetic helicity density fluxes. Furthermore, it rapidly evolved into a complex β − γ − δ structure and produced three X-class flares (including an X-6.3, an X-1.9 and an X-1.7 flare) between the third and fourth day of its appearance. Here, the magnetic helicity analysis also reveals a dominance of current-carrying helicity, particularly near the occurrence of large flares, including the X-6.3 flare, helicity imbalance reaching the value of ∼4 × 1017 G2 km2 s−1 during the trigger of X-flares. The helicity imbalance peaks are not isolated in this case, in contrast to that of AR 13514, which is due to the fact that AR 13590 appeared as a mature AR. Overall, besides the three X-class flares, AR 13590 produced 9 M-class flares and 60 C-class flares. The global analysis of the magnetic toroids shows that AR 13590 emerged into the enhanced tipped-away longitude location. This is the typical flare-prone location, where emerging ARs lead to major storms, as has already been noted in the case of big storm-producing ARs in solar cycles 23 (Dikpati et al. 2021) and 24 (Raphaldini et al. 2023).
In summary, we find that in both cases, the biggest and second-biggest storms occurred from the ARs located in the tipped-away portions of the toroids, no matter whether the tip is most enhanced or not. The local dynamics in both cases suggest that the strongest flares get triggered by a strong influx of current-carrying helicity. This study highlights the value of combining approaches at different spatial scales to obtain a complete view of the circumstances that lead to enhanced flare activity.
Acknowledgments
This work is supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under cooperative agreement 1852977. We acknowledge support from several NASA grants, namely, M.D. and B.R. acknowledge NASA-LWS grant No. 80NSSC20K0355 and NASA-HSR grant No. 80NSSC21K1676. M.D., B.R. and K.J. acknowledge COFFIES Phase II NASA-DRIVE Center for the subaward from Stanford with grant No. 80NSSC22M0162. A.S.W.T. has been supported by Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP; grant 2020/14162-6). This work utilizes data from HMI onboard NASA’s SDO spacecraft, courtesy of NASA/SDO and the HMI Science Teams.
References
- Afraimovich, E., Demyanov, V., Gavrilyuk, N., Ishin, A., & Smolkov, G. Y. 2009, Cosmic Res., 47, 126 [Google Scholar]
- Alielden, K., MacTaggart, D., Ming, Q., Prior, C., & Raphaldini, B. 2023, RASTI, 2, 398 [NASA ADS] [Google Scholar]
- Arnold, V. I., & Khesin, B. A. 2009, Topological Methods in Hydrodynamics (New York: Springer) [Google Scholar]
- Badalyan, O., & Obridko, V. 2011, New Astron., 16, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, M. A., & Field, G. B. 1984, J. Fluid Mech., 147, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, G., Ilieva, M., & Åkesson, S. 2019, Biol. Lett., 15, 20180918 [CrossRef] [Google Scholar]
- Biskamp, D. 2003, Magnetohydrodynamic Turbulence (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Bluestein, H. B. 1992, Synoptic-Dynamic Meteorology in Midlatitudes: Observations and Theory of Weather Systems (Taylor& Francis) [Google Scholar]
- Bobra, M. G., Sun, X., Hoeksema, J. T., et al. 2014, Sol. Phys., 289, 3549 [Google Scholar]
- Branch, M. A., Coleman, T. F., & Li, Y. 1999, SIAM J. Sci. Comput., 21, 1 [CrossRef] [Google Scholar]
- Chae, J. 2001, ApJ, 560, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Moon, Y.-J., & Park, Y.-D. 2004, Sol. Phys., 223, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2020, Liv. Rev. Sol. Phys., 17, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., & Gilman, P. A. 1999, ApJ, 512, 417 [Google Scholar]
- Dikpati, M., Cally, P. S., McIntosh, S. W., & Heifetz, E. 2017, Sci. Rep., 7, 14750 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., McIntosh, S. W., Bothun, G., et al. 2018, ApJ, 853, 144 [Google Scholar]
- Dikpati, M., McIntosh, S. W., Chatterjee, S., et al. 2021, ApJ, 910, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., Anderson, J. L., Belucz, B., et al. 2023, BAAS, 55, 097 [NASA ADS] [Google Scholar]
- Green, L., Thalmann, J., Valori, G., et al. 2022, ApJ, 937, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, G., Smolarkiewicz, P., Dal Pino, E. D. G., Kosovichev, A., & Mansour, N., 2016, ApJ, 819, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, G., Smolarkiewicz, P. K., de Gouveia Dal Pino, E. M., et al. 2017, IAU Symp., 328, 61 [NASA ADS] [Google Scholar]
- Gurgenashvili, E., Zaqarashvili, T. V., Kukhianidze, V., et al. 2017, ApJ, 845, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2002, ApJ, 577, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2004, ApJ, 610, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F., Xiang, N., Xie, J., & Xu, J. 2019, ApJ, 873, 121 [NASA ADS] [CrossRef] [Google Scholar]
- MacTaggart, D., Prior, C., Raphaldini, B., Romano, P., & Guglielmino, S. L. 2021, Nat. Commun., 12, 6621 [NASA ADS] [CrossRef] [Google Scholar]
- Moon, Y.-J., Chae, J., Choe, G., et al. 2002, ApJ, 574, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Moraitis, K., Sun, X., Pariat, É., & Linan, L. 2019, A&A, 628, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norton, A. A., & Gilman, P. A. 2005, ApJ, 630, 1194 [NASA ADS] [CrossRef] [Google Scholar]
- Omatola, K., & Okeme, I. 2012, Arch. Appl. Sci. Res., 4, 1825 [Google Scholar]
- Pariat, E., Valori, G., Linton, M., Zuccarello, F., & Dalmasse, K. 2017, A&A, 601, A125 [CrossRef] [EDP Sciences] [Google Scholar]
- Pedlosky, J. 2013, Geophysical Fluid Dynamics (Springer Science& Business Media) [Google Scholar]
- Prior, C., & MacTaggart, D. 2020, Proc. R. Soc. A, 476, 20200483 [NASA ADS] [CrossRef] [Google Scholar]
- Raphaldini, B., Prior, C. B., & MacTaggart, D. 2022, ApJ, 927, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Raphaldini, B., Dikpati, M., Norton, A. A., et al. 2023, ApJ, 958, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, H., & Lopes, I. 2017, Ap&SS, 362, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X., & Norton, A. A. 2017, Res. Notes AAS, 1, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Svalgaard, L., Cliver, E. W., & Kamide, Y. 2005, Geophys. Res. Lett., 32, L01104 [NASA ADS] [CrossRef] [Google Scholar]
- Teruya, A. S., Raphaldini, B., & Raupp, C. F. 2022, Front. Astron. Space Sci., 9 [CrossRef] [Google Scholar]
- Teruya, A. S., Mayta, V. C., Raphaldini, B., Silva Dias, P. L., & Sapucci, C. R. 2024, Meteorol., 3, 141 [CrossRef] [Google Scholar]
- Teubler, F., & Riemer, M. 2021, Weather Clim. Dyn., 2, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, N. R., Rodger, C. J., & Dowden, R. L. 2004, Geophys. Res. Lett., 31, L06803 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. A., Brown, G. M., & Scherrer, P. H. 1989, J. Geophys. Res.: Atmos., 94, 14783 [NASA ADS] [CrossRef] [Google Scholar]
- Upton, L. A., & Hathaway, D. H. 2023, J. Geophys. Res.: Space Phys., 128, e2023JA031681 [CrossRef] [Google Scholar]
- van Driel-Gesztelyi, L., & Green, L. M. 2015, Liv. Rev. Sol. Phys., 12, 1 [Google Scholar]
- Zaqarashvili, T., Oliver, R., Ballester, J., & Shergelashvili, B. 2007, A&A, 470, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Carbonell, M., Oliver, R., & Ballester, J. L. 2010a, ApJ, 724, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Carbonell, M., Oliver, R., & Ballester, J. L. 2010b, ApJ, 709, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Zuccarello, F. P., Pariat, E., Valori, G., & Linan, L. 2018, ApJ, 863, 41 [Google Scholar]
Appendix A: Synoptic maps of all ARs tagged on December 7 and 31 and February 21
Here, we present the third panel, from the top, of Fig. 2, the top panel of Fig. 6 and the third panel of Fig. 7 with all emerged ARs marked by NOAA numbers.
 |
Fig. A.1. All ARs numbered by NOAA are spotted and marked on February 21, 2024, synoptic map constructed from SDO/HMI daily fits files. The double-arrowed topbar indicates which ARs are on the front side. Here, ARs resulting in X-class Flares are highlighted in red, while ARs resulting in M-class flares are highlighted in orange. |
 |
Fig. A.2. Same as in Fig A.1, but for the synoptic map on December 7, 2023. Here, ARs resulting in X-class Flares are highlighted in red, while ARs resulting in M-class flares are highlighted in orange. |
 |
Fig. A.3. Same as in Fig A.1, but for the synoptic map on December 31, 2023. Note that December 7’s ARs 13513 and 13514 at 137-degree longitude in Fig. A.2 rotate to the back side and reappear to the front as AR 13537 and 13536 respectively at the same longitude on December 31. Here, ARs resulting in X-class flares are highlighted in red, while active regions resulting in M-class flares are highlighted in orange. |
All Tables
Comparison of helicity (in G2 Km2 s−1, accumulated helicity normalized by cadence time unit = 720 s) parameters of ARs present on the disk on February 22, 2024.
All Figures
 |
Fig. 1. Evolution of global patterns of AR distributions in tight-fit toroids in the interval of a week from the top to the bottom panels. AR13590 appears at an absolute heliographic longitude of 224 degree in the north toroidal band, and erupted to produce X-flare on February 21. Here, the solid blue line represents the fit for the AR centroids in the northern toroid band, while the solid red line represents that for the AR centroids in the southern toroid, respective dashed lines represent the spreads in the respective “trust-region” derived optimized fits. |
| In the text | |
 |
Fig. 2. Evolution of Helicity parameters for AR 13590. (a) Magnetic helicity accumulation for AR 13590 together with its potential and current-carrying components, (b) Helicity imbalance for AR 13590. Purple vertical lines indicate X-class flares, while yellow vertical lines indicate M-class flares. Accumulated helicity time series is normalized by cadence time unit t = 720 s. |
| In the text | |
 |
Fig. 3. Evolution of the magnetic flux (left) and magnetic helicity density flux (right) for AR 13590. |
| In the text | |
 |
Fig. 4. Comparison of the evolution of the total accumulated helicity of the ARs in Table 1. Time series are normalized by cadence time unit t = 720 s. |
| In the text | |
 |
Fig. 5. Evolution of global patterns of AR distributions in tight-fit toroids in the interval of a week from the top to the bottom panels. AR13514 appears at the absolute heliographic longitude of 137 degree in the north toroidal band, and erupted to produce X-flare on December 14. |
| In the text | |
 |
Fig. 6. Evolution of hemispheric sunspot number in the northern and southern hemispheres. Here, the time series are smoothed with a one Carrington-rotation smoothing window. The two shaded gray regions denote the periods of the two storms addressed here. |
| In the text | |
 |
Fig. 7. Post-storm toroid-patterns’ evolution containing AR 13514, which continued to produce big flares until December 31 and January 1. |
| In the text | |
 |
Fig. 8. Evolution of the helicity parameter for AR 13514. (a) Magnetic helicity accumulation for AR 13514 together with its potential and current-carrying components and (b) helicity imbalance for AR 13514. Purple vertical lines indicate X-class flares, while yellow vertical lines indicate M-class flares. Accumulated helicity time series is normalized by cadence time unit t = 720 s. |
| In the text | |
 |
Fig. 9. Evolution of the magnetic flux (left) and magnetic helicity density flux (right) for AR 13514. |
| In the text | |
 |
Fig. A.1. All ARs numbered by NOAA are spotted and marked on February 21, 2024, synoptic map constructed from SDO/HMI daily fits files. The double-arrowed topbar indicates which ARs are on the front side. Here, ARs resulting in X-class Flares are highlighted in red, while ARs resulting in M-class flares are highlighted in orange. |
| In the text | |
 |
Fig. A.2. Same as in Fig A.1, but for the synoptic map on December 7, 2023. Here, ARs resulting in X-class Flares are highlighted in red, while ARs resulting in M-class flares are highlighted in orange. |
| In the text | |
 |
Fig. A.3. Same as in Fig A.1, but for the synoptic map on December 31, 2023. Note that December 7’s ARs 13513 and 13514 at 137-degree longitude in Fig. A.2 rotate to the back side and reappear to the front as AR 13537 and 13536 respectively at the same longitude on December 31. Here, ARs resulting in X-class flares are highlighted in red, while active regions resulting in M-class flares are highlighted in orange. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.