| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202451288 | |
| Published online | 31 October 2024 | |
The HST Large Programme on ω Centauri
VII. The white dwarf cooling sequence
1
Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, Via Giuseppe Saragat 1, Ferrara 44122, Italy
2
Istituto Nazionale di Astrofisica, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, Padova 35122, Italy
3
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
4
Istituto Nazionale di Astrofisica, Osservatorio Astronomico d’Abruzzo, Via Mentore Maggini, Teramo 64100, Italy
5
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore MD 21218, USA
6
Dipartimento di Fisica e Astronomia “Galileo Galilei”, Università di Padova, Vicolo dell’Osservatorio 3, Padova 35122, Italy
7
Department of Astronomy, Indiana University, Swain West, 727 E. 3rd Street, Bloomington IN 47405, USA
8
Département de Physique, Université de Montréal, C.P. 6128, Succ. Centre-Ville, Montréal, Quebec H3C 3J7, Canada
9
Department of Astronomy & Astrophysics, University of California, San Diego, La Jolla, California 92093, USA
10
Department of Astronomy and Steward Observatory, The University of Arizona, 933 N. Cherry Avenue, Tucson, AZ 85721, USA
11
Lunar and Planetary Laboratory, The University of Arizona, 1629 E. University Blvd., Tucson, AZ 85721, USA
⋆ Corresponding author; michele.scalco@inaf.it
Received:
27
June
2024
Accepted:
5
September
2024
We present a study of the white dwarf (WD) cooling sequence (CS) in the globular cluster (GC) Omega Centauri (or NGC 5139; hereafter, ω Cen), the primary goal of a dedicated Hubble Space Telescope (HST) programme. We find that the peak at the termination of the WD CS is located at mF606W = 30.1 ± 0.2 (equivalent to V ∼ 31). The brighter part of ω Cen’s WD CS is consistent with the presence of massive He-core WDs, in agreement with previous HST analyses with ultraviolet and blue filters. Comparative analyses of the WD luminosity function (LF) and theoretical counterparts show that a single-age population for the cluster is compatible with the data. However, an analysis of only the WD LF cannot entirely exclude the possibility of an age range, due to uncertainties in the present-day WD mass function, with a star formation history potentially spanning up to 5 billion years, predominantly comprising stars about 13 Gyr old, with a minority potentially as young as 8 Gyr. This underscores the need for global spectroscopic and photometric investigations that simultaneously include both the WD populations and the previous evolutionary phases, in order to fully understand the cluster’s diverse chemical compositions and ages.
Key words: white dwarfs / globular clusters: individual: NGC 5139
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The white dwarf (WD) cooling sequence (CS) of globular clusters (GCs) lies in one of the faintest and least explored regions of the colour-magnitude diagram (CMD). Deep imaging with Hubble Space Telescope (HST) has reached the peak of the WD number distribution at the faint end of the CS in four GCs: NGC 6397 (Anderson et al. 2008a), M 4 (Bedin et al. 2009), 47 Tucanae (Kalirai et al. 2012), and NGC 6752 (Bedin et al. 2019, 2023). Each of these GCs hosts multiple stellar populations (mPOPs) characterized by small mean spreads in initial helium abundances (Milone et al. 2018), and their WD CSs align with predictions for single-population (i.e. WD population) systems (Richer et al. 2013; Campos et al. 2016).
Omega Centauri (ω Cen) is a moderately low-reddening GC that is relatively close (∼5 kpc) to the Sun, making it an ideal target for an efficient study of its faint WD population. It is also one of the most extreme cases of a GC hosting mPOPs. Spectroscopy has shown that ω Cen’s stars display a range of [Fe/H] and a very complex pattern of light-element anti-correlations at each [Fe/H] (Marino et al. 2012), and optical CMDs have shown two main groups of stars with a large difference in their initial helium content (Y ∼ 0.40 for the He-rich component King et al. 2012), as evidenced by ω Cen’s split main sequence (MS) in optical filters (Bedin et al. 2004). In addition, a wide range of initial chemical abundances is revealed by UV-based CMDs, which display a MS with at least 15 sub-populations (Bellini et al. 2017b).
Regarding the WD population, the upper part of the CS in ω Cen exhibits a bifurcation into two sequences, as reported by Bellini et al. (2013): a blue CS populated by standard CO-core WDs, and a red CS populated by low-mass WDs with both CO and (mainly) He cores (the presence of a sizeable population of He-core WDs was already disclosed by Monelli et al. 2005 and Castellani et al. 2007).
The prevailing hypothesis suggests that the blue WD CS is populated by the final stages of evolution of the He-normal stars of ω Cen, while the red WD CS is populated by the final stages of evolution of the He-rich stars. Observing the complete WD CS of this cluster allows us (1) to investigate the effect of a chemically complex system such as ω Cen on the termination of the WD CS (which is an age indicator used in stellar population studies), and (2) to set independent constraints on the cluster age spread.
This study represents the seventh paper in a series dedicated to the exploitation of an HST multi-cycle large programme centred on ω Cen. The previous publications focused on the analysis of the parallel fields collected as a part of the programme:
-
Milone et al. (2017, hereafter Paper I) focused on the analysis of the mPOPs of ω Cen at very faint magnitudes.
-
Bellini et al. (2018a, hereafter Paper II) analysed the internal kinematics of these mPOPs.
-
Libralato et al. (2018, hereafter Paper III) presented the absolute proper motion (PM) estimate for ω Cen.
-
Scalco et al. (2021, hereafter Paper IV) released the astro-photometric catalogue for two parallel fields of the programme.
-
Gerasimov et al. (2022 hereafter Paper V) presented a set of stellar models designed to investigate low-mass stars and brown dwarfs in ω Cen.
-
Finally, Scalco et al. (2024, hereafter Paper VI) presented a comprehensive analysis of the radial distribution of the mPOPs of ω Cen across an extensive part of the cluster.
The focus of this study is the WD CS of the cluster and its LF in the primary deep field of this HST large programme.
The paper is organized as follows: Section 2 outlines the observations, and Sect. 3 gives details about the data reduction. Section 4 offers a concise overview of the artificial star tests (ASTs) we have performed. The selection criteria employed to construct the cluster CMD are laid out in Sect. 5. The decontamination of the cluster sample using PMs is discussed in Sect. 6. Section 7 presents the empirical WD LF derived from the data, and Sect. 8 discusses the theoretical interpretation of the WD LF. Finally, Sect. 9 provides a brief summary of the results.
2. Observations
This study is based on images collected with the Wide Field Channel (WFC) of the Advanced Camera for Surveys (ACS) onboard HST under the multicycle large programme ‘The end of the White Dwarf Cooling Sequences of Omega Centauri’ (programme IDs: GO-14118 and GO-14662, PI: Bedin). Data were collected over a total of 132 HST orbits across six epochs, spanning a temporal baseline of ∼3 years (from 2015 to 2018). In each epoch, we took 24 deep exposures (of ∼1100–1200 s) in the F606W filter and 20 in the F814W filter, resulting in a total of 216 exposures taken with the F606W filter and 180 exposures with the F814W filter. The dataset also includes 12 F606W and 10 F814W short exposures (of ∼40–50 s). A finding chart of the studied field at two scales, and its position relative to the cluster centre, is shown in Fig. 1.
 |
Fig. 1. Left: 1° ×1° infrared image from the Digital Sky Survey 2 centred on ω Cen. The image is aligned with North up and East towards the left. The region indicated in magenta is the field of view covered by our HST deep field from programmes GO-14118 and GO-14662. Middle: Three-chromatic stacked image of the entire ACS/WFC primary field (∼5′×5′). Right: Zoom-in view of a dark sub-region (of ∼1′×1′) of the ACS/WFC primary field (indicated by the green box in the centre panel), at a scale where individual pixels are visible. |
3. Data reduction
The data reduction closely follows the procedure outlined in Bedin et al. (2019, 2023) and other papers in this series (see Paper II; Paper IV; Paper VI). For a detailed description of the reduction process, we refer readers to those papers.
We initially conducted what we call a first-pass analysis, wherein fluxes and positions for relatively bright, unsaturated stars were extracted from each image using the FORTRAN routine hst1pass (see, Anderson 2022). Each image was analysed independently to generate a tailored effective Point Spread Function (ePSF), allowing for adjustments to accommodate spatial and temporal variations relative to the library ePSFs provided by Anderson (2006). The tailoring of ePSFs was performed using the method introduced by Anderson & Bedin (2017) for the ultraviolet and visible (UVIS) channel of the Wide Field Camera 3 (WFC3), later extended to ACS/WFC by Bellini et al. (2018b). Both positions and fluxes were corrected for the geometric distortion of the detector following the methods outlined by Anderson (2006). We then created a common, distortion-free reference frame, based on cluster members, to which all individual images were linked using a six-parameter linear transformation.
With the tailored ePSF and transformations obtained during the first-pass analysis, we conducted a second-pass analysis employing the FORTRAN code KS2 introduced by Sabbi et al. (2016), Bellini et al. (2017a) (see also Anderson et al. 2008b Paper II; Paper III; Paper IV; Nardiello et al. 2018 for a comprehensive description of the software). The KS2 code iteratively identifies, models, and subtracts point sources from the image, initially targeting the brightest sources and progressively addressing fainter sources within the subtraction residuals. This iterative process determines stars’ positions and fluxes, alongside crucial diagnostic parameters such as the local sky noise (rmsSKY) and the RADXS parameter (introduced in Bedin et al. 2009), which assesses the resemblance of the source flux distribution to that of the ePSF. For a detailed description of these parameters, we direct readers (Paper II; Paper IV, and Nardiello et al. 2018).
Photometry was calibrated to the ACS/WFC Vega-mag system using the procedure outlined in Bedin et al. (2005), employing encircled energy and zero points available from STScI1.
In panel (a) of Fig. 2, we present a preliminary mF606W versus mF606W − mF814W CMD for sources satisfying |RADXS|< 0.1 in both F606W and F814W filters. This CMD was used exclusively to define the fiducial line of the WD CS (see Sect. 4). For the subsequent analysis, a CMD obtained with different selection criteria was employed.
 |
Fig. 2. (a) Preliminary mF606W versus mF606W − mF814W CMD of sources within the studied field. Only those having |RADXS|< 0.1 in both F606W and F814W filters are shown. The magenta line denotes the fiducial line for the WD CS, while the green lines bound the region in the CMD used for counting the WDs. (b) CMD for ASs, which is presented on the same scale. The magenta and green lines from panel (a) are retained. The green lines define an area generous enough to encompass both the majority of observed real WDs in panel (a) and the ASs introduced along the WD fiducial line, which were recovered despite exhibiting substantial photometric errors. |
4. Artificial stars
The ASTs were conducted following the guidelines outlined by Bedin et al. (2019, 2023). In summary, a fiducial line was established by hand along the bulk of the observed WDs in the preliminary CMD presented in panel (a) of Fig. 2, extending down to where they appeared to stop, and then extrapolated to fainter magnitudes.
Using KS2, 105 artificial stars (ASs) were introduced along this fiducial line, distributed uniformly with a mF606W magnitude between 24 and 32 and a homogeneous spatial distribution across the field of view. The methodology outlined in (Bedin et al. 2009, Sect. 2.3) was followed to correct for input-output systematic errors in both real and artificial magnitudes.
To determine if an inserted star was successfully recovered, criteria were set such that if an AS was not detected within 0.753 magnitudes (∼−2.5log 2) in both filters and within 1 pixel from the inserted position in both x and y detector coordinates, it was considered unrecovered. Panel (b) of Fig. 2 shows the inserted artificial sources (in magenta) and those that were successfully recovered (grey dots).
The combined information from the panels of Fig. 2 was used to bound the region used for counting the WDs of ω Cen. This region was defined by hand-drawn green lines, striking a balance between encompassing observed WDs with significant photometric scatter and excluding the majority of field objects.
5. Colour-magnitude diagram and selections
Following the approach by Bedin et al. (2019, 2023), in Fig. 3, we show the impact of our progressive selection criteria on ASs, and then apply the same criteria to real sources. In each panel, the top-right corner is labelled either with an (a) for ASs or with an (r) for real sources. The aim of these selections was to strike a balance that maximizes the inclusion of well-measured WD members of ω Cen, while minimizing the inclusion of spurious or poorly measured detections. It is important to note that in the subsequent analysis, we exclusively utilized the long exposures, as they provide the necessary depth to study the WD CS.
The areas shaded in light blue and dark blue represent the 5σ and 3σ regions, respectively, where σ denotes the background noise as measured by Bedin et al. (2019) in both filters. For our analysis, we only considered sources above the 3σ limits as significantly detected.
Panel (a1) displays all artificial sources as inserted (in magenta) and as recovered (blue dots). In panel (a2), sources are limited to those within areas observed in at least ∼40% of the F814W and F606W images, resulting in a significant reduction of the field of view used for the investigation.
Panel (a3) further restricts sources to regions where the rmsSKY matches the noise within empty sky patches, indicating areas suitable for detecting faint objects. Panel (a4) excludes all ASs recovered outside the region enclosed within the two green lines shown in panel (a3).
In panel (c1), instead of a CMD, the magnitude versus completeness curve is presented (black line). It also shows the ’good’ completeness, cg, in blue, representing the completeness calculated within the ’good’ regions based on the rmsSKY value (see Bedin et al. 2008, for details). This panel indicates that sources passing these selections are 50% complete down to mF606W = 29.45 and 25% complete at mF606W = 30.04.
Panel (a5) displays the result after applying the RADXS parameter to reject non-stellar objects. Panel (c2) shows the completeness curves after the final RADXS selection.
The same selections applied to ASs are then applied to observed real sources in the top panels of Fig. 3. Panel (r5) shows the final sample for ω Cen’s WD candidates.
 |
Fig. 3. Progression of cumulative selections employed to derive a sample of well-measured WDs along ω Cen’s WD CS. The sequence progresses from left to right, with the top panels representing real stars and the bottom panels representing ASs. The number of real stars after each selection is reported in the bottom left of the panels. In panel (a1), a magenta line indicates where ASs were introduced. Panels (c) display the resulting completeness, depicted as (c1), without, and (c2), with, the inclusion of the selection on RADXS, a highly effective parameter for identifying well-measured point sources. Panel (s1) illustrates the impact of RADXS selection on stars both within and outside the defined WD region, enclosed by two green lines (see text for details). Lastly, in panel (s2), a direct comparison between real and artificial stars reveals no distinct decline in the number of ASs below mF606W ∼ 30.1. |
Panel (s1) displays all stars that meet the selection criteria, including those outside the area defined by the two thin green lines in panel (a3). The stars outside this region will be utilized to model field contamination within the WD region in the CMD. The fiducial line defined in Sect. 4 (and shown in magenta) well represents the mean observed CMD location for the WD CS of ω Cen.
Panel (s2) shows real stars and ASs that meet all selection criteria: ASs – as selected in panel (a5) – are shown in orange, while real sources – as selected in panel (r5) – are shown in blue. This comparison suggests that the majority of the observed real WD CS might not extend to magnitudes as faint as those of the recovered ASs. This could indicate that the peak of the WD CS LF of ω Cen has potentially been reached and surpassed.
6. Proper motion decontamination
We also investigated whether the PMs can help in disentangling field objects found within the WD region of ω Cen’s CMD and cluster members. To do this, we evaluated PMs following the approach by Bedin et al. (2023), that is, combining the bulk of the first three epochs (∼2016.1) to obtain averaged positions for the sources, which are then compared to their averaged positions as measured in the last three epochs of the data (∼2018.1). In the following analysis, we considered only sources shown in green in panel (s1) of Fig. 3 but for which it was possible to estimate the PM.
The PM analysis is presented in Fig. 4. We colour code the stars, with those surviving the WD selection defined by the two thin green lines in blue, and all other stars in orange.
 |
Fig. 4. (a)–(b)–(c) Vector point diagrams for the samples shown in the corresponding panels below. (d) CMD of the sources in panel (s1) of Fig. 3. In all panels, sources within the WD region (between the two green lines) are represented in blue, while all other sources are shown in orange. The light grey and dark grey shaded areas indicate the 5σ and 3σ limit, respectively, of significant detection for the sources of interest. (e) One-dimensional PM, μR, as a function of the mF606W magnitude. Bright stars (down to mF606W ∼ 28) exhibit a μR distribution with a tight dispersion (< 1.5 mas yr−1), along with a tail displaying a much broader dispersion. We arbitrarily define two regions, indicated by the red line: one enclosing the bulk of the μR values at different magnitudes (indicated by filled circles), and the other containing objects with larger μR (indicated by crosses). (f)–(g) CMDs for the stars within and beyond the red line defined in panel (e). Neither of the two CMDs solely consists of members or field objects (see text for details). |
In panels (a), (b), and (c) we present the vector-point diagrams (VPDs) of the sources in our sample. Since PMs were calculated relative to the cluster’s overall motion, the cluster members’ distribution in the VPD is centred at (0,0). Panels (d), (f), and (g) display the CMDs. Panel (e) from the left shows the observed one-dimensional PM (μR, obtained by summing in quadrature the PM in the two directions) plotted against mF606W. Among brighter stars, we observe a narrow distribution in μR for ω Cen’s members, predominantly clustered well below μR < 1.5 mas yr−1, while a broader tail extends towards higher μR, peaking between 2 < μR < 10 mas yr−1, indicative of field objects. However, as we approach a magnitude mF606W ∼ 28, the random errors in positional measurements, compounded over the first and last three epochs, become significant for fainter stars. By mF606W ∼ 28.5, it becomes notably challenging to disentangle cluster members and field objects. We defined a PM selection consistent with the PM errors at different magnitudes represented by a red line. Stars satisfying this selection are shown as filled circles, while stars not passing this selection are indicated with crosses. The subsequent panels display the VPD and CMD for sources positioned to the left or right of the red-line criterion, maintaining the blue colour code for WD candidates. The PM selection effectively separates outliers and objects with large PMs. However, it struggles to distinguish between WDs and field objects fainter than mF606W ∼ 28.5. This challenge arises mainly due to the minimal separation between field and cluster members, which is much smaller than measurement errors at magnitudes fainter than mF606W ∼ 28.5.
Since PMs are not effective in distinguishing between WDs and field objects for faint sources, we decided not to use PMs in our analysis.
7. The corrected WD CS LF
We applied a correction to the observed WD CS LF to mitigate the effects of field contamination by unresolved blue galaxies, following the method outlined by Bedin et al. (2023). The process is presented in Fig. 5 and described as follows. In panel (a), we show the CMD of sources identified in panel (s1) of Fig. 3. Using the two lines defined in Fig. 3, we establish on the CMD what we term the WD region. Additionally, we define two other regions with the same colour width at each magnitude of the WD region, one at bluer colours and the other at redder colours, referred to as the Blue and Red regions, respectively. These regions are symmetrically offset from the WD region by a fixed colour interval at each magnitude.
 |
Fig. 5. (a) CMD partitioned into three regions along the WD CS. The azure-shaded region indicates sources that pass the selection on the blue side of the WDs, while the red-shaded region represents those on the redder side. (b) WD CS LF, displaying histograms depicting the number of sources per magnitude interval for observed stars within the WD region and for stars in the two shaded regions. The magenta histogram represents our model for field distribution. (c) WD CS LF derived by subtracting the field model from the observed WD CS LF. (d) Observed field-corrected WD CS LF, adjusted for completeness, depicted in black. Grey-shaded areas indicate the 5- and 3-σ levels, where below 3-σ findings and completeness become unreliable. Errors were linearly propagated and then corrected for completeness. |
We counted the sources within each of these three regions and, shown in panel (b), generated the LFs for each one of them, with error bars representing statistical Poisson errors. The number of contaminants within the CMD WD region is determined as the average of the number of objects observed in the Blue and Red regions at various magnitudes. This model is shown in magenta, with corresponding errors estimated through linear propagation of Poisson noise.
In panel (c), we compare the observed LF with the resulting WD LF corrected for the field-contamination model. The field-corrected LF was obtained by subtracting the field model from the observed LF, with errors propagated linearly.
Finally, in panel (d), we present the completeness-corrected and field-corrected WD CS LF for ω Cen. The errors on this LF were corrected for completeness using a simple approximation involving linear propagation of the errors.
The WD CS LF exhibits a peak at an estimated magnitude of mF606W = 30.1 ± 0.2, followed by a rapid decline leading to zero. Despite the low completeness at these faint magnitudes, which falls well below the commonly accepted limit of 50%, we consider this result valid as the peak exceeds the 3σ threshold (dark grey area) that we set as the lower limit for valid measurements.
8. Theoretical interpretation of the WD LF
As briefly summarized in the introduction, ω Cen hosts a very complex population of stars, composed of several sub-populations that show themselves as multiple sequences in CMDs displayed in appropriately chosen filter combinations. These multiple sequences are originated by the range of initial chemical composition – and possibly age– of the cluster’s stars.
Spectroscopic studies have determined a range of iron abundances ∼ − 2.2 < [Fe/H]< ∼ −0.6 (see, e.g., Johnson & Pilachowski 2010; Marino et al. 2011; Nitschai et al. 2024), with the main component characterized by [Fe/H] ∼ − 1.7, and the canonical GC light-element abundance anti-correlations (e.g. the O-Na anti-correlation) present at all [Fe/H]. In addition, there is a sizeable component of stars with [Fe/H] ∼ − 1.3 and an enhanced helium mass fraction, that is, Y ∼ 0.36 − 0.40 (see, e.g., Piotto et al. 2005; King et al. 2012). From the point of view of the stellar ages, the situation is much less clear. For example, Sollima et al. (2005) found an age spread Δt ≤2 Gyr from their analysis of the CMD of the cluster sub-giant branch (SGB) region, a result in agreement with the analysis by Calamida et al. (2009) based on deep near-infrared photometry, and Tailo et al. (2016) derived a negligible Δt from the joint analysis of the HB and SGB. On the other hand, the studies by Villanova et al. (2007) and Villanova et al. (2014) of the SGB provided Δt equal to several Gyr.
Here, we theoretically investigated the observed WD CS and the LF of Fig. 5 in light of this complex chemical abundance (and possibly age) distribution, by employing sets of WD cooling tracks and isochrones. To model the CO-core WDs from progenitors not belonging to the very He-enhanced Y ∼ 0.4 cluster sub-population, we employed the BaSTI-IAC WD tracks by Salaris et al. (2022) with hydrogen envelopes and metal-poor progenitors, calculated with the Cassisi et al. (2007) electron conduction opacities, complemented by the Cummings et al. (2018) initial-final mass relation and progenitor lifetimes from the α-enhanced Pietrinferni et al. (2021) models to calculate the corresponding WD isochrones. For the WDs produced by the Y ∼ 0.4 sub-population, given the lack of He-core WD tracks and progenitor models with Y ∼ 0.40 in the BaSTI-IAC database, we employed the models by Althaus et al. (2017) for Y = 0.40 and a metal mass fraction Z = 0.001, close to the value appropriate for the He-rich stars in the cluster (characterized by [Fe/H] ≃−1.3). Althaus et al. (2017) calculations follow the evolution from the MS to the WD stage of models with masses from 0.6M⊙ to 2 M⊙ and Y = 0.40, and therefore also provide a theoretical initial-final mass relation and progenitor lifetimes for these WDs, enabling us to calculate WD isochrones for the Y ∼ 0.4 cluster sub-population. According to these calculations, MS stars with initial masses up to 0.65M⊙ produce He-core WDs, while more massive objects produce CO-core WDs. At ages around 10–13 Gyr, WD isochrones calculated from these models predict, along the bright CS, He-core WDs with masses equal to 0.44–0.46M⊙, consistent with the results by Bellini et al. (2013). Significantly, we note that (1) Althaus et al. (2017) calculations (both progenitors and WDs) do not employ the same physics inputs of the BaSTI-IAC, although some of the main inputs are in common (for example the equation of state for the model WD cores), and (2) Althaus et al. (2017) calculate progenitor models only up to 2M⊙, which produces a CO-core WD model with mass equal to 0.81M⊙. More massive WDs are therefore missing from the isochrones calculated with Althaus et al. (2017) models.
Figure 6 compares three 12 Gyr isochrones and the corresponding LFs (the result of this comparison does not depend on the chosen age, at least for ages older than a few Gyr), after applying the distance modulus and extinctions assumed for ω Cen. Throughout our analysis, we used (m − M)0 = 13.67 determined by Baumgardt & Vasiliev (2021) as an average of Gaia Early Data Release 3 parallax and kinematic distances, HST kinematic distance, and 26 literature estimates (listed in Table B.1) based on pulsating variables, eclipsing binaries, CMD fitting, and tip of the red giant branch. The adopted value agrees well with the eclipsing binary distance by Thompson et al. (2001).
 |
Fig. 6. Upper panel: Two 12 Gyr WD isochrones for the progeny of He-normal cluster sub-populations with [Fe/H] = −1.9 and −0.9 (solid blue and dotted orange lines, respectively), and a 12 Gyr WD isochrone for the progeny of the Y = 0.4 cluster sub-population (dashed green line). See text for details. Lower panel: LFs calculated from the three isochrones in the upper panel (same line styles and colours). The number of stars in each LF is the same, approximately equal to the total number of objects in the cluster LF. |
For the reddening, we employed E(B − V) = 0.12 (King et al. 2012), close to the average value E(B − V) = 0.11 from multiple sources recommended by Lub (2002), and consistent with the mean value determined by Calamida et al. (2005) using Strömgren photometry. Using this value of E(B − V), we applied extinction corrections to the F606W and F814W filters dependent on the model Teff calculated as in Bedin et al. (2005).
These LFs (with the same bin size of the observed cluster LF) and all other theoretical LFs discussed later have been calculated using a power-law mass function for the progenitors with a Salpeter exponent x = −2.3 and, with a Monte Carlo technique, include the photometric error law for the ω Cen CS derived from the AS analysis, as described in Bedin et al. (2023). Two isochrones have been calculated for CO-core WDs from He-normal progenitors with [Fe/H] = −1.90 and −0.90, respectively, while the third isochrone has been calculated for the progeny of the Y ∼ 0.40 population. This isochrone includes He-core models down to mF606W ∼ 28.5 and CO-core models at fainter magnitudes.
The isochrones for the two He-normal populations almost completely overlap and are very similar at their faint end, the age indicator of the population. This is a consequence of the fact that progenitors’ metallicity variations affect the WD cooling speed mainly due to the variation of the 22Ne abundance in the core that affects the energy released by 22Ne diffusion and distillation (see, e.g., Deloye & Bildsten 2002; Althaus et al. 2010; Blouin & Daligault 2021; Salaris et al. 2022, 2024, and references therein); however, at the low metallicities of GCs, these effects are negligible because of the low abundance of 22Ne in the WD cores. Moreover, the faint end of the isochrone, where the colours turn to the blue, is populated by the more massive WDs (with decreasing radii), coming from progenitors whose lifetime is much shorter than the isochrone age. As a consequence – remembering that at each point along a WD isochrone the sum of the cooling age of the WD evolving at that point and its progenitor lifetime is constant and equal to the isochrone age– the corresponding magnitudes are set by the cooling times of the WD progeny, and are unaffected by small changes in the progenitor lifetimes due to variations in their metallicity. The ‘hook’ at the blue end of the isochrones is caused by the most massive objects (masses ∼1 − 1.1M⊙) that have cooled down faster at this isochrone age, due to an earlier onset of crystallization and phase separation, and are slightly fainter compared to the less massive WDs.
The isochrone for the He-rich population is redder for most of its magnitude extension because it is populated by lower mass objects, and eventually approaches the other two isochrones when the evolving masses become similar. The magnitude of the bottom end of this isochrone is slightly fainter, and the colour extension shorter; this latter effect is due to the lack of models with mass above 0.81M⊙ (the other two isochrones include WD models up to 1.1M⊙).
Despite these differences, once photometric errors are included, the LFs calculated from the three isochrones are almost equivalent, especially when considering the errors in the observed star counts of the observed LF.
As mentioned in the Introduction, Bellini et al. (2013) near-UV and B HST photometry of the bright part of the cluster CS has demonstrated that there are two parallel sequences. Analysis of these sequences –which also made use of Cassisi et al. (2009) study of the extreme blue part of the cluster HB– has revealed the redder sequence to be populated essentially by He-core WDs with a mass around 0.45M⊙, the progeny of the He-rich sub-population, while the blue sequence hosts the standard CO-core WDs with a mass around 0.55M⊙ expected to populate the bright CS of GCs.
The bright part of our optical CS however does not show a split sequence, due to the small sample of objects and especially the low sensitivity of the (F606W−F814W) colour to Teff at high temperatures, as shown by the following test.
Figure 7 displays a qualitative comparison between the cluster CS and a 12 Gyr (a representative age) synthetic CS made of two components (for the synthetic CS, we used the cluster distance modulus and extinction, discussed before). The main component, which includes 89% of the synthetic population, represents the WDs produced by all cluster sub-populations other than the Y ∼ 0.4 one. Given the result of the isochrone comparison in Fig. 6, we employed a single WD isochrone for a representative [Fe/H] = −1.7 to produce this WD population. The remaining 11% of the synthetic CS has been calculated using the isochrone calculated with Althaus et al. (2017)Y = 0.4 progenitors and WDs. These percentages come from the analysis of the radial distribution of the cluster sub-populations presented in Paper IV, taking into account that the observed field is located at a radial distance from the centre equal to 2.6 times the half-light radius.
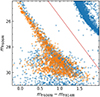 |
Fig. 7. Cluster CS (blue circles) compared to a 12 Gyr synthetic CMD of the cluster WD population (orange circles). The red line is used to define the sample of stars used in our analysis. See text for details. |
The magnitudes along the synthetic CS (which include the photometric errors as determined from the artificial star analysis) have been calculated as described in Bedin et al. (2023). Here, we also account for the effect of completeness (we display only objects that pass the completeness test), considering how the completeness fraction varies with mF606W according to the AS analysis.
The number of synthetic objects is 1498, the same as on the observed CS, defined in this comparison as the sequence of cluster’s stars to the left of the straight line in the figure, with colours larger than −0.5 mag and F606W magnitudes lower than 30.5.
The synthetic sequence appears in good overall qualitative agreement with the observations, in terms of shape and colour spread at a given magnitude, apart from the brighter magnitudes below mF606W ∼ 26, where the synthetic CS appears to be slightly bluer than the observations. The synthetic population supports the idea that, with this observed CMD, we do not expect to see a well-defined bimodal CS even at the brightest magnitudes where the photometric error is small.
Before trying to interpret the cluster LF in terms of age and age spread of the various sub-populations, we first compared it in Fig. 8 with three theoretical LFs for 8, 10, and 13 Gyr respectively, calculated for He-normal populations and [Fe/H] = −1.71. The theoretical LFs were normalized to have the same total number of objects as in the empirical LF for mF606W < 28.0. As shown by Fig. 6, a LF calculated using a single initial chemical composition for the progenitors is appropriate, to represent the whole range of chemical compositions of the cluster sub-populations (including the Y ∼ 0.40 sub-population).
 |
Fig. 8. Cluster LF (filled circles with error bars) compared to theoretical LFs for ages equal to 13 (solid blue line), 10 (dotted orange line) and 8 Gyr (dashed green line). See text for details. |
The width of the peak at the faint end of the LF encompasses the theoretical LFs for ages between 8 and 13 Gyr, but neither a single age nor a combination of ages between 8 and 13 Gyr can match the observed star counts between mF606W of 29.5 and 30.3. This is very likely an indication that the mass distribution of the WDs along the CS predicted by our choice of a Salpeter progenitor mass function is inappropriate. (see, e.g., the discussion in Bedin et al. 2023), due to the cluster dynamical evolution. A more top-heavy mass function would increase the relative number of massive WDs and therefore increase the number counts across the region of the peak of the LF.
Figure 9 indeed shows how an exponent x = −1.6 for the progenitor mass function produces theoretical LFs (normalized as described before) that better match the star counts in the region of the peak of the LF, for various selected combinations of ages. The maximum age range compatible with the observations is 5 Gyr, with 8 Gyr as the minimum age to match the rising branch of the peak region of the LF, while an age of 13 Gyr is required to match the faint, descending branch of the peak region. A single-age population for the cluster provides a good fit to the data, also taking into account that the local maximum of the LF centred at mF606W = 29.3 (not matched by the theoretical LF) is very likely a statistical fluctuation; when considering the error bars, the star counts in this magnitude bin are different from the values at the two adjacent bins by less than 2σ.
 |
Fig. 9. Cluster LF compared to theoretical LFs calculated with an exponent x = −1.6 for the WD progenitor mass function, and various age combinations. Panel a: single age 13 Gyr old population; Panel b: 12% of the population 8 Gyr old, and 88% is 13‘Gyr old; Panel c: 4% of the population is 8 Gyr, 16% is 10 Gyr old, and 80% is 13 Gyr old; Panel d: 8% of the population is 8 Gyr old, 8% is 12 Gyr old, and 84% is 13 Gyr old. |
That said, an age range among the cluster population cannot be ruled out, so long as the large majority of stars (at least ∼80%) in the cluster have an age of 13 Gyr, as shown by the three selected examples in Fig. 9. A high fraction of stars with an age of 13 Gyr is required to match the two points at mF606W = 30.1 and 30.3, while the fraction of stars with ages as low as 8 Gyr has to be small, less than ∼10%, otherwise the ratio between the star counts around mF606W = 29 and the number of stars around mF606W = 30 becomes too high compared to the observed LF. The quality of the matches between theory and observations in Fig. 9 is very similar for all four representative cases, and ad hoc tweaks of the mass function can improve the match in each of them. We find, therefore, that an age range between 8 and 13 Gyr among ω Cen stars cannot be ruled out from the analysis of the WD CS, but if stars younger than 13 Gyr do exist, they should not make up more than ∼20% of the total, with less than 10% can having an age as young as 8 Gyr.
9. Summary
We have presented our study of the complete WD CS in ω Cen, the primary objective of the HST GO-14118+14662 programme. We have produced the CMD and corresponding completeness-corrected LF of the WD CS, which displays a peak at the termination of the CS, located at a magnitude mF606W = 30.1 ± 0.2.
We have created a synthetic WD CS for ω Cen, consisting of a main component made of CO-core objects that are the progeny of the He-normal cluster sub-populations (89% of the WDs) and a component made of CO-core and He-core objects produced by the He-rich cluster sub-population. This synthetic CS aligns well with observational data, except at brighter magnitudes where the synthetic sequence appears slightly bluer.
Our analysis has shown that the chemical complexity of the cluster stellar population has a minor impact on the theoretical interpretation of the observed LF. For a fixed age, LFs calculated for CO-core WDs with varying progenitors’ initial chemical compositions, and for He-core WDs produced by the He-rich cluster sub-population are very similar, particularly when considering the observational errors.
We found that, overall, a single-age population can match the observed LF, but an age range cannot be entirely ruled out using just the WD LF, given the uncertainties in the present-day WD mass function. LF comparisons suggest that ω Cen’s star formation history could potentially span an age range of up to ∼5 Gyr, however, the majority of stars (at least 80%) must be approximately 13 Gyr old, and only a small fraction (less than 10%) could potentially be as young as 8 Gyr.
Further studies, simultaneously analysing the WD LF together with both spectroscopic and photometric data of the previous evolutionary phases, are essential to fully understand the formation and evolution of this extreme GC. In particular, we note that observations of these very same fields are approved and scheduled with JWST under the https://www.stsci.edu/jwst/science-execution/program-information?id = 5110 program (PI: Bedin).
Acknowledgments
Michele Scalco and Luigi Rolly Bedin acknowledge support by MIUR under the PRIN-2017 programme #2017Z2HSMF, and by INAF under the PRIN-2019 programme #10-Bedin.
References
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., De Gerónimo, F., Córsico, A., Torres, S., & García-Berro, E. 2017, A&A, 597, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, J. 2006, The 2005 HST Calibration Workshop: Hubble After the Transition to Two-Gyro Mode (NASA), 11. [Google Scholar]
- Anderson, J., 2022, One-Pass HST Photometry with hst1pass (Instrument Science Report WFC3), 55 [Google Scholar]
- Anderson, J., & Bedin, L. R. 2017, MNRAS, 470, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., King, I. R., Richer, H. B., et al. 2008a, AJ, 135, 2114 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008b, AJ, 135, 2055 [Google Scholar]
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Piotto, G., Anderson, J., et al. 2004, ApJ, 605, L125 [Google Scholar]
- Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., King, I. R., Anderson, J., et al. 2008, ApJ, 678, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Salaris, M., Piotto, G., et al. 2009, ApJ, 697, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Salaris, M., Anderson, J., et al. 2019, MNRAS, 488, 3857 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Salaris, M., Anderson, J., et al. 2023, MNRAS, 518, 3722 [Google Scholar]
- Bellini, A., Anderson, J., Bedin, L. R., et al. 2017a, ApJ, 842, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Anderson, J., Salaris, M., et al. 2013, ApJ, 769, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Milone, A. P., Anderson, J., et al. 2017b, ApJ, 844, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Libralato, M., Bedin, L. R., et al. 2018a, ApJ, 853, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Anderson, J., & Grogin, N. A. 2018b, Focus-diverse, Empirical PSF Models for the ACS/WFC (Instrument Science Report ACS), 8 [Google Scholar]
- Blouin, S., & Daligault, J. 2021, ApJ, 919, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Stetson, P. B., Bono, G., et al. 2005, ApJ, 634, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Calamida, A., Bono, G., Corsi, C. E., et al. 2009, Mem. Soc. Astron. It., 80, 73 [NASA ADS] [Google Scholar]
- Campos, F., Bergeron, P., Romero, A. D., et al. 2016, MNRAS, 456, 3729 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Salaris, M., Anderson, J., et al. 2009, ApJ, 702, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, V., Calamida, A., Bono, G., et al. 2007, ApJ, 663, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Cummings, J. D., Kalirai, J. S., Tremblay, P. E., Ramirez-Ruiz, E., & Choi, J. 2018, ApJ, 866, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Deloye, C. J., & Bildsten, L. 2002, ApJ, 580, 1077 [Google Scholar]
- Gerasimov, R., Burgasser, A. J., Homeier, D., et al. 2022, ApJ, 930, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., & Pilachowski, C. A. 2010, ApJ, 722, 1373 [NASA ADS] [CrossRef] [Google Scholar]
- Kalirai, J. S., Richer, H. B., Anderson, J., et al. 2012, AJ, 143, 11 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R., Bedin, L. R., Cassisi, S., et al. 2012, AJ, 144, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Libralato, M., Bellini, A., Bedin, L. R., et al. 2018, ApJ, 854, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Lub, J. 2002, ASP Conf. Ser., 265, 95 [NASA ADS] [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2011, ApJ, 731, 64 [Google Scholar]
- Marino, A. F., Milone, A. P., Piotto, G., et al. 2012, ApJ, 746, 14 [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Bedin, L. R., et al. 2017, MNRAS, 469, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Marino, A. F., Renzini, A., et al. 2018, MNRAS, 481, 5098 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Corsi, C. E., Castellani, V., et al. 2005, ApJ, 621, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Nardiello, D., Libralato, M., Piotto, G., et al. 2018, MNRAS, 481, 3382 [NASA ADS] [CrossRef] [Google Scholar]
- Nitschai, M. S., Neumayer, N., Häberle, M., et al. 2024, ApJ, 970, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Villanova, S., Bedin, L. R., et al. 2005, ApJ, 621, 777 [Google Scholar]
- Richer, H. B., Goldsbury, R., Heyl, J., et al. 2013, ApJ, 778, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Lennon, D. J., Anderson, J., et al. 2016, ApJS, 222, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Cassisi, S., Pietrinferni, A., & Hidalgo, S. 2022, MNRAS, 509, 5197 [Google Scholar]
- Salaris, M., Blouin, S., Cassisi, S., & Bedin, L. R. 2024, A&A, 686, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scalco, M., Bellini, A., Bedin, L. R., et al. 2021, MNRAS, 505, 3549 [NASA ADS] [CrossRef] [Google Scholar]
- Scalco, M., Bedin, L., & Vesperini, E. 2024, A&A, 688, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sollima, A., Pancino, E., Ferraro, F. R., et al. 2005, ApJ, 634, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Tailo, M., Di Criscienzo, M., D’Antona, F., Caloi, V., & Ventura, P. 2016, MNRAS, 457, 4525 [CrossRef] [Google Scholar]
- Thompson, I. B., Kaluzny, J., Pych, W., et al. 2001, AJ, 121, 3089 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Piotto, G., King, I. R., et al. 2007, ApJ, 663, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Villanova, S., Geisler, D., Gratton, R. G., & Cassisi, S. 2014, ApJ, 791, 107 [Google Scholar]
All Figures
 |
Fig. 1. Left: 1° ×1° infrared image from the Digital Sky Survey 2 centred on ω Cen. The image is aligned with North up and East towards the left. The region indicated in magenta is the field of view covered by our HST deep field from programmes GO-14118 and GO-14662. Middle: Three-chromatic stacked image of the entire ACS/WFC primary field (∼5′×5′). Right: Zoom-in view of a dark sub-region (of ∼1′×1′) of the ACS/WFC primary field (indicated by the green box in the centre panel), at a scale where individual pixels are visible. |
| In the text | |
 |
Fig. 2. (a) Preliminary mF606W versus mF606W − mF814W CMD of sources within the studied field. Only those having |RADXS|< 0.1 in both F606W and F814W filters are shown. The magenta line denotes the fiducial line for the WD CS, while the green lines bound the region in the CMD used for counting the WDs. (b) CMD for ASs, which is presented on the same scale. The magenta and green lines from panel (a) are retained. The green lines define an area generous enough to encompass both the majority of observed real WDs in panel (a) and the ASs introduced along the WD fiducial line, which were recovered despite exhibiting substantial photometric errors. |
| In the text | |
 |
Fig. 3. Progression of cumulative selections employed to derive a sample of well-measured WDs along ω Cen’s WD CS. The sequence progresses from left to right, with the top panels representing real stars and the bottom panels representing ASs. The number of real stars after each selection is reported in the bottom left of the panels. In panel (a1), a magenta line indicates where ASs were introduced. Panels (c) display the resulting completeness, depicted as (c1), without, and (c2), with, the inclusion of the selection on RADXS, a highly effective parameter for identifying well-measured point sources. Panel (s1) illustrates the impact of RADXS selection on stars both within and outside the defined WD region, enclosed by two green lines (see text for details). Lastly, in panel (s2), a direct comparison between real and artificial stars reveals no distinct decline in the number of ASs below mF606W ∼ 30.1. |
| In the text | |
 |
Fig. 4. (a)–(b)–(c) Vector point diagrams for the samples shown in the corresponding panels below. (d) CMD of the sources in panel (s1) of Fig. 3. In all panels, sources within the WD region (between the two green lines) are represented in blue, while all other sources are shown in orange. The light grey and dark grey shaded areas indicate the 5σ and 3σ limit, respectively, of significant detection for the sources of interest. (e) One-dimensional PM, μR, as a function of the mF606W magnitude. Bright stars (down to mF606W ∼ 28) exhibit a μR distribution with a tight dispersion (< 1.5 mas yr−1), along with a tail displaying a much broader dispersion. We arbitrarily define two regions, indicated by the red line: one enclosing the bulk of the μR values at different magnitudes (indicated by filled circles), and the other containing objects with larger μR (indicated by crosses). (f)–(g) CMDs for the stars within and beyond the red line defined in panel (e). Neither of the two CMDs solely consists of members or field objects (see text for details). |
| In the text | |
 |
Fig. 5. (a) CMD partitioned into three regions along the WD CS. The azure-shaded region indicates sources that pass the selection on the blue side of the WDs, while the red-shaded region represents those on the redder side. (b) WD CS LF, displaying histograms depicting the number of sources per magnitude interval for observed stars within the WD region and for stars in the two shaded regions. The magenta histogram represents our model for field distribution. (c) WD CS LF derived by subtracting the field model from the observed WD CS LF. (d) Observed field-corrected WD CS LF, adjusted for completeness, depicted in black. Grey-shaded areas indicate the 5- and 3-σ levels, where below 3-σ findings and completeness become unreliable. Errors were linearly propagated and then corrected for completeness. |
| In the text | |
 |
Fig. 6. Upper panel: Two 12 Gyr WD isochrones for the progeny of He-normal cluster sub-populations with [Fe/H] = −1.9 and −0.9 (solid blue and dotted orange lines, respectively), and a 12 Gyr WD isochrone for the progeny of the Y = 0.4 cluster sub-population (dashed green line). See text for details. Lower panel: LFs calculated from the three isochrones in the upper panel (same line styles and colours). The number of stars in each LF is the same, approximately equal to the total number of objects in the cluster LF. |
| In the text | |
 |
Fig. 7. Cluster CS (blue circles) compared to a 12 Gyr synthetic CMD of the cluster WD population (orange circles). The red line is used to define the sample of stars used in our analysis. See text for details. |
| In the text | |
 |
Fig. 8. Cluster LF (filled circles with error bars) compared to theoretical LFs for ages equal to 13 (solid blue line), 10 (dotted orange line) and 8 Gyr (dashed green line). See text for details. |
| In the text | |
 |
Fig. 9. Cluster LF compared to theoretical LFs calculated with an exponent x = −1.6 for the WD progenitor mass function, and various age combinations. Panel a: single age 13 Gyr old population; Panel b: 12% of the population 8 Gyr old, and 88% is 13‘Gyr old; Panel c: 4% of the population is 8 Gyr, 16% is 10 Gyr old, and 80% is 13 Gyr old; Panel d: 8% of the population is 8 Gyr old, 8% is 12 Gyr old, and 84% is 13 Gyr old. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


