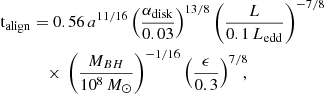| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450897 | |
| Published online | 29 October 2024 | |
Spectral aging analysis of the 3C 219 double-double radio galaxy
Astronomical Observatory, Jagiellonian University, Orla 171, PL-30-244 Krakow, Poland
⋆ Corresponding author; kamil.wolnik@doctoral.uj.edu.pl
Received:
28
May 2024
Accepted:
5
September 2024
Context. Double-double radio galaxies are characterized by intermittent jet-formation activity. The exact reasons for this behavior are not yet fully understood. Studying these objects and their environment allows us to find common characteristics and compare them with the general population of radio galaxies. 3C 219 is a well-known and thoroughly studied radio galaxy. Among the many explanations for its unusual “partial jet” structure, intermittent activity seems to be the leading one. However, this hypothesis has never been tested using aging analysis.
Aims. The aim of this paper is to put constraints on the active galactic nucleus duty cycle and dynamics of radio lobe expansion in 3C 219, in both the inner and outer double. This will provide us with information on the behavior of the central engine and the interaction of the radio lobes with the ambient medium, allowing us to verify whether the structure of 3C 219 is the result of intermittent activity and to search for its possible causes.
Methods. We performed a spectral aging analysis of the 3C 219 double-double radio galaxy using archival Karl G. Jansky Very Large Array and Low Frequency Array data. We present detailed spectral age maps and constructed a spectral age profile. We compared ratios of linear sizes and luminosities in individual phases of activity with lobe expansion velocities in the plane of the sky derived from the age profile to infer hot-spot advance velocities through the surrounding medium and the orientation of the jet axes.
Results. The galaxy shows a general asymmetry in the distribution of plasma with respect to the inferred jet axis in the original phase of activity, suggesting an influence of the intracluster medium on the formation of the radio structure. The advance speed of hot spots in the outer double is typical of classical FRII sources expanding into an ambient thermal medium, while for the inner double, the lower limit is estimated to be ∼0.28 c. The radio galaxy has experienced a very short quiescent period of no more than 2 Myr, which is ≲7% of its total lifetime.
Conclusions. The most plausible explanation for the double-double radio structure in 3C 219 is a rapid jet reorientation along the line of sight, which may be the result of a minor merger. Further study of the 3C 219 inner double is needed. High-resolution maps are required to probe its structure in sufficient detail, while high-frequency observations are necessary to better constrain the durations of the quiescent and restarted phases.
Key words: galaxies: active / galaxies: individual: 3C 219 / radio continuum: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
3C 219 is a Fanaroff-Riley type II (FR II;Fanaroff & Riley 1974) radio galaxy, whose host is a 17.m5 cD1-type galaxy (according to the Yerkes classification: Morgan 1958) in a D5 envelope (Matthews et al. 1964; MacDonald et al. 1968) located in a rich cluster. The host of 3C 219 is the cluster’s brightest member in the optical regime and is surrounded by a few companions visible in the near-infrared (Taylor et al. 1996). The closest, SDSS J092109.15+453851.0, with a spectroscopic redshift difference Δz = 0.0015 (Dawson et al. 2016), is connected to 3C 219 by a faint bridge (Maltby et al. 1963; Matthews et al. 1964; MacDonald et al. 1968). However, McLure et al. (1999) found no direct evidence for recent interactions in Hubble Space Telescope (HST) observations. The central supermassive black hole (SMBH) has a mass of  (Marchesini et al. 2004) and may be accreting matter at a super-Eddington rate (Ito et al. 2008). The Chandra X-ray Observatory map shows an emission region spanning almost the entire volume of the radio lobes, most likely due to inverse Compton scattering of cosmic microwave background (CMB) photons (Comastri et al. 2003) – a property that allows for the magnetic field strength to be estimated independently of the usual equipartition or minimum energy methods.
(Marchesini et al. 2004) and may be accreting matter at a super-Eddington rate (Ito et al. 2008). The Chandra X-ray Observatory map shows an emission region spanning almost the entire volume of the radio lobes, most likely due to inverse Compton scattering of cosmic microwave background (CMB) photons (Comastri et al. 2003) – a property that allows for the magnetic field strength to be estimated independently of the usual equipartition or minimum energy methods.
In the past, 3C 219 has also been intensively studied in the radio regime, with particular interest paid to its inner structure. It has the form of a bright and narrow jet with a deconvolved full width at half maximum (FWHM) of  , superimposed on a wider and fainter FWHM ≈ 3″ component interpreted as an inner cocoon (Clarke et al. 1992). The jet has two bright segments offset by ∼11° and connected by a faint bridge. There are also several local emission peaks interpreted as jet knots (Bridle et al. 1986). Polarimetric observations reveal a magnetic field roughly aligned with the jet along its entire length (De Young et al. 1979; Perley et al. 1980), while high-resolution maps show systematic ∼25° deviations with a beam depolarization at the tip (Bridle et al. 1986), possibly indicating a reorientation of the magnetic field lines. A small clump of emission interpreted as a counter-jet was discovered to the northeast of the radio core by Bridle et al. (1986). In the outer double, there is an asymmetry in the morphology of the hot spots. The southern hot spot is V-shaped, and the northern one is circular (Perley et al. 1980). Bridle et al. (1986) interpreted this asymmetry as a deviation of the jet axis from the plane of the sky.
, superimposed on a wider and fainter FWHM ≈ 3″ component interpreted as an inner cocoon (Clarke et al. 1992). The jet has two bright segments offset by ∼11° and connected by a faint bridge. There are also several local emission peaks interpreted as jet knots (Bridle et al. 1986). Polarimetric observations reveal a magnetic field roughly aligned with the jet along its entire length (De Young et al. 1979; Perley et al. 1980), while high-resolution maps show systematic ∼25° deviations with a beam depolarization at the tip (Bridle et al. 1986), possibly indicating a reorientation of the magnetic field lines. A small clump of emission interpreted as a counter-jet was discovered to the northeast of the radio core by Bridle et al. (1986). In the outer double, there is an asymmetry in the morphology of the hot spots. The southern hot spot is V-shaped, and the northern one is circular (Perley et al. 1980). Bridle et al. (1986) interpreted this asymmetry as a deviation of the jet axis from the plane of the sky.
Clarke et al. (1992) presented a “born-again relativistic jet” model to explain the inner structure. According to this model, after the quenching of the jet formation in the initial phase of activity and a period of quiescence, the restarted jet propagates through the interior of the cocoon. The authors cite two problems with the model: (a) the presence of compact hot spots in the outer double, which should dissipate when their energy supply is terminated; and (b) a mismatch between the observed and predicted slope of the inner double radio continuum. Clarke et al. (1992) also proposed an alternative model of “passive magnetic fields” in which a combination of toroidal and poloidal magnetic fields in the jets is amplified by shocks arising from their interaction with the ambient medium, thereby producing an observable radio structure. However, using this model, the authors were unable to reproduce the exact morphology of the 3C 219 inner double.
Schoenmakers et al. (2000), Saikia & Jamrozy (2009), and Kuźmicz et al. (2017) describe 3C 219 as a double-double radio galaxy (DDRG) based on its morphology – a claim that we aim to verify in this paper. DDRGs are a class of objects that have two (or more) co-axial pairs of lobes, most likely due to intermittent activity of the active galactic nucleus (AGN; Schoenmakers et al. 2000). They are typically explained as a result of merging (Schoenmakers et al. 2000; Kuźmicz et al. 2017) or an accretion-feedback mechanism (e.g., Heckman & Best 2014, and references therein) in clusters of galaxies. A few dozen of these sources have been cataloged (see, e.g., Kuźmicz et al. 2017), and in recent years a number of DDRG candidates have been discovered (e.g., Mahatma et al. 2019; Kozieł-Wierzbowska et al. 2020). Few of these sources have been thoroughly studied with the use of spectral aging analysis, so the mechanisms leading to their formation are not yet fully understood. Multifrequency radio observations of such objects allow for radiative age modeling of relativistic plasma injected into the lobes, using models such as those presented in Jaffe & Perola (1973, hereafter JP) or by Kardashev (1962) and Pacholczyk (1970). In FRII radio sources, the most energetic particles are found around the hot spots, and the least energetic are in the radio cocoon around the center. Deviations from this pattern could indicate a more complex history of the central engine activity, such as periods of quiescence and a reignition of jet-forming activity (e.g., Konar et al. 2006; Marecki et al. 2016). The study of variations in radiative age between different regions of the source could also provide (qualitative) information about the dynamics of radio lobe growth and interactions between the lobe and the external medium, such as an adiabatic expansion of the lobes or a varying hot-spot advance speed (e.g., Konar et al. 2012, 2013).
Using archival data, including previously unpublished 15 GHz maps, and a recently developed tool for spectral aging analysis, Broadband Radio Astronomy ToolS1 (BRATS; Harwood et al. 2013, 2015), we aim to verify the status of 3C 219 as a DDRG and a source with recurrent jet activity. Through this study, we also address the issues with the “born-again relativistic jet” model identified by Clarke et al. (1992).
In this paper we assume a Λ cold dark matter cosmological model, with parameters H0 = 67.3 km s−1 Mpc−1, ΩΛ = 0.69, and Ωm = 0.31 (Planck Collaboration VI 2020). The 3C 219 redshift z = 0.17456 (Ahn et al. 2012) translates to a luminosity distance DL = 875.2 Mpc and an angular size distance Dθ = 634.4 Mpc. Hereafter, a spectral index convention, Sν ∝ ν−α, is used, meaning that positive values of α indicate a declining power law.
2. Observations and data reduction
This study is based on archival Karl G. Jansky Very Large Array (VLA) data in the form of previously published maps and re-reduced observations extracted from the National Radio Astronomy Observatory (NRAO) archive, with the addition of a LOw Frequency ARray (LOFAR) LoTSS Data Release 2 (DR2) map (Shimwell et al. 2022) at 144 MHz. A summary of all the archival maps and datasets is given in Table 1.
Basic properties of the archival data used in the analysis.
2.1. Archival data reduction
All the datasets were imported into the Common Astronomy Software Applications2 (CASA) software and reduced using standard procedures3. The flux scales were calibrated using the Perley & Butler (2017) models.
Outer double maps were cleaned using a visibility weighting that would bring the FWHM of the restoring beam as close as possible to 20″ without exceeding it. High-resolution data were used for the analysis of the inner double. The datasets were imaged with uniform weighting, and baselines shorter than 6 kλ were removed in order to remove diffuse emission coming from the outer lobes that could interfere with further analysis. A few runs of phase self-calibration were performed to correct the visibility phase.
All the maps were then re-gridded to a common reference frame where necessary and convolved to beam sizes of 20″ for the outer double maps and  for the inner double maps. These beam sizes allow us to include the largest possible amount of data while still providing a satisfactory level of details in spectral age variations. A larger beam size usually translates to an overall better sensitivity per arcsec2, which helps highlight weak diffuse emission such as the inner FWHM ≈ 3″ component (see Sect. 1) .
for the inner double maps. These beam sizes allow us to include the largest possible amount of data while still providing a satisfactory level of details in spectral age variations. A larger beam size usually translates to an overall better sensitivity per arcsec2, which helps highlight weak diffuse emission such as the inner FWHM ≈ 3″ component (see Sect. 1) .
2.2. Reliability of flux measurements
Since the angular size of the outer double is about 3′, there is a possibility of losing flux due to the finite length of the shortest baselines. This could be a particular problem in the X (8.46 GHz) and Ku (14.94 GHz) bands, where the largest angular scales are 145″and 97″, respectively. The magnitude of the flux loss was estimated by re-imaging the L-band data with the inner baselines removed to match the characteristics of synthesized apertures in the X and Ku bands. The resulting maps were later compared with a regular L-band map to determine the missing fraction of the flux. The expected total flux loss is ≲5% in the X band and ≲10% in the Ku band. These values are within the assumed 10% uncertainty of the flux scale calibration, so no further steps were taken to compensate for this effect.
However, it is worth noting that the flux loss effect may be the strongest in the oldest, and the most diffuse, parts of the source. This could contribute to the dimming of these regions, normally associated with plasma aging, artificially increasing the perceived spectral age. In the maps presented in Fig. 1, the dimming of the outer double may appear to be further enhanced by differences in beam sizes, with the beams generally smaller at higher frequencies. The angular extent of the inner double is 20″, which is smaller than the largest angular scales for the bands and array configurations used. Therefore, considering flux loss effects in the inner double is unnecessary.
 |
Fig. 1. Total intensity contour maps of 3C 219, showing changes in its morphology over the entire available frequency range. The contour levels are (3, 6, 9, 15, 24,39, 63, 102, 165, 267, 432, 699, 1131)×σrms. The basic properties of individual maps together with noise levels, σrms, are given in Table 1. Beams are shown in the bottom-left corners and center frequencies in the top-right corners of each panel. |
For the purpose of calculating flux measurement errors, in addition to the assumed 10% uncertainty of the flux scale calibration, the σrms noise level in individual maps was also taken into account according to the equation
where Sν is the flux measurement at a given frequency, Ωregion is the angular extent of the measured region, and Ωbeam is the beam size. The flux measurements reported in Table 2 are mostly dominated by flux scale calibration uncertainty. They are close to 10%.
Flux density measurements from 3C 219 lobes.
3. Results
The collected data cover frequencies from 144 MHz to 15 GHz for the outer lobes and from 1.5 GHz to 15 GHz for the inner lobes. A series of maps in Figs. 1 and 2 show 3C 219 over these frequency ranges. Detailed information on each map is given in Table 1, and flux density measurements for each lobe are given in Table 2.
 |
Fig. 2. Total intensity contour maps of the inner structure of 3C 219, showing changes in its morphology over the entire available frequency range. Diffuse outer lobe emission was removed as described in Sect. 2. The contour levels are (3, 6, 9, 15, 24, 39, 63, 102, 165, 267, 432)×σrms. The basic properties of individual maps together with noise levels, σrms, are given in Table 1. Beams are shown in the bottom-left corners and center frequencies in the top-right corners of each panel. |
3.1. Total power radio maps
The main feature of the outer lobes is the asymmetric backflow extending to the west from the northern hot spot. There is a hint of a similar structure extending to the northeast from the southern hot spot. The pronounced hot spots suggest that this phase of activity must have ended relatively recently. At lower frequencies, the emission from the outer lobes dominates, leaving the inner parts unresolved. At higher frequencies, the emission from the oldest parts of the lobes around the center fades and eventually becomes undetectable in the X and Ku bands, revealing the core and the inner lobe. The angular sizes of the northern (N) and southern (S) lobes (lN = 73″ and lS = 73″), counted as the distance from the core to the hot spots, and the brightness (L1.5 GHz, N = 3.0 ⋅ 1033 erg s−1 and L1.5 GHz, S = 3.6 ⋅ 1033 erg s−1) are similar.
The small emission region to the north of the core, which is treated as a northern counterpart to the pronounced southern inner lobe, is unresolved at  and poorly resolved even at
and poorly resolved even at  (Bridle et al. 1986; Clarke et al. 1992). Bridle et al. (1986) showed that the region lies directly on the continuation of the southern jet axis and is elongated along this axis. The authors also cited a paper by Ledden et al. (1980) to conclude that it is very unlikely to be a random confusing source. Archival HST images4 show no detections of background sources at the position of the northern inner lobe. The inner lobes show a significant asymmetry in both linear size (lN = 5″ and lS = 17″) and brightness (L1.5 GHz, N = 2.8 ⋅ 1031 erg s−1 and L1.5 GHz, S = 1.1 ⋅ 1032 erg s−1), possibly as the result of the relativistic Doppler effect, suggesting a deviation of the jet axis from the plane of the sky. The main features of the southern inner lobe are two emission peaks, one located at each end of the structure and visible over the entire frequency range. Higher-resolution observations (Bridle et al. 1986) reveal an 11° offset of these two regions in addition to a larger number of emission peaks along the jet.
(Bridle et al. 1986; Clarke et al. 1992). Bridle et al. (1986) showed that the region lies directly on the continuation of the southern jet axis and is elongated along this axis. The authors also cited a paper by Ledden et al. (1980) to conclude that it is very unlikely to be a random confusing source. Archival HST images4 show no detections of background sources at the position of the northern inner lobe. The inner lobes show a significant asymmetry in both linear size (lN = 5″ and lS = 17″) and brightness (L1.5 GHz, N = 2.8 ⋅ 1031 erg s−1 and L1.5 GHz, S = 1.1 ⋅ 1032 erg s−1), possibly as the result of the relativistic Doppler effect, suggesting a deviation of the jet axis from the plane of the sky. The main features of the southern inner lobe are two emission peaks, one located at each end of the structure and visible over the entire frequency range. Higher-resolution observations (Bridle et al. 1986) reveal an 11° offset of these two regions in addition to a larger number of emission peaks along the jet.
Small patches of emission to the north and to the west of the core in the high-resolution 4.85 GHz and 14.94 GHz (Fig. 2) maps come from a smaller background radio-galaxy referred to as “Baby 3C 219” by Clarke et al. (1992). It is located in a close angular proximity to the core of 3C 219 and superimposed on the outer cocoon. In further analysis of the outer lobes, the central regions of 3C 219 together with the position of Baby 3C 219 are masked. However, due to beam smearing, some residual emission from this background galaxy may still be present and cause systematic errors. Its flux S1.5 GHz < 1 mJy (Clarke et al. 1992) is on the order of the observational uncertainty, so no further steps are taken to correct for it.
3.2. Spectral index maps
The spectral index maps (Fig. 3) were calculated by minimizing χ2 of a pure power-law model of the radio continuum against the full dataset of eight maps of the outer double between 144 MHz and 15 GHz, where the beam size was convolved to 20″, and four maps of the inner double between 1.5 GHz and 15 GHz, where the beam size was convolved to  .
.
 |
Fig. 3. Spectral index maps of 3C 219 presented as color maps, with color bars representing the scales given next to each panel. Top left: Spectral index map of the whole radio galaxy. A convolved 4.89 GHz contour map is overlaid for reference. The contour levels are (3, 39, 267, 600, 1830)×0.17 mJy/b.a.. The size of the circular beams for the color and contour maps is 20″. Top right: Spectral index map of the inner double with diffuse relic emission removed. The convolved 4.85 GHz contour map was overlaid for reference. The contour levels are (3,24,63) × 0.17 : mJy/b.a. The size of the circular beams for the color and contour maps is 2.7″. Bottom left: Spectral index 1σ error map of the whole radio galaxy. The contour map is the same as in the top-left panel. Bottom right: Spectral index 1σ error map of the inner double. The contour map is the same as in the top-right panel. |
The overall structure of the outer lobes has, as expected, a relatively flat spectrum in the hot-spot areas that gets progressively steeper toward the center, which is the result of spectral aging. In the center, the spectral index assumes lower values due to the influence of the inner double and the inverted spectrum radio core. There is a small discrepancy between the spectral indices in the northern (α ≃ 0.73) and the southern (α ≃ 0.66) hot spot. However, due to relatively high errors of spectral index in these regions, where 1σ uncertainties reach Δα ≃ 0.04 − 0.05, these measurements are in agreement.
The map of the inner double spectral index is in agreement with the one presented by Clarke et al. (1992), where α ≃ 0.7, and is extended by using 8 GHz and 15 GHz maps. Smearing the data with  serves to highlight the emission from the inner FWHM ≈ 3″ component. The southern inner lobe has two separate regions, one at each end, with a relatively low spectral index, α ≃ 0.73, which is similar to that of the outer northern hot spot. They are separated by a region with a steep spectrum (α ≃ 0.85), spatially coincident with the faint bridge (see Sect. 1). High values of α at the edges of the inner southern lobe, together with high errors, are most likely due to a low signal-to-noise ratio (S/N) and mixing of the spectrum with residual diffuse outer double emission. The northern inner lobe shows slightly higher values of the spectral index α ≃ 0.82. This was already noted by Clarke et al. (1992) and explained as the result of the differential Doppler shifting of the spectral curvature between the approaching and the receding jet. However, due to the large spectral index errors, reaching Δα ≃ 0.5, discussing such fine details may be unjustified. The high uncertainties in the inner double spectral index maps compared to the outer double spectral index maps, are most likely the result of a shorter range of frequencies, spanning only one order of magnitude instead of two, over which the measurement was made. Additionally, the errors are the highest in the regions of low S/N, at the edges of the inner structure.
serves to highlight the emission from the inner FWHM ≈ 3″ component. The southern inner lobe has two separate regions, one at each end, with a relatively low spectral index, α ≃ 0.73, which is similar to that of the outer northern hot spot. They are separated by a region with a steep spectrum (α ≃ 0.85), spatially coincident with the faint bridge (see Sect. 1). High values of α at the edges of the inner southern lobe, together with high errors, are most likely due to a low signal-to-noise ratio (S/N) and mixing of the spectrum with residual diffuse outer double emission. The northern inner lobe shows slightly higher values of the spectral index α ≃ 0.82. This was already noted by Clarke et al. (1992) and explained as the result of the differential Doppler shifting of the spectral curvature between the approaching and the receding jet. However, due to the large spectral index errors, reaching Δα ≃ 0.5, discussing such fine details may be unjustified. The high uncertainties in the inner double spectral index maps compared to the outer double spectral index maps, are most likely the result of a shorter range of frequencies, spanning only one order of magnitude instead of two, over which the measurement was made. Additionally, the errors are the highest in the regions of low S/N, at the edges of the inner structure.
An inverted core spectrum may indicate that 3C 219 is a peaked spectrum source (e.g., O’Dea & Saikia 2021, and references therein), which could be associated with restarting sources. However, confirming the status of 3C 219 as a peaked spectrum source and studying its properties would require extending the flux measurements to even higher frequencies and modeling of the spectral turnover, taking into account processes such as synchrotron self-absorption (see, e.g., Jeyakumar 2016), which is beyond the scope of this paper. There exist short narrowband observations of 3C 219 at 22.5 GHz and 43 GHz, but these are not presented here, as we were unable to recover any extended emission from the inner structure due to high noise levels.
4. Spectral aging analysis
The main energy loss mechanisms for particles inside radio lobes are synchrotron radiation and inverse Compton scattering of CMB photons. These processes are described in similar terms and are often considered jointly by adding the energy densities of the magnetic field uB and the CMB photon field uCMB.
In this paper, two models of particle aging are considered. The JP model assumes that after the initial injection, synchrotron particles with a power-law energy spectrum lose energy in a tangled magnetic field of constant strength, where the pitch angles of their velocities with respect to the magnetic field lines are constantly changing. The Tribble (1993) variant of the JP model (hereafter JP-Tribble) modifies the above assumptions by allowing the magnetic field strength to vary over the lifetime of the particles according to the Maxwell-Boltzmann distribution.
For the purposes of aging analysis of radio-galaxy lobes, the JP model is often used (e.g., Jamrozy et al. 2008; Konar et al. 2013; Nandi et al. 2019), although in recent discussions (e.g., Hardcastle 2013; Harwood et al. 2013) the advantages of the JP-Tribble variant are pointed out.
4.1. Magnetic field estimation
In this study, the “classical-1” method of magnetic field strength estimation proposed by Konar et al. (2008, Appendix A) is used. It is based on the classical minimum energy approach, where we consider a system of relativistic particles with energy (1 + κ)ue and a magnetic field with energy uB. The total energy of this system is (in cgs units)
where κ is the contribution of protons to the particle energy, which is assumed to be negligible in this paper, B is the magnetic field strength, V is the volume of the radiating region, and ϕ is the pitch angle of synchrotron electrons with respect to the magnetic field lines, which is later averaged. A is the result of integrating the source luminosity over an aged spectrum determined from spectral age modeling, instead of a pure power-law spectrum. The expression is (in cgs units)
Konar et al. (2008) give their equations for the minimum energy condition, where  . To make the results of this paper easier to compare with other similar works (e.g., Jamrozy et al. 2007; Nandi et al. 2019), these equations were rescaled to equipartition magnetic field strengths by a factor of (4/3)2/7, which results from assuming (1 + κ)ue = uB.
. To make the results of this paper easier to compare with other similar works (e.g., Jamrozy et al. 2007; Nandi et al. 2019), these equations were rescaled to equipartition magnetic field strengths by a factor of (4/3)2/7, which results from assuming (1 + κ)ue = uB.
A rather large beam required to extract the weak diffuse emission from the outer and inner lobes made accurate volume estimation challenging. The angular dimensions of the source were measured between the 3σ contours assuming a cylindrical shape, which would lead to overestimation of the volume. To account for this, a volume filling factor of 1/2 was introduced everywhere except for the northern outer lobe, where the value was changed to 1/3, due to the asymmetric back-flow that additionally increases the perceived dimensions. Since the northern inner lobe is unresolved, it was assumed to be a sphere rather than a cylinder, with a diameter of 1″. Conservative uncertainties of ±50% were assumed for the volume estimates given in Table 3. These uncertainties were taken into account while calculating the magnetic field strengths that are also given in Table 3.
Basic lobe parameters and the results of spectral age modeling.
The estimates of B are similar to those obtained in the previous studies of 3C 219 (Burch 1979; Bridle et al. 1986). The slightly weaker magnetic field in the inner southern lobe might be due to an overestimation of its volume in this paper. Observations of the X-ray inverse Compton emission (Comastri et al. 2003) enabled an independent estimation of the magnetic field strengths in the outer lobes. They are noticeably lower than the equipartition strengths, with BN ∼ 2.9 μ G and BD ∼ 3.6 μ G, the difference being a factor of ∼2.2 and ∼1.9 for the northern and southern lobes, respectively. A comparison between equipartition and inverse Compton magnetic field strengths in a sample of FR II radio sources was performed by Croston et al. (2005). The authors found that equipartition magnetic field estimates typically differ from inverse Compton magnetic field estimates by a factor of ∼0.8 − 5, and for most of the sources the factor is around 1.5. 3C 219 is unremarkable in this regard, as it fits well within these limits.
4.2. Modeling method
For the purposes of modeling, the following assumptions were made: (1) the initial energy spectrum of the particles injected into the lobes follows a declining power law spanning an energy range between Lorentz factors γmin = 10 and γmax = 106, with the power law index p = 2αinj + 1 constant over the entire activity phase, where αinj is an injection spectral index; (2) only synchrotron radiation and inverse Compton scattering energy losses are considered; (3a) the magnetic field strength is constant over particle’s lifetime in the JP model and assumes an equipartition value; (3b) the magnetic field strength assumes the Maxwell-Boltzmann distribution over the lifetime of the particle in the JP-Tribble model with the calculated equipartition value as the average; (4) the timescale of the particle pitch angle isotropization is much shorter than their lifetime; and (5) the plasma in individual regions of the source was injected all at once.
In this study, the BRATS (Harwood et al. 2013, 2015) package is used. The software splits the source into regions based on a minimum S/N criterion and then proceeds to model particle aging for each region independently according to the above assumptions. All four radio lobes of 3C 219 were modeled in BRATS separately, which allowed independent estimates of αinj and B (Table 3) to be used as fitting parameters. The αinj indices were estimated using the built-in FINDINJECT task, based on integrated flux densities (Table 2) for individual lobes. The results of the individual radio lobe modeling were then combined to produce spectral age maps (Figs. 4 and 5). All the reported errors of spectral age modeling are 1σ.
 |
Fig. 4. Results of spectral aging analysis for the outer structure of 3C 219 presented with color maps, with color bars representing scales given next to each panel. In each panel, a 4.89 GHz contour map is overlaid for reference. The contour levels are (3, 39, 267, 600, 1830)×0.17 mJy/b.a.. The size of the circular beams for the color and contour maps is 20″. Top left: Spectral age map. The gray line marks a section through the source, the results of which are presented in Fig. 8Top right: χred2 map. Regions with χred2 > 2.8 (99% confidence level) are marked in red. Bottom left: Upper error map of the spectral age. Bottom right: Lower error map of the spectral age. |
 |
Fig. 5. Results of spectral aging analysis for the inner structure of 3C 219 presented with color maps, with color bars representing scales given next to each panel. In each panel a 4.85 GHz contour map is overlaid for reference. The contour levels are (3, 24, 63)×0.17 mJy/b.a. The size of the circular beams for the color and contour maps is 2.7″. Due to its size, the northern lobe was modeled as a single region – the results are presented in Table 3 and in Fig. 7Top left: Spectral age map. The gray line marks a section through the source, the results of which are presented in Fig. 8Top right: χred2 map. Regions with χred2 > 4.61 (99% confidence level) are marked in red. Bottom left: Upper error map of the spectral age. Bottom right: Lower error map of the spectral age. |
4.3. Break frequency and reliability of the age estimation
As the plasma continues to lose energy, its radio spectrum evolves by developing a break, beyond which it steepens. The relation between break frequency and radiative age is described by the equation
where the radiative age τrad is expressed in Myr, the magnetic field B in μG, and the break frequency νbr in GHz. The equivalent CMB magnetic field strength is BCMB = 3.18(1 + z)2 μG.
An aged synchrotron spectrum does not deviate significantly from a pure power law in its pre-break part. For reliable spectral age estimation, it is necessary to include high-frequency measurements – close to or even above the break frequency. Otherwise, even a small systematic error could substantially change the result. In this study, the maximum available frequency is 15 GHz, which corresponds to a spectral age of ∼16 Myr for B = 6.9 μG and ∼1.5 Myr for B = 39 μG.
Another consideration regarding modeling reliability is related to χ2 goodness of fit. A criterion was adopted: regions with χ2 exceeding the 99% confidence level are rejected. These regions are marked in Figs. 4 and 5.
5. Discussion
The spectral age maps are shown in Figs. 4 and 5. In the outer double map, the central regions were masked to exclude the emission from the inner double and the core, which could introduce errors into the fit. The spectral ages are lowest around the hot spots and gradually increase toward the center, reaching ∼20 Myr at the mask cutoff.
The youngest regions in the northern and southern lobes of the outer double are  Myr and
Myr and  Myr, respectively. Considering the linear size of the lobe and the travel time of the plasma from the core to the hot spot, an approximate moment when the AGN switched off could be derived. The minimum travel time, assuming a bulk velocity of the jet plasma close to c, is ∼0.7 Myr. Assuming that the process was symmetric on both sides, the initial phase of activity ended
Myr, respectively. Considering the linear size of the lobe and the travel time of the plasma from the core to the hot spot, an approximate moment when the AGN switched off could be derived. The minimum travel time, assuming a bulk velocity of the jet plasma close to c, is ∼0.7 Myr. Assuming that the process was symmetric on both sides, the initial phase of activity ended  Myr ago. The youngest regions are located asymmetrically to the east of the jet axis and coincide with the low spectral index “fans” discovered by Clarke et al. (1992). These are likely to be the regions where freshly shocked particles move after leaving the hot spot.
Myr ago. The youngest regions are located asymmetrically to the east of the jet axis and coincide with the low spectral index “fans” discovered by Clarke et al. (1992). These are likely to be the regions where freshly shocked particles move after leaving the hot spot.
In the outer double, there is an asymmetry with respect to the jet axis (which is roughly approximated by the gray line in Fig. 4) in the distribution of different plasma populations (Fig. 6). There is a noticeable excess of young (< 5 Myr) regions, as well as a generally higher number of emitting regions on the eastern side. There is also an outflow from the northern hot spot to the west, visible in the total power maps. This asymmetric back-flow may be a result of the outer double expanding into an inhomogeneous medium.
 |
Fig. 6. Histogram showing the distribution of different plasma populations in the outer double with respect to the jet axis. |
The inner southern lobe shows two separate regions with ages of  Myr, one at each end of the lobe, that are spatially coincident with the total power emission peaks. They are separated by a region of slightly older emission of age
Myr, one at each end of the lobe, that are spatially coincident with the total power emission peaks. They are separated by a region of slightly older emission of age 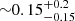 Myr. Normally, this type of structure suggests the existence of a new emission phase. However, due to questions about the reliability of the fit (Sect. 4.3) and rather large relative spectral age uncertainties, this would be a hasty conclusion. Expanding the study with higher-frequency observations would be necessary to prove or disprove it. For the purpose of further analysis, the 0-age region close to the core is omitted and the maximum age of the inner southern lobe is assumed to be
Myr. Normally, this type of structure suggests the existence of a new emission phase. However, due to questions about the reliability of the fit (Sect. 4.3) and rather large relative spectral age uncertainties, this would be a hasty conclusion. Expanding the study with higher-frequency observations would be necessary to prove or disprove it. For the purpose of further analysis, the 0-age region close to the core is omitted and the maximum age of the inner southern lobe is assumed to be  Myr. The oldest regions of the inner lobe appear along its edges. This is most likely due to residual emission from the outer lobes.
Myr. The oldest regions of the inner lobe appear along its edges. This is most likely due to residual emission from the outer lobes.
An interesting pattern emerges in the χ2 map of the inner lobes, there are several local peaks along the jet axis. This suggests that there may be additional components to the perceived spectrum that cause it to deviate from a pure aged power law, such as emission from jet knots (Bridle et al. 1986; Clarke et al. 1992), which could be due to reacceleration and compression of the jet fluid in internal shocks arising from jet recollimation by external pressure (Bridle et al. 1986).
The northern inner lobe was modeled as a single region due to its meager size. The results of this fitting are given in Table 3. In the same table, the average spectral ages for the other lobes are also included. They were calculated from the fluxes integrated over the full volumes of individual lobes (Table 2). The flux density measurements along with fitted spectra are presented in Fig. 7.
 |
Fig. 7. Results of spectral aging analysis for individual lobes based on integrated flux densities. The scale on the frequency and flux axes is logarithmic. A summary of each model is given in Table 3. Left: Outer lobes. The JP-Tribble model was used. In order to separate the plots, the measured and modeled fluxes for the northern lobe were rescaled by a factor of 0.5. Right: Inner lobes. The JP model was used. |
When considering the integrated flux densities, the JP and JP-Tribble models are equivalent within the uncertainties, giving very similar ages and the same χ2 goodness of fit, with the JP-Tribble giving slightly but systematically higher estimates. However, when 3C 219 is split into regions, there are differences in favor of the JP-Tribble model in the outer lobes and the JP model in the inner lobes. An immediate explanation would be that older particles are more likely to have experienced significant variations in magnetic field strength over their lifetime.
There appears to be a discrepancy in the best-fit injection spectral index values in 3C 219 outer and inner doubles (Table 3). However, due to rather large errors in the estimation of αinj in the inner lobes, the results of the injection spectral index fitting in the inner and outer lobes are similar within the uncertainties. Extending the flux measurements of the 3C 219 inner double to lower frequencies would be necessary to put tighter constraints on αinj. Confirmation of this αinj discrepancy could provide an interesting result, since Konar & Hardcastle (2013) showed a correlation between injection indices in subsequent phases of activity in DDRGs. With the addition of a complementary correlation between injection index and jet power, they argue that different αinj could indicate a large-scale perturbation of the central SMBH during the quiescent period.
5.1. Age profile, jet axis orientations, and lobe expansion velocities
Sections through spectral age maps and complementary error maps (Figs. 4 and 5) were made, resulting in a plot shown in Fig. 8. A model of linear expansion was fitted to the outer lobes. Both fit the model well. Their extrapolation toward the center gives values for the maximum age of the outer northern and southern lobes  Myr and
Myr and  Myr. There is a slight discrepancy between the two estimates, which is also reflected in different transverse expansion velocities βT that were recovered from the slopes of the model. For the outer northern and southern lobes they assume values βT, out, N = 0.035 ± 0.001 and βT, out, S = 0.028 ± 0.001, respectively.
Myr. There is a slight discrepancy between the two estimates, which is also reflected in different transverse expansion velocities βT that were recovered from the slopes of the model. For the outer northern and southern lobes they assume values βT, out, N = 0.035 ± 0.001 and βT, out, S = 0.028 ± 0.001, respectively.
 |
Fig. 8. Spectral age profile of 3C 219. Measurements made along the sections marked in Figs. 4 and 5, together with spectral age errors, are shown as black points with error bars. Top: Outer lobes. Best-fit linear expansion models are shown as black lines. Bottom: Inner lobes. |
Due to the relativistic Doppler effect and the finite travel time of light, a lobe expanding at a constant linear velocity β at an angle of inclination to the line of sight θ appears to have a transverse velocity of
The same effects are also responsible for an apparent mismatch between the linear sizes and luminosities of the opposite lobes, where one expands toward the observer and the other away from the observer. An additional assumption is that the linear expansion velocities in both lobes are the same, and that the lobes expand along collinear axes. Then, the ratios of linear sizes and the k-corrected luminosities are given by the equations
The measured values of linear sizes and luminosities given in Sect. 3.1, as well as the values of βT presented in this section, were substituted into the above equations to recover β and θ. For the outer double, βoutcosθout is in the range 0–0.024, with the lower limit estimated from the ratio of linear sizes and the upper limit from the ratio of luminosities. This discrepancy could be due to inhomogeneities in the ambient medium, which could cause the lobes to expand at different velocities or along non-collinear axes. The linear expansion speed βout is in the range 0.027–0.043 and the inclination θout is in the range 45–90°, with the southern lobe being the approaching one. The discrepancies of βoutcosθout and βT, out were taken into account in making these estimates.
The inclination range is consistent with the observations of Perley et al. (1980), who noted a V-shaped hot spot in the south and a ring-like one in the north and explained that this is the result of Doppler (de)beaming (e.g., simulations by Wilson & Scheuer 1983; Komissarov & Falle 1996). The clear hot-spot asymmetry suggests that θ is closer to 45°. The derived value of β≃0.035 is a typical expansion speed that generally does not exceed ≃0.1–0.15 in the wide population of radio-galaxies (Scheuer 1995; Arshakian & Longair 2000).
A similar analysis was performed for the pair of inner lobes. A model of linear expansion for the southern lobe gives poor fit, so the maximum age of the southern inner lobe is assumed to be  Myr. Radiative age of the northern counterpart is
Myr. Radiative age of the northern counterpart is  . This gives an estimation of the southern and northern inner lobe transverse expansion velocities βT, in, S = 0.63 with a lower limit equal to 0.27, and a lower limit for βT, in, N equal to 0.26. Since the uncertainty ranges of radiative ages reach 0 Myr, it is impossible to estimate the upper limits of βT, in in a straightforward way. βincosθin is in the range 0.18–0.55 with the lower limit derived from the luminosity ratio and the upper limit derived from the linear size ratio. The maximum possible value of βT, in for which βin < 1 is then ∼1.2, which is used as the upper limit. Substituting these values into the above equations, a lower limit for the linear expansion speed βin = 0.28 was derived. An expansion speed higher than in the initial phase of activity is consistent with a model that assumes that the restarted jet expands into the relic cocoon, where it encounters less resistance than in the thermal ambient medium (e.g., Safouris et al. 2008; Konar & Hardcastle 2013). θin in the range 12–45°, with the southern lobe being the approaching one, suggests that a reorientation of the jet axis may have occurred during the quiescent phase.
. This gives an estimation of the southern and northern inner lobe transverse expansion velocities βT, in, S = 0.63 with a lower limit equal to 0.27, and a lower limit for βT, in, N equal to 0.26. Since the uncertainty ranges of radiative ages reach 0 Myr, it is impossible to estimate the upper limits of βT, in in a straightforward way. βincosθin is in the range 0.18–0.55 with the lower limit derived from the luminosity ratio and the upper limit derived from the linear size ratio. The maximum possible value of βT, in for which βin < 1 is then ∼1.2, which is used as the upper limit. Substituting these values into the above equations, a lower limit for the linear expansion speed βin = 0.28 was derived. An expansion speed higher than in the initial phase of activity is consistent with a model that assumes that the restarted jet expands into the relic cocoon, where it encounters less resistance than in the thermal ambient medium (e.g., Safouris et al. 2008; Konar & Hardcastle 2013). θin in the range 12–45°, with the southern lobe being the approaching one, suggests that a reorientation of the jet axis may have occurred during the quiescent phase.
It is possible to use the estimate of the βT, in upper limit to derive lower limits of tmax, in for the inner lobes based on the minimum travel time of the hot spots. Applying this method to the above values gives  Myr for the southern lobe and
Myr for the southern lobe and  Myr for the northern lobe. Due to the light travel time, the northern lobe is observed at an earlier stage of evolution, so only tmax, S is used to derive the duration of the quiescent phase.
Myr for the northern lobe. Due to the light travel time, the northern lobe is observed at an earlier stage of evolution, so only tmax, S is used to derive the duration of the quiescent phase.
5.2. Active and quiescent phase durations
With the derived values of: (1) tmax,I = 30.9 ± 2.5 Myr – average extrapolated maximum spectral age of the old lobes; (2)  Myr – initial phase of activity switch-off time; (3)
Myr – initial phase of activity switch-off time; (3)  Myr – estimated maximum spectral age of the young lobes; (4) ths,II = 0 Myr – hot-spot age of the young lobes; it is possible to estimate the duration of the active and quiescent phases, assuming that the young phase is still ongoing and neglecting the possible third phase of activity. The expressions for the active time of the initial phase tact,I, the duration of the quiescent phase tqui, and the active time of the current phase tact,II are as follows:
Myr – estimated maximum spectral age of the young lobes; (4) ths,II = 0 Myr – hot-spot age of the young lobes; it is possible to estimate the duration of the active and quiescent phases, assuming that the young phase is still ongoing and neglecting the possible third phase of activity. The expressions for the active time of the initial phase tact,I, the duration of the quiescent phase tqui, and the active time of the current phase tact,II are as follows:
In comparison with the typical duration of the quiescent phase in DDRGs in the range ∼105–107 yr with some reaching as much as ∼108 yr (Konar et al. 2013), 3C 219 restarted very quickly. It spent as little as 2% of its lifetime being inactive. This result explains the existence of confined hot spots in the outer double.  is on the order of the travel time from the core to the hot spot, implying that plasma may still be supplied to the outer double hot spots.
is on the order of the travel time from the core to the hot spot, implying that plasma may still be supplied to the outer double hot spots.
5.3. Comparison with a dynamical model of the outer double
Machalski et al. (2021) performed dynamical modeling based on the integrated total radio continuum of 3C 219, which was extended down to 26 MHz (Laing & Peacock 1980), using a KDA EXT model (Kuligowska 2017). They have found an injection index αinj = 0.56, a value much lower than the one derived in this paper. The discrepancy is likely the result of a possible spectrum turnover at decametric wavelengths (Artyukh et al. 1994). Not surprisingly, this leads to a higher estimate of the outer double age tdyn = 76 Myr.
To check, whether the two approaches (dynamical and radiative) are in agreement, the JP-Tribble model with αinj = 0.56 was applied to the outer double, similarly as in Sect. 4. The resulting fit is rather poor with an average χred2 = 2.29. The result was then extrapolated toward the center to give an age estimate trad ≃ 33 Myr, which is a marginal increase and still over 50% shorter than the dynamical age.
The discrepancy between radiative and dynamical age estimates (with radiative ages being much lower) is well known and discussed in literature. Recent findings of Mahatma et al. (2020) suggest that the classical equipartition method leads to a substantial overestimation of the magnetic field strength B, which contributes to the widening of the gap. They suggest developing a revised method for estimating B or using inverse Compton measurements. In addition, heavy mixing of the synchrotron plasma can occur in radio lobes (Turner et al. 2018), which would invalidate assumption (5) in Sect. 4.2 and the applicability of the JP model.
Following the mixing argument, the outer lobes were assumed to be two separate regions into which fresh plasma is continuously injected (the “CI model”; Pacholczyk 1970) as an approximation of the process. In addition, magnetic field strengths inferred from the X-ray observations were assumed (see Sect. 4.1). The required flux density measurements are given in Table 2, and the assumed αinj is 0.56 to keep it consistent with the dynamical model. The results are as follows:  with
with  for the northern lobe and
for the northern lobe and  with χred2 = 0.32 for the southern lobe. These continuous injection estimates of radiative ages are in agreement with the results of dynamical modeling performed by Machalski et al. (2021).
with χred2 = 0.32 for the southern lobe. These continuous injection estimates of radiative ages are in agreement with the results of dynamical modeling performed by Machalski et al. (2021).
5.4. Scenarios for the reorientation of the jet axis
In Sect. 5.1 we show that the jet axis was most likely reoriented between the two phases of activity; however, this is not immediately visible, as the reorientation occurred along the line of sight. If 3C 219 was observed from a different perspective, it could resemble 3C 293 (Machalski et al. 2016) or 3C 403 (Dennett-Thorpe et al. 2002), which are classified as X-shape radio sources. There are several models aiming to explain the origins of X-shaped radio structures (for a comprehensive review, see, e.g., Gopal-Krishna 2012). We decided to apply these models to 3C 219 to find the most likely scenario for the reorientation of the jet axis.
First of the possible scenarios is the jet–shell interaction model proposed by Gopal-Krishna (2012). The jet may get deflected when it encounters one of the clouds that form a shell surrounding galaxies in post-merger systems (e.g., Hernquist & Spergel 1992) in low-density environments. These shells may be a common feature of elliptical galaxies hosting radio sources (e.g., Sikkema et al. 2007), although it may be difficult to observe them in systems outside of the local Universe due to technical limitations (Gopal-Krishna 2012). Two of the main advantages of this model are: (a) it does not require interruption in the AGN activity – the cause of the jet reorientation lies outside of the central engine; and (b) it could occur even a long time after a merger event, which is important in the case of 3C 219 because the host galaxy shows no obvious signs of recent interactions (McLure et al. 1999) on the scales of the HST resolution (equivalent to ∼300 pc at z = 0.17456). However, the shells are mostly aligned with the major axes of elliptical galaxies (Malin & Carter 1983), and the projected jet axis of 3C 219 in the original phase of activity is at a position angle of ∼75° (Saripalli & Subrahmanyan 2009) with respect to the major axis of the host galaxy. Furthermore, 3C 219 is located in a rich cluster (Matthews et al. 1964; MacDonald et al. 1968). This makes the jet–shell interaction model an unlikely explanation.
Another possibility is the presence of a binary SMBH system producing two separate pairs of jets (Lal & Rao 2005, 2007), which could explain two pairs of edge-brightened lobes oriented in different directions. No obvious signs of a recent interaction in the host galaxy of 3C 219 (McLure et al. 1999) would suggest that such a binary system would have to avoid coalescence for ∼108–109 yr, which is the typical timescale for galaxy mergers (e.g., Conselice 2006; Lotz et al. 2008). Spectroscopic observations reveal double-peaked Balmer lines (Strateva et al. 2006). However, it is more likely that the double-peaked profile of the spectral lines is reflective of the accretion disk structure and kinematics rather than the presence of a binary black hole system, since fewer than one in 104 AGNs are expected to show such signatures of binary motion. Furthermore, for the double-peaked emission to come from a binary black hole, the combined mass of such a system would have to be in the range 1010–1011 M⊙ (Eracleous et al. 1997), which is inconsistent with the mass of the SMBH in 3C 219 given by Marchesini et al. (2004) equal MBH = 6.3 ⋅ 108 M⊙. The generally low probability of finding a binary system where both components launch jets simultaneously forces us to reject this model.
The third model assumes a steady conical precession of the jet axis (Parma et al. 1985), which could be due to the presence of a secondary black hole (Sillanpaa et al. 1988) or the Bardeen & Petterson (1975) effect. A jet precessing over longer periods of time should leave obvious traces that could be seen in radio total power morphology, as is the case in J1328+2752 (Nandi et al. 2021) or NGC 326 (Ekers et al. 1978). Additionally, we should be able to trace jet precession in a spectral age map as spectral age of the plasma increases laterally from the hot spots, whereas the age profile of the 3C 219 outer double is unperturbed (Fig. 4), gradually changing from the youngest plasma around the hot spots to the oldest plasma around the center, which is characteristic of “regular" FRII radio galaxies. The inconsistency of the precession model with the results of spectral aging analysis means that this is not the correct explanation.
The most promising model is rapid jet reorientation due to binary black hole coalescence (Merritt & Ekers 2002) or the accretion of matter from a tilted disk (Natarajan & Pringle 1998). In the first case, the flip would be nearly instantaneous. In the second case, the timescale of jet realignment (in Myr) is given by Natarajan & Pringle (1998) as
where 0 < a < 1 is the dimensionless black hole spin, ϵ is the radiative efficiency of the black hole, and αdisk is the dimensionless viscosity parameter (Shakura & Sunyaev 1973). In this paper, we assume αdisk = 0.03, following the reasoning of Natarajan & Pringle (1998). Ledd is the Eddington luminosity, and L is the radiated energy. Ito et al. (2008) estimated that L is in the range ∼0.65–10 Ledd in 3C 219. Here, we assumed the lower limit. We chose to vary a and ϵ between 0.1 and 1, as we have no information about the exact values of spin and radiative efficiency in 3C 219. The timescale for the spin flip of the black hole is then in the range ∼0.01–0.3 Myr, which is on the order of the quiescent phase duration. The amount of plasma injected into the lobes during this period would be negligible when compared to the > 20 Myr of the previous evolution, so there should be no visible distortion to the spectral age map of the outer lobes. Dennett-Thorpe et al. (2002) argue that even in the absence of obvious traces of recent interactions, it is possible for a spin flip to occur due to either a binary black hole merger or an acquisition of a smaller galaxy that supplies material to the SMBH. Given the richness of the 3C 219 environment and the consistency of the derived realignment time with the quiescent phase duration, we consider the “acquisition” explanation to be the most plausible. This model also does not require the consideration of a break in the AGN activity to explain the formation of the edge-brightened inner double. After the realignment is complete the jet propagates through the interior of the cocoon as if it was restarting after a period of inactivity long enough for the original jet channel to collapse (∼104 yr; Brocksopp et al. 2011).
6. Conclusions
We performed a spectral aging analysis of the DDRG 3C 219 using multifrequency survey and archival data. The inner and outer lobes were split and modeled independently using BRATS software. Maps of the spectral age were obtained and are presented in Sect. 4. These maps were used to construct a radiative age profile and to fit a model of linear expansion of the radio lobes.
In interpreting the inner double of 3C 219 as a “rejuvenated jet”, we find that, in order to explain the modeled ages of the outer and inner doubles and the observed asymmetry in length and brightness of the inner lobes, the jet axis must have been reoriented on a timescale of ∼105 yr. The formation of this structure could be attributed to a spin flip of the black hole due to accretion of matter with a different angular momentum that was supplied by a merger minor enough that it did not leave any other obvious observable traces. 3C 219 could be a case of a “hidden X-shape” radio source, where the projection of the X-shaped structure onto the plane of the sky hides its true nature from observers. It is also worth noting that in the case of 3C 219, it was possible to bring the dynamical and radiative estimates of the outer double ages into agreement by using the continuous injection model with a magnetic field strength BIC derived from X-ray observations.
To confirm the results of this study, the inner lobes of 3C 219 require further investigation. Higher-frequency observations, for example by VLA in bands K (18–26 GHz) and possibly Q (40–50 GHz), need to be included to verify whether the spectral age map of the inner southern lobe is accurate. Extending the study to lower frequencies, for example by observing with the International LOFAR Telescope, would allow tighter constraints to be placed on the injection index in the inner double. High-resolution maps are also necessary to probe the internal structure of the inner double in greater detail. Finally, dynamical modeling of the inner double could be performed to gain further insight into the dynamics of the inner double expansion.
Acknowledgments
This research work was partially supported by the National Science Center (NCN) OPUS-15 grant, no. UMO2018/29/B/ST9/01793. We would like to thank M. Krośniak and an anonymous reviewer for valuable comments and suggestions. LOFAR data products were provided by the LOFAR Surveys Key Science project (LSKSP; https://lofar-surveys.org/) and were derived from observations with the International LOFAR Telescope (ILT). LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources), and which are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orleans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland; The Istituto Nazionale di Astrofisica (INAF), Italy. This research used the Dutch national e-infrastructure with support of the SURF Cooperative (e-infra 180169) and the LOFAR e-infra group. The Jülich LOFAR Long Term Archive and the German LOFAR network are both coordinated and operated by the Jülich Supercomputing Centre (JSC), and computing resources on the supercomputer JUWELS at JSC were provided by the Gauss Centre for Supercomputing e.V. (grant CHTB00) through the John von Neumann Institute for Computing (NIC). This research used the University of Hertfordshire high performance computing facility and the LOFAR-UK computing facility located at the University of Hertfordshire and supported by STFC [ST/P000096/1], and of the Italian LOFAR IT computing infrastructure supported and operated by INAF, and by the Physics Department of Turin university (under an agreement with Consorzio Interuniversitario per la Fisica Spaziale) at the C3S Supercomputing Centre, Italy. Based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA). The National Radio Astronomy Observatory running the VLA is a facility of the National Science Foundation operated under a cooperative agreement by Associated Universities, Inc.
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2012, ApJS, 203, 21 [Google Scholar]
- Arshakian, T. G., & Longair, M. S. 2000, MNRAS, 311, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Artyukh, V. S., Tyul’bashev, S. A., & Ogannisyan, M. A. 1994, Astron. Lett., 20, 146 [NASA ADS] [Google Scholar]
- Bardeen, J. M., & Petterson, J. A. 1975, ApJ, 195, L65 [Google Scholar]
- Bridle, A. H., Perley, R. A., & Henriksen, R. N. 1986, AJ, 92, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Brocksopp, C., Kaiser, C. R., Schoenmakers, A. P., & de Bruyn, A. G. 2011, MNRAS, 410, 484 [CrossRef] [Google Scholar]
- Burch, S. F. 1979, MNRAS, 186, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, D. A., Bridle, A. H., Burns, J. O., Perley, R. A., & Norman, M. L. 1992, ApJ, 385, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Brunetti, G., Dallacasa, D., et al. 2003, MNRAS, 340, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Harris, D. E., et al. 2005, ApJ, 626, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, K. S., Kneib, J.-P., Percival, W. J., et al. 2016, AJ, 151, 44 [Google Scholar]
- Dennett-Thorpe, J., Scheuer, P. A. G., Laing, R. A., et al. 2002, MNRAS, 330, 609 [NASA ADS] [CrossRef] [Google Scholar]
- De Young, D. S., Hogg, D. E., & Wilkes, C. T. 1979, ApJ, 228, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Ekers, R. D., Fanti, R., Lari, C., & Parma, P. 1978, Nature, 276, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Eracleous, M., Halpern, J. P., Gilbert, M. A., Newman, J. A., & Filippenko, A. V. 1997, ApJ, 490, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Gopal-Krishna, Biermann P. L., Gergely, L. Á., & Wiita, P. J., 2012, Res. Astron. Astrophys., 12, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J. 2013, MNRAS, 433, 3364 [Google Scholar]
- Harwood, J. J., Hardcastle, M. J., Croston, J. H., & Goodger, J. L. 2013, MNRAS, 435, 3353 [NASA ADS] [CrossRef] [Google Scholar]
- Harwood, J. J., Hardcastle, M. J., & Croston, J. H. 2015, MNRAS, 454, 3403 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 52, 589 [Google Scholar]
- Hernquist, L., & Spergel, D. N. 1992, ApJ, 399, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Ito, H., Kino, M., Kawakatu, N., Isobe, N., & Yamada, S. 2008, ApJ, 685, 828 [CrossRef] [Google Scholar]
- Jaffe, W. J., & Perola, G. C. 1973, A&A, 26, 423 [NASA ADS] [Google Scholar]
- Jamrozy, M., Konar, C., Saikia, D. J., et al. 2007, MNRAS, 378, 581 [Google Scholar]
- Jamrozy, M., Konar, C., Machalski, J., & Saikia, D. J. 2008, MNRAS, 385, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Jeyakumar, S. 2016, MNRAS, 458, 3786 [NASA ADS] [CrossRef] [Google Scholar]
- Kardashev, N. S. 1962, Sov. Ast., 6, 317 [NASA ADS] [Google Scholar]
- Komissarov, S. S., & Falle, S. A. E. G. 1996, ASP Conf. Ser., 100, 327 [NASA ADS] [Google Scholar]
- Konar, C., & Hardcastle, M. J. 2013, MNRAS, 436, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Konar, C., Saikia, D. J., Jamrozy, M., & Machalski, J. 2006, MNRAS, 372, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Konar, C., Jamrozy, M., Saikia, D. J., & Machalski, J. 2008, MNRAS, 383, 525 [Google Scholar]
- Konar, C., Hardcastle, M. J., Jamrozy, M., Croston, J. H., & Nandi, S. 2012, MNRAS, 424, 1061 [Google Scholar]
- Konar, C., Hardcastle, M. J., Jamrozy, M., & Croston, J. H. 2013, MNRAS, 430, 2137 [NASA ADS] [CrossRef] [Google Scholar]
- Kozieł-Wierzbowska, D., Goyal, A., & Żywucka, N. 2020, ApJS, 247, 53 [CrossRef] [Google Scholar]
- Kuligowska, E. 2017, A&A, 598, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuźmicz, A., Jamrozy, M., Kozieł-Wierzbowska, D., & Weżgowiec, M. 2017, MNRAS, 471, 3806 [CrossRef] [Google Scholar]
- Laing, R. A., & Peacock, J. A. 1980, MNRAS, 190, 903 [Google Scholar]
- Lal, D. V., & Rao, A. P. 2005, MNRAS, 356, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Lal, D. V., & Rao, A. P. 2007, MNRAS, 374, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Ledden, J. E., Broderick, J. J., Condon, J. J., & Brown, R. L. 1980, AJ, 85, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., & Primack, J. R. 2008, MNRAS, 391, 1137 [Google Scholar]
- MacDonald, G. H., Kenderdine, S., & Neville, A. C. 1968, MNRAS, 138, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Machalski, J., Jamrozy, M., Stawarz, Ł., & Weżgowiec, M. 2016, A&A, 595, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Machalski, J., Kozieł-Wierzbowska, D., & Goyal, A. 2021, ApJS, 255, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Mahatma, V. H., Hardcastle, M. J., Williams, W. L., et al. 2019, A&A, 622, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahatma, V. H., Hardcastle, M. J., Croston, J. H., et al. 2020, MNRAS, 491, 5015 [Google Scholar]
- Malin, D. F., & Carter, D. 1983, ApJ, 274, 534 [Google Scholar]
- Maltby, P., Matthews, T. A., & Moffet, A. T. 1963, ApJ, 137, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., Celotti, A., & Ferrarese, L. 2004, MNRAS, 351, 733 [CrossRef] [Google Scholar]
- Marecki, A., Jamrozy, M., & Machalski, J. 2016, MNRAS, 463, 338 [CrossRef] [Google Scholar]
- Matthews, T. A., Morgan, W. W., & Schmidt, M. 1964, ApJ, 140, 35 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Kukula, M. J., Dunlop, J. S., et al. 1999, MNRAS, 308, 377 [CrossRef] [Google Scholar]
- Merritt, D., & Ekers, R. D. 2002, Science, 297, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, W. W. 1958, PASP, 70, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Nandi, S., Saikia, D. J., Roy, R., et al. 2019, MNRAS, 486, 5158 [CrossRef] [Google Scholar]
- Nandi, S., Caproni, A., Kharb, P., Sebastian, B., & Roy, R. 2021, ApJ, 908, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., & Pringle, J. E. 1998, ApJ, 506, L97 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Saikia, D. J. 2021, A&ARv, 29, 3 [Google Scholar]
- Pacholczyk, A. G. 1970, Radio astrophysics. Nonthermal processes in galactic and extragalactic sources (San Francisco: Freeman) [Google Scholar]
- Parma, P., Ekers, R. D., & Fanti, R. 1985, A&AS, 59, 511 [NASA ADS] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2017, ApJS, 230, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Bridle, A. H., Willis, A. G., & Fomalont, E. B. 1980, AJ, 85, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safouris, V., Subrahmanyan, R., Bicknell, G. V., & Saripalli, L. 2008, MNRAS, 385, 2117 [NASA ADS] [CrossRef] [Google Scholar]
- Saikia, D. J., & Jamrozy, M. 2009, BASI, 37, 63 [NASA ADS] [Google Scholar]
- Saripalli, L., & Subrahmanyan, R. 2009, ApJ, 695, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Scheuer, P. A. G. 1995, MNRAS, 277, 331 [NASA ADS] [Google Scholar]
- Schoenmakers, A. P., de Bruyn, A. G., Röttgering, H. J. A., van der Laan, H., & Kaiser, C. R. 2000, MNRAS, 315, 371 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shimwell, T. W., Hardcastle, M. J., Tasse, C., et al. 2022, A&A, 659, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sikkema, G., Carter, D., Peletier, R. F., et al. 2007, A&A, 467, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sillanpaa, A., Haarala, S., Valtonen, M. J., Sundelius, B., & Byrd, G. G. 1988, ApJ, 325, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, I. V., Brandt, W. N., Eracleous, M., Schneider, D. P., & Chartas, G. 2006, ApJ, 651, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. L., Dunlop, J. S., Hughes, D. H., & Robson, E. I. 1996, MNRAS, 283, 930 [CrossRef] [Google Scholar]
- Tribble, P. C. 1993, MNRAS, 261, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., Rogers, J. G., Shabala, S. S., & Krause, M. G. H. 2018, MNRAS, 473, 4179 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, M. J., & Scheuer, P. A. G. 1983, MNRAS, 205, 449 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Total intensity contour maps of 3C 219, showing changes in its morphology over the entire available frequency range. The contour levels are (3, 6, 9, 15, 24,39, 63, 102, 165, 267, 432, 699, 1131)×σrms. The basic properties of individual maps together with noise levels, σrms, are given in Table 1. Beams are shown in the bottom-left corners and center frequencies in the top-right corners of each panel. |
| In the text | |
 |
Fig. 2. Total intensity contour maps of the inner structure of 3C 219, showing changes in its morphology over the entire available frequency range. Diffuse outer lobe emission was removed as described in Sect. 2. The contour levels are (3, 6, 9, 15, 24, 39, 63, 102, 165, 267, 432)×σrms. The basic properties of individual maps together with noise levels, σrms, are given in Table 1. Beams are shown in the bottom-left corners and center frequencies in the top-right corners of each panel. |
| In the text | |
 |
Fig. 3. Spectral index maps of 3C 219 presented as color maps, with color bars representing the scales given next to each panel. Top left: Spectral index map of the whole radio galaxy. A convolved 4.89 GHz contour map is overlaid for reference. The contour levels are (3, 39, 267, 600, 1830)×0.17 mJy/b.a.. The size of the circular beams for the color and contour maps is 20″. Top right: Spectral index map of the inner double with diffuse relic emission removed. The convolved 4.85 GHz contour map was overlaid for reference. The contour levels are (3,24,63) × 0.17 : mJy/b.a. The size of the circular beams for the color and contour maps is 2.7″. Bottom left: Spectral index 1σ error map of the whole radio galaxy. The contour map is the same as in the top-left panel. Bottom right: Spectral index 1σ error map of the inner double. The contour map is the same as in the top-right panel. |
| In the text | |
 |
Fig. 4. Results of spectral aging analysis for the outer structure of 3C 219 presented with color maps, with color bars representing scales given next to each panel. In each panel, a 4.89 GHz contour map is overlaid for reference. The contour levels are (3, 39, 267, 600, 1830)×0.17 mJy/b.a.. The size of the circular beams for the color and contour maps is 20″. Top left: Spectral age map. The gray line marks a section through the source, the results of which are presented in Fig. 8Top right: χred2 map. Regions with χred2 > 2.8 (99% confidence level) are marked in red. Bottom left: Upper error map of the spectral age. Bottom right: Lower error map of the spectral age. |
| In the text | |
 |
Fig. 5. Results of spectral aging analysis for the inner structure of 3C 219 presented with color maps, with color bars representing scales given next to each panel. In each panel a 4.85 GHz contour map is overlaid for reference. The contour levels are (3, 24, 63)×0.17 mJy/b.a. The size of the circular beams for the color and contour maps is 2.7″. Due to its size, the northern lobe was modeled as a single region – the results are presented in Table 3 and in Fig. 7Top left: Spectral age map. The gray line marks a section through the source, the results of which are presented in Fig. 8Top right: χred2 map. Regions with χred2 > 4.61 (99% confidence level) are marked in red. Bottom left: Upper error map of the spectral age. Bottom right: Lower error map of the spectral age. |
| In the text | |
 |
Fig. 6. Histogram showing the distribution of different plasma populations in the outer double with respect to the jet axis. |
| In the text | |
 |
Fig. 7. Results of spectral aging analysis for individual lobes based on integrated flux densities. The scale on the frequency and flux axes is logarithmic. A summary of each model is given in Table 3. Left: Outer lobes. The JP-Tribble model was used. In order to separate the plots, the measured and modeled fluxes for the northern lobe were rescaled by a factor of 0.5. Right: Inner lobes. The JP model was used. |
| In the text | |
 |
Fig. 8. Spectral age profile of 3C 219. Measurements made along the sections marked in Figs. 4 and 5, together with spectral age errors, are shown as black points with error bars. Top: Outer lobes. Best-fit linear expansion models are shown as black lines. Bottom: Inner lobes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.






![$$ \begin{aligned} \tau _{\rm rad} = 1590.6\frac{B^{1/2}}{B^2+B_{\rm CMB}^2}\left[\nu _{br}(1+z)\right]^{-1/2}, \end{aligned} $$](/articles/aa/full_html/2024/11/aa50897-24/aa50897-24-eq20.gif)