| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202449453 | |
| Published online | 30 October 2024 | |
The missing rings around Solar System moons
1
Departamento de Ciencias, Facultad de Artes Liberales, Universidad Adolfo Ibáñez,
Av. Padre Hurtado 750,
Viña del Mar,
Chile
2
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
3
Núcleo Milenio Formación Planetaria – NPF,
Chile
4
School of Mathematical and Physical Sciences, Macquarie University,
Balaclava Road,
North Ryde,
NSW
2109,
Australia
5
The Macquarie University Astrophysics and Space Technologies Research Centre, Macquarie University,
Balaclava Road,
North Ryde,
NSW
2109,
Australia
6
SEAP/FACom, Instituto de Física – FCEN, Universidad de Antioquia,
Calle 70 No. 52-21,
Medellín,
Colombia
7
Departamento de Física, Universidad Técnica Federico Santa María,
Avenida España 1680,
Valparaíso,
Chile
★ Corresponding author; mario.sucerquia@univ-grenoble-alpes.fr
Received:
2
February
2024
Accepted:
20
August
2024
Context. Rings are complex structures that surround various bodies within the Solar System, such as giant planets and certain minor bodies. While some formation mechanisms could also potentially promote their existence around (regular or irregular) satellites, none of these bodies currently bear these structures.
Aims. We aim to understand the underlying mechanisms that govern the potential formation, stability, and/or decay of hypothetical circumsatellital rings (CSRs) orbiting the largest moons in the Solar System. This extends to the exploration of short-term morphological features within these rings, providing insights into the ring survival timescales and the interactions that drive their evolution.
Methods. To conduct this study, we used numerical N-body simulations under the perturbing influence of the host planet and other moon companions.
Results. We found that, as suspected, moons with a lower Roche-to-Hill radius can preserve their rings over extended periods. Moreover, the gravitational environment in which these rings are immersed influences the morphological evolution of the system (e.g. ring size), inducing gaps through the excitation of eccentricity and inclination of constituent particles. Specifically, our results show that the rings of Iapetus and Rhea experience minimal variations in their orbital parameters, enhancing their long-term stability. This agrees with the hypothesis that some of the features of Iapetus and Rhea were produced by ancient ring systems, for example, the huge ridge in the Iapetus equator as a result of a decaying ring.
Conclusions. From a dynamical perspective, we found that there are no mechanisms that preclude the existence of CSRs, and we attribute their current absence to non-gravitational phenomena. Effects such as stellar radiation, magnetic fields, and the influence of magnetospheric plasma can significantly impact the dynamics of constituent particles and trigger their decay. This highlights the importance of future studies of these effects.
Key words: methods: numerical / planets and satellites: dynamical evolution and stability / planets and satellites: rings
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Planetary rings are fascinating features that have captured the interest of researchers for centuries, since the advent of the telescope and the first observations of Saturn’s rings by Galileo Galilei in 1610. These structures are made up of many small particles that range in size from micrometres to several metres, and their composition can also vary depending on the characteristics of the planet, such as its size, gravity, and magnetic field, and the environment surrounding these systems (for a complete review, see Tiscareno 2013).
Planetary rings have been extensively studied by both remote and in situ observations. In recent decades, flyby encounters by spacecraft such as Pioneer, Voyager, New Horizons, and other missions that visited the giant planets have revealed a wealth of fascinating features in these objects (e.g. Tiscareno 2013; Sicardy et al. 2018; Lauer et al. 2018; Tiscareno & Murray 2018), such as Saturn’s Cassini Division, density waves caused by resonances with nearby moons, spokes, arcs ringlets, and propeller-shaped features (see e.g. Charnoz et al. 2018 and references therein).
The characteristics found within the rings are largely acknowledged to arise from the intricate interplay between individual ring particles and their surrounding environment. This intricate environment encompasses the gravitational influence of the host planet, the proximity of other satellites situated within or near the rings, the influx of interplanetary matter that interacts with the rings, collision events, radiation pressure, electrostatic forces, photophoresis, cosmic rays, and others. Rings are also continuously replenished through material emanating from neighbouring satellites. Hence, comprehending the dynamics and behaviour inherent to these intricate systems necessitates a multidisciplinary method that amalgamates observational data, theoretical models, and numerical simulations.
Rings have also been observed to encircle various small objects, including the centaurs Chariklo and Chiron (Braga-Ribas et al. 2014; Ortiz et al. 2015; Wood et al. 2017; Bérard et al. 2017), and the trans-Neptunian dwarf planets Haumea and Quaoar (Ortiz et al. 2017; Morgado et al. 2023; Sicardy et al. 2022), through stellar occultations. Nonetheless, neither the rocky planets of the inner Solar System nor the moons of any planet possess planetary rings. This is intriguing, because rings are expected to form easily in the Solar System through close encounters with comets and asteroids or grazing collisions on their surfaces, which might eject substantial amounts of material into orbit (e.g. Charnoz et al. 2018).
It is important to mention that on the one hand, satellites have experienced periods of great violence due to impacts from comets, asteroids, and possibly other nearby moons, leading to the formation of high-speed ejecta from their surfaces (Zahnle et al. 2003; Kirchoff & Schenk 2010; Rickman et al. 2017). On the other hand, moons such as Io, Europa, Ganymede, Enceladus, and Triton show evidence of high-energy volcanic or cryovolcanic activity (e.g. Geissler 2015). In both scenarios, the resulting material should be ejected towards the orbits of the satellites, aided by their low-intensity gravitational fields. However, there is currently no evidence for dense circumsatellital rings (CRS) around moons orbiting close planets.
In Sucerquia et al. (2022), we recently explored the dynamics of rings around moons for exoplanets that are in close proximity to their host star. This study showed that different paths through moons can give rise to a ring, and we also concluded from numerical simulations that rings made of either ice or dust could survive long enough to be detected and characterised. These rings were dubbed “cronomoons” because of their resemblance to the famous rings of Saturn (Chronos in Greek mythology).
In this paper, we proceed and aim to explore from a dynamical perspective whether some of the moons of the Solar System can retain CSRs. We take the perturbative effects of the gravitational environment of the host planet and other moons within the system into account. This work provides some clues that explain the current absence of these features, and we also revisit the origins of some satellites in orbit and surface features of certain satellites that can be elucidated by the presence of ancient rings around actual moons. Examples such as the hypothetical rings of Rhea and the equatorial ridge of Iapetus, which we introduce and discussed in detail below, are pertinent to this discussion. Furthermore, we seek to understand the morphological and dynamical characteristics of these hypothetical structures, and their evolution over time.
To provide a background for our study, we briefly describe the properties of Solar System satellites and rings in Sec. 2. We describe our simulation setup in Sec. 3 and present the findings of our simulations in Sec. 4. Finally, in Sec. 5, we discuss the implications of our results for the search and characterisation of rings around moons and planets in the Solar System and beyond.
2 Solar System satellites and rings
The Solar System has at least 290 moons1, most of which orbit giant planets and a few rocky and dwarf planets. The majority of the moons around giant planets are regular satellites, namely, satellites with direct orbits and close-by orbits that formed in situ around the planet. However, irregular moons, that is, moons that were probably captured from the interplanetary environment, differ from regulars in terms of their physical and orbital properties, such as an exotic composition or retrograde spin and orbital motion (Hall 2016). Irregular moons do not constitute long-lived isolated objects, but evolve and decay rather rapidly through gravitational and tidal interactions with the host planets and other sister moons (see e.g. Sucerquia et al. 2019, 2020, and references therein). These moons can also undergo constant collisions that transform their surface and form circumplanetary ring systems from the remnants of a tidal break-up.
Jupiter and Saturn have the largest number of moons in the Solar System. According to the moon classification by Hall (2016), Jupiter is currently orbited by 4 large moons, 12 small moons, and 51 very small moons, while Saturn has one large moon, 4 medium-sized moons, 21 small moons, and 36 very small moons2. The Uranus system is the smallest in terms of mass, with 27 moons, 4 of which are medium-sized moons, and 23 are small moons (no large, regular moons orbit the planet). Neptune has the smallest number of moons, with a total of 14 moons, of which only one, Triton, is classified as a large moon, although its origin is still debated. Fig. 1 shows the main properties of the large and medium-sized moons of the giant planets (Jupiter and Saturn) and the ice giants (Uranus and Neptune), including their normalised position to the radius of the host planet. The moon size as well as the size of their ring system is normalised using Titan as a standard (see Sec. 3 for their definitions).
The rings of the giant planets have a wide variety of features, some of which are common and some of which are quite different. For example, most of them are confined to between two and three times the radius of the planet and are thinner than their diameter. However, their composition, origin, and morphological characteristics can vary from one system to the next. For instance, Saturn’s rings consist of countless small particles that are mostly made of water ice mixed with some rocky material. There are various major divisions within Saturn’s rings, including the Cassini Division and the Encke and Keeler gaps. The rings are continuously shaped by several small moons, known as “shepherd moons”, which exert gravitational forces on the particles and shape and structure the rings. Particles within the rings can create waves and wakes as they interact with each other and with the nearby moons. The rings of Saturn also exhibit mysterious radial features known as “spokes”, which are sometimes visible and thought to be the result of electrostatic forces (Hartquist et al. 2003).
In contrast, Jupiter’s rings are made up of small particles of icy and rocky dust. The majority of these particles are tiny, with sizes ranging from micrometres to a few centimetres. These rings are much thinner and less massive than those of Saturn and have a relatively narrow width of only a few thousand kilometres. The density of material in Jupiter’s rings is very low, with only a few particles per cubic centimetre. Additionally, small shepherding moons, such as Metis and Adrastea, confine the rings and maintain their narrow orbits, similar to Prometheus and Pandora shepherding Saturn’s F ring Hall (2016).
The rings of Uranus consist of small particles of ice and dust, similar to those of Jupiter. Like Saturn and Jupiter, Uranus also has small moons that help to shape and maintain the structure of the rings, whose vertical high scale is relatively narrow, and which are divided into several distinct regions with different densities and particle sizes (Porco & Goldreich 1987; Goldreich & Porco 1987). The rings of Uranus are thought to be relatively young. They are estimated to be only a few hundred million years old (Esposito 2002; Esposito & Colwell 1989).
Following De Pater et al. (2018), the rings of Neptune differ from those of other giant planets in a few key ways. Composed primarily of dust particles and small rocks, with some water ice, these rings (e.g. the Adams and Le Verrier rings) are maintained by small moons that help shape their structure (e.g. Galatea and Despina). Notably, Neptune’s rings contain bright arcs or segments that are thought to be the product of gravitational resonances with nearby moons. Additionally, the rings are divided into several distinct regions, each with varying densities and particle sizes.
The satellites of the giant planets and their rings are closely related. Satellites may be destroyed by planetary tidal forces to form massive rings, and, due to the gravitational viscosity (the process in which particles within the rings interact through their gravitational fields, leading to angular momentum and energy transfer) of very old rings, they may end up forming small satellites with portions of their material (Charnoz et al. 2010; Ćuk et al. 2020). Some authors have also postulated that Jupiter’s tenuous ring system may have been formed from material ejected from the moons Amalthea, Thebe, Metis, Adrastea, and other parent bodies during high-velocity impacts (see e.g. Burns et al. 2004). The Saturn F ring may have formed when Prometheus and Pandora collided with each other and were partially disrupted, and the very active E ring of Saturn is thought to be maintained by the particles that were ejected by cryovolcanic activity on the surface of Enceladus and by particles that were released after continued micro-meteoroid collisions with this moon (Hyodo & Ohtsuki 2015; Spahn et al. 2006).
Despite the rich diversity of moons within the Solar System, it is intriguing to note the absence of ring systems around them. While many moons are known to encircle giant planets, the phenomenon of moon-hosted rings remains notably absent. This peculiarity prompts the question why moons lack the ring structures that are so commonly observed around their parent planets. In the subsequent section, we delve into our approach of employing numerical simulations to explore the long-term stability and morphological attributes of these enigmatic structures.
 |
Fig. 1 Moon mass vs. moon semi-major axis for our sample of large moons around giant planets (two upper panels) and ice giants (two lower panels). The x-axis of each panel is normalised with respect to the radius of each host planet. The radius of the filled circles represents the moon size, and the shaded area around them shows the size of the ring system (as defined in Sec. 3). The moon and ring sizes are scaled using Titan as a standard size. The colour bar represents the lunar density. |
3 Simulation setup
Our study of the dynamical stability of circumsatellital particles involved integrating the equations of motion of a set of test particles that evolved under the gravitational influence of the moon, the planet, and the sibling satellites. This approach, for instance, allowed us to constrain the radii of the inner and outer rings, as well as their stability, lifespan, fate, and morphology.
We decided to exclude satellites with a mass lower than 1019 kg (on the order of the mass of Mimas) and those with an average density lower than that of water ice from our numerical experiments to ensure that they possessed a spherical shape. In other words, we included all major, intermediate, and some selected minor moons, as presented in Fig. 1 and Table A.1. To establish the initial conditions of the particles, we used data imported from the NASA Horizons programme for the main planet and its moons at an arbitrary date chosen after the Juno mission3. The physical and orbital parameters for the bodies involved in each simulation are provided in Table A.1. The ring particles were initialised in circular orbits (e = 0) and were coplanar with the lunar orbit, sharing the same inclination and longitude of the ascending node, as indicated in the aforementioned table. Additionally, we considered the Roche limit (rR) as a guide for the maximum outer limit of the rings, but this was not necessarily a restriction. The Roche limit ensures that circumsatellite particles do not coalesce into larger particles to form new sub-satellites. We assumed that the planet and satellite were spherical and that the hypothetical rings were coplanar and co-rotated with the satellite orbit around the planet. The Roche limit is defined as the orbital limit within which a body’s self-attraction (particles) is exceeded by the tidal forces of a primary body (host moon),
![$\[r_{\mathrm{R}}=r_{\mathrm{m}}\left(2 \frac{\rho_{\mathrm{m}}}{\rho_{\mathrm{part}}}\right)^{\frac{1}{3}},\]$](/articles/aa/full_html/2024/11/aa49453-24/aa49453-24-eq1.png) (1)
(1)
where rm and ρm are the radius and density of the moon, respectively; and ρpart is the density of the CSR, assumed to be equal to that of water ice (0.917 g/cm3).
Additionally, it is pertinent to elaborate on the so-called Hill radius (both primary and secondary; see Fig. 1). This radius represents the extent of the gravitational domain of a secondary object in the presence of a primary object, and it also defines the maximum distance at which particles maintain dynamic stability around the secondary object. The Hill radius is defined here following the notation by Domingos et al. (2006)
![$\[r_{\mathrm{H}} \approx c ~a(1-e) \sqrt[3]{\frac{m}{3 M}},\]$](/articles/aa/full_html/2024/11/aa49453-24/aa49453-24-eq2.png) (2)
(2)
where a, e, m are the semi-major axis, eccentricity, and mass of the secondary (in this case, the satellite), M is the mass of the primary (the host planet), and c is a constant value related to the dynamical stability of the particles: if c = 1, we recover the traditional expression for the primary Hill radius, if c ≈ 0.4895 or c ≈ 0.9309, the expression is the secondary Hill radius, or the stability limit for prograde and retrograde satellites, respectively (Domingos et al. 2006). Beyond this critical threshold, it is widely postulated that particles are subject to the perturbations of evection or eviction resonances (Vaillant & Correia 2022), rendering them dynamically unstable on short timescales.
By calculating the ratio of the Roche limit to the Hill limit (rR/rH) for each of the selected satellites, we therefore gain insights into the stability of potential sub-satellites (a satellite of a satellite) or rings. For instance, the closer these limits are to each other, the more susceptible the particles become to escaping, colliding with the planet, or colliding with each other due to excitation of their eccentricities. Fig. 2 presents a comparison of these dynamical stability boundaries. This can be interpreted as follows: The higher the ratio rR/rH for each moon, the more unstable the hypothetical rings surrounding it. For instance, particles surrounding Io, Mimas, Enceladus, Miranda, and Proteus are likely to be unstable, as the ratio of the Roche limit and the Hill limit is close to 0.49. Particularly in the case of Mimas, where this ratio exceeds 0.5, we predict that its rings are entirely unstable. Conversely, rings around Iapetus are expected to be the most stable in the set of moons we analysed.
Based on these assumptions, we established the boundaries of the CSR. We set the inner ring radius to 1.05 times the satellite radius, Rs, and its outer radius to 1.2 rR. The rationale for selecting an outer radius like this stems from the fact that if the rings originated from a collision, the resulting debris could be ejected over long distances4. Moreover, to avoid oversampling problems, we randomly generated the initial positions of 1000 particles that compose the ring system, employing blue-noise sampling algorithms. In particular, we used the fibpy algorithm based on the work of Vogel (1979)5. Additionally, to complete our setup, we included the host planet and its other large moons. Furthermore, we did not consider the zonal coefficients Ji of each planet to reduce the computational load. Including these coefficients in future work could improve the description of the gravitational field, and thus, the prediction of satellite and ring orbits. In the case of Earth’s moon, we also included the perturbative effect of the Sun due to its relative proximity. Finally, we ran our simulations employing the REBOUND N-body code (Rein & Liu 2012), with the integration being performed over 1000 years using the symplectic Wisdom-Holman integrator, WHFast (Rein & Tamayo 2015; Wisdom & Holman 1991). The integration duration corresponds to approximately 450 periods of Iapetus, the moon with the longest orbital period included in our simulations, which is about 79 Earth days. We used a time-step of about a few minutes.
To assess the stability and morphological evolution of the CPRs, we conducted the following experiments:
Moon stability: We simulated the evolution of each planet’s satellites over a span of one million years to verify the regularity of the orbits within the gravitational scheme of our interest.
Long-term integration: We studied the dynamics of representative ring particles, specifically, the inner- and outermost particles of the system. Their orbits were then classified after one million years of evolution within a system composed of the planet and the satellites that met the above criteria.
MEGNO analysis: We computed the mean exponential growth factor of nearby orbits (MEGNO) parameter in order to test the dynamical structure of the ring particles and evaluate their long-term orbital stability.
Gravitational environment: We studied a specific case wherein the evolution of ring morphology was compared for a system in which the rings are isolated (i.e. only the planet, satellite, and rings were included) and when the gravitational perturbations of other sibling moons (or the Sun, in the case of Earth’s moon) is taken into account.
Morphology: We analysed the evolution of the ring system for each satellite in an environment that considered the perturbation of the planet and other satellites. This allowed us to evaluate their influence on particles that leads to the dissipation of the rings or the emergence of resonant structures in their orbital elements.
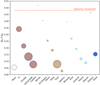 |
Fig. 2 Ratio of the gravitational domain (Hill radius) and the theoretical ring size (Roche limit) for our sample of large moons in the Solar System. Each colour denotes a different host planet. The dashed horizontal red line marks the orbital stability threshold above which ring particles are likely to remain gravitationally bound. |
 |
Fig. 3 Orbital characteristic evolution of the moons within the Saturn system over a span of 1 Myr. The three horizontal panels display from top to bottom the evolution of the semi-major axis (a), eccentricity (e), and inclination (i) for each moon. |
4 Results and analysis
4.1 Satellite stability
Using the same initialisation system as delineated in the preceding section, we numerically integrated the moon systems of Earth, Jupiter, Saturn, Uranus, and Neptune. This was undertaken to ensure that in the simulations of the ring particles, the moon system behaved regularly, as anticipated from long-timescale integrations such as those presented by Kane & Li 2022, and references therein. For instance, Fig. 3 shows the orbital evolution of Saturn’s satellites, in which no significant changes in the evolution of the semi-major axes are discernible. Concurrently, the eccentricity and inclination undergo regular periodic variations in their evolution, and no secular perturbations destabilise the system within the evaluated time interval. Saturn was used as an example, but the other systems showed a similar behaviour.
4.2 Long-term stability
We simulated the orbital dynamics of mass-less individual ring particles around the Solar System moons for a duration of one million years to identify potential sources of instability that may result in considerable variations in the primary orbital elements. For the initial conditions, particles positioned at the inner and outer ring edges of the respective moon were selected as the more representative particles from the ring. We limited this simulation to only a few particles because their orbital period is relatively short and spans only a few hours. This implies that integrating over timescales such as millions of years results in high computational cost (e.g. each simulation took ~3.5 days). Therefore, our approach was to seek an optimal balance between the duration of the integration and the associated computational cost.
In Fig. 4, we present the maximum excitation of the orbital elements of the particles (δamax., δemax., and δimax.) at the end of the simulation for the inner (upper panel) and outer particles (lower panel). For all systems, at least one of these evaluated characteristics displays substantial variations in general. For instance, in the case of Iapetus, the particle shows minuscule δamax./Rs and δemax. (about 10−5 to 10−4) but a significant secular excitation in its inclination with δi ~ 30° for both particles, suggesting that the observed change in inclination is the result of a dynamical behaviour that is shared among the ring particles. Finally, Triton and Io exhibit the most significant changes of the evaluated systems. Here, their semi-major axis and eccentricity display erratic and irregular behaviour (see Fig. 5). The nature of the instabilities observed might be linked to the relation between the Roche limit and the Hill radius (see Fig. 2), as well as the gravitational stress exerted by the surroundings in the cases of Io and Enceladus. In the case of Triton, these instabilities might be attributed to its retrograde translation, considering that the simulation only included the gravitational effects of the distant and relatively minor moon Proteus, as well as the planet itself.
Table 1 summarises the behaviour of the inner- and outermost particles in the ring system, corresponding to each satellite evaluated in our simulations, based on a visual analysis of the orbital elements associated to each moon. The behaviours of each orbital parameter for these orbits can be categorised into one of two distinct types. Periodic or regular orbits (R) are characterised by their repetitive nature. They recur over fixed intervals of time (see the left panels of Fig. 5). On the other hand, irregular orbits (I) denote a state of unpredictability, perturbed by the gravitational influence of other objects within the system, such as the parent planet or moons (see the right panels of Fig. 5).
 |
Fig. 4 Long-term orbital variations of ring particles around the moons over a span of 1 Myr. Upper panel summarises δa, δβ, and δi (colour bar) for an isolated inner particle, while the lower panel represents an outer particle orbiting the moons. The missing label for Enceladus in the lower panel indicates that the orbit was unbound. |
 |
Fig. 5 Orbital elements as a function of time for particles orbiting Iapetus (left panels) and Triton (right panels). Iapetus and Triton are the most extreme cases observed in the upper panel of Fig. 4. The horizontal blue line represents the initial inclination (i0) of the particles. |
Long-term stability of ring particles.
4.3 MEGNO
The computational technique Mean Exponential Growth factor of Nearby Orbits (MEGNO, Cincotta & Simó 2000) is used to distinguish between a regular and a chaotic behaviour within a dynamical system. Its functionality relies on examining the exponential divergence or convergence of trajectories in phase space over time. In the context of this study, MEGNO was employed to assess the long-term stability of trajectories within the system. The MEGNO value approaches 2 for regular orbits, and for chaotic orbits, it yields higher average values, thus providing insights into the dynamical stability of the ring system. We calculated the MEGNO values for 100 constituent particles of the rings, integrating their equation of motion over a period of 1ky years. The constraints on the time span and the number of particles were chosen to strike a balance between the accuracy of the mean results and computational cost. This approach was particularly necessary because, as detailed below, each individual moon required 100 independent simulations for five or more bodies (planet and moons) over the defined simulation time.
It should be emphasised that MEGNO evaluates the overall stability of the system. For example, the MEGNO value deviates from 2 for the entire system when even a single particle within the ring becomes unstable, which can create an illusion of irregularity. The need to evaluate this parameter for each individual particle within the ring led to the following sequence of steps. Firstly, we established the arrangement of the planets, moons, and rings according to Sec. 3. Then, we selected a ring particle, allowed the system to evolve over a predetermined period of time, and computed the relevant parameter. We recalculated the orbit using another particle with a different set of parameters until all the particles in the ring were covered. This method not only verified our numerical parameters, but also provided a comprehensive understanding of the temporal progress of these ring systems. A summary of the implementation of this approach, using the REBOUND software, is depicted in Fig. 6.
In this regard, the prevalence of MEGNO values near 2 suggests the existence of relatively stable orbits, indicating a coherent and predictable motion for a significant portion of particles. In contrast, striking spikes in the MEGNO values indicate localised instability and indicate the potential for chaotic behaviour in these regions. Fig. 6 substantially corroborates the instability of the rings around the satellites Mimas, Miranda, and Proteus. This result indicates that only a few sharp ringlets could orbit Mimas and Proteus. The MENGO analysis for Enceladus and Io reveals instability in the outermost regions of their orbiting rings, thus constraining their width. MEGNO suggests that the remaining moons might be stable over the evaluated period. However, a more comprehensive understanding of the structural dynamics of these systems can be achieved only by analysing the behaviour of semi-major axes, eccentricities, and inclinations (see Sec. 4.5).
It is worth noting that the application of the MEGNO technique as described in this study does not consider any interactions between ring particles. These interactions were not studied in this work, but may add either instability or stability. They are discussed below.
 |
Fig. 6 Orbital stability within the ring systems of selected satellites. The horizontal axis represents the initial semi-major axis a0,s in satellite radii Rs of the particles in the rings, and the vertical axis lists the various satellites. The MEGNO (Y) parameter values for each particle are depicted by the colour scale, with shades varying according to the detected degree of orbital stability. |
4.4 Effect of the neighbourhood
Sucerquia et al. (2022) examined the dynamics of rings encircling isolated moons. This scenario applies for Earth, but not for other planets in the Solar System, where moons are typically accompanied by other objects of comparable sizes. The perturbations of these bodies can significantly influence the evolution of ring systems.
This highlights the importance of studying the impact of environmental conditions on ring systems. To do this, we undertook dynamic experiments using the complete assembly of ring particles to assess and compare the collective behaviour of the system under two distinct conditions. The first scenario assumed the ring system to be fully isolated from perturbations triggered by neighbouring satellites, whereas the second scenario considered the ring system to be situated within the gravitational field of these satellites. Both scenarios were examined over a period of 1 kyr and included the host planet.
As our study case, we chose Europa as the primary ringed satellite and devised two contrasting test scenarios. The isolated scenario referred to the Jupiter-Europa system alone, and the integrated, scenario also incorporated its sibling moons Io, Ganymede, and Callisto. For this experiment, the rings did not lie on the orbital plane of the moon to enhance the perturbation effects.
Fig. 7 depicts the outcome of the system evolution. It clearly illustrates the effects of the environment on the orbital evolution of particles. In the top panel (isolated), the absence of resonant interactions in Europa’s complex ring system leads to a lack of structure in specific regions, maintaining a more uniform morphology of the ring particles over time. In contrast, the bottom panel (integrated) shows that these resonant interactions generate noticeable structures that alter the morphology of the rings. The colour of the dots in the figure indicates changes in particle eccentricity, which are more intense in the integrated case and mostly affect the outer ring particles. These perturbations may lead to the loss of particles through collisions and further constrain the size of the ring and even its lifespan. However, a detailed investigation of this phenomenon is beyond the scope of this study, as is analysing the effects of companion moons on these hypothetical rings individually: it is virtually impossible to isolate these moons. In the following sections, we present the results we obtained for the remaining moons.
 |
Fig. 7 Comparison of the orbital elements δi and δe in the ring particles of Europa as a function of their initial semi-major axis a0,s with (integrated) and without (isolated) other Galilean satellites. This comparison reveals that these satellites influence the distribution and behaviour of the particles. |
4.5 Evolution of the ring morphology
Studying the dynamics of particles within a ring system can lead to a better understanding of the gravitational environment that encompasses the system and might reveal regions in which the influence of nearby celestial bodies is either more or less prominent. This can help us understand the complex gravitational interactions within the system. Furthermore, this knowledge might offer insights into phenomena such as gravitational resonances, which play a pivotal role in shaping the system morphology. An illustrative example are the Kirkwood gaps in the main asteroid belt. They are primarily caused by orbital resonances with Jupiter. An orbital resonance occurs when two orbiting bodies, in this case, an asteroid and Jupiter, exert a periodic gravitational influence on each other because their orbital periods are in a simple ratio (e.g., 2:1 or 3:2). For a moon with numerous sources of perturbation, such as its sibling moons, it is feasible that these features may emerge and persist. These perturbations can have a pronounced effect on the ring and might even lead to its dispersal or to the confinement of its edges.
In the pursuit of identifying morphological structures within the rings, we adopted two approaches. Firstly, we analysed the orbital widening of the test particles that comprise them. Secondly, we examined the rings as a whole, assessing the emergence of substructures within them. For the first approach, we defined the maximum orbital width of each particle, Δr,p, as the difference between the maximum apoapsis, Qi,max, and the minimum periapsis, qi,min, of each particle throughout the total integration time, as expressed in the following equation:
![$\[\Delta_{\mathrm{r}, \mathrm{p}}=Q_{\mathrm{i}, \max }-q_{\mathrm{i}, \min }.\]$](/articles/aa/full_html/2024/11/aa49453-24/aa49453-24-eq3.png) (3)
(3)
This indicator reflects how a particle orbit expands or contracts during its interaction with the environment. Consequently, substantial variations in Δr,p (measured in units of Δr, the initial ring width) might lead to collisions between particles. These collisions might in turn accelerate the decay of their orbits, contribute to the formation of moonlets (see e.g. Crida & Charnoz 2012; Ćuk et al. 2020), or result in the loss of particles in specific regions. The results are summarised in Fig. 8.
According to this figure, Mimas, Miranda, and Proteus undergo significant changes in this parameter, thus aligning with the results obtained from evaluating the MEGNO parameter (Fig. 6). There is also a noticeable orbital widening of the particles in the rings of Io, Europa, Enceladus, Dione, Ariel, and Umbriel, which, as shown in Fig. 2, are situated in the uppermost positions close to the region of orbital instability. Furthermore, the presence of narrow regions in the rings of the Moon, Callisto, and Titan, where the orbital width is high, suggests the emergence of gaps due to resonant interactions with the environment.
We also inspected morphological structures in the rings through variations in the semi-major axis, eccentricity, and inclination of the particles. Figs. 9 and 10 illustrates the collective evolution of CSRs, which are organised to show the least dispersed data at the top and the most dispersed at the bottom, with respect to their eccentricity. In Fig. 9, the excitation of particle eccentricity relative to their initial semi-major axis is shown. Generally, it is noticeable that there are three modes in the data dispersion: firstly, rings whose dispersion is minimal, such as in the case of Iapetus; secondly, those whose orbits closest to the satellite experience greater excitation, as with the rings of Oberon and Triton; and thirdly, those where the outer regions are the most disturbed, as in the remaining cases we studied. However, it is important to mention that the rings of the Moon, Ganymede, and Oberon exhibit δi < 0.01, suggesting a general stability of the rings.
Figs. 9 and 10 also show that certain moons display evident perturbation patterns that can be seen as peaks in the data. This is the case for Callisto, Titan, the Moon, Titania, and Ganymede, suggesting regions of instability in the ring in which particles could collide with each other, decay, and/or form gaps. These gaps would be located in different regions of the rings: in the inner part for Titania and Ganymede, in the central part for Callisto and Titan, and in the outermost region of the Moon’s rings.
For Io and Enceladus, about 50% of the ring particles vanished within just a decade. This significant loss can be attributed to factors such as close encounters with the moon that lead to ejections or collisions, and the influence of Jupiter’s strong gravitational field, amplified by the perturbations from its other moons. For both moons, these patterns of particle dispersion were observed over simulation periods of 33 and 11 years, respectively.
Fig. 10 illustrates the maximum excitation of the inclination for each satellite ring system, and they are presented in the same order as in the left panel. In general, the excitations in inclination are relatively low, except for Io, where δi ~ 2.5°, and Enceladus, whose values reach 28° for the surviving particles. For the remaining rings, these variations are less than 1.5 degrees on average, and the rings of Iapetus are affected most.
Additionally, several of the structures exhibit a wave-like behaviour (e.g. Iapetus, Callisto, Titan, Oberon, and Triton), which could be interpreted as density waves traversing the rings. However, these patterns may be damped by the mutual gravitational interactions between particles with mass, which are not considered in this work (e.g. Lehmann et al. 2019). In contrast, other structures, regardless of the scale, appear quite flat (e.g. Titania, Rhea, Dione, Ariel, and others), with slight dispersion in the inclinations that mostly do not exceed one hundredth of a degree. Ganymede, Europa, and Umbriel show areas in which particles experience great excitation in their inclination compared to their companions. For example, the triple peak shown by Ganymede does not have the same location as the eccentricity peak in the respective figure in the left panel, so that the rings of this moon could be very rich in substructures. The other moons showed a flatter behaviour and did not exhibit major features in the studied orbital elements.
Moons such as Io, Callisto, Dione, Rhea, Ariel, Oberon, and Titania display a discernible relation between inclination variations and the initial semi-major axis a0,s. Specifically, within Io, δi appears to be more pronounced for particles that are positioned at greater distances. Conversely, for Callisto and Titania, the inclination variation decreases with their proximity to the moon. Hence, both Io and Enceladus might retain ringlets in closer orbits, but additional factors (radiation, magnetic fields, or higher-order gravitational effects) might challenge their stability.
Iapetus exhibits a constrained dispersion, primarily at low δe values, implying very little eccentricity perturbation for particles in its vicinity. The plot scale underlines the subtle nature of these eccentricity shifts. It suggests that particles around Iapetus exist in a relatively stable environment in which rings could thrive over extended timescales, despite its slight variation in inclination of about 1.5°.
Significant inclination variations of particles are evident in specific scenarios. The case of Iapetus stands out. Positioned approximately 60 planetary radii from Saturn, with Titan, its nearest neighbour, 20 planetary radii away, Iapetus could be perceived as relatively isolated. In spite of this, the Iapetus ring system shows non-negligible inclination changes, while the eccentricity variations remain trivial. These unique excitations may be linked to the marked inclinations of Iapetus to multiple reference planes: 17.28° relative to the ecliptic, 15.47° to Saturn’s equator, and 8.13° towards the Laplace plane6. These prominent inclinations might induce the activation of ν-type secular resonances in inclination, which involve interactions between the precession frequencies of orbital nodes or pericenters and can potentially alter the trajectories of ring particles. A detailed analysis of these ν-type resonances and their impact on ring particles will be the subject of future work. Moreover, as discussed in Sect. 4.4, we found that the eccentricity peaks appear when only the planet is included in the simulations, that is, without the influence of sibling moons. On the other hand, the inclusion of nearby massive satellites generates the wavy pattern in inclination. This parameter is not significantly affected by the planet alone.
In the case of the Earth’s Moon, the peaks in its rings are caused by the Earth itself. Experiments with or without the Sun showed no significant changes in the ring system, indicating that the Sun’s dynamic influence is negligible due to its distance and the extent of the ring.
Finally, a summary of the experiments and their outcomes is presented in Table 2. Notably, these results align perfectly with Fig. 2, demonstrating that the particles most affected by their environment are located at the top of the graph, while the most stable particles are at the bottom.
 |
Fig. 8 Orbital behaviour of particles within the ring systems of the investigated satellites. The horizontal axis signifies the initial semimajor axis a0 in terms of the satellite radii R0 for each constituent particle of the ring. The colour map illustrates the corresponding maximum orbital widening Δrp of each ring particle, expressed as a fraction of the initial ring width, upon the completion of the simulations. |
 |
Fig. 9 Numerical simulation outcomes for rings around moons. δe and δi represent the maximum amplitude of the excitation of the ring particle eccentricity and tilt, respectively. |
 |
Fig. 10 Numerical simulation outcomes for rings around moons. δe and δi represent the maximum amplitude of the excitation of the ring particle eccentricity and tilt, respectively. N denotes the number of surviving particles after a simulation time of tend. |
5 Discussion and conclusions
We explored the complexities of the dynamics and evolution of hypothetical CSRs within the Solar System. To achieve this, we selected the most representative moons in the Solar System based on their mass and size. These moons were equipped with rings that were positioned within their orbital planes. The ring particles were treated as test particles and were randomly distributed using blue-noise generation techniques (Sec. 3). All particles were initialised at the same time, and different strategies were implemented to determine the fate of these rings. This involved evaluating the orbital stability of the moons alone (without rings, see Sec. 4.1), integrating representative ring particles (the innermost and outermost) for one million years (Sec. 4.2), analysing the MEGNO parameter for each particle (Sec. 4.3), observing the broadening of the orbital domains for each particle (orbital widening), studying the effect of the gravitational environment on the rings, and investigating the morphological evolution of the whole system (Sects. 4.4 and 4.5).
As a result of these analyses, we found that CSRs can demonstrate stability around most of the Solar System moons within the time frame evaluated. However, it is worth noting that moons such as Mimas, Miranda, and Proteus are less likely to have sustained these structures over long periods of time. We also observed that the constituent particles forming the rings of Io, Europa, Enceladus, Ariel, and Umbriel are prone to significant orbital excitation, making the particle system susceptible to collisions and subsequent fading. In addition, resonance patterns were identified within the rings, suggesting the possible prevalence of structures such as gaps and other phenomena.
The absence of rings around moons is particularly intriguing because astrophysical mechanisms exist that might facilitate their formation. Unfortunately, the processes of ring formation around planets have not yet been directly observed, but the mechanisms underlying their formation have been seen in action. An important event in this respect was the collision of comet Shoemaker-Levy 9 with Jupiter, which occurred after its fragmentation by the tidal forces of the gas giant (see e.g. Zahnle & Mac Low 1994). If the comet had hit Jupiter under different impact parameters, it is highly likely that it would have dispersed some or all of its constituent material around the planet (see e.g. Hyodo & Charnoz 2017). Among other mechanisms, the most significant for forming rings around moons would be the grazing collisions of asteroids or comets with these moons, and the continuous emission of particles through cryovolcanic activity.
It is tempting to explain the absence of CSRs by invoking the complexity of the gravitational environment in which moons are immersed. In this environment, the gravitational field intensity undergoes significant variations over time, imprinting a chaotic behaviour on particles that would ultimately destabilise the entire ring system. This was the hypothesis we tested in this work. However, we know that circumplanetary rings (CPRs) are structures with unique and complex origins and rapid evolution.
Currently, there is no consensus on the lifespan of CPRs as they are immersed in highly dynamic environments in which their durability is influenced by various factors, including particle size, composition, interactions with electric and magnetic fields or solar wind particles, and orbital decay (e.g. Durisen & Estrada 2023). The last scenario has been studied by Sucerquia et al. (2022) for constituent particles in CSRs. The authors found that these rings can be relatively durable at low inclinations, that is, when the rings are face-on with respect to the star. Nevertheless, dusty CPRs are thought to be sustained by the continuous replenishment of dust particles. For instance, interplanetary dust can be captured by the planetary gravity and added to the ring (Colwell & Horányi 1996; Colwell et al. 1998). Additionally, impact ejecta from circumplanetary objects such as moons can also contribute to the continuous replenishment of dust particles (Burns et al. 1999; Krüger et al. 1999, 2000; Krivov et al. 2002). In the case of CSRs, cryovolcanism could be the source that replenished ring particles for their own rings.
The existence of CSRs has long been discussed. In 2005, the Cassini mission inferred the existence of a ring around Rhea, Saturn’s second-largest moon, by observing changes in the flow of electrons trapped by Saturn’s magnetic field during its proximity to the moon. This anomaly was attributed to a faint ring or cloud of particles around Rhea, which cause electron absorption (Kerr 2008). However, later data from the same mission failed to confirm these rings (Tiscareno et al. 2010). Additionally, Iapetus, another of Saturn’s large moons, features the Iapetus ridge, a unique geological formation extending to 75% of the satellite circumference and reaching up to 20 km in height. Various hypotheses have been proposed for its formation, including endogenous causes such as high rotation and exogenous causes such as material deposition from a former massive ring. A consensus on its origin remains elusive.
An endogenous factor potentially causing CSR instability is the strongly prolate shape of some satellites, such as Rhea (see Fig. A.1). This raises questions about whether the gravitational field of a non-spherical object could sustain a ring system. Lehébel & Tiscareno (2015) demonstrated that Rhea’s gravitational potential allows stable rings only within the equatorial plane, restricting the parameters for long-term stability. Our simulations suggest that Rhea’s rings could have short excursions (~ 0.3°) on their inclinations, favouring Rhea potential to host CSRs. However, the referenced study does not account for the influence of nearby moons. Our findings demonstrate that the impact of these moons on the rings is minimal, thus motivating further investigations that incorporate both gravitational effects.
Our simulations revealed that of the satellites we considered, Iapetus has the most stable ring structures. This supports the hypothesis that its prominent equatorial ridge might have originated from the collapse of a dense ring system onto its surface. It is crucial to note that because of the significant orbital inclination of Iapetus (see Sec. 4.5), the dynamics of its rings could be markedly influenced by electromagnetic phenomena in addition to gravitational fields. This inclination causes Iapetus to traverse various regions of Saturn’s magnetosphere during its orbit, resulting in a complex interaction between charged particles and the changing magnetic field. However, the extent of the planetary orbit partially mitigates this effect, as evidenced by the considerable Hill radius of the satellite, as illustrated in Fig. 1. Consequently, the past existence of sub-moons (a moon of a moon; Kollmeier & Raymond 2019) becomes a plausible scenario, which could explain the formation of the Iapetus ridge as a result of the collapse and fragmentation of a submoon at its Roche limit, followed by subsequent decay due to non-gravitational phenomena.
Additionally, we highlight the dynamic interactions within Jupiter’s magnetosphere, particularly concerning its Galilean satellites. Jupiter’s extensive magnetic field, encompassing its ring system and the orbits of its four Galilean moons, plays a dynamic role in the interactions within its magnetosphere. These moons, situated near the magnetic equator, serve both as sources and sinks of magnetospheric plasma. Energetic particles, synchronized with Jupiter’s rotation and moving at higher speeds than the moons, orbits, collide with their surfaces, causing sputtering and chemical changes via radiolysis (Johnson et al. 2004). This interaction leads to wear and drag on the surfaces and could similarly affect potential low-mass ring particles around the moons, influencing their orbital stability and accelerating decay and erosion processes. These phenomena, which might also occur in other moon systems within the Solar System, add complexity to these hypothetical celestial bodies.
In the specific case of Io, Jupiter’s corotational plasma plays a vital role in considering the potential instability of its hypothetical rings. The velocity of this plasma, synchronized with Jupiter’s rotation, ranges from a few km/s to high-energy tails of approximately 30–100 km/s (Wilson et al. 2002). Since Jupiter’s rotation period exceeds Io’s Keplerian velocity, the corotating plasma impacts Io with high-energy ions, potentially inducing instability in any rings Io might possess. This interaction emphasises that we need to understand ejected particle dynamics, atmospheric sputtering, and charge exchange. It also suggests a mechanism for the blurring or dispersion of planetary rings not only in Jupiter, but in other satellite systems with similar magnetic and orbital configurations. This highlights the intricate relation between magnetic fields, orbital dynamics, and ring stability, with broader implications for our understanding of the ring systems in our Solar System and beyond.
We did not investigate in depth why the particles in the hypothetical ring of Triton, despite the large mass of the moon, exhibit one of the highest eccentricity and inclination excursion. As pointed out in Sec. 4.2, this is the only regular moon in our sample on a retrograde orbit, and we speculate that this might be one of the main reasons for these instabilities. A more detailed theoretical investigation of the case of Triton and proper numerical simulations might confirm our hypothesis or reveal other reasons. However, since our preliminary results here reveal that the probability of a ring around this moon is very low, we did not consider this particular case in more detail.
We studied the dynamics and evolution of hypothetical circumsatellital rings (CSRs) within the Solar System using a representative selection of moons based on their bulk properties. While we have advanced our understanding of these intricate systems, unanswered questions and areas for future investigation remain, for instance, whether the orbital and surface features of Rhea and Iapetus are a byproduct of a decaying CSR. This work supports this scenario. However, including the effects of planet and moon deformities, particle interaction with magnetic fields, and radiative effects is paramount to clarifying the nuances of CSR dynamics. A continued exploration of these systems will not only enrich our understanding of satellite evolution within our own Solar System, but also offer valuable insights into the dynamical interactions between rings and moons, the understanding of which can help us identify these characteristics in distant planetary systems (Zuluaga et al. 2022; Veenstra et al. 2024).
Summary of the results of the simulations.
Data availability
The data underlying this article was stored in the SimulationArchive format (Rein & Tamayo 2017) to ensure full reproducibility, and it will be shared on reasonable request to the corresponding author.
Acknowledgements
MS acknowledges support from ANID (Agencia Nacional de Investigación y Desarrollo) through FONDECYT postdoctoral 3210605. MS, JC & MM thank ANID – Millennium Science Initiative programme – NCN19_171. MM acknowledges financial support from FONDECYT Regular 1241818. This project received funding from the European Research Council (ERC) under the European Union Horizon Europe programme (grant agreement No. 101042275, project Stellar-MADE). This research has made use of NASA’s Astrophysics Data System Bibliographic Services, a modified A&A bibliography style file for the preprint version of the article (https://github.com/yangcht/AA-bibstyle-with-hyperlink).
Appendix A Orbital and physical parameters
 |
Fig. A.1 Triaxial dimensions of moons with masses greater than 1019 kg. The bars represent the principal axes a, b, and c for each moon, showcasing their deviation from a perfect sphere. |
Tab. A.1 and Fig. A.1 summarise the physical and orbital parameters of the satellites used in this work. The initial conditions for the planets and moons presented in Tab. A.1 were generated using the ephemeris service of NASA’s Horizons programme (https://ssd.jpl.nasa.gov/horizons/app.html#/), while the physical parameters of Fig. A.1 were obtained from the “Physical Data for Solar System Planets and Satellites” compiled by Wm. Robert Johnston, available at https://www.johnstonsarchive.net/astro/solar_system_phys_data.html.
Physical and orbital properties of the moons and planets used in the simulations.
References
- Bérard, D., Sicardy, B., Camargo, J. I. B., et al. 2017, AJ, 154, 144 [CrossRef] [Google Scholar]
- Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2014, Nature, 508, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A., Showalter, M. R., Hamilton, D. P., et al. 1999, Science, 284, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A., Simonelli, D. P., Showalter, M. R., et al. 2004, in Jupiter. The Planet, Satellites and Magnetosphere, 1, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon, 241 [Google Scholar]
- Charnoz, S., Salmon, J., & Crida, A. 2010, Nature, 465, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Charnoz, S., Canup, R. M., Crida, A., & Dones, L. 2018, in Planetary Ring Systems. Properties, Structure, and Evolution, ed. M. S. Tiscareno, & C. D. Murray, 517 [CrossRef] [Google Scholar]
- Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colwell, J. E., & Horányi, M. 1996, J. Geophys. Res., 101, 2169 [NASA ADS] [CrossRef] [Google Scholar]
- Colwell, J. E., Horanyi, M., & Gren, E. 1998, Science, 280, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., & Charnoz, S. 2012, Science, 338, 1196 [Google Scholar]
- Ćuk, M., Minton, D. A., Pouplin, J. L. L., & Wishard, C. 2020, ApJ, 896, L28 [CrossRef] [Google Scholar]
- De Pater, I., Renner, S., Showalter, M. R., & Sicardy, B. 2018, in Planetary Ring Systems. Properties, Structure, and Evolution, ed. M. S. Tiscareno, & C. D. Murray, 112 [CrossRef] [Google Scholar]
- Domingos, R. C., Winter, O. C., & Yokoyama, T. 2006, MNRAS, 373, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Durisen, R. H., & Estrada, P. R. 2023, Icarus, 400, 115221 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, L. W. 2002, Rep. Progr. Phys., 65, 1741 [CrossRef] [Google Scholar]
- Esposito, L. W., & Colwell, J. E. 1989, Nature, 339, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Geissler, P. 2015, in The Encyclopedia of Volcanoes, 2nd edn., ed. H. Sigurdsson (Amsterdam: Academic Press), 763 [CrossRef] [Google Scholar]
- Goldreich, P., & Porco, C. C. 1987, AJ, 93, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. A. 2016, Moons of the Solar System: From Giant Ganymede to Dainty Dactyl [CrossRef] [Google Scholar]
- Hartquist, T. W., Havnes, O., & Morfill, G. E. 2003, Astron. Geophys., 44, 5.26 [NASA ADS] [CrossRef] [Google Scholar]
- Hyodo, R., & Charnoz, S. 2017, AJ, 154, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Hyodo, R., & Ohtsuki, K. 2015, Nat. Geosci., 8, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Carlson, R. W., Cooper, J. F., et al. 2004, in Jupiter. The Planet, Satellites and Magnetosphere, 1, eds. F. Bagenal, T. E. Dowling, & W. B. McKinnon, 485 [Google Scholar]
- Kane, S. R., & Li, Z. 2022, Planet. Sci. J., 3, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, R. A. 2008, Science, 319, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Kirchoff, M. R., & Schenk, P. 2010, Icarus, 206, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Kollmeier, J. A., & Raymond, S. N. 2019, MNRAS, 483, L80 [CrossRef] [Google Scholar]
- Krivov, A. V., Krüger, H., Grün, E., Thiessenhusen, K.-U., & Hamilton, D. P. 2002, J. Geophys. Res. (Planets), 107, 5002 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, H., Krivov, A. V., Hamilton, D. P., & Grün, E. 1999, Nature, 399, 558 [CrossRef] [Google Scholar]
- Krüger, H., Krivov, A. V., & Grün, E. 2000, Planet. Space Sci., 48, 1457 [CrossRef] [Google Scholar]
- Lauer, T. R., Throop, H. B., Showalter, M. R., et al. 2018, Icarus, 301, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Lehébel, A., & Tiscareno, M. S. 2015, A&A, 576, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehmann, M., Schmidt, J., & Salo, H. 2019, A&A, 623, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morgado, B. E., Sicardy, B., Braga-Ribas, F., et al. 2023, Nature, 614, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Duffard, R., Pinilla-Alonso, N., et al. 2015, A&A, 576, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ortiz, J. L., Santos-Sanz, P., Sicardy, B., et al. 2017, Nature, 550, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., & Goldreich, P. 1987, AJ, 93, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Tamayo, D. 2015, MNRAS, 452, 376 [Google Scholar]
- Rein, H., & Tamayo, D. 2017, MNRAS, 467, 2377 [NASA ADS] [Google Scholar]
- Rickman, H., Wiśniowski, T., Gabryszewski, R., et al. 2017, A&A, 598, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sicardy, B., El Moutamid, M., Quillen, A. C., et al. 2018, Rings beyond the giant planets, eds. M. S. Tiscareno, & C. D. Murray (Cambridge University Press), 517 [Google Scholar]
- Sicardy, B., Morgado, B., Braga-Ribas, F., et al. 2022, in European Planetary Science Congress, EPSC2022-82 [Google Scholar]
- Spahn, F., Schmidt, J., Albers, N., et al. 2006, Science, 311, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Sucerquia, M., Alvarado-Montes, J. A., Zuluaga, J. I., Cuello, N., & Giuppone, C. 2019, MNRAS, 489, 2313 [NASA ADS] [CrossRef] [Google Scholar]
- Sucerquia, M., Ramírez, V., Alvarado-Montes, J. A., & Zuluaga, J. I. 2020, MNRAS, 492, 3499 [NASA ADS] [CrossRef] [Google Scholar]
- Sucerquia, M., Alvarado-Montes, J. A., Bayo, A., et al. 2022, MNRAS, 512, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Tiscareno, M. S. 2013, in Planets, Stars and Stellar Systems. Volume 3: Solar and Stellar Planetary Systems, eds. T. D. Oswalt, L. M. French, & P. Kalas, 309 [CrossRef] [Google Scholar]
- Tiscareno, M. S., & Murray, C. D. 2018, Planetary Ring Systems. Properties, Structure, and Evolution [CrossRef] [Google Scholar]
- Tiscareno, M. S., Burns, J. A., Cuzzi, J. N., & Hedman, M. M. 2010, Geophys. Res. Lett., 37, L14205 [NASA ADS] [CrossRef] [Google Scholar]
- Vaillant, T., & Correia, A. C. M. 2022, A&A, 657, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veenstra, A. K., Zuluaga, J. I., Alvarado-Montes, J. A., Sucerquia, M., & Stam, D. M. 2024, A&A, submitted [arXiv:2404.16606] [Google Scholar]
- Vogel, H. 1979, Math. Biosci., 44, 179 [CrossRef] [Google Scholar]
- Wilson, J. K., Mendillo, M., Baumgardner, J., et al. 2002, Icarus, 157, 476 [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [Google Scholar]
- Wood, J., Horner, J., Hinse, T. C., & Marsden, S. C. 2017, AJ, 153, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K., & Mac Low, M.-M. 1994, Icarus, 108, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zahnle, K., Schenk, P., Levison, H., & Dones, L. 2003, Icarus, 163, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Zuluaga, J. I., Sucerquia, M., & Alvarado-Montes, J. A. 2022, Astron. Comput., 40, 100623 [NASA ADS] [CrossRef] [Google Scholar]
For updates, see https://ssd.jpl.nasa.gov/
All Tables
Physical and orbital properties of the moons and planets used in the simulations.
All Figures
 |
Fig. 1 Moon mass vs. moon semi-major axis for our sample of large moons around giant planets (two upper panels) and ice giants (two lower panels). The x-axis of each panel is normalised with respect to the radius of each host planet. The radius of the filled circles represents the moon size, and the shaded area around them shows the size of the ring system (as defined in Sec. 3). The moon and ring sizes are scaled using Titan as a standard size. The colour bar represents the lunar density. |
| In the text | |
 |
Fig. 2 Ratio of the gravitational domain (Hill radius) and the theoretical ring size (Roche limit) for our sample of large moons in the Solar System. Each colour denotes a different host planet. The dashed horizontal red line marks the orbital stability threshold above which ring particles are likely to remain gravitationally bound. |
| In the text | |
 |
Fig. 3 Orbital characteristic evolution of the moons within the Saturn system over a span of 1 Myr. The three horizontal panels display from top to bottom the evolution of the semi-major axis (a), eccentricity (e), and inclination (i) for each moon. |
| In the text | |
 |
Fig. 4 Long-term orbital variations of ring particles around the moons over a span of 1 Myr. Upper panel summarises δa, δβ, and δi (colour bar) for an isolated inner particle, while the lower panel represents an outer particle orbiting the moons. The missing label for Enceladus in the lower panel indicates that the orbit was unbound. |
| In the text | |
 |
Fig. 5 Orbital elements as a function of time for particles orbiting Iapetus (left panels) and Triton (right panels). Iapetus and Triton are the most extreme cases observed in the upper panel of Fig. 4. The horizontal blue line represents the initial inclination (i0) of the particles. |
| In the text | |
 |
Fig. 6 Orbital stability within the ring systems of selected satellites. The horizontal axis represents the initial semi-major axis a0,s in satellite radii Rs of the particles in the rings, and the vertical axis lists the various satellites. The MEGNO (Y) parameter values for each particle are depicted by the colour scale, with shades varying according to the detected degree of orbital stability. |
| In the text | |
 |
Fig. 7 Comparison of the orbital elements δi and δe in the ring particles of Europa as a function of their initial semi-major axis a0,s with (integrated) and without (isolated) other Galilean satellites. This comparison reveals that these satellites influence the distribution and behaviour of the particles. |
| In the text | |
 |
Fig. 8 Orbital behaviour of particles within the ring systems of the investigated satellites. The horizontal axis signifies the initial semimajor axis a0 in terms of the satellite radii R0 for each constituent particle of the ring. The colour map illustrates the corresponding maximum orbital widening Δrp of each ring particle, expressed as a fraction of the initial ring width, upon the completion of the simulations. |
| In the text | |
 |
Fig. 9 Numerical simulation outcomes for rings around moons. δe and δi represent the maximum amplitude of the excitation of the ring particle eccentricity and tilt, respectively. |
| In the text | |
 |
Fig. 10 Numerical simulation outcomes for rings around moons. δe and δi represent the maximum amplitude of the excitation of the ring particle eccentricity and tilt, respectively. N denotes the number of surviving particles after a simulation time of tend. |
| In the text | |
 |
Fig. A.1 Triaxial dimensions of moons with masses greater than 1019 kg. The bars represent the principal axes a, b, and c for each moon, showcasing their deviation from a perfect sphere. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


