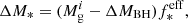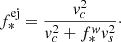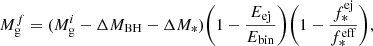| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A182 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202451481 | |
| Published online | 08 October 2024 | |
Exploring a primordial solution for early black holes detected with JWST
Kapteyn Astronomical Institute, University of Groningen, PO Box 800 9700 AV Groningen, The Netherlands
Received:
12
July
2024
Accepted:
24
August
2024
Aims. With its rest-frame optical sensitivity, the James Webb Space Telescope (JWST) has unearthed black holes as massive as 106.2−8.1 M⊙ at redshifts of z ∼ 8.5 − 10.6. In addition to these unexpectedly high masses, many systems show unexpectedly high ratios of the black hole to stellar mass of MBH/M* ≳ 30% at these early epochs. This poses a crucial challenge for theoretical models.
Methods. We collated data for all of the black holes that were confirmed with the JWST (through spectroscopy, X-rays, or high-ionization emission lines). Using analytic calculations, we explored the combination of astrophysical seeding mechanisms and Eddington accretion rates that can explain the observed objects. We then appeal to cosmological primordial black hole (PBH) seeds and show that these present an alternative path for the seeding of early structures and their baryonic contents.
Results. When we assume seeding (via astrophysical means) at a redshift of zseed = 25 and continuous accretion, all of the black holes we studied can analytically either be explained through super-Eddington accretion (at an Eddington fraction of fEdd ≲ 2.1) onto low-mass seeds (100 M⊙) or through Eddington-limited accretion onto high-mass seeds (105 M⊙). The upper limit at which we assume a primordial origin for all of these black holes yields a continuous primordial black hole mass function (between 10−5.25 and 103.75 M⊙) and a fractional PBH value ≲10−12. This agrees well with observational constraints. We then show that PBHs can seed a halo around themselves and assemble their baryonic (gas and stellar contents) starting at the redshift of matter-radiation equality (z ∼ 3400). We were able to reproduce the observed stellar and black hole masses for two of the highest-redshift black holes (UHZ1 and GHZ9 at z ∼ 10.3) with the same parameters as those that govern star formation, black hole accretion, and their feedbacks. Exploring a wide swathe of model parameter space for GHZ9, we find ratios of black hole to stellar mass between 0.1 − 1.86. This means that in some cases (of high supernova feedback), the black hole grows to be more massive than the stellar mass of its host halo. This is an attractive alternative to seeding these puzzling early systems.
Key words: galaxies: high-redshift / quasars: supermassive black holes / cosmology: theory / early Universe
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
With its unparalleled sensitivity, the James Webb Space Telescope (JWST) has been crucial in shedding light on the black hole population in the first billion years of the Universe. These black holes comprise both intrinsically faint (Harikane et al. 2023; Maiolino et al. 2024a,b; Juodžbalis et al. 2024) and heavily reddened compact sources, the so-called little red dots (LRDs; e.g. Labbé et al. 2023a,b; Furtak et al. 2023, 2024; Kokorev et al. 2023, 2024; Matthee et al. 2024; Greene et al. 2024). These early observations have given rise to a number of tantalising issues, for instance (i) clearly broadened Balmer lines have been used to infer black hole masses ranging between 107−8.6 M⊙ at redshifts z ∼ 6 − 8.5 (Kokorev et al. 2023; Harikane et al. 2023; Maiolino et al. 2024a; Furtak et al. 2024; Juodžbalis et al. 2024; Greene et al. 2024). Additionally, high-ionization lines (Maiolino et al. 2024b) and X-ray detections (Bogdán et al. 2024; Kovács et al. 2024) have been used to infer black hole masses as high as 106.2−7.9 M⊙ as early as z ∼ 10.3 − 10.6. These high masses pose a crucial challenge for theoretical models of black hole seeding and growth due to the lack of cosmic time available for their assembly (see reviews by e.g. Inayoshi et al. 2020; Fan et al. 2023). (ii) Another issue is an over-abundance of black holes in the first billion years (Harikane et al. 2023; Maiolino et al. 2024a; Greene et al. 2024); and (iii) in contrast to local relations that indicate ratios of black hole (MBH) to stellar mass (M*) of ≲0.3% for high-mass ellipticals (e.g. Volonteri & Reines 2016) or even lower than 0.01% (e.g. Suh et al. 2020), many of these early systems show unprecedentedly high ratios of MBH/M* ≳ 30% (Kokorev et al. 2023; Juodžbalis et al. 2024; Bogdán et al. 2024; Kovács et al. 2024) that deviate from local relations at the > 3-σ level (Pacucci et al. 2023). Interestingly, however, it has been shown that many of these black holes are compatible with local MBH-velocity dispersion or MBH-dynamical mass relations, suggesting that while baryons might exist in the correct number in the host haloes, they are inefficient at forming stars (e.g. Maiolino et al. 2024a).
A number of works, however, have urged caution in taking black hole and stellar masses at face value. Drawing a parallel with ultraluminous X-ray sources (ULXs), King (2024) warned that the emission from these sources could be beamed, which would severely over-estimate the inferred luminosity. They also cautioned that standard virial indicators cannot be used because the line velocity width broadening could be dominated by outflows in un-virialised broad-line regions (BLRs). Using BLR models in different accretion regimes, Lupi et al. (2024) showed that in many cases, super-Eddington accretion is preferred over the standard Shakura & Sunyaev (Shakura & Sunyaev 1973) accretion disk, yielding black hole masses that are lower by an order of magnitude than those inferred by applying standard local relations to single-epoch broad lines (from e.g. Greene & Ho 2007; Vestergaard & Osmer 2009; Reines & Volonteri 2015). The offset of the inferred high-redshift MBH − M* relation from local relations might be explained by a combination of selection biases (e.g. finite detection limits and broad-line detection requirements) and measurement uncertainties (Li et al. 2024), and only over-massive black holes may be able to outshine their hosts and make them detectable by the JWST (Volonteri et al. 2023).
Observational issues notwithstanding, these puzzles have naturally prompted a flurry of research exploring the variety of black hole seeding and growth mechanisms allowed. In terms of astrophysical black hole seeds, low-mass seeds with a mass of ∼102 M⊙ can be created by the collapse of metal-free (Population III) stars in mini-haloes at high redshifts (e.g. Carr et al. 1984; Abel et al. 2002; Bromm et al. 2002). Intermediate-mass seeds (∼ 103−4 M⊙) can form in dense, massive stellar clusters through a number of pathways (see e.g. Sect. 2.3.1, Amaro-Seoane et al. 2023), including dynamical interactions (e.g. Devecchi & Volonteri 2009), the runaway merger of stellar mass black holes (e.g. Belczynski et al. 2002), or the growth of stellar mass black holes in conjunction with mergers (e.g. Leigh et al. 2013; Alexander & Natarajan 2014). Finally, high-mass seeds, the so-called direct-collapse black holes (DCBHs; ∼ 105 M⊙), can form via supermassive star formation (e.g. Loeb & Rasio 1994; Begelman et al. 2006; Habouzit et al. 2016), although this mechanism produces fewer viable seeds (Dayal et al. 2019). Theoretical works allow a range of solutions for the existence of such massive black holes at early epochs so far, including requiring high-mass seeding mechanisms (Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024a; Natarajan et al. 2024), extremely efficient accretion, and merger-driven growth of either low-mass (Furtak et al. 2024) or intermediate-mass seeds (Dayal et al. 2024), or high-mass seeds that grow through mergers with low-mass seeds and/or efficient accretion (Bhowmick et al. 2024). High- or intermediate- to low-mass seeds subjected to episodic super-Eddington accretion phases are another option (Schneider et al. 2023; Maiolino et al. 2024b), although the sustainability and effectiveness of super-Eddington accretion remains unclear (e.g. Regan et al. 2019; Massonneau et al. 2023). It has also been postulated that the dense and dust-rich environments of LRDs, in particular, could enable rapidly spinning black holes that are maintained by prolonged mass accretion, which might result in over-massive black holes at these early epochs (Inayoshi & Ichikawa 2024). Theoretical analyses have also been used to demonstrate the need for both low- and high-mass seeding mechanisms (Fragione & Pacucci 2023), suggesting a continuum of seed masses rather than a bimodal distribution (Regan & Volonteri 2024).
However, cosmology provides an additional tantalising seeding mechanism in terms of primordial black holes (PBHs; Hawking 1971; Carr & Hawking 1974). We refer to excellent reviews (e.g. Carr 2005; Carr & Green 2024) that describe in detail how PBHs could be generated by a number of mechanisms, including collapse from scale-invariant fluctuations (or cosmic strings), by cosmological phase transitions, or by a temporary softening of the equation of state in the early Universe. We draw inspiration from a number of previous works that described that the Coulomb effect of a single black hole can generate an initial density fluctuation through the seed effect, which can grow through gravitational instability to bind (dark matter) mass around itself. This means that individual PBHs can essentially act as seeds of structure formation (Hoyle & Narlikar 1966; Ryan 1972; Carr & Rees 1984; Mack et al. 2007; Carr & Silk 2018; Carr & Kühnel 2020). These PBHs have already been used to provide solutions for dwarf galaxy anomalies (Silk 2017), act as the seeds of high-redshift massive structures and massive black holes (Mack et al. 2007; Carr & Silk 2018; Cappelluti et al. 2022; Liu & Bromm 2023), and to explain the excesses seen in the cosmic X-ray background (Ziparo et al. 2022) and radio wave background (Mittal & Kulkarni 2022).
In this work, our aim is to determine whether PBHs that assemble (isolated) haloes around themselves offer a viable pathway for generating the massive black holes detected by the JWST. We start by collating data on all of the spectroscopically confirmed black holes detected by the JWST and their physical properties in Sect. 2. Assuming a seed redshift of zseed = 25 appropriate for astrophysical origins, we explore the seed masses (low to high) and growth (Eddington limited to super-Eddington accretion) mechanisms required to explain this data. For black holes that cannot be explained by different seed masses and Eddington-limited growth mechanisms, we apply cosmology and infer the PBH masses at the epoch of matter-radiation equality (z = 3400), which are used to construct the PBH mass function. We ignore any growth of PBHs before this era because this is beyond the scope of this work. Finally, starting at z = 3400, we present an illustrative formalism of how these seeds might grow a halo around themselves, in addition to building their gas content and stellar components yielding values of MBH/M* ∼ 0.1 − 1.86, in Sect. 3.1. We discuss the role of the model free parameters in Sect. 3.2 before we conclude in Sect. 4.
We adopt a Λ cold dark matter model with dark energy, dark matter, and baryonic densities in units of the critical density as ΩΛ = 0.673, Ωm = 0.315, and Ωb = 0.049, respectively, a Hubble constant H0 = 100 h km s−1 Mpc−1 with h = 0.673, a spectral index n = 0.96, and a normalisation σ8 = 0.81 (Planck Collaboration VI 2020). Throughout this work, we use a Salpeter initial mass function (IMF; Salpeter 1955) between 0.1 − 100 M⊙ for the mass distribution of stars in a newly formed stellar population.
2. Inferring the primordial black hole mass function in light of JWST data
Analytically, the time evolution of the black hole mass, MBH(t), can be expressed as
Here, Mseed(tseed) is the seed mass at the starting time of tseed, fEdd is the Eddington fraction, G is the universal gravitational constant, mp is the proton mass, c is the speed of light, σT is the Thomson scattering cross-section, and ϵ is the radiative efficiency, for which we use a value of 0.1 throughout the work. We explored the growth of black holes assuming seeding at a redshift of zseed = 25 (corresponding to ∼134 Myr after the Big Bang) and seed masses ranging between 102−5 M⊙, and we allowed both Eddington-limited and super-Eddington accretion. With continuous accretion onto the black hole, this formalism implicitly assumes a maximal duty cycle of 100%.
We then collated data for all black holes confirmed by the JWST at z ≳ 4. As summarised in Table 1, a total of 34 such black holes were identified through broad (∼1000 − 6000 km s−1) hydrogen balmer lines, which are assumed to trace the kinematics of gas in broad-line regions (Kokorev et al. 2023; Kocevski et al. 2023; Harikane et al. 2023; Maiolino et al. 2024a; Furtak et al. 2024; Greene et al. 2024), through high-ionization lines of nitrogen and neon (Maiolino et al. 2024b), or through X-ray counterparts in deep Chandra observations (Bogdán et al. 2024; Kovács et al. 2024). These were used to infer the existence of massive black holes as large as 107.5 −108.1 M⊙ at z ≳ 8.5, only 600 million years after the Big Bang. A key caveat, however, is that these observations apply locally calibrated single-epoch relations to infer black hole masses from observed spectra/X-ray luminosities. This is driven by two key reasons: The first reason is that this provides a redshift-independent estimate of the black hole mass. The second reason is that local relations between line broadening (or X-ray emission) and the black hole mass are associated with small-scale (< parsec scale) physics and dynamics that are not expected to show any significant dependence on the redshift (although see King 2024; Lupi et al. 2024).
Black holes confirmed by the JWST at z ≳ 4.
Fig. 1 shows that continuous Eddington-limited accretion onto low-mass (100 M⊙) seeds starting at zseed = 25 is able to yield black hole masses of 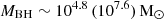 by z ∼ 10.3 (7). As a result, this model is able to explain 26 of the 34 JWST-observed black holes, leaving only 6 outliers. These comprise 2 of the z ∼ 7 massive black holes (Harikane et al. 2023; Juodžbalis et al. 2024) and all objects observed at z ≳ 8.5 (Kokorev et al. 2023; Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024b). An explanation of these last 6 outliers with low-mass seeds requires invoking continuous super-Eddington accretion with fEdd = 2.1 that allows assembling
by z ∼ 10.3 (7). As a result, this model is able to explain 26 of the 34 JWST-observed black holes, leaving only 6 outliers. These comprise 2 of the z ∼ 7 massive black holes (Harikane et al. 2023; Juodžbalis et al. 2024) and all objects observed at z ≳ 8.5 (Kokorev et al. 2023; Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024b). An explanation of these last 6 outliers with low-mass seeds requires invoking continuous super-Eddington accretion with fEdd = 2.1 that allows assembling 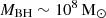 as early as z ∼ 10.3.
as early as z ∼ 10.3.
 |
Fig. 1. Growth of the black hole mass as a function of redshift (or cosmic time). Assuming seeding at a redshift of zseed = 25, we show the black hole growth considering both Eddington-limited (fEdd = 1) and super-Eddington (fEdd > 1) accretion for seed masses of 100, 104, and 105 M⊙, as marked. As detailed in Table 1 and marked in the plot, we compare these models to black holes confirmed by Bogdán et al. (2024), Furtak et al. (2024), Kocevski et al. (2023), Maiolino et al. (2024a,b), Harikane et al. (2023), Greene et al. (2024), Kokorev et al. (2023), Kovács et al. (2024), and Juodžbalis et al. (2024). |
An intermediate starting seed mass of 104 M⊙ at zseed = 25 allows us to assemble a mass of 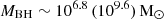 by z ∼ 10.3 (7), which encompasses all of the observed black holes, except for the two highest-redshift objects at z ≳ 10 (Bogdán et al. 2024; Kovács et al. 2024). Explaining these with such massive seeds requires invoking fEdd = 1.4. Finally, already assembling a mass of
by z ∼ 10.3 (7), which encompasses all of the observed black holes, except for the two highest-redshift objects at z ≳ 10 (Bogdán et al. 2024; Kovács et al. 2024). Explaining these with such massive seeds requires invoking fEdd = 1.4. Finally, already assembling a mass of 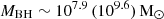 by z ∼ 10.3 (7), continuous Eddington accretion onto massive (105 M⊙) seeds is able to explain all of the current observations, precluding the need for super-Eddington accretion.
by z ∼ 10.3 (7), continuous Eddington accretion onto massive (105 M⊙) seeds is able to explain all of the current observations, precluding the need for super-Eddington accretion.
To summarise, Eddington-limited accretion onto low- and intermediate-mas seeds results in 6 and 2 outliers (out of 34 objects), respectively. Seeds that start at a high mass of 105 M⊙ at z = 25 can explain all of the current data.
We then carried out a Gedankenexperiment in which we assumed a primordial origin for black holes and calculated the PBH mass assuming that (i) all of the black holes observed by JWST to have been seeded primordially. This yields the upper limit to the JWST-motivated PBH mass function. (ii) We then assumed that only the (6) BHs that cannot be explained by Eddington accretion onto low-mass seeds are primordial, and we assumed (iii) that only the (2) BHs that cannot be explained by Eddington accretion onto intermediate-mass seeds are primordial. For each of these cases, we calculated the PBH seed mass (MPBH) by reversing Eq. (1) assuming a redshift of z = 3400. We reasonably ignored any growth of PBHs before this era of matter-radiation equality. Calculating the PBH mass function also requires a number density associated with each seed. We used the number densities quoted in the literature for this (see Table 1). These numbers were usually obtained from the luminosity function (Column 6). When several objects contributed to a given luminosity function bin, we assigned each of them the same weight in order to derive the number density per object (Column 7), which are the values used here. The PBH mass function for each of these cases is shown in Fig. 2 with the PBH seed masses for each object noted in Column 9 of Table 1.
Case (i) above yields an extended PBH mass function that range between 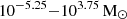 , reflecting the range of black hole masses and redshifts measured by the JWST. The mass function decreases by more than two orders of magnitude from a value of about 10−3.1 cMpc−3 at
, reflecting the range of black hole masses and redshifts measured by the JWST. The mass function decreases by more than two orders of magnitude from a value of about 10−3.1 cMpc−3 at 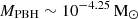 to 10−5.3 cMpc−3 at
to 10−5.3 cMpc−3 at 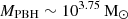 . This reflects the few outliers in terms of mass and redshift as opposed to a large number of reasonable-mass black holes detected at z ≲ 7. The massive end of the PBH mass function (for
. This reflects the few outliers in terms of mass and redshift as opposed to a large number of reasonable-mass black holes detected at z ≲ 7. The massive end of the PBH mass function (for 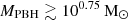 ) is completely dominated by the outliers in case (ii) above, that is, those lying above the Eddington-accretion-limited mass onto low-mass seeds. Finally, given their similar masses and redshifts, the outliers in case (iii) above yield PBHs of very similar masses, resulting in a single number density value of 10−5.3 cMpc−3 at
) is completely dominated by the outliers in case (ii) above, that is, those lying above the Eddington-accretion-limited mass onto low-mass seeds. Finally, given their similar masses and redshifts, the outliers in case (iii) above yield PBHs of very similar masses, resulting in a single number density value of 10−5.3 cMpc−3 at 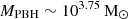 . We note that assuming super-Eddington accretion would shift the mass function towards lower masses. Conversely, decreasing the seeding redshift would shift the mass function to higher masses.
. We note that assuming super-Eddington accretion would shift the mass function towards lower masses. Conversely, decreasing the seeding redshift would shift the mass function to higher masses.
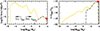 |
Fig. 2. PBH mass function as a function of the primordial black hole mass (left panel) and the fraction of dark matter composed of these objects (right panel). In both panels, these estimates are obtained assuming Eddington-limited accretion onto all black holes observed by the JWST (solid line; upper limit) and for those that cannot be explained by Eddington-limited accretion onto low-mass seeds (dashed line) and intermediate-mass seeds (point). As shown by arrows in the left panel, super-Eddington accretion would shift the mass function towards lower masses. Decreasing the seeding redshift would shift the mass function to higher masses. |
We also calculated the density parameter for PBHs as a function of their mass and converted it into the usual notation of the fraction of dark matter in the form of PBHs as f = ΩPBH/Ωm. We show these results in the right panel of Fig. 2. We find that even in the maximum scenario in which all JWST black holes are assumed to be primordial, the fractional PBH density parameter reaches ∼10−19 for 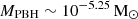 , which increases to a maximum of ∼10−12 for
, which increases to a maximum of ∼10−12 for 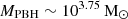 . For this mass range, observational bounds mostly come from microlensing, gravitational waves, accretion, and dynamical effects (Kavanagh 2024; Carr & Green 2024), and they typically allow values of f ≲ 10−2 − 10−3. Being ten orders of magnitude lower, our results agree with current constraints, and as expected, they show that JWST-detected black holes contribute very little to the dark matter content.
. For this mass range, observational bounds mostly come from microlensing, gravitational waves, accretion, and dynamical effects (Kavanagh 2024; Carr & Green 2024), and they typically allow values of f ≲ 10−2 − 10−3. Being ten orders of magnitude lower, our results agree with current constraints, and as expected, they show that JWST-detected black holes contribute very little to the dark matter content.
3. Primordial black holes as seeds of early galaxy assembly
We now carry out illustrative calculations to show that the PBH masses calculated for the two outliers (UHZ1 and GHZ9) in case (iii) above (requiring super-Eddington accretion onto 104 M⊙ seeds) could evolve into the systems observed by the JWST.
3.1. Theoretical model
In the seed effect, a PBH of mass MPBH at redshift zh can bind a dark matter halo mass (Mh) equal to (Carr & Silk 2018)
Here, zmreq = 3400 is the redshift of matter-radiation equality, which is when we assume that the black hole can start to assemble a halo around itself. In this formalism, at redshift z = 30, the halo mass is higher by two orders of magnitude than the black hole. Providing the dominant potential, at this point, we assume that the halo transitions grow by smoothly accreting dark matter from the intergalactic medium (IGM). We use the results from high-resolution N-body (dark matter) simulations for this, in which the average halo accretion rate evolves with redshift as (Trac et al. 2015)
We caution that this relation was derived for haloes ranging between 108−13 M⊙ at z ∼ 6 − 10. However, we assumed that this relation holds out to z ∼ 30 given the lack of numerically derived results at these early epochs and just used the average relation (without any scatter) for simplicity.
According to the spherical top-hat collapse model for halo formation, the virial temperatures of bound haloes evolve as (Barkana & Loeb 2001)
where we used a mean molecular weight value of μ = 1.22 as appropriate for neutral primordial gas, Δc = 18π2 + 82d − 39d2, where d = Ωmz − 1. Finally, Ωmz = [Ωm(1 + z)3][Ωm(1 + z)3 + ΩΛ]−1. At the high redshifts (z ≳ 6) considered in this work, Ωmz ≈ 1, that is, d = 0 and Δc = 18π2. We then modelled the response of baryons to dark matter potential wells (we refer the reader to Sect. 3.2 of the excellent review by Barkana & Loeb 2001). At z ≲ 160, the gas temperature is decoupled from that of the cosmic microwave background (CMB) and evolves as ![$ \bar{T} \approx 170[(1 + z)/100]^2\,\mathrm{K} $](/articles/aa/full_html/2024/10/aa51481-24/aa51481-24-eq45.gif) (Barkana & Loeb 2001). Furthermore, the over-density of baryons in a virialised object whose gravitational potential is driven by cold dark matter particles can be written as
(Barkana & Loeb 2001). Furthermore, the over-density of baryons in a virialised object whose gravitational potential is driven by cold dark matter particles can be written as
where ρb is the gas density, and the bar values denote background quantities. From Eqs. (4) and (5), we can calculate the minimum halo mass (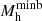 ) that can host gas with a baryonic over-density of δb = 200 at any redshift. We caution that this solution is approximate because it assumes gas to be stationary throughout the object and ignores entropy production in the virialisation shock.
) that can host gas with a baryonic over-density of δb = 200 at any redshift. We caution that this solution is approximate because it assumes gas to be stationary throughout the object and ignores entropy production in the virialisation shock.
When the assembling halo exceeded the 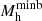 value, we allowed it to start building its gas content assuming that the assembling halo is able to drag in gas at a cosmological baryon-to-dark matter fraction, that is, the gas mass assembles at a rate of
value, we allowed it to start building its gas content assuming that the assembling halo is able to drag in gas at a cosmological baryon-to-dark matter fraction, that is, the gas mass assembles at a rate of 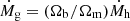 . We used a redshift step of Δz = 0.1 to obtain the total halo and gas mass that are accreted in any given redshift step (or corresponding time-step). We allowed the central black hole to grow by accreting a fraction of this gas,
. We used a redshift step of Δz = 0.1 to obtain the total halo and gas mass that are accreted in any given redshift step (or corresponding time-step). We allowed the central black hole to grow by accreting a fraction of this gas,
The black hole can therefore grow by accreting the minimum between the Eddington mass and a fraction (fBH) of the available gas mass at the start of the redshift step (Mgi).
We finally allowed star formation to take place at z = 30. The gas that was left over after black hole accretion was allowed to form stars with an efficiency that is limited by feedback from Type II supernova (SNII; exploding stars more massive than 8 M⊙), such that (see Dayal et al. 2014; Mauerhofer & Dayal 2023)
where ![$ f_{*}^{\mathrm{eff}} = \mathrm{min}[f_*^{\mathrm{ej}}, f_*] $](/articles/aa/full_html/2024/10/aa51481-24/aa51481-24-eq52.gif) is the effective star formation efficiency. Physically, this is the minimum between the star formation efficiency that produces enough SNII energy to unbind the remainder of the gas (f*ej) and a maximum star formation efficiency parameter (f*). While f* is a free parameter,
is the effective star formation efficiency. Physically, this is the minimum between the star formation efficiency that produces enough SNII energy to unbind the remainder of the gas (f*ej) and a maximum star formation efficiency parameter (f*). While f* is a free parameter, 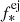 can be calculated for any halo as
can be calculated for any halo as
Here, vc is the virial velocity of the host halo, f*w is the fraction of SNII energy that couples to the gas component, and vs2 = νE51 = 611 km s−1. Here, ν = [134 M⊙]−1 is the number of SNII per stellar mass formed for our IMF, and each SNII was assumed to impart an explosion energy of E51 = 1051 erg. We assumed black hole and SNII feedback to act instantaneously on the gas component that was left after black hole accretion and star formation, leaving a final gas mass at the end of a redshift step of
where the second and third terms on the right-hand side account for black hole and SNII feedback, respectively. Here, 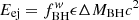 is the ejection energy provided by the accreting black hole, Ebin is the binding energy of gas in the halo (for details see Dayal et al. 2019), and
is the ejection energy provided by the accreting black hole, Ebin is the binding energy of gas in the halo (for details see Dayal et al. 2019), and 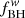 is the fraction of black hole energy that couples to gas. This final gas mass in a given redshift step was added to the accreted gas mass to form the new initial gas mass for the next redshift step. Because we assumed black hole and SNII feedback to act instantaneously, the order of star formation or black hole accretion has no impact on the results.
is the fraction of black hole energy that couples to gas. This final gas mass in a given redshift step was added to the accreted gas mass to form the new initial gas mass for the next redshift step. Because we assumed black hole and SNII feedback to act instantaneously, the order of star formation or black hole accretion has no impact on the results.
The free parameters of the model (summarised in Table 2) are: the fraction of gas that is accreted onto the black hole (fBH), the threshold star formation efficiency (f*), and the fraction of black hole and SNII energies that couple to gas (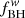 and f*w). In the interest of simplicity, in our fiducial model, we assumed extremely weak feedback and used
and f*w). In the interest of simplicity, in our fiducial model, we assumed extremely weak feedback and used 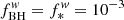 . We find that black holes can always accrete at the Eddington rate, rendering fBH a redundant parameter. We then find the value of f* by matching to stellar mass measured for UHZ1 (Bogdán et al. 2024) using the PBH mass calculated in Sect. 2 and detailed in Table 1: We find a value of f* = 0.7, as shown in the left panel of Fig. 3. For this object, we started with a PBH seed mass of
. We find that black holes can always accrete at the Eddington rate, rendering fBH a redundant parameter. We then find the value of f* by matching to stellar mass measured for UHZ1 (Bogdán et al. 2024) using the PBH mass calculated in Sect. 2 and detailed in Table 1: We find a value of f* = 0.7, as shown in the left panel of Fig. 3. For this object, we started with a PBH seed mass of 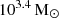 at z = 3400, which initially binds the same mass in dark matter. By z = 30, the halo assembling around the black hole reaches a mass of
at z = 3400, which initially binds the same mass in dark matter. By z = 30, the halo assembling around the black hole reaches a mass of 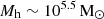 . Only at z ∼ 60 is the halo is large enough to exceed
. Only at z ∼ 60 is the halo is large enough to exceed 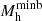 and can start assembling its gas content. At this point, the black hole was allowed to start to accrete, and it grew its mass by a factor of 4 between z = 60 and 30. As a result, by z = 30, this halo had a black hole mass of
and can start assembling its gas content. At this point, the black hole was allowed to start to accrete, and it grew its mass by a factor of 4 between z = 60 and 30. As a result, by z = 30, this halo had a black hole mass of 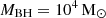 , a gas mass of
, a gas mass of 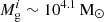 , and M* = 0. At z ≲ 30, the halo transitions to smoothly accreting dark matter from the IGM at a rate given by Eq. (3), resulting in a halo mass of 108.8 M⊙ by the source redshift of 10.3. This was accompanied by smooth accretion of IGM gas, which we (reasonably) assumed to have a cosmological ratio of the gas to dark matter. This means that the gas mass tracked the halo mass, as shown in the same figure. We note that in this simplistic model of an isolated halo, accretion is the only mode through which the system can gain gas. In terms of the black hole mass, we find that it is able to grow efficiently at the Eddington rate. By z = 10.3, this black hole achieves a mass
, and M* = 0. At z ≲ 30, the halo transitions to smoothly accreting dark matter from the IGM at a rate given by Eq. (3), resulting in a halo mass of 108.8 M⊙ by the source redshift of 10.3. This was accompanied by smooth accretion of IGM gas, which we (reasonably) assumed to have a cosmological ratio of the gas to dark matter. This means that the gas mass tracked the halo mass, as shown in the same figure. We note that in this simplistic model of an isolated halo, accretion is the only mode through which the system can gain gas. In terms of the black hole mass, we find that it is able to grow efficiently at the Eddington rate. By z = 10.3, this black hole achieves a mass 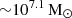 , comparable to the observationally inferred mass for UHZ1. Finally, given the low halo mass, star formation always proceeds at the ejection efficiency (
, comparable to the observationally inferred mass for UHZ1. Finally, given the low halo mass, star formation always proceeds at the ejection efficiency (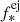 ) such that at any time, the only gas mass available is the mass accreted in that time-step. Given the higher efficiency of the process, the stellar mass starts to exceed the black hole mass as early as z ∼ 25.4 and reaches a final value of
) such that at any time, the only gas mass available is the mass accreted in that time-step. Given the higher efficiency of the process, the stellar mass starts to exceed the black hole mass as early as z ∼ 25.4 and reaches a final value of 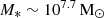 by the observed redshift. In this case, the final ratio of black hole to stellar mass is about 0.25.
by the observed redshift. In this case, the final ratio of black hole to stellar mass is about 0.25.
 |
Fig. 3. Assembly of early galaxies in the scenario in which primordial black holes act as the seeds of (isolated) structure formation. The left and right panels show the inferred stellar (blue points) and black hole (red points) masses for UHZ1 and GHZ9, observed at z ∼ 10.3 − 10.4. As marked, we show the assembly of the black hole mass (long-dash line), the halo mass (solid line), the accreted gas mass (dotted line), and the stellar mass (short-dash line). In each panel, the dot-dashed line shows the evolution of the minimum halo mass that is able to bind haloes with a baryonic over-density value of δb = 200. |
Parameter values.
We then applied the same parameters to GHZ9 (right panel of Fig. 3) as a sanity check. The stellar mass of this object ranges between 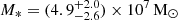 (Atek et al. 2023) and
(Atek et al. 2023) and 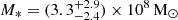 (Castellano et al. 2023). This object starts with a 2.8 times higher primordial black hole with a mass of
(Castellano et al. 2023). This object starts with a 2.8 times higher primordial black hole with a mass of 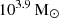 , which allows its halo to exceed
, which allows its halo to exceed 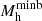 as early as z ∼ 90. By the observed redshift of z = 10.4, this object has a halo mass of
as early as z ∼ 90. By the observed redshift of z = 10.4, this object has a halo mass of 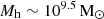 . Additionally, without any change in parameters, we obtain final stellar and black hole mass values of 108.5 and 107.6 M⊙, that is, MBH/M* ∼ 0.12, which agrees very well with the observed values of the black hole mass (Kovács et al. 2024) and the stellar mass (as inferred by Castellano et al. 2023), as shown.
. Additionally, without any change in parameters, we obtain final stellar and black hole mass values of 108.5 and 107.6 M⊙, that is, MBH/M* ∼ 0.12, which agrees very well with the observed values of the black hole mass (Kovács et al. 2024) and the stellar mass (as inferred by Castellano et al. 2023), as shown.
3.2. Impact of free parameters on the model results
As detailed in Table 2, we explored a wide range of models, including extreme combinations of the gas-mass fractions available for black hole accretion/star formation and the fraction of black hole/SNII feedback coupling to the gas content. We applied these models to GHZ9 to highlight the impact of the parameter values on the assembled stellar and black hole masses. The results of these calculations are also shown in Fig. 4. We start by noting that the exact order of black hole accretion or star formation has no bearing on our results, and black holes always accrete at the Eddington rate. As a result, the black hole assembly is the same in every model, even though we used different values that spanned the extrema of the parameter space.
 |
Fig. 4. Assembly of GHZ9 with primordial black holes acting as the seeds of structure formation. In the top row (panels a and b), we show the assembly of the stellar mass (solid lines) and black hole mass (dashed lines) for three different models exploring the parameter space (see Table 2). The bottom row (panels c and d) shows the ratios of black hole to stellar mass for each model. While the left panel shows results for different feedback models in the case where black hole accretion is more efficient (BHe-) than star formation, the right panel shows results for the cases where star formation is allowed to be more efficient (SFe). The second part of the label in each panel shows the key feedback source. 0fb stands for no feedback, BHfb for feedback from black holes alone, and SNfb for SNII feedback alone. |
We start by discussing the set of models in which black holes are allowed to accrete the minimum between the Eddington mass and 90% of the available gas mass, with 10% of the gas forming stars at most, at any step. As shown in panel a of Fig. 4, in the model without feedback (BHe-0fb), the stellar mass reaches a final value of 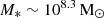 , in agreement with the inferred value from Castellano et al. (2023), that is, MBH/M* ∼ 0.23, as shown in panel c. When the impact of black hole feedback is included (BHe-BHfb), a stellar mass is reached that is almost five times lower and has a value of
, in agreement with the inferred value from Castellano et al. (2023), that is, MBH/M* ∼ 0.23, as shown in panel c. When the impact of black hole feedback is included (BHe-BHfb), a stellar mass is reached that is almost five times lower and has a value of 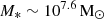 (in agreement with the mass estimate from Atek et al. 2023). Interestingly, in this case, the model yields a black hole mass that exceeds the stellar mass, with a value of MBH/M* ∼ 1.01 (panel c). Finally, when we consider SNII feedback (BHe-SNfb), a very slow buildup of the stellar mass is caused that reaches a final value of only
(in agreement with the mass estimate from Atek et al. 2023). Interestingly, in this case, the model yields a black hole mass that exceeds the stellar mass, with a value of MBH/M* ∼ 1.01 (panel c). Finally, when we consider SNII feedback (BHe-SNfb), a very slow buildup of the stellar mass is caused that reaches a final value of only 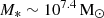 , again yielding a black hole mass that exceeds the stellar mass by a factor 1.86, as shown in panel c.
, again yielding a black hole mass that exceeds the stellar mass by a factor 1.86, as shown in panel c.
The case of efficient star formation, in which the minimum between the ejection efficiency up to 90% of the gas is allowed to form stars, is shown in panel b of the same figure. In this case, in the cases without feedback (SNe-0fb) and with black hole feedback (SNe-BHfb), the stellar mass is only 0.1 dex higher than that from the fiducial relation, resulting in MBH/M* ∼ 0.1, as shown in panel d. These stellar masses agree with the higher mass estimates of Castellano et al. (2023). In the SNII feedback case (SNe-SNfb), a combination of high star formation rates and high feedback results in a final stellar mass of 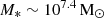 , which agrees with the values inferred by Atek et al. (2023). This results in MBH/M* ∼ 1.86 (panel d).
, which agrees with the values inferred by Atek et al. (2023). This results in MBH/M* ∼ 1.86 (panel d).
To summarise, essentially the entire parameter space we explored is compatible with the black hole and stellar masses inferred for GHZ9 given the wide range of M* values that are observationally allowed for this object. Interestingly, the ratios of the black hole to stellar mass inferred from the different models we explored range between 0.1 − 1.86, which means that in some cases (high supernova feedback), the black hole even grows to be more massive than its host halo.
4. Conclusions and discussion
The JWST has been instrumental in shedding light on black holes in the first billion years of the Universe. These unprecedented datasets have raised a number of tantalising issues, including an over-abundance of black holes (Harikane et al. 2023; Maiolino et al. 2024a; Greene et al. 2024), the presence of overly huge black holes (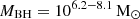 ) as early as z ∼ 8.5 − 10.6 (Kokorev et al. 2023; Maiolino et al. 2024b; Bogdán et al. 2024; Kovács et al. 2024), and systems with unprecedentedly high ratios of the stellar to black hole mass of MBH/M* ≳ 30% (Kokorev et al. 2023; Juodžbalis et al. 2024; Bogdán et al. 2024; Kovács et al. 2024), compared to local relations, where these values are lower by two orders of magnitude (e.g. Volonteri & Reines 2016).
) as early as z ∼ 8.5 − 10.6 (Kokorev et al. 2023; Maiolino et al. 2024b; Bogdán et al. 2024; Kovács et al. 2024), and systems with unprecedentedly high ratios of the stellar to black hole mass of MBH/M* ≳ 30% (Kokorev et al. 2023; Juodžbalis et al. 2024; Bogdán et al. 2024; Kovács et al. 2024), compared to local relations, where these values are lower by two orders of magnitude (e.g. Volonteri & Reines 2016).
A number of works have cautioned about the use of standard virial indicators in estimating black hole masses for these systems (King 2024), and others used BLR models to estimate black hole masses that were lower by an order of magnitude (Lupi et al. 2024). Finally, it has been noted that selection biases and measurement uncertainties might account for the offset of the inferred high-redshift MBH − M* relation (Li et al. 2024). These caveats notwithstanding, an enormous body of theoretical work has focused on astrophysical solutions, including high-mass seeding mechanisms (Bogdán et al. 2024; Kovács et al. 2024; Maiolino et al. 2024a; Natarajan et al. 2024), episodic super-Eddington accretion phases (Schneider et al. 2023; Maiolino et al. 2024b), extremely efficient accretion onto low- or intermediate-mass seeds (Furtak et al. 2024; Dayal et al. 2024), or high-mass seeds that grow through mergers with low-mass seeds and/or efficient accretion (Bhowmick et al. 2024).
We explored a complementary cosmological solution provided by PBHs. These are seeded in the early Universe through mechanisms including collapse from scale-invariant fluctuations, cosmic strings, cosmological phase transitions, or a temporary softening of the equation of state (see excellent reviews by e.g. Carr 2005; Carr & Green 2024). A key advantage of this scenario is that individual PBHs can act as seeds of structure formation by binding their dark matter halo around themselves (Hoyle & Narlikar 1966; Ryan 1972; Carr & Rees 1984; Mack et al. 2007; Carr & Silk 2018).
Starting by collating data on all of the 34 JWST-detected black holes confirmed at z ≳ 4 (summarised in Table 1), we carried out analytic calculations to estimate the seed masses and accretion rates that would allow their assembly. We used these observations to derive limits on the PBH mass function. We then developed an illustrative model to show a PBH that assembles its dark matter and baryonic content in the seed scenario. This was successfully applied to the highest-redshift outlying black holes observed (UHZ1 and GHZ9). Our key findings are listed below.
-
Starting at a redshift of z = 25, continuous Eddington-limited accretion onto low-mass (100 M⊙) seeds is able to explain 26 of the 34 JWST-observed black holes, leaving only 6 outliers (2 at z ∼ 7 and all of the 4 at z ≳ 8.5). Explaining these requires invoking continuous super-Eddington accretion with fEdd = 2.1. Eddington accretion onto intermediate-mass seeds (104 M⊙) explains 32 of the observed black holes except for the two highest-redshift objects at z ≳ 10 (Bogdán et al. 2024; Kovács et al. 2024). These objects can be explain by invoking fEdd = 1.4. Continuous Eddington accretion onto massive (105 M⊙) seeds is able to explain all of the current observations, precluding the need for super-Eddington accretion.
-
Assuming a PBH origin for all JWST black holes yields the upper limit to the PBH mass function. This shows an extended shape, with number densities ∼10−3.1 cMpc−3 at
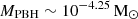 to 10−5.3 cMpc−3 at
to 10−5.3 cMpc−3 at 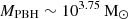 . However, even in this maximum scenario, the fractional PBH density parameter has a maximum value ∼10−12, which is lower by ten orders of magnitude than current constraints. This implies that PBHs from these JWST-detected early sources contribute very little to the dark matter content.
. However, even in this maximum scenario, the fractional PBH density parameter has a maximum value ∼10−12, which is lower by ten orders of magnitude than current constraints. This implies that PBHs from these JWST-detected early sources contribute very little to the dark matter content. -
Considering PBHs to form the seeds of structure formation, we successfully showed that the two highest-redshift sources (UHZ1 at z ∼ 10.3 and GHZ9 at z ∼ 10.4) assemble their dark matter and baryonic contents with the same parameters that govern star formation and black hole accretion and their associated feedbacks.
-
Exploring a wide swathe of parameter space in terms of black hole gas accretion, star formation efficiency, and their associated feedbacks applied to GHZ9, we find ratios of the black hole to stellar mass between 0.1 − 1.86, which means that in some cases (high supernova feedback), the black hole even grows to be more massive than its host halo.
We end with a few caveats: From the observational side, as noted, black hole masses are inferred using single-epoch measurements calibrated against local relations. Furthermore, the inferred stellar masses intricately depend on the assumed star formation history and stellar population properties (nebular emission inclusion, metallicity, and dust attenuation) and, most crucially, on the initial mass function. Systematic uncertainties arising from these quantities can change the stellar mass estimates by about an order of magnitude (Wang et al. 2024). Finally, we note that the black holes that are currently being observed only form a subset of the underlying population, which might induce systematics in the observed relations (e.g. Li et al. 2024).
In terms of the theoretical model, we have presented what is mostly an illustrative model of how a black hole can seed a halo and its baryonic components. We note that a number of assumptions were made that must be improved further: We transitioned from a linear (black hole dominated) growth of the halo to non-linear when the halo exceeds the black hole by two orders of magnitude, which must be investigated further. The accretion rates used here were also derived for higher-mass haloes at lower redshifts. Star formation and black hole accretion and their associated feedback could all be modelled in more detail. We also assumed that the black hole is able to remain stable at the centre of the halo and continue to accrete with a duty cycle of 100%.
In addition to the JWST, facilities such the Laser Space Interferometer Antenna (LISA) and Athena will be utterly crucial in the next decades for our understanding of black holes and their hosts in the first billion years.
Acknowledgments
PD acknowledge support from the NWO grant 016.VIDI.189.162 (“ODIN”) and warmly thanks the European Commission’s and University of Groningen’s CO-FUND Rosalind Franklin program. PD thanks A. Mazumdar for illuminating discussions and L. Furtak, J. Greene and M. Mosbech for their comments that have added crucially to the quality of the work.
References
- Abel, T., Bryan, G. L., & Norman, M. L. 2002, Science, 295, 93 [CrossRef] [Google Scholar]
- Alexander, T., & Natarajan, P. 2014, Science, 345, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Amaro-Seoane, P., Andrews, J., Arca Sedda, M., et al. 2023, Liv. Rev. Relat., 26, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Atek, H., Chemerynska, I., Wang, B., et al. 2023, MNRAS, 524, 5486 [NASA ADS] [CrossRef] [Google Scholar]
- Barkana, R., & Loeb, A. 2001, Phys. Rep., 349, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Bhowmick, A. K., Blecha, L., Torrey, P., et al. 2024, MNRAS, 531, 4311 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdán, Á., Goulding, A. D., Natarajan, P., et al. 2024, Nat. Astron., 8, 126 [Google Scholar]
- Bromm, V., Coppi, P. S., & Larson, R. B. 2002, ApJ, 564, 23 [Google Scholar]
- Cappelluti, N., Hasinger, G., & Natarajan, P. 2022, ApJ, 926, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B. J. 2005, ArXiv e-prints [arXiv:astro-ph/0511743] [Google Scholar]
- Carr, B. J., & Green, A. M. 2024, ArXiv e-prints [arXiv:2406.05736] [Google Scholar]
- Carr, B. J., & Hawking, S. W. 1974, MNRAS, 168, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B., & Kühnel, F. 2020, Annu. Rev. Nucl. Part. Sci., 70, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B. J., & Rees, M. J. 1984, MNRAS, 206, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B., & Silk, J. 2018, MNRAS, 478, 3756 [NASA ADS] [CrossRef] [Google Scholar]
- Carr, B. J., Bond, J. R., & Arnett, W. D. 1984, ApJ, 277, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Castellano, M., Fontana, A., Treu, T., et al. 2023, ApJ, 948, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., Dunlop, J. S., & Pacucci, F. 2014, MNRAS, 445, 2545 [CrossRef] [Google Scholar]
- Dayal, P., Rossi, E. M., Shiralilou, B., et al. 2019, MNRAS, 486, 2336 [Google Scholar]
- Dayal, P., Volonteri, M., Greene, J. E., et al. 2024, A&A, submitted [Google Scholar]
- Devecchi, B., & Volonteri, M. 2009, ApJ, 694, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Bañados, E., & Simcoe, R. A. 2023, ARA&A, 61, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Fragione, G., & Pacucci, F. 2023, ApJ, 958, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Wang, B., Weaver, J., et al. 2023, ArXiv e-prints [arXiv:2308.11609] [Google Scholar]
- Furtak, L. J., Zitrin, A., Plat, A., et al. 2023, ApJ, 952, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Furtak, L. J., Labbé, I., Zitrin, A., et al. 2024, Nature, 628, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2007, ApJ, 670, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Labbe, I., Goulding, A. D., et al. 2024, ApJ, 964, 39 [CrossRef] [Google Scholar]
- Habouzit, M., Volonteri, M., Latif, M., Dubois, Y., & Peirani, S. 2016, MNRAS, 463, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Harikane, Y., Zhang, Y., Nakajima, K., et al. 2023, ApJ, 959, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hawking, S. 1971, MNRAS, 152, 75 [Google Scholar]
- Hoyle, F., & Narlikar, J. V. 1966, Proc. Roy. Soc. London Ser. A, 290, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Inayoshi, K., & Ichikawa, K. 2024, ArXiv e-prints [arXiv:2402.14706] [Google Scholar]
- Inayoshi, K., Visbal, E., & Haiman, Z. 2020, ARA&A, 58, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Juodžbalis, I., Maiolino, R., Baker, W. M., et al. 2024, ArXiv e-prints [arXiv:2403.03872] [Google Scholar]
- Kavanagh, B. J. 2024, https://doi.org/10.5281/zenodo.10641173 [Google Scholar]
- King, A. 2024, MNRAS, 531, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Kocevski, D. D., Onoue, M., Inayoshi, K., et al. 2023, ApJ, 954, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kokorev, V., Fujimoto, S., Labbe, I., et al. 2023, ApJ, 957, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Kokorev, V., Caputi, K. I., Greene, J. E., et al. 2024, ApJ, 968, A38 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, O. E., Bogdán, Á., Natarajan, P., et al. 2024, ApJ, 965, L21 [CrossRef] [Google Scholar]
- Labbé, I., Greene, J. E., Bezanson, R., et al. 2023a, ArXiv e-prints [arXiv:2306.07320] [Google Scholar]
- Labbé, I., van Dokkum, P., Nelson, E., et al. 2023b, Nature, 616, 266 [CrossRef] [Google Scholar]
- Leigh, N. W. C., Böker, T., Maccarone, T. J., & Perets, H. B. 2013, MNRAS, 429, 2997 [Google Scholar]
- Li, J., Silverman, J. D., Shen, Y., et al. 2024, ArXiv e-prints [arXiv:2403.00074] [Google Scholar]
- Liu, B., & Bromm, V. 2023, ArXiv e-prints [arXiv:2312.04085] [Google Scholar]
- Loeb, A., & Rasio, F. A. 1994, ApJ, 432, 52 [Google Scholar]
- Lupi, A., Trinca, A., Volonteri, M., Dotti, M., & Mazzucchelli, C. 2024, A&A, 689, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mack, K. J., Ostriker, J. P., & Ricotti, M. 2007, ApJ, 665, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Scholtz, J., Curtis-Lake, E., et al. 2024a, A&A, in press, https://doi.org/10.1051/0004-6361/202347640 [Google Scholar]
- Maiolino, R., Scholtz, J., Witstok, J., et al. 2024b, Nature, 627, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Massonneau, W., Volonteri, M., Dubois, Y., & Beckmann, R. S. 2023, A&A, 670, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matthee, J., Naidu, R. P., Brammer, G., et al. 2024, ApJ, 963, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Mauerhofer, V., & Dayal, P. 2023, MNRAS, 526, 2196 [NASA ADS] [CrossRef] [Google Scholar]
- Mittal, S., & Kulkarni, G. 2022, MNRAS, 510, 4992 [NASA ADS] [CrossRef] [Google Scholar]
- Natarajan, P., Pacucci, F., Ricarte, A., et al. 2024, ApJ, 960, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pacucci, F., Nguyen, B., Carniani, S., Maiolino, R., & Fan, X. 2023, ApJ, 957, L3 [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Regan, J., & Volonteri, M. 2024, Open J. Astrophys., 7, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Regan, J. A., Downes, T. P., Volonteri, M., et al. 2019, MNRAS, 486, 3892 [CrossRef] [Google Scholar]
- Reines, A. E., & Volonteri, M. 2015, ApJ, 813, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, M. P. 1972, ApJ, 177, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Schneider, R., Valiante, R., Trinca, A., et al. 2023, MNRAS, 526, 3250 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Silk, J. 2017, ApJ, 839, L13 [Google Scholar]
- Suh, H., Civano, F., Trakhtenbrot, B., et al. 2020, ApJ, 889, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Trac, H., Cen, R., & Mansfield, P. 2015, ApJ, 813, 54 [Google Scholar]
- Vestergaard, M., & Osmer, P. S. 2009, ApJ, 699, 800 [Google Scholar]
- Volonteri, M., & Reines, A. E. 2016, ApJ, 820, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Volonteri, M., Habouzit, M., & Colpi, M. 2023, MNRAS, 521, 241 [CrossRef] [Google Scholar]
- Wang, B., Leja, J., Atek, H., et al. 2024, ApJ, 963, 74 [CrossRef] [Google Scholar]
- Ziparo, F., Gallerani, S., Ferrara, A., & Vito, F. 2022, MNRAS, 517, 1086 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Growth of the black hole mass as a function of redshift (or cosmic time). Assuming seeding at a redshift of zseed = 25, we show the black hole growth considering both Eddington-limited (fEdd = 1) and super-Eddington (fEdd > 1) accretion for seed masses of 100, 104, and 105 M⊙, as marked. As detailed in Table 1 and marked in the plot, we compare these models to black holes confirmed by Bogdán et al. (2024), Furtak et al. (2024), Kocevski et al. (2023), Maiolino et al. (2024a,b), Harikane et al. (2023), Greene et al. (2024), Kokorev et al. (2023), Kovács et al. (2024), and Juodžbalis et al. (2024). |
| In the text | |
 |
Fig. 2. PBH mass function as a function of the primordial black hole mass (left panel) and the fraction of dark matter composed of these objects (right panel). In both panels, these estimates are obtained assuming Eddington-limited accretion onto all black holes observed by the JWST (solid line; upper limit) and for those that cannot be explained by Eddington-limited accretion onto low-mass seeds (dashed line) and intermediate-mass seeds (point). As shown by arrows in the left panel, super-Eddington accretion would shift the mass function towards lower masses. Decreasing the seeding redshift would shift the mass function to higher masses. |
| In the text | |
 |
Fig. 3. Assembly of early galaxies in the scenario in which primordial black holes act as the seeds of (isolated) structure formation. The left and right panels show the inferred stellar (blue points) and black hole (red points) masses for UHZ1 and GHZ9, observed at z ∼ 10.3 − 10.4. As marked, we show the assembly of the black hole mass (long-dash line), the halo mass (solid line), the accreted gas mass (dotted line), and the stellar mass (short-dash line). In each panel, the dot-dashed line shows the evolution of the minimum halo mass that is able to bind haloes with a baryonic over-density value of δb = 200. |
| In the text | |
 |
Fig. 4. Assembly of GHZ9 with primordial black holes acting as the seeds of structure formation. In the top row (panels a and b), we show the assembly of the stellar mass (solid lines) and black hole mass (dashed lines) for three different models exploring the parameter space (see Table 2). The bottom row (panels c and d) shows the ratios of black hole to stellar mass for each model. While the left panel shows results for different feedback models in the case where black hole accretion is more efficient (BHe-) than star formation, the right panel shows results for the cases where star formation is allowed to be more efficient (SFe). The second part of the label in each panel shows the key feedback source. 0fb stands for no feedback, BHfb for feedback from black holes alone, and SNfb for SNII feedback alone. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



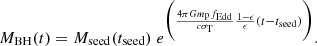
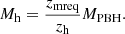
![$$ \begin{aligned} \langle \dot{M}_{\rm h} \rangle = 0.21 \bigg (\frac{M_{\rm h}}{10^8\,\mathrm{M}_{\odot }}\bigg )^{1.06} \bigg (\frac{1+z}{7}\bigg )^{2.5} \bigg [\frac{\mathrm{M}_{\odot }}{\mathrm{yr}}\bigg ]\cdot \end{aligned} $$](/articles/aa/full_html/2024/10/aa51481-24/aa51481-24-eq43.gif)
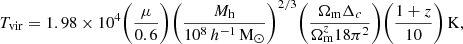
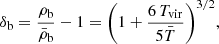
![$$ \begin{aligned} \Delta M_{\rm BH} = \mathrm{min}[M_{\rm Edd},f_{\rm BH} M_{\rm g}^i]. \end{aligned} $$](/articles/aa/full_html/2024/10/aa51481-24/aa51481-24-eq50.gif)