EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A347 Full HTML
Highlight
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A347
Number of page(s) 14
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202451324
Published online 22 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Ultra-luminous X-ray sources (ULXs) are binary systems with X-ray luminosities exceeding ∼3 × 1039 erg s−1, which is the Eddington luminosity limit for a 20 M⊙ black hole (Kaaret et al. 2017; King et al. 2023). Typically, ULXs are situated close to young massive star clusters, preferably in low-metallicity galaxies (Poutanen et al. 2013; Kovlakas et al. 2020).

Initially, ULXs were considered hosts of the elusive intermediate-mass black holes. However, the discovery of coherent pulsations in the ULX M82 X-2 proved that the compact object in this system is a neutron star (Bachetti et al. 2014). Since the apparent X-ray luminosities of ULXs are more than 100 times larger than the Eddington luminosity of a neutron star, this led to a paradigm shift – the study of ULXs is now largely concentrating on understanding the supercritical accretion regime.

At the same time, the discovery of gravitational wave (GW) emission from merging black holes stirred interest in the final evolutionary stages of massive binary stars. Current binary evolution models and population synthesis codes firmly predict that black holes with masses comparable to those detected by the GW observatories (M• > 20 M⊙ ) should exist in binary systems, preferably in low-metallicity galaxies (Fragos et al. 2013; Mondal et al. 2020). Some of these systems should have ULX-like X-ray luminosities when accreting close to their Eddington limit (Marchant et al. 2017; Hainich et al. 2018).

Both models – supercritical accretion onto light compact objects and standard accretion onto more massive black holes – are capable of explaining the ULX luminosities. Therefore, to determine the true nature of compact objects in individual ULXs, a detailed multi-wavelength analysis and a comparison with the different model predictions are needed.

Hydrodynamic simulations of supercritical accretion show that large amounts of mass and angular momentum should be removed from ULXs by jets and powerful outflows from accretion discs (e.g. Toyouchi et al. 2024, and references therein). However, the simulations are not yet capable of making quantitative predictions about the outflow velocities, outward mass flux, and other key parameters. These quantities determine the multi-wavelength spectral appearance of ULXs and are required for direct comparison with observations. Therefore, empirical studies are needed to gauge and guide the theory.

Observationally, the smoking gun of supercritical accretion is the spectral signature of strong outflows. Signatures of ultra-fast disc outflows (up to ∼0.2c) have already been spotted as blue-shifted absorption lines in high-resolution X-ray spectra of some ULXs (Pinto et al. 2016; Kosec et al. 2018a). Attempts have been made to search for such X-ray absorption features in a large sample of sources using statistical methods, but the results remain inconclusive (Kosec et al. 2018b).

Another important and promising avenue for searching the signatures of outflows is provided by UV and optical spectroscopy. The strong winds are manifested in the ultraviolet (UV) as resonance lines of metals (such as C IVλ1550 Å) with P Cygni line profiles (Morton 1967; Lamers & Cassinelli 1999). Indeed, the detection of P Cygni line profiles in the UV spectra of low-mass X-ray binaries (LMXBs) has been considered as proof of the presence of accretion disc winds, and consequently of supercritical accretion during X-ray outbursts (Castro Segura et al. 2022). The signatures of disc winds were also found in optical and near-infrared (near-IR) spectra of ULXs and LMXBs, typically during outbursts, as broad emission lines of hydrogen, helium, and metals, resembling characteristics of a Wolf-Rayet (WR)-type spectrum (Zhou et al. 2023; Muñoz-Darias et al. 2020; Panizo-Espinar et al. 2022; Sánchez-Sierras et al. 2023).

Thus, over the last decade, an apparent consensus has emerged in the literature: the detection of wind signatures in ULX spectra proves that the compact object in the source accretes supercritically (e.g. Fabrika et al. 2015). However, it remains unclear whether the absence of wind signatures implies that a source accretes in a standard regime, implying that the compact object is a black hole with M• > 20 M⊙. Additional, circumstantial evidence is needed to address this problem.

Such evidence is provided by considering the nature and ionisation mechanisms of the circumstellar nebulae, which are commonly found around ULXs (Pakull & Mirioni 2002). Strong outflows, characteristic of supercritical accretors, should leave their fingerprints on the ULX nebulae. In contrast, if there are no strong outflows, the nebulae should be largely photoionised by the intense X-ray radiation field of the ULX.

The situation is especially complex when the donor star in a ULX has an OB or WR spectral type. The OB and WR stars are hot, emit most of their light in the UV, and drive powerful stellar winds. If, as binary evolution models predict, the donor star in a ULX is a hot massive star, then its radiation must significantly contribute to or even dominate the binary UV and optical spectra, including wind lines. Previously, the UV spectra of ULXs have been interpreted as originating in the donor star winds rather than in the accretion disc wind (Long et al. 2002; Liu et al. 2004). This aligns with UV and optical observations of high-mass X-ray binaries (HMXBs, Ramachandran et al. 2022). In HMXBs, the accretion proceeds at a sub-Eddington rate and their UV and optical spectra can be safely attributed to the donor.

There are only a few ULXs with securely identified counterparts in the optical and UV. The question arises as to whether optical and UV counterparts of ULXs should be attributed to their donor stars or to their accretion discs, or whether perhaps they have contributions from both. Joint multi-wavelength analysis of donor star, accretion disc, and nebula is required to answer this fundamental question and provide a comprehensive understanding of ULXs. Such an analysis is attempted in this paper.

As the object of our study, we chose Holmberg II X-1 (Ho II X-1 hereafter) – a well-studied template ULX located at a distance of 3.05 Mpc in a star-forming region of a dwarf galaxy with low-metallicity (Hoessel et al. 1998; Kaaret et al. 2004). Ho II X-1 is surrounded by a large photoionised nebula, the Foot Nebula (Fig. 1), and is situated near a young cluster of OB-type stars from which it likely escaped (Stewart et al. 2000; Pakull & Mirioni 2002; Kaaret et al. 2004; Egorov et al. 2017). It is a perfect ULX for a multi-wavelength analysis due to its comparatively bright optical counterpart and low foreground extinction.

thumbnail Fig. 1.

False-colour HST ACS image of the area around the ULX Ho II X-1 with the adjacent H II region known as the ‘Foot Nebula’. This composite image comprises observations taken with the F502N (blue), F658N (green), and F814W (red) filters. The white circle highlights the He III bubble generated by ionising X-ray radiation emitted by the ULX, and has a diameter of 2 . ″ $ \overset{\prime \prime }{.} $5, corresponding to 37 pc at the distance of the Holmberg II galaxy. The ULX optical counterpart is seen as the white spot centred in the cycle. In the lower right corner, the acquisition image of our HST COS observations is displayed. The 2 . ″ $ \overset{\prime \prime }{.} $5 diameter aperture (shown as a red circle) encompasses the ULX, the He III bubble, and two neighbouring UV-bright stars. North is up and east is to the left.

Ho II X-1 has an X-ray luminosity (0.3 − 10 keV) that varies from > 1039 to ∼3 × 1040 erg s−1 (Grisé et al. 2010; Gúrpide et al. 2021a). Its X-ray properties are typical for a variable soft ULX (Gúrpide et al. 2021b). Ho II X-1 is not an X-ray pulsar and no definite evidence of fast outflows has been found in its X-ray spectra, which rules out that Ho II X-1 is accreting at a high super-Eddington rate (Kosec et al. 2018b; Barra et al. 2023).

Its optical counterpart and the circumstellar nebula were first reported by Pakull & Mirioni (2002), and it was suggested that the nebula is photoionised by the ULX. Subsequent analysis set the bolometric luminosity of the source at ∼1040 erg s−1, and suggested an OB-type donor star or an X-ray illuminated accretion disc as the origin of the optical counterpart (Kaaret et al. 2004; Berghea et al. 2010a,b). Furthermore, Kaaret et al. (2004) reinforced the hypothesis of photoionisation by the examination of the relative morphologies of the He IIλ 4686 Å, H β, and [O I] λ 6300 Å emission lines. These nebular analyses, however, have never been done consistently with the analyses of the ionising source.

Fabrika et al. (2015) presented an optical spectrum of Ho II X-1 obtained with the Faint Object Camera And Spectrograph (FOCAS) at the 8.2 m telescope Subaru. The authors claimed that the spectrum has a sufficiently high signal-to-noise ratio (S/N) for spectral analysis and fully attributed it to the accretion disc. They also claimed the detection of disc wind signatures in the spectra, which was considered as proof that Ho II X-1 and other ULXs accrete supercritically (see Sect. 4.2 for a more detailed discussion of their results). In this paper, we retrieve and analyse the same spectra, complementing them with newer data.

At radio wavelengths, Cseh et al. (2014, 2015) discovered a collimated jet emission from Ho II X-1, which first had a kinematic luminosity of ∼1039 erg s−1 but faded out by a factor of ∼7 during the ∼1.5 years between the observations. Heida et al. (2014) reported the detection of the near-IR counterpart of Ho II X-1, which Lau et al. (2017) attributed to the circumstellar disc of a B[e]-type donor star.

In the UV, Ho II X-1 has been observed twice. Tao et al. (2012) presented Hubble Space Telescope (HST) observations conducted with the prism grating of the Solar Blind Channel (SBC) of the Advanced Camera for Surveys (ACS). They acquired the spectrum of the ULX and two neighbouring stars (see Fig. 1). However, the resolving power of this instrument is not sufficient to resolve spectral lines, preventing a detailed spectroscopic analysis.

Vinokurov et al. (2022) used the UV AstroSat telescope to obtain UV photometry of Ho II X-1. Due to the low spatial resolution of the instrument, the data are likely highly contaminated by the surrounding nebula and the contribution from the neighbouring stellar cluster. To mitigate this, the authors performed a dedicated background subtraction; however, their reported values do not agree with the fluxes measured with the HST (Tao et al. 2012).

In both works, UV and optical photometry were combined to construct the spectral energy distribution (SED) and compared to theoretical models of irradiated accretion discs and various donor stars to elucidate the nature of the UV and optical counterpart of Ho II X-1. Both studies remain inconclusive, claiming that the SED is consistent with a disc or stellar origin.

In this paper, we aim to consistently analyse the optical and UV observations, modelling the source’s emission using stellar atmosphere and photoionisation models. In Sect. 2, we report all the data used for the analysis, as well as the data reduction process. In Sect. 3, a detailed overview of the modelling process is given, and in Sect. 4 we present our results. Finally, we discuss the results and present an evolutionary scenario in Sect. 5. Finally, in Sect. 6 we summarise our conclusions.

2. Observations and data reduction

2.1. Ultraviolet spectroscopy

The spectroscopic UV observations of Ho II X-1 were carried out during February and March 2021, in the TIME-TAG mode with the Cosmic Origin Spectrograph (COS, Green et al. 2012), onboard the HST (Programme ID: 16182, PI: L. Oskinova). The low-resolution (R ∼ 2000) G140L grating centred at 1280 Å was used to ensure a good wavelength coverage (1230–2050 Å). The spectrum was secured over 17 orbits, grouped in five visits (Table A.1).

Next to the ULX, still within the COS aperture (white and red circles in Fig. 1), there is a pair of point-like sources that are only a bit fainter in the UV than our target (in the following, we consider our target as source 1 and the narrow pair that is about 0 . ″ $ {{\overset{\prime\prime}{.}}} $8 to the south as source 2). The focus of HST’s main mirror suffers from spherical aberration, which is not corrected for the beam that feeds the COS spectrograph. Although we already restricted the scheduling of our observations such that the roll-angle of the spacecraft yielded the maximum separation between the two sources in the cross-dispersion direction, the spectra partially overlap on the detector. As the data reduction pipeline does not separate the sources, we developed a dedicated algorithm to disentangle their spectra.

We employed the COS pipeline to obtain the flat-fielded detector images. These 2-D images have the wavelength dispersion as the x-axis and the position in the cross-dispersion direction as the y-axis. In these images, the positions of two maxima can be identified in the cross-dispersion direction, separated by seven pixels according to the separation of the two sources, but largely overlapping.

We downloaded the calibration file from the HST database for a single-point source with the same spectrograph set-up to obtain the cross-dispersion instrumental profile. This allowed us to construct a mock instrumental profile for our pair of sources with their given position and separation. We kept this profile normalised, so the only free parameter during the process is the count ratio between the two sources, q(x). At each x-coordinate, the brightness ratio varies, searching for the value at which the deviation from the observation (χ2) is smallest. q(x) is applied to the pipeline-reduced total spectrum, yielding the spectra of both sources separately (Fig. 2).

thumbnail Fig. 2.

Ultraviolet spectra extracted from the HST COS observations of Ho II X-1. As is shown in the insert in Fig. 1, there are three point-like sources within the COS aperture. The black line shows the combined spectrum of all three sources. The spectra are disentangled (Sect. 2.1) to separate the ULX from the neighbouring sources, presumably OB-type stars. The red line shows the spectrum of the UV counterpart of Ho II X-1, while the combined spectra of two other sources within the COS field of view are plotted in blue.

However, the faintness of the ULX in the UV limits our method. Although we have already added all 17 exposures (weighted by their respective exposure time, Table A.1), the number of counts per detector pixel is still very small. Therefore, the brightness-ratio function q(x) has its own uncertainty which impacts the disentangled spectra. To reduce noise, we binned the images (both observation and calibration ones) in the wavelength direction by convolution with a Gaussian, and thus degrading the spectral resolution. For the blue part (1300–1900 Å) of our spectrum, an additional smoothing with 2 Å is a good compromise; at longer wavelengths, the instrumental profile degrades (James 2022) and the signal is anyhow too low to result in useful data, disentangled or not.

2.2. Ultraviolet photometry

We obtained UV photometric measurements of Ho II X-1 using archival HST observations taken with the prism grating PR130L (λeff = 1761 Å, Δλ = [1271 − 1981] Å) of the SBC/ACS on November 27 2006 (Proposal ID: 10814, PI: J. Bregman, previously analysed in Tao et al. 2011). We used the drizzled images obtained following the standard pipeline calibration. The photometry was performed using the APPHOT package in IRAF with an aperture of 0 . ″ $ \overset{\prime \prime }{.} $25. For the background subtraction, an annulus around the source of 0 . ″ $ \overset{\prime \prime }{.} $3 was taken. The UV counterpart of Ho II X-1 has a UV magnitude of 18.70 mag, while each of the other two sources within the HST COS aperture is roughly one magnitude fainter (Fig. 1). In order to compare with the UV observations, in which the nebula cannot be subtracted, we also measured the total UV flux of the point-like source, including the nebula contribution (see Table 1).

Table 1.

HST photometric data used to construct the SED.

2.3. Optical spectroscopy

To complement the UV observations, optical archival data were retrieved. Ho II X-1 has been observed only three times with long-enough exposure times to ensure a sufficiently high S/N and resolution to perform a spectroscopic analysis.

FOCAS observed the ULX, between February 26 and March 1 2011 (Proposal ID: o11104, PI: Yoshihiro Ueda). The telescope was operated with the 300B grism without a filter and a 0 . ″ $ \overset{\prime \prime }{.} $4 slit due to the good seeing. With this configuration, a resolving power of R ∼ 1000 was achieved for the spectral range of 3800–7000 Å, and an angular resolution of 0 . ″ $ \overset{\prime \prime }{.} $1 per pixel.

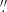The two other observations were performed by the Gran Telescopio de Canarias (GTC), between November and January during the winter campaigns of 2010–2011 and 2011–2012, with the OSIRIS long-slit spectrograph (Programme IDs: GTC20-11B and GTC38-10B, PI: F. Vilardell). The instrument was operated with a 0 . ″ $ \overset{\prime \prime }{.} $6 slit and the R2000B grism, which has a spectral range of 3950–5700 Å. With this configuration, a spectral resolving power of R  ∼  2165 and an angular sampling of 0 . ″ $ \overset{\prime \prime }{.} $25 per pixel were achieved.

All the obtained spectra were reduced using standard IRAF tasks; for the GTC data, the GTCMOS pipeline (Gómez-González et al. 2016) was employed. During the process, we also corrected the data for Galactic extinction. Due to the strong nebular contribution in the ULX spectra, the background subtraction was carried out in three independent ways, following three different approaches. These were applied to all the optical data.

In the first one, the spectrum of the ULX is extracted only from the point-like source at the coordinates of Ho II X-1. On the detector image, a narrow region contains the continuum of the point-like source, while the emission lines are extended. To subtract the contribution from the innermost nebula regions close to the ULX, on the detector image we select narrow regions adjacent to the continuum but still covering the emission lines. The rationale for this approach is that the ionisation conditions within the nebula strongly depend on the distance from the ionising source. After the background subtraction, no emission nor absorption lines are present in the resulting spectra, neither for the Subaru nor for the GTC observations.

For the second approach, we checked whether the emission line of He IIλ 4686 Å has a composite profile formed by the superposition of a broad wind line and a narrow nebular line. To achieve this, the spectra are extracted from a region comprising the point-like source plus the He IIλ 4686 Å emission. We noted that on the detector image, the extent of the He IIλ 4686 Å line is smaller compared to the extent of hydrogen lines, but has similar extent as the photoionised He III region (Pakull & Mirioni 2002). We found, however, that the He IIλ 4686 Å line, similar to other nebular lines, is described by a Gaussian profile with a width corresponding to the resolution of the spectrograph. This procedure is also repeated for other nebular lines, such as the forbidden [O III] λ 5007 Å, with the same result.

As a third and last approach, the spectrum from a region corresponding to the whole COS 2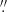 . ″ $ \overset{\prime \prime }{.} $5 aperture is extracted, and the contribution of the adjacent nebular region is subtracted. This allows a consistent analysis with the HST spectrum.

2.4. X-rays

To model the nebular spectra it is necessary to take the ionising X-ray spectrum of Ho II X-1 into account. In this work, we use archival observations by the XMM-Newton telescope taken fortuitously on the same dates as our HST COS observations on March 19 2021 (ObsID:0864550501, PI: M. Middleton). The XMM-Newton telescope delivers pipeline-reduced data ready for analysis. Since in this work, we need only the number of ionising photons and the crude spectral shape, the pipeline data are sufficient.

3. Methods and data analysis

The spectra analysed in this work are displayed in Figs. 3–5. The UV spectrum of Ho II X-1 (Fig. 2) shows narrow absorption lines of C IIλλ 1334,1335 Å, Si IIλ 1527 Å, Fe IIλ 1608 Å, Al IIλ 1671 Å and Al IIIλ 1855 Å. These lines are unresolved, as their widths do not exceed the low spectral resolution of the observations. They correspond to transitions from ground levels of low ionisation stage ions (Kramida et al. 2020). On this basis, we conclude that these lines are due to the line-of-sight absorption in the interstellar medium (ISM). The spectrum shows strong emission lines, which are generated in the high-excitation nebula around the ULX. These emission lines are somewhat broader than the ISM absorption lines, because the nebula emission fills the entire 2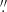 . ″ $ \overset{\prime \prime }{.} $5 aperture of COS, smearing the lines and effectively reducing the spectral resolution.

thumbnail Fig. 3.

Ultraviolet spectrum of Ho II X-1 normalised to the stellar model continuum. Solid blue: the COS disentangled spectrum; dotted green: the modelled PoWR stellar spectrum of a B0.5I supergiant (T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3, see Sect. 3.1); dotted purple: the CLOUDY nebular model for an X-ray ionising source modelled with diskir (see Sect. 3.3); dotted red: the combined PoWR and CLOUDY spectra. This last one also accounts for interstellar absorption lines (i.s.)

thumbnail Fig. 4.

Optical spectrum of Ho II X-1 taken with the Subaru telescope. The spectrum is normalised to the stellar model continuum and corrected for extinction. In blue, the observations, in dotted green the synthetic stellar spectrum from the PoWR model for a B0.5I supergiant (T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3), in dotted purple the CLOUDY nebular model for an X-ray ionising source modelled with diskir, and in dotted red the combined PoWR and CLOUDY spectra. The most relevant features are identified in black, while those identified in green correspond to high ionisation stages of iron and calcium overpredicted by the CLOUDY model (Sect. 3.3).

thumbnail Fig. 5.

Same as Fig. 4, but with the observed spectrum taken with the GTC.

The optical spectra of Ho II X-1 (Figs. 4 and 5) are dominated by its high excitation nebula. The emission lines are unresolved, with their widths corresponding to the spectral resolution of the FOCAS and OSIRIS spectrographs.

To proceed with the data analysis, we construct the SED of Ho II X-1 by combining our UV photometric data with the measurements in the optical and near-IR from Tao et al. (2012). The authors reported the average fluxes of non-simultaneous observations, with and without nebular subtraction, in the F814W, F555W, F450W and F336W filters. The SED of the ULX is shown in Fig. 6 (see Sect. 4.1 for a detailed discussion of the results) and the flux values are reported in Table 1.

thumbnail Fig. 6.

Spectral energy distribution (SED) of the ULX Ho II X-1 from UV to optical. Upper panel A: The blue line shows the data extracted from the observations with HST COS (UV), GTC OSIRIS and Subaru FOCAS (both in the optical). The blue boxes display photometric measurements from the HST ACS SBC F165LP in the UV and from HST WFPC2 in the optical (Sect. 4.1). The black lines at the bottom represent the filter wavelength ranges, each of them identified by the name of the filter. The red line indicates the synthetic PoWR SED for a B0.5I supergiant with T* =  26 k K, log g =  3.1 cm s−2 and log L/L⊙ =  5.3. The red hatched boxes show the modelled photometry. Bottom panel B: The blue boxes are the photometric measurements of the Ho II X-1 counterpart from HST filters without any correction for the nebular contribution. The purple line shows the synthetic CLOUDY SED for a nebula photoionised by an X-ray source, as is described by a diskir model (Sect. 3.2, Table 2), and with a luminosity of Lbol =  1.4 × 1040 erg s−1. The green line represents the synthetic PoWR SED for a B0.5I supergiant with T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3. The red line is the combination of both PoWR and CLOUDY models, and the red-hatched boxes represent the modelled photometry for the combined model.

3.1. Spectral modelling of the donor star

Model calculations of the donor star spectrum are performed with the Potsdam Wolf-Rayet (PoWR ) model atmosphere code. PoWR is a state-of-the-art code for stellar atmosphere in spherical symmetry and with winds. Local thermodynamic equilibrium is not presumed (non-LTE) (Hainich et al. 2019; Todt et al. 2015; Sander et al. 2015; Hamann & Gräfener 2004; Gräfener et al. 2002). The basic input parameters for a model are the luminosity (L*), the stellar temperature (T*), the surface gravity (log g), and the mass-loss rate (Ṁ) of the star. Also, the abundances have to be specified. We include C, N, O, Si, P, Al, S, Mg and the Fe-group elements, and adopt their down-scaled solar abundances according to the metallicity of 0.07 Z⊙ found for the host galaxy Holmberg II (Kaaret et al. 2004).

As there is no clear evidence for stellar lines in the optical and only marginal evidence for such lines in the UV, the stellar parameters can only be roughly constrained. Motivated by the work of Fabrika et al. (2015), we first compare the observations with PoWR models for WR stars at low-metallicity. However, they cannot reproduce either the SED or the UV and optical spectra, as they predict very broad emission lines that would be visible even with the strong nebular contribution.

Models for OB-type stars are tested next. The stellar temperature and luminosity can be estimated from the SED (Sect. 4.1), particularly from the lack of a Balmer jump. This restricts the temperature to within 20 to 40 kK. Thus, if the observed continuum belongs to the donor star in the system, it could be an early B supergiant. More constraints on the temperature are obtained from the UV spectrum. The lack of a blue-shifted absorption component in the C IV doublet at 1548/50 Å and the He II line at 1640 Å, in addition to the tentative presence of weak absorption lines at wavelengths above 1700 Å (Fig. 3), constrain the temperature range even more, between 20 and 30 kK. This is also consistent with the tentative detection of C IIλλ 1334,1335 Å and Al IIλλ 1855,1863 Å.

The surface gravity and the wind mass-loss rate are poorly constrained due to the lack of observed non-nebular spectral lines. To get a rough estimate of these parameters, we employ a pre-computed grid of stellar atmosphere models (Hainich et al. 2019), based on the MIST stellar evolution models (Dotter 2016; Choi et al. 2016; Paxton et al. 2011). As customary in stellar spectroscopy, we select our preferred model by comparison with the observations through multiple iterations. During this process, we systematically adjust the model’s stellar parameters and conduct visual inspections. The selected model is the one that best reproduces the following spectral features: absence of a noticeable Balmer jump; lack of strong blue-shifted absorption components of the UV lines C IVλλ 1548, 1550 Å and He IIλ 1640 Å; weak absorption lines of N IIIλλ 1747, 1754 Å and iron, and lack of strong absorption features. Thus, the derived donor star parameters (T* ≃ 26 kK, log L/L⊙ ≃ 5.3, log g ≃ 3.1 [cm s−2], log Ṁ ≃−8.5 [M⊙ yr−1]) correspond to a star of spectral type B0.5 I (Searle et al. 2008; Martins & Palacios 2021), which is a common type of a donor star in high mass X-ray binaries (Martínez-Núñez et al. 2017).

3.2. X-ray spectral modelling

The EPIC-PN spectrum of Ho II X-1 is analysed using the XSPEC spectral fitting package (Arnaud 1996). Four different models were tested. The irradiated disc model, diskir (Gierliński et al. 2009), can reproduce the UV and optical photometric measurements of Ho II X-1 (Tao et al. 2012). Another model is a composite of a blackbody, bbody, and a slim disc, diskpbb (Mineshige et al. 1994), commonly used in the analysis of the ULX X-ray spectra (Kajava et al. 2012). The next model combines two multi-temperature blackbody discs, diskbb (Mitsuda et al. 1984; Gúrpide et al. 2021a). Finally, we test a multicolour blackbody disc together with a Comptonising component, comptt (Titarchuk 1994; Pintore et al. 2014). The best-fit parameters of all these models are given in Table 2. We note that the diskir model might not be fully physically motivated in the case of Ho II X-1, as the parameters fout and log rout are unconstrained. However, this model reproduces fluxes in the UV and optical wavelength range, making it a suitable choice for extrapolating the ionising spectrum from X-ray to UV and optical wavelengths. The other three models do not reproduce the photometric data in the UV and optical ranges. Therefore, they need to be combined with our donor star model (B0.5 I star with T* = 26 kK and log L/L⊙ = 5.3) to explain the UV and optical measurements. In this way, we construct four alternative SEDs as ionising spectra input for the nebula models.

Table 2.

Parameters of the best-fit spectral models to the observed XMM-Newton EPIC PN spectrum of Ho II X-1 (ObsID:0864550501).

3.3. Spectral modelling of the Foot Nebula

To obtain a synthetic spectrum of the nebular emission, we used the photoionising code CLOUDY (Ferland et al. 2017). The key input parameters for the nebula model are the luminosity and the SED of the ionising source; that is, the broadband X-ray and UV (XUV) flux and spectrum of Ho II X-1. The bolometric luminosity of the source is fixed at its average value of Lbol = 1.4 × 1040 erg s−1 (Grisé et al. 2010; Berghea et al. 2010a). While Ho II X-1 has strong X-ray variability on a timescale of days (Gúrpide et al. 2021b), this approach is reasonable as the recombination timescale of the nebula is on the order of thousands of years.

To produce the broadband XUV SED, we extrapolate the spectral models from X-rays to UV (Sect. 3.2). While the source is well observed in X-rays and UV, the extreme UV wavelength range that is at the ionisation threshold of He II (around λ 227.84 Å) cannot be observed. Therefore, the spectral shape at these wavelengths is model-dependent. We test four alternative SEDs obtained when fitting the X-ray spectrum (Sect. 3.2). As they are all normalised to the same X-ray luminosity, the main difference between them is the contribution to the extreme UV range predicted by the different disc models. For each of the four SEDs, a grid of CLOUDY models is computed by varying the density and the inner radius of the He III nebula.

Further input parameters to the CLOUDY model include the hydrogen density, the inner radius of the nebula, and the nebular chemical abundances. The electron density and temperature of nebulae are typically constrained using flux ratios between certain forbidden metal lines, such as [S II] λλ 6716, 6731 Å and [O III] λλ 4363, 4959, 5007 Å (Osterbrock & Ferland 2006). Fortunately, the Subaru spectra cover these important diagnostic lines. Using these methods we roughly constrain the electron temperature to 14.5 kK and the electron density to 125 cm−3. These values are used as input for an initial CLOUDY model. However, the agreement with the observed spectrum is not perfect. Likely, this is because the [O II]λλ 3426, 3729, 7319, 7330 Å auroral lines, which are needed to better constrain the electron density, are outside of the wavelength range of the available spectra. To improve the quality of our models, we compute a grid of models for densities between 10 to 200 cm−3 with steps of 10 cm−3. This procedure is repeated for each of the four SEDs.

For the geometry of the nebula, we choose spherical symmetry. The inner radius is a free parameter of our CLOUDY models. In the HST image shown in the insert in Fig. 1 the nebula around the point source does not have a ring-like structure. Thus, taking into account the spatial resolution of the telescope, the maximum value of the inner radius must be smaller than 1 pc (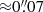 ≈ 0 . ″ 07 $ {\approx}0{{\overset{\prime\prime}{.}}}07 $ at Ho II X-1 distance). We compute models for inner radii between 10−5 to 1 pc and conclude that the effect on the synthetic spectrum is negligible.

Finally, the nebular abundances of oxygen, nitrogen, sulfur, neon, and argon are adopted from Croxall et al. (2009). They obtained these values after performing a spectroscopic analysis of the H II region around Ho II X-1s. The abundances of other elements are scaled down from solar values (Asplund et al. 2009) to 0.07Z⊙. Although Egorov et al. (2013) reported a higher mean metallicity for the host galaxy, Holmberg II, these authors also adopted the values from Croxall et al. (2009) for the region containing the Foot Nebula.

Following these criteria, we computed a grid of nebula models. To identify models suitable for comparison with the observations, we first examine the size of the He III region surrounding the ULX Ho II. The observed radius of ∼15 pc (Kaaret et al. 2004, Fig. 1) is compared with the predicted sizes from our models. Given the model SED, this procedure constrains the electron density of the gas. For the diskir and diskbb+diskbb models (Sect. 3.2 and Table 2), the size of the He III region is reproduced when the gas density is rather low, ne = 20 ± 10 cm−3, in rough agreement with (Kaaret et al. 2004). On the other hand, the diskbb+comptt and bbody+diskpbb models (Sect. 3.2 and Table 2), favour higher electron densities, ne = 140 ± 10 cm−3 and 50 ± 10 cm−3, respectively. To proceed, we compute a grid of synthetic spectra combining models for X-rays, the donor star, and the nebula, which could be directly compared with the observations.

4. Results

4.1. Photometry and spectral energy distribution

Before comparing the synthetic stellar and nebular SEDs with the photometric data, we correct the models for extinction, taking into account both the Galactic and the Holmberg II contributions. The synthetic SED of the donor star matches the photometry in the UV and the optical (upper panel of Fig. 6). Furthermore, the combined stellar and nebular model also matches the photometric measurements that also comprise the nebular contribution (bottom panel of Fig. 6). At this point, it is necessary to point out that no optical excess is observed as would be expected if the system were accreting supercritically. During super Eddington accretion, the disc must contribute to the total luminosity significantly, producing a measurable bump in the optical wavelength range (Ambrosi & Zampieri 2018).

In the IR wavelength range, an excess in the SED of Ho II X-1 has been reported by Lau et al. (2017, 2019) and attributed to a circumbinary disc of heated dust around the donor star. The IR excees could also indicate that the system is undergoing a rapid phase of Roche Lobe overflow that fuels the accretion process and forms a circumbinary disc where dust formation occurs. Although the dust emission might, in principle, contaminate the redmost data we consider here (see the HST WFPC2 filter F814W in Fig. 6), our models indicate that this is not the case, since the combined (stellar plus nebular) SED contribution matches the photometry very well (lower panel in Fig. 6).

4.2. Ultraviolet and optical spectra of Ho II X-1

Even though the UV spectrum of Ho II X-1 seems to be completely dominated by interstellar absorption and nebular lines, when it is compared with our combined stellar plus nebula model one can see tentative evidence of stellar contribution (see Fig. 3). It cannot be ruled out that the C II doublet at 1334/1335 Å is blended with the Si IIIλλ 1341,1342,1343 Å triplet, which, according to our selected donor star model, is present in the stellar atmosphere. Furthermore, the profile of the nebular O IVλλ 1401,1404 Å lines could be influenced by stellar contribution from Si IVλλ 1394,1402 Å. Importantly, the PoWR model does not predict any other stellar feature that would be detectable in the observations, given the limited S/N and the blending with strong nebular emission.

Previous analysis of optical spectra from Ho II X-1 claimed the detection of broad emission lines He IIλ 4686 Å, Hα and Hβ (Fabrika et al. 2015). On this basis, the optical spectrum was misclassified as a WR-type. Based on the presence of He II and H lines but the absence of He I lines, it was suggested that the optical counterpart of the ULX originates from the accretion disc. This was presented as proof that the compact object in Ho II X-1 accretes supercritically (i.e. at a rate highly above the Eddington limit). However, our observations with two times higher spectral resolution and our quantitative analysis show that the line width was mistakenly attributed to an expanding wind. Instead, the line broadening is fully explained by instrumental broadening and is in accordance with the low spectral resolution of the Subaru FOCAS. These lines are much narrower in the higher-resolution spectra obtained with the GTC OSIRIS. Hence, our independent analysis does not confirm the presence of disc-wind lines (Figs. 4, 5), removing another reason for suggesting accretion in a supercritical regime.

Standard accretion (or decretion) discs often display emission lines, such as Hα, Hβ or He IIλ 4686 Å and the Bowen blend, in their optical spectra. Depending on inclination, the lines might have a characteristic double peak profile as indeed observed in the optical spectra of black hole LMXBs (Soria et al. 2000; Panizo-Espinar et al. 2022). The emission lines that could be attributed to the accretion disc are not detected in the optical spectrum of Ho II X-1. However, the optical spectra of Ho II X-1 are quite noisy and strongly dominated by the nebula lines and the donor star continuum. Therefore, any possible spectral feature of the accretion disc is most likely strongly diluted and not detectable in our data. Interestingly, the disc lines are also not detected in the optical spectra of the prominent black hole HMXB M33 X-7, because the radiation of the OB donor star in the optical and UV is significantly brighter compared to the possible disc contribution (Ramachandran et al. 2022).

To perform the combined analysis of the UV and optical data of Ho II X-1 and its nebula, we first scale the synthetic CLOUDY spectra to the different aperture (COS) and slit sizes of the spectrographs (FOCAS & OSIRIS). Then, the model flux in the H β line and the ratios between fluxes in metal lines and in H β are compared with those measured from the observed spectra. The XSPEC+CLOUDY model that reproduces the line ratios best has the SED described by the diskir model and the nebular electron density of ne = 20 ± 10 cm−3. Combining this model with the PoWR stellar model for the donor star allows us, for the first time, to consistently reproduce the multi-wavelength, UV and optical, spectrum of Ho II X-1 (Figs. 3, 4, 5).

Still, there are some small deviations between the modelled and observed optical spectra. All synthetic spectra overpredict the line strengths of the high ionisation stages of iron, and underpredict the lines that are likely to be the result of shock ionisation, such as [S II]λλ 6716, 6731 Å. We attribute these mild discrepancies to the deviation from the spherical symmetry, probable inhomogeneities, and other contributions to the ionisation such as the shocks produced by jets or the possible contribution to the nebula from the bow-shocked gas caused by Ho II X-1 moving away from its natal cluster (Egorov et al. 2017).

5. Discussion

The first consistent analysis of the X-ray, UV and optical spectra of Ho II X-1 and its nebula presented in this paper successfully identifies the donor star and reproduces the observations without invoking super-Eddington accretion. Indeed, spectral features associated with powerful and fast outflows, as predicted and observed in supercritically accreting X-ray binaries, are absent in the UV and optical as well as in the X-ray spectra (Barra et al. 2023) of Ho II X-1 at the moment of our observations. This gives important information about the nature of the compact object in Ho II X-1, suggesting that it is a massive black hole.

5.1. New estimates of the black hole mass and accretion rate in Ho II X-1

The results presented in this paper suggest that Ho II X-1 consists of a B supergiant donor star and a black hole accreting at or below the Eddington limit. This allows us to use the X-ray luminosity for estimating the black hole mass.

The X-ray emission of Ho II X-1 is variable but its spectral appearance is persistent and typical for sources accreting close to the Eddington limit (Kaaret et al. 2017; King et al. 2023). The time-averaged X-ray luminosity is best estimated from nebula analysis. To reproduce the UV and optical spectra of the He III region around Ho II X-1, an X-ray luminosity of LX ∼ 1 × 1040 erg s−1 is required, which is in excellent agreement with the actual X-ray luminosity during our HST COS observations (see Table 2). Assuming spherical symmetry and electron scattering as the principal source of opacity, the Eddington luminosity of a black hole is given by LEdd ≈ 2.5 × 1038(1 + X)−1M/M⊙ erg s−1, where X = 0.65 is the typical hydrogen mass fraction of the accreted matter; that is, the donor star atmosphere (van Paradijs & Stollman 1984; Poutanen et al. 2007). Using the X-ray luminosity during XMM-Newton observations conducted simultaneously with our HST spectroscopic observations (Table 2), the mass of the black hole in Ho II X-1 is M• ≳ 66 M⊙. The X-ray luminosity, and this the implied black hole mass, might be overestimated if the radiation is beamed towards us. However, our analysis shows no evidence of beaming on Ho II X-1, as the X-ray luminosity estimated from the nebula analysis and the X-ray observations agree. Additionally, there are no indications of beaming in the existing literature for this ULX.

The accretion rate can be inferred from a thin disc model with an inner temperature constrained by the X-ray modelling. Following Shakura & Sunyaev (1973), Ho II X-1 is accreting with Ṁacc ∼ 1.8 × 10−6 M⊙ yr−1; that is, at a rate that is marginally below the Eddington limit.

5.2. Previous works suggesting that Ho II X-1 is powered by a black hole

The nature of the compact object in Ho II X-1 has been extensively discussed in the literature with many authors agreeing that the compact object in this ULX is a black hole. One of the strongest evidence for this hypothesis is the presence of a collimated jet (Cseh et al. 2014, 2015). The large kinematic energy carried away by the jet implies a minimum black hole mass of M• > 25 M⊙. This agrees with previous analysis of the source based on its X-ray luminosity (Grisé et al. 2010).

More detailed studies of the X-ray spectra of Ho II X-1 have been performed to better constrain the mass of the compact object and the accretion rate. As ULXs are variable X-ray sources, it is possible to analyse the changes in the relationship between the accretion disc luminosity and temperature. In the standard thin accretion disc model (Shakura & Sunyaev 1973), the disc luminosity and temperature are related as L ∝ T4. If confirmed from the analysis of X-ray spectra, the presence of such correlation provides strong support to the assumption that the luminosity of a source is < 0.3LEdd. Such analysis has been conducted for Ho II X-1. Feng & Kaaret (2009) concluded that Ho II X-1 might be accreting below the Eddington limit, but they stressed the necessity of repeating the analysis with a larger spectral sample. This is achieved in Barra et al. (2023) who analysed 17 XMM-Newton observations of Ho II X-1 spanning over ≈20 yr. They fit the X-ray spectra using a spectral model that combines two modified black body components (see details in Barra et al. 2023) and found that the luminosity of the lower temperature component does correlate with T4. Still, the correlation breaks for the hotter component when the bolometric luminosity exceeds 5 × 1039 erg s−1. They consider this value as the LEdd in Ho II X-1, and, on this basis, estimate M• ≈ 36 M⊙.

Unfortunately, there are caveats in this method because the disc temperature is deduced from the fitting of X-ray spectra using a handful of existing ready-to-use models, and hence is highly model-dependent. When considering the same data as analysed in Barra et al. (2023) we notice that some observations are mildly piled up, which may affect the spectral fitting results. Furthermore, the temperatures derived from spectral analysis depend on the spectral model describing interstellar absorption. For example, for the observations ObsID 0864550501 (simultaneous with the HST observations) we determine LX(0.2–12.0 keV) ≈ 1040 erg s−1, which is twice higher than the one reported in Barra et al. (2023). Taking at face value, the estimated black hole mass is M• ≈ 70 M⊙. Interestingly, Barra et al. (2023) report the largest deviation from the L ∝ T4 relation for the observation ObsID 0724810101. For the same data we derive NH = (8.4 ± 1.2)×1021 cm−2 using the standard absorption model (Morrison & McCammon 1983) and lower temperatures, kT1 = 0.29 ± 0.05 keV and kT2 = 1.86 ± 0.07 keV (χ2 = 108 for 78 d.o.f.) compared to Barra et al. (2023).

An upper limit for the compact object was proposed by Goad et al. (2006) by comparing the X-ray properties of Ho II X-1 with that of the microquasar GRS 1915+105. The authors concluded that the black hole in Ho II X-1 should be more massive than a stellar compact object, but less massive than 100 M⊙. Clearly, a better understanding of circumstellar gas around Ho II X-1 and more physically motivated disc models are needed to test whether Ho II X-1 sometimes accretes supercritcally.

Further evidence for a massive black hole in Ho II X-1 was presented by Ambrosi et al. (2022) who compared binary stellar evolution models with photometric measurements and obtained M• ∼ 50 M⊙.

5.3. The donor star and a possible evolution scenario for Ho II X-1

Ho II X-1 is located in a star-forming region of the Holmberg II galaxy (Fig. 1) right next to a young, 4 Myr old, OB star cluster, suggesting that it has escaped from that cluster and has a similar age. (Stewart et al. 2000; Egorov et al. 2017). This excludes an evolved low-mass star as the donor. The donor star in Ho II X-1 can only be a young, massive star. The absence of broad emission lines in the optical and UV spectra rules out that the companion is a WR star, while the photometry across UV, optical, and infrared wavelengths is not consistent with the donor star being a red supergiant either (Lau et al. 2017). Instead, all measurements are consistent with the donor being an OB-type supergiant (Tao et al. 2011; Lau et al. 2017; Vinokurov et al. 2022; Ambrosi et al. 2022).

Our new detailed spectroscopic analysis suggests that the donor star has B0.5I spectral type, and hence is only a few million years old. The donor star parameters are listed in Table 3. Unfortunately, the nebular contamination of the donor star spectra prevents any measurement of radial velocity variations, and hence impedes a direct constrain on the binary’s period. To estimate the period, we relied on the current radius and mass of the donor (22 R⊙ and 22 M⊙, respectively), and the estimated black hole mass (M• ≳ 66 M⊙). Making the plausible assumption of the donor filling its Roche lobe and transferring mass onto the black hole and following the approximation for the Roche lobe radius from Eggleton (1983), the binary period is Porb ∼ 6 d.

Table 3.

Stellar parameters for the donor star in the Ho II X-1 obtained from spectroscopic analysis.

A 4 Myr old binary system in which the primary has evolved to a 66 M⊙ black hole, and the secondary fills its Roche lobe, should have special properties. Initially, the primary star should be more massive than 150 M⊙, while the secondary should have a mass of ∼25 M⊙ (Ambrosi et al. 2022). The binary must have initially been in a wide orbital configuration with Porb ∼ 102 d − 103 d, which is wide enough for the primary to develop a massive core. However, the orbital separation should be small enough to allow the system to enter a common envelope phase at later evolutionary stages. We speculate that during the common envelope phase, the secondary (current donor) does not accrete any material and the primary directly collapses into a black hole. The secondary continues its evolution until it starts filling its Roche lobe and the system enters the current ULX phase.

During the accretion phase, the black hole accretes at the Eddington limit with Ṁacc ∼ 1.8 × 10−6 M⊙ yr−1. Assuming that the mass-transfer phase lasts less than 106 years, the black hole will accrete less than 2 M⊙ during this phase. This implies that the spin of the black hole is not expected to change significantly during the mass-transfer phase (Fragos & McClintock 2015).

It is worth noting that during the mass-transfer phase, the surface abundances of H, He, C, N, and O of the donor star are expected to change (Marchant et al. 2017), as is indeed commonly found in the blue supergiant donor stars in high-mass X-ray binaries (Hainich et al. 2020). That is, the surface hydrogen abundance drops to values of about XH ≈ 0.65 and the C, N, and O abundances change to the CNO equilibrium values. For consistency, we tested if our stellar atmosphere model is also consistent with these values and no discrepancies can be found. This is supported by the enhanced nitrogen abundance deduced from the high-resolution X-ray spectra of Ho II X-1 (Barra et al. 2023).

Eventually, the donor star will lose about half of its mass during the mass-transfer event, leaving behind a helium star of about 10–15 M⊙ that will collapse into a black hole or a neutron star. Since the mass ratio of the system is always q = M•/M* ≫ 1 the orbit of the system is expected to further shrink during the mass-transfer, bringing the components closer together. Their masses and proximity make this system a potential progenitor of a GW event, and might provide the missing link to explain the systems with extreme mass ratios as observed with LIGO/Virgo (Abbott et al. 2020).

6. Summary and conclusions

We present the first consistent multi-wavelength analysis of the ULX Ho II X-1 and its surrounding nebula. For this work, we have gathered archival optical and X-ray data, and presented the first medium-resolution UV spectrum obtained with the HST.

The detailed spectroscopic analysis reveals the lack of signatures of strong outflows in the UV spectra, contrary to the expectations for a supercritically accreting system. The absence of strong outflows is further corroborated by the lack of broad emission lines in the optical spectra, which also refutes claims of strong disc winds in Ho II X-1.

We successfully reproduce the composite spectrum of Ho II X-1 and the surrounding He III nebula. Using a combination of stellar atmosphere and photoionising codes, we consistently explain the observations and simultaneously characterise the nebula and its ionising source.

Furthermore, by analysing the SED and modelling the UV spectra, we obtain compelling evidence that the donor is a B supergiant with an estimated mass of M* ∼ 22 M⊙.

Based on the nebula modelling, we estimated the averaged X-ray luminosity of the ULX, and thus constrained the mass of the compact object as M• ≳ 66 M⊙. This aligns with previous works suggesting the presence of a heavy black hole in Ho II X-1.

We conclude that the ULX Ho II X-1 is a close binary system consisting of a black hole with M• ≳ 66 M⊙ and a B-type supergiant with M* ≈ 22 M⊙ filling its Roche lobe. Black holes within this mass range have so far only been observed via gravitational wave events (Abbott et al. 2020). This work not only enhances our understanding of ULXs but also contributes to the broader knowledge of massive black hole formation and evolution in binary systems.

Acknowledgments

We thank the referee for their useful comments. Based on observations with the NASA/ESA Hubble Space Telescope obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. Support for Programme number HST-GO-16182 was provided through a grant from the STScI under NASA contract NAS5-26555. Based on data from the GTC Archive at CAB (CSIC -INTA). The GTC Archive is part of the Spanish Virtual Observatory project funded by MCIN/AEI/10.13039/501100011033 through grant PID2020-112949GB-I00. S.R.S. and D.P. acknowledge financial support by the Deutsches Zentrum für Luft und Raumfahrt (DLR) grants FKZ 50OR2108 and 50OR2005. AACS and VR acknowledge support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) in the form of an Emmy Noether Research Group – Project-ID 445674056 (SA4064/1-1, PI Sander). AACS and VR further acknowledge support from the Federal Ministry of Education and Research (BMBF) and the Baden-Württemberg Ministry of Science as part of the Excellence Strategy of the German Federal and State Governments. TB was supported by the NCN grant n 2023/49/B/ST9/02777. The collaboration of co-authors was facilitated by support from the International Space Science Institute (ISSI, Bern).

References

  1. Abbott, R., Abbott, T. D., Abraham, S., et al. 2020, Phys. Rev. Lett., 125, 101102 [Google Scholar]
  2. Ambrosi, E., & Zampieri, L. 2018, MNRAS, 480, 4918 [Google Scholar]
  3. Ambrosi, E., Zampieri, L., Pintore, F., & Wolter, A. 2022, MNRAS, 509, 4694 [Google Scholar]
  4. Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
  5. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
  7. Barra, F., Pinto, C., Middleton, M., et al. 2024, A&A, 682, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Berghea, C. T., Dudik, R. P., Weaver, K. A., & Kallman, T. R. 2010a, ApJ, 708, 354 [NASA ADS] [CrossRef] [Google Scholar]
  9. Berghea, C. T., Dudik, R. P., Weaver, K. A., & Kallman, T. R. 2010b, ApJ, 708, 364 [NASA ADS] [CrossRef] [Google Scholar]
  10. Castro Segura, N., Knigge, C., Long, K. S., et al. 2022, Nature, 603, 52 [NASA ADS] [CrossRef] [Google Scholar]
  11. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  12. Croxall, K. V., van Zee, L., Lee, H., et al. 2009, ApJ, 705, 723 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cseh, D., Kaaret, P., Corbel, S., et al. 2014, MNRAS, 439, L1 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cseh, D., Miller-Jones, J. C. A., Jonker, P. G., et al. 2015, MNRAS, 452, 24 [NASA ADS] [CrossRef] [Google Scholar]
  15. Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
  16. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  17. Egorov, O. V., Lozinskaya, T. A., & Moiseev, A. V. 2013, MNRAS, 429, 1450 [NASA ADS] [CrossRef] [Google Scholar]
  18. Egorov, O. V., Lozinskaya, T. A., & Moiseev, A. V. 2017, MNRAS, 467, L1 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fabrika, S., Ueda, Y., Vinokurov, A., Sholukhova, O., & Shidatsu, M. 2015, Nat. Phys., 11, 551 [NASA ADS] [CrossRef] [Google Scholar]
  20. Feng, H., & Kaaret, P. 2009, ApJ, 696, 1712 [Google Scholar]
  21. Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
  22. Fragos, T., Lehmer, B., Tremmel, M., et al. 2013, ApJ, 764, 41 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fragos, T., & McClintock, J. E. 2015, ApJ, 800, 17 [Google Scholar]
  24. Gierliński, M., Done, C., & Page, K. 2009, MNRAS, 392, 1106 [CrossRef] [Google Scholar]
  25. Goad, M. R., Roberts, T. P., Reeves, J. N., & Uttley, P. 2006, MNRAS, 365, 191 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gómez-González, V. M. A., Mayya, Y. D., & Rosa-González, D. 2016, MNRAS, 460, 1555 [Google Scholar]
  27. Gräfener, G., Koesterke, L., & Hamann, W. R. 2002, A&A, 387, 244 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Green, J. C., Froning, C. S., Osterman, S., et al. 2012, ApJ, 744, 60 [NASA ADS] [CrossRef] [Google Scholar]
  29. Grisé, F., Kaaret, P., Feng, H., Kajava, J. J. E., & Farrell, S. A. 2010, ApJ, 724, L148 [Google Scholar]
  30. Gúrpide, A., Godet, O., Koliopanos, F., Webb, N., & Olive, J. F. 2021a, A&A, 649, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Gúrpide, A., Godet, O., Vasilopoulos, G., Webb, N. A., & Olive, J. F. 2021b, A&A, 654, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Hainich, R., Oskinova, L. M., Shenar, T., et al. 2018, A&A, 609, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Hainich, R., Ramachandran, V., Shenar, T., et al. 2019, A&A, 621, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Hainich, R., Oskinova, L. M., Torrejón, J. M., et al. 2020, A&A, 634, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Hamann, W. R., & Gräfener, G. 2004, A&A, 427, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Heida, M., Jonker, P. G., Torres, M. A. P., et al. 2014, MNRAS, 442, 1054 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hoessel, J. G., Saha, A., & Danielson, G. E. 1998, AJ, 115, 573 [NASA ADS] [CrossRef] [Google Scholar]
  38. James, B. L. 2022, COS Instrument Handbook v. 14.0, 14, 14 [Google Scholar]
  39. Kaaret, P., Ward, M. J., & Zezas, A. 2004, MNRAS, 351, L83 [NASA ADS] [CrossRef] [Google Scholar]
  40. Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
  41. Kajava, J. J. E., Poutanen, J., Farrell, S. A., Grisé, F., & Kaaret, P. 2012, MNRAS, 422, 990 [NASA ADS] [CrossRef] [Google Scholar]
  42. King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96 [Google Scholar]
  43. Kosec, P., Pinto, C., Walton, D. J., et al. 2018a, MNRAS, 479, 3978 [NASA ADS] [Google Scholar]
  44. Kosec, P., Fabian, A., Walton, D., & Pinto, C. 2018b, in 42nd COSPAR Scientific Assembly, 42, E1.13 [Google Scholar]
  45. Kovlakas, K., Zezas, A., Andrews, J. J., et al. 2020, MNRAS, 498, 4790 [Google Scholar]
  46. Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2020, NIST Atomic Spectra Database (ver. 5.10) (Gaithersburg, MD: National Institute of Standards and Technology), [Online]. Available: https://physics.nist.gov/asd [2023, November 14] [Google Scholar]
  47. Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds [Google Scholar]
  48. Lau, R. M., Heida, M., Kasliwal, M. M., & Walton, D. J. 2017, ApJ, 838, L17 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lau, R. M., Heida, M., Walton, D. J., et al. 2019, ApJ, 878, 71 [NASA ADS] [CrossRef] [Google Scholar]
  50. Liu, J.-F., Bregman, J. N., & Seitzer, P. 2004, ApJ, 602, 249 [NASA ADS] [CrossRef] [Google Scholar]
  51. Long, K. S., Charles, P. A., & Dubus, G. 2002, ApJ, 569, 204 [NASA ADS] [CrossRef] [Google Scholar]
  52. Marchant, P., Langer, N., Podsiadlowski, P., et al. 2017, A&A, 604, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Martínez-Núñez, S., Kretschmar, P., Bozzo, E., et al. 2017, Space Sci. Rev., 212, 59 [Google Scholar]
  54. Martins, F., & Palacios, A. 2021, A&A, 645, A67 [EDP Sciences] [Google Scholar]
  55. Mineshige, S., Hirano, A., Kitamoto, S., Yamada, T. T., & Fukue, J. 1994, ApJ, 426, 308 [NASA ADS] [CrossRef] [Google Scholar]
  56. Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
  57. Mondal, S., Belczyński, K., Wiktorowicz, G., Lasota, J.-P., & King, A. R. 2020, MNRAS, 491, 2747 [Google Scholar]
  58. Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [Google Scholar]
  59. Morton, D. C. 1967, ApJ, 147, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  60. Muñoz-Darias, T., Armas Padilla, M., Jiménez-Ibarra, F., et al. 2020, ApJ, 893, L19 [CrossRef] [Google Scholar]
  61. Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei [Google Scholar]
  62. Pakull, M. W., & Mirioni, L. 2002, ArXiv e-prints [arXiv: astro-ph/0202488] [Google Scholar]
  63. Panizo-Espinar, G., Armas Padilla, M., Muñoz-Darias, T., et al. 2022, A&A, 664, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  65. Pinto, C., Middleton, M. J., & Fabian, A. C. 2016, Nature, 533, 64 [Google Scholar]
  66. Pintore, F., Zampieri, L., Wolter, A., & Belloni, T. 2014, MNRAS, 439, 3461 [Google Scholar]
  67. Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
  68. Poutanen, J., Fabrika, S., Valeev, A. F., Sholukhova, O., & Greiner, J. 2013, MNRAS, 432, 506 [NASA ADS] [CrossRef] [Google Scholar]
  69. Ramachandran, V., Oskinova, L. M., Hamann, W. R., et al. 2022, A&A, 667, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Sánchez-Sierras, J., Muñoz-Darias, T., Casares, J., et al. 2023, A&A, 673, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Sander, A., Shenar, T., Hainich, R., et al. 2015, A&A, 577, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Searle, S. C., Prinja, R. K., Massa, D., & Ryans, R. 2008, A&A, 481, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  74. Soria, R., Wu, K., & Hunstead, R. W. 2000, ApJ, 539, 445 [NASA ADS] [CrossRef] [Google Scholar]
  75. Stewart, S. G., Fanelli, M. N., Byrd, G. G., et al. 2000, ApJ, 529, 201 [NASA ADS] [CrossRef] [Google Scholar]
  76. Tao, L., Feng, H., Grisé, F., & Kaaret, P. 2011, ApJ, 737, 81 [NASA ADS] [CrossRef] [Google Scholar]
  77. Tao, L., Kaaret, P., Feng, H., & Grisé, F. 2012, ApJ, 750, 110 [NASA ADS] [CrossRef] [Google Scholar]
  78. Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
  79. Todt, H., Sander, A., Hainich, R., et al. 2015, A&A, 579, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Toyouchi, D., Hotokezaka, K., Inayoshi, K., & Kuiper, R. 2024, MNRAS, 532, 4826 [NASA ADS] [CrossRef] [Google Scholar]
  81. van Paradijs, J., & Stollman, G. M. 1984, A&A, 137, L12 [NASA ADS] [Google Scholar]
  82. Vinokurov, A., Atapin, K., Bordoloi, O. P., et al. 2022, Astrophys. Bull., 77, 231 [NASA ADS] [CrossRef] [Google Scholar]
  83. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
  84. Zhou, C., Feng, H., & Bian, F. 2023, ApJ, 947, 52 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Observation log tables

Table A.1.

Observation log for the HST-COS data. Programme ID: 16182, PI: L. Oskinova

Table A.2.

Observation log for the Subaru-FOCAS data. Proposal ID: o11104, PI: Y. Ueda

Table A.3.

Observation log for the GTC-OSIRIS data. Programme IDs: GTC20-11B and GTC38-10B, PI: F. Vilardell

All Tables

Table 1.

HST photometric data used to construct the SED.

In the text
Table 2.

Parameters of the best-fit spectral models to the observed XMM-Newton EPIC PN spectrum of Ho II X-1 (ObsID:0864550501).

In the text
Table 3.

Stellar parameters for the donor star in the Ho II X-1 obtained from spectroscopic analysis.

In the text
Table A.1.

Observation log for the HST-COS data. Programme ID: 16182, PI: L. Oskinova

In the text
Table A.2.

Observation log for the Subaru-FOCAS data. Proposal ID: o11104, PI: Y. Ueda

In the text
Table A.3.

Observation log for the GTC-OSIRIS data. Programme IDs: GTC20-11B and GTC38-10B, PI: F. Vilardell

In the text

All Figures

thumbnail Fig. 1.

False-colour HST ACS image of the area around the ULX Ho II X-1 with the adjacent H II region known as the ‘Foot Nebula’. This composite image comprises observations taken with the F502N (blue), F658N (green), and F814W (red) filters. The white circle highlights the He III bubble generated by ionising X-ray radiation emitted by the ULX, and has a diameter of 2 . ″ $ \overset{\prime \prime }{.} $5, corresponding to 37 pc at the distance of the Holmberg II galaxy. The ULX optical counterpart is seen as the white spot centred in the cycle. In the lower right corner, the acquisition image of our HST COS observations is displayed. The 2 . ″ $ \overset{\prime \prime }{.} $5 diameter aperture (shown as a red circle) encompasses the ULX, the He III bubble, and two neighbouring UV-bright stars. North is up and east is to the left.
In the text
thumbnail Fig. 2.

Ultraviolet spectra extracted from the HST COS observations of Ho II X-1. As is shown in the insert in Fig. 1, there are three point-like sources within the COS aperture. The black line shows the combined spectrum of all three sources. The spectra are disentangled (Sect. 2.1) to separate the ULX from the neighbouring sources, presumably OB-type stars. The red line shows the spectrum of the UV counterpart of Ho II X-1, while the combined spectra of two other sources within the COS field of view are plotted in blue.
In the text
thumbnail Fig. 3.

Ultraviolet spectrum of Ho II X-1 normalised to the stellar model continuum. Solid blue: the COS disentangled spectrum; dotted green: the modelled PoWR stellar spectrum of a B0.5I supergiant (T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3, see Sect. 3.1); dotted purple: the CLOUDY nebular model for an X-ray ionising source modelled with diskir (see Sect. 3.3); dotted red: the combined PoWR and CLOUDY spectra. This last one also accounts for interstellar absorption lines (i.s.)
In the text
thumbnail Fig. 4.

Optical spectrum of Ho II X-1 taken with the Subaru telescope. The spectrum is normalised to the stellar model continuum and corrected for extinction. In blue, the observations, in dotted green the synthetic stellar spectrum from the PoWR model for a B0.5I supergiant (T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3), in dotted purple the CLOUDY nebular model for an X-ray ionising source modelled with diskir, and in dotted red the combined PoWR and CLOUDY spectra. The most relevant features are identified in black, while those identified in green correspond to high ionisation stages of iron and calcium overpredicted by the CLOUDY model (Sect. 3.3).
In the text
thumbnail Fig. 5.

Same as Fig. 4, but with the observed spectrum taken with the GTC.
In the text
thumbnail Fig. 6.

Spectral energy distribution (SED) of the ULX Ho II X-1 from UV to optical. Upper panel A: The blue line shows the data extracted from the observations with HST COS (UV), GTC OSIRIS and Subaru FOCAS (both in the optical). The blue boxes display photometric measurements from the HST ACS SBC F165LP in the UV and from HST WFPC2 in the optical (Sect. 4.1). The black lines at the bottom represent the filter wavelength ranges, each of them identified by the name of the filter. The red line indicates the synthetic PoWR SED for a B0.5I supergiant with T* =  26 k K, log g =  3.1 cm s−2 and log L/L⊙ =  5.3. The red hatched boxes show the modelled photometry. Bottom panel B: The blue boxes are the photometric measurements of the Ho II X-1 counterpart from HST filters without any correction for the nebular contribution. The purple line shows the synthetic CLOUDY SED for a nebula photoionised by an X-ray source, as is described by a diskir model (Sect. 3.2, Table 2), and with a luminosity of Lbol =  1.4 × 1040 erg s−1. The green line represents the synthetic PoWR SED for a B0.5I supergiant with T* =  26 k K, log g =  3.1 [cm s−2] and log L/L⊙ =  5.3. The red line is the combination of both PoWR and CLOUDY models, and the red-hatched boxes represent the modelled photometry for the combined model.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.