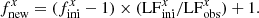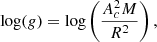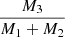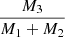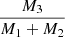| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 22 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450797 | |
| Published online | 08 October 2024 | |
Spectroscopy of eclipsing compact hierarchical triples
I. Low-mass double-lined and triple-lined systems
1
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Rabiańska 8, 87-100 Toruń, Poland
2
Villanova University, Dept. of Astrophysics and Planetary Sciences, 800 East Lancaster Avenue, Villanova, PA 19085, USA
3
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warszawa, Poland
4
Facultad de Ingeniería y Ciencias, Universidad Adolfo Ibáñez, Av. Diagonal las Torres, 2640 Peñalolén, Santiago, Chile
5
Millennium Institute for Astrophysics, Monseñor Nuncio Sótero Sanz 100, Of. 104, Providencia, Santiago, Chile
6
Data Observatory Foundation, Eliodoro Yáñez, 2990 Providencia, Santiago, Chile
7
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, 21218 MD, USA
Received:
20
May
2024
Accepted:
29
June
2024
Context. Eclipsing compact hierarchical triples (CHTs) are systems in which a tertiary star orbits an eclipsing binary (EB) in an orbit of fewer than 1000 days. In a CHT, all three stars exist in a space that is less than 5 AU in radius. A low-mass CHT is an interesting case through which we can understand the formation of multiple stars and planets at such small scales.
Aims. In this study, we combine spectroscopy and photometry to estimate the orbital, stellar, and atmospheric parameters of stars in a sample of CHTs. Using the complete set of parameters, we aim to constrain the metallicity and age of the systems.
Methods. We used time-series spectroscopy to obtain radial velocities (RVs) and disentangled spectra. Using RV modelling, EB light curve modelling, and spectral analysis, we estimated the metallicities and temperatures. Using isochrone fitting, we constrained the ages of the system. We then combined observations of masses, outer eccentricities (e2), orbital periods, and age estimates of the systems from the literature. We compared the distributions of e2, and the tertiary mass ratio, q3 = M3/(M1 + M2), for three different metallicity ranges and two age ranges.
Results. We have estimated the masses, radii, temperatures, metallicities, and ages of 12 stars in four CHTs. The CHT CD-32 6459 shows signs of von Zeipel-Lidov-Kozai oscillations, while CD-62 1257 can evolve to form a triple common envelope. The rest of the CHTs are old and have an M-dwarf tertiary. We find that the q3 distribution for CHTs with sub-solar metallicity has a uniform distribution but the systems with solar and above-solar metallicity peak between 0.5 and 1. When dividing them according to their ages, we find the q3 of old systems to be around 0.5. The eccentricity, e2, favours a value of around 0.3 irrespective of metallicity or age. The distributions of q3 and e2 resemble the distributions of the mass ratio and eccentricity of close field binaries.
Key words: binaries: eclipsing / binaries: spectroscopic / stars: evolution / stars: formation / stars: fundamental parameters
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Stellar multiplicity is a well-established phenomenon (Duchêne & Kraus 2013). While thousands of binaries and multiples were observed in the 19th century (Herschel et al. 1874), Harrington (1972) was one of the first to use the observations to understand multiple stars as a separate population. Later, with better samples and improved theories, we started having a better understanding of triple (and multiple) stars around the new millennium (Eggleton & Kiseleva 1995; Mardling & Aarseth 2001).
The previous and present decades have seen a revolution in observing and understanding multiple stars. While it was radial velocity (RV) surveys (Tokovinin 2004) that helped us to identify different hierarchies of multiple-star systems, most of the new detections have been from photometric surveys like the Optical Gravitational Lensing Experiment (OGLE; Udalski et al. 1992) and the All Sky Automated Survey (ASAS; Pojmanski 1997). Recently, space-based surveys like Kepler (Borucki et al. 2010) and the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) have been revolutionary in detecting and characterising binaries, triples, and multiple stars.
Triples, especially, have been the subject of renewed interest recently. They are emerging as possible explanations for several problems in stellar astrophysics. This includes triple dynamics as an explanation for asymmetry of planetary nebula (Jones et al. 2019) formation of Thorne-Zytków objects (Eisner et al. 2022), blue stragglers (Perets & Fabrycky 2009), recurrent novae (Knigge et al. 2022), and Type Ia supernovae (Naoz & Fabrycky 2014).
A special class of triple stars, compact hierarchical triples (CHTs), have seen increased incidence rates, which is surprising as they were considered rare before (Tokovinin 2004). Compact hierarchical triples are hierarchical systems in which the tertiary orbits an inner binary with an orbital period of less than 1000 days (Borkovits 2022). This, in principle, can cause dynamic changes in these systems that can be characterised by a few years of observation. If we have an eclipsing binary (EB) as the inner binary, we can extract the parameters of each component in the system. This has led to eclipse timing programs helping us find hundreds of new CHTs from different EB catalogues (Borkovits et al. 2016; Hajdu et al. 2019; Mitnyan et al. 2024).
Estimating the precise stellar and orbital parameters of CHTs opens up an avenue through which to study stellar evolution coupled with dynamical evolution. Further, using the distribution of orbital parameters and masses, we can understand star formation at scales at which planet formation usually occurs (≤5 AU). While triply eclipsing systems (E3CHTs) can provide ultra-precise mass and radius measurements (Borkovits et al. 2019), using time-series spectroscopy of doubly eclipsing systems (E2CHTs) can also help us fill the same parameter space (Moharana et al. 2023).
In this paper, we present the total parameters of four E2CHTs using high-resolution spectroscopy coupled with TESS photometry. Two of these systems, CD-58 963 (hereby CD58) and BD+11 359 (hereby BD11), are spectroscopic double-lined (ST2) systems, while CD-62 1257 (hereafter CD62) and CD-32 6459 (hereby CD32) are triple-lined (ST3) systems. Three of these systems (CD32, CD62, and BD11) are newly identified CHTs.
CD32 was first classified as an eccentric EB by (Shivvers et al. 2014) using observations from the All Sky Automated Survey (ASAS; Pojmanski 2002). Kim et al. (2018) was the first to observe variation in eclipse times in the system, but they did not find any tertiary star signatures. While these works provide accurate estimates of the period and eccentricity, we provide the first measurements of stellar parameters of the EB stars and the tertiary companion. Though CD32 is not a CHT by the strictest of definitions (outer period of ∼1300 d), we try to see if they are any different.
CD62 was first flagged as an EB in the first TESS EB catalogue (Prša et al. 2022). The first light curve (LC) analysis was done by Ulaş & Ayan (2023), but with the assumption that the system is a binary. This affected the estimated parameters as the tertiary in the system contributes a significant amount of third light (∼50%), which was assumed to be zero in their analysis.
CD58 was first identified as a multiple system with EB by Borkovits et al. (2020a). It was one of the first CHTs discovered with TESS, as it is in the continuous viewing zone (CVZ) and has been observed since the first year of TESS. With eclipse timing from Wide-Angle Search for Planets (WASP; Pollacco et al. 2006), Borkovits et al. (2020a) showed that CD58 is a hierarchical quadruple on a wide 2661 d orbit around the CHT. We do not find any signs of the quadruple but the point to note is that we do not have good coverage over the quadruple period. CD58 is the tightest CHT in this sample, with an outer-orbit period of 76.32 d. Such systems are considered very rare, as it is difficult to survive the migration evolution from early formation (Tokovinin & Moe 2020).
BD11 was identified as an EB in the ASAS survey and its first spectroscopic and LC solution was given by Hełminiak et al. (2009). Later, Kozłowski et al. (2014) used it as a test object for their BACHES spectrograph and also presented an initial orbital solution. None of those works describes BD11 as a triple.
2. Observations
2.1. Photometry
All of the targets were observed by TESS1 for at least two sectors. For our work, we chose the best sectors considering (i) minimal cadence, (ii) low stellar activity or out-of-eclipse variations, and (iii) long-term coverage to detect eclipse depth variations (EDVs), if any. All the chosen sectors had a minimal cadence of two minutes. CD58 has been studied before, using sectors 1 to 12. We analysed the system with new observations from sectors 62 to 69. We extracted LCs using the LIGHTKURVE2 package. We extracted the photometry using the standard pipeline aperture.
While CD32 (TIC 24972851) and CD58 (TIC 220397947) are well isolated in the TESS frames, CD62 (TIC 387107961) and BD11 (TIC 408834852) have close-by stars. We checked for any contaminant signature (e.g. pulsations, eclipses, or transits) but did not find any, and therefore used the pipeline photometry.
The detrending was done with WOTAN3 (Hippke et al. 2019). We used the bi-weight de-trending method in a window 0.5−3 times the orbital period (depending on the trends). The normalised output from WOTAN was then converted to the magnitude scale by using zero-points that adjusted the out-of-eclipse magnitude to the TESS magnitude registered in the TESS catalogue.
2.2. Spectroscopy
The spectroscopy was obtained from a set of high-resolution spectrographs that includes a Fibre-fed Extended Range Optical Spectrograph (FEROS; R ∼ 48 000) at the MPG/ESO 2.2m telescope in La Silla (Kaufer et al. 1999), CHIRON (R ∼ 28 000 in the fiber mode) at the CTIO 1.5m telescope in Cerro Tololo (Tokovinin et al. 2013), CORALIE (R ∼ 70 000) at the 1.2m Euler telescope in La Silla (Queloz et al. 2000), the High-Resolution Spectrograph (HRS; R ∼ 67 000) at the 9.2m SALT in Sutherland (Crause et al. 2014), and the High Accuracy Radial velocity Planet Searcher (HARPS; R ∼ 115 000) at the 3.6m ESO telescope in La Silla (Mayor et al. 2003) (see Table 1). Additionally, for BD11 we also used RV measurements from Hełminiak et al. (2009) that were based on data obtained with the University College London Echelle Spectrograph (UCLES) at the 3.9m AAT in Siding Spring Observatory. We did not use BACHES data from Kozłowski et al. (2014), as they are of significantly lower quality.
All the spectroscopic observations used for RV extraction.
The CORALIE and FEROS spectrographs both work in a simultaneous object-calibration manner. Spectra were reduced with the dedicated python-based pipeline (Jordán et al. 2014; Brahm et al. 2017), optimised to derive high-precision RVs, which also performs barycentric corrections. The pipeline reduces CORALIE spectra to 70 rows spanning from 3840 to 6900 Å, of which we used only 45 rows (4400–6500 Å), to avoid the broad Hα line and the blue part with a very low signal. For FEROS, the output was reduced to 21 rows covering 4115–6519 Å, of which we used 20 (4135–6500 Å).
The CHIRON spectra were reduced with the pipeline developed at Yale University (Tokovinin et al. 2013). Wavelength calibration was based on ThAr lamp exposures taken just before the science observation. Barycentric corrections are not applied by the pipeline; thus, we calculated them ourselves under IRAF4 with the bcvcor task.
The HRS spectra were obtained by the long-term programme 2021-2-MLT-006 (PI: Moharana), which focused on the spectroscopic monitoring of CHTs. They were made available after reduction with the MIDAS HRS pipeline (Kniazev et al. 2016, 2017). While the products included spectra in the blue arm (370−550 nm) and the red arm (550−890 nm), we used the blue arm to avoid contamination by the static telluric lines. The barycentric correction was also done with bcvcor.
The HARPS data were reduced on site, including wavelength calibration and barycentric correction, with ESO’s data reduction system (DRS). They are available through the ESO Archive.
3. Analysis
3.1. Radial velocity extraction and fitting
The RVs were calculated with a TODCOR method (Zucker & Mazeh 1994), with synthetic spectra computed with ATLAS9 code as templates. Measurement errors were calculated with a bootstrap approach, and used for weighting the measurements during the orbital fit, as they are sensitive to the signal-to-noise ratio (S/N) of the spectra and rotational broadening of the lines. Though this code is optimised for double-lined spectroscopic binaries (SB2) and provides velocities for two stars (u1, u2), it can still be used for ST3 as well. In an ST3, the tertiary’s velocities were found from a local maximum, where u1 was set for the tertiary, and u2 for the brighter component of the eclipsing pair.
The orbital solutions were found using our procedure called V2FIT (Konacki et al. 2010). It applies a Levenberg-Marquardt minimisation scheme to find orbital parameters of a double-Keplerian orbit, which can optionally be perturbed by several effects, like a circumbinary body. We fitted for the binary period (PA), time of periastron passage of the inner orbit (TpA), inner eccentricity (eA), argument of periastron (ω), semi-amplitudes of the EB (KAa, KAb), projection of the semi-major axis (aAsin i1), and systemic velocity (γA). The fitting follows the procedure defined in Hełminiak et al. (2017), Moharana et al. (2023), and references therein.
In addition, for each observation for which three sets of lines were sufficiently separated, we also calculated the systemic velocities, γ(ti), of the inner pair using the formula
where v1, 2(ti) are the measured RVs of the inner binary, and q is its mass ratio, found from the RV fit with a circumbinary perturbation. With these values as the centre-of-mass (COM) RVs of the binary, and RVs of the tertiary component, we can treat the long-period outer orbit as a spectroscopic double-lined system, and independently look for its parameters. The final values of PAB, Kout, eAB, and so on, come from such fits. For the triple spectroscopic double-lined systems (ST2), this is the only way of estimating the orbital parameters of the third body and its projected mass (MBsin iAB).
The results of our orbital RV fits are presented in Table 2. The RV measurements and modelled curves are shown in Figures 1 and 2 for the ST3 and ST2 cases, respectively. Individual measurements are given in Appendix A.
Orbital parameters of the binary and tertiary orbit obtained by RV modelling.
 |
Fig. 1. RVs and orbital solutions of the ST3 systems CD32 (top) and CD62 (bottom). The left panels present the inner binary Aa+Ab corrected for its COM. Primary components are marked with red triangles and secondary ones with blue squares. The right panels present the outer orbit, with the inner binary’s COM (calculated with Equation 1) represented by purple squares and the tertiary’s RVs by green triangles. The dashed line marks the γ velocity of the whole system. |
 |
Fig. 2. Same as Fig. 2 but for ST2 systems CD58 (top) and BD11 (bottom). Since there are no RVs of the tertiary, the right panels show only the binary’s COM. |
3.2. Light curve fitting
We used version 40 of the JKTEBOP code (Southworth 2013) for our LC modelling. JKTEBOP models a star as a sphere or as a biaxial spheroid and calculates the LC by numerical integration of concentric circles. This allows it to fit only detached EBs. With binary periods of more than two days, JKTEBOP is well suited for solving our systems. We modelled every TESS sector separately except for CD58, where we modelled only half of the LC for a sector. In our modelling process, we first fixed certain parameters from RV modelling, and/or from prior knowledge about the type of stars. The fixed parameters are (i) mass-ratio (q), and (ii) limb-darkening coefficients. We took initial values for PA from the RV solution but varied them during our modelling. We also took a visual estimate of the time of super-conjugation (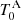 ) and optimised it later. We optimised the following LC parameters: (i) PA, (ii)
) and optimised it later. We optimised the following LC parameters: (i) PA, (ii) 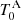 , (iii) the scale-factor (which determines the scaling or the magnitude of the out-of-eclipse portion), (iv) the surface brightness ratio (J), (v) the third light (L3), (vi) eA and ω in the form of esin ω and e cos ω, (vii) the inclination of inner binary (iA), (viii) the radius ratio (k), and (ix) the sum of fractional radii (r1 + r2), where the fractional radii are represented as the radius divided by the semi-major axis (aA). The optimisation was iterated until we got the best fit. To test the convergence, we randomly fixed certain parameters and optimised the others to check the stability. We then estimated the errors on the parameters by using the Monte Carlo (MC) module available on JKTEBOP. We followed this exact prescription for all the targets except CD58. CD58 has shallow eclipses (the primary eclipse has a depth of ∼0.04 mag) and shows stellar activity that varies with every sector. On top of that, the tertiary orbital period is 77 d. This causes eclipse timing variations (ETVs) that affect radii measurement in one TESS sector and that is why we used half a sector for our modelling. To get a consistent solution over sectors, we first fixed the third light to zero. JKTEBOP allows one to set the light ratio from spectroscopy as a constraint, so we constrained the optimisation by fixing the light ratio of the components as the values obtained from broadening function (BF) fitting (see Sect. 3.4.1). The rest of the optimisation process was the same as before. The MC sampling for CD58 was initiated with the final optimised parameters but without constraints from the light ratio. The final fits to the LC are shown in Figure 3. The final results for all the targets for all the modelled sectors are given in Appendix B. We adopted the final estimates of all the parameters as the average of all the sectors.
, (iii) the scale-factor (which determines the scaling or the magnitude of the out-of-eclipse portion), (iv) the surface brightness ratio (J), (v) the third light (L3), (vi) eA and ω in the form of esin ω and e cos ω, (vii) the inclination of inner binary (iA), (viii) the radius ratio (k), and (ix) the sum of fractional radii (r1 + r2), where the fractional radii are represented as the radius divided by the semi-major axis (aA). The optimisation was iterated until we got the best fit. To test the convergence, we randomly fixed certain parameters and optimised the others to check the stability. We then estimated the errors on the parameters by using the Monte Carlo (MC) module available on JKTEBOP. We followed this exact prescription for all the targets except CD58. CD58 has shallow eclipses (the primary eclipse has a depth of ∼0.04 mag) and shows stellar activity that varies with every sector. On top of that, the tertiary orbital period is 77 d. This causes eclipse timing variations (ETVs) that affect radii measurement in one TESS sector and that is why we used half a sector for our modelling. To get a consistent solution over sectors, we first fixed the third light to zero. JKTEBOP allows one to set the light ratio from spectroscopy as a constraint, so we constrained the optimisation by fixing the light ratio of the components as the values obtained from broadening function (BF) fitting (see Sect. 3.4.1). The rest of the optimisation process was the same as before. The MC sampling for CD58 was initiated with the final optimised parameters but without constraints from the light ratio. The final fits to the LC are shown in Figure 3. The final results for all the targets for all the modelled sectors are given in Appendix B. We adopted the final estimates of all the parameters as the average of all the sectors.
 |
Fig. 3. JKTEBOP models (purple lines) for the first and the last used in our modelling of TESS observations (centre and last panel, respectively). The variable stellar activity can be seen in the sector-wise observations and models. The eccentric and near-circular systems can be distinguished from the phased LC observations and models (first panel). |
3.3. Estimate of orbital configuration
Combining both the LC and RV analyses, we can get a picture of the orbital architecture of the systems, except the estimate of the mutual inclination (imut). This is possible for both ST2 and ST3 systems if we observe dynamical effects in ETVs. For ST3 systems specifically, we can estimate imut using inclinations of the binary (iA) and tertiary (iAB) orbits. Using equations described in Moharana et al. (2023), we get two different sets of limits for the imut. With the estimated value of imut for ST3 systems, and an arbitrary value for ST2 systems, we can simulate the orbits using numerical integration. We used REBOUND5 (Rein & Liu 2012), an n-body numerical integration code, to obtain the architecture of the systems. The configuration of the orbits in the XZ plane (the Z axis is towards the observer) is shown in Figure 4.
 |
Fig. 4. Orbital configuration of the targets viewed perpendicular to the observers’ plane (XY plane). The COM of the system is at (0,0). |
3.4. Spectroscopic analysis
For our spectroscopic analysis, we need a set of homogeneous spectroscopic data; in other words, from a single instrument. We selected a set of time-series spectroscopy for each target with clean line profiles and good S/N. This resulted in a set of 9 CHIRON spectra for CD32, 7 HRS spectra for CD62, 13 HRS spectra for CD58, and 8 FEROS spectra for BD11. All further analyses were done on these sets of spectra.
3.4.1. Broadening functions
We used BFs (Rucinski 1999) to (i) estimate light fractions (LF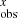 ), and (ii) estimate the projection of rotational velocity (vxsin i) of the component, x. The BF was generated with a variation of the BF code, BF-RVPLOTTER6. Clean BFs (where we can see all spectral components) were modelled with the rotational profile from Gray (2005) using the formula
), and (ii) estimate the projection of rotational velocity (vxsin i) of the component, x. The BF was generated with a variation of the BF code, BF-RVPLOTTER6. Clean BFs (where we can see all spectral components) were modelled with the rotational profile from Gray (2005) using the formula
where A is the area under the profile and vmax is the maximum velocity shift that occurs at the equator. The terms c1 and c2 are constants that are a function of limb darkening themselves, while l and k are correction factors to the BF ‘continuum’. The final LF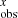 , and vxsin i values were taken as the average of all the epochs of spectra, with respective standard deviations as errors. These values are presented in the lower panel of Table 3.
, and vxsin i values were taken as the average of all the epochs of spectra, with respective standard deviations as errors. These values are presented in the lower panel of Table 3.
Atmospheric parameters obtained from our spectroscopic analysis on the disentangled spectra.
3.4.2. Spectral disentangling
We separated the individual spectra from the composite spectra using the method of spectral disentangling with the shift-and-add algorithm (González & Levato 2006) implemented in the code DISENTANGLING_SHIFT_AND_ADD7 (DSAA; Shenar et al. 2020, 2022). DSAA disentangles spectra in the velocity space by applying simple velocity shifts corresponding to one component and creating an averaged spectrum. This is iterated for every component until the final individual spectra have no contribution from the rest of the components. The code takes in orbital parameters along with a list of times of epoch to disentangle the spectra. We disentangled spectra in the wavelength range from 4870 Å to 5300 Å. This region was selected to avoid wide lines and due to the availability of sufficient narrow lines for spectral analysis. We initially assumed equal light fractions for the component. The final disentangled spectra were accepted after using DSAA for 30 000 iterations. In addition to the convergence checks built into the code, we also calculated cross-correlation plots on the final output to check for any contaminant lines in the spectra due to the disentangling process. The disentangled spectra had trends in the continuum, which were a result of bias in normalisation, light-fraction variation, et cetera (Hensberge et al. 2008). The amplitude of these trends varies depending on the number, the extent of convolution of line profiles, and the wavelength range of the spectra used for disentangling. Further, it depended on the spectrograph, which we attribute to either the stability of the spectrograph or the accuracy of the spectral reduction method. To address the first source of bias, we selected the best spectra by preliminary trials with the wavelength range and set of spectra. Further, we cleaned this additive form of bias by modelling this trend and subtracting it from the component spectra, following the process in Hensberge et al. (2008). We then scaled the spectra for a component, x, to the observed values (from BF) of the light fraction, using the formula
3.4.3. Synthetic spectral fitting
For the measurement of effective temperature (Teff), metallicity ([M/H]), and log of surface gravity (log g), we used ISPEC (Blanco-Cuaresma et al. 2014; Blanco-Cuaresma 2019) on the disentangled spectra. All the disentangled spectra were checked for any RV offset caused by the disentangling method. We did not normalise the spectra further, as the SPD and the bias-cleaning already give us normalised spectra. We obtained the atmospheric parameters using the synthetic spectral fitting (SSF) technique. The SSF technique generates synthetic spectra on the go and then does a χ2 optimisation at selected spectral lines. This method is better than a simple grid fitting (Blanco-Cuaresma 2019). We implemented different fitting procedures for the eclipsing stars and the tertiary, respectively. For the eclipsing stars, we fixed the log g estimated from LC and RV modelling using
where M is the mass in units of M⊙, R is the radius in R⊙, calculated from LC and RV modelling, and 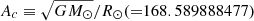 is a constant necessary for transformation to solar units. The resolution of FEROS and HRS was high enough to give us the precise projected rotational velocity (v sin i) from SSF, but for CHIRON we fixed it to the value obtained with BF. The set-up for synthetic spectra generation includes model atmospheres from MARCS8 (Gustafsson et al. 2008), solar abundances from Asplund et al. (2009), and the radiative transfer code SPECTRUM9. We calculated the parameters using two different line lists. We first fitted for Teff, [M/H], α, and v sin i using line list LL1, which is prescribed for abundance measurement. We adopted [M/H] and α from this run and then fitted for Teff and v sin i using line list LL2, which is prescribed for parameter estimation. For the eclipsing systems, we kept the log g fixed as the values (Tables 4 and 5) that we obtained from LC and RV modelling, since the spectroscopic log g matched well but had a lower precision. We kept the log g free for the tertiary spectra. The final spectroscopic estimates for all the systems are given in Table 3 and the best-fit models are shown in Figure 5.
is a constant necessary for transformation to solar units. The resolution of FEROS and HRS was high enough to give us the precise projected rotational velocity (v sin i) from SSF, but for CHIRON we fixed it to the value obtained with BF. The set-up for synthetic spectra generation includes model atmospheres from MARCS8 (Gustafsson et al. 2008), solar abundances from Asplund et al. (2009), and the radiative transfer code SPECTRUM9. We calculated the parameters using two different line lists. We first fitted for Teff, [M/H], α, and v sin i using line list LL1, which is prescribed for abundance measurement. We adopted [M/H] and α from this run and then fitted for Teff and v sin i using line list LL2, which is prescribed for parameter estimation. For the eclipsing systems, we kept the log g fixed as the values (Tables 4 and 5) that we obtained from LC and RV modelling, since the spectroscopic log g matched well but had a lower precision. We kept the log g free for the tertiary spectra. The final spectroscopic estimates for all the systems are given in Table 3 and the best-fit models are shown in Figure 5.
Adopted values of all major parameters for the studied ST3 systems.
 |
Fig. 5. Synthetic spectroscopic models of primary (red), secondary (blue), and tertiary (green) spectra compared to the disentangled spectra (black) for the different systems. The panels for ST2 systems (CD58 and BD11) show only the primary and secondary spectral models. |
3.5. Isochrone fitting
Most CHTs with detailed analysis have been found to have co-evolving stars. This implies that we can use a single isochrone to explain the masses, radii, and temperatures of all stars. While there have been cases in which non-coeval stars seem to exist in a CHT (David et al. 2019; Marcadon et al. 2020), we used this assumption to check and estimate the age of the system as a whole. We used our fitting code ISOFITTER, which searches through the grid of MIST (MESA Isochrones and Stellar Tracks; Choi et al. 2016; Dotter 2016) and finds the best-fit model that explains the masses, radii, metallicities, and temperatures of all three stars. There is also an option to add Gaia distances and flux ratios as constraints in the minimisation routine. Details of the routine can be found in Moharana et al. (2023). We made two runs for the ST3 systems. In one run, we used the observed constraints from all three stars, and in the other we used only the inner binary (also adding the binary flux ratio as a constraint). The best-fit tertiary models (in black) and binary models (in purple) are shown in Figures 6 and 7 for CD32 and CD62, respectively. The same routine was used for the ST2s, with their stellar parameters, flux ratio, and Gaia distance used as constraints. Assuming co-evolution, we can also estimate the third star’s radius for a range of tertiary masses. We used this to estimate the radius and temperature of the ST2 tertiaries, assuming M3 between the lower limit from RV fits and M2. For ST2s, we also rejected models that predict a distance of more than 3σ from the Gaia value (Appendix C).
 |
Fig. 6. Results of the isochrone fitting for CD32. The black line is the best-fitting isochrone for the run with all constraints (grey lines are exemplary of other isochrones within the constraints), and the purple line is for the run in which only the inner binary was used. Apart from the low log g of the tertiary (mostly due to a noisy disentangled spectrum), the parameters observed are consistent with isochrone estimates within 5σ errors. |
4. Results and discussion
In the following text, we use A–B notation to denote the CHT, where B is the tertiary and A is the EB with components Aa and Ab. Here, Aa corresponds to the primary, which is the most massive star in the inner binary. We use the short form for a star’s name along with the alphabetical notation to exclusively denote each star; for example, the secondary of CD62 is referred to as CD62Ab.
4.1. CD-32 6459 ≡ TIC024972851
CD32 is the widest of all our systems (largest aAB value). The inner binary is also the largest of all four systems (largest aA value). The binary masses are above-solar with a primary and secondary mass of 1.406 M⊙ and 1.211 M⊙, respectively. With radii of 1.54 R⊙ and 1.44 R⊙ for CD32Aa and CD32Ab, respectively, both are in the main-sequence regime. It is the only system with a non-negligible eccentricity of eA = 0.221, but with an inner binary period of ∼4 d, the orbit should be circularised after ∼500 Myr (according to the formalism of Zahn & Bouchet 1989). The mutual inclination regimes lie in two possible sets of solutions: (i) 34.3° to 136.7° or (ii) 43.3° to 145.7°. These limits are close to the limits for Von Zeipel-Lidov-Kozai (ZLK; von Zeipel 1910; Lidov 1962; Kozai 1962) oscillations, which could be the reason behind the large value of eA. ZLK oscillations in such close binaries make it a good candidate to see Kozai cycles with tidal friction (KCTF; Kiseleva et al. 1998) in action. Simulations predict that the product of KCTF will have a large period ratio, a mutual inclination close to the critical limit, and a circular inner orbit (Fabrycky & Tremaine 2007). CD32 shows all the above properties except a circular inner orbit. This makes CD32 a case with which to study ongoing KCTF or a candidate for a failed KCTF process (see estimated age in the following discussions).
The ZLK oscillations in CD32 can also cause it to show EDVs. To check the possibility of observing the variations in the future, we simulated the system for a period of 100 years using REBOUND with imut values of 44° and 67°. We find that while the cycles themselves have a period of more than 4000 years, the short-term higher-order perturbations have amplitudes close to the precision limits (from LC modelling) for iA values (Figure 8). This is because according to Brown (1936), the amplitudes for medium-period and short-period perturbations are of the order of PA/PAB and (PA/PAB)2, respectively, which are small for CD32. The simulations did not include tidal effects that would further subdue the chances of detecting EDVs.
 |
Fig. 8. REBOUND simulations of iA variations (upper panel) of CD32 (in purple). Estimated inclinations from LC modelling are shown with black dots. |
The disentangled spectrum for CD32B (Figure 5; third panel from top) is quite poor because of the faintness of the component, the comparatively low resolution (∼28 000), and a low number of spectra. Therefore, we fixed most of the atmospheric parameters using approximations for metallicity and α from the inner binary. The final log g and radius estimates had large error bars. The temperatures are above solar values and the system is metal-poor (−0.25 dex). Isochrone fitting with these values suggested a log(age) of 9.2 or 1.58 Gyr, i.e. more than the inner orbit circularisation timescale. While the estimated log(g) of CD32B is way off the isochrone value, the temperature matched the isochrone temperature within 5σ errors. Because of the poor spectroscopic estimate, we adopted the isochrone radius estimate for the tertiary (0.9 R⊙). Isochrones from binary fitting were consistent with the tertiary one. Therefore, we consider this system to be a co-evolving system.
4.2. CD-62 1257 ≡ TIC387107961
CD62 is the only system in the sample that has a tertiary more massive than the inner binary stars (M3 = 1.6 M⊙). This is visible in the high third light in the LC and also prominent in the spectra and the BFs. The binary is relatively close, with a period of 2.71456 d and a semi-major axis of 11.17 R⊙. The outer orbit is eccentric (eAB ∼ 0.3). The mutual inclination ranges are (i) 16.4° to 162.4° or (ii) 17.6° to 163.6°. Spectroscopic analysis shows that the system is metal-rich, with the inner binary stars showing an [M/H] value of 0.3 dex and the tertiary being at 0.13 dex. Isochrone fitting gives us an age of 2.45 Gyr for the tertiary-constrained case and 2.19 Gyr for the binary-constrained case but with a negative metallicity. The more massive tertiary seems to be still on the main sequence even though the isochrone log g expects it to be in the sub-giant phase. While the spectroscopic estimations are precise (compared to CD32B), our fitting is affected by large errors in the CD62B’s mass. While it is consistent with co-evolving temperatures, we do not completely rule out the case that the tertiary is evolving differently with its different metallicity and log(g). With the current configuration, CD62B seems to be evolving towards the red giant branch (RGB). Since the tertiary mass ratio is the highest in the sample, we checked for the possibility of Roche lobe mass transfer and subsequently a triple common envelope (TCE) formation. We used a MESA evolutionary grid for a 1.6 M⊙ star to see the radius evolution. The calculation of the Roche limit was done using the expression in Eggleton (1983) and the assumption that the CHT is a wide binary with the eclipsing pair as a single star with a mass of ∼2.5 M⊙. We found that the tertiary will evolve beyond the Roche limit in 20 Myr and could form a TCE (see Figure 9).
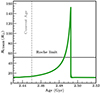 |
Fig. 9. Radius evolution of CD62B. The star evolves in the outer orbit of the CHT and reaches the Roche limit after 40 Myr. This can prompt a mass transfer that leads to a TCE system. |
4.3. CD-58 963 ≡ TIC220397947
CD58 has the shortest outer orbital period in our sample and (most likely) the smallest aAB value. Borkovits et al. (2020b) found a solution in which the two stars, despite having slightly different masses (1.15 and 1.10 M⊙ at i = 82.3°), had very similar radii (∼1.21 R⊙). This led to the conclusion that the system is young (18.2 Myr). In our solution, the radii are significantly different from each other, and the inclination is somewhat lower. We obtained a good isochrone fit to our results for the age of 3.01 Gyr, with all the parameters (including Gaia distance) properly reproduced. It places all three stars on the main sequence. Despite having masses close to the solar one, the Aa and Ab components are significantly hotter, due to their lower metallicity.
From the isochrone fit (Figure 10), we can also estimate the properties of the tertiary: MB = 0.45 M⊙, RB = 0.42 R⊙, and Teff, B = 3730 K. The value of MB is close to the lower limit from the RV solution, suggesting a nearly edge-on outer orbit, and likely a co-planar geometry.
 |
Fig. 10. Results of the isochrone fitting for CD58. The parameters observed for Aa+Ab are consistent with isochrone estimates within 3σ errors. Tertiary parameters are evaluated from the isochrone fit. |
There are several discrepancies between our results and Borkovits et al. (2020b), mainly in the radii of Aa and Ab, and the properties of the tertiary. One of the reasons behind those discrepancies might be the extent of TESS data. New observations were obtained during Cycle 5 (only had access to Cycle 1 Borkovits et al. 2020b). By that time, the shape of the LC has changed (see Fig. 3), leading to different estimates of the radii and inclination. Furthermore, Borkovits et al. (2020b) did not have any RV measurements, only ETVs of the inner binary, and thus no direct dynamical reference scale for masses and orbit sizes. We also argue that the presence of the fourth (0.21 M⊙) body at the 2661 d orbit did not affect our analysis, since its contribution to the total flux seems to be negligible, and our RV data were taken within a much shorter time frame.
4.4. BD+11 359 ≡ TIC408834852
BD11 was the first CHT identified in the CRÉME survey, already appearing (but not identified by name) in Figure 2 of Hełminiak et al. (2015). In the solutions by Hełminiak et al. (2009) and Kozłowski et al. (2014), one can note systematic effects in RV residuals. In those works, only a few RV measurements were used, and the system was treated as a ‘lone’ binary; thus, our current results are more reliable. The inner binary is composed of two main-sequence stars of sub-solar metallicity and similar, yet unequal, masses, radii, and temperatures. We obtained a very good isochrone fit for the age of 2.95 Gyr (Figure 11). The fit predicts the tertiary to be a 0.58 M⊙, 0.54 R⊙, 4085 K dwarf. The mass is also close to the lower limit from RVs, which suggests an edge-on outer orbit and possibly a co-planar geometry.
5. Distributions of parameters from detailed CHT solutions
While spectroscopy is important in extracting precise and accurate parameters of stars in E2CHT, many such detailed solutions have been obtained using E3CHT and photodynamical modelling of long-term LCs. Such studies in the literature have estimated the metallicity of the systems (and sometimes of the individual stars) with the help of spectral energy distributions and isochrone fitting. While some part of the methodology assumes co-evolution and is model-dependent, it contributes substantially to the understanding of these rare systems. Going through the literature, we found 48 systems that have undergone such an analysis; these are listed in Table D.1. To check for hints of formation and evolution channels, we looked at statistics of all the well-studied systems. We added our measurements from Moharana et al. (2023, 2024) and this work.
5.1. Metallicity dependence of parameter distributions
The distributions of the outer eccentricity, e2, the tertiary period, P2, and the tertiary to binary mass ratio (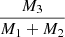 ) as a function of metallicity ([Fe/H]) are shown in Figure 12. We divided the [Fe/H] into three regions (to account for any errors in measurements): sub-solar (< −0.15 dex), solar (−0.15 to +0.15 dex), and above-solar (> +0.15 dex). The P2 distribution peaks below 200 days, which is likely a bias due to the majority of the systems being E3CHT. The lack of low
) as a function of metallicity ([Fe/H]) are shown in Figure 12. We divided the [Fe/H] into three regions (to account for any errors in measurements): sub-solar (< −0.15 dex), solar (−0.15 to +0.15 dex), and above-solar (> +0.15 dex). The P2 distribution peaks below 200 days, which is likely a bias due to the majority of the systems being E3CHT. The lack of low 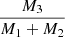 for periods of less than 200 days is suggestive of the brown-dwarf desert analogue (Grether & Lineweaver 2006), which we find to be [Fe/H]-independent. The distributions of
for periods of less than 200 days is suggestive of the brown-dwarf desert analogue (Grether & Lineweaver 2006), which we find to be [Fe/H]-independent. The distributions of 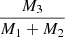 for solar and above-solar metallicities both peak between 0.5 and 1, which are possible values for scenarios in which all three masses are equal, and the tertiary and binary masses are equal, respectively. However, the sub-solar systems seem to be spread uniformly. The two solar and above-solar systems at the low
for solar and above-solar metallicities both peak between 0.5 and 1, which are possible values for scenarios in which all three masses are equal, and the tertiary and binary masses are equal, respectively. However, the sub-solar systems seem to be spread uniformly. The two solar and above-solar systems at the low 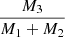 end are EDV systems and one of them has [Fe/H] very close to our limits for being metal-poor ([Fe/H] = −0.12). Interestingly, in a study of close binaries, Bate (2019) found that metal-poor environments have low opacities and high cooling rates of dense gas, which enhances small-scale fragmentation in the star-forming cloud. Objects of all [Fe/H] values show a favoured outer eccentricity of 0.3, and some E3CHT systems contribute to a peak at 0. This peak was observed in the Kepler sample of CHTs in Borkovits et al. (2016), Hajdu et al. (2019), and Czavalinga et al. (2023). We computed the cumulative distribution of e2 for all [Fe/H] values and found it to be similar to the above studies, which show a non-flat and non-thermal e2 distribution (see left panel of Figure 13). This eccentricity distribution was also observed in field binaries, as was noted by Duchêne & Kraus (2013). The lower [Fe/H] distribution shows signs of a flat distribution around 0.2 but this could be the result of an incomplete, low-number statistic.
end are EDV systems and one of them has [Fe/H] very close to our limits for being metal-poor ([Fe/H] = −0.12). Interestingly, in a study of close binaries, Bate (2019) found that metal-poor environments have low opacities and high cooling rates of dense gas, which enhances small-scale fragmentation in the star-forming cloud. Objects of all [Fe/H] values show a favoured outer eccentricity of 0.3, and some E3CHT systems contribute to a peak at 0. This peak was observed in the Kepler sample of CHTs in Borkovits et al. (2016), Hajdu et al. (2019), and Czavalinga et al. (2023). We computed the cumulative distribution of e2 for all [Fe/H] values and found it to be similar to the above studies, which show a non-flat and non-thermal e2 distribution (see left panel of Figure 13). This eccentricity distribution was also observed in field binaries, as was noted by Duchêne & Kraus (2013). The lower [Fe/H] distribution shows signs of a flat distribution around 0.2 but this could be the result of an incomplete, low-number statistic.
 |
Fig. 12. Distribution of the tertiary mass-ratio ( |
 |
Fig. 13. Cumulative eccentricity (e2) distribution of the tertiary orbit of CHTs listed in Table D.1. Left: Cumulative e2 distribution of CHTs of different [fe/H] values. Yellow represents metal-rich samples, red represents solar ones, and purple represents metal-poor ones. Right: Cumulative e2 distribution for young (blue) and old (red) systems. The black line represents the expected trend for a flat distribution and the dashed green line is the expected trend for a thermal distribution of e2. The grey lines in both panels show the total distribution of all the listed CHTs. |
5.2. Age dependence of parameter distributions
To see any signatures of dynamical changes in these distributions over time, we differentiated them based on the system age. Due to the lack of very young systems (log(age) ∼ 6), we made a separation between young and old systems at a log(age) of 9. We see similar e2 distributions with no drastic differences between young and old systems (see right panel of Figure 13). Meanwhile, the young systems favoured a mass ratio closer to 1 than the old systems, which peaked at around 0.5 (Figure 14). The change in the peak mass ratio between young and old systems can be a result of the migration of the tertiary. To see any signatures of migration of the tertiary, we plot the age dependency of the imut10 in Figure 15. The distribution shows all old systems, below a period of 500 d, to be planar. All young systems below a period of 300 d are planar. While there is a young system with a high value of imut, it is still planar, though in a retrograde orbit. These imut-P2 cut-offs are similar to the eccentricity-period cut-offs seen in observations of binaries in the solar neighbourhood (Raghavan et al. 2010). Simulations of close binary formation attribute this to tidal dissipation (Moe & Kratter 2018). The simulations also predict that the cut-offs move towards longer periods as the systems get old, similar to the trends seen in Figure 15. This planarisation of CHTs may be powered by tidal dissipation (possibly KCTF), along with mass loss, which can explain the different mass ratios for old and young systems. The other plausible scenario is that lower-mass-ratio systems are dynamically more stable and hence survive longer.
 |
Fig. 14. Same as Figure 12 but systems are marked with colours according to their age estimate (in log scale). The systems in red are old systems with log(age) > 9 (in Gyr), while the systems in blue are classified as old with log(age) < 9. |
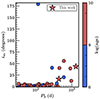 |
Fig. 15. Distribution of mutual inclination (imut) vs period of the outer orbit (P2). The blue circles represent young systems, while the red circles represent old systems. Stars denote systems observed in this work. |
Considering the current state of trends, it is possible that the outer hierarchical orbit of a CHT is formed in a similar way to that of close, field binaries. While the dependencies of these distributions are prone to error because of the small sample, it is an interesting property to study that could help us better understand star formation at these scales.
6. Conclusions
In this work, we present an analysis of three newly discovered CHTs and one already identified. We used LC modelling, RV modelling, spectral disentangling, and spectral analysis to get the orbital, stellar, and atmospheric parameters of all three stars in ST3 systems and two stars in the inner binary of our ST2 systems. For ST3 systems, we used the parameters of all three stars to constrain their ages and distances. For ST2 systems, we used parameters of the inner binary to estimate the ages and then estimate the tertiary mass and radius with constraints from the estimated minimum mass and Gaia distances. All inner binaries have their masses estimated with high or very high precision. Except for CD58 Aa and Ab, the radii are precise to a level of 1% or better. The four systems are summarised below:
-
CD-32 6459: This system is the widest in our sample. The tertiary star is a 0.97 M⊙ main-sequence star. This is a metal-poor system with an age of 1.58 Gyr. The inner binary is eccentric and has a similar eccentricity to the tertiary orbit (∼0.2). The mutual inclination limits are close to the limiting angle for ZLK oscillations, which could explain the large inner eccentricity. This system is a candidate to observe KCTF in process.
-
CD-62 1257: This is a system with a larger and more massive tertiary than the stars in the eclipsing pair. The tertiary will evolve below the Roche limit of the A–B orbit, and the system will undergo a TCE phase.
-
CD-58 963: This system has the shortest outer period and lowest mass in our sample. The inner binary, composed of 1.16 and 1.06 M⊙ stars, is accompanied by a 0.45 M⊙ red dwarf. Despite it previously being suggested that this is a young (∼20 Myr) system (Borkovits et al. 2020b), we found a good isochrone fit for an older age (∼3 Gyr).
-
BD+11 359: This system is the first CHT identified by the CRÉME survey. The inner binary, composed of 1.27 and 1.25 M⊙ stars, is accompanied by a 0.58 M⊙ red dwarf.
We compiled CHT systems from the literature with age and metallicity estimates and used them with our results to look at the dependencies of the tertiary mass ratio and eccentricity. We found that metal-poor stars have no preferred mass ratio but metal-rich and solar-metallicity stars prefer mass ratios around 0.5. Such a dependency of mass ratios upon metallicity was observed in simulations of close binaries. We also found that older systems (> 1 Gyr) also prefer a mass ratio of around 0.5. Older CHTs with outer periods less than 500 d and younger systems with outer periods less than 300 d are near planar in configuration. The outer eccentricities of all CHTs follow the same distribution that was observed previously for CHTs, and also field binaries. This is suggestive of a CHT formation scenario similar to that of close, field binaries. However, these distributions are biased due to the abundance of triply eclipsing systems. They also suffer from a lack of systems, and this is why there is a need for more homogeneous and detailed studies of CHT parameters in the future.
IRAF is distributed by the National Optical Astronomy Observatory (NOAO), which is operated by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. https://iraf-community.github.io/
Acknowledgments
The authors thank Dr. Tomer Shenar for his help with using his disentangling code, DSAA. This work is funded by the Polish National Science Centre (NCN) through grant 2021/41/N/ST9/02746. K.G.H. acknowledges support from NCN grant 2023/49/B/ST9/01671. A.M., F.M., T.P., and M.K. are supported by NCN through grant 2017/27/B/ST9/02727. F.M. gratefully acknowledges support from the NASA TESS Guest Investigator grant 80NSSC24K0498 (PI: F. Marcadon). Observations for CD-62 1257, CD-32 6459, and CD-58 963 were obtained with the Southern African Large Telescope (SALT). Polish participation in SALT is funded by grant No. MEiN nr 2021/WK/01. This work is based on observations collected at the European Southern Observatory, Chile under programmes 088.D-0080, 089.D-0097, 089.C-0415, 090.D-0061, 091.D-0145, and through CNTAC proposals 2012B-036, 2013A-093, 2013B-022, 2014B-067, and 2015A-074. This paper includes data collected with the TESS mission, obtained from the Mikulski Archive for Space Telescopes (MAST) data archive at the Space Telescope Science Institute (STScI). Funding for the TESS mission is provided by the NASA Explorer Program. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5–26555. This work also presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular, the institutions participating in the Gaia MultiLateral Agreement (MLA).
References
- Alonso, R., Deeg, H. J., Hoyer, S., et al. 2015, A&A, 584, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bate, M. R. 2019, MNRAS, 484, 2341 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T. 2022, Galaxies, 10, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., & Mitnyan, T. 2023, Universe, 9, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Derekas, A., Kiss, L. L., et al. 2013, MNRAS, 428, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [Google Scholar]
- Borkovits, T., Rappaport, S., Kaye, T., et al. 2019, MNRAS, 483, 1934 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Rappaport, S. A., Hajdu, T., et al. 2020a, MNRAS, 493, 5005 [Google Scholar]
- Borkovits, T., Rappaport, S. A., Tan, T. G., et al. 2020b, MNRAS, 496, 4624 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Mitnyan, T., Rappaport, S. A., et al. 2022a, MNRAS, 510, 1352 [Google Scholar]
- Borkovits, T., Rappaport, S. A., Toonen, S., et al. 2022b, MNRAS, 515, 3773 [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
- Brahm, R., Jordán, A., & Espinoza, N. 2017, PASP, 129, 034002 [Google Scholar]
- Brown, E. W. 1936, MNRAS, 97, 62 [NASA ADS] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
- Crause, L. A., Sharples, R. M., Bramall, D. G., et al. 2014, SPIE Conf. Ser., 9147, 91476T [Google Scholar]
- Czavalinga, D. R., Borkovits, T., Mitnyan, T., Rappaport, S. A., & Pál, A. 2023, MNRAS, 526, 2830 [NASA ADS] [CrossRef] [Google Scholar]
- David, T. J., Hillenbrand, L. A., Gillen, E., et al. 2019, ApJ, 872, 161 [Google Scholar]
- Derekas, A., Kiss, L. L., Borkovits, T., et al. 2011, Science, 332, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrov, W., Lehmann, H., Kamiński, K., et al. 2017, MNRAS, 466, 2 [CrossRef] [Google Scholar]
- Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Eggleton, P., & Kiseleva, L. 1995, ApJ, 455, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, N. L., Johnston, C., Toonen, S., et al. 2022, MNRAS, 511, 4710 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Gaulme, P., Borkovits, T., Appourchaux, T., et al. 2022, A&A, 668, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González, J. F., & Levato, H. 2006, A&A, 448, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [Google Scholar]
- Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hajdu, T., Borkovits, T., Forgács-Dajka, E., et al. 2019, MNRAS, 485, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, R. S. 1972, Celest. Mech., 6, 322 [Google Scholar]
- Hełminiak, K. G., Konacki, M., Ratajczak, M., & Muterspaugh, M. W. 2009, MNRAS, 400, 969 [Google Scholar]
- Hełminiak, K. G., Konacki, M., Złoczewski, K., et al. 2011, A&A, 527, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hełminiak, K. G., Konacki, M., Ratajczak, M., et al. 2015, ASP Conf. Ser., 496, 76 [NASA ADS] [Google Scholar]
- Hełminiak, K. G., Ukita, N., Kambe, E., et al. 2017, MNRAS, 468, 1726 [CrossRef] [Google Scholar]
- Hensberge, H., Ilijić, S., & Torres, K. B. V. 2008, A&A, 482, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herschel, J. F. W., Main, R., & Pritchard, C. 1874, Mem. Roy. Astron. Soc., 40, 1 [Google Scholar]
- Hippke, M., David, T. J., Mulders, G. D., & Heller, R. 2019, AJ, 158, 143 [Google Scholar]
- Jones, D., Pejcha, O., & Corradi, R. L. M. 2019, MNRAS, 489, 2195 [NASA ADS] [CrossRef] [Google Scholar]
- Jordán, A., Brahm, R., Bakos, G. Á., et al. 2014, AJ, 148, 29 [CrossRef] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kim, C. H., Kreiner, J. M., Zakrzewski, B., et al. 2018, ApJS, 235, 41 [Google Scholar]
- Kiseleva, L. G., Eggleton, P. P., & Mikkola, S. 1998, MNRAS, 300, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kniazev, A. Y., Gvaramadze, V. V., & Berdnikov, L. N. 2016, MNRAS, 459, 3068 [NASA ADS] [CrossRef] [Google Scholar]
- Kniazev, A. Y., Gvaramadze, V. V., & Berdnikov, L. N. 2017, ASP Conf. Ser., 510, 480 [NASA ADS] [Google Scholar]
- Knigge, C., Toonen, S., & Boekholt, T. C. N. 2022, MNRAS, 514, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Konacki, M., Muterspaugh, M. W., Kulkarni, S. R., & Hełminiak, K. G. 2010, ApJ, 719, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kozłowski, S. K., Konacki, M., Ratajczak, M., et al. 2014, MNRAS, 443, 158 [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
- Marcadon, F., Hełminiak, K. G., Marques, J. P., et al. 2020, MNRAS, 499, 3019 [NASA ADS] [CrossRef] [Google Scholar]
- Mardling, R. A., & Aarseth, S. J. 2001, MNRAS, 321, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mitnyan, T., Borkovits, T., Rappaport, S. A., Pál, A., & Maxted, P. F. L. 2020, MNRAS, 498, 6034 [NASA ADS] [CrossRef] [Google Scholar]
- Mitnyan, T., Borkovits, T., Czavalinga, D. R., et al. 2024, A&A, 685, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moe, M., & Kratter, K. M. 2018, ApJ, 854, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Moharana, A., Hełminiak, K. G., Marcadon, F., et al. 2023, MNRAS, 521, 1908 [NASA ADS] [CrossRef] [Google Scholar]
- Moharana, A., Hełminiak, K. G., Marcadon, F., et al. 2024, MNRAS, 527, 53 [Google Scholar]
- Naoz, S., & Fabrycky, D. C. 2014, ApJ, 793, 137 [Google Scholar]
- Orosz, J. A. 2023, Universe, 9, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., & Fabrycky, D. C. 2009, ApJ, 697, 1048 [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [Google Scholar]
- Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., Kochoska, A., Conroy, K. E., et al. 2022, ApJS, 258, 16 [CrossRef] [Google Scholar]
- Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [Google Scholar]
- Rappaport, S. A., Borkovits, T., Gagliano, R., et al. 2022, MNRAS, 513, 4341 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S. A., Borkovits, T., Gagliano, R., et al. 2023, MNRAS, 521, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S. A., Borkovits, T., Mitnyan, T., et al. 2024, A&A, 686, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Rucinski, S. 1999, ASP Conf. Ser., 185, 82 [Google Scholar]
- Shenar, T., Bodensteiner, J., Abdul-Masih, M., et al. 2020, A&A, 639, L6 [EDP Sciences] [Google Scholar]
- Shenar, T., Sana, H., Mahy, L., et al. 2022, A&A, 665, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shivvers, I., Bloom, J. S., & Richards, J. W. 2014, MNRAS, 441, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2013, A&A, 557, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tokovinin, A. 2004, Rev. Mex. Astron. Astrofis. Conf. Ser., 21, 7 [NASA ADS] [Google Scholar]
- Tokovinin, A., & Moe, M. 2020, MNRAS, 491, 5158 [NASA ADS] [CrossRef] [Google Scholar]
- Tokovinin, A., Fischer, D. A., Bonati, M., et al. 2013, PASP, 125, 1336 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Ulaş, B., & Ayan, V. 2023, RAA, 23, 035016 [Google Scholar]
- von Zeipel, H. 1910, Astron. Nachr., 183, 345 [Google Scholar]
- Yenawine, M. E., Welsh, W. F., Orosz, J. A., et al. 2022, ApJ, 924, 66 [Google Scholar]
- Zahn, J. P., & Bouchet, L. 1989, A&A, 223, 112 [NASA ADS] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: RV measurements
We present all RV measurements used in this work in Tables A1 and A2. We included the data from Hełminiak et al. (2009) for BD11. When a measurement cannot be done at a certain epoch due to various effects, for example line blending, it is marked with ‘—’. There is no data, obviously, for the tertiaries in ST2 systems.
RV measurements of ST3s used in this work. All values are given in km s−1.
RV measurements of ST2s used in this work. All values are given in km s−1.
Appendix B: JKTEBOP tables
We made LC models with JKTEBOP for each TESS sector separately. The parameters obtained from the fitting for each fun are given in Table B1 (CD32), Table B2 (BD11), Table B3 (CD62), and Table B4 (CD58). For our final estimates, we use only the solutions which have J close to the spectroscopic value. Some sectors have nonphysical solutions due to strong effects of stellar activity. This also affects the estimation of other orbital parameters, i.e., high eccentricity in S62 due to high J value (see Table B4).
JKTEBOP Solutions for CD32.
JKTEBOP Solutions for BD11.
JKTEBOP Solutions for CD62.
JKTEBOP Solutions for CD58.
Appendix C: ISOFITTER results
The isochrone fitting code ISOFITTER calculates grids of χ2 using models from MIST and the measured parameters. In Figure C1 we show the χ2 map for isochrone metallicity ([Fe/H]), log of the system age (log(age)), reddening-free distance (D0), extinction (as E(B − V)) and estimated radius of the tertiary (R3). The top panel for each star shows grids where the χ2 was weighted with Gaia distance and the lower panels were free of this weight. For ST3 systems, we calculate separate grids using three-star constraints (TC; Figure C1-left) and binary constraints (BC; Figure C1-right). For the case of ST2 systems, we use only BC and we show the expected mass of the tertiary (M3) as well.
 |
Fig. C.1. ISOFITTERχ2 grids for specific parameters for different constraints. Orange denotes grids calculated with constraints from all stars while purple denotes grids calculated using only the eclipsing pair. |
Appendix D: Table of detailed CHT solutions
There are 48 systems in the literature with a complete set of orbital, stellar and atmospheric parameters of all stars in a CHT. We list all these systems in Table D.1. The systems are characterised according to their method of estimation of orbital parameters, metallicity, and ages.
CHTs with detailed parameters, and their sources.
All Tables
Atmospheric parameters obtained from our spectroscopic analysis on the disentangled spectra.
All Figures
 |
Fig. 1. RVs and orbital solutions of the ST3 systems CD32 (top) and CD62 (bottom). The left panels present the inner binary Aa+Ab corrected for its COM. Primary components are marked with red triangles and secondary ones with blue squares. The right panels present the outer orbit, with the inner binary’s COM (calculated with Equation 1) represented by purple squares and the tertiary’s RVs by green triangles. The dashed line marks the γ velocity of the whole system. |
| In the text | |
 |
Fig. 2. Same as Fig. 2 but for ST2 systems CD58 (top) and BD11 (bottom). Since there are no RVs of the tertiary, the right panels show only the binary’s COM. |
| In the text | |
 |
Fig. 3. JKTEBOP models (purple lines) for the first and the last used in our modelling of TESS observations (centre and last panel, respectively). The variable stellar activity can be seen in the sector-wise observations and models. The eccentric and near-circular systems can be distinguished from the phased LC observations and models (first panel). |
| In the text | |
 |
Fig. 4. Orbital configuration of the targets viewed perpendicular to the observers’ plane (XY plane). The COM of the system is at (0,0). |
| In the text | |
 |
Fig. 5. Synthetic spectroscopic models of primary (red), secondary (blue), and tertiary (green) spectra compared to the disentangled spectra (black) for the different systems. The panels for ST2 systems (CD58 and BD11) show only the primary and secondary spectral models. |
| In the text | |
 |
Fig. 6. Results of the isochrone fitting for CD32. The black line is the best-fitting isochrone for the run with all constraints (grey lines are exemplary of other isochrones within the constraints), and the purple line is for the run in which only the inner binary was used. Apart from the low log g of the tertiary (mostly due to a noisy disentangled spectrum), the parameters observed are consistent with isochrone estimates within 5σ errors. |
| In the text | |
 |
Fig. 7. Same as Figure 6 but for CD62. |
| In the text | |
 |
Fig. 8. REBOUND simulations of iA variations (upper panel) of CD32 (in purple). Estimated inclinations from LC modelling are shown with black dots. |
| In the text | |
 |
Fig. 9. Radius evolution of CD62B. The star evolves in the outer orbit of the CHT and reaches the Roche limit after 40 Myr. This can prompt a mass transfer that leads to a TCE system. |
| In the text | |
 |
Fig. 10. Results of the isochrone fitting for CD58. The parameters observed for Aa+Ab are consistent with isochrone estimates within 3σ errors. Tertiary parameters are evaluated from the isochrone fit. |
| In the text | |
 |
Fig. 11. Same as Fig. 10 but for BD11. |
| In the text | |
 |
Fig. 12. Distribution of the tertiary mass-ratio ( |
| In the text | |
 |
Fig. 13. Cumulative eccentricity (e2) distribution of the tertiary orbit of CHTs listed in Table D.1. Left: Cumulative e2 distribution of CHTs of different [fe/H] values. Yellow represents metal-rich samples, red represents solar ones, and purple represents metal-poor ones. Right: Cumulative e2 distribution for young (blue) and old (red) systems. The black line represents the expected trend for a flat distribution and the dashed green line is the expected trend for a thermal distribution of e2. The grey lines in both panels show the total distribution of all the listed CHTs. |
| In the text | |
 |
Fig. 14. Same as Figure 12 but systems are marked with colours according to their age estimate (in log scale). The systems in red are old systems with log(age) > 9 (in Gyr), while the systems in blue are classified as old with log(age) < 9. |
| In the text | |
 |
Fig. 15. Distribution of mutual inclination (imut) vs period of the outer orbit (P2). The blue circles represent young systems, while the red circles represent old systems. Stars denote systems observed in this work. |
| In the text | |
 |
Fig. C.1. ISOFITTERχ2 grids for specific parameters for different constraints. Orange denotes grids calculated with constraints from all stars while purple denotes grids calculated using only the eclipsing pair. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



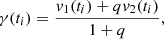
![$$ \begin{aligned} G(v)=A \left[c_{1}\sqrt{1-\left(\frac{v}{v_{\rm max}}\right)^{2}}+c_{2}\left(1-\left(\frac{v}{v_{\rm max}}\right)^{2}\right)\right]+l v+k, \end{aligned} $$](/articles/aa/full_html/2024/10/aa50797-24/aa50797-24-eq5.gif)