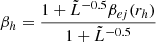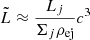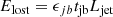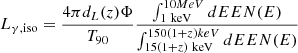| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202450201 | |
| Published online | 11 October 2024 | |
Letter to the Editor
Disk mass after a binary neutron star merger as a constraining parameter for short gamma-ray bursts
1
Institut für Theoretische Physik, Goethe Universität Frankfurt, Max-von-Laue-Str.1, 60438 Frankfurt am Main, Germany
2
Department of Physics, National and Kapodistrian University of Athens, Panepistimiopolis, GR 15783 Zografos, Greece
3
Research Center for Astronomy, Academy of Athens, Soranou Efessiou 4, GR-11527 Athens, Greece
e-mail: anathanail@academyofathens.gr
Received:
1
April
2024
Accepted:
27
August
2024
Context. The coincident detection of GW170817 and gamma-ray burst GRB170817A marked a milestone for the connection between binary neutron star (BNS) mergers and short gamma-ray bursts (sGRBs). These mergers can lead to the formation of a black hole that is surrounded by a disk and to the generation of a powerful jet. It spends energy to break free from the merger ejecta, and then a portion of it is dissipated to produce observable emissions.
Aims. Our primary goal is to enhance our comprehension of BNS mergers by constraining the disk mass for a selection of sGRBs. To do this, we used the isotropic gamma-ray luminosity and corresponding emission times as key indicators.
Methods. We leveraged data from GW170817 to estimate the disk mass surrounding the BNS merger remnant, and we subsequently inferred the efficiency of the accretion onto the jet. We then statistically examined other sGRB observations to estimate whether they might have been induced by BNS mergers
Results. Our findings suggest that when similar physical parameters are employed as in the only observed BNS-powered GRB event, GRB170817A, a substantial fraction of sGRBs would need an unrealistically massive disk remnant.
Conclusions. This observation raises the possibility that either a different mechanism powered those events or that the post-collapse disk efficiency varies significantly in different BNS merger scenarios.
Key words: stars: black holes / gamma-ray burst: general / stars: neutron
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The detection of GRB170817A (Goldstein et al. 2017), which was observed simultaneously with the gravitational-wave event GW170817, provided the first direct evidence that at least a subset of sGRBs is produced by the merger of two neutron stars (NS) (Abbott et al. 2017a). The identification of an electromagnetic optical counterpart to GW170817 (Coulter et al. 2017; Pian et al. 2017; McCully et al. 2017; Evans et al. 2017) provided useful insight into open problems in cosmology (Abbott et al. 2017b) and the production of heavy elements (Tanvir et al. 2017), but also determined the host galaxy of the event, allowing for a long-term multiwavelength monitoring of the evolution of the event. This uncovered an additional nonthermal counterpart that was eventually established as being the afterglow of an off-axis relativistic jet (Mooley et al. 2018; Ghirlanda et al. 2019).
The dynamics of a binary neutron star (BNS) merger that lead to a short-duration GRB are strongly affected by the merger process (Giacomazzo et al. 2013). The two NSs spiral together and emit gravitational waves. As they approach each other, they are tidally deformed. This tidal deformation leads to the ejection of matter from the system, which can produce a short-lived bright electromagnetic transient known as a kilonova (Li & Paczyński 1998; Metzger et al. 2010). After the violent merger and the dynamical ejection of mass (Sekiguchi et al. 2015; Bovard et al. 2017; Radice et al. 2018), secular mechanisms further eject mass through magnetic- and neutrino-driven winds from the accretion disk and the remnant before its eventual collapse into a black hole (Fujibayashi et al. 2018; Gill et al. 2019; Ascenzi et al. 2021, and references therein)
During the merger process, a massive hot accretion disk is produced around the central object. When a black hole is formed, the accretion of matter onto it can power the production of a relativistic jet (Blandford & Znajek 1977; Cruz-Osorio et al. 2022). The jet then propagates through the surrounding ejecta, and when it can break out from the ejecta, dissipation of energy in radiation can be observed (Rees & Meszaros 1994; McKinney & Uzdensky 2012; Zhang & Yan 2011). The subsequent interaction of the jet with the surrounding medium can give rise to afterglow emission, which is observed at longer wavelengths after the prompt gamma-ray emission has faded (Rees & Meszaros 1992).
Multimessenger observation of GRB170817A allowed us to estimate that the kinetic energy of the jet is approximately Ek, jet ≈ 1050 erg. A combination of observables indicated that the remnant collapsed into a black hole in tcoll ≈ 1 s after merger (Gill et al. 2019). The surrounding disk mass was estimated within the limits dictated by numerical relativity simulations Mdisk > 0.04 M⊙ (Radice & Dai 2019). From the deduced energetics of the jet and the estimated disk mass, it was possible to infer the efficiency of the accretion power into jet energy (Salafia & Giacomazzo 2021).
In this work, we take into account the continued mass ejection that feeds the ejecta through the survival time of the BNS merger remnant. The jet propagation through the ejecta is connected with the observed short gamma-ray burst (sGRB) parameters (tGRB, LGRB, iso), and this allows us to determine a posterior distribution for the disk mass. Finally, using the inferred disk mass distribution, we compute the probability that a specific short GRB comes from a BNS merger scenario based on the value of the inferred disk mass. Our main assumption is the use of the posterior distribution for the efficiency of converting the mass accretion energy into jet energy for GRB170817A (Salafia & Giacomazzo 2021).
This Letter is organized as follows: In Sect. 2 we describe the way the observables are combined with theory to produce posterior distributions for the efficiency and eventually, for the disk mass for short GRB observations. In Sect. 3 we present the results, and we conclude in Sect. 4.
2. Estimating dynamical quantities
We present the algorithm that we designed to estimate various dynamical quantities based on observed parameters, such as the isotropy-equivalent GRB luminosity (LGRB, iso) and the burst duration (T90). Our goal was to deduce the mass of the accretion disk surrounding the remnant black hole by applying robust statistical assumptions.
To do this, we needed to link observables to dynamical quantities. We initially associated the isotropy-equivalent jet power Ljet, iso with LGRB, iso using a fixed efficiency parameter (ϵGRB = 0.15) that remained constant throughout our calculations. This parameter typically fell within the range of 10–20% in the literature (Kumar & Zhang 2015), so that even when a distribution within the standard range is considered, the impact on the results is insignificant. To estimate the available amount of jet energy, we took two fundamental factors into account: First, the mass of the remnant disk that is accreted during the collapse process, and second, the efficiency of converting the accretion energy from the infalling matter into jet energy (ϵdisk). For each quantity involved in our calculations, we adopted the following approach.
Jet-breakout time (tjb): We considered a jet with constant power that is launched inside an ejecta envelope with a power-law density profile. We followed the uncollimated approximation presented by Bromberg et al. (2011); for more details, see Appendix A).
Accretion-into-jet efficiency (ϵdisk): We considered a posterior distribution for this efficiency. To model this distribution, we examined two cases. First, we derived the distribution for the efficiency of the accretion onto the jet, derived from Salafia & Giacomazzo (2021), who used the kinetic energy distribution from Ghirlanda et al. (2019). Second, following the same method, we calculated the posterior distribution for the efficiency of the accretion onto the jet using a different kinetic energy distribution. More specifically, we used the energy profile that is aligned with afterglow observations of GRB170817A, assuming a strongly magnetized jet (Nathanail et al. 2021). Since the BNS merger systems are qualitatively similar, we generalized the efficiency results for all sGRB cases.
Total disk mass upon merger (Mdisk): We determined the total disk mass upon merger using fitting formulas derived from numerical simulations. These formulas primarily depend on the masses and tidal deformabilities of the NSs (Fujibayashi et al. 2018; Radice et al. 2018; Krüger & Foucart 2020; Barbieri et al. 2021). For instance, in the case of GW170817, Laser Interferometer Gravitational-Wave Observatory (LIGO) provided posteriors for the tidal deformability and mass of the binary components, allowing us to parametrically estimate the remnant mass. Additionally, a portion of the total mass is extracted due to the ejection mechanism before collapse, following the profile provided in Appendix A of Barbieri et al. (2021), which can be summarized as follows:
where M1, M2, and 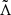 are the mass of the primary star, the mass of the secondary star, and the dimensionless tidal deformability parameter of the binary, with parameter values of α = 0.097, β = 0.241, and Λ0 = 245. The index 1 of each quantity was calculated after interchanging 1 with 2. Then, the disk mass of the system after the merger was calculated as
are the mass of the primary star, the mass of the secondary star, and the dimensionless tidal deformability parameter of the binary, with parameter values of α = 0.097, β = 0.241, and Λ0 = 245. The index 1 of each quantity was calculated after interchanging 1 with 2. Then, the disk mass of the system after the merger was calculated as
Jet opening angle (θjet): We used a profile constructed from the observations of a larger sample of short GRBs (Rouco Escorial et al. 2023) to determine the distribution of the jet opening angle. This approach allowed us to generalize our results to both past and future short GRB candidates. Notably, this analysis revealed a double peak in the jet angle distribution at approximately 5 and 15 degrees. For the specific case of GRB170817A, an estimated opening angle of 5–6 degrees (Ghirlanda et al. 2019; Troja et al. 2019; Mooley et al. 2018) or 15 degrees for a strongly magnetized jet was assumed (Nathanail et al. 2021).
Engine time (teng): We assumed that the jet is launched at the time of collapse. Gamma-ray emission begins after the jet breaks out of the ejecta and ends when the jet ceases (ignoring the remaining jet travel time, which reflects the time the jet spends inside the ejecta while the engine is turned off). Consequently, we associated the engine time with the sum of the observed quantity T90 and the jet break-out time (tjb).
For the calculation of dynamical quantities, we used the relations detailed below.
Isotropy-equivalent jet power (Ljet, iso):
Jet opening angle (θjet):
Emission (T90) and gamma-ray burst (tGRB) time:
Mass that must be penetrated by the jet (Mej):
Effective disk mass (Mdisk, eff):
Energy available for the jet (Ejet):
Probability distributions for various quantities.
 |
Fig. 1. Comparison of posteriors for accretion-to-jet efficiency and application of our model. Left panel: Posteriors for the accretion to jet efficiency for the case of GRB170817A. The green line represents the efficiency derived from ou algorithm, and the red line shows the efficiency from Salafia & Giacomazzo (2021). They both use the kinetic energy distribution from Ghirlanda et al. (2019). The blue line corresponds to the kinetic energy distribution from a strongly magnetized jet from Nathanail et al. (2021). The overplotted points refer to efficiencies from general relativity magnetohydrodynamics simulations. Right panel: Resulting posterior distributions analyzing GRB201221D with our algorithm, assuming an efficiency similar to GRB170817A. |
Total emitted gamma-ray energy (EGRB):
Here, ϵjb is the percentage of energy lost during the break-out of the jet. By definition, ϵjb = Ecocoon/Ljettjet,where, Ecocoon = (tjb − rjb/c)Ljet, and rjb is the jet break-out radius. Therefore, of the energy released by the engine during break-out, which is equal to Ejb = tjbLjet, only a portion is lost. This fraction is displayed in the lower panel of Fig. A.11.
The amount of ejected mass and the mass that is observed as either a red or blue kilonova remains to be clarified. These components of the ejected mass are denoted Mblue and Mred and were calculated using the analytical formulas presented in Gill et al. (2019). Importantly, their determination relies solely on the parameter tcoll, which is the collapse time of a supermassive NS into a black hole. The portion of the mass denoted as Mred is mostly concentrated in large angles toward the equator. It mostly comes from the dynamical ejecta and partially from the disk before the remnant collapses (Bovard et al. 2017). Thus, the mass that the jet has to travel through is the Mblue component (see Eq. (8)).
The set of equations outlined above served a dual purpose. One purpose was to use the equations to derive an Mdisk value by analyzing GW170817, similar to the method employed by Salafia & Giacomazzo (2021). The set of equations also allowed us to derive the efficiency of the conversion of the accretion into jet energy.
3. Applications
3.1. Jet efficiency
First, we recalculated the distribution of the efficiency of the accretion onto the jet for the specific case of GW170817 by solving for ϵdisk in Eq. (10). With a Monte Carlo simulation, we drew the dimensionless tidal deformability parameter 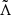 from Abbott et al. (2017a). Based on the formula form Barbieri et al. (2021), we calculated
from Abbott et al. (2017a). Based on the formula form Barbieri et al. (2021), we calculated 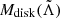 . Then, we calculated Mdisk, eff as (1 − fw)Mdisk with fw = 0.4, according to Salafia & Giacomazzo (2021) (only for the red curve), or by Eq. (9) with tcoll = 1. For the jet energy deposit, we drew from the posterior presented in either Ghirlanda et al. (2019) or Nathanail et al. (2021). Last, a trivial calculation gave us ϵdisk. A summary is shown in Table 1. The results for the efficiency of converting accretion energy into jet energy are illustrated in left panel of Fig. 1 and are represented by the green line. They are comparable to the outcomes obtained by Salafia & Giacomazzo (2021), which are indicated by red in the same figure. Furthermore, we examined the efficiency for a kinetic energy distribution based on 3D general relativistic magnetohydrodynamics (GRMHD) simulations conducted by Nathanail et al. (2021). However, the analytical solution we followed did not include magnetization effects, and we treated each kinetic distribution hydrodynamically. Notably, the resulting efficiency exhibited a slightly higher mean value for the latter kinetic energy distribution.
. Then, we calculated Mdisk, eff as (1 − fw)Mdisk with fw = 0.4, according to Salafia & Giacomazzo (2021) (only for the red curve), or by Eq. (9) with tcoll = 1. For the jet energy deposit, we drew from the posterior presented in either Ghirlanda et al. (2019) or Nathanail et al. (2021). Last, a trivial calculation gave us ϵdisk. A summary is shown in Table 1. The results for the efficiency of converting accretion energy into jet energy are illustrated in left panel of Fig. 1 and are represented by the green line. They are comparable to the outcomes obtained by Salafia & Giacomazzo (2021), which are indicated by red in the same figure. Furthermore, we examined the efficiency for a kinetic energy distribution based on 3D general relativistic magnetohydrodynamics (GRMHD) simulations conducted by Nathanail et al. (2021). However, the analytical solution we followed did not include magnetization effects, and we treated each kinetic distribution hydrodynamically. Notably, the resulting efficiency exhibited a slightly higher mean value for the latter kinetic energy distribution.
 |
Fig. 2. Disk mass required, according to our model, for the production of a short gamma-ray burst. The background color represents the mass of the disk in both cases, calculated as the mean value of our posteriors. The red points represent observational events (see the main text for details). The vertical dashed blue line corresponds to the core luminosity of GRB170817A. The shaded region indicates where the disk mass exceeds 0.3 M⊙, which is an approximate limit derived from numerical relativity simulations. The solid gray line marks the boundary between these two regions. In the left panel, we used the efficiency profile from Salafia & Giacomazzo (2021), and in the right panel, we adopted the corresponding efficiency for a jet profile from Nathanail et al. (2021). |
Since GRB170817A was observed off-axis, the measured luminosity cannot be directly used in our analysis. To address this, we needed to account for the isotropic luminosity as if the observation were on-axis. Ghirlanda et al. (2019) argued that if this jet were observed directly along its axis, its gamma-ray emission would have displayed an isotropic equivalent luminosity of at least LGRB, iso = 1(± 0.35)×1051 erg s−1, assuming a 10% efficiency in converting kinetic energy to radiation and attributing a 35% typical error. Another assumption for GRB170817A concerns the association between T90 and tGRB. While this connection is evident for on-axis observations, the dependence of the observed duration on the viewing angle is not well understood. These points have to be revised if any observation of an on-axis short GRB accompanying a BNS gravitational-wave (GW) event is observed in the future.
For the collapse time, we relied on the findings of Gill et al. (2019). Their method involves determining the survival time of the merger remnant by integrating two distinct constraints. First, they calculated the time required for the generation of the requisite mass of blue ejecta. Simultaneously, they accounted for the duration necessary for the relativistic jet to penetrate the expanding ejecta. Through this dual constraint approach, it was established that the remnant resulting from GW170817 must have transitioned into a black hole after a collapse time of 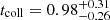 seconds. An alternative interpretation of the delay time, the time difference between the GW detection and the onset of a GRB, was presented in Beniamini et al. (2020).
seconds. An alternative interpretation of the delay time, the time difference between the GW detection and the onset of a GRB, was presented in Beniamini et al. (2020).
3.2. Disk mass distribution for short GRBs
Our next objective was to draw more generalized conclusions about the disk mass distribution for observed short GRBs and determine whether the obtained result can be within the allowed limits for a BNS merger event.
We systematically explored the parameter space encompassing T90 and LGRB, iso, requiring the associated disk mass necessary to generate a GRB event corresponding to a specific point within this parameter space. The details of our use of short GRBs and their observed parameters throughout the algorithm can be found in Appendix B. Under the assumption that the efficiency of the accretion onto the jet is universal to BNS merger events, we used the posterior distribution obtained in the previous section, specifically based on the characteristics of GRB170817A. To comprehensively examine the influence of the collapse time, we considered several scenarios ranging from a duration of 10−2 s to 9 s.
For each combination of (tGRB, LGRB, iso), we generated a mass distribution by running a Monte Carlo simulation for a total of one million samples. To ensure a smoother dataset, we incorporated an additional 100 data points for each draw, following a normalized distribution with a σ value equal to that sample variance. An illustrative example of the resulting distribution is presented in the right panel of Figure 1 for the case of GRB201221D.
Our primary interest was to determine an upper limit for the disk mass for each combination T90, Ljet in the parameter space, which is what is observed from a regular short GRB with a known distance. We focused on the most probable value of the disk mass and assessed its feasibility within the context of BNS mergers. In Figure 2, we present the results of this analysis using a color-scale representation. The solid gray line within the plot defines the region in which the disk mass is aligned with the approximate maximum derived from advanced numerical relativity simulations. The estimated maximum is lower than 0.3 M⊙, as reported in previous studies (Radice et al. 2018; Krüger & Foucart 2020; Nedora et al. 2021; Barbieri et al. 2021). To ensure a conservative upper limit for the disk mass, we set it at 0.3 M⊙. Notably, even for binary systems with a total mass of approximately 3.3 M⊙ and significant asymmetry, which generally leads to higher disk masses, the maximum disk mass remains limited to around 0.1 M⊙ (Camilletti et al. 2022). The shaded olive areas in the plot represent regions with higher disk mass values and essentially delineate the areas within the T90, Ljet parameter space in which observational events are statistically unlikely to be progenitors of BNS mergers for the chosen efficiency values.
In our model, the ejecta mass is controlled by the collapse time (see Eq. (8)). Each panel sets the collapse time constant and therefore the ejecta mass. An examination of horizontal line sets constant LGRB, iso. Therefore, also the jet break-out time remains a constant (see Fig. A1). Consequently, the engine time can be rewritten as T90 + tjb for these points. When the engine time decreases, the merger ejecta consumes a larger portion of the disk energy deposit. Therefore, the region in which the collapse time significantly influences the disk mass posterior primarily lies in the lower T90 range, where Teng ≳ tjb (LGRB, iso, tcoll).
However, it becomes evident that the efficiency of the accretion onto the jet is an even more crucial parameter that can span orders of magnitude. One approach to allow the shaded region to encompass disk masses compatible with short GRBs from BNS mergers is to allow the efficiency to vary across the (T90, LGRB, iso) parameter space. However, this is not easily visualized in a plot like Fig. 2, and can be better understood from the discussion for Table B.2 in Appendix B.
4. Conclusions
We developed a comprehensive algorithm for estimating the dynamical quantities involved in sGRB events, with a specific focus on the mass of the accretion disk that formed after a BNS merger. Our approach linked observational parameters, such as isotropic GRB luminosity (LGRB, iso) and burst duration (T90), to the properties of the merger remnant and its ability to power a GRB event.
Our results highlight the significance of the jet efficiency and opening angle in determining the disk mass required for a GRB event. The analysis indicates that in the parameter space of T90 and LGRB, iso, the majority of observational data corresponds to disk masses near 0.1 solar masses (M⊙), which is consistent with current simulations. Importantly, some short GRB events exhibit a significantly higher disk mass, which raises questions about their origin. This suggests the possibility that BNS mergers may involve different mechanisms for jet launching than the well-studied GRB170817A, indicating a potential lack of universality in the underlying physics. Specifically, when the efficiency parameter ϵdisk is changed, the observables that require high disk masses vary greatly. Future observations of sGRBs that will allow the calculation of this efficiency will verify or reject this assumption.
With the advancement of numerical relativity, general restrictions can be drawn with greater confidence based on these methods.
Acknowledgments
The authors would like to thank P. Singh, R. Gill, S.I. Stathopoulos and L. Rezzolla for useful discussions. Support also comes from the ERC Advanced Grant “JETSET: Launching, propagation and emission of relativistic jets from binary mergers and across mass scales” (Grant No. 884631).
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 119, 161101 [Google Scholar]
- Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., & Serra-Ricart, M. 2017b, Nature, 551, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Arcavi, I., Hosseinzadeh, G., Howell, D. A., et al. 2017, Nature, 551, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ascenzi, S., Oganesyan, G., Branchesi, M., & Ciolfi, R. 2021, J. Plasma Phys., 87, 845870102 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [Google Scholar]
- Barbieri, C., Salafia, O. S., Colpi, M., Ghirlanda, G., & Perego, A. 2021, A&A, 654, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beniamini, P., Duran, R. B., Petropoulou, M., & Giannios, D. 2020, ApJ, 895, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Best, W. M. J., Magnier, E. A., Liu, M. C., et al. 2018, ApJS, 234, 1 [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bovard, L., Martin, D., Guercilena, F., et al. 2017, Phys. Rev. D, 96, 124005 [NASA ADS] [CrossRef] [Google Scholar]
- Bromberg, O., Nakar, E., Piran, T., & Sari, R. 2011, ApJ, 740, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Camilletti, A., Chiesa, L., Ricigliano, G., et al. 2022, MNRAS, 516, 4760 [CrossRef] [Google Scholar]
- Coulter, D., Foley, R., Kilpatrick, C., et al. 2017, Science, 358, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz-Osorio, A., Fromm, C. M., Mizuno, Y., et al. 2022, Nat. Astron., 6, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Drout, M. R., Piro, A. L., Shappee, B. J., et al. 2017, Science, 358, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Duffell, P. C., Quataert, E., Kasen, D., & Klion, H. 2018, ApJ, 866, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, P. A., Cenko, S. B., Kennea, J. A., et al. 2017, Science, 358, 1565 [NASA ADS] [CrossRef] [Google Scholar]
- Fujibayashi, S., Kiuchi, K., Nishimura, N., Sekiguchi, Y., & Shibata, M. 2018, ApJ, 860, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [Google Scholar]
- Ghirlanda, G., Salafia, O. S., Paragi, Z., et al. 2019, Science, 363, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Giacomazzo, B., Perna, R., Rezzolla, L., Troja, E., & Lazzati, D. 2013, ApJ, 762, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, R., Nathanail, A., & Rezzolla, L. 2019, ApJ, 876, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Goldstein, A., Veres, P., Burns, E., et al. 2017, ApJ, 848, L14 [CrossRef] [Google Scholar]
- Kasen, D., Metzger, B., Barnes, J., Quataert, E., & Ramirez-Ruiz, E. 2017, Nature, 551, 80 [Google Scholar]
- Kasliwal, M. M., Nakar, E., Singer, L. P., et al. 2017, Science, 358, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Krüger, C. J., & Foucart, F. 2020, Phys. Rev. D, 101, 103002 [CrossRef] [Google Scholar]
- Kumar, P., & Zhang, B. 2015, Phys. Rep., 561, 1 [Google Scholar]
- Li, L.-X., & Paczyński, B. 1998, ApJ, 507, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D., Perego, A., Arcones, A., et al. 2015, ApJ, 813, 2 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Hiramatsu, D., Howell, D. A., et al. 2017, ApJ, 848, L32 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Uzdensky, D. A. 2012, MNRAS, 419, 573 [Google Scholar]
- Metzger, B. D., MartÃnez-Pinedo, G., Darbha, S., et al. 2010, MNRAS, 406, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Mooley, K. P., Deller, A. T., Gottlieb, O., et al. 2018, Nature, 561, 355 [Google Scholar]
- Nathanail, A., Gill, R., Porth, O., Fromm, C. M., & Rezzolla, L. 2021, MNRAS, 502, 1843 [NASA ADS] [CrossRef] [Google Scholar]
- Nava, L., Ghirlanda, G., Ghisellini, G., & Celotti, A. 2011, A&A, 530, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nedora, V., Radice, D., Bernuzzi, S., et al. 2021, MNRAS, 506, 5908 [CrossRef] [Google Scholar]
- Pian, E., D’Avanzo, P., Benetti, S., et al. 2017, Nature, 551, 67 [Google Scholar]
- Radice, D., & Dai, L. 2019, Eur. Phys. J. A, 55, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Radice, D., Perego, A., Hotokezaka, K., et al. 2018, ApJ, 869, 130 [Google Scholar]
- Rees, M. J., & Meszaros, P. 1992, MNRAS, 258, 41 [Google Scholar]
- Rees, M. J., & Meszaros, P. 1994, ApJ, 430, L93 [Google Scholar]
- Rouco Escorial, A., Fong, W.-F., Berger, E., et al. 2023, ApJ, 959, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Salafia, O. S., & Giacomazzo, B. 2021, A&A, 645, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sekiguchi, Y., Kiuchi, K., Kyutoku, K., & Shibata, M. 2015, Phys. Rev. D, 91, 064059 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Simon, J. D., Drout, M. R., et al. 2017, Science, 358, 1574 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, M., & Hotokezaka, K. 2019, Annu. Rev. Nucl. Part. Sci., 69, 41 [Google Scholar]
- Smartt, S. J., Chen, T. W., Jerkstrand, A., et al. 2017, Nature, 551, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Levan, A. J., González-Fernández, C., et al. 2017, ApJ, 848, L27 [CrossRef] [Google Scholar]
- Troja, E., van Eerten, H., Ryan, G., et al. 2019, MNRAS, 489, 1919 [NASA ADS] [Google Scholar]
- Troja, E., Fryer, C. L., O’Connor, B., et al. 2022, Nature, 612, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., & Yan, H. 2011, ApJ, 726, 90 [Google Scholar]
Appendix A: Jet’s evolution
We solve for the dynamics of an arbitrary jet, following the uncollimated case of Bromberg et al. (2011). We assume an identical prescription for the rest of our work, regarding the jet’s dynamical evolution. We will briefly describe the governing equations
For simplicity, we consider a jet with constant power, that is launched inside an ejecta envelope. The ejecta envelope consists of mass ejected through various channels. The main mechanisms can be recognized as the dynamical ejection (Best et al. 2018), the neutrino-driven winds(Martin et al. 2015), and the magnetically-driven winds(Fujibayashi et al. 2018). Ejecta reach semi-relativistic velocities and they also act as a "barrier" that the jet has to drill through before reaching the interstellar medium (ISM).
The velocity profile is the following:
which is close to numerical values (Shibata & Hotokezaka 2019) and observational constraints (Arcavi et al. 2017; Drout et al. 2017; Shappee et al. 2017; Pian et al. 2017; Kasliwal et al. 2017; Kasen et al. 2017; Evans et al. 2017; Smartt et al. 2017).
For the ejecta density profile, we adopt a simple power-law
where rout(t) is the outer radius of the ejecta envelope, and is moving accordingly as the ejecta moves outwards. t is the time passed after the collapse. The radius is calculated via
where rout, 0 = 3 × 106cm. Mej(t) denotes the mass of the blue component of the ejecta, which is produced by the BNS compact remnant, before collapsing to a black hole at tcol. Its value is calculated from the formula reported in Gill et al. (2019).
Assuming that the jet injection starts at the collapse time, we analytically find the velocity of the jet’s head, which is slowed down by the double shock that is ignited upon collision with the ejecta. The jet’s head velocity, while inside the ejecta envelope, is dictated by the ram pressure equilibrium in the head’s frame.
 |
Fig. A.1. Key dynamical quantities for the jet. Upper panel: jet break-out time (in color) for the uncollimated case. Lower panel: the fraction of the jet energy lost for break-out ϵjb (in color). Quantities in both panels are plotted as functions of tcoll and LGRB, iso. The cyan region corresponds to 1 and 2−σ estimations of GRB170817A. |
where ρ and h are the mass density and specific enthalpy of each fluid and β the velocity. With the sub indices j, h and ej we denote the jet, the jet’s head and the ejecta. Assuming a relativistic jet that penetrates through cold ejecta, it can be concluded that:
where rh is the jet’s head position and 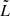 is the ratio of the jet energy density, to the ejecta density at that position.
is the ratio of the jet energy density, to the ejecta density at that position.
With given tcoll, Ljet, iso, and the assumption of uncollimated jet, the system described above can be solved for the jet evolution. The break-out time computed is shown on the upper panel of Fig. A.1, as a function of tcoll and Ljet, iso. Under the assumption of quasi-spherical ejecta, meaning that within the opening angle of the jet, the ejecta are spherically symmetric, this quantity does not depend on the opening angle of the jet.
The drilling that the jet has to go through, reduces its available energy which is dissipated later to produce the observed emission. The higher the resistance, meaning the more massive the ejecta to be bypassed, the greater the losses in energy before break out. The energy lost, is better expressed as follows:
Notice the similarities between this formulation presented and the one developed in Gill et al. (2019) - see sections 5 and 6 -. In Gill et al. (2019) reference case is GRB170817A, which from a dynamical point of view, there is no reason to consist an exception compared to the other sGRBs examined in this work. Other simplified and intuitive approximations, as the one from Duffell et al. (2018), where numerical results are employed, could not be adapted to our scheme, since in the latter for example, the ejecta radius is set to a constant upon jet launching, when in our case, it varies based on the collapse time, which dictates how much time the outer shell of the ejecta has, to freely expand. However, modifying the notation presented, to the same parameters as in Duffell et al. (2018), the break-out time differed mostly by an order of ∼2, which can be explained by slightly modifying the constant parameters in the fitting procedure.
Appendix B: Observables
 |
Fig. B.1. Variation in the percentage of short GRBs data classified as incompatible with BNS-merger as a function of collapse time (see Fig. 2). The differently colored columns represent different levels of disk mass selection for each observation event: the ranges covering 33%, 50%, and 67% of the disk mass posterior. The data reveals an increasing trend with higher collapse time. |
In this appendix, we thoroughly explore real observations of short GRBs within the (T90, LGRB, iso) parameter space as shown in Figure 2. Our objective is to assess what percentage of these observations can be reliably interpreted as a result of BNS mergers. To achieve this, we utilize publicly available data from the GRB archive of the Neil Gehrels Swift Observatory (Gehrels et al. 2004). We specifically focus on short GRBs, characterized by observed T90 durations less than 2 seconds. Additionally, we filter this subset to include only events with known redshift measurements, which are essential for estimating the isotropic γ-ray luminosity.
To calculate the isotropic γ-ray luminosity (Lγ, iso), we use the BAT fluence (Φ) along with the luminosity distance (dL(z)), redshift (z), and the Band function (Band et al. 1993) parameters (a = −0.5, b = −2.25) to model the differential photon spectrum within the 1 keV-10 MeV energy range. We assume a rest-frame peak energy of Ep = 800keV (Nava et al. 2011).
Sources for Various Quantities
Following the calculation of the isotropic γ-ray luminosity, and maintaining the assumption of tcoll = 1s. Our algorithm generates a posterior distribution for the disk mass by the following way. First, we select every source from the aforementioned subset, and calculate Ljet, iso from Eq. B.1. Then we draw disk to jet efficiency, from the distribution presented in Fig. 1, and an opening angle from (Rouco Escorial et al. 2023). We can then calculate for each observation Ljet, iso -we use a constant ϵGRB-. We solve for Ejet from Eq. 11. Then, a simple calculation from Eq. 10 gives Mdisk, eff, and since collapse time is constant, we employ Eq. 9, to solve for Mdisk . This distribution is exemplified in the right panel of Figure 1, illustrating the specific case of GRB 211221D. From this distribution, and for each observation, we derive the mean value and the 1-σ range. These short GRB events are then mapped onto the T90, Ljet parameter space, as illustrated in Figure 2. We assess the compatibility of each event with a BNS merger based on its position within the shaded region. Notably, we include GRB 211211A, even though it belongs to the category of long-duration GRBs, as it is classified as a burst originating from a compact object merger, supported by kilonova measurements and host property analysis (Troja et al. 2022).
To quantify the percentage of incompatible cases, we use blue, red, and black lines to represent 33%, 50%, and 67% quantiles of the posterior distribution. These lines correspond to the mean value minus 1-σ, the mean value, and the mean value plus 1-σ, respectively. The results of this analysis are displayed in Fig. B.1, where we also explore the influence of varying the collapse time, extending from the expected tcoll = 1s for GRB 170817A to smaller and larger values. The left panel of Fig. B.1 assumes the efficiency derived by Salafia & Giacomazzo (2021) for an empirical structured jet, while for the right one the energy efficiency distribution is based on the kinetic energy from Nathanail et al. (2021).
The handling of each parameter is shown in Table B.1. Fig. B.1 demonstrates that the variation in collapse time has a rather limited impact on the results compared to other factors, where we followed the exact same procedure described earlier, but for different collapse times. Our in-depth analysis highlights the greater significance of parameters like efficiency and opening angle. However, we observed a positive correlation between the percentage of possible BNS merger events and shorter collapse times.
Probability for BNS event and corresponding Disk Mass in log10[M⊙] with tcol = 1sec
For each short GRB event in the sample, while maintaining tcol = 1sec, we are investigating, we estimate the probability of the event originating from a BNS merger, with a specific focus on the mass of the disk surrounding the merger remnant. The approach to assigning a probability is as follows: from the normalized posterior distribution, which integrates to a sum of 1, we compute the integral for the region with a lower mass than the conservative upper limit for the disk mass, which is set to 0.3M⊙. This value represents the probability. These results are reported in Table B.2. We provide the disk mass values calculated based on the accretion-to-jet energy efficiency profiles from both Salafia & Giacomazzo (2021) (left columns) and Nathanail et al. (2021) (right columns).
All Tables
Probability for BNS event and corresponding Disk Mass in log10[M⊙] with tcol = 1sec
All Figures
 |
Fig. 1. Comparison of posteriors for accretion-to-jet efficiency and application of our model. Left panel: Posteriors for the accretion to jet efficiency for the case of GRB170817A. The green line represents the efficiency derived from ou algorithm, and the red line shows the efficiency from Salafia & Giacomazzo (2021). They both use the kinetic energy distribution from Ghirlanda et al. (2019). The blue line corresponds to the kinetic energy distribution from a strongly magnetized jet from Nathanail et al. (2021). The overplotted points refer to efficiencies from general relativity magnetohydrodynamics simulations. Right panel: Resulting posterior distributions analyzing GRB201221D with our algorithm, assuming an efficiency similar to GRB170817A. |
| In the text | |
 |
Fig. 2. Disk mass required, according to our model, for the production of a short gamma-ray burst. The background color represents the mass of the disk in both cases, calculated as the mean value of our posteriors. The red points represent observational events (see the main text for details). The vertical dashed blue line corresponds to the core luminosity of GRB170817A. The shaded region indicates where the disk mass exceeds 0.3 M⊙, which is an approximate limit derived from numerical relativity simulations. The solid gray line marks the boundary between these two regions. In the left panel, we used the efficiency profile from Salafia & Giacomazzo (2021), and in the right panel, we adopted the corresponding efficiency for a jet profile from Nathanail et al. (2021). |
| In the text | |
 |
Fig. A.1. Key dynamical quantities for the jet. Upper panel: jet break-out time (in color) for the uncollimated case. Lower panel: the fraction of the jet energy lost for break-out ϵjb (in color). Quantities in both panels are plotted as functions of tcoll and LGRB, iso. The cyan region corresponds to 1 and 2−σ estimations of GRB170817A. |
| In the text | |
 |
Fig. B.1. Variation in the percentage of short GRBs data classified as incompatible with BNS-merger as a function of collapse time (see Fig. 2). The differently colored columns represent different levels of disk mass selection for each observation event: the ranges covering 33%, 50%, and 67% of the disk mass posterior. The data reveals an increasing trend with higher collapse time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



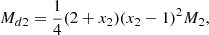
![$$ \begin{aligned} x_2&= 2\left[\left(1+\dfrac{M_1}{M_2}\right)^{-1} + \lambda _2 ^{-1} -1\right],\end{aligned} $$](/articles/aa/full_html/2024/10/aa50201-24/aa50201-24-eq2.gif)
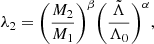
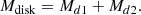
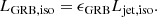
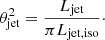
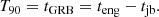
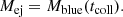
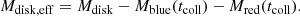
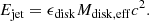
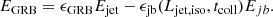
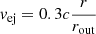
![$$ \begin{aligned} \rho (r,t) = \dfrac{1}{4\pi }\dfrac{M_{ej}(t)}{r_{\mathrm{out,0} ^3}} \bigg [\dfrac{r}{r_\mathrm{out} (t)}\bigg ]^{-2} \end{aligned} $$](/articles/aa/full_html/2024/10/aa50201-24/aa50201-24-eq19.gif)
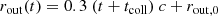
![$$ \begin{aligned} \rho _{j}h_{j}[\Gamma _{j}\Gamma _{h}(\beta _{j}-\beta _{h})]^{2} = \rho _{ej}h_{ej}[\Gamma _{ej}\Gamma _{h}(\beta _{h}-\beta _{ej})]^{2} \end{aligned} $$](/articles/aa/full_html/2024/10/aa50201-24/aa50201-24-eq21.gif)