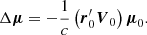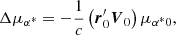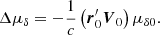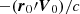| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | L24 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202451053 | |
| Published online | 12 August 2024 | |
Letter to the Editor
Secular aberration drift in stellar proper motions
An additional term due to the change in line-of-sight direction
1
School of Astronomy and Space Science, Key Laboratory of Modern Astronomy and Astrophysics (Ministry of Education), Nanjing University, Nanjing 210023, PR China
2
University of Chinese Academy of Sciences, Nanjing 211135, China
Received:
10
June
2024
Accepted:
26
July
2024
Context. The motion of the Solar System barycenter (SSB), the spatial origin of the International Celestial Reference System, causes a directional displacement known as secular aberration. The secular aberration drift caused by the galactocentric acceleration of the SSB has been modeled in the third generation of the International Celestial Reference Frame.
Aims. We aim to address another secular aberration drift effect due to the change in the line-of-sight direction and study its implications for stellar proper motions.
Methods. We derived a complete formula for the secular aberration drift and computed its influence on stellar proper motion based on the astrometric data in Gaia Data Release 3.
Results. We find that the secular aberration drift due to the change in the line-of-sight direction tends to decrease the observed proper motions for stars with galactic longitudes between 0° and 180°, and increase the observed proper motion for stars in the remaining region. If this secular aberration drift effect is ignored, it will induce an additional proper motion of > 1 mas yr−1 for 84 stars and > 0.02 mas yr−1 for 5 944 879 stars, which is comparable to or several times greater than the typical formal uncertainty of the Gaia proper motion measurements at G < 13.
Conclusions. The secular aberration drift due to the change in the line-of-sight direction and the acceleration of the SSB should be modeled to make the stellar reference frame consistent with the extragalactic reference frame.
Key words: methods: data analysis / astrometry / proper motions / reference systems
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The International Celestial Reference System (ICRS; Feissel & Mignard 1998) adopts the Solar System barycenter (SSB) as the spatial origin and uses extragalactic sources as the fiducial points in the sky. It has long been established that the motion of the SSB in space causes a displacement in the source direction, known as the secular aberration effect (see, e.g., the review in Gaia Collaboration 2021). This effect was previously assumed to be constant and thus was not considered in astrometric data reduction. This assumption relies on two underlying premises: (i) the SSB moves uniformly in space, and (ii) the direction of the line of sight for a given source does not change. However, these two premises do not always hold valid.
First, Galactic rotation suggests that the SSB does not exhibit uniform motion. Kovalevsky (2003) first formulated the secular aberration drift due to the acceleration of the SSB; according to their calculations, this drift causes an apparent proper motion field of extragalactic sources with an amplitude of approximately 5 microarcsecond per year (μas yr−1). This effect, also referred to as Galactic aberration (e.g. Malkin 2023), has been detected in the astrometric measurements of extragalactic sources by very long baseline interferometry (VLBI; MacMillan et al. 2019) and Gaia (Gaia Collaboration 2021). The Galactic aberration effect results in an apparent rotation of the ICRS (Liu et al. 2012) and then a non-negligible drift of the celestial pole (Yao et al. 2022). In the construction of the third generation of the International Celestial Reference Frame (ICRF3; Charlot et al. 2020), the VLBI delay model integrates the effect of the galactocentric acceleration of the SSB. This new model corrects for the observational effect due to the curvature of the SSB motion, making the ICRF3 more consistent with the ICRS concept than its predecessors.
Second, the assumption that the direction of the line of sight remains constant does not always hold. Due to their enormous distances, extragalactic sources are not supposed to show any proper motion with respect to the current observational accuracy and precision. This is also one of the basic assumptions behind the ICRS concept. The Galactic objects, however, show non-negligible proper motions, which alter the direction of the line of sight and, consequently, the magnitude of the secular aberration. This effect manifests as additional proper motion and is, as we will demonstrate, proportional to the stellar proper motion. Therefore, this effect is several orders of magnitude greater than that caused by the acceleration of the SSB and will bias the proper motion measurement for sources with high proper motion.
This Letter aims to address the secular aberration drift in stellar proper motions due to both the acceleration of the SSB and the change in the direction of the line of sight. The complete formula of the secular aberration drift effect is developed in Sect. 2. In Sect. 3 we determine the implications for stellar proper motions based on Gaia Data Release 3 (DR3; Gaia Collaboration 2016, 2023).
2. Secular aberration drift effect
For a fictitious observer at the SSB who is at rest with respect to the extragalactic background, the coordinate direction of an object at the observational epoch, T, is denoted as the unit vector, u. The difference in the coordinate direction caused by the motion of the SSB can be expanded as1
where V⊙ is the velocity vector of the SSB with respect to the extragalactic background at T, and c is the speed of light. This formula ignores the relativistic aberrational effect, that is, terms higher than the second order with respect to 1/c.
Following the standard model of stellar motion (ESA 1997; Lindegren et al. 2016), the position and motion of the source can be described by six astrometric parameters. Five of these parameters are the classical parameters: the right ascension (α), declination (δ), trigonometric parallax (ϖ), and the proper motion in the right ascension (μα*) and declination (μδ). For the sixth parameter, we used the radial proper motion (μr) instead of the radial velocity (vr), which is defined as
where A is the astronomical unit expressed in km s−1 yr. The normal triad at the location of this source can then be defined as
Therefore, the proper motion of the source can be expressed as
Since the six parameters change with time, these parameters are conventionally given with respect to a reference epoch, Tref. We subsequently used the difference between the reference epoch and the observation epoch, t = Tobs − Tref, as the time argument and a subscript 0 to denote the quantities at the reference epoch (i.e., t = 0). Let us introduce a factor, f, to account for the change in the distance as
and a sum vector of the (tangential) proper motion and the radial proper motion as
The propagated coordinate direction, u, at t can thus be written as
The light-time effect is ignored since it can cause only small displacements of 0.1 mas over 100 yr (Butkevich & Lindegren 2014) and hence is negligible for the investigation in this work. The Galactic rotation of the observed stars, as in previous studies (e.g. Liu et al. 2013), is also ignored here.
Considering the acceleration term (e.g., the Galactic rotation), the velocity of the SSB can be written as
where V0 is the initial velocity vector of the SSB at Tref. We adopted the results of the Galactic kinematic analysis in Reid et al. (2019); other studies yielded consistent results (e.g., Bobylev et al. 2021). The velocity of the SSB is
where AG is the transform matrix between the equatorial and galactic systems (see ESA 1997, Vol. 1, Sect. 1.5.3). The distance to the Galactic center, R0, is approximately 8.15 kpc. The acceleration of the SSB is dominated by the galactocentric acceleration.
By substituting Eqs. (7) and (8) into Eq. (1), the secular aberration effect can be expanded as
The secular aberration effect apparently changes with time due to both the acceleration of the SSB and the change in the line-of-sight direction of the source.
For extragalactic sources, the proper motion and radial proper motion are nominally assumed to be zero, which leads to f = 1. As a result, Eq. (10) becomes
The first term in Eq. (11) represents the constant secular aberration, while the second term is caused by the acceleration of the SSB and manifests as a dipole field of the apparent proper motion. Using the values given in Reid et al. (2019) in the computation, we have
for constant aberration displacement and
for the apparent proper motion. Although the magnitude of the constant aberration greatly exceeds the accuracy of microarcsecond astrometry, the effect itself does not vary with time; thus, it is omitted in practical data analyses. The effect of the acceleration of the SSB depends on the location of the source, resulting in a dipolar proper motion field with an amplitude of approximately 5 μas yr−1. This effect has been well studied and will not be discussed further in this work.
As the proper motions of the Galactic stars are non-negligible, the variation in the secular aberration effect is more complicated. Here, we were more concerned with the secular aberration drift since it will be absorbed in the observed stellar proper motion if it is neglected. For a source with an extremely high proper motion of 10 arcsec yr−1, the amplitudes of the quadratic and cubic terms of t could reach 0.04 μas yr−2 and 1.2 × 10−8 μas yr−3, respectively. These two terms might need to be considered for astrometric data reductions that cover a long time baseline; they can be safely omitted in this work. We used the Taylor expansions up to the first order to approximate f2, which yields
Then, we substituted Eq. (14) into Eq. (10) and kept only the constant and linear terms of t, leading to
This equation suggests that the apparent proper motion due to the secular aberration effect contains an additional term compared to extragalactic sources. This term can be regarded as an effect related to the change in the line-of-sight direction of the source, whose magnitude not only depends on the celestial coordinate but is also proportional to the proper motion of the source by a factor of V0/c ≃ 8.0 × 10−4. In Gaia DR3, the source with the largest total proper motion is Barnard’s star (Gaia DR3 4472832130942575872), whose total proper motion is approximately 10393.349 mas yr−1 with a formal uncertainty of 0.04 mas yr−1. For this star, the magnitude of the third term in Eq. (15) reaches 8 mas yr−1, which is three orders of magnitude greater than the magnitude of the second term in Eq. (15) and two orders of magnitude greater than the formal uncertainty of the Gaia proper motion measurement. This kind of secular aberration drift effect, therefore, should be taken into consideration. Conversely, with a required accuracy of 1 μas yr−1 and 10 μas yr−1 in proper motion, the secular aberration drift due to the proper motion of a source may need to be considered if the stellar proper motion reaches 1.2 mas yr−1 and 12 mas yr−1, respectively.
In short, the secular aberration drift induces two additional terms in the observed proper motion for the stars, one caused by the acceleration of the SSB and the other caused by the proper motion of the source. The first term has been well investigated and determined in previous studies; however, the second term is rarely discussed in the literature. In this work, we focus on the second term.
We note that the terms proportional to r0 in Eq. (15) do not lead to proper motion changes. Therefore, the additional proper motion caused by the secular aberration drift due to the change in the line-of-sight direction can be written as
This equation suggests that this effect will only change the magnitude of the proper motion by a factor of 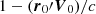 . The corresponding components in right ascension and declination are
. The corresponding components in right ascension and declination are
Figure 1 displays the relative change in the observed total proper motion, according to Eq. (16), in the galactic coordinate system. This pattern suggests that secular aberration drift will cause the observed proper motion to decrease for stars of 0 < l < 180° but increase in the region of 180° < l < 360°.
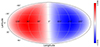 |
Fig. 1. Distribution of the factor |
3. Implication for stellar proper motion
We searched for stellar objects (i.e., with in_qso_candidates = false and in_galaxy_candidates = false) that had either a five- or a six-parameter solution and a total proper motion, μ0, greater than 1 mas yr−1 (pm > 1) in Gaia DR3. The query returned a sample of 1 417 503 136 sources. We then computed the additional proper motion due to secular aberration drift using Eqs. (16)–(18). Figure 2 depicts the distribution of additional proper motion components. The greatest additional proper motion is 5.214 mas yr−1 for Gaia DR3 4810594479418041856 (HD 33793). The number of stars whose additional proper motion exceeds 1 mas yr−1 in an absolute sense is 43 in right ascension, 29 in declination, and 84 for the total proper motion. Considering that the typical formal uncertainty of the Gaia proper motion at G < 13 is approximately 0.02 mas yr−1 (Lindegren et al. 2021), the corresponding numbers of stars with additional proper motion exceeding 0.02 mas yr−1 are 2 875 610 for right ascension, 2 422 948 for declination, and 5 944 879 for total proper motion. The uncertainties of the proper motions in the next Gaia data release will be improved by at least a factor of 0.35 compared to those in Gaia DR3 (Lindegren et al. 2021), making the additional proper motion effect more pronounced.
 |
Fig. 2. Distribution of the additional proper motion components in right ascension (Δμα*) and declination (Δμδ) caused by secular aberration drift due to the change in the line of sight for Galactic stars with a total proper motion exceeding 1 mas yr−1. (a) Scatter plot of Δμα* versus Δμδ. The ten sources with the greatest additional proper motion are highlighted, with their names labeled near the data points. (b) Histogram of Δμα*. (c) Histogram of Δμδ. |
To quantify the significance of the additional proper motion, we computed the ratio between the additional proper motions and the formal uncertainties of Gaia proper motion measurements. The formal uncertainty of the Gaia total proper motion was computed as
where σμα* and σμδ are the uncertainties in proper motion in right ascension and declination, respectively, and Cμα*, μδ is the covariance between them.
As shown in Fig. 3, large values of the additional total proper motion are usually associated with large values of significance. For more than 70 000 stars, the additional total proper motion is significant at the 3σ level or higher and thus cannot be ignored for these stars. Figure 4 depicts the distribution of the significance of the additional total proper motion as a function of Gaia G magnitude, clearly showing that significant additional proper motions due to the secular aberration drift mainly occur in the magnitude range 6 < G < 16.
 |
Fig. 3. Distribution of the additional total proper motions (Δμ) and their significance (Δμ/σμ) caused by secular aberration drift due to the change in the line of sight for Galactic stars with a total proper motion exceeding 1 mas yr−1. (a) Scatter plot of Δμ versus Δμ/σμ. The ten sources with the greatest additional proper motion are highlighted, with their names labeled near the data points. (b) Histogram of Δμ. (c) Histogram of Δμ/σμ. |
 |
Fig. 4. Distribution of the significance of the additional total proper motion (Δμ/σμ) caused by secular aberration drift due to the change in the line of sight as a function of Gaia G magnitude for Galactic stars with a total proper motion exceeding 1 mas yr−1. The horizontal lines in green and red are at vertical axis values of 1 and 3, respectively. |
We examined the dependence of the additional proper motion on distance. Using the built-in function for distance estimation in the STILTS package (Taylor 2006), we computed stellar distances from Gaia parallaxes. This estimation is based on the exponentially decreasing space density prior defined in Astraatmadja & Bailer-Jones (2016); we set the length scale, L, to 1.35 kpc as done therein. Figure 5 depicts the dependence of the additional proper motion as a function of the stellar distance. We find that the additional proper motion generally decreases with distance. Moreover, for stars within 2 kpc, the additional proper motion can reach up to 0.1 mas yr−1, which highlights the potential impact of secular aberration drift on Galactic kinematic analyses, particularly for nearby stars.
 |
Fig. 5. Distribution of the additional total proper motions caused by secular aberration drift due to the change in the line of sight as a function of distances for Galactic stars with total proper motions exceeding 1 mas yr−1. The green line indicates the medians, calculated using the built-in Epanechnikov kernel smoothing function in the TOPCAT package (Taylor 2011). |
4. Discussion
In the construction of the ICRF3, the secular aberration effect due to the galactocentric acceleration of the SSB has been modeled, enhancing the consistency of ICRF3 with the concept of the ICRS. It is anticipated that the Gaia celestial reference frame will also model and correct for this effect. To ensure that the stellar reference frame of Gaia aligns with the extragalactic reference frame, it is necessary to account for the secular aberration drift due to stellar proper motion.
For the extragalactic frame, it is sufficient to consider the galactocentric acceleration of the SSB. However, the stellar frame must address the secular aberration drift caused by stellar proper motion. As demonstrated in the previous section, the secular aberration drift from stellar proper motion can be several times greater than the effect of the SSB’s acceleration and the formal uncertainties in Gaia proper motion measurements, particularly for bright stars with high proper motions. Therefore, we recommend that the term “Galactic aberration effect”, commonly used in the ICRF community, encompass the secular aberration drift in (apparent) proper motions due to both the SSB’s acceleration and stellar proper motion to ensure consistency between the stellar frame and the extragalactic frame.
Fully correcting the stellar proper motion terms related to secular aberration drift requires knowledge of the position and motion of the SSB within our Galaxy. However, this information is usually derived from Galactic kinematic analyses, which utilize stellar proper motion data. As a result, correcting for secular aberration drift in stellar proper motion necessitates an iterative process. We propose addressing this issue in four steps:
-
(i)
Determine the acceleration vector of the SSB from the proper motion measurements of extragalactic sources, and then correct for the secular aberration drift due to the acceleration of the SSB for both the Galactic and extragalactic sources.
-
(ii)
Adopt the state-of-the-art estimates from the literature as the initial guess for the velocity of the SSB and correct for the secular aberration drift due to the proper motion for Galactic stars.
-
(iii)
Perform a Galactic kinematic analysis using the corrected stellar proper motions to determine the velocity of the SSB.
-
(iv)
Repeat steps (ii) and (iii) until the results converge to the required accuracy.
By following these steps, we can achieve a more accurate and consistent celestial reference frame that accounts for both the SSB’s acceleration and the proper motions of stars.
5. Conclusions
We investigated the secular aberration drift due to stellar proper motion in addition to the effect caused by the acceleration of the Solar System. Our findings demonstrate that this previously neglected term can induce systematic errors in observed stellar proper motion, depending on both the celestial position and the magnitude of the stellar proper motion. For several dozen stars with high proper motion, this drift can bias the Gaia proper motion by 1 mas yr−1 or more. Such a bias exceeds the precision of Gaia’s proper motion measurements at G < 13 and should therefore be considered in the reduction of Gaia astrometric data, especially for stars at 6 < G < 16.
By fully accounting for the secular aberration drift in proper motion, we can bring the stellar and extragalactic reference frames more in line with the definition of the ICRS. This correction is crucial for maintaining a consistency between the stellar frame and the extragalactic frame and for advancing our understanding of stellar kinematics.
Acknowledgments
We sincerely thank the anonymous referee for their constructive comments and useful suggestions, which improve the work a lot. N. Liu, J.-C. Liu, and Z. Zhu were supported by the National Natural Science Foundation of China (NSFC) under grant Nos. 12373074, 11833004, and 12103026. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research had also made use of several Python packages, including Numpy (van der Walt et al. 2011), IPython (Perez & Granger 2007), Astropy (http://www.astropy.org) (Astropy Collaboration 2013, 2018), the 2D plotting library Matplotlib (Hunter 2007), healpy, and HEALPix (http://healpix.sf.net). All the necessary files (e.g., codes) to reproduce the results in the this Letter can be found at https://git.nju.edu.cn/astrometry/sadonpm
References
- Astraatmadja, T. L., & Bailer-Jones, C. A. L. 2016, ApJ, 833, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bobylev, V. V., Bajkova, A. T., Rastorguev, A. S., & Zabolotskikh, M. V. 2021, MNRAS, 502, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Butkevich, A. G., & Lindegren, L. 2014, A&A, 570, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Jacobs, C. S., Gordon, D., et al. 2020, A&A, 644, A159 [EDP Sciences] [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues. Astrometric and Photometric Star Catalogues Derived from the ESA Hipparcos Space Astrometry Mission (Noordwijk, Netherlands: ESA Publications Division), 1200 [Google Scholar]
- Feissel, M., & Mignard, F. 1998, A&A, 331, L33 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Klioner, S. A., et al.) 2021, A&A, 649, A9 [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Liu, J. C., Capitaine, N., Lambert, S. B., Malkin, Z., & Zhu, Z. 2012, A&A, 548, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, J. C., Xie, Y., & Zhu, Z. 2013, MNRAS, 433, 3597 [NASA ADS] [CrossRef] [Google Scholar]
- MacMillan, D. S., Fey, A., Gipson, J. M., et al. 2019, A&A, 630, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malkin, Z. 2023, Res. Notes Am. Astron. Soc., 7, 133 [NASA ADS] [Google Scholar]
- Perez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
- Taylor, M. B. 2006, ASP Conf. Ser., 351, 666 [Google Scholar]
- Taylor, M. 2011, Astrophysics Source Code Library [record ascl:1101.010] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- Yao, J., Liu, J. C., Liu, N., et al. 2022, A&A, 665, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. Distribution of the factor |
| In the text | |
 |
Fig. 2. Distribution of the additional proper motion components in right ascension (Δμα*) and declination (Δμδ) caused by secular aberration drift due to the change in the line of sight for Galactic stars with a total proper motion exceeding 1 mas yr−1. (a) Scatter plot of Δμα* versus Δμδ. The ten sources with the greatest additional proper motion are highlighted, with their names labeled near the data points. (b) Histogram of Δμα*. (c) Histogram of Δμδ. |
| In the text | |
 |
Fig. 3. Distribution of the additional total proper motions (Δμ) and their significance (Δμ/σμ) caused by secular aberration drift due to the change in the line of sight for Galactic stars with a total proper motion exceeding 1 mas yr−1. (a) Scatter plot of Δμ versus Δμ/σμ. The ten sources with the greatest additional proper motion are highlighted, with their names labeled near the data points. (b) Histogram of Δμ. (c) Histogram of Δμ/σμ. |
| In the text | |
 |
Fig. 4. Distribution of the significance of the additional total proper motion (Δμ/σμ) caused by secular aberration drift due to the change in the line of sight as a function of Gaia G magnitude for Galactic stars with a total proper motion exceeding 1 mas yr−1. The horizontal lines in green and red are at vertical axis values of 1 and 3, respectively. |
| In the text | |
 |
Fig. 5. Distribution of the additional total proper motions caused by secular aberration drift due to the change in the line of sight as a function of distances for Galactic stars with total proper motions exceeding 1 mas yr−1. The green line indicates the medians, calculated using the built-in Epanechnikov kernel smoothing function in the TOPCAT package (Taylor 2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \delta \boldsymbol{u} = \dfrac{1}{c} \left[{\boldsymbol{V}}_{\odot } - \left({\boldsymbol{u}}^{\prime }{\boldsymbol{V}}_{\odot }\right)\boldsymbol{u}\right] + O\,(c^{-2}), \end{aligned} $$](/articles/aa/full_html/2024/08/aa51053-24/aa51053-24-eq1.gif)
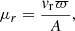
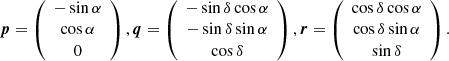
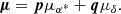
![$$ \begin{aligned} f = \left[1 + 2\mu _{r0} t + \left(\mu ^{2}_{0} + \mu ^{2}_{r0}\right) t^2\right]^{-1/2} \end{aligned} $$](/articles/aa/full_html/2024/08/aa51053-24/aa51053-24-eq5.gif)
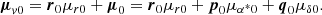
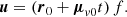
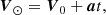
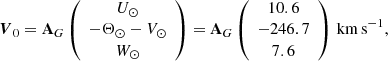
![$$ \begin{aligned} \begin{aligned} \delta \boldsymbol{u} =&\dfrac{1}{c} \left[{\boldsymbol{V}}_{0} - \left({\boldsymbol{r}}_{0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{r}}_0 f^2\right] \\&+ \dfrac{t}{c} \left[\boldsymbol{a} - \left({\boldsymbol{r}}_{0}^{\prime } \boldsymbol{a}\right) {\boldsymbol{r}}_0 f^2 \right] - \dfrac{f^2 t}{c} \left[\left({\boldsymbol{\mu }}_{v0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{r}}_0 + \left({\boldsymbol{r}}_{0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{\mu }}_{v0}\right] \\&-\dfrac{f^2 t^2}{c} \left[\left({\boldsymbol{r}}_0^{\prime }\boldsymbol{a} + {\boldsymbol{\mu }}_{v0}^{\prime }{\boldsymbol{V}}_0\right) {\boldsymbol{\mu }}_{v0} + \left({\boldsymbol{\mu }}^{\prime }_{v0} \boldsymbol{a}\right) {\boldsymbol{r}}_0\right] - \dfrac{f^2 t^3}{c} \left({\boldsymbol{\mu }}^{\prime }_{v0} \boldsymbol{a}\right) {\boldsymbol{\mu }}_{v0}. \end{aligned} \end{aligned} $$](/articles/aa/full_html/2024/08/aa51053-24/aa51053-24-eq10.gif)
![$$ \begin{aligned} \delta \boldsymbol{u} = \dfrac{1}{c} \left[{\boldsymbol{V}}_{0} - \left({\boldsymbol{r}}_{0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{r}}_0\right] + \dfrac{t}{c} \left[\boldsymbol{a} - \left({\boldsymbol{r}}_{0}^{\prime } \boldsymbol{a}\right) {\boldsymbol{r}}_0\right]. \end{aligned} $$](/articles/aa/full_html/2024/08/aa51053-24/aa51053-24-eq11.gif)
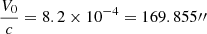
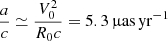
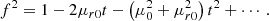
![$$ \begin{aligned} \begin{aligned} \delta \boldsymbol{u} =&\dfrac{1}{c} \left[{\boldsymbol{V}}_{0} - \left({\boldsymbol{r}}_{0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{r}}_0\right] + \dfrac{t}{c} \left[\boldsymbol{a} - \left({\boldsymbol{r}}_{0}^{\prime } \boldsymbol{a}\right){\boldsymbol{r}}_0\right] \\&-\dfrac{t}{c} \left[\left({\boldsymbol{\mu }}_{v0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{r}}_0 + \left({\boldsymbol{r}}_{0}^{\prime } {\boldsymbol{V}}_0\right) {\boldsymbol{\mu }}_{v0}\right] + \cdots \end{aligned} \end{aligned} $$](/articles/aa/full_html/2024/08/aa51053-24/aa51053-24-eq15.gif)