| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A199 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202449536 | |
| Published online | 26 July 2024 | |
Thermonuclear 28P(p, γ)29S reaction rate and astrophysical implication in ONe nova explosion
1
Key Laboratory of High Precision Nuclear Spectroscopy, Institute of Modern Physics, Chinese Academy of Sciences,
509 Nanchang Rd,
Lanzhou
730000, PR China
e-mail: sqhou@impcas.ac.cn
2
School of Nuclear Science and Technology, University of Chinese Academy of Sciences,
19A Yuquan Rd, Shijingshan District,
Beijing
100049, PR China
3
Departament de Física, Universitat Politècnica de Catalunya,
08019
Barcelona, Spain
4
Institut d’Estudis Espacials de Catalunya, Universitat Politècnica de Catalunya,
08034
Barcelona, Spain
5
NuGrid Collaboration,
http://www.nugridstars.org
6
Konkoly Observatory, HUN-REN,
H-1121 Budapest,
Konkoly Thege M. út
15–17, Hungary
7
CSFK, MTA Centre of Excellence,
Budapest,
Konkoly Thege Miklós út 15–17,
1121,
Hungary
8
E. A. Milne Centre for Astrophysics, University of Hull,
Cottingham Rd,
Kingston upon Hull
HU6 7RX, UK
9
Joint Institute for Nuclear Astrophysics – Center for the Evolution of the Elements,
640 S Shaw Lane,
East Lansing, MI
48824, USA
10
Department of Physics, North Carolina State University,
Raleigh, NC
27695, USA
11
Triangle Universities Nuclear Laboratory,
Durham, NC
27708, USA
12
Department of Physics and Astronomy, Texas A&M University-Commerce,
Commerce, TX
75429, USA
Received:
8
February
2024
Accepted:
11
April
2024
Context. An accurate 28P(p, γ)29S reaction rate is crucial to defining the nucleosynthesis products of explosive hydrogen burning in ONe novae. Using the recently released nuclear mass of 29S, together with a shell model and a direct capture calculation, we reanalyzed the 28P(p, γ)29S thermonuclear reaction rate and its astrophysical implication.
Aims. We focus on improving the astrophysical rate for 28P(p, γ)29S based on the newest nuclear mass data. Our goal is to explore the impact of the new rate and associated uncertainties on the nova nucleosynthesis.
Methods. We evaluated this reaction rate via the sum of the isolated resonance contribution instead of the previously used Hauser-Feshbach statistical model. The corresponding rate uncertainty at different energies was derived using a Monte Carlo method. Nova nucleosynthesis is computed with the 1D hydrodynamic code SHIVA.
Results. The contribution from the capture on the first excited state at 105.64 keV in 28P is taken into account for the first time. We find that the capture rate on the first excited state in28 P is up to more than 12 times larger than the ground-state capture rate in the temperature region of 2.5 × 107 K to 4 × 108 K, resulting in the total 28P(p, γ)29S reaction rate being enhanced by a factor of up to 1.4 at ~1 × 109 K. In addition, the rate uncertainty has been quantified for the first time. It is found that the new rate is smaller than the previous statistical model rates, but it still agrees with them within uncertainties for nova temperatures. The statistical model appears to be roughly valid for the rate estimation of this reaction in the nova nucleosynthesis scenario. Using the 1D hydrodynamic code SHIVA, we performed the nucleosynthesis calculations in a nova explosion to investigate the impact of the new rates of 28P(p, γ)29S. Our calculations show that the nova abundance pattern is only marginally affected if we use our new rates with respect to the same simulations but statistical model rates. Finally, the isotopes whose abundance is most influenced by the present 28P(p, γ)29S uncertainty are 28Si, 33,34S, 35,37Cl, and 36Ar, with relative abundance changes at the level of only 3% to 4%.
Key words: nuclear reactions, nucleosynthesis, abundances / stars: abundances / novae, cataclysmic variables
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Nova explosions stand out as relatively frequent cataclysmic events. They occur in interacting binary systems consisting of a white-dwarf and a main-sequence (or a red-giant) companion, with an estimated Galactic frequency of 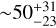 novae per year (Shafter 2017). It is worth noting that only a fraction of these events, around ten per year, are actually obscured by interstellar dust. In contrast to type Ia supernovae, neither the white dwarf nor the binary system is expected to be disrupted during a classical nova. In fact, novae constitute recurrent phenomena, exhibiting periodicities spanning between 104 and 105 yr. In the subclass of recurring novae (by definition, novae observed in outburst more than once), recurrence times vary from 1 to 100 yr. The question of whether these recurrence times constitute a nearly continuous sequence, encompassing the shorter values observed for recurrent novae and the longer periods predicted for classical novae, is still a matter of debate.
novae per year (Shafter 2017). It is worth noting that only a fraction of these events, around ten per year, are actually obscured by interstellar dust. In contrast to type Ia supernovae, neither the white dwarf nor the binary system is expected to be disrupted during a classical nova. In fact, novae constitute recurrent phenomena, exhibiting periodicities spanning between 104 and 105 yr. In the subclass of recurring novae (by definition, novae observed in outburst more than once), recurrence times vary from 1 to 100 yr. The question of whether these recurrence times constitute a nearly continuous sequence, encompassing the shorter values observed for recurrent novae and the longer periods predicted for classical novae, is still a matter of debate.
Classical novae are characterized by the ejection of approximately 10–7 to 10–4 M⊙ of nuclear-processed material, at typical velocities exceeding 1000 km s–1 (Starrfield et al. 2008, 2016; José & Shore 2008; José et al. 2016). Spectral analysis has proven instrumental in unraveling crucial details concerning the properties of expanding nova ejecta; it particularly sheds light on its chemical composition. Observationally, the nova ejecta exhibits significant amounts of carbon (C), nitrogen (N), and oxygen (O). In the case of ONe novae, which constitute approximately one-third of the total, there are discernible overabundances of additional elements, such as neon (Ne), as first reported by Gehrz et al. (1998). In fact, spectroscopic analyses have revealed that the inferred metallicity within the ejecta typically falls within the range of Z ~ 0.2–0.5. The origin of these metallicity enhancements in the ejecta remains unexplained, although prevailing hypotheses attribute them to mixing episodes occurring at the core-envelope boundary. Among the different mechanisms proposed to date, one of the most promising involves Kelvin-Helmholtz hydrodynamic instabilities within the context of 3D turbulent convection (Casanova et al. 2011; José et al. 2020). This dynamic framework offers a compelling explanation for the observed metallicity enhancements, providing a deeper understanding of the intricate processes underlying nova events. An alternative mechanism was recently proposed, which is based on deep, shear-driven mixing (Bellomo et al. 2024).
The main nuclear processes during nova outbursts involve proton captures, (p, γ) and (p, α), and ß+ -decays, with the main nuclear path running close to the valley of stability. Current models for novae predict peak temperatures below 4 × 108 K, precluding the occurrence of α-capture reactions and the potential extension of the nuclear path through CNO breakout. Calcium (Ca) is thought to be the endpoint in nova nucleosynthesis (José et al. 2006, 2001). From a nuclear physics perspective, novae represent unique stellar explosions; the relatively confined nuclear activity, involving approximately one hundred species (below mass A < 40) linked through a few hundred nuclear processes, as well as the limited range of temperatures attained during the outburst, T ~ 107 to 4 × 108 K, allow us to rely primarily on experimental information (José et al. 2006).
Nova nucleosynthesis in the Si–Ca region is mainly governed by the 30P(p, γ)31S reaction (in competition with 30P(ß+)30Si), which determines the final 30Si/28Si ratio in the ejecta; this is a valuable tool for identifying presolar grains of a putative nova origin (Downen et al. 2012). Other reactions, such as 28P(p, γ)29S, also have an obvious influence on nova nucleosynthesis in this mass region. As pointed out by Iliadis et al. (2002) in a thorough sensitivity study, a 28P(p, γ)29S rate variation by a factor of 100 results in a noticeable change in the final abundances of 33,34S, 35Cl, and36 Ar in some nova models, by factors between 0.92 and 1.4. Proton captures on 29S cannot proceed in a nova explosion because of the −480 keV proton separation energy in 30Cl. Thus, the reaction flow passing through 28P is responsible for the synthesis of intermediate-mass elements in this region, either by 28P(p, γ)29S(ß+)29P, or by 28P(ß+)28Si(p, γ)29P. In light of this, accurate 28P(p, γ)29S rates are needed for a comprehensive understanding of the main nova nucleosynthesis path as well as for the abundance patterns of elements ranging from Si to Ca (José et al. 2001).
There currently exist four different rates for the 28P(p, γ)29S reaction in the literature. The earliest evaluation was presented by Wallace & Woosley (1981), but the method used to derive the rate was not clarified. Later, this rate was reevaluated by Rauscher & Thielemann (2000), Cyburt et al. (2010), and Sallaska et al. (2013) based on Hauser-Feshbach statistical estimates. It is well known that the statistical model is only applicable for the case of sufficient high-level density in the compound nucleus (Rauscher & Thielemann 2000; Cyburt et al. 2010). However, this condition is not met for 29S, especially in the low-energy domain of nova interest. The reaction rate for nova nucleosynthesis is mainly determined by the near-threshold isolated resonances, and it is substantially influenced by the nuclear masses of the nuclei involved in the reaction. Therefore, for an arbitrary reaction, accurate nuclear masses are crucial for determining the reaction rates. For the 28P(p, γ)29S reaction, the Q values used in the previous four works are nearly identical: about 3290(50) keV (Rauscher & Thielemann 2000; Cyburt et al. 2010; Sallaska et al. 2013; Wallace & Woosley 1981). However, the recently released nuclear mass data of 28P and 29S in the evaluation of atomic mass (AME2020) (Wang et al. 2021) provides a highest precision reaction Q value of 3235(13) keV, which allows us to reduce the uncertainty of the reaction rates.
In order to verify whether the Hauser-Feshbach statistical model is suitable for the evaluation of this reaction rate, especially for the nova temperature domain, in this work we derive the28 P(p, γ)29S rate by using the contributions from narrow and isolated resonances, rather than by the statistical model used in previous works (Rauscher & Thielemann 2000; Cyburt et al. 2010; Sallaska et al. 2013). In addition, considering the realistic stellar evolution scenario, the effect of the thermally populated excited states of target nuclei should also be considered. The new reaction rate includes the contribution from proton capture on the first excited state of 28P at 105.64 keV. With the new rate, we also explore its impact on the nucleosynthesis process in ONe novae.
The paper is structured as follows. Section 2 introduces the basic formalism for astrophysical reaction-rate calculations. We derive the new reaction rate for 28P(p, γ)29S, including both the contribution from ground-state and first-excited state capture, in Sect. 3. In Sect. 4, we investigate the impact of the new rates on the nova nucleosynthesis when using the 1D hydrodynamic code SHIVA. The conclusions are discussed in Sect. 5.
2 28P(p, γ)29S reaction rate
2.1 Shell model calculation
The 29S energy structure information currently remains unknown, except the ground state and the other five excited states at 1222 keV, 1727 keV, 2887 keV, 7.4 MeV, and 10 MeV (Shamsuzzoha Basunia 2012). However, none of these excited states resides in the energy region of nova interest. Furthermore, the energy levels of its mirror nucleus29 Al obtained from the ߯ decay of 29Mg by Guillemaud-Mueller et al. (1984) are poorly understood; the assignment of spin and parity and the branching ratios of γ transitions for the specific excited states are still not confirmed, with only upper limits provided. The spectroscopic factors of proton emission for our target states used to calculate the resonant rates are also unknown. It is reported that the shell model can guarantee the typical uncertainty of around 100 keV in level energies for the sd-shell nuclei (Brown & Wildenthal 1988; Herndl et al. 1995). Therefore, we performed a shell-model calculation to derive the energy structure information used to calculate the resonant reaction rates. We calculate the 29S energy levels using the KSHELL shell-model code (Shimizu et al. 2019) and the sd-shell-model space involving the π0d5/2, π0d3/2, π1s1/2, v0d5/2, v0d3/2 and v1s1/2 valence orbits. Here, π denotes the proton and v denotes the neutron. The new isospin-breaking USDC interaction was used in the present work (Magilligan & Brown 2020). The calculated results on the energy levels of 29S and the mirror nucleus 29Al are shown in Fig. 1. For comparison, the available experimental energy levels of this pair of mirror nuclei are also added. We can see that the energy levels of 29Al predicted by the shell-model match closely the experimental result. The other critical information used to calculate the resonant reaction rates, such as reduced transition probabilities B(M1) and B(E2) and the spectroscopic factor of 28P(p, γ)29S, are also obtained through the shell model.
 |
Fig. 1 Comparison of experimental and theoretical excitation energies for mirror nuclei29 S and29 Al, where “SM” is the result of the Shell-model, and “Exp” is the result from the experiment. The numbers on the dashed lines represent the energy level differences in megaelectronvolt for the corresponding energy levels. |
2.2 Reaction-rate calculation
The thermonuclear 28P(p, γ)29S reaction rate can be calculated as the incoherent sum of all resonant and nonresonant capture contributions. It is well known that only the resonances located in the energy window of astrophysical interest (called the Gamow window) significantly contribute to the reaction rate. For isolated narrow resonances, the resonant reaction rate for capture on a nucleus in an initial state i can be calculated as a sum over all relevant compound nucleus states j above the proton threshold (Fowler & Hoyle 1964; Hou et al. 2023b):
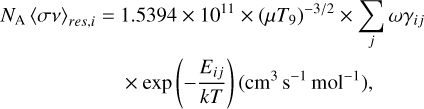 (1)
(1)
where NA is Avogadro’s constant, µ is the reduced mass of the 28P+p system in atomic mass units, T9 is the temperature in gigakelvin (GK), and k is the Boltzmann constant. The resonance energy in the center-of-mass system, Eij = Ej – Q – Ei, is calculated from the excitation energies of the initial Ei and compound nucleus Ej· state, where the resonance strengths ωγij are given in units of MeV and can be calculated for proton capture as
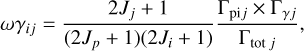 (2)
(2)
where Ji is the spin of the target and Jp = 1/2 is the spin of a proton. Jj, Γpij and Tγj are spin, proton and γ-decay width of the compound nucleus state j, respectively. The total width Γtot j is given by Γtot j = Γpij + Γγj. The proton width can be obtained from the proton spectroscopic factor multiplied by the single-particle proton width Γspi j, as Γpi j = C2SijΓspi j (Iliadis 1997).
The γ-decay widths are obtained from electromagnetic reduced transition probabilities B(ΩL; Ji → Jf ), where Ω stands for electric or magnetic, which carry the nuclear structure information of the resonance states and the final bound states. The reduced transition probabilities were computed within the framework of the shell model. The corresponding γ-decay widths for the most contributed transitions (M1 and E2) can be expressed as Herndl et al. (1995)
![$\matrix{ {{{\rm{\Gamma }}_{M1}}[eV] = 1.16 \times {{10}^{ - 2}}E_\gamma ^3[{\rm{MeV}}]B(M1)\left[ {\mu _N^2} \right],{\rm{and}}} \cr {{{\rm{\Gamma }}_{E2}}[eV] = 8.13 \times {{10}^{ - 7}}E_\gamma ^5[{\rm{MeV}}]B(E2)\left[ {{e^2}f{m^4}} \right].} \cr }$](/articles/aa/full_html/2024/07/aa49536-24/aa49536-24-eq4.png) (3)
(3)
In a stellar plasma, the low-lying excited states of the target nucleus are thermally populated and might have considerable influence on the actual astrophysical reaction rate. Thus, the rate contribution from the first excited state of 105.64 keV in 28P should also be taken into account. In this work, the mass excesses of 28P and29 S were taken from AME2020 (Wang et al. 2021), where the specific values are −7147.9 (1.1) keV and −3094 (13) keV, respectively. Then, the proton separation energy (Sp) is fixed at 3235.1 (13) keV, as marked in Fig. 2. For classical ONe nova explosions with a peak temperature of 4 × 108 K (Starrfield et al. 2016), the upper limit of the nova Gamow window is less than 485 keV. In other words, the reaction rate, which includes contributions from all excited states of 29S with excitation energies below 3.72 MeV, is sufficient for the accurate simulation of nova nucleosynthesis. However, considering that this reaction may be used in another proton capture process that occurs in X-ray bursts, we include 13 energy levels above the threshold here to ensure that the reaction rate is also reliable for X-ray bursts, even those with an extreme peak temperature of 1.95 × 109 K (Schatz et al. 2001). Here, it needs to be clarified that not all energy levels of the above 13 states are from shell-model predictions. There are five resonant states in mirror nucleus 29Al known experimentally, which are at 3.433 MeV (1/2+), 3.577 MeV (9/2+), 3.641 MeV (5/2+ ), 4.403 MeV (7/2+), and 4.656 MeV (5/2+), respectively. For reliability, here we use the excitation energies of the corresponding five energy levels in 29S obtained by adding the shell model’s calculated level shift to the respective energy level of mirror states in 29Al instead of the absolute prediction of the shell model. The remaining eight levels are taken from the shell-model calculation. The 13 energy levels above the proton threshold are shown in Fig. 2, and the relevant parameters for the 28P(p, γ)29S resonant rate calculation are summarized in Table 1. The upper part of the table is for ground-state capture, while the lower part is for capture on the first excited state in28 P. Columns 5–7 refer to the spectroscopic factors of the corresponding 0d5/2, 1s1/2, and 0d3/2 orbits.
For the nonresonant reaction rate, it is directly related to the astrophysical S factor (S(E)) via the following expression (Rolfs & Rodney 1988; Iliadis 2015):
![$\matrix{ {{N_{\rm{A}}}{{\left\langle {\sigma v} \right\rangle }_{dc\,\,i}} = 7.8327 \times {{10}^9} \times \,{{\left( {{{{Z_p}{Z_T}} \over {\mu T_9^2}}} \right)}^{1/3}}\, \times {S_{i{\rm{eff}}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left[ { - 4.2487{{\left( {{{Z_p^2Z_T^2\mu } \over {{T_9}}}} \right)}^{1/3}}} \right]\left( {{\rm{c}}{{\rm{m}}^3}\,{{\rm{s}}^{ - 1}}\,{\rm{mo}}{{\rm{l}}^{ - 1}}} \right),} \hfill \cr }$](/articles/aa/full_html/2024/07/aa49536-24/aa49536-24-eq6.png) (4)
(4)
where Sieff can be parameterized by the formula
![${S_{i\,\,{\rm{eff}}}} \approx {S_i}(0)\left[ {1 + 0.09807{{\left( {{{{T_9}} \over {Z_p^2Z_T^2\mu }}} \right)}^{1/3}}} \right],$](/articles/aa/full_html/2024/07/aa49536-24/aa49536-24-eq7.png) (5)
(5)
and S (0) is the sum of the individual S factors of the transitions from the initial state i into all bound states in the final nucleus; η is the Sommerfeld parameter.
The S (0) for direct capture into the bound states of 29S were calculated with a RADCAP code (Bertulani 2003) based on a Woods-Saxon nuclear potential (central + spin-orbit) and a Coulomb potential of a uniform charge distribution. The nuclear potential parameters were determined by matching the bound-state energies. The spectroscopic factors were calculated using the shell-model code calculation. Table 2 lists the individual S factors found for transitions into the seven bound states of 29S from the 28P ground state and the first excited state. Our uncertainty of S (0) for direct capture is set to 42%. This includes not only an assumed uncertainty of 40%, as in Downen et al. (2022), but also the contribution due to uncertainty of the g-value of 13 keV.
 |
Fig. 2 Simplified level scheme of29 S. The drawing is not to scale. The mass excesses and single proton separation energy (Sp) are from AME2020 (Wang et al. 2021), whereas the energies of the excited states are from the shell-model calculation. |
Parameters for present 28P(p, γ)29S resonant-rate calculation.
3 New reaction rate
In stellar plasma, the total reaction rate is the sum of the capture rate on all thermally excited states in the target nucleus weighted with their individual population factors (Fowler & Hoyle 1964; Schatz et al. 2005):
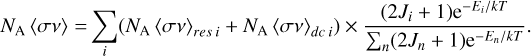 (6)
(6)
In this work, we only considered capture on the ground state and the first excited state in 28P, since the 885 keV energy of the second excited state is too high to have an effective influence on the reaction rate. The ground state is experimentally known to have spin and parity 3+. However, the spin and parity assignment of the experimentally known first excited state at 105.64 keV have not been confirmed. For the calculation of the reaction rate, we assign a spin parity of 2+ based on the comprehensive consideration of both the level structure of the mirror nucleus 28Al and our shell-model calculations.
The resonance energy uncertainty used in our evaluation is 158.5 keV, mainly contributed by the uncertainty in excited state energy of the 158 keV, which is thought to be the maximum energy difference between the shell-model prediction and the experimental measurements for an arbitrary state below 5.0 MeV in mirror nucleus 29Al. The gamma width uncertainties are uniformly assumed to be a factor of three, as in Hou et al. (2023a). For the spectroscopic factor C2 S predicted from the shell model, we assign a corresponding uncertainty factor of 2, 5,10 for cases of C2S > 0.2, 0.01 ≤ C2S ≤0.2, and C2S < 0.01, respectively. Using the resonance and the direct reaction information introduced above, the reaction rate and associated upper and lower limits can be consistently obtained by Monte Carlo sampling of all corresponding uncertainties in the resonance energy, spectroscopic factor, and gamma transition width (Longland et al. 2010; Iliadis et al. 2010a,b,c). Table 3 is for the ground-state capture, and Table 4 is for capture on the first excited state in 28P.
The first excited state rate is overall larger than the ground-state rate, and the maximum difference is up to two orders of magnitude, as shown in Fig. 3. We also plot the fractional contributions of different resonances to the reaction rate in Figs. 4 (capture on the ground state) and 5 (capture on the first excited state). For ground-state capture, the resonant rate at 0.03 < T9 < 2 is dominated by the resonances at Er =241 and 523 keV, and the resonances at 292 keV and 711 keV also make a substantial contribution in a certain temperature region. The direct reaction contribution dominates for temperatures below 0.03 × 109 K. The rate contribution for capture on the first excited state is mostly from three resonances at Er = 187, 418, and 606 keV for the temperature range of 0.02 × 109−2 × 109 K.
After taking into account the effect of the thermally excited state population by Eq. (6), the final reaction rate can be obtained as listed in Table 5. Figure 6 shows the new total rate of 28P(p, γ)29S and the associated uncertainties. For comparison, the previous rates collected in the Joint Institute for Nuclear Astrophysics Reaction Library (JINA REACLIB) database from Rauscher & Thielemann (2000), Cyburt et al. (2010), and Wallace & Woosley (1981), and the latest one proposed in STAR-LIB (Sallaska et al. 2013) (hereafter rath, ths8, wawo, and starlib, respectively), are also added. Our result is, overall, larger than the wawo rate, except for the narrow temperature interval of 0.17 × 109−0.26 × 109 K. Compared with the statistical model rates, our new rate shows different patterns of discrepancy from each one of them (ths8, rath, starlib) over the temperature range T < 1 × 108 K, and the largest difference is over four orders of magnitude. HF rate predictions are expected to behave worse in a low temperature zone because of the lower nuclear level density close to the threshold. However, for temperatures from 1 × 108 K to 1.1 × 109 K, which covers the entire temperature region of nova interest, our rate agrees with the previous HF rates within uncertainties, indicating that the statistical model is a reasonable approximation for the prediction of the 28P(p, γ)29S rate in this temperature region. For temperatures ≥1.1 × 109 K, which are suitable for X-ray bursts, the statistical model rates are about a factor of two above our high rate.
The new rate in units of cm3 mol−1 s−1 can be fitted (less than 3% error in 0.01–10 × 109 K) by the following analytic expression, using the standard seven-parameter REA-CLIB format:
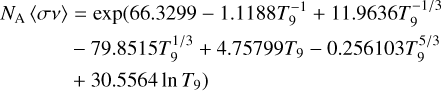
 (7)
(7)
The stellar enhancement factor (SEF) is often used to describe the effect of the stellar medium on the actual capture rate relative to the ground-state capture rate obtained in the laboratory. Hence, SEF is defined as the ratio of the actual capture rate including thermal excitations of the target nucleus to the ground-state capture rate. We calculate the corresponding SEF at different temperatures caused by the first excited state capture in 28P, as listed in the fifth column of Table 5. The first excited state capture has an obvious enhancement effect on the reaction rate over temperature region from 0.2 × 109 K to 10 × 109 K, even up to 40% around 1 × 109 K.
Spectroscopic factors C2S and astrophysical S factors S(0) for direct capture into bound states in 29S.
New reaction rate for the ground-state capture for the 28P(p, γ)29s.
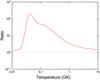 |
Fig. 3 Ratio of first excited state capture rate to that from the ground-state capture. |
New reaction rate for capture on the first excited state in28 P forthe28P(p, γ)29S.
 |
Fig. 4 Fractional contributions to the total 28P(p, γ)29S reaction rate. Resonances are labeled by their center-of-mass resonance energies, and the label “DC” refers to the direct capture process. The contribution ranges are shown as colored bands, with the band thickness representing the uncertainty of the contribution. Resonances that contribute less than 15% are not shown here. |
Final new reaction rate for the 28P(p, γ)29S.
 |
Fig. 6 Ratio of previous 28P(p, γ)29S rates normalized to present recommended rate (the median rates in Table 5). The different line patterns correspond to the rates from Rauscher & Thielemann (2000), Cyburt et al. (2010), Wallace & Woosley (1981), and Sallaska et al. (2013), as marked in rath, ths8, wawo, and starlib, respectively. The shallow blue shaded areas correspond to 68% coverage probabilities, labeled as “Low” and “High” in Table 5. The vertical shallow gray band indicates the typical temperature range of nova nuclear burning. |
4 Astrophysical impact for classical nova
The impact of the new 28P(p, γ)29S rates on nova nucleosynthesis has been analyzed in a series of four simulations performed with the spherically symmetric, Lagrangian, 1-D hydrodynamic code SHIVA, which has been extensively used in the modeling of nova outbursts (José 2016; José & Hernanz 1998). SHIVA includes a general equation of state, with contributions from the degenerate electron gas, the ion plasma, and radiation. Coulomb corrections to the electron pressure component are taken into account, and both radiative and conductive opacities are considered in the energy transport. Nuclear-energy generation is determined by means of a reaction network that contains 120 species (ranging from 1H to 48Ti); this is linked through 630 nuclear processes with updated rates from the STARLIB database (Sallaska et al. 2013; Iliadis, 2013, priv. comm.). Matter accreted from the stellar companion, at a typical rate of 2 × 10−10 M⊙ yr−1 is assumed to mix with material from the outermost layers of the underlying white dwarf to a characteristic level of 50% to match observations of ONe novae. In all the hydrodynamic simulations reported in this paper, a 1.35 M⊙ ONe white dwarf, with an initial luminosity of ~0.01 L⊙, has been adopted. All simulations are identical, except for the specific prescriptions adopted for the forward and reverse 28P(p, γ)29S rates: STARLIB rates were adopted in the first simulation; for the additional three simulations, low, recommended and high 28P(p, γ)29S, and 29S(γ, p)28P rates were used.
Table 6 summarizes the mean composition of ejecta, expressed in mass fractions of Si–Ca group elements, corresponding to three models computed with the newly established low, recommended, and high rates (Cols. 2–4). The simulations reveal that the adoption of the new rates does not substantially alter the abundance pattern of these isotopes when compared to the model computed with STARLIB rates, with differences amounting to less than 1.5%. The last column provides the percentage change in abundances between the simulations with upper and lower limits on the rates. Except for 28Si, the most abundant Si–Ca nuclei – 32S, 30Si, 31P, and 29Si- are only marginally affected by the current uncertainties in the 28P(p, γ)29S and 29S(γ, p)28 rates. The most significant impact is observed in 28Si, 33,34S, 35,37Cl, and 36Ar, with relative abundance variations at the level of 3% to 4%. It is important to emphasize that, while the new rates do not exert a significant influence on element production in novae, the uncertainty of these rates has now been significantly reduced. The present reaction rate is accurate enough, making novae nucleosynthesis predictions sound.
Averaged mass fraction of ejecta (Si–Ca) from 1.35 M⊙ ONe white-dwarf models.
5 Conclusion
Accurate nuclear masses and excitation energies are crucial quantities for improving the accuracy of proton-capture reaction rates on short-lived and proton-rich nuclei. In this study, using the updated proton threshold of Sp = 3235.1(13) keV determined by the 29S new mass of high-accuracy, together with the energy structure information of 29S by shell model, we recalculated the thermonuclear reaction rate of 28P(p, γ)29S and its associated uncertainty via a Monte Carlo method. In particular, we considered the contribution from the capture on the first excited state of28 P for the first time. We find that the first excited state in 28P at 105.6 keV has an enhancement effect of over 30% on the final reaction rate over the temperature range from 4 × 108 K to 2.5 × 109 K, which is not considered in previous evaluations. In comparison to the HF statistical model rates, it is found that our new rate shows different discrepancy patterns from the ths8, rath, and starlib rates in different temperature regions. Despite the fact that HF predictions cannot be safely used for the case of the compound nucleus with insufficient high-level densities, in this specific case we see that the new rate still agrees with those within uncertainties at typical nova temperatures.
To investigate the impact of the new reaction rates on the hydrogen burning that occurred in ONe novae, we performed a series of nucleosynthesis calculations in which four groups of different reaction rates of 28P(p, γ)29S were used. Compared with the result using previous starlib rates, it is found that the adoption of new rates has no significant effect on the final yields of intermediate-mass isotopes from Si to Ca produced in a 1.35 M⊙ ONe nova explosion, and the largest differences are no larger than 1.5%. Comparing two simulations using upper and lower limits of reaction rates, we also find that the rate uncertainty of up to two orders of magnitude at typical nova temperatures has a limited impact on the final isotope abundance of the ejecta from ONe nova outburst. Nuclides with the largest changes in relative abundance are 28Si, 33,34S, 35,37Cl, and 36Ar, approximately at the level of 3%–4%.
Acknowledgements
This work was financially supported by the National Key R&D Program of China Grant No. 2022YFA1603300, Longyuan Youth Talent Program of Gansu Province, the Strategic Priority Research Program of Chinese Academy of Sciences Grant No. XDB34020204, and in part by the National Science Foundation under Grant No. OISE-1927130 (IReNA). J.J. acknowledges support from the MINECO grant PID2020-117252GB-I00, by the EU Feder funds, and by the AGAUR/Generalitat de Catalunya grant SGR-386/2021. C.A.B. acknowledges support by the U.S. DOE grant DE-FG02-08ER41533 and the Helmholtz Research Academy Hesse for FAIR. M.P. and TT acknowledge the ongoing access to viper, the University of Hull High Performance Computing Facility. J.J., M.P. and T.T. acknowledge the support of the European Union’s Horizon 2020 research and innovation programme (ChETEC-INFRA – Project no. 101008324). M.P. acknowledges the support from the “Lendulet-2023” LP2023-10 Programme of the Hungarian Academy of Sciences (Hungary), and the support from the NKFI via K-project 138031 (Hungary). J.G.L. acknowledges support from the National Natural Science Foundation of China under Grants No. 12205340; the Gansu Natural Science Foundation under Grant No. 22JR5RA123. R.L. acknowledges support from the U.S. Department of Energy, Office of Science, Office of Nuclear Physics, under Award Number DE-SC0017799 and Contract Nos. DE-FG02-97ER41033 and DE-FG02-97ER41042.
References
- Bellomo, M., Shore, S. N., & José, J. 2024, A&A, submitted [Google Scholar]
- Bertulani, C. 2003, Comput. Phys. Commun., 156, 123 [CrossRef] [Google Scholar]
- Brown, B. A., & Wildenthal, B. H. 1988, Annu. Rev. Nucl. Part. Sci., 38, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Casanova, J., José, J., Garcia-Berro, E., Shore, S., & Calder, A. 2011, Nature, 478, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Downen, L. N., Iliadis, C., José, J., & Starrfield, S. 2012, ApJ, 762, 105 [Google Scholar]
- Downen, L. N., Iliadis, C., Champagne, A. E., et al. 2022, Phys. Rev. C, 105, 055804 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, W. A., & Hoyle, F. 1964, ApJS, 9, 201 [Google Scholar]
- Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Guillemaud-Mueller, D., Detraz, C., Langevin, M., et al. 1984, Nucl. Phys. A, 426, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Herndl, H., Görres, J., Wiescher, M., Brown, B. A., & Van Wormer, L. 1995, Phys. Rev. C, 52, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, S. Q., Iliadis, C., Pignatari, M., et al. 2023a, A&A, 677, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hou, S. Q., Liu, J. B., Trueman, T. C. L., et al. 2023b, ApJ, 950, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C. 1997, Nucl. Phys. A, 618, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C. 2015, Nuclear Physics of Stars, 2nd edn. (Weinheim: Wiley-VCH Verlag) [Google Scholar]
- Iliadis, C., Champagne, A., José, J., Starrfield, S., & Tupper, P. 2002, ApJS, 142, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A., & Coc, A. 2010a, Nucl. Phys. A, 841, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A., & Coc, A. 2010b, Nucl. Phys. A, 841, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A., Coc, A., & Fitzgerald, R. 2010c, Nucl.Phys. A, 841, 31 [CrossRef] [Google Scholar]
- José, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton, FL: CRC/Taylor and Francis) [Google Scholar]
- José, J., & Hernanz, M. 1998, ApJ, 494, 680 [Google Scholar]
- José, J., & Shore, S. N. 2008, in Classical Novae, eds. M. F. Bode, & A. Evans, 2nd edn. (Cambridge, UK: Cambridge University Press), 121 [CrossRef] [Google Scholar]
- José, J., Coc, A., & Hernanz, M. 2001, ApJ, 560, 897 [CrossRef] [Google Scholar]
- José, J., Hernanz, M., & Iliadis, C. 2006, Nucl. Phys. A, 777, 550 [Google Scholar]
- José, J., Halabi, G. M., & El Eid, M. F. 2016, A&A, 593, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- José, J., Shore, S. N., & Casanova, J. 2020, A&A, 634, A5 [EDP Sciences] [Google Scholar]
- Longland, R., Iliadis, C., Champagne, A., et al. 2010, Nucl. Phys. A, 841, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Magilligan, A., & Brown, B. A. 2020, Phys. Rev. C, 101, 064312 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [Google Scholar]
- Rolfs, C. E., & Rodney, W. S. 1988, Cauldrons in the Cosmos (Chicago: University of Chicago Press) [Google Scholar]
- Sallaska, A. L., Iliadis, C., Champange, A. E., et al. 2013, ApJS, 207, 18 [Google Scholar]
- Schatz, H., Aprahamian, A., Barnard, V., et al. 2001, Phys. Rev. Lett., 86, 3471 [CrossRef] [PubMed] [Google Scholar]
- Schatz, H., Bertulani, C. A., Brown, B. A., et al. 2005, Phys. Rev. C, 72, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W. 2017, ApJ, 834, 196 [CrossRef] [Google Scholar]
- Shamsuzzoha Basunia, M. 2012, Nucl. Data Sheets, 113, 909 [CrossRef] [Google Scholar]
- Shimizu, N., Mizusaki, T., Utsuno, Y., & Tsunoda, Y. 2019, Comput. Phys.Commun., 244, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, W. R. 2008, Classical Novae, eds. M. F. Bode, & A. Evans (Cambridge: Cambridge University Press), 43, 77 [NASA ADS] [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, W. R. 2016, PASP, 128, 051001 [Google Scholar]
- Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Huang, W. J., Kondev, F. G., Audi, G., & Naimi, S. 2021, Chin. Phys.C, 45, 030003 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Spectroscopic factors C2S and astrophysical S factors S(0) for direct capture into bound states in 29S.
New reaction rate for capture on the first excited state in28 P forthe28P(p, γ)29S.
All Figures
 |
Fig. 1 Comparison of experimental and theoretical excitation energies for mirror nuclei29 S and29 Al, where “SM” is the result of the Shell-model, and “Exp” is the result from the experiment. The numbers on the dashed lines represent the energy level differences in megaelectronvolt for the corresponding energy levels. |
| In the text | |
 |
Fig. 2 Simplified level scheme of29 S. The drawing is not to scale. The mass excesses and single proton separation energy (Sp) are from AME2020 (Wang et al. 2021), whereas the energies of the excited states are from the shell-model calculation. |
| In the text | |
 |
Fig. 3 Ratio of first excited state capture rate to that from the ground-state capture. |
| In the text | |
 |
Fig. 4 Fractional contributions to the total 28P(p, γ)29S reaction rate. Resonances are labeled by their center-of-mass resonance energies, and the label “DC” refers to the direct capture process. The contribution ranges are shown as colored bands, with the band thickness representing the uncertainty of the contribution. Resonances that contribute less than 15% are not shown here. |
| In the text | |
 |
Fig. 5 Same as Fig. 4, but for capture on the first excited state of 28P. |
| In the text | |
 |
Fig. 6 Ratio of previous 28P(p, γ)29S rates normalized to present recommended rate (the median rates in Table 5). The different line patterns correspond to the rates from Rauscher & Thielemann (2000), Cyburt et al. (2010), Wallace & Woosley (1981), and Sallaska et al. (2013), as marked in rath, ths8, wawo, and starlib, respectively. The shallow blue shaded areas correspond to 68% coverage probabilities, labeled as “Low” and “High” in Table 5. The vertical shallow gray band indicates the typical temperature range of nova nuclear burning. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


