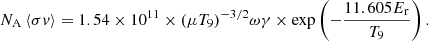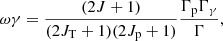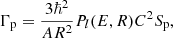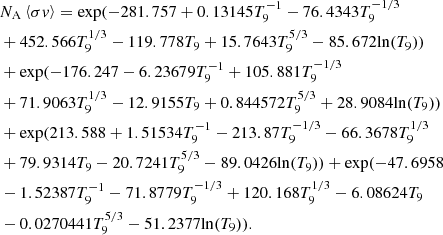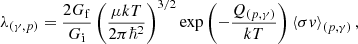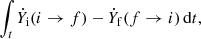| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 7 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202347054 | |
| Published online | 18 September 2023 | |
Improved thermonuclear rate of 42Ti(p,γ)43V and its astrophysical implication in the rp process
1
Key Laboratory of High Precision Nuclear Spectroscopy, Institute of Modern Physics, Chinese Academy of Sciences, 509 Nanchang Rd, Lanzhou, 730000
PR China
e-mail: sqhou@impcas.ac.cn
2
School of Nuclear Science and Technology, University of Chinese Academy of Sciences, 19A Yuquan Rd, Shijingshan District, Beijing, 100049
PR China
3
Department of Physics & Astronomy, 120 E. Cameron Ave., University of North Carolina at Chapel Hill, NC, 27599-3255
USA
4
Triangle Universities Nuclear Laboratory (TUNL), 116 Science Drive, Duke University, Durham, NC, 27708-0308
USA
5
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Eötvös Loránd Research Network (ELKH), Konkoly Thege M. út 15-17, 1121 Budapest, Hungary
6
CSFK, MTA Centre of Excellence, Konkoly Thege Miklós út 15-17, Budapest, 1121
Hungary
7
E. A. Milne Centre for Astrophysics, University of Hull, Cottingham Rd, Kingston upon Hull, HU6 7RX
UK
8
Joint Institute for Nuclear Astrophysics, Center for the Evolution of the Elements, 640 S Shaw Lane, East Lansing, MI, 48824
USA
Received:
30
May
2023
Accepted:
10
July
2023
Context. Accurate 42Ti(p,γ)43V reaction rates are crucial for understanding the nucleosynthesis path of the rapid capture process (rp process) that occurs in X-ray bursts.
Aims. We aim to improve the thermonuclear rates of 42Ti(p,γ)43V based on more complete resonance information and a more accurate direct component, together with the recently released nuclear masses data. We also explore the impact of the newly obtained rates on the rp process.
Methods. We reevaluated the reaction rate of 42Ti(p,γ)43V by the sum of the isolated resonance contribution instead of the Hauser-Feshbach statistical model. We used a Monte Carlo method to derive the associated uncertainties of new rates. The nucleosynthesis simulations were performed via the NuGrid post-processing code ppn.
Results. The new rates differ from previous estimations due to the use of a series of updated resonance parameters and a direct S factor. Compared with the previous results from the Hauser-Feshbach statistical model, which assumes compound nucleus 43V with a sufficiently high-level density in the energy region of astrophysical interest, large differences exist over the entire temperature region of rp-process interest, up to two orders of magnitude. We consistently calculated the photodisintegration rate using our new nuclear masses via the detailed balance principle, and found the discrepancies among the different reverse rates are much larger than those for the forward rate, up to ten orders of magnitude at the temperature of 108 K. Using a trajectory with a peak temperature of 1.95×109 K, we performed the rp-process nucleosynthesis simulations to investigate the impact of the new rates. Our calculations show that the adoption of the new forward and reverse rates result in abundance variations for Sc and Ca of 128% and 49%, respectively, compared to the variations for the statistical model rates. On the other hand, the overall abundance pattern is not significantly affected. The results of using new rates also confirm that the rp-process path does not bypass the isotope 43V.
Conclusions. Our study found that the Hauser-Feshbach statistical model is inappropriate to the reaction rate evaluation for 42Ti(p,γ)43V. The adoption of the new rates confirms that the reaction path of 42Ti(p,γ)43V(p,γ)44Cr(β+)44V is a key branch of the rp process in X-ray bursts.
Key words: nuclear reactions / nucleosynthesis / abundances
NuGrid Collaboration, http://www.nugridstars.org
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
As the most frequent thermonuclear explosions in the galaxy, Type I X-ray bursts take place on the surface of a neutron star that accretes matter from a nearby companion star. They are powered by unstable thermonuclear burning of freshly accreted hydrogen and helium material, where three nuclear-burning patterns of a triple-α reaction, rapid proton-capture (rp) process, and α-capture proton-emission (αp) process are involved (Taam et al. 1993; Woosley et al. 2004; Fisker et al. 2008; José et al. 2010). Therein, the rp process can approach the proton drip line far from the valley of stability via consecutive proton capture on seed nuclei despite the fact that in some cases the proton capture has to wait for a β+ decay before continuing. Finally, heavier elements with atomic mass number A = 60–100 can be synthesized (Wallace & Woosley 1981; Schatz et al. 1998, 2001; Koike et al. 2004).
A large number of short-lived and neutron-deficient nuclei are involved during the rp process, as the reaction path of the rp process is far from the valley of stability. Along the rp-process path, the unstable nuclei at which the proton capture process fiercely competes with the β+ decay are called the rp-process branching nuclei. We note that 42Ti is a typical rp-process branching nucleus, from which a splitting of the rp-process nucleosynthesis path is created. The branching ratio of the proton capture and the β+ decay for 42Ti depends on the quantity of the net proton capture flow through 42Ti, which is determined by the competition between the 42Ti(p,γ)43V reaction and its reverse process 43V(γ,p)42Ti. Thus, both the accurate forward and reverse reaction rates of 42Ti(p,γ)43V are important for the study of the reaction path in the rp process.
We know from Fowler et al. (1967) that the forward and reverse reaction rates can be converted mutually via an exp( − Q/kT) involved term, which means the reverse reaction can be directly obtained if the forward reaction rate and reaction Q value are available. Since the 42Ti(p,γ)43V reaction Q value is less than 200 keV, the role of the photodisintegration reaction 43V(γ,p)42Ti played in the rp process is highly sensitive to the uncertainties of nuclear masses of the nuclei involved. Indeed, the photodisintegration can more efficiently hinder the proton capture for the reaction with a small Q value relative to that with a large Q value. In addition, the forward reaction rate of 42Ti(p,γ)43V is substantially influenced by the nuclear masses of the involved nuclei: the alteration of nuclear masses can lead to the change of the resonance energy, which sensitively affects the resonant reaction rate. Therefore, in order to have a complete and comprehensive understanding of the role of the 42Ti(p,γ)43V reaction in the rp process, it is worthwhile to carry out a detailed investigation of its forward and reverse reaction rates.
The 42Ti(p,γ)43V reaction rate has previously been studied in several papers (Van Wormer et al. 1994; Herndl et al. 1995; Rauscher & Thielemann 2000; Cyburt et al. 2010; He et al. 2014). These can be classified into two categories, based upon the way in which the final reaction rates are obtained. In the first category, the rate is thought to be the sum of the rate contribution from each isolated resonance separately; in the second, the reaction rate is obtained based on the Hauser-Feshbach statistical model, which is only appropriate when the nuclear level density in the compound nucleus is sufficiently high to make the resonances completely overlap. The studies of Van Wormer et al. (1994), Herndl et al. (1995), and He et al. (2014) belong to the first category. The earliest study of this reaction was presented by Van Wormer et al. (1994), who used a proton separation energy of 88 keV from Wapstra & Audi (1985) and considered only four excited states closest to the proton threshold, based on the assumption of 43V holding exactly the same level structure as its mirror nuclide 43Ca. One year later, Herndl et al. (1995) re-evaluated this rate using different energy levels of 43V, predicted from large-basis shell model calculations instead of assuming the same excitation energies as its mirror states. Furthermore, they considered fewer resonance states, including only the first and second excited states. In He et al. (2014), this reaction rate was updated using an 83 keV proton separation energy, obtained from the nuclear masses from AME2012 (Wang et al. 2012), and for the first time considered the contribution from the 7/2+ resonance at 2.067 MeV in addition to the first and second excited states. For the reaction rates obtained by the Hauser-Feshbach statistical model code NON-SMOKER (Rauscher & Thielemann 2000), there currently exist two versions collected in the Joint Institute for Nuclear Astrophysics Reaction Library (JINA REACLIB), which were presented by Rauscher & Thielemann (2000) and Cyburt et al. (2010). In their evaluations, the proton separation energies of 43V are thought to be −0.411 MeV and −0.0189 MeV, respectively. As mentioned above, this statistical model is suited only to cases of high-level densities in the compound nuclei (Woosley et al. 1978; Cowan et al. 1991). However, as we know that the energy level density of 43V near the proton threshold is low, the results from this statistical model probably contain large uncertainties when calculating the reaction rate of 42Ti(p,γ)43V. In this sense, the approach that computes the reaction rate to be the sum of the individual resonance contribution seems more appropriate for the rate estimation of 42Ti(p,γ)43V. The major sources of error in applying this approach to calculate the 42Ti(p,γ)43V rate are the uncertainties of proton separation energy and the level energy of the 43V-excited states.
A recent evaluation of atomic mass (AME2020) presents the data for the newest nuclear masses from experiments and theoretical evaluation (Wang et al. 2021), from which the new proton separation energy (Sp) of 43V is determined to be 105 keV, with an uncertainty of 40 keV, which is currently the highest precision of Sp. In previous works (Van Wormer et al. 1994; Herndl et al. 1995; He et al. 2014), some resonant states that have appreciable contributions to the final reaction rate of the temperature larger than 1.1 × 109 K were not included. For this work, we recalculated the reaction rate of 42Ti(p,γ)43V, using the newest nuclear masses and including those resonant states previously neglected, and explored its impact on the rp-process nucleosynthesis for X-ray burst trajectory extracted from Schatz et al. (2001) with a peak temperature of 1.95 × 109 K.
This paper is organized as follows: Sect. 2 introduces the basic formalism for astrophysical reaction rate calculations and we explain how we derived the new forward and reverse reaction rates for 42Ti(p,γ)43V using new nuclear data. We investigate the impact of the new rates on the rp process by virtue of a post-processing code in Sect. 3. The conclusions are discussed in Sect. 4.
2. 42Ti(p,γ)43V reaction rate
2.1. The resonant reaction rate
The astrophysical reaction rate consists of a resonant contribution and non-resonant contribution, with the latter term consisting of the contributions from direct reaction and subthreshold resonances. For the reaction of 42Ti(p,γ)43V, it has been confirmed that no subthreshold resonances exist, since the first excited state of 43V from all theoretical predictions remains much higher than the newest proton threshold of 105(40) keV. For the proton capture reactions in the rp process, it is often thought that they proceed via narrow and isolated resonances (Timofeyuk et al. 2006). From the classic textbook of nuclear astrophysics (Iliadis 2015), it is known that the reaction rate for a single narrow resonance is expressed as
Here, μ refers to the reduced mass of the colliding system in atomic units. With the same units as the resonance energy Er (in units of mega electron volts), the resonance strength ωγ is defined as
where Jp, JT, and J denote the spin of the proton, target nucleus, and the resonant state, respectively, and Γp and Γγ are the partial width of the entrance channel and exit channel, respectively. The total width Γ can be approximated as the sum of Γp and Γγ, since other channels are closed in the energy range of our study. Here, the proton width Γp can be obtained by the following formula:
where R = 1.25(1+421/3) fm is the nuclear channel radius, Pl(E, R) is the Coulomb penetrability that can be calculated numerically, and C2Sp is the spectroscopic factor of a particular state. Both C2Sp and Γγ can be supplied via a shell model calculation when no experimental information is available. In the case of several narrow and isolated resonances dominating the cross sections, the total reaction rate is equal to the sum of the individual contributions from every single resonance.
As seen in Eq. (1), the reaction rate is determined by two key quantities which are the resonance energy of exponential dependence and the resonance strength of linear dependence, respectively. From the expression of Eq. (3), we know that the resonance strength is also sensitive to the resonance energy because of its sensitivity to the Coulomb penetration factor, which dramatically influences the proton width. For proton capture reactions, the resonance energy refers to the energy difference between the excitation energy of the compound nucleus state and the proton separation energy. As mentioned in the introduction, due to the adoption of the more accurate mass excesses of 42Ti and 43V in AME2020, the new value of Sp is fixed at 105(40) keV, which is about 21.5 keV larger than that used by He et al. (2014). More importantly, this new value has the smallest error up to now. Another key factor in determining the resonance energy is the excitation energy of near-threshold states in 43V. In the current situation, the accurate excitation energy of the 43V- excited states remains unclear because of the vast difficulties in conducting such experiments for the short-lived nucleus 43V. Therefore, one has to resort to other avenues, such as theoretical predictions.
At present, three different values for the peak temperatures reached during X-ray bursts have been proposed in the literature (Koike et al. 2004; Fisker et al. 2008; Schatz et al. 2001), ranging approximately from 1.0 × 109 K to 1.95 × 109 K. According to the estimation of the astrophysical effective energy region, all of the excited states of 43V with excitation energies below 2.17 MeV should be included, provided that the peak temperature is set at 1.95 × 109 K. However, the majority of states below 2.17 MeV are not included in previous works, because the authors thought that the first and second excited states dominated the reaction rate. Actually, for cases with a peak temperature of up to 1.95 × 109 K (Schatz et al. 2001), every resonant state that has a noticeable contribution to the 42Ti(p,γ)43V reaction rate should be taken into account. The resonance excited states that need to carry more than three units of orbit angular momentum to populate are excluded from our study, owing to the fact that these states usually play a negligible role in astrophysical processes (Setoodehnia et al. 2020). All of the states of interest are listed in the first column of Table 1.
Parameters of resonant states used in the calculation of 42Ti(p,γ)43V resonant reaction rate, including excitation energy, resonance energies, spin and parity, spectroscopic factor, partial width of gamma and proton, and resonance strength.
Because the experimental information of the level structure of the short-lived nucleus 43V remains very limited, the excitation energies of the first and second excited states of 43V used in the previous two evaluations (Herndl et al. 1995; He et al. 2014) were both derived from shell model calculation. However, we know that the high-precision prediction of level structures for a certain nucleus still presents a large challenge to shell model theory. In the present work, six more excited states of 43V are also considered in addition to the first and second excited states. In this case, instead of adopting a shell model prediction, we chose the approach used by Van Wormer et al. (1994) in which the energy level structures for mirror pair 43V and 43Ca are assumed to be identical, but with 100 keV uncertainties assigned to 43V energy levels. We agree with this assumption based upon the plethora of experimental evidence supporting the fact that the mirror energy differences of pf-shell nuclei are within 100 keV for low spin states (O’Leary et al. 1997; Davies et al. 2013). Because of the uncertainty of 40 keV of the new proton separation energy, the uncertainty of resonance energy is determined to be 108 keV.
From Eq. (3), we also know that another key quantity in the determination of the proton emission width is the spectroscopic factor C2S. However, the spectroscopic factors of our target states in 43V remain unknown, due to a scarcity of relevant experiments. Luckily, the corresponding C2S of its mirror states has been studied extensively in experiments, including the stripping reaction (d, p) and pick-up reaction (p, d). For radiative reactions, the spectroscopic factor should correspond to the value determined by the stripping reaction. Unlike the adoption of the values from the pick-up reaction for the first resonance by He et al. (2014), we adopted a different path to ascertain the C2S of each resonance. Specifically, the average values of C2S from studies on the stripping reaction (Dorenbusch et al. 1966; Brown et al. 1974; Endt 1977; Endt & Van Der Leun 1978) were used for states at 0.593, 0.99, 1.394, 1.957, and 2.046 MeV. However, for resonances at 0.373, 1.931, and 2.067 MeV, we had to rely on the shell model calculation. For the uncertainties of the spectroscopic factor C2S of every resonance we considered, we assumed a factor varying from 1.6 to 3 for C2S values from previous stripping reaction studies and a factor of ten for those from our shell model calculations. The detailed information can be seen in column five of Table 1.
Using the resonance energy determined from new data, in combination with the new C2S values of the states we considered, the new proton width Γp for each considered excited state can be obtained via Eq. (3), as listed in column seven of Table 1. Regarding the Γγ gamma widths of these resonance states, we adopted the values estimated from the lifetime of the corresponding mirror state in 43Ca via the Γγ = ℏ/τ, where τ is the lifetime of the corresponding excited state. The uncertainty of Γγ is uniformly assumed to be a factor of three, which is simply estimated by the formula of the γ transition width, together with the energy level difference between 43V and 43Ca. All of the information used for the calculation of the resonance strength is summarized in Table 1.
2.2. Direct reaction contribution
For this work, the direct capture (DC) contribution was recalculated via a method using a hard sphere scattering potential (Iliadis & Wiescher 2004), which can exclude the possibility that the potential resonance contribution created by the particular choice of the scattering potential is mistakenly taken as a part of the direct contribution, as in He et al. (2014). The actual direct S factor we obtained can be described by a truncated polynomial Sdc(E) = S(0)+S′(0)E + S″(0)E2, where the corresponding polynomial coefficients were set as S = 0.0042 MeV⋅b, S′ = 0.0039 b, S″ = 5.54 × 10−5 b⋅MeV−1 via a χ2-fit. Our value is approximately ten times smaller than those used in previous works (Herndl et al. 1995; He et al. 2014).
2.3. Total reaction rate
For the present work, the interference effects between the direct and the resonant capture are negligible1. Based on the information of resonances and direct reaction introduced above, the total reaction rate and associated upper and lower limits can be directly obtained by Monte Carlo sampling of all corresponding uncertainties listed in Table 2 (Longland et al. 2010). The final result is shown in Fig. 1. It is clearly seen that the direct reaction and the resonance at Er = 268 keV dominate in the temperature range of T9 ≤ 0.04 and 0.04 < T9 < 0.16 (temperature T9 = 109 K), respectively. The reaction rate over the temperature of 0.16 < T9 < 1.6 is entirely determined by the Er = 488 keV resonant state. The resonances at Er = 0.885, 1.289, 1.826, and 1.962 MeV contribute to the rate in the temperature range of T9 > 1.1 considerably, while those of Er = 1.852, 1.941 MeV contribute minimally. Figure 2 plots the new total rate and the associated uncertainties arising from the uncertainties of the resonance energy and the spectroscopic factor. For comparison, the rates from previous studies, including those compiled in JINA REACLIB and He et al. (2014), were also added. It can be seen that our result is consistent with the results from Herndl et al. (1995) and He et al. (2014, hereafter hg95 and He14, respectively) over a wide temperature range from 2 × 108 K to 1 × 109 K, except for the region with a temperature larger than 1 × 109 K and less than 2 × 108 K. However, large differences arise if we compare our result with the results from Cyburt et al. (2010) and Rauscher & Thielemann (2000, hereafter ths8 and rath, respectively), due to them both being obtained by the statistical model. Regarding the difference between the rate from Van Wormer et al. (1994; hereafter laur) and ours, it is caused mainly by different resonance strengths and resonance energies.
 |
Fig. 1. Fractional contributions to the total 42Ti(p,γ)43V reaction rate. Resonances are labeled by their center-of-mass resonance energies and the label DC refers to the direct capture process. The contribution ranges are shown as colored bands, with the band thicknesses representing the uncertainty of the contribution. |
 |
Fig. 2. Ratio of previous rates 42Ti(p,γ)43V normalized to present recommended rates (the median rates in Table 2). The different patterns of lines correspond to the rates from Van Wormer et al. (1994, laur), Herndl et al. (1995, hg95), Rauscher & Thielemann (2000, rath), Cyburt et al. (2010, ths8), and He et al. (2014, He14). The shallow blue-shaded areas correspond to 68% coverage probabilities, shown as Low and High in Table 2. |
New total reaction rate for 42Ti(p,γ)43V.
The newly obtained reaction rate can be well fitted (less than 2.63% error in the temperature range 0.01 − 10 × 109 K) by the following analytic expression in the standard seven-parameter format of REACLIB:
It is well known that the forward and reverse reaction rates are tightly connected by the detailed balance principle. For the 42Ti(p,γ)43V reaction, its reverse reaction rate (also called the photodisintegration rate) can be calculated directly by the following expression (Fowler et al. 1967; Schatz & Ong 2017)
where Gi and Gf are the partition functions of the initial and final nuclei. The ratio of the (γ, p) reaction rate to the (p, γ) rate depends exponentially on Q(p, γ) and is therefore very sensitive to nuclear masses. In light of the new nuclear masses used in this study, we investigated the impact of the variation of nuclear masses of the nuclei involved in this reaction on the λ(γ, p) rate. The calculation shows that the two rates from the statistical model (rath and ths8) are much higher than our new λ(γ, p) rate and others obtained by the sum of the contributions from narrow and isolated resonances. This large discrepancy is mainly due to their negative reaction Q values, which are −18.9 keV for ths8 and −411 keV for rath. Generally speaking, larger λ(γ, p) rates mean stronger effects of impeding the proton capture on 42Ti, resulting in a reduction of the net reaction flux pass through the 42Ti(p,γ)43V reaction.
3. Astrophysical impact for X-ray bursts
The new forward and reverse rates for 42Ti(p,γ)43V are remarkably different from the previous rates in the temperature region of 1 × 107 K to 2 × 109 K. Therefore, it is worthwhile to explore the impact of the new rates on the rp process in Type I X-ray bursts. We performed the rp-process simulation using the one-zone post-processing nucleosynthesis code ppn, a branch of the Nucleosynthesis Grid (NuGrid) framework (Herwig et al. 2009; Denissenkov et al. 2014). We chose here a trajectory from Schatz et al. (2001), with a peak temperature of 1.95 × 109 K. The solar abundances from AG89 (Anders & Grevesse 1989) were used as the initial composition of the accreted material from the companion star. Three runs were performed on the condition that all the nuclear physics and model inputs be kept unchanged except for the forward and reverse reaction rates for 42Ti(p,γ)43V taken from different sources. In the first run, we used our new rates. The ths8 rates were used for the second run and rates from rath in the third run. Our rp-process simulations show that the adoption of different rates for the 42Ti(p,γ)43V reaction does not have a noticeable influence on the sum of the energies released from nuclear reactions (which is indicative of the nuclear energy generation rate), but can result in considerable abundance variations for some isotopes. Table 3 shows a comparison of the calculated abundances of such isotopes for different values of the forward and reverse rates of the 42Ti(p,γ)43V reaction. The largest variations were obtained for the radioactive isotopes 43V and 44Cr, both on the order of a magnitude of four, while the abundances of the rest isotopes in Table 3 changed modestly. In general, this result is due to the adoption of new forward and reverse rates for 42Ti(p,γ)43V. However, this is in essence a natural consequence of local (p, γ)–(γ, p) equilibrium that formed in the extreme environment of an X-ray burst. When equilibrium is achieved, the abundances of isotopes within an isotonic chain are determined by the proton separation energies rather than the proton capture rates (Schatz et al. 1998), which is confirmed by our investigation that both a forward and reverse rate multiplied by a factor of ten results in the largest abundance difference less than 0.7%. The adoption of new proton separation energies of 105 keV in 43V directly lead to the prominent increase in equilibrium abundances of 43V and 44Cr along the isotonic chain from 42Ti to 44Cr compared with cases using negative ones of −18.9 keV and −411 keV from ths8 and rath, respectively.
Calculated abundances for stable and unstable isotopes primarily affected by three groups of forward and reverse rates of the 42Ti(p,γ)43V with different sources (new, ths8, and rath).
To investigate the impact of the variation of the 42Ti(p,γ)43V reaction rate on the final rp-process composition in the X-ray burst, we calculated the final composition of hydrogen-burning ashes. The element abundance after the full decay of all the unstable isotopes is plotted in Fig. 3. The abundances of Ca and Sc were found to have a prominent change for the case using our new rate, compared with the two cases using ths8 and rath rates. The decrease of 49% in calcium abundance was caused by 42Ti decay to 42Ca, while the increase of 128% in scandium abundance was due to 45Ti, 45V, and 45Cr decay to 45Sc. On the other hand, the overall abundance distribution obtained from the calculations was not modified. The abundances shown in Table 3 differ from the predicted abundances shown by He et al. (2014), who used the trajectory from Koike et al. (2004, hereafter K04). This is due to the much higher temperatures reached by the Schatz et al. (2001) trajectory compared to a temperature peak of 1.35 × 109 K obtained by K04. In order to test the impact of such a relevant difference, we performed analogous nucleosynthesis calculations also using the K04 trajectory. Similar results previously discovered for the Schatz et al. (2001) trajectory were obtained, with the largest variations still in the Ca–Sc region (up to a 73% decrease in calcium abundance and 200% increase in scandium abundance), yet with the overall abundance pattern unchanged.
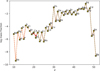 |
Fig. 3. Decayed elemental abundance distribution in the rp process for cases with different forward and reverse reaction rates for 42Ti(p,γ)43V. The red triangle, black square, and yellow cross correspond to cases using new rate, ths8, and rath, respectively. |
To explore the impact of different rates on the rp-process path, the net reaction flow between two nuclei i and f is defined as
where Ẏi(i → f) is the partial rate of change of the isotopic abundance Yi, induced by the particular reaction under consideration that converts the initial nuclide i into the final nuclide f. As with the definition in Schatz & Ong (2017), the main reaction flow for an X-ray burst was identified by requiring a net reaction flow integrated over the burst duration leading either to or from the nuclide of at least 10−5 mol g−1. Figure 4 plots the main reaction flux integrated over the entire rp-process duration. Panel (a) shows the case using the new forward and reverse rate of 42Ti(p,γ)43V, and panels b and c show the ths8 rate and the rath rate, respectively. It can be seen that the main rp-process paths are essentially the same for cases using the new rates and the ths8 rates. The obvious difference between them is that the net flow from β+ decay of 43V becomes larger when using the new rates. This is attributed to the fact that a larger leakage occurs by decay if a nucleus has a higher abundance in an isotonic chain during local (p, γ)–(γ, p) equilibrium. The new proton separation energy with a value larger than that from ths8 leads to a higher equilibrium abundance of 43V. This increases the abundance flow through β+ decay of 43V. For panel c of Fig. 4, the nucleosynthesis path varies dramatically. The reaction flow passing 42Ti(p,γ)43V is entirely prevented by the extremely strong 43V(γ,p)42Ti rate, which is due to the reaction Q value of −411 keV. The path marked by the purple arrow becomes the only channel to guide the reaction flow into the higher Z region. We have seen that in this specific case the overall production of heavier isotopes is not affected, and only a strong impact on the local isotopes is obtained. Nevertheless, the results would be different for branching points involving heavier isotopes, especially those with long lifetimes, such as 64Ge and 72Kr (Schatz 2006; Schatz & Ong 2017). This is due to the significant lifetime difference between 64Ge and 65As can more efficiently regulate the progress of the rp process through the (p, γ) and β decay of 64Ge. The rate variation of the longer lifetime branching nuclei involved reaction is expected to have an overall effect on the production of heavier isotopes in comparison to those of reactions involving short lifetime branching nuclei, such as 42Ti. Therefore, accurate nuclear masses and reaction rates are crucial for a comprehensive understanding of the rapid proton capture in X-ray bursts.
 |
Fig. 4. Main reaction flows in the rp process for the adoption of different forward and reverse reaction rates for 42Ti(p,γ)43V. Panels (a)–(c) represent the cases using the new rate, the ths8 rate, and the rath rate, respectively. The reaction flow is integrated over the entire X-ray burst duration. The thickness of the arrow depicts the magnitude of the reaction flux. |
4. Conclusion
Based on a series of improvements on crucial information of the 42Ti(p,γ)43V rate calculation, including the spectroscopic factors of the resonances of interest in 43V, neglected resonances in previous works, and the new nuclear masses of 42Ti and 43V, we reevaluated the thermonuclear rate of 42Ti(p,γ)43V and its associated uncertainty, via a Monte Carlo method. The reverse reaction rate is updated consistently using the new proton separation energy. The present study shows that the previous reaction rates from the statistical model dramatically differ from our new rates. Specifically, the largest differences can measure up to two orders of magnitude for the forward reaction, and four orders of magnitude for the reverse reaction over the temperature range of X-ray burst interest. In order to explore the influence of new rates in the rp process, we performed nucleosynthesis simulations in which three different reaction rates of 42Ti(p,γ)43V were used. In comparison to the results obtained using the ths8 and rath rates, our new rates have no significant impact on the final elemental abundances, except for a decrease of 49% in calcium and an increase of 128% in scandium. Furthermore, in contrast to the experiment using rath rates in which the rp-process path bypasses the nucleus 43V, our results show that the main reaction path passes through 43V, which is the same as using the ths8 rates, but with a larger leakage through 43V decays.
From Eq. (A.38) of Rolfs (1973), interference appears in the total cross section only when the orbital angular momenta for the resonant and DC are equal. In addition, the Z1 coefficient is only nonzero in the total cross section if the multipolarities of the DC process (E1) and resonant capture are equal. Since the DC process to the ground state proceeds via an incoming orbital angular momentum of 2, interference effects are possible only with the Er = 885 keV (3/2+) and 1289 keV (5/2+) resonances. Furthermore, because the ground state transition from the former resonance must proceed via a M2 transition, it cannot interfere with the E1 DC. For the latter resonance, the interference effect is also negligible since the mirror state in 43Ca (Ex = 1394 keV) has a reported branching of only 9(3)% to the ground state.
Acknowledgments
We thank C.X. Yuan for his shell model calculation on the properties of 43V excited states. This work was financially supported by the National Key R&D Program of China Grant no. 2022YFA1603300, the Youth Innovation Promotion Association of Chinese Academy of Sciences under Grant No. 2019406, the Strategic Priority Research Program of Chinese Academy of Sciences Grant No. XDB34020204, and in part by the National Science Foundation under Grant No. OISE-1927130 (IReNA). This work was also supported in part by the DOE, Office of Science, Office of Nuclear Physics, under grants DE-FG02-97ER41041 (UNC) and DE-FG02-97ER41033 (TUNL). M.P. acknowledges significant support to NuGrid from the ERC Consolidator Grant (Hungary) funding scheme (Project RADIOSTAR, G.A. n. 724560), from the ChETEC COST Action (CA16117), supported by the European Cooperation in Science and Technology, from the IReNA network supported by NSF AccelNet, from the National Science Foundation (NSF, USA) under grant No. PHY-1430152 (JINA Center for the Evolution of the Elements), from the “Lendulet-2014” Program of the Hungarian Academy of Sciences (Hungary), and from the European Union’s Horizon 2020 research and innovation programme (ChETEC-INFRA – Project no. 101008324). M.P. also acknowledges the support from the NKFI (Hungary) via K-project 138031 and the access to viper, the University of Hull High Performance Computing Facility. J.G.L. acknowledges the support from the National Natural Science Foundation of China under Grants No. 12205340; the Gansu Natural Science Foundation under Grant No. 22JR5RA123.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Brown, G., Denning, A., & Haigh, J. 1974, Nucl. Phys. A, 225, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, J. J., Thielemann, F.-K., & Truran, J. W. 1991, Phys. Rep., 208, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, P. J., Bentley, M. A., Henry, T. W., et al. 2013, Phys. Rev. Lett., 111, 072501 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Truran, J. W., Pignatari, M., et al. 2014, MNRAS, 442, 2058 [NASA ADS] [CrossRef] [Google Scholar]
- Dorenbusch, W. E., Belote, T. A., & Hansen, O. 1966, Phys. Rev., 146, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Endt, P. 1977, At. Data Nucl. Data Tables, 19, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Endt, P., & Van Der Leun, C. 1978, Nucl. Phys. A, 310, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fisker, J. L., Schatz, H., & Thielemann, F.-K. 2008, ApJS, 174, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Fowler, W. A., Caughlan, G. R., & Zimmerman, B. A. 1967, ARA&A, 5, 525 [NASA ADS] [CrossRef] [Google Scholar]
- He, J. J., Parikh, A., Brown, B. A., et al. 2014, Phys. Rev. C, 89, 035802 [NASA ADS] [CrossRef] [Google Scholar]
- Herndl, H., Görres, J., Wiescher, M., Brown, B. A., & Van Wormer, L. 1995, Phys. Rev. C, 52, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Diehl, S., Fryer, C. L., et al. 2009, PoS, NIC X, 023 [Google Scholar]
- Iliadis, C. 2015, Nuclear Physics of Stars, 2nd edn. (Weinheim: Wiley-VCH Verlag) [Google Scholar]
- Iliadis, C., & Wiescher, M. 2004, Phys. Rev. C, 69, 064305 [NASA ADS] [CrossRef] [Google Scholar]
- José, J., Moreno, F., Parikh, A., & Iliadis, C. 2010, ApJS, 189, 204 [CrossRef] [Google Scholar]
- Koike, O., Hashimoto, M.-A., Kuromizu, R., & Fujimoto, S.-I. 2004, ApJ, 603, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Longland, R., Iliadis, C., Champagne, A., et al. 2010, Nucl. Phys. A, 841, 1 [NASA ADS] [CrossRef] [Google Scholar]
- O’Leary, C. D., Bentley, M. A., Appelbe, D. E., et al. 1997, Phys. Rev. Lett., 79, 4349 [CrossRef] [Google Scholar]
- Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [Google Scholar]
- Rolfs, C. 1973, Nucl. Phys. A, 217, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H. 2006, Int. J. Mass Spectrom., 251, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., & Ong, W.-J. 2017, ApJ, 844, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Aprahamian, A., Görres, J., et al. 1998, Phys. Rep., 294, 167 [CrossRef] [Google Scholar]
- Schatz, H., Aprahamian, A., Barnard, V., et al. 2001, Phys. Rev. Lett., 86, 3471 [CrossRef] [PubMed] [Google Scholar]
- Setoodehnia, K., Chen, A. A., Chen, J., et al. 2020, Phys. Rev. C, 102, 045806 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R., Woosley, S., Weaver, T., & Lamb, D. 1993, ApJ, 413, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Timofeyuk, N. K., Descouvemont, P., & Johnson, R. C. 2006, in The 2nd International Conference on Nuclear Physics in Astrophysics, eds. Z. Fülöp, G. Gyürky, & E. Somorjai (Berlin: Springer), 269 [CrossRef] [Google Scholar]
- Van Wormer, L., Görres, J., Iliadis, C., Wiescher, M., & Thielemann, F. K. 1994, ApJ, 432, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, R. K., & Woosley, S. E. 1981, ApJS, 45, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Audi, G., Wapstraand, A. H., et al. 2012, Chin. Phys. C, 36, 1603 [CrossRef] [Google Scholar]
- Wang, M., Huang, W. J., Kondev, F. G., Audi, G., & Naimi, S. 2021, Chin. Phys. C, 45, 030003 [CrossRef] [Google Scholar]
- Wapstra, A., & Audi, G. 1985, Nucl. Phys. A, 432, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Fowler, W. A., Holmes, J. A. G., & Zimmerman, B. A. 1978, At. Data Nucl. Data Tables, 22, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., Cumming, A., et al. 2004, ApJS, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters of resonant states used in the calculation of 42Ti(p,γ)43V resonant reaction rate, including excitation energy, resonance energies, spin and parity, spectroscopic factor, partial width of gamma and proton, and resonance strength.
Calculated abundances for stable and unstable isotopes primarily affected by three groups of forward and reverse rates of the 42Ti(p,γ)43V with different sources (new, ths8, and rath).
All Figures
 |
Fig. 1. Fractional contributions to the total 42Ti(p,γ)43V reaction rate. Resonances are labeled by their center-of-mass resonance energies and the label DC refers to the direct capture process. The contribution ranges are shown as colored bands, with the band thicknesses representing the uncertainty of the contribution. |
| In the text | |
 |
Fig. 2. Ratio of previous rates 42Ti(p,γ)43V normalized to present recommended rates (the median rates in Table 2). The different patterns of lines correspond to the rates from Van Wormer et al. (1994, laur), Herndl et al. (1995, hg95), Rauscher & Thielemann (2000, rath), Cyburt et al. (2010, ths8), and He et al. (2014, He14). The shallow blue-shaded areas correspond to 68% coverage probabilities, shown as Low and High in Table 2. |
| In the text | |
 |
Fig. 3. Decayed elemental abundance distribution in the rp process for cases with different forward and reverse reaction rates for 42Ti(p,γ)43V. The red triangle, black square, and yellow cross correspond to cases using new rate, ths8, and rath, respectively. |
| In the text | |
 |
Fig. 4. Main reaction flows in the rp process for the adoption of different forward and reverse reaction rates for 42Ti(p,γ)43V. Panels (a)–(c) represent the cases using the new rate, the ths8 rate, and the rath rate, respectively. The reaction flow is integrated over the entire X-ray burst duration. The thickness of the arrow depicts the magnitude of the reaction flux. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.