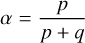| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A277 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202449297 | |
| Published online | 23 July 2024 | |
Asteroid spin and shape properties from Gaia DR3 photometry★
1
INAF, Osservatorio Astrofisico di Torino,
via Osservatorio 20,
10025
Pino Torinese (TO),
Italy
e-mail: alberto.cellino@inaf.it
2
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange,
Bd de l’Observatoire, CS 34229,
06304
Nice Cedex 4,
France
e-mail: Paolo.Tanga@oca.eu
3
Department of Physics, University of Helsinki,
Gustaf Hällströmin katu 2,
PO Box 64,
00014 U.
Helsinki,
Finland
e-mail: karri.muinonen@helsinki.fi
4
Finnish Geospatial Research Institute FGI,
Vuorimiehentie 5,
02150
Espoo,
Finland
Received:
21
January
2024
Accepted:
7
May
2024
Context. The third data release of Gaia, in June 2022, included the first large sample of sparse photometric data for more than 150 000 Solar System objects (SSOs), mainly asteroids.
Aims. The SSO photometric data can be processed to derive information on the physical properties for a large number of objects, including spin properties, surface photometric behaviour in a variety of illumination conditions, and overall shape.
Methods. After selecting a set of 22 815 objects for which an adequate number of accurate photometric measurements had been obtained by Gaia, we applied the ‘genetic’ algorithm of photometric inversion developed by the Gaia Data Processing and Analysis Consortium to process SSO photometric data. Given the need to minimise the required data processing time, the algorithm was set to adopt a simple triaxial ellipsoid shape model.
Results. Our results show that in spite of the limited variety of observing circumstances and the limited numbers of measurements per object at present (in the majority of cases no greater than 40 and still far from the number expected at the end of the mission of about 60–70), the proportion of correct determinations for the spin period among the observed targets is about 85%. This percentage is based on a comparison with reliable literature data following a moderate filtering procedure developed to remove dubious solutions.
Conclusions. The analysis performed in this paper is important in the context of developing further improvements to the adopted data reduction procedure. This includes the possible development of better solution filtering procedures that take into account, for each object, the possible presence of multiple, equivalent spin period solutions that have not been systematically investigated in this preliminary application.
Key words: methods: data analysis / techniques: photometric / minor planets, asteroids: general
Full table A.1 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/687/A277
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The Gaia space mission of the European Space Agency was launched in 2013, and since then it has continued to scan the sky to collect astrometric, photometric, and spectroscopic data for a huge number of astrophysical sources down to a visual magnitude around 21. The primary purpose of the mission is to obtain measurements of unprecedented accuracy of the positions and proper motions of the stars in a wide region of our galaxy (Gaia Collaboration 2016), but the results of the mission are of extraordinary importance for a broad variety of astrophysical investigations. The third release of Gaia data (hereinafter: DR3) was made available to the public on June 13, 2022. Among a huge number of measurements of different classes of targets, the DR3 catalogue includes a list of 3 069 170 observations (transits in the focal plane) of Solar System objects (SSOs), corresponding to multiple observations on different CCD devices across the Gaia field of view of 158 152 SSOs. Among them, 156 801 are asteroids. An exhaustive presentation of the SSO data in DR3 is given by Tanga et al. (2023).
The DR3 photometric measurements are important because they can be used to derive information on several physical properties of these objects. In particular, it is possible to obtain estimates of the rotation properties, including the rotation period, the sense of rotation (clockwise or counter-clockwise), and the orientation of the spin axis. The relation between magnitude and phase angle at the epochs of different observations can also be studied. As explained by Tanga et al. (2023), the general behaviour of the phase-mag relation has been one of the tools adopted for the validation of DR3 data for SSOs. In addition, the measured changes in brightness at different epochs are the main input data used to derive the shape parameters.
In this paper, we extend the results of photometric inversion already carried out for a small sample of asteroids for the purpose of validation of DR3 SSO photometry (Tanga et al. 2023). Here, however, we consider a much larger sample, including thousands of asteroids for which no photometric data were previously available. As explained in Sect. 2, we have used the same technique of SSO photometric inversion already adopted to interpret SSO photometric data that were available in the second Gaia data release (Cellino et al. 2019). The main difference is that in DR3 we have a much improved dataset, both in size and in terms of a better sampling of a larger variety of observing circumstances per object. The latter is a key feature for the success of photometric inversion, as we explain in Sect. 2.
The results we describe in this paper are not yet final and represent an intermediate step in the exploitation of Gaia SSO photometric measurements. It is only at the end of the mission, when all the recorded photometric measurements for each object, covering a longer time span and a wider variety of observational circumstances, become available that we will have access to a definitive Gaia catalogue of SSO rotational properties. Possible uncertainties and errors present in the results of the present paper will then be significantly reduced. This catalogue will be published directly as a product of the data processing pipelines for the Solar System, in the framework of a forthcoming release.
Even at this stage, however, DR3 data represent a very large database which can be exploited to derive a preliminary picture of the rotation periods of a reasonably large sample of the entire asteroid population. The main purpose of this paper is to present the results of the analysis of DR3 data focusing on the determination of the rotation period of the objects. Another major goal is to assess the performances of the photometric inversion algorithm developed by the Gaia Data Processing and Analysis Consortium (DPAC) to process SSO photometric data.
2 The photometric inversion of DR3 SSO photometric data
The most important property of DR3 photometric data for SSOs is that they are sparse and cover a long time span. In this respect, they differ from the kind of data most frequently used in asteroid photometry, namely, the analysis of measurements collected over relatively short time spans (generally covering one or a few nights), most often referred to as ‘light curves’. Light curves are most commonly used to obtain a reliable determination of the rotation period for the target object, namely, this refers to the time needed to complete a full rotational cycle.
The photometric inversions described in this paper have been obtained using the genetic algorithm developed to process Gaia SSO photometric data (Cellino et al. 2009; Santana-Ros et al. 2015, and references therein). The data used for the purposes of photometric inversion consist of epochs corrected for light time and magnitude reduced to unit distance from both the Sun and Gaia.
The inversion algorithm accepts in input the differences between the first recorded magnitude for any given object and the other magnitudes of the same object, recorded by Gaia at different epochs. Working in terms of magnitude differences, instead of simple magnitudes, offers the advantage that any absolute dependence of the magnitudes upon light scattering properties of the surface can be removed, assuming that the surface of any given object has homogeneous properties.
It is also assumed, for the sake of minimisation of the runtime, that the shape of each object can be conveniently represented by a triaxial ellipsoid. Under this assumption, imposed by the need of minimising the time needed to process very large amounts of data, the algorithm determines for each asteroid the best set of unknown parameters that would minimise the differences between the magnitudes measured at different epochs and those predicted at the same epochs. This is based on the assumed values of the relevant physical parameters characterising an object.
The unknown parameters which determine the observed magnitude differences are: the object’s rotation period; its pole coordinates expressed in ecliptic longitude and latitude; the b/a and c/a axial ratios; the slope of an assumed linear phase-magnitude relation computed at a phase angle of 20° (Muinonen et al. 2022); the rotational phase of the object at the epoch of the first Gaia measurement. Because it is very important to deal with data of a sufficiently good quality in this kind of analysis, single photometric measurements having a nominal uncertainty greater than 0.05 mag have not been used.
The number of accepted measurements is critically important for the purposes of photometric inversion. The results described in this paper have been obtained for a sample of 22 815 objects, for the vast majority main-belt asteroids (see Tanga et al. 2023), for which a minimum number of 25 sparse photometric measurements are available in the Gaia DR3 catalogue. This choice of the minimum number of acceptable measurements per object is based upon the experience achieved in a large number of inversion tests based on both real and simulated data (see e.g. Cellino et al. 2009, 2019; Santana-Ros et al. 2015).
The genetic inversion algorithm makes a trial and error search for the unknown physical parameters of the object. Its “genetic” attribute refers to the way it progressively identifies better sets of the parameters, using a strategy that is inspired by the genetic evolution of living organisms (Cellino et al. 2009). In particular, starting from an initial population of 20 completely random solutions, the algorithm performs a number of l0 000 steps. At each step, one of the existing solutions is randomly chosen, and is either coupled with another solution, randomly taking each parameter from one of the two “parent” solutions, or it is randomly modified in one or more of its parameter. The corresponding residuals of the computed magnitudes with respect to the recorded magnitudes are then computed. The new solution is then accepted if its residuals enter the top 20 solution ranking among the “parent” population. At the end of this procedure, a small number of possible solutions are obtained, each one consisting of a full set of parameters. The set of parameters giving the smallest residuals constitutes the solution of the inversion attempt. The algorithm is run 15 times for each object. This is done because (due to the intrinsic properties of the adopted algorithm) any single solution obtained by running only once the genetic algorithm is not sufficient to ensure that it corresponds to the minimum possible value of the residuals. In different runs, the algorithm can converge to a range of local minima of the residuals; therefore, a variety of executions is needed to ensure we are reasonably confident in the solution corresponding to the minimum possible value of the residuals, using the adopted shape model. The execution time depends upon the number of recorded magnitude data. On a server booted up two years ago, running under Linux Ubuntu, the execution time is of the order of 1 min for an object with 25 measurements available, while it is a little less than 2 min 45 s for an object with 60 measurements.
It is important to note that the approach described above allows for a simultaneous determination of the whole set of inversion parameters (as opposed to individually). Moreover, the sense of rotation is also immediately indicated by the sign assigned to the rotation period. In this respect, we followed IAU recommendations, and always assigned a positive sign to the latitude of the pole. Retrograde rotation is indicated by a negative rotation rate. As a consequence of this choice, when comparing our obtained rotation periods with literature values given without a sign, we use the modules of our obtained values. This is the case for several figures shown in this paper.
We have found that in a non-negligible number of cases, multiple equivalent solutions can be found by the algorithm (the residuals differing from those of the best obtained solution by less than 0.0015 mag). It may happen that a solution in very good agreement with ground-based results can be among the best equivalent solutions, but not specifically the one giving the smallest residuals. For the moment, we have not analysed these cases. In this paper we have decided to adopt and test a simple approach, by disregarding all possible equivalent spin rate solutions for any object. We note, however, that based on a still-limited number of tests, we found that (in most cases) objects having more than one equivalent period solution tend to give erroneous results. In such cases, neither the nominal best solution, nor the second-best one in terms of residuals, is found to be in agreement with the literature data. In the future, we will probably remove inversion solutions characterised by multiple rotation periods, but for the moment we have not taken any action related to this subject. Some discrepancies between the spin periods listed in the literature for several objects and the computed spin periods determined in this paper could therefore disappear in the future by analysing the existence of multiple period solutions and possibly removing them.
We are confident that adding large amounts of new data for each object in the next data releases will significantly remove many uncertainties and will result in much more robust and unique solutions. On the other hand, we are aware that as new data become available, a number of increasingly fainter objects will always exist, having numbers of acceptable measurement close to the minimum acceptable value. However, this tail of the distribution of non-optimally observed objects will be limited to a fraction of increasingly small asteroids as Gaia continues to collect new data.
3 Results and reliability tests
Table A.1 summarises the results of our photometric inversion study for a tiny sub-sample of objects, whereas the full Table will be made publicly available at the Centre de Don-nées astronomiques de Strasbourg (CDS)1. For each object, the table lists the asteroid number, the number of recorded measurements, the computed ecliptic coordinates of the pole, the rotation period, axial ratios, phase-magnitude slope for the best obtained solution, and the corresponding solution residuals. We note that the table does not indicate the errors associated with each solution parameter. This is because we are not interested on the uncertainty of the pole and shape solutions, while the formal uncertainty of the rotation period turns out to be always very small, of the order of some or few seconds. The value of the solution residuals is sufficient to give an estimate of the solution uncertainty. In turn, the latter depends heavily on the fact that in our photometric inversion computations we are not using an advanced shape model, although the triaxial ellipsoid shape model has been proven to give reasonable solutions even when applied to objects having much more complex shapes (see e.g. Martikainen et al. 2021).
The histogram of the computed rotational frequencies (cycles per day, expressed as 24 divided by the period expressed in hours) for the whole sample of 22 815 asteroids having a minimum number of 25 transits in DR3 is given in Fig. 1. We note, as mentioned above, that the adopted genetic algorithm produces solutions for the rotation period including a sign to distinguish between objects found to have a prograde rotation, and those having a retrograde rotation. A surprising feature of the distribution shown in Fig. 1 is the large fraction of slow rotators, having rotation periods above 50 h. This is not a totally unexpected result, because other authors have recently pointed out that the fraction of slow-rotators among the asteroid population may have been severely underestimated in the past (Marciniak et al. 2021, 2023). This is also confirmed by a very recent analysis of DR3 asteroid photometric data carried out by Ďurech & Hanuš (2023). The presence of some secondary peaks in the distribution of rotational frequencies, corresponding to rotation periods of 12 and 6 h, is also evident in Fig. 1. This is an intriguing phenomenon and deserves some explanation. Such an explanation is closely related to the fundamental question we want to answer in this paper, namely, the extent to which the rotation periods derived using our technique of photometric inversion are reliable.
This is a fundamental task, taking into account that no information about rotational properties is available for most asteroids analysed in this paper2. Our primary goal is therefore to assess, based on a comparative analysis limited to the objects for which some information is currently available from other sources, whether the results of our photometric inversions can be found to be generally correct, and the expected fraction of probably erroneous (discrepant) rotation period solutions.
Therefore, we address a dataset of independent determinations of asteroid spin properties, determined by means of different, and fully independent, data, mainly taking advantage of decades of ground-based asteroid photometric measurements.
The ground-based data used in this paper have been taken from the most recent version (April 24, 2023) of the Asteroid Lightcurve Database (LCDB) (Warner et al. 2021). In particular, in the LCDB data table, we considered only the entries for numbered objects (33 869 objects). These list for each object the rotation period and its associated ‘quality code’, which comprises the essential information we use for comparison with DR3 photometric inversion results. The LCDB lists also a number of other important physical parameters, including but not limited to the absolute magnitude H, usually in the (H,G) photometric system, the corresponding G parameter, the size, the taxonomic classification, and the geometric albedo. Among the 22 815 numbered asteroids for which we have a Gaia DR3 photometric inversion, 6 258 are included in the LCDB list, with an assigned quality code of >0 (see later). These objects can be used for the purposes of comparison with DR3 results.
We note that the LCDB lists, when available, also the ecliptic coordinates of the derived spin axis orientation. However, we have to take into account that the pole orientation is not uniquely determined in many cases discussed in the literature, especially when a simple and symmetrical shape model is adopted. Moreover, for pole determination purposes it is critically necessary to take advantage of the maximum possible variety of observing circumstances, in the case of Gaia this will be available only at the end of the mission. For these reasons, we postpone an analysis of the asteroid poles to a future paper, although here we include (for the sake of completeness) some preliminary results on spin axis determination in Table A.1. In particular, because we do not consider here the possible presence of more than one equivalent solutions (as mentioned above) in Table A.1 we list for each object one pole solution only; namely, the one producing the smallest residuals. In many cases we have obtained equivalent solutions corresponding to the same spin period but to different pole coordinates. The fact that more than one solution for the pole of an asteroid can often be found is well known in the literature. These alternative solutions are not considered in this paper.
Apart from a limited number of cases for which the assigned LCDB quality code is zero (meaning the listed period is totally unreliable), the LCDB quality code assigned to the spin period listed for each object can vary between 1 (very tentative), 2 (moderate uncertainty) and 3 (very reliable and accurate). Apart from minor details (some objects can be assigned a quality code of e.g. 1−, 1, 1+) the meaning of the assigned QC can be summarised as follows:
QC = 1: the listed period may be completely wrong (223 objects having at least 25 Gaia-measured transits).
QC = 2: the listed period is not firmly established based on a complete coverage of the light curve. It may be wrong by something of the order of 30% or more in less favourable cases. We note that QC= 2 often corresponds to survey data such as the Transiting Exoplanets Survey Satellite (TESS) or the Palo-mar Transient Factory (PTF), which, as Gaia, did not produce asteroid light curves, but sparse photometric data. 4380 QC = 2 objects have at least 25 Gaia-measured transits.
QC = 3: very good coverage of the light curve. The derived period is unambiguous and unique (1655 objects having at least 25 Gaia-measured transits).
In our analysis, we did not consider asteroids having LCDB period QC = 0 (little more than 100 asteroids). We also did not make use of those having LCDB QC = 1 (223 objects).
The distribution of the rotational frequencies for different LCDB quality codes exhibits important differences, shown in the plots in Fig. 2. The distribution of QC = 3 periods (right panel of this figure) is much depleted in long periods. This is expected when taking into account the difficulty in obtaining full light curves and, consequently, accurate periods for very slowly rotating objects. This effect is not present for QC = 2 asteroids (shown in the left panel), which exhibit a maximum at rotation periods between 24 and 48 h. In Fig. 3 we show, for a comparison, a histogram of the rotation periods resulting from inversion of the sub-sample of 6035 DR3 objects which are present, with a period quality code of ≥2, in the LCDB dataset. The presence of an important fraction of slow-rotators, in agreement with the large number of LCDB QC = 2 objects, is confirmed by our Gaia DR3 inversions.
Some important comparisons between Gaia-derived rotational frequencies of individual asteroids and the corresponding LCDB values are shown in Fig. 4. We note again that, whenever comparing LCDB periods with those obtained from inversion of DR3 data, we do not take into account the nominal sign of the latter, but we use its absolute value.
Broad differences exist in the plots comparing ground-based frequencies of asteroids having different LCDB QCs. There are only 223 QC = 1 asteroids, and we have not taken them into account in our analysis, due to their unreliability. As opposite, QC = 2 asteroids are much more common (4380 objects). In the left panel of Fig. 4, a large fraction of the objects are found along the line of P(LCDB) = P(Gaia). However, an intricate web of sharp lines mutually intersecting in the freq-freq plane is evident (see the left panel in Fig. 4). Most features correspond to linear combinations of the frequencies, m/P(LCDB) + n/P(Gaia) = 1 where m and n are small integers. Another, much weaker feature in this plot is an oblique alignment produced by objects for which P(Gaia) is twice the P(LCDB). It is difficult to infer in quantitative terms from this plot the relative abundance of the objects populating all these unexpected alignments. In the case of LCDB QC = 3, the plot shown in the right panel of Fig. 4, displaying the cases of 1655 objects, is cleaner, with the majority of objects apparently lying on the line corresponding to P(Gaia) = P(LCDB). The most important spurious alignments present in the case of QC = 2 objects, however, are still present, though apparently weaker. The oblique alignment corresponding to P(Gaia) being equal to twice P(LCDB), which is sharper for QC = 2 asteroids in the left panel of Fig. 4, is also still recognisable.
The interpretation of the above results is not straightforward. In the case of objects having LCDB QC = 2, even taking into account that for them the listed LCDB periods can be affected by significant uncertainties, the existence of the observed alignments in the frequency-frequency plot suggests that some unexpected effects may play a role, The same is true for LCDB QC = 3 objects; however, in that case, the number of objects that have discrepant rotation period is much reduced, but not really negligible. We also note that, according to the recent analysis by Ďurech & Hanuš (2023), the number of wrong LCDB periods having QC = 3 turns out to be quite low. These authors found that only 20 out of 848 QC = 3 objects have periods differing by more than 10% from those determined by their own inversion of DR3 data. If this figure is correct, and we assume that the photometric inversion results by Ďurech & Hanuš (2023) are all correct3, this means that, for 1655 LCDB QC = 3 objects, we should expect no more than about 2.5% wrong periods, corresponding to about 30 objects. It is easy to see that in Fig. 4 the number of objects belonging to the strange alignments is much higher than that.
In most general terms, some unexpected behaviour can be due to a variety of reasons. One possibility is that the regular shape of the ellipsoid, with its full symmetry with respect to the geometric centre point and three planes for mirror symmetries, causes some problems. Another possibility is that for certain values of the true period of an object, a particular sequence of transit epochs and corresponding magnitudes may produce a situation in which the inversion algorithm tends to preferentially find a number of erroneous period values producing a reasonable agreement with the available transits. These period solutions might correspond to the anomalous peaks at 12 and 6 h (visible in the histogram shown in Fig. 1) and might be responsible also of the unusual alignments seen in Fig. 4. The mechanism producing such effects may be possibly influenced by the Gaia sky-scanning periodicities. The possible effect of the intrinsic periodicity in the data acquisition due to the properties of the Gaia sky scanning law has been extensively analysed and the details and conclusions are deferred to Appendix B. It should be noted, however, that the analysis given in Appendix B is based on comparisons of “true” periodicities of some phenomena (with generally small associated errors) and those computed using their measurements under the assumption that the data collection is on its own affected by some intrinsic periodicity. In the case of the plots of Gaia-determined spin frequency versus ground-based frequency, however, the situation is not exactly the same, because in most cases the “true” spin frequencies determined by ground-based data (LCDB periods) cannot be considered as really “true” values. QC = 2 periods can have errors up to 30%. Only periods that are designated QC = 3 can be considered to be sufficiently accurate and reliable, although some errors are still possible even in these cases.
We also note that for what concerns the cases of P(Gaia) = 2 P(LCDB), which are present in Fig. 4 in both the plots for LCDB QC = 2 and LCDB QC = 3, these cases may be, at least partially, explained in terms of surface albedo heterogeneity (Cellino et al. 2009, 2016).
A different, more quantitative way to consider the differences between rotation periods computed using DR3 data and the corresponding LCDB periods is given in Fig. 5. This figure shows (on logarithmic scales, and separately for LCDB QC = 2 and QC = 3) the histograms of the difference in rotation period between DR3 and LCDB solutions, normalised to the latter. We note that, in these histograms, all the values of the normalised period differences smaller than a value of about 0.01 or 0.02 correspond to very good agreement between DR3 inversions, and LCDB values. For values of the order of 0.1 or 0.2, the agreement can still be reasonable, mainly for slowly rotating asteroids having periods longer than some tens of hours, for which the associated uncertainties are generally very important. A value of the normalised period difference of 1 identifies cases in which DR3-derived periods are twice the corresponding value in LCDB. Figure 5 shows that in the case of asteroids having LCDB QC = 2, the agreement with the DR3 results is reasonable, except for a fraction of cases in which the DR3-derived periods tend to be much larger than the corresponding LCDB periods. We note also the presence of a sharp peak in this histogram, corresponding to objects for which the DR3-derived periods are twice the LCDB values. In the case of objects having the maximum reliability in LCDB, namely those having QC = 3, there is an agreement between DR3 and LCDB rotation periods in about 60% of cases, including up to a fraction of about 5% of objects having a DR3 period twice the LCDB value.
We note that the agreement between our DR3-derived periods and those listed in the LCDB tends to be independent of the rotation period itself, across a range of rotation period from a couple of hours up to values of the order of 100 h or more.
In about 40% of the cases, however, the Gaia-determined periods can be wrong. As we have noted several times, Gaia DR3 data are still relatively scarce, the numbers of measurements per object being smaller than 40 in about 75% of the cases, and yet they do not offer a satisfactory sampling of the full variety of possible observing circumstances for each object. The number of available measurements is of the highest importance, because each observation provides a constraint for the computation of the inversion solution. Moreover, we should not forget that we are disregarding in this analysis the cases in which equivalent period solutions are found for some objects, as mentioned above. In spite of these facts, the proportion of wrong period determinations is high. This led us to find some way to improve the results, even at the cost of decreasing the total number of inverted objects.
 |
Fig. 1 Distribution of the rotational frequency for the sample of 22 815 Solar System objects (SSOs) having a minimum of 25 recorded transits in DR3. |
 |
Fig. 2 Distribution histograms of LCDB rotation periods for objects in the DR3 database with at least 25 measured transits and present in the LCDB with a period quality code 2 or 3. |
 |
Fig. 3 Same as Fig. 2, but for all the objects in the DR3 database that are present in the LCDB with a period quality code of ≥2. |
 |
Fig. 4 Comparison between rotation frequencies computed for asteroids included in the DR3 catalogue and the corresponding frequencies listed for the same objects in the LCDB. Left panel: all objects for which the LCDB period quality code is 2. Right panel: the same, but for objects having LCDB quality code of 3. |
 |
Fig. 5 Differences (in absolute values) between our DR3-derived rotation period and the corresponding LCDB rotation period, normalised to the LCDB period. Left panel: all objects for which the LCDB period quality code is equal to 2. Right panel: same, but for objects having LCDB quality code of 3. |
 |
Fig. 6 Distribution of the solution residuals for the objects whose rotation period solution is in disagreement with LCDB for objects having QC = 3 (left). Same details as in the left panel, but for the distribution of the b/a axial ratio (right). |
 |
Fig. 7 Same as in Fig. 6, but in this case the distribution of the slope of the phase-magnitude relation for the objects whose rotation period solution is in disagreement with LCDB for objects having QC = 3 (left). The distribution of the ecliptic latitude of the pole is on the right. |
3.1 Solution filtering
It is important to assess whether the introduction of data filtering can substantially improve the results of DR3 photometric inversions presented above.
There are some circumstances where it may be a priori difficult to perform a correct photometric inversion. We have already mentioned the importance of having a high number of reliable photometric measurements covering the maximum possible variety of observing circumstances. In this respect, it is clear that the cases of objects for which the range of measured magnitudes is small do not favour the chances to find a correct solution. As some trivial example, we may mention the cases of nearly spherical or spheroidal objects, independently of the direction of the rotation axis and the cases of objects having a small orbital inclination with respect to the ecliptic, along with spin orientations at very high ecliptic latitudes. Whenever the visible and illuminated surface of an object tends to be quite similar at all epochs, the chance to find a correct inversion solution after a limited number of attempts decreases significantly.
There are also cases for which we can have a posteriori evidence that for any possible reason, the obtained inversion solution is not good. These are cases in which the resulting slope of the magnitude-phase slope turns out to have extreme, unrealistic values. We know (Belskaya & Shevchenko 2000) that the phase-magnitude slope is related to the geometric albedo of the surface. This means that, in our photometric inversions, values of the photometric slope corresponding to albedo values very close to 0 (or higher than 1) should be forbidden. Another alarm can be raised whenever the inversion solution gives extremely low values for the rotation period. In particular, we refer here to the existence of the so-called spin barrier at about 2.1 h, which characterises the spin period of asteroids larger than about 300 m in size (see e.g., Pravec & Harris 2000; Pravec et al. 2008, and references therein).
To develop a criterion to reject bad solutions, we have performed an analysis of the sample of incorrectly recovered rotation periods, including 681 LCDB QC = 3 objects (41% of the total sample). For these asteroids, we looked at the distributions of different solution parameters, and we evaluated their possible role in determining the resulting wrong solutions for the rotation period. In Figs. 6 and 7 we show, for these photometric inversions giving period solutions in disagreement with LCDB periods, the distributions of the resulting solution residuals, of the b/a axial ratio, of the slope of the phase-magnitude linear relation, and of the resulting ecliptic latitude of the pole.
Figures 6 and 7 show several interesting features. In particular, we see that the distribution of the phase-mag linear coefficient includes at its ends significant peaks of hardly acceptable values, which are not seen in classical, ground-based photometric data; according to Belskaya & Shevchenko (2000) these would correspond to extreme values of the albedo. One more result is that there is a clear overabundance of wrong solutions characterised by high b/a axial ratios, above 0.80. Another result is that many wrong solutions exhibit high values of the solution residuals, above 0.05 mags. In addition, we have examined also the distribution of the resulting latitude of the computed pole, shown in the right panel of Fig. 7. Although this is not apparent in this figure, we have found that the fraction of solutions giving a very low ecliptic latitude of the pole plays a non-negligible role in determining the total fraction of wrong period solutions. This is in qualitative agreement with some results by Ďurech & Hanuš (2023), who found that in their solutions, which are in generally excellent agreement with LCDB QC = 3 solutions, there is a clear under-abundance of objects having the pole latitude close to the ecliptic and, more in general, close to the orbital plane. In general terms, main-belt asteroids (whose orbital inclination with respect to the ecliptic is always modest) do not exhibit large variations in apparent magnitude in cases for which the b/a ratio tends to be high and the ecliptic latitude of the pole is low. These are cases for which the role played by the c axis in determining the magnitude in most observing circumstances tends to be very limited, and the assumed triaxial ellipsoid shape model tends to have problems. The fact that a low ecliptic latitude of the pole tends to negatively affect the quality of photometric inversion results using the genetic algorithm described in Sect. 2 was also found in the extensive analysis by Santana-Ros et al. (2015).
Based on the results of this analysis, and taking also into account the asteroid spin barrier mentioned above, we have developed the following rejection filter. Solutions are rejected when any of the following conditions occur:
The linear slope of the phase-magnitude relation is ≤0.02 or ≥0.05 mag deg−1.
The solution residuals are ≥0.05 mag.
The rotation period solution is, in module, ≤2.l h.
The resulting b/a axial ratio ≥0.80.
The resulting ecliptic latitude of the pole is <10°.
By applying the above filter, we find that 8670 inversion solutions are acceptable. Among them, 679 out of 1655 solutions for objects having LCDB QC = 3 are acceptable (41% of the cases). Among these accepted solutions, 571 out of 679 give a rotation period in agreement with LCDB (i.e. 84% of the sample).
In Figs. 8 and 9 we show the distribution of rotation frequency for the total DR3 sample of solutions passing the rejection filter, and the comparison of the DR3 filtered rotation frequencies with those of LCDB QC = 3 results, respectively. We note that, compared to the distribution of rotation frequencies for the whole DR3 sample shown in Fig. 1, the anomalous peaks corresponding to rotation periods of 12 and 6 h are no longer present in Fig. 8, as we would generally expect in the case the anomalous peaks are produced by incorrect period determinations, as discussed in Sect. 3.
Another difference is that in Fig. 8 we see a slight asymmetry in the distribution of rotation frequencies, which is produced by the presence of an overabundance of objects having prograde rotation and periods between 24 and 12 h. Whether this is a real property of the distribution, or an artefact created by our algorithm of photometric inversion, is a question that will be answered when a much larger dataset of Gaia photometric data will be available in future data releases.
In Fig. 9 we show that, compared to the case of non-filtered inversion solutions, the number of cases of rotation frequencies producing anomalous alignments (as those seen in Fig. 4) is much reduced. This offers a visual representation of the fact that filtered solutions should include only a modest (about 16%) fraction of incorrectly determined rotation periods.
 |
Fig. 8 Same as Fig. 1, but here only DR3 inversion solutions passing the filter discussed in the text are displayed. This means a total of 8670 objects, for which we can be confident that 84% of them should be correct. |
 |
Fig. 9 Same as in the right panel of Fig. 4, but plotting only inversion solutions passing the rejection filter discussed in the text. |
3.2 Comparison with the results of Ďurech and Hanuš
In a recent paper, Ďurech & Hanuš (2023) published the outcome of an independent solution of photometric inversion of Gaia DR3 data. Instead of assuming a priori a fixed shape model, they used their own method of photometric inversion to find the best-fit asteroid model to be compared with available Gaia data. Their model consists of a sidereal rotation period, a spin axis direction, and a low-resolution convex shape. The Ďurech & Hanuš (2023) method is conceptually more flexible than the simple model adopted by us. In terms of results, the above authors found that in most cases the number of data points was insufficient to obtain a photometric inversion. However, they were able to uniquely determine the spin state, together with a low-resolution convex shape model for a sample of 8596 asteroids out of a total number of more than 150 000 objects included in the Gaia DR3 database. In order to identify and remove unstable period solutions, the above authors applied what they call a “jackknife” procedure, to test the stability of the obtained period solutions against small changes of the available data for each object. This led to a set of 6269 models based on a convex-shape period search and 5784 models based on a period search using a triaxial ellipsoid shape model. After taking into account the intersection of these two samples and removing a small number of objects having non-consistent periods, this procedure led to a total number of 8602 solution models. Among these photometric inversion solutions, 3690 could be compared with an LCDB period estimate. Among them, only reliable LCDB periods, having a QC of 3, were selected for a comparison, corresponding to 848 asteroids. Among these, only 20 period solutions were found to differ by more than 10% with respect to the LCDB listed values. After looking at the original publications from which LCDB periods had been compiled, the above authors concluded that only five periods had been incorrectly determined in their analysis of Gaia DR3 data. We note that differences of the order of 10% in the determination of the period correspond to a value of 0.1 when comparing with the normalised period differences with respect to LCDB values, as shown in Fig. 5 of this paper. Such a value is certainly acceptable when dealing with objects with long rotation periods, as determined by ground-based photometry.
The number of 8602 reliable inversion solutions obtained by Ďurech & Hanuš (2023) is markedly similar to the number of 8670 filtered solutions found in the present paper, as explained in this section. It is interesting to note that two different algorithms of photometric inversion, applied to Gaia DR3 data, are found to produce solutions for a so similar fraction of the whole DR3 asteroid sample. The number of asteroids whose DR3 photometric data make it possible to find a solution is still relatively small with respect to the total number of objects included in the DR3 sample. However, we can be confident that in next data releases, the availability of significantly larger numbers of photometric measurements (about 350 000 asteroids are expected to be included in Gaia DR4, and the number of acceptable photometric measurements per object will increase correspondingly) will produce a significant improvement in the situation.
Looking at the DR3 results, it is important to note that the intersection of the two above-mentioned samples of inverted objects includes 3585 objects, only. In other words, about one-half of our 8670 filtered solutions and of the 8602 Ďurech & Hanuš (2023) solutions refer to asteroids that are not in common in the two samples. Interestingly, the agreement between our period solutions and those of Ďurech & Hanuš (2023) for the 3585 asteroids included in both samples is excellent, about 95%. This is an encouraging result. In spite of their different assumptions, our photometric inversion method, when applying the filtering criterion described in this section, and the Ďurech & Hanuš (2023) inversion method give results in very good agreement for the objects that turn out to be inverted using both methods.
Our adopted triaxial ellipsoid shape model can, in principle, be responsible for a less-than-optimal agreement of our obtained spin periods with those of LCDB QC=3 objects. The better agreement obtained by Ďurech & Hanuš (2023) has also been made possible by their choice of using a more flexible convex shape model, which, in many cases, led to the determination of a rotation period in very good agreement with LCDB data. The fact that the sample of our obtained period determinations is in excellent agreement with Ďurech & Hanuš (2023) for the objects that are in common, whereas our agreement with LCDB QC=3 objects is slightly worse (around 85%) may be due to the fact that a simple triaxial ellipsoid shape model has some limitations when applied to Gaia DR3 photometric data in a still relevant fraction of cases. We should recall that our inversion algorithm determines the parameters characterising a triaxial ellipsoid solution which produces a best-fit of available photometric data. As shown by the results of Ďurech & Hanuš (2023) discussed above, there are objects that are intrinsically very well approximated by a triaxial ellipsoid shape, but in other less favourable cases this can be no longer true. We can expect, however, that in the next Gaia data releases, which will include up to about ten times the number of single photometric measurements for the asteroid population4, the performances of our photometric inversion algorithm might improve significantly.
 |
Fig. 10 Plot of proper eccentricity vs. proper semi-major axis (left) for the members of asteroid dynamical families taken from the list of Milani et al. (2014), also available on the AstDyS web site. The sub-sample of family members whose Gaia DR3 photometric data pass the solution rejection filter described in this paper is displayed using a colour code to indicate their resulting sense of rotation. Right: the same, but for sine of proper inclination vs. proper semi-major axis. In these plots, red points indicate family members displaying retrograde sense of rotation, while blue symbols are used for objects displaying prograde rotation, according to the results of photometric inversion. Black symbols are used for family members for which we have not obtained a photometric inversion. |
3.3 A few important results
One of the results obtained in this preliminary analysis of DR3 photometric results, is that, as already mentioned in Sect. 3, the distribution of Gaia-derived periods include, as shown in Fig. 1, confirmed by the sample of filtered solutions shown in Fig. 8, a sharp peak corresponding to long rotation periods. This is also in reasonable agreement with the distribution of LCDB QC = 2 rotation frequency (see Fig. 2). These findings seem to confirm that, in agreement with previous results by Marciniak et al. (2021, 2023), Pál et al. (2020), and the most recent analysis by Ďurech & Hanuš (2023), slow rotators having spin periods above some tens or even hundreds of hours are not rare among main-belt asteroids. They are under-represented in the lists of the most reliable asteroid rotation periods based on ground-based light curve data, because the identification of long rotation periods requires long observing times and cannot usually be derived with very good accuracy. We also note that (as indicated in Fig. 8) the total number of DR3 inversion solutions passing the rejection filter is 8670. This is definitely smaller than the total number of DR3 computed periods (more than 25 000), but it is nevertheless a large number of asteroid period solutions that are not expected to include a fraction much larger than about 16% of erroneous determinations (see Sect. 3.1).
Another important piece of evidence comes from an analysis of the spinning state of asteroid families. Figure 10 shows, for the sample of asteroids identified as members of the dynamical families taken from the list produced by Milani et al. (2014)5, the results of photometric inversion, whenever available, for the sub-sample of objects passing the selection filter. In this figure, family members are plotted in different colours, according to the resulting sense of rotation obtained by DR3 photometric inversion. Red symbols are used to display retrograde rotators, whereas blue symbols is used for prograde rotators (black symbols represent family members for which we do not have yet a photometric inversion solution).
An observed ‘polarisation’ of the sense of rotation for family-member asteroids had been already noted by Hanuš et al. (2013), corresponding to what should be expected based on the Yarkovsky effect acting on the long timescale dynamical evolution of objects characterised by opposite sense of rotation (see Bottke et al. 2001; Milani et al. 2017), with retrograde rotation tending to move the objects towards lower values of orbital semi-major axis, and prograde rotation tending to produce an increase of semi-major axis. The effect is size-dependent, and produces a drifting in semi-major axis for increasingly smaller asteroids. This effect has been exploited by different authors to estimate the ages of different asteroid families (see e.g. Spoto et al. 2015; Milani et al. 2017, and references therein). It is interesting to note when looking specially at the α-sin(i) plot in Fig. 10, that this ‘polarisation’ effect is clearly visible in our plots, although the overlapping of different families in the same regions of the proper elements space tends to produce a blurring in several cases, mostly in the α-e plot. It is also possible to see that the members of families located very close to some important mean-motion resonances with Jupiter (corresponding to some of the sharpest ‘Kirkwood gaps’), tend to have an under-abundance of objects having sense of rotation corresponding to an orbital drift tending to bring them towards the neighbouring resonance. This general feature, already noted by Hanuš et al. (2013), is visible, for instance, in the case of the great Themis family. Its members have proper semi-major axes between 3.1 and 3.2 au, close to the inner border of the powerful 2:1 mean-motion resonance with Jupiter. The same is true for other families located close to the outer border of the 3:1 mean-motion resonance, like the families of Eunomia and Maria. In all these cases, a natural explanation is that a dynamical evolution dominated by the Yarkovsky effect has led many small family members to move into a powerful, neighbouring mean-motion resonance, and to be removed from the asteroid main belt. Another interesting case is that of the big Eos family, whose members have semi-major axes around 3 au. This family is crossed by the relatively weak 9:4 mean-motion resonance with Jupiter, centred at a heliocentric distance of 3.03 au (Źappalá et al. 2000). In the right panel of Fig. 10 the sharp inversion of rotation sense for objects located at heliocentric distances surrounding the two borders of the resonance seems particularly sharp. This also confirms that the 9:4 resonance can be crossed without big consequences in many cases by Eos family members, although, as shown by Źappalá et al. (2000), some of the resonance crossers can be perturbed and removed from the family.
It is important to note that the plots shown in Fig. 10 are certainly influenced by our adopted choice of family membership, but the cases discussed above concern big and very robust families.
The observed distribution of the sense of rotation of family members is another (indirect) piece of evidence that supports the overall reliability of filtered DR3 photometric inversions, even in terms of determining the sense of rotation.
Figure 11 shows in log-log scale the computed rotational frequency as a function of diameter for all DR3 asteroids whose inversions passed the rejection filter and for which some reliable estimate of the size can be found in the literature. The total number of plotted asteroids is 2405. Family members are displayed in red. The figure shows another, potentially important result. In particular, two lines, taken from Fig. 11 of the paper by Pravec et al. (2005) are displayed. The upper, dashed-dotted line, delimits the region below which non-principal axis rotators (NPAs) have been known or suspected to exist when the paper by Pravec et al. (2005) was published. In particular, the line corresponds to the limit for which NPA rotation had been detected based on deviations from the single periodicity of the objects, but the second period had not been resolved. The lower, dashed lines corresponds to situations for which the time of relaxation of NPA to a principal axis rotation was estimated to be equal or longer than the age of the Solar System. According to Pravec et al. (2005), most asteroids whose position in this plot is lower than the dashed line, are NPA rotators.
An important difference between our Fig. 11 and Fig. 11 in Pravec et al. (2005) is that in the case of our plot of DR3 data, the region corresponding to objects smaller than about a couple of kilometres is nearly empty, due to the limiting magnitude attainable by Gaia, or simply because the number of measurements available in DR3 are not yet sufficient to compute a rotation period. On the other hand, Fig. 11 includes a much larger amount of asteroids which are located in the region where, according to Pravec et al. (2005), NPA objects have long relaxation times, even longer than the age of the solar system. In particular, only a couple of objects displaying values of the rotational frequency lower that 0.1 (240 h) were known at the time of the Pravec et al. (2005) paper. Interestingly, this region of the plot includes now a fairly large number of objects in our Fig. 11, including several having rotation frequencies ten times lower. All this is related to the relative abundance of slow and very slow rotators mentioned in previous sections. Whether this can be interpreted as the discovery by Gaia of a population of tumblers is a very interesting subject of investigation, which is beyond the scope of the present paper. We plan to devote a more exhaustive analysis of this result and its possible implications in a separate work.
 |
Fig. 11 Rotational frequency vs. diameter for the sample of asteroids having photometric inversion solutions passing the rejection filter described in Sect. 3.1 (8670 objects). Red symbols are used to indicate asteroid family members according to Milani et al. (2014). They are displayed in red just to emphasise the large contribution of asteroid dynamical families in our inventory of objects having sizes smaller than about 10 km, including many slow-rotators. |
4 Conclusions
Summarising the results presented in this paper, we find that we have good reasons to conclude that the rotation periods we have obtained for the available set of DR3 data are reasonably satisfactory. This includes a significant fraction of the solutions for asteroids with no prior information from ground-based observations. By applying the filtering procedure described in Sect. 3.1, there is a clear improvement in the quality of photometric inversion results, based on comparisons with the most reliable rotation periods currently available in the literature. This comes at the cost of flagging a high percentage of our solutions as likely erroneous, including some which might be correct. On the other hand, the final number of supposedly reliable computations of the rotation period includes those for 8670 asteroids. For this set, a comparison with LCDB QC = 3 periods indicates that the fraction of correctly determined periods is around 84%. As discussed in Sect. 3.2, the above fraction is not dramatically worse than that of successful inversion solutions obtained by Ďurech & Hanuš (2023), who used an approach that also included the determination of complex convex shapes. A comparison of our filtered inversion results with those of 3585 objects that are in common with the sample of objects successfully inverted by Ďurech & Hanuš (2023) gives a fraction of about 95% of identical spin period solutions.
The investigation presented in this paper gives an answer to one of the most urgent open questions, concerning the overall reliability of the photometric inversion algorithm developed for Gaia, which makes use of a very simple shape model. The choice of such a shape model is dictated by the need of minimising the execution time of the data processing, which is expected to be very time consuming, when dealing with data for tens of thousands objects at the end of the mission. The results of our analysis are quite encouraging, in spite of the limitations and uncertainties due to the adopted shape model. We should not neglect the fact that the analysis described in this paper concerns the treatment of data obtained far from the more favourable conditions we expect to have in the next Gaia data releases, when the number of photometric measurements per object will be of the order of 70 in the DR4 and twice that number in the very last release. In this respect, we remind again that in DR3 we process asteroids for which we have less than 40 sparse data points in about 75% of cases. There are only 16 asteroids for which we have a number ≥60 of photometric measurements which pass the rejection filter. We find that 15 end up with a correct period determination, in spite of the incomplete coverage of observing circumstances.
The reliability of the DR3 results presented in this paper is strengthened by the fact that the resulting directions of rotation for asteroid family members are in agreement with expectations based on the Yarkovsky effect, and supported also by the recent investigation by Ďurech & Hanuš (2023). A major results of our analysis of asteroid periods derived from inversion of DR3 data is the relatively high abundance of objects characterised by long rotation periods, well above some tens of hours. This fact can have consequences on our understanding of the collisional evolution of the objects, and of the efficiency of non-dynamical mechanisms of evolution, including the YORP effect (Pravec et al. 2005). A large abundance of slow rotators may indicate that the abundance of NPA rotating asteroids may be much greater than previously believed. These are important topics that will be more adequately discussed in forthcoming papers.
Acknowledgements
The authors thank the referee for his positive and constructing review. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular, the institutions participating in the Gaia Multilateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/Gaia. The Gaia archive website is https://archives.esac.esa.int/Gaia. PT and AC were supported by the Action National d'Observation Gaia of INSU (France). A.C. acknowledges support by the Agenzia Spaziale Italiana (ASI) through contracts I/037/08/0, I/058/10/0, 2014-025-R.0, 2014-025-R.1.2015, and 2018-24-HH.0 to the Italian Istituto Nazionale di Astrofisica (INAF), contract 2014-049-R.0/1/2 to INAF for the Space Science Data Centre (SSDC, formerly known as the ASI Science Data Center, ASDC), contracts I/008/10/0, 2013/030/I.0, 2013-030-I.0.1-2015, and 2016-17-I.0 to the Aerospace Logistics Technology Engineering Company (ALTEC S.p.A.), INAF, and the Italian Ministry of Education, University, and Research (Ministero dell'Istruzione, dell'Università e della Ricerca) through the Premiale project ‘MIning The Cosmos Big Data and Innovative Italian Technology for Frontier Astrophysics and Cosmology’ (MITiC). K.M.’s research was supported by the Research Council of Finland grants No. 336546 and No. 345115.
Appendix A Results of the inversion of DR3 SSO data
Example of results of photometric inversion of Gaia DR3 data for a few objects among those analysed in this paper.
Appendix B Period search with Gaia time sampling
B.1 Empirical facts
Figure 4 shows obvious patterns of discrete aliasing, something not fully surprising with the rather regular and repetitive sky scanning with Gaia. We have investigated this feature specifically for the sequencing found with Gaia, not strictly periodic but definitely with enough underlying regularities to generate aliasing in harmonic analysis. See also Holl et al. (2023) for a more general approach of the Gaia time series and the appearance of spurious periods in the context of binary systems. An alias is defined here as a spurious frequency seen in a time signal produced by a discrete sampling when the data points of a noisy signal of frequency v0 can be fitted with a better quality to a signal with a frequency, v, different from v0. Due to the noise, the power found in this spurious frequency v, can be larger than the power seen at the frequency v0. These features are particularly visible in Fig. B.1 for a pure noisy (S/N = 1.5) harmonic signal sampled with Gaia sequencing and then analysed to find its frequency. The main line of slope one from left to right corresponds to the 70% of the cases when the input frequency is recovered. All the other more or less straight lines are either undertones or aliases. The most conspicuous alias is the line of frequency, v, which is v + v0 = 12 cy/day. The presence of this integral value is surprising and in addition 12 cy/day is a frequency value entirely unknown to Gaia. Eventually all the details of this plot are understood with simulations and mathematical analysis.
 |
Fig. B.1 Retrieved frequencies of a simulated periodic signal sampled with Gaia repeated visits on different regions of the sky. The noise is at a S/N = 1.5 in this example. 70% of the solutions come out with the correct frequency and the remainder is divided between the 1/2 undertone and aliases. |
They depend only on the Gaia sampling coupled with the limited frequency range in which the signal is analysed.
As mentioned earlier the time sampling of the satellite is neither regular, nor random. It has some regularity, but far from being close to a uniform or periodic sampling. There are essentially two timescales:
- 1.
A short timescale lasting a few hours with sequences of passages in the two fields of view of the rotating satellite (PFOV and FFOV, standing for ‘preceding’ and ‘following’ field of view), repeated a few times consecutively, and exceptionally for several days in a row. This is driven by the 6-h spin period of the satellite and the angle of 106.5 deg between the two FOVs;
- 2.
A longer timescale between two epochs of visibility ranging from a few weeks to a few months. This is driven by the precession period of ~ 2 months and the annual solar motion.
 |
Fig. B.2 Retrieved frequencies of a simulated time signal sampled with the toy model. The noise is such that S/N = 1.5 in this example. 91% of the solutions come out with the correct frequency and the remainder is divided between the 1/2 undertone and aliases. |
Regarding the true signal, in the case of asteroids, the rotation period can range between a few hours for the fast rotators and up to several hundreds of hours for the very slow rotators. We have run extensive simulations to see the impact of the scanning parameters in the case of period determination of asteroids observed by Gaia. We extracted the real-time sampling for 30 000 objects and kept in the analysis only those having a number of observed transits ≥ 12. A periodic signal was generated over these samplings: S(t) = sin 2πvt, with v randomly chosen between 0 and 10 or 15 cycles per day. A random white noise was added, giving S/N values between 1 and 20. Then a period search was carried out using standard procedures, and exploring the frequency range from 0.01 to 15 cycles/day. An analysis of performance was carried out, as a function of the number of available transits, and of the true frequency of the signal.
The results of these experiments can be summarised as follows:
the main pattern in the Gaia period search as shown in Fig. B.1 comes from the short timescales linked to the spin period and the inter-FOV intervals;
the presence of the spurious and unexpected frequency of 12 cycles/day is well explained by this analysis;
by tuning the free parameters we were able to reproduce and account for the grid-like pattern so conspicuous in the data analysis.
Our toy-model imitates the Gaia sequencing by dividing the spin period P into two adjustable fractions of αP and (1 − α)P, where 0 < α < 0.5, or equivalently for Gaia adjusting the basic angle or the time span between the two FOVs within the spin period. This flexibility proved essential for the complete understanding of the alias intricate pattern. For Gaia one has α = 106.5/360 = 0.29583 and P = 6 h. Therefore the normal Gaia sampling from PFOV to FFOV, then to PFOV after 6h, and this being repeated after long gaps of several weeks, is replaced by much shorter sequences of continuous repetitions of PFOV-FFOV-PFOV without long gaps. However the number of samples is constrained to remain in agreement with that found in Gaia DR3. This is a different instrument, but this simplified version retains the important sampling structure over the short timescale.
The main result in Fig. B.2 shows the same set as before but sampled with the toy-model to emphasise the role played by the short timescale. The patterns seen in Fig. B.1 are still there but stand out much more neatly without their fuzzy margins. This brings the conviction that the alias pattern is primarily produced by the timescales linked to the spin period of six hours and not to the longer modulation of several weeks. Understanding this pattern with the simplified sampling provides also the answers for the patterns seen with the true Gaia sampling. In particular the main alias appears at frequency, v, whereby νtrue + νfitted ≈ 12cy/d, with this puzzling whole number. Changing the period from 6 hours to 5 h or 7 h has shown that the integral number of 12 cy/d, is contingent and closely related to the 6-h period and not a sort of magic whole number.
B.2 Mathematical modelling
Aliases are easily understood when the sampling is periodical and this topic is dealt with in textbooks on signal processing. Briefly stated we consider a periodic sampling with interval τ between successive samples, or equivalently the sampling rate is η = 1/τ. The Nyquist frequency is vN = η/2 = 1/(2τ). Then, for a signal with true frequency of 0 < vtrue < vN two infinite families of aliases may show up as
 (B.1)
(B.1)
 (B.2)
(B.2)
forming a regular pattern of straight lines with slopes ±1 in the plane (vtrue, vfitted). Fundamentally the samplings at interval τ of these signals are all identical and none of these signals can be unambiguously recovered from its sample values. The direct problem (sample values) has a single solution, the inverse problem (the original signal from its sampling) has infinitely many solutions.
In the case of irregular sampling, meaning non-periodic, the situation is much more complicated. If for a mathematician a signal is periodic of not, for the applied scientists, a signal can depart gradually from a pure periodic one and so the pattern of aliases will slowly depart from perfect replicas. Sampling with our toy model is clearly not purely periodic, but this is the super-imposition of two periodic samplings shifted by the interval αP. We consider the case where
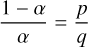 (B.3)
(B.3)
where p and q are integers and the fraction p/q is in its simplest form. Therefore there is an interval τ in [0,1] such that α = qτ and 1 − α = pτ and then
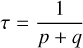 (B.5)
(B.5)
The regular sampling with alternating intervals of lengths α, 1 − α is in fact an under-sampling of a periodic sampling with a smaller interval of length τ, since both α and 1 − α are multiple of τ. As a consequence, there are the two families of aliases,
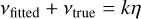 (B.6)
(B.6)
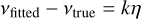 (B.7)
(B.7)
with η = 1/τ = p + q and k positive or negative integers. Scaling with the period, P, in hours, this is equivalent to η = 24/(Pτ) = 24(p + q)/P in cy/day. It could be very large if p + q >> 1, and not visible in practice if the frequency range of the fit is below this number. However, good rational approximations are often obtained with rather small integers and p + q is not necessarily large.
 |
Fig. B.3 Same conditions as in Fig. B.2 with frequencies searched up to 40 cy/d. The effect of the weak rational approximations has vanished (almost no alias at 12 and 16 cy/d) replaced by the stronger approximations and their aliases at 28 and 40 cy/d. |
Aliases arising from the best rational approximations of the Gaia duty cycle between the PFOV and the FFOV.
With the real Gaia data one has α = 0.29583 apparently not related to a simple rational number. Certainly it has two very poor approximations like 1/4,1/3 but also some not so bad con-vergents like 2/7, 3/10, 5/17 with relatively small p, q. Applying (B.6) with η = 4(p + q) cy/d, we have the possible aliases at reachable frequencies, They are given in Table B.1 for the relevant rational approximations. The first three are for the two weak approximations and show up in the diagram only when the frequency search is limited in range to vfitted < 20 cy/d, as illustrated in Fig. B.3. The aliases at 12 and 16 cy/d associated with the weak rational approximations have disappeared and are replaced by the strong aliases at 28 and 40 cy/day coming from the stronger rational approximations of the Gaia fraction of the spin period spent between the PFOV and FFOV. They captured many of the noisy signals because the power at these frequencies happens to be larger than the power at the simulated frequencies. The remaining fuzzy lines with slopes ±1/2 are the aliases of the undertone.
Comparing this pattern to the data in Fig. 4, it is clear that we have reproduced most of the features, but with a factor of 2 in the frequency values. This can be accounted for by the use of the frequency of the photometric signal in this appendix while the rotation period is used elsewhere and also in the data model. For a triaxial ellipsoid, the period seen in the light curves is half the rotation period, or its frequency double of the rotation frequency. When provision is made for this difference we see that all the lines are explained by the Gaia scan parameters related to the 6h spin period and well understood.
References
- Belskaya, I. N., & Shevchenko, V. G. 2000, Icarus, 147, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Brož, M., et al. 2001. Science, 294, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Hestroffer, D., Tanga, P., et al. 2009, A&A, 506, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cellino, A., Ammannito, E., Magni, G., et al. 2016, MNRAS, 456, 248 [Google Scholar]
- Cellino, A., Hestroffer, D., Lu, X.-P., et al. 2019, A&A, 631, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dell’Oro, A., Paolicchi, P., Cellino, A., et al. 2001, Icarus, 153, 52 [CrossRef] [Google Scholar]
- Ďurech, J., & Hanuš, J. 2023, A&A, 675, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.), 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Brož, M., Durech, J., et al. 2013, A&A, 559, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holl, B., Fabricius, C., Portell, J., et al. 2023, A&A, 674, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Durech, J., Alí-Lagoa, G., et al. 2021, A&A, 654, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marciniak, A., Durech, J., Choukroun, A., et al. 2023, A&A, 679, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martikainen, J., Muinonen, K., Penttilä, A., et al. 2021, A&A, 649, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milani, A., Cellino, A., Kneževic, Ź., et al. 2014, Icarus, 239, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., Kneževic, Ź., Spoto, F., et al. 2017, Icarus 288, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Muinonen, K., Uvarova, E., Martikainen, J., et al. 2022, Front. Astron. Space Sci., 9, 821125 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Szakáts, R., Kiss, et al. 2020, ApJS, 247, 26 [CrossRef] [Google Scholar]
- Pravec, P., & Harris, A.W. 2000, Icarus, 148, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., & Scheirich, P. 2005, Icarus 173, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A. W., Vokrouhlický, D., et al. 2008, Icarus, 197, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Santana-Ros, T., Bartczac, P., Michalowski, T., et al. 2015, MNRAS, 450, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Spoto, F., Milani, A., & Kneževic, Ź. 2015, Icarus 257, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Tanga, P., Pauwels, T., Mignard, F., et al. 2023, A&A, 674, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Źappalá, V., Bendjoya, Ph., Cellino, A., et al. 2000, Icarus, 145, 4 [CrossRef] [Google Scholar]
This is true even considering the recent analysis of Gaia DR3 data performed by Ďurech & Hanuš (2023) (see Sect. 3.2).
For some more detailed comparisons of our results with those obtained by Ďurech & Hanuš (2023), see Sect. 3.2.
DR4 will cover 66 months (to be compared with 36 months in DR3). This is larger by a factor of 1.8; we also expect to collect data by a factor of 2.2 in terms of number of objects. Therefore, we can expect an increase by a factor of 4 as far as DR4 is concerned. This will increase up to a factor of about 8 by the end of the extended mission.
These families and their members can be found at the web site https://newton.spacedys.com/astdys/index.php?pc=5
All Tables
Example of results of photometric inversion of Gaia DR3 data for a few objects among those analysed in this paper.
Aliases arising from the best rational approximations of the Gaia duty cycle between the PFOV and the FFOV.
All Figures
 |
Fig. 1 Distribution of the rotational frequency for the sample of 22 815 Solar System objects (SSOs) having a minimum of 25 recorded transits in DR3. |
| In the text | |
 |
Fig. 2 Distribution histograms of LCDB rotation periods for objects in the DR3 database with at least 25 measured transits and present in the LCDB with a period quality code 2 or 3. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but for all the objects in the DR3 database that are present in the LCDB with a period quality code of ≥2. |
| In the text | |
 |
Fig. 4 Comparison between rotation frequencies computed for asteroids included in the DR3 catalogue and the corresponding frequencies listed for the same objects in the LCDB. Left panel: all objects for which the LCDB period quality code is 2. Right panel: the same, but for objects having LCDB quality code of 3. |
| In the text | |
 |
Fig. 5 Differences (in absolute values) between our DR3-derived rotation period and the corresponding LCDB rotation period, normalised to the LCDB period. Left panel: all objects for which the LCDB period quality code is equal to 2. Right panel: same, but for objects having LCDB quality code of 3. |
| In the text | |
 |
Fig. 6 Distribution of the solution residuals for the objects whose rotation period solution is in disagreement with LCDB for objects having QC = 3 (left). Same details as in the left panel, but for the distribution of the b/a axial ratio (right). |
| In the text | |
 |
Fig. 7 Same as in Fig. 6, but in this case the distribution of the slope of the phase-magnitude relation for the objects whose rotation period solution is in disagreement with LCDB for objects having QC = 3 (left). The distribution of the ecliptic latitude of the pole is on the right. |
| In the text | |
 |
Fig. 8 Same as Fig. 1, but here only DR3 inversion solutions passing the filter discussed in the text are displayed. This means a total of 8670 objects, for which we can be confident that 84% of them should be correct. |
| In the text | |
 |
Fig. 9 Same as in the right panel of Fig. 4, but plotting only inversion solutions passing the rejection filter discussed in the text. |
| In the text | |
 |
Fig. 10 Plot of proper eccentricity vs. proper semi-major axis (left) for the members of asteroid dynamical families taken from the list of Milani et al. (2014), also available on the AstDyS web site. The sub-sample of family members whose Gaia DR3 photometric data pass the solution rejection filter described in this paper is displayed using a colour code to indicate their resulting sense of rotation. Right: the same, but for sine of proper inclination vs. proper semi-major axis. In these plots, red points indicate family members displaying retrograde sense of rotation, while blue symbols are used for objects displaying prograde rotation, according to the results of photometric inversion. Black symbols are used for family members for which we have not obtained a photometric inversion. |
| In the text | |
 |
Fig. 11 Rotational frequency vs. diameter for the sample of asteroids having photometric inversion solutions passing the rejection filter described in Sect. 3.1 (8670 objects). Red symbols are used to indicate asteroid family members according to Milani et al. (2014). They are displayed in red just to emphasise the large contribution of asteroid dynamical families in our inventory of objects having sizes smaller than about 10 km, including many slow-rotators. |
| In the text | |
 |
Fig. B.1 Retrieved frequencies of a simulated periodic signal sampled with Gaia repeated visits on different regions of the sky. The noise is at a S/N = 1.5 in this example. 70% of the solutions come out with the correct frequency and the remainder is divided between the 1/2 undertone and aliases. |
| In the text | |
 |
Fig. B.2 Retrieved frequencies of a simulated time signal sampled with the toy model. The noise is such that S/N = 1.5 in this example. 91% of the solutions come out with the correct frequency and the remainder is divided between the 1/2 undertone and aliases. |
| In the text | |
 |
Fig. B.3 Same conditions as in Fig. B.2 with frequencies searched up to 40 cy/d. The effect of the weak rational approximations has vanished (almost no alias at 12 and 16 cy/d) replaced by the stronger approximations and their aliases at 28 and 40 cy/d. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.