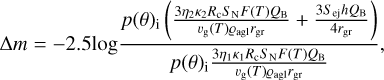| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A248 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202449573 | |
| Published online | 18 June 2024 | |
Determination of bolometric albedo based on spectroscopic measurements for selected dust analogues and its impact on the change of cometary brightness during its outburst
1
University of Rzeszów, College of Natural Sciences, Institute of Physics,
Pigonia 1 Street,
35-310
Rzeszów,
Poland
e-mail: mwesolowski@ur.edu.pl
2
University of Rzeszów, College of Natural Sciences, Institute of Materials Science and Engineering,
Pigonia 1 Street,
35-310
Rzeszów,
Poland
Received:
12
February
2024
Accepted:
29
April
2024
The paper presents the results of spectroscopic measurements for selected dust analogues, based on which change in cometary brightness was determined. In the first part of the article, we present the results of laboratory measurements of hemispherical albedo for selected dust analogues using a Cary 5000 spectrometer with an integrating sphere. In the case of this system and the tested samples, the obtained hemispherical albedo values ranged from 0.35 ± 0.07% to 41.58 ± 0.07%. The obtained measurement results were used to determine the bolometric albedo and geometric albedo. For the analogue consisting of charcoal, the Bond albedo was equal to AB(charcoal) = 2.15%, whereas the geometric albedo was equal to pv(charcoal) = 6.76%. The second part of the paper presents an analytical method allowing us to calculate the amplitude of the change of cometary brightness during the outburst. The calculations show that the upper value of the amplitude is 6.5 magnitudes, which is within the medium range amplitude of the outburst. Calculations have shown that as the bolometric albedo increases for a given agglomerate porosity, the temperature decreases, which determines a smaller sublimation flux, which translates into a larger change in the cometary brightness.
Key words: comets: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The cometary activity is most commonly associated with the emission of dust that forms a coma and tail. The process of emission of matter can occur as a result of quiet sublimation, through jets, and during the outburst of a comet. Sublimation of cometary ice plays a key role in describing these processes. As a result of these processes, the cometary matter is emitted into the coma. The influence of this matter significantly contributes to increasing the total scattering cross-section, the main parameter of which is the mass ejected or the surface that has been destroyed (Wesołowski 2021a, 2022). In addition, the increase in this cross-section is associated with a more effective scattering of sunlight, which translates into a change in the cometary brightness that is its outburst (Gronkowski & Wesołowski 2016; Saki et al. 2021). A cometary outburst is commonly understood as a sudden unexpected increase in brightness by at least one magnitude. Analyzing cometary outbursts, we can notice that they occur at different heliocentric distances and are characterized by different outburst amplitude values. Let us add that the average value of the change in the cometary brightness as a result of the outburst oscillates around 3 magnitudes. It is worth noting that sporadically there are outbursts whose amplitude is much larger (for example the outburst of comet 17P/Holmes in 2007; Montalto et al. 2008; Moreno et al. 2008, the outburst of comet 174P/Echechlus in 2005; Choi & Weissman 2006; Wesołowski 2020a, and some outbursts of comet 29P/Schwassmann-Wachmann; Miles 2016a,b). In addition to outbursts with a relatively large amplitude, mini-outbursts occur much more often that is, those whose amplitude is less than one magnitude. A direct example of these is almost all the outbursts of comet 67P/Churyumov-Gerasimenko (hereafter 67P) that were recorded during the Rosetta mission (Vincent et al. 2016).
Despite many years of research, the phenomenon of cometary outbursts remains one of the incompletely explained issues related to modern astrophysics. Many different mechanisms have been proposed in the literature to address this problem. The following mechanisms deserve special attention: crystallization of amorphous ice (Prialnik & Bar-Nun 1992), a model of cometary cavities, which is associated with the destruction of the upper layer (crust) as a result of the increase in pressure in the subsurface layers (Ipatov 2011; Gronkowski & Wesołowski 2015; Vincent et al. 2015), formation of a landslide that can transform into a local avalanche (Steckloff & Melosh 2016; Wesołowski et al. 2020b), cliff collapse (Pajola et al. 2017). In the context of a cometary outburst, it follows from almost all mechanisms of the phenomenon that the key parameters are the mass ejected and the active surface both in the phase of quiet sublimation (η1) and during the outburst (η2). In particular, the last two parameters are difficult to estimate in the general case because they are assessed visually. As an example, we consider the two following cases. Observations of comet 1P/Halley during its last approach to the Sun in 1986 showed that the size of the total active surface was 36 km2, which translates to 10% of the total surface area of the nucleus (Keller et al. 1987). The rest of the surface seemed to be covered with a so-called crust (Gundlach et al. 2015) which made sublimation difficult. Thanks to the Rosetta mission and the EPOXI mission, it was shown that most of the illuminated surfaces, including those passing into the terminator, were sublimating. In the case of comet 67P, sublimation of water ice occurred from those parts of the nucleus that were illuminated by the Sun (Gicquel et al. 2016). In the case of shadowed areas, CO2 ice was responsible for the sublimation activity (Keller et al. 2017). The detailed morphology of the presence of bright regions associated with exposed water ice on the surface of comet 67P nucleus was recently reported by Fornasier et al. (2023). Their analysis shows that only a small fraction of the total surface of the nucleus are bright areas, which confirms that the surface of comet 67P is dominated by refractory dark areas.
When determining the amplitude of the cometary outburst, it should be noted that one of the key parameters is to determine the fraction of the surface of the nucleus that was actively sublimating. The level of surface activity is related to the location of the comet in the solar system (in the case of gravitational comets associated with the Sun), the structure of the mantle (crust) covering the nucleus, and the sublimation activity which is controlled by the given cometary ice. In addition to these three main factors directly related to the comet, the key issue is also the distance from the nucleus at which the observations were made. Let us recall that the observations of comet 1P/Halley were related only to the passage of space probes, for example, Vega 1 and Vega 2, Giotto at a distance of several hundred kilometers from its nucleus. The Vega 1 and Vega 2 space probes approached Comet 1P/Halley on March 6 and 9, 1986, respectively.The research apparatus consisting of 14 instruments collected data on the comet’s optical characteristics, dust emission, and neutral gas, plasma and electromagnetic field environment (Sagdeev et al. 1986). Thanks to the Giotto spacecraft, the first results of imaging the nucleus of comet 1P/Halley were obtained using the Halley Multicolor Camera (HMC) (Keller et al. 1986).
In the case of comet 67P, in addition to observations at close range, the Philae lander made the first-ever landing on the surface of a comet. Thanks to the Rosetta space mission and the equipment used, they were able to observe the development of cometary activity both in the phase of quiet sublimation (t1) and during outbursts (t2). In addition, thanks to the very accurate imaging of the surface of the comet 67P nucleus, they were able to observe many interesting structures, for example, dune fields, landslides, and pits both young (that is active) and old (that is inactive). Taking into account the mentioned two cases of the comet, it seems reasonable that in the numerical calculations, a wide range of the active surface can be used when determining the amplitude of the change in the brightness of the comet. Hopefully, future cometary missions will contribute to a more accurate estimation of η1 parameter.
This paper aims to present the results of hemispherical albedo measurements for selected dust analogues, which were made using a Cary 5000 spectrometer with an integrating sphere. In laboratory tests, sand, ash, and charcoal were used as dust analogues, which after mixing will create three subsequent samples. Recall that sand is commonly used as an analogue of dust in laboratory tests (Stöffler et al. 1991; Rotundi et al. 2002; Feller et al. 2022; Kossacki et al. 2022a,b). Let us note that two analogues used (ash and charcoal) were intended to darken the tested sample. Thanks to this approach, our samples, at least visually, had a color similar to the color of the surface of comet 67P. Then, using the measurement results, a new numerical model was developed, based on which the amplitude of the cometary outburst.
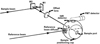 |
Fig. 1 Optical design of the DRA system. The diagram is available in the spectrometer manual. The measurement process can be described in five steps: 1. The sample beam hits mirror M1 and is then reflected to M2. 2. The beam travels through the lens and is focused into the transmission port, and onto the reflectance port. 3. The reflected beam is diffused throughout the sphere before being measured by the detector. 4. The reference beam enters the sphere directly through the reference port and is scattering. 5. The hemisphere albedo was then measured. |
2 Measurement of hemispherical albedo
2.1 Measuring apparatus
A Cary 5000 double-beam spectrometer was used for hemispherical albedo measurements. The light sources in this spectrometer are a halogen-tungsten lamp and a deuterium lamp (UV). The spectral range for the deuterium lamp is 175–375 nm, while for the halogen lamp, the range is in the range from 375 to 3300 nm. The light beam regulated by the slit falls on the Lit-trow monochromator (two diffraction gratings 1200 lines/mm in the Uv-Vis range). The monochromator is controlled by a stepper motor whose function is to separate the monochromatic light beam from the lamp light. The stepper motor also changes the position of the monochromator gratings, which results in a change in the wavelength of monochromatic light. Then a beam of monochromatic light with a wavelength changing over time falls on the sample. Before measurements were taken, the spectrometer was calibrated using a reference reflection spectrum to establish a baseline that is a line representing the signal level when the sample is not absorbing and transmitting light and only reflects the light) based on the Labsphere certified reflectance standard USRS-99-020 AS-01159-60. The zero line was calibrated against a quartz window. Let us add that calibration of the zero line (zero correction) against quartz eliminates the error resulting from examining the sample through a quartz window. The purpose of zeroing is to balance both the reference beam and the sample beam. By adjusting to zero, the instrument readings reflect the absence of a sample. We use the DRA system (Diffuse Reflection Accessory, see Fig. 1) to perform the measurements described in this paper.
The basic configuration of the Cary 5000 spectrophotometer used to determine hemispherical albedo is an integrating sphere. In this configuration, a light ray of a certain wavelength is incident perpendicularly on the sample placed on the front surface outside the integrating sphere. The sample scatters the light into the integrating sphere, where, as a result of multiple reflections from the surface of the sphere, it is focused into a beam of light falling on the detector. The measuring range of the spectrometer together with the integrating sphere is from 200 to 2500 nm. The measuring accuracy of the spectrometer based on the data provided by the manufacturer for the wavelength in the Uv-Vis range is Δλ = ± 0.08 nm, while in the case of the hemispherical albedo, the accuracy is ∆Ah = 0.07%. Each spectrum consists of over 2300 measurement points.
 |
Fig. 2 Scanning electron microscope image showing sand particles. The individual parameters mean: HV is the accelerating voltage the value of which was 7 kV (it is the highest possible accelerating voltage that does not cause contamination for a given sample), mag is the image magnification, HFW is the horizontal field width, WD is the distance between the lens and the sample (working distance), det ETD is the ETD detector recording the secondary electron signal, pressure in the chamber, mode SE is the operating mode, using a detector recording secondary electrons. |
2.2 Preparation of samples for study
Three samples of dust analogues were used to carry out laboratory tests. The basic component of each sample was sand taken from a sand mine whose geographic location is 50°07′08.7″N 21°45′32.8″E. Moreover, this area is exploited commercially1. The sand sample was taken from a depth of about 50 cm to avoid contamination of the surface layer. The material was then dried and dry sieved through six standardization sieves with different mesh diameters: 1.5, 0.49, 0.43, 0.385, 0.30, and 0.06 mm. To make the radius of the sand grains close to the real size of the particles present in the coma during the outburst, sand grains with the smallest diameter were used in laboratory tests. This means that we were dealing with a fraction whose grain diameter met the following relationship: 0 < dgr < 0.06 × 10−3 m. Two types of organic materials (ash and charcoal) were used as admixtures, for which the analogous fractionation procedure was repeated. The charcoal used in the research came from commercial sources2. Beech wood, which was subjected to the pyrolysis process, was used to produce charcoal. This process is also called dry distillation and consists of the thermal decomposition of materials, most often of organic origin, occurring under the influence of high temperature and carried out in anaerobic conditions. On the other hand, the ash that was used in the research was created as a result of burning beech wood (this process was supervised by us). The main purpose of using admixtures was to obscure the tested sample (Haack et al. 2021; Lethuillier et al. 2022). For the considered analogs (for each one separately), microscopic photos and an analysis of the chemical composition were made using a Scanning Electron Microscope Quanta 3D 200i, which is equipped with the EDS (Energy Dispersive Spectroscopy) system. The EDS detector enables qualitative and quantitative analysis of the chemical composition of the tested area of the sample. The value of the radiation energy allows the identification of individual elements present in the sample, while the intensity or height of the peaks is related to the quantitative analysis. Since the tested samples resembled powdered material, a special carbon tape was used to secure the vacuum pump, which is used to better fix the sample on the microscope stage. In addition, the tape provided better electrical conductivity, and the carbon contained in it allowed the sample to be charged. Thanks to this, the effect of electron accumulation on the surface of the sample placed in a vacuum is eliminated. The use of carbon tape ensures the high quality of the images obtained. Photos of individual dust analogues are presented in Figs. 2–4, and the analysis of the chemical composition for these analogues is presented in Table 1.
Using three dust analogs (sand, ash, and charcoal) three samples were prepared which resulted from their mixing. For this purpose, the mass method was used, and the process of sample preparation consisted in precisely weighing the same mass for each of the analogs using a laboratory scale with a measurement accuracy of ∆m = 0.001 g. Then, the individual components of the samples were combined and mixed by repeated shaking. Note that due to the density of the analogs, the volume fraction of both ash and charcoal was much higher than that of sand. As a result, the following samples were obtained:
sample A is a mixture of sand and ash in a mass ratio of 1:1,
sample B is sand with ash and charcoal in a mass ratio of 1:1:1,
sample C is sand and charcoal in a mass ratio 1:1.
 |
Fig. 3 Scanning electron microscope image showing ash particles. |
 |
Fig. 4 Scanning electron microscope image showing charcoal particles. |
 |
Fig. 5 Hemispherical albedo distribution in a function of wavelength in the range from 200 to 2500 nm. An integrating sphere was used in these measurements. The presented measurement results concern three analogues (sand, ash, charcoal) that were examined in this paper. |
2.3 Research results and their analysis
Using a Cary 5000 spectrometer and an integrating sphere, the spectrum of the hemispherical albedo was determined as a function of the wavelength of the incident light in the range from 200 to 2500 nm. In the first step, the spectrum of hemispherical albedo was determined for three pure analogues (sand, ash, charcoal–Fig. 5). In the second step, the spectrum of hemispherical albedo was determined for the three samples considered in this paper (sample A, sample B and sample C–Fig. 6).
Based on the spectroscopic measurements performed, we can formulate the following conclusions:
In the case of pure analogues, especially sand and ash, we observe a significant increase in hemispherical albedo with wavelength in the studied spectral range. However, in the case of charcoal, this increase is insignificant and starts above 1200 nm (see Fig. 5). In the case of sand grains, the hemispherical albedo range was from 3.57 to 41.58%, for ashes from 4.89 to 35.36%, and in the case of charcoal, the hemispherical albedo range was from 0.35 to 4.08%. Analyzing the obtained result, we can conclude that the main determinant in the case of hemispherical albedo measurement is the observed color of the sample, which translates into its reflectivity. The main factors influencing the photometric properties of a sample are its color, wavelength range and the angle of incidence of light on the sample, which in the case of our system is 90 degrees. This means that the visually brighter the sample, the greater its hemispherical albedo.
In the case of sand and ash, the greatest dynamics of the hemispherical albedo increase as a function of wavelength is observed in the visible region, while in the infrared the dynamics of the hemispherical albedo increase is smaller. A similar relationship also occurs in the case of the three tested mixtures.
For sand and ash, there is a clear dependence of the hemispherical albedo on the wavelength, while for charcoal this dependence is negligible. The inclination of individual spectral lines is different and is related to the visual color of a given analogue in reflected scattered light: the sand sample was yellow, the ash was gray, and the charcoal was black.
Comparing the hemispherical albedo values at a wavelength of λ = 2500 nm, it can be seen that sand is more than 10 times more reflective than charcoal, and ash is more than 8 times more reflective.
In the case of sand, due to the much higher hemispherical albedo compared to charcoal, we observe clear extremes in the spectral distribution near the wavelengths: 750, 950, 1450, 1900 and 2200 nm. Analyzing the hemispherical albedo in the case of ash, one can also notice the occurrence of several local extremes, which occur at slightly different wavelengths than in the case of sand. The occurrence of these local extremes is most likely related to the chemical composition of the tested samples.
In the case of three mixtures (sample A, sample B and sample C), we can observe an increasing trend of hemispherical albedo in the studied spectral range. Even in sample C, a composite of sand and charcoal in a 1:1 mass ratio, a more pronounced upward trend in the hemispherical albedo is visible in virtually the entire spectral range.
For two samples A and B, we can notice a clear decrease in hemispherical albedo in comparison to the sand, which is related to the admixture of ash in the case of sample A or ash and charcoal in the case of sample B. This result clearly shows that for darker materials their hemispherical albedo is lower. However, in the case of sample C, due to the addition of sand to the charcoal, we obtained an increase in hemispherical albedo due to its visual brightening in comparison to the charcoal. For sample A, the hemispherical albedo range was from 2.41 to 36.23%, for sample B from 4.34 to 12.26%, and for sample C, the hemispheric albedo range was from 4.04 to 6.99%. Example comparison of hemispherical albedo for sand and sample A is shown in Fig. 7, for ash and sample B is shown in Fig. 8, and for charcoal and sample C is shown in Fig. 9.
Moreover, the hemispherical albedo values obtained for the tested mixtures are a consequence of significant differences in their bulk density (see Table 2). Moreover, the volume fraction of sand in individual samples was much smaller than in the case of the admixtures considered (ash, charcoal).
By comparing the hemispherical albedo between the individual materials tested and the samples obtained from them, we can notice that the smallest differences occur in the case of sand and sample A (ΔAh = 6.22% for λ = 2500 nm), and the largest in the case of ash and sample B (ΔAh = 23.10% for λ = 2500 nm). Moreover, in the case of three mixtures (sample A, sample B and sample C) there are also visible local extremes that occur near the same wavelengths as in the case of pure materials.
The slope of a given spectrum depends on the visual color of the sample being examined. The darker the color of a given sample, the smaller the angle of inclination of the spectrum relative to the wavelength axis, which is a consequence of the hemispherical albedo of the tested sample.
 |
Fig. 6 Hemispherical albedo distribution as a function of wavelength in the range from 200 to 2500 nm for the three samples (sample A, sample B and sample C) considered in this paper. As in the case of pure analogues, an integrating sphere was used for measurements. |
2.4 Analysis of reflectivity results based on measurements from the Rosetta mission
During the Rosetta mission, the equipment on board the probe made it possible to study, among other things, the reflectances and albedoes of real irregular dust-ice particles. These measurements were performed using the following equipment: COSIMA - Cometary Secondary Ion Mass Analyzer (Langevin et al. 2017, 2020), OSIRIS - Optical, Spectroscopic, and Infrared Remote Imaging System (Fornasier et al. 2015; Feller et al. 2016; Quirico et al. 2016; Hasselmann et al. 2017) and VIRTIS - Visible and Infrared Thermal Spectrometer (Ciarniello et al. 2015; Bockelée-Morvan et al. 2019; Langevin et al. 2020). A detailed analysis of the results obtained regarding the above measurements is presented in the paper (Wesołowski et al. 2024). It should be noted that in the case of COSIMA and VIRTIS measurements, the obtained values are larger than the geometric albedo of comet 67P (AN–67P = 6.5+0.2% at 649 nm (Fornasier et al. 2015), which may suggest that these particles contained a more reflective material, such as sand. Moreover, the geometric albedo was with local variations of up to 16% in the Hapi region (Fornasier et al. 2015). By comparing the obtained hemispherical albedo values with the VISIR reflectance spectrum from nineteen regions defined on the surface of comet 67P, we can see quantitative and qualitative agreement with our spectra. In particular, this applies to two samples B and C, which were characterized by a low hemispherical albedo (which is consistent with a feature typical of small bodies originally orbiting in the Solar System) compared to sample A. Moreover, in the case of our samples in the range from 200 to 1000 nm, we can observe a dynamic increase in the hemispherical albedo compared to the rest of the spectrum for which the dynamics height is smaller. Note that the same growth dynamics were confirmed for the actual spectrum of comet 67P for the same spectral range (Filacchione et al. 2016).
Let us note that processes such as ice sublimation and the influence of solar wind radiation on the one hand drive the activity of the comet, and on the other hand, make direct observations of the nucleus difficult. In particular, the sublimation of cometary ice is responsible for the initiation of processes that contribute to the morphological changes visible on the surface of comets, such as landslides, avalanches, dust migrations and the formation of dunes (Kossacki et al. 2022a,b; Wesołowski et al. 2020b; Wesołowski 2023a). All this means that the actual results of albedo measurements during a given orbital period may differ even for the same comet.
 |
Fig. 7 Comparison of hemispherical albedo in the case of sand and sample A in the studied spectral range. |
 |
Fig. 8 Comparison of hemispherical albedo in the case of ash and sample B in the studied spectral range. |
 |
Fig. 9 Comparison of hemispherical albedo in the case of charcoal and sample C in the studied spectral range. |
Most important values of basic parameters that were used in numerical simulations.
2.5 Geometric albedo
The basic photometric term commonly used in astronomy is geometric albedo (physical albedo), which is defined as the ratio of the brightness of a body to the brightness of a perfect Lambert disk with the same radius and the same distance as the body, but illuminated and observed perpendicularly.
Using the results of hemispherical albedo measurements, we can calculate the geometric albedo value in two steps. In the first step, we need to calculate the Bond albedo (bolometric albedo), which accounts for all of the light scattered from a body at all wavelengths and all phase angles, it is a necessary quantity for determining how much energy a body absorbs. Then we can express the Bond albedo using Eq. (1):
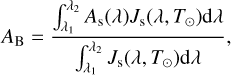 (1)
(1)
where As(λ) is the spectral spherical albedo, Js(λ, T⊙) is approximately the Planck function for a black body at a temperature of 5770 K. The range of wavelengths in which the hemispherical albedo measurement was performed that is the range from λ1 = 200 nm to λ2 = 2500 nm, was adopted as the integration limits. It should be noted that our experimental setup does not allow direct measurement of the spherical albedo but the measured hemispherical albedo (Ah(λ)) can be used as an upper limit for the spherical albedo. In the second step, we used the relationship between the Bond albedo and the geometric albedo, which we can express as:
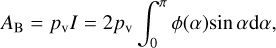 (2)
(2)
where pv is the geometric albedo, ϕ(α) is the ratio of apparent brightness at the phase angle α to the brightness at α = 0, or in short, the phase function. The value of the phase integral (I) in Eq. (2) is equal to I = 0.318. Examples of geometric albedo values for the two most representative samples dominated by charcoal (sample C and the sample consisting of charcoal) are presented in Table 2.
3 The cometary outburst
3.1 The energy balance
When considering the outburst of a comet, it should be emphasized that the key thermodynamic parameter is the surface temperature. In particular, this applies to those outburst mechanisms that are closely related to the cometary nucleus (examples of such mechanisms are listed in the introduction to this paper). Due to the irregular surface of the cometary nucleus, uneven heating, cooling and thermal conductivity to the interior of the nucleus must be taken into account in the energy balance. It is worth noting that the temperature on the surface of the cometary nucleus can be determined based on direct observation (Tosi et al. 2019), or by numerically solving the energy balance equation, which can be expressed as (Wesołowski & Potera 2024):
![$\eqalign{ & {\left( {{{{r_ \odot }} \over {{r_{\rm{E}}}}}} \right)^2}\int_0^{2\pi } {\int_0^{{\pi \over 2}} {\int_{{\lambda _1}}^{{\lambda _2}} {\left[ {{J_{\rm{s}}}\left( {\lambda ,{T_ \odot }} \right)\left( {1 - {A_{\rm{h}}}(\lambda )} \right)} \right]} } } \sin \theta \cos \theta {\rm{d}}\lambda {\rm{d}}\theta {\rm{d}}\phi {{\cos \zeta } \over {r_{\rm{h}}^2}} \cr & & = \sigma {T^4} + HF(T) + \lambda (T)\nabla T{\rm{. }} \cr} $](/articles/aa/full_html/2024/06/aa49573-24/aa49573-24-eq3.png) (3)
(3)
In Eq. (3) the following notation is adopted: r⊙ is the radius of the sun photosphere (r⊙ = 695 700 km), rE is the distance of the Earth from the center of the Sun (rE ≈ 1.496 × 108 km), θ and ϕ can be expressed using spherical coordinates. Moreover, the remaining symbols used in Eq. (3) mean: rh is the heliocentric distance of a comet, ζ is the solar zenithal angle (the angle Sun-comet-Earth, also known as the phase angle), ϵ is the infrared emissivity of the nucleus, σ is the Stefan Boltzmann constant, H is the latent heat of sublimation, F(T) is the mass flux of subliming vapor, λ(T) is the heat conductivity inside the nucleus, and VT is the average gradient of the temperature at the equilibrium, respectively. To solve the Eq. (3), we must take into account the dependence describing the sublimation flux F(T) (Kossacki et al. 2022a):
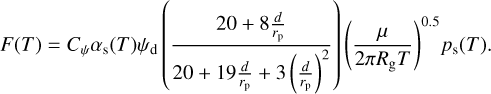 (4)
(4)
In Eq. (4), the individual symbols mean: Cψ is the parametric function (Cψ = (1.73 − 5.16ψ + 3.96ψ2)), ψ is the porosity of the agglomerates, ψd is the porosity of the dust layer, d is the thickness of layer, rp is the radius of pores, µ is the molar mass of water ice, Rg is the universal gas constant, and ps (T) is the pressure of the phase equilibrium (ps is calculated using the simple classical formulation:
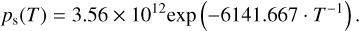 (5)
(5)
Let us add that Eq. (4) which was used to calculate the water ice sublimation flux was tested only on samples that did not contain agglomerates with a radius larger than 1 cm. In addition, in Eq. (4) there is an important parameter that determines the sublimation coefficient αs(T) which depends on the temperature. The value of this coefficient was calculated based on the formula specified by (Kossacki et al. 2022b):
![${\alpha _s}(T) = \left( {1 - {1 \over {{a_1}}}} \right) + {1 \over {{a_1}}}\tanh \left[ { - {a_3}\tan \left( {\pi {{T - {a_2}} \over {273 - {a_2}}} - {\pi \over 2}} \right)} \right],$](/articles/aa/full_html/2024/06/aa49573-24/aa49573-24-eq6.png) (6)
(6)
where α1 = 2.36±0.21, a2 = 139.34±1.94, and α3 = 7.80±2.30 are numerical coefficients (Kossacki et al. 2022b), and its distribution for a wide temperature range is presented in the paper (Wesołowski 2024). The remaining physical constants used in the numeric model are presented in Table 2.
3.2 The amplitude of the outburst
Determining the amplitude of the change in the brightness of the comet during the outburst, we continue our previous considerations presented in papers (Gronkowski et al. 2018; Wesołowski 2020b; Wesołowski et al. 2020a,b, 2022). In this paper, we present an outburst model that takes into account the influence of the bolometric albedo on the total change in the cometary brightness. According to previous assumptions, the measure of the outburst amplitude is the increase in the total scattering cross-section. This increase is the result of the destruction of a fragment of the surface of the cometary nucleus and the emission of porous dust agglomerates on which the incident sunlight scatters more effectively. Let us emphasize that an agglomerate means a porous model particle consisting of grains with a density corresponding to our analogues. Submicron dust grains are composed of amorphous carbon, and submicron silicate mass is usually dominated by amorphous silicate materials rich in magnesium and iron. The presence of these chemical elements in our analogues was confirmed based on the analysis presented in Table 1. Furthermore, porous agglomerates approximately reproduce the highly irregular and fluffy dust morphology in the Solar System (Zubko 2020). Therefore, based on Pogson’s law, the change in the cometary brightness during the outburst can be expressed as:
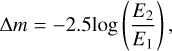 (7)
(7)
where E1 and E2 represent the illuminance of the comet as seen from Earth in the quiet sublimation (t1) and during the outburst (t2). Since these intensities are proportional to the individual scattering cross-sections, Eq. (7) takes the form:
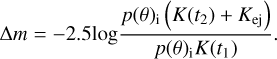 (8)
(8)
In Eq. (8), the individual symbols mean: p(θ)i is a phase function that depends on the phase angle and the asymmetry factor. The value of this function was calculated based on the Henyey-Greenstein equation (Wesołowski et al. 2020a). Other symbols mean: K(t1) and K(t2) are scattering cross-sections originating from dust particles that were lifted into the coma during the quiet sublimation phase (t1) and outburst phase (t2), respectively. Whereas Kej is the scattering cross-section associated with the destruction of a fragment of the cometary surface. The individual scattering cross-sections can be defined as:
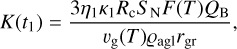 (9)
(9)
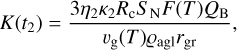 (10)
(10)
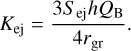 (11)
(11)
In Eqs. (9)—(11), individual symbols mean: η1, η2 is the area fraction that was active in the quiet sublimation phase (t1) and during the outburst phase (t2), respectively. The relationship between these two parameters is as follows: (η1 = η1 + Sej•(SN)−1). Moreover, κ1 is the dust-gas mass ratio in the quiet phase, κ2 is the dust-gas mass ratio in the outburst phase, Rc is the radius of the coma, RN is the radius of cometary nucleus, υg(T) is the velocity of sublimation gas molecules, ϱagl is the density of agglomerate, QB is the scattering factor for the considered analogues (QB ≈ 1 + AB), h is the thickness of the layer, Sej is the surface exposed after the destruction, SN is the total surface and rgr is the average value of the radius of the particles, which we calculate using the power law f(r) = r−q, where q is the power index. Taking into account the above measurement results, we can determine the density of individual agglomerates based on the following relationship given in Eq. (12):
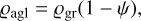 (12)
(12)
where ϱgr is the density of the tested analogues and ψ is their porosity.
When determining the value of the outburst amplitude, we take into account two models. In the first one (model A), we assume that the incident sunlight is scattered on both dust and ice particles. Therefore, in this approach, it is important to determine the volume fraction of both ice particles (υice) and dust particles (υdust) in the total number of grains contained in a coma. The assumed volume fractions of ice particles and dust particles were selected so that: υice + υdust = 1 (Wesołowski et al. 2020a). In the second model (model B), the scattering of incident sunlight occurs on dust particles. Based on the Eqs. (7)–(11), we can write two relationships:
where Qice is the scattering coefficient for particles consisting of water ice. Moreover, we assume that the outburst took place from the part of the comet that was illuminated by the Sun. Then the value of the η1 parameter can be equal to even 50%. By the considerations presented in the introduction of this paper, four exemplary values have been adopted for the η1 parameter. Using the above considerations, Figs. 10–13 presents the change of cometary brightness during its outburst, which took place at a heliocentric distance of rh = 1.5 au.
When analyzing the calculation results, it should be noted that the measure of the change in brightness is the total scattering cross-section. The measure of this cross-section is the number of particles present in the coma on which the incident sunlight is scattered. The following conclusions can be drawn from the performed calculations:
Because cometary outbursts occur in a very short time of the order of several hours, the phase angle practically does not change. Due to the short duration of the outburst, it can be safely assumed that just before and during the outburst its phase angle is practically the same. Then the phase function will have the same value which we can simplify and the equations determining the amplitude of outbursts will have a simpler form.
The amplitude of the cometary outburst depends on the surface of both the one that was active in the quiet sublimation phase and the surface that was destroyed. Moreover, as the η1 parameter increases, the amplitude of the cometary outburst decreases at the same value of the area that was destroyed.
In model A, the highest scattering efficiency was obtained when the volume fraction of ice particles in the coma was the highest. However, the lowest scattering efficiency was obtained in the case of the highest volume fraction of dust particles in the coma. However, these differences are approximately 0.5 magnitude and are a consequence of the assumed density value for both ice particles and porous dust particles.
We will obtain similar differences in the amplitude of outburst by analyzing the bolometric albedo contribution for the tested samples, regardless of the η1 parameter. This applies in particular to comparisons in the case of extreme volume fractions of individual particles. However, when comparing the same volume fractions, the contribution from our bolometric albedo generates differences in amplitude of approximately 0.2 magnitude.
In the case of model B, for the given bolometric albedo value, the differences in amplitude for the extreme values of the η1 parameter are 2.25 magnitudes. This means that the main factor that should be used when numerically modeling the amplitude of an outburst is the parameter η1 because the contribution is the most significant. However, accurate determination of this parameter requires direct observation of a given comet from a close distance (or even from its surface), as was the case during the Rosetta mission. Therefore, in numerical modeling, a wide range of values for the η1 parameter should be assumed.
Analyzing the contribution of bolometric albedo (for the analogues considered in this paper), we can notice that it generates a distribution of the change in cometary brightness ranging from 6.50 to 4.02 magnitudes, depending on the η1 parameter. In addition, different values of bolometric albedo affect thermodynamic parameters such as the sublimation flux and gas velocity, which results in a difference in the change of cometary brightness that ranges from 0.19 to 0.27 magnitudes for a given η1 parameter.
Considering the influence of the volume fraction of individual particles, it is easy to see that the greater the share of ice particles, the greater the scattering efficiency. Additionally, as the bolometric albedo increases for a given porosity of the agglomerate, the temperature decreases, which determines a smaller water ice sublimation flux, which translates into a greater change in the cometary brightness.
 |
Fig. 10 Distribution of changes in brightness as a function of the surface that has undergone destruction. The presented calculation results refer to model A, in which we take into account the volumetric share of dust and ice particles in their total amount contained in the coma. The calculations assumed that the parameter η1 = 10%. |
 |
Fig. 11 Distribution of changes in brightness as a function of the surface that has undergone destruction. The presented calculation results refer to model A, in which we take into account the volumetric share of dust and ice particles in their total amount contained in the coma. The calculations assumed that the parameter η1 = 50%. |
 |
Fig. 12 Distribution of changes in brightness as a function of the surface that has undergone destruction. The calculations assumed that the activity of the comet is controlled by the sublimation of water ice, and the scattering of incident sunlight occurs on porous dust agglomerates. Additionally, four example values of the active surface during quiet sublimation and one example value of bolometric albedo were taken into account in the calculations. The presented simulation results refer to model B. |
 |
Fig. 13 Distribution of brightness changes as a function of the damaged surface. These calculations took into account the influence of bolomet-ric albedo and η1 parameters of the change in cometary brightness. The presented simulation results refer to model B. |
4 Summary and conclusions
The considerations presented in the article are divided into two main parts. The first part concerns the measurement of hemispherical albedo for selected dust analogues. A Cary 5000 spectrometer with an integrating sphere was used for the measurements. The tested dust analogue is a mixture of sand, ash, and charcoal. As expected, each sample was visually characterized by a different color resulting from the volume fraction of individual admixtures (ash and charcoal). The use of these two admixtures allowed us to obtain relatively dark samples, and their color influenced their optical properties, including the determined value of hemispherical albedo. The obtained measurement results were used to calculate the bolometric albedo and individual thermodynamic parameters. In the second part of the paper, using Pogson’s law, equations (model A and model B) were derived, based on which we could determine the amplitude of the cometary outburst. In addition, the amplitude of the outburst was dependent on the bolometric albedo. The upper limit of the outburst amplitude oscillated around 6.5 magnitudes. At the same time, this value is almost half the amplitude of the mega-outburst of comet l7P/Holmes from 2007.
Analyzing real cases of cometary outbursts, we can notice that smaller amplitude outbursts occur much more often. In particular, for outbursts with an amplitude of less than 1 magnitude, these outbursts may be missed by observers. This is because the vast majority of astronomical observations are made visually by tracking a given part of the night sky. Taking into account the obtained values of the change in brightness, it is worth noting that they are comparable to real outbursts. Here are some examples of comets whose actual outburst amplitudes are close to our results:
1P/Halley outburst in 1836 with an amplitude of ∆m = 5.0 magnitude,
12P/Pons-Brooks outburst in 1883 with an amplitude of ∆m = 5.0 magnitude,
186P/Garradd outburst in 1975 with an amplitude of ∆m = 2.4 magnitude,
1P/Halley outburst in 1991 with an amplitude of ∆m = 6.0 magnitude,
l74P/Echechlus outburst in 2005 with an amplitude of ∆m = 3.5 magnitude,
63P/Wild 1 outburst in 2013 with an amplitude of Δm = 2.5 magnitude,
273P/Pons-Gambart outburst in 2014 with an amplitude of Δm = 3.0 magnitude,
15P/Finlay outburst in 2014 with an amplitude of Δm = 3.0 magnitude,
C/2013 C2 (Tenagra) outburst in 2015 with an amplitude of Δm = 3.3 magnitude,
12P/Pons-Brooks outburst in the second half of 2023, eight outbursts were recorded, the amplitude of which was in the range from 0.30 to 5.1 magnitudes,
29P/Schwassmann-Wachmann an average of seven outbursts per year with amplitudes ranging from 0.4 to 6 magnitudes.
Let us add that these actual outbursts took place at different heliocentric distances, which means that their sublimation activity was driven by different cometary ices. As an example, numerous outbursts of comet 29P/Schwassmann-Wachmann can be considered, which was initiated by the sublimation of CO ice (Wierzchos & Womack 2020; Harrington et al. 2022). In the context of cometary outbursts, it is extremely important to regularly study the level of pollution of the sky with artificial light and its impact on the visibility of comets during their outbursts (Gronkowski et al. 2018; Wesołowski 2019, 2023b). An additional important tool for detecting early cometary outbursts is the LCO Outbursting Objects Key (LOOK) research project (Lister et al. 2022). The data that will be collected as part of the project will make it possible to redefine the morphology of the outburst, and above all, its evolution over time. In addition, these data will allow us to study the frequency and distribution of flares, and thus contribute to a better understanding of this unique and at the same time the most spectacular phenomenon that we can observe in the night sky.
The phenomenon of cometary outbursts is a complex issue that requires further research and analysis. On the one hand, new mechanisms that initiate the outburst should be searched for, and on the other hand, in the case of known mechanisms, the mathematical formalism should be improved. In particular, this concerns the analysis of the sublimation flux, which is the basic process describing the sublimation activity of a comet.
Let us emphasise that the obtained ranges of comet brightness changes are based on certain approximations resulting from the complex structure of the cometary nucleus. Some of the parameters used are well defined (for example the dimensions of cometary particles) and others are determined with some uncertainty (for example the fracture strength of the cometary nucleus). Moreover, it is worth emphasising the following fact comets are diverse both in terms of size and the percentage of water ice in relation to other ices.
The results of measurements and calculations of the change of cometary brightness presented in this paper should be treated as an extension of our previous paper (Wesołowski & Potera 2024). The obtained results are therefore of qualitative value, and the presented analytical model is universal and can be used to determine the change in the brightness of any comet whose activity is controlled by the sublimation of water ice.
Acknowledgements
This paper has been done due to the support the author received from the Centre for Innovation and Transfer of Natural Sciences and Engineering Knowledge, University of Rzeszów, Poland (RPPK.01.03.00-18-001/10-00).
References
- Bockelée-Morvan, D., Leyrat, C., Erard, S., et al. 2019, A&A, 630, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capaccioni, F., Coradini, A., Filacchione, G., et al. 2015, Science, 347, aaa0628 [Google Scholar]
- Ciarniello, M., Capaccioni, F., Filacchione, G., et al. 2015, A&A, 583, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, B. E., Veverka, J., Helfenstein, P., et al. 1999, Icarus, 140, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, Y.-J., & Weissman, P. 2006, BAAS, 38, 551 [NASA ADS] [Google Scholar]
- Choukroun, M., Altwegg, K., Kührt, E., et al. 2020, Space Sci. Rev., 216, 44 [CrossRef] [Google Scholar]
- Feller, C., Fornasier, S., Hassemann, P. H., et al. 2016, MNRAS, 462, S287 [NASA ADS] [CrossRef] [Google Scholar]
- Feller, C., Pommerol, A., Lethuillier, A., & Gundlach, B. 2022, 16th Europlanet Science Congress 2022, held 18-23 September 2022 at Palacio de Congresos de Granada, Spain, EPSC2022-1082 [Google Scholar]
- Filacchione, G., Capaccioni, F., Ciarniello, M., et al. 2016, Icarus, 274, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Fornasier, S., Hasselmann, P. H., & Barucci, M. A. 2015, A&A, 583, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fornasier, S., Hoang, H. V., Fulle, M. Quirico, E., & Ciarniello, M. 2023, A&A, 672, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fulle, M., Blum, J., Rotundi, A., et al. 2020, MNRAS, 493, 4039 [CrossRef] [Google Scholar]
- Gicquel, A., Vincent, J.-B., Agarwal, J., et al. 2016, MNRAS, 462, S57 [NASA ADS] [CrossRef] [Google Scholar]
- Gronkowski, P., & Wesolowski, M. 2015, MNRAS, 451, 3068 [CrossRef] [Google Scholar]
- Gronkowski, P., & Wesolowski, M. 2016, Earth Moon Planets, 119 23 [NASA ADS] [CrossRef] [Google Scholar]
- Gronkowski, P., Tralle, I., & Wesolowski, M. 2018, Astron. Nachr., 339, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Groussin, O., & Lamy, P. 2003, A&A, 412, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groussin, O., Attree, N., Brouet, Y., et al. 2019, Space Sci. Rev. 215 29 [Google Scholar]
- Gundlach, B., Blum, J., Keller, H. U., & Skorov, Y. V. 2015, A&A, 583, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haack, D., Lethuillier, A., Kreuzig, C., et al. 2021, A&A, 649, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasselmann, P. H., Barucci, M. A., Fornasier, S., et al. 2017, MNRAS, 469, S550 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington Pinto, O., Womak, M., Fernandez, Y., & Bauer, J. 2022, Planet. Sci. J., 3 247 [NASA ADS] [CrossRef] [Google Scholar]
- Ipatov, S. I. 2011, EPSC-DPS Joint Meeting 2011, held 2-7 October 2011 in Nantes, France, 586 [Google Scholar]
- Keller, H. U., Arpigny, C., Barbieri, C., et al. 1986, Nature, 321, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, H. U., Delamere, W. A., Reitsema, H. J., Huebner, W. F., & Schmidt, H. U., 1987, A&A, 187, 807 [NASA ADS] [Google Scholar]
- Keller, H. U., Mottola, S., Hviid, S. F., et al. 2017, MNRAS, 469, S357 [Google Scholar]
- Kossacki, K. J., Wesolowski, M., Skóra, G., & Staszkiewicz, K. 2022a, Icarus, 379, 114946 [NASA ADS] [CrossRef] [Google Scholar]
- Kossacki, K. J., Wesolowski, M., Szutowicz, S., & Mikolajków, T. 2022b, Icarus, 388, 115209 [NASA ADS] [CrossRef] [Google Scholar]
- Langevin, Y., Hilchenbach, M., Vincendon, M., et al. 2017, MNRAS, 469, S5350 [NASA ADS] [CrossRef] [Google Scholar]
- Langevin, Y., Merouane, S., Hilchenbach, M., et al. 2020, Planet. Space Sci., 182, 104815 [NASA ADS] [CrossRef] [Google Scholar]
- Lethuillier, A., Feller, C., Kaufmann, E., et al. 2022, MNRAS, 515, 3420 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Z.-Y., Knollenberg, J., Vincent, J.-B., et al. 2017, MNRAS, 469, 731 [Google Scholar]
- Lister, T., Kelley, M. S. P., Holt, C. E., et al. 2022, Planet. Sci. J., 3, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Miles, R. 2016a, Icarus, 272, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Miles, R. 2016b, Icarus, 272, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M., Riffeser, A., Hopp, U., Wilke, S., & Carraro, G. 2008, A&A, 479, 45 [Google Scholar]
- Moreno, F. J. L., Santos-Sanz, P., Morales, N., et al. 2008, ApJ, 677, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Pajola, M., Höfner, S., Vincent, J. B., et al. 2017, Nat. Astron., 1, 0092 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Bar-Nun, A., 1992, A&A, 258, L9 [NASA ADS] [Google Scholar]
- Quirico, E., Moroz, L. V., Schmitt, B., et al. 2016, Icarus, 272, 32 [CrossRef] [Google Scholar]
- Rotundi, A., Brucato, J. R., Colangeli, L., et al. 2002, Meteor. Planet. Sci., 37, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Sagdeev, R. Z., Blamont, J., Galeev, A. A., et al. 1986, Nature, 321, 2590 [Google Scholar]
- Saki, M., Gibb, E., Bonev, B. P., et al. 2021, AJ, 162, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Steckloff, J., & Melosh, H. J. 2016, AAS meeting, 48, 206.06 [Google Scholar]
- Stöffler, D., Duren, H., Knolker, J., Hische, R., & Bischoff, A., 1991, Geophys. Res. Lett., 18, 285 [CrossRef] [Google Scholar]
- Tosi, F., Capaccioni, F., Capria, M. T., et al. 2019, Nat. Astron., 3, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, J.-B., Bodewits, D., Besse, S., et al. 2015, Nature, 523, 63 [Google Scholar]
- Vincent, J.-B., A’Hearn, M. F., Lin, Z.-Y., et al. 2016, MNRAS, 462, 184 [Google Scholar]
- Wesołowski, M. 2019, J. Astrophys. Astron., 40, 20 [CrossRef] [Google Scholar]
- Wesołowski, M. 2020a, Icarus, 351, 113950 [CrossRef] [Google Scholar]
- Wesołowski, M. 2020b, Planet. Space Sci., 194, 105117 [CrossRef] [Google Scholar]
- Wesołowski, M. 2021a, MNRAS, 505, 3525 [CrossRef] [Google Scholar]
- Wesołowski, M. 2021b, Icarus, 357, 114116 [CrossRef] [Google Scholar]
- Wesołowski, M. 2021c, RAA, 21, 69 [Google Scholar]
- Wesołowski, M. 2022, MNRAS, 512, 4683 [CrossRef] [Google Scholar]
- Wesołowski, M. 2023a, MNRAS, 521, 1570 [CrossRef] [Google Scholar]
- Wesołowski, M. 2023b, Sci. Rep., 13, 17091 [CrossRef] [Google Scholar]
- Wesołowski, M. 2024, Icarus, 411, 115937 [CrossRef] [Google Scholar]
- Wesołowski, M., & Potera, P. 2024, Icarus, 416, 116087 [CrossRef] [Google Scholar]
- Wesołowski, M., Gronkowski, P., Tralle, I. 2020a, Planet. Space Sci., 184, 104867 [CrossRef] [Google Scholar]
- Wesołowski, M., Gronkowski, P., & Tralle, I. 2020b, Icarus, 352, 114005 [CrossRef] [Google Scholar]
- Wesołowski, M., Gronkowski, P., & Kossacki, K. J. 2022, MNRAS, 517, 4950 [CrossRef] [Google Scholar]
- Wesołowski, M., Potera, P., Gronkowski, P. Skala, P., & Sobaszek, J. 2024, MNRAS, 527, 7613 [Google Scholar]
- Wierzchos, K., & Womack, M. 2020, AJ, 159, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Zubko, E. 2020, MNRAS, 492, 810 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Most important values of basic parameters that were used in numerical simulations.
All Figures
 |
Fig. 1 Optical design of the DRA system. The diagram is available in the spectrometer manual. The measurement process can be described in five steps: 1. The sample beam hits mirror M1 and is then reflected to M2. 2. The beam travels through the lens and is focused into the transmission port, and onto the reflectance port. 3. The reflected beam is diffused throughout the sphere before being measured by the detector. 4. The reference beam enters the sphere directly through the reference port and is scattering. 5. The hemisphere albedo was then measured. |
| In the text | |
 |
Fig. 2 Scanning electron microscope image showing sand particles. The individual parameters mean: HV is the accelerating voltage the value of which was 7 kV (it is the highest possible accelerating voltage that does not cause contamination for a given sample), mag is the image magnification, HFW is the horizontal field width, WD is the distance between the lens and the sample (working distance), det ETD is the ETD detector recording the secondary electron signal, pressure in the chamber, mode SE is the operating mode, using a detector recording secondary electrons. |
| In the text | |
 |
Fig. 3 Scanning electron microscope image showing ash particles. |
| In the text | |
 |
Fig. 4 Scanning electron microscope image showing charcoal particles. |
| In the text | |
 |
Fig. 5 Hemispherical albedo distribution in a function of wavelength in the range from 200 to 2500 nm. An integrating sphere was used in these measurements. The presented measurement results concern three analogues (sand, ash, charcoal) that were examined in this paper. |
| In the text | |
 |
Fig. 6 Hemispherical albedo distribution as a function of wavelength in the range from 200 to 2500 nm for the three samples (sample A, sample B and sample C) considered in this paper. As in the case of pure analogues, an integrating sphere was used for measurements. |
| In the text | |
 |
Fig. 7 Comparison of hemispherical albedo in the case of sand and sample A in the studied spectral range. |
| In the text | |
 |
Fig. 8 Comparison of hemispherical albedo in the case of ash and sample B in the studied spectral range. |
| In the text | |
 |
Fig. 9 Comparison of hemispherical albedo in the case of charcoal and sample C in the studied spectral range. |
| In the text | |
 |
Fig. 10 Distribution of changes in brightness as a function of the surface that has undergone destruction. The presented calculation results refer to model A, in which we take into account the volumetric share of dust and ice particles in their total amount contained in the coma. The calculations assumed that the parameter η1 = 10%. |
| In the text | |
 |
Fig. 11 Distribution of changes in brightness as a function of the surface that has undergone destruction. The presented calculation results refer to model A, in which we take into account the volumetric share of dust and ice particles in their total amount contained in the coma. The calculations assumed that the parameter η1 = 50%. |
| In the text | |
 |
Fig. 12 Distribution of changes in brightness as a function of the surface that has undergone destruction. The calculations assumed that the activity of the comet is controlled by the sublimation of water ice, and the scattering of incident sunlight occurs on porous dust agglomerates. Additionally, four example values of the active surface during quiet sublimation and one example value of bolometric albedo were taken into account in the calculations. The presented simulation results refer to model B. |
| In the text | |
 |
Fig. 13 Distribution of brightness changes as a function of the damaged surface. These calculations took into account the influence of bolomet-ric albedo and η1 parameters of the change in cometary brightness. The presented simulation results refer to model B. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\Delta m = - 2.5\log {{p{{(\theta )}_{\rm{i}}}\left( {{{3{\eta _2}{\kappa _2}{R_2}{S_{\rm{N}}}F(T){Q_{\rm{B}}}} \over {{v_{\rm{g}}}(T){\varrho _{{\rm{ag}}f}}{r_{{\rm{gr}}}}}} + {{3{S_{{\rm{ej}}}}h} \over {4{r_{{\rm{gr}}}}}}\left[ {{v_{{\rm{ice}}}}{Q_{{\rm{ice}}}} + {v_{{\rm{Dust }}}}{Q_{\rm{B}}}} \right]} \right)} \over {p{{(\theta )}_{\rm{i}}}{{3{\eta _1}{\kappa _1}{R_{\rm{c}}}{S_{\rm{N}}}F(T){Q_{\rm{B}}}} \over {{v_{\rm{g}}}(T){\varrho _{{\rm{agg}}}}{r_{{\rm{gr}}}}}}}},$](/articles/aa/full_html/2024/06/aa49573-24/aa49573-24-eq13.png)