| Issue |
A&A
Volume 686, June 2024
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202348895 | |
| Published online | 04 June 2024 | |
Simultaneous NICER and NuSTAR observations of the ultraluminous source NGC 4190 ULX-1
1
Instituto Argentino de Radioastronomía (CCT La Plata, CONICET; CICPBA; UNLP), C.C.5, (1894), Villa Elisa, Argentina
e-mail: jorgearielcombi@gmail.com
2
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, B1900FWA La Plata, Argentina
3
Instituto de Astrofísica de Canarias (IAC), Vía Láctea s/n, La Laguna, 38205 S/C de Tenerife, Spain
4
Departamento de Astrofísica, Universidad de La Laguna, La Laguna, 38205 S/C de Tenerife, Spain
5
Departamento de Física (EPS), Universidad de Jaén, Campus Las Lagunillas s/n, A3, 23071 Jaén, Spain
Received:
9
December
2023
Accepted:
18
March
2024
Aims. We present an X-ray analysis of three different XMM-Newton observations together with simultaneous NICER and NuSTAR observations of the ultraluminous X-ray source NGC 4190 ULX-1. Our goal is to constrain the structure of the accretion disk and the geometrical properties of the source.
Methods. We performed temporal and spectral analyses in the 0.4−30 keV energy range in which the source is significantly detected in dedicated XMM-Newton, NICER, and NuSTAR observations.
Results. The temporal analysis shows no flaring activity in the light curves. No pulsation is detected throughout. The source exhibits a typical ULX spectrum, which can be fitted with two thermal blackbody components plus a Comptonization tail at high energies. The luminosity–temperature (L − T) relation of each thermal spectral component is consistent with the L ∝ T2 relation expected from an advection-dominated supercritical disk.
Conclusions. We interpret these results as a super-Eddington accreting black hole seen almost face-on. A dense wind ejected from the disk obscures the central source, and a hot electron plasma is evacuated through the funnel formed above the hole. Geometric beaming is responsible for the ULX soft emission, whereas the hard tail is the result of the Comptonization of soft photons by the electrons ejected through the funnel.
Key words: accretion / accretion disks / stars: black holes / stars: individual: NGC 4190 ULX-1
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Ultraluminous X-ray sources (ULXs) provide one of the best opportunities to study super-Eddington accretion in nearby galaxies (Kaaret et al. 2017). In the last decade, the nature of these off-nuclear point sources with luminosities ≥1039 erg s−1 has been the subject of considerable debate. Several hypotheses have been proposed to explain the high X-ray luminosities. These include (i) intermediate-mass black holes (BHs) accreting at sub-Eddington rates (Colbert & Mushotzky 1999), (ii) sub-Eddington accreting compact stellar-mass objects with jets (Begelman et al. 2006), (iii) stellar-mass BHs accreting at supercritical rates (Poutanen et al. 2007; Fabrika et al. 2021), and (iv) neutron stars (NSs) accreting at supercritical rates (Mushtukov et al. 2017; Koliopanos et al. 2017).
Ultraluminous X-ray sources are classified into different states based on their X-ray spectral components and hardness (Sutton et al. 2013; Kaaret et al. 2017). The most common state is the ultraluminous state, which is characterized by a power-law tail with a cutoff (Gladstone et al. 2009). Ultraluminous X-ray sources in this state can be further classified as hard ultraluminous (HUL) or soft ultraluminous (SUL) sources depending on their hardness (Sutton et al. 2013). Soft bright states are generally in a higher luminosity range compared to hard intermediate states, due to the down-scattering of photons by the dense medium of clumpy winds at high accretion rates. Other ULX states are the broadened disk (BD) state and the super-soft ultraluminous (SSUL) state. Broadened disk states are characterized by a pure accretion disk model with a temperature of 1−2.5 keV, while SSUL states are dominated by single-component cool blackbody emissions. It should be noted that the distinction between the above classifications is not always clear. A significant number of ULXs exhibit spectral transitions between these different states or regimes (e.g. Gúrpide et al. 2021a). These changes are likely due to variations in the accretion rate, disk occultation, wind outflow strength, precession of the accretion disk, and various other physical parameters. In recent years, observations performed with a new generation of X-ray telescopes like XMM-Newton, Chandra, NICER, or NuSTAR have allowed us to establish the emission mechanism for the majority of ULX sources as super-Eddington accretion from a stellar mass X-ray binary system (Walton et al. 2013; Mukherjee et al. 2015). This result was further supported by the remarkable discovery that several ULXs are actually powered by accreting NSs (Bachetti et al. 2014).
The first physical models of super-Eddington accretion involved a geometrically thin and optically thick disk around the central compact object (Shakura & Sunyaev 1973). One of the main predictions of these models is massive radiation-driven outflows of ionized gas from regions close to the compact object, escaping at slightly relativistic velocities. However, most current models consider disk inflation inside the critical radius, where the radiation pressure exceeds the gravitational attraction. In this inner region, the disk is unstable and most of the matter is evacuated by a very dense, opaque wind. Photon trapping and advection remove energy from the disk, feeding the BH at a rate close to the Eddington accretion rate (Ohsuga et al. 2003; Fukue 2004; Dotan & Shaviv 2011; Ogawa et al. 2017).
In this context, of particular interest is the study of super-Eddington accretion in the ULX system NGC 4190 ULX1, located at a distance, D ≈ 2.9 Mpc (Tully et al. 2013). This source was recently studied by Ghosh & Rana (2021). Of the detailed analysis of X-ray spectra from several XMM-Newton observations, the authors conclude that ULX1 in NGC 4190 it is not in a standard canonical accretion state, but in an ultraluminous regime. In addition, the positive luminosity-temperature relation suggests that the multicolor disk model seems to favor the L ∝ T2 relation, consistent with an advection-dominated inflated disk emission.
Recently, Abaroa et al. (2023) implemented a physical model that fits the available XMM-Newton data for this source. The model is based on a BH of MBH = 10 M⊙ accreting at Ṁ ∼ 10 ṀEdd (where ṀEdd ≈ 2.2 × 10−8 MBH yr−1 is the Eddington rate). The system is viewed almost face-on, with an inclination of i ≈ 0°.
In this paper we present an analysis of archival XMM-Newton, NICER, and NuSTAR observations of the ULX source NGC 4190 ULX-1 to better constrain the geometry and structure of the accretion disk around the BH, to detect spectral signatures of outflows, and to search for possible pulsations.
The paper is organized as follows. In Sect. 2 we provide details about the observations used in this work. In Sect. 3 we describe the main results of the temporal and spectral analyses, while in Sect. 4 we discuss the behavior of the thermal components and present an improved model of the source. Finally, in Sect. 5 we present our conclusions.
2. Observation and data analysis
2.1. XMM-Newton data
XMM-Newton observed NGC 4190 ULX1 on May 6, 2010 with an exposure time of 21 ks (ObsID 0654650101), on May 8, 2010 with an exposure time of 27 ks (ObsID 0654650201), and November 25, 2010 with an exposure time of 20 ks (ObsID 0654650301). In the three observations, the MOS and pn cameras were in full-frame mode.
The XMM-Newton data were reduced using v21.0.0 of the XMM-Newton Science Analysis System (SAS) software and up-to-date CCFs as of October 2023, producing calibrated event files with epproc and emproc and removing periods of high background. We extracted data products using circular regions of 30 and 60 arcsec radius for the source and background, respectively, with background regions located on the same chip at a similar distance from the readout node. We selected events with FLAG == 0, with PATTERN ≦ 12 for the EPIC-MOS cameras and PATTERN ≦ 4 for the EPIC-pn cameras. In all cases, spectra were grouped into having a minimum of 20 counts per bin. Redistribution matrices and auxiliary response files were generated with the tasks rmfgen and armgen, respectively.
2.2. NICER data
The Neutron star Interior Composition ExploreR (NICER; Gendreau et al. 2016) is an instrument on board the International Space Station equipped with an X-ray timing instrument (XTI) detector. The X-ray timing instrument detects soft X-rays in the 0.2−12 keV energy range with a high temporal resolution. We analyzed four NICER’s ObsIDs 3645010101/2/3/4 performed between April 26, 2020 and April 28, 2020, with exposures of ∼0.7, 13, 17, and 2.9 ks, respectively. We followed the standard data processing using HEASoft v.6.32.1 and NICER data analysis software (xti20221001). We extracted light curves and spectra using the nicerl3 task. In addition, for each observation, we obtained the background light curve and spectrum with the Space Weather background model (Remillard et al. 2022). We applied a barycentric correction using the barycorr tool.
2.3. NuSTAR data
The NuSTAR telescope (Nuclear Spectroscopic Telescope Array; Harrison et al. 2013) is an X-ray satellite equipped with two detectors, FPMA and FPMB, operating in the 3 to 78 keV energy band. NuSTAR observed NGC 4190 ULX-1 in April 2020 (ObsID 30601009002), with an exposure of ∼73 ks. We reduced the data using the analysis software NuSTARDAS-v. 2.0.0 from HEASoft v.6.32.1 and CALDB (V.20130509) calibration files. We took source events that accumulated within a circular region of a 60 arcsec radius around the focal point. The chosen radius encloses ∼75% of the point spread function (PSF). Background regions for FPMA/B modules were selected far from contamination of the source and detector edges, with a radius of 100 arcsec.
We used the nupipeline task to create level 2 data products, with saacalc=1, saamode=OPTIMIZED, and tentacle=NO to filter high background epochs, obtained from the South Atlantic Anomaly (SAA) filtering report. This led to us losing ∼0.6% of the observation total exposure. We extracted the light curves and spectra with the nuproducts task. We obtained the barycenter-corrected light curves using the barycorr task with a nuCclock20100101v136 clock correction file. We used celestial coordinates α = 183.434049 deg and δ = +36.631493 deg for the barycentric correction. For this, we used JPL-DE200 as the Solar System ephemeris. We finally added the light curves of both detectors with the task LCMATH.
3. Results
3.1. Light curve analysis
Figure 1 shows the background-corrected barycentered light curves observed simultaneously by NICER and NuSTAR over a time interval of ∼50 h. We did not observe any flaring activity in the light curve. In both light curves there is a slight decrease in the count rate toward the end of the observation. To investigate this phenomenon, we obtained light curves in several energy bands with both instruments (0.3−3 keV, 3−12 keV, 12−79 keV) and found that such a decrease in counts is observed up to ∼12 keV. Above 12 keV, the light curves show a constant behavior, with an average rate of ∼0.15 c s−1. We presume that the observed soft flux decrease and spectral change can be attributed to changes in local absorption.
 |
Fig. 1. NICER (0.3−12 keV, top panel) and NuSTAR (3−79 keV, bottom panel) background subtracted light-curves of NGC 4190 ULX-1 with a time bin of 30 s and 120 s respectively. |
We used spectral timing routines from the HENDRICS (Bachetti 2018) and Stingray (Huppenkothen et al. 2019) packages to search for possible pulsations on NICER and NuSTAR data within 0.01−10 Hz frequency interval. We visually inspected power spectra of both instruments and found no pulsations that were significantly above noise. We applied the HENACCELSEARCH tool, which searches for the best pulsation candidates within a given frequency interval, and with varying period derivatives up to 10−9 Hz s−1. The number of harmonics in the 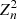 statistic was limited to two. No pulsation candidates were found using the above criteria.
statistic was limited to two. No pulsation candidates were found using the above criteria.
In order to derive an upper limit on the pulsed fraction (PF) that any signal could have, we applied the HENZ2VSPF tool. This task simulates N datasets with the same good time intervals (GTIs) and number of events as the real data, and produces a  versus PF for each simulated dataset. Thus, for N = 10 000 simulations we derive an upper limit on the PF (within 90% confidence) of ≲7% for NICER data (0.3−12 keV), and of ≲18% for NuSTAR (3−79 keV, FPMA+B) data.
versus PF for each simulated dataset. Thus, for N = 10 000 simulations we derive an upper limit on the PF (within 90% confidence) of ≲7% for NICER data (0.3−12 keV), and of ≲18% for NuSTAR (3−79 keV, FPMA+B) data.
3.2. Spectral analysis
We performed the X-ray spectral analysis using XSPEC v.12.13.0c (Arnaud 1996). The spectra were grouped with the optimal binning method from Kaastra & Bleeker (2016) with a minimum of 20 counts per bin to properly use the χ2 statistics. Unabsorbed luminosities were estimated using the CGLUMIN convolution model, assuming a distance of 2.9 Mpc (Tully et al. 2013).
A broadband spectral analysis of the data was performed to characterize the source spectrum. The source were modeled simultaneously using all three detectors (FPMA, FPMB, and XTI). To account for the systematic differences among the three detectors, a calibration constant was assigned to each one. For the NICER spectra, we noticed channels between 0.3 and 9 keV where the source was above the background. Similarly, for the NuSTAR spectrum, we noticed channels between 3 and 30 keV. Consequently, we modeled the entire spectra between 0.3 and 30 keV.
To investigate the properties of NGC 4190 ULX-1, we have constructed two tentative scenarios. First, we hypothesize a non-magnetic accretor, such as a BH. Second, we consider a magnetic accretor, such as a ULX pulsar, although no pulsations have been detected in NGC 4190 ULX-1 so far. Two neutral absorption models were included in this study, where we fixed the first model to a galactic absorption column of 2.4 × 1020 cm−2 derived from the NH tool1 and left the second model free to account for local absorption. For the neutral absorption we used the abundances from Wilms et al. (2000) and the effective cross sections from Verner et al. (1996).
Two thermal components were used to represent the accretion flow scenario for non-magnetic objects. The DISKBB model (Mitsuda et al. 1984) was adopted to describe the flow in the outer region or wind with significant opacity, while the DISKPBB model (Mineshige et al. 1994) was implemented to describe the flow in the inner region where it is expected to deviate from the thin disk approximation. The DISKBB model assumes a thin disk profile with a fixed exponent p value of 0.75. Conversely, the DISKPBB model allows p to be set as a free parameter. This combination of models is often implemented to fit low-energy X-ray data (E < 10 keV) when analyzing the spectrum of ULXs (Stobbart et al. 2006; Walton et al. 2014, 2017; Rana et al. 2015; Mukherjee et al. 2015).
The high-energy emission (E > 10 keV) is probably associated with Compton scattering of photons from the disk in a hot electron plasma. This process is similar to what occurs in X-ray binaries with BHs below the Eddington limit and in active galactic nuclei (Haardt & Maraschi 1991). Therefore, we modeled the emission by including an extra high-energy power-law component. To avoid incorrect extrapolations of this power-law emission at extremely low energies, we used the SIMPL model (Steiner et al. 2009). This additional component complements the DISKPBB component, which is the hotter of the two with respect to the disk.
The case of a magnetic accretor, specifically a ULX pulsar, is based on the framework outlined in Walton et al. (2018a,b). Such a framework consists of two thermal blackbody components that represent the accretion flow emanating from the magnetosphere, the point where the NS’s magnetic field cuts off the disk, causing the accreted material to stick to the magnetic field lines instead of falling directly onto the star. In addition, the central accretion columns formed by the material flow at the magnetic poles are described by a power-law component with an exponential cutoff (CUTOFFPL).
For the thermal components, we again adopted the DISKBB+DISKPBB combination often used in ULX pulsar studies. The spectral shape of the accretion columns in the NGC 4190 ULX1 source cannot be determined directly, since no pulsations have been detected. To model the high-energy part of the spectrum (E > 10 keV), we used a method similar to Walton et al. (2018b) by assigning the spectral parameters to the average values detected in the pulsed emission of the four ULX pulsars identified so far. These values include Γ = 0.59 and Ecut = 7.9 keV for the CUTOFFPL component (Brightman et al. 2016; Walton et al. 2018a).
The results of applying both phenomenological models to the NICER+NuSTAR data are shown in Table 1 and Fig. 2. We obtain good fits overall in both cases, with reduced χ2 of ∼1.1. Both models show similar local absorption columns of NH ∼ 0.1 × 1022 cm−2, cold DISKBB temperatures of ∼0.4 keV, and hot DISKBB temperatures higher than 1 keV, with p indices greater than 0.7. The unabsorbed luminosity of NGC 4190 ULX1 yields ∼7.6 × 1039 erg s−1 for a distance of 2.9 Mpc in the 0.3 − 30 keV energy range.
 |
Fig. 2. NICER+NuSTAR unfolded spectrum and residuals from both tested models. The NICER background dominated above 9 keV, while the NuSTAR background dominated above 30 keV. Left panel: SIMPL model. Right panel: CUTOFFPL model. |
Best fit parameters.
We used MCMC chains to compute the errors after generating chains of 106 samples using the XSPEC CHAIN task with walkers equal to 16 times the number of free parameters, and checking that each parameter converged successfully (i.e., auto-correlation time close to unity; see Fogantini et al. 2023; Saavedra et al. 2023 for more details).
We also modeled archival XMM-Newton pn+MOS observations separately, using both proposed scenarios, in order to use the associated temperatures in the next section. The same XMM-Newton dataset was presented and analyzed, firstly by Ghosh & Rana (2021). As the EPIC background was significant above 10 keV in all observations, in order to properly account for the high-energy-emission components, we froze the SIMPL parameters to those obtained using NICER+NuSTAR data. We left only the SIMPL and CUTOFFPL normalization parameters free to vary. The parameters of each model are detailed in Table A.1.
4. Discussion
We examined the entire collection of archived X-ray observations from NGC 4190 ULX-1, with particular emphasis on the concurrent NICER and NuSTAR observations. Our analysis included examination of the power spectra in the 0.01−10 Hz range, which showed no associated pulsations. We placed an upper limit on the detectable PFs for NICER and NuSTAR derived from simulations. We applied phenomenological models to fit the time averaged spectra, focusing on scenarios involving compact objects with and without magnetic fields, such as an NS or BH.
To classify the source, we compared its spectral parameters with those of other sources and created a hardness–luminosity diagram. We used the energy range of 0.3−1.5 keV as the soft band and 1.5−10 keV as the hard band, following Gúrpide et al. (2021b). The ratio between the hard and soft bands was found to be ∼2.4, placing it in the same region as both pulsating and non-pulsating ULXs. Moreover, the flux ratio between the CUTOFFPL component and the total 0.3−30 keV flux is ∼28%, placing NGC 4190 ULX1 closer to non-pulsating sources (Walton et al. 2018a). Additionally, we observed that the spectra are similar to that of NGC 5204 X-1 in an HUL state (Gúrpide et al. 2021a).
We now focus on the temporal analysis of the behavior of the thermal components, examining their evolution in a plot of luminosity versus temperature. We calculated the unabsorbed luminosity of each thermal component over a wide energy range, from 0.3 to 30 keV. Figure 3 shows a comparison of temperature and luminosity for DISKBB and DISKPBB components. In each panel we have plotted the T2 and T4 trends.
 |
Fig. 3. Luminosity–temperature relationship derived from NICER+NuSTAR (diamond marker) and XMM-Newton (circle marker) spectral fits. Unabsorbed luminosity was calculated assuming a distance of 2.9 Mpc (Tully et al. 2013). Left panel: DISKBB component. Right panel: DISKPBB model. In both cases, T2 and T4 trends were added for reference. |
It is valuable to compare the observed trends with those projected in theoretical scenarios of the luminosity-temperature relation, such as a Shakura-Sunyaev sub-Eddington thin disk (where L is proportional to T4 for a constant emitting area, Shakura & Sunyaev 1973), or a thick disk where advection is significant (where L is proportional to T2, Watarai et al. 2000). Based on the analyzed archive data from NICER, NuSTAR, and XMM-Newton, it is clear that it favors a proportional relationship between L and T2, no matter which compact object scenario we consider. This implies the presence of advection in the system.
We now present a more physical model consistent with the newly available data, based on the phenomenological fit of the X-ray observations. The model extends that presented by Abaroa et al. (2023), which was based on XMM-Newton data alone. A physically motivated model offers deeper insights into the possible mechanisms operating in the source and opens the possibility to new observational tests.
4.1. Disk and wind
We assumed that the accreting object is a BH of 10 M⊙. It forms a close binary with an evolved massive star. Gladstone et al. (2013) imposed constraints on the optical counterpart, suggesting that if MBH = 10 M⊙, the mass of the star should be < 50 M⊙ and its radius < 86 R⊙. These constraints are met by a star of type B2V, for example.
We assumed that the BH accretes matter from the star at a rate of 10 ṀEdd (we will discuss this assumption when we present the results). We denoted this initial rate as Ṁinput. Then, at some critical distance, rcrit, from the BH, the radiation pressure of the disk exceeds the gravitational attraction of the compact object. Hydrodynamic equilibrium in the vertical direction is no longer maintained, and the disk begins to lose mass in the form of a wind. The critical radius is given by rcrit ∼ 40 ṁinput rg, with rg = GMBH/c2 and ṁinput = Ṁinput/ṀEdd (Fukue 2004). The Eddington rate is
with LEdd the Eddington luminosity (defined as the luminosity required to balance the attractive gravitational pull of the BH by radiation pressure), η ≈ 0.1 the accretion efficiency, and c the speed of light. The critical radius divides the disk into two regions: a standard outer disk that is optically thick but geometrically thin (Shakura & Sunyaev 1973) and a radiation-dominated inner disk with advection (Fukue 2004). In this inner disk, the advection is parameterized as a fraction, f, of the viscous heating, Qadv = fQvis, and the disk becomes geometrically thick. The ejection of winds by the radiation force helps to regulate the mass accretion rate onto the BH (Ṁacc) at the Eddington rate. We then have Ṁacc = Ṁinput in the outer region of the disk and Ṁacc = Ṁinput(rd/rcrit) in the inner region (Fukue 2004) (rd is the radial distance to the BH on the equatorial plane of the disk). The difference is the mass rate injected into the wind: Ṁw = Ṁinput − Ṁacc(rd).
A self-similar solution for optically thick supercritical disks with mass loss can be found for the effective disk temperature, as in the appendix of Fukue (2004). The solution reads
with 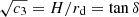 , where H is the scale height of the disk, δ is the disk opening angle, and fin = 1 − rin/rd ≈ 1 (since rd > rcrit, then rd ≫ rin). Here, rin is the location of the inner edge of the disk. The coefficient, c3, depends on the advection parameter, the adiabatic index of the gas, γ = 5/3, and the viscosity, α (see appendix in Fukue 2004). Here we assumed a disk with f = 0.5 and α = 0.5; that is, we assumed equipartition between advection and viscous heating. The scale height of the disk (and thus its semi-opening angle) is completely determined by the coefficient, c3, and therefore by γ, f, and α. The values assumed for these parameters lead to a disk opening angle of δ ∼ 30°. It should also be noted that in the critical region of the disk Teff ∝ r−1/2, contrary to what is expected for a standard disk (see Watarai et al. 2000 for details).
, where H is the scale height of the disk, δ is the disk opening angle, and fin = 1 − rin/rd ≈ 1 (since rd > rcrit, then rd ≫ rin). Here, rin is the location of the inner edge of the disk. The coefficient, c3, depends on the advection parameter, the adiabatic index of the gas, γ = 5/3, and the viscosity, α (see appendix in Fukue 2004). Here we assumed a disk with f = 0.5 and α = 0.5; that is, we assumed equipartition between advection and viscous heating. The scale height of the disk (and thus its semi-opening angle) is completely determined by the coefficient, c3, and therefore by γ, f, and α. The values assumed for these parameters lead to a disk opening angle of δ ∼ 30°. It should also be noted that in the critical region of the disk Teff ∝ r−1/2, contrary to what is expected for a standard disk (see Watarai et al. 2000 for details).
The effects of the radiation on the matter located at the escape surface of the disk in the region, rd ≤ rcrit, have been calculated in detail by Abaroa et al. (2023). The radiation field transfers both energy and angular momentum to the wind, which escapes the system with a strong equatorial component, forming a funnel above the BH. The wind itself is opaque until it reaches the photospheric radius, where it becomes transparent to its own radiation. This photosphere is defined by the condition that the optical depth, τphoto, is unity for an observer at infinity. If the velocity of the wind is relativistic, the optical depth in the observer’s frame depends in general on the magnitude of the velocity and the viewing angle. The position of the apparent photosphere from the equatorial plane, zphoto, is given by Abaroa & Romero (2023)
where γdw is the wind Lorentz factor, κco is the opacity in the comoving frame, and ρco is the comoving wind density. Since we assumed a fully ionized wind, the opacity is dominated by free electron scattering (κco = σT/mp).
4.2. Emission
When the system is viewed face-on (i.e., with an inclination angle of i ≈ 0°), the only X-ray emission visible from the disk is that which escapes through the funnel. This emission is produced near the innermost part. The radiation from the rest of the disk is absorbed and reprocessed in the wind and shifted to lower energies (see Abaroa et al. 2023).
The effect of geometrical beaming is to cause an observer to infer an isotropic luminosity given by
where b is the beaming factor (King 2008). This factor varies with the accretion rate (in Eddington units) as b ∝ ṁ−2 (King et al. 2023)2; in our case, we obtain b = 0.73. However, the emission extends to energies higher than 10 keV that cannot be produced in the disk; the hard X-rays found in our observations require an additional component. Such a component could be a hot plasma in the funnel above the BH. This plasma can be heated by magnetic reconnection, and a nonthermal particle population could be created by turbulent acceleration (del Valle et al. 2016). The relativistic electrons in the plasma then Comptonize the softer photons from the disk, producing the nonthermal tail.
We modeled the X-ray emission discussed in Sect. 3 using the model just described. The adopted and derived parameters are presented in Table 2.
Parameters of the model.
The results are shown in the top panel of Fig. 4, where we plot the disk emission, along with the Comptonization produced by the nonthermal electrons in the funnel. To explore the space parameter that is physically allowed by the observation, we show our results for three different accretion rates: 1, 10, and 15 Eddington rates. As can be seen from the spectral energy distribution (SED), the model is in good agreement with the observational data for the set of parameters presented in Table 2, extending the results of Abaroa et al. (2023). We obtain a chi-square value of χ2 ∼ 6.06 for six spectral bins and show the residuals in the bottom panel of Fig. 4. An accretion rate higher than 10 ṀEdd flattens the spectrum, resulting in a hardening of the emission at soft X-rays, which mismatches the observational data at low energies. Additionally, the accretion rate influences two other parameters: the beaming factor and the available power for the hot gas, causing variations in the observed luminosity with Ṁinput. In Fig. 5 we present an alternative model with a smaller BH. The results are similar: essentially a lighter BH is possible, as long as the accretion rate remains at a level of ten Eddington rates. This result is natural, since the luminosity of the innermost region of the disk depends weakly on the normalized accretion rate (see Eq. (4)), and hence on the mass of the BH. However, this set of values is less conservative than the one in Fig. 4.
 |
Fig. 4. Top: SED of the X-ray emission of NGC 4190 ULX-1 on a logarithmic scale. We plot the radiation from the innermost part of the disk that escapes through the funnel (blue line) and the radiation produced by Comptonization of the disk emission by nonthermal electrons in the funnel (orange line). The black line represents the total SED, while red dots correspond to energy-binned observations from NICER and NuSTAR. We also present, for comparison, the application of our model assuming an accretion rate of 1 ṀEdd (dashed lines) and of 15 ṀEdd (dash-dotted lines). Bottom: residuals of the best fit. The six spectral bins correspond to the data in the 0.4 − 20 keV energy range. |
 |
Fig. 5. Alternative model: SED of the X-ray emission of NGC 4190 ULX-1 on a logarithmic scale for a different, less conservative, set of parameters. Here we fixed the BH mass to 5 M⊙, the viscosity parameter to 0.1, and the content of relativistic particles to 0.25. We also show for comparison the application of our model assuming an accretion rate of 1 ṀEdd (dashed lines) and of 15 ṀEdd (dash-dotted lines). |
4.3. Further remarks
Fukue (2005) estimated the final velocity of a radiation-driven jet in a supercritically accreting BH. He found that the final Lorentz factor should be γ∞ ≈ 1 + 0.223Γ, with Γ = L/LEdd, where L is the disk luminosity. Since the wind regulates the disk luminosity to L ∼ LEdd, one typically get set γ∞ ∼ 1.2 for the jet. This is essentially the same value that we obtained by considering the effect of the radiation force on a particle in the funnel, following the calculation method described in Abaroa et al. (2023), see Table 2.
Since the radiation pressure in the funnel above the BH exceeds the gravitational pull, the plasma cannot be at rest and must be constantly removed and replenished. Since heating the gas to Comptonization temperatures requires time for thermalization, we prefer to assume a nonthermal component flowing through the funnel. Whether this gas is considered a non-static corona or a mildly relativistic jet is more a matter of convention. Markoff et al. (2005) have shown that the observational features are quite similar in both cases.
A collimated jet can manifest its effects at greater distances when it strikes the interstellar medium. There, a system of shocks may form. The forward shock is expected to be radiative and inefficient for particle acceleration, but the reverse shock could reaccelerate electrons to relativistic energies and produce radio synchrotron emission. This radiation could be detected by radio interferometric observations. If the jet has a hadronic content and the surrounding medium is dense enough, a γ-ray source could also be produced through the p + p → p + p + π0 channel, although it would be undetectable in the case of an extragalactic source like NGC 4190 ULX1. In galactic super-Eddington sources such as SS433, γ-rays have instead been reported by various instruments (e.g. Bordas et al. 2015). Another potential super-Eddington microquasar with γ-ray emission seems to be 4FGL J1405.1−6119 (see Saavedra et al. 2022).
The conditions in the funnel are not expected to be very stable, due to various instabilities, clumping of the wind, and magnetic reconnection. Hence, some degree of rapid variability could be present, in accordance with some of the hints in this sense from our light curves. Longer observations will test this in real time. Differences with the results presented in the soft X-ray band presented by Ghosh & Rana (2021) are already indicative of changes in the beaming.
A final note on ultraviolet (UV) radiation: the predicted emission in the UV range from the source is ∼1037 erg s−1, which corresponds to the radiation from the inner disk. This is orders of magnitude lower than that of the ULX NGC 6946 X-1 investigated by Kaaret et al. (2010). Two possible explanations for the difference in the UV luminosity between NGC 4190 ULX1 and this source could be: (i) the blackbody emission of the companion massive star in NGC 6946 X-1, whose spectrum peaks in the UV range; and (ii) the accretion rate of the compact object (higher Ṁinput leading to a spectrum flattening), resulting in increased luminosities at lower energies (see e.g., Fukue 2004).
Future high-resolution observations of NGC 4190 ULX1 with Chandra and VLBI may help to complete the picture of this source; in particular, its impact on the surrounding medium.
5. Conclusions
In this paper we have performed a temporal and spectral study of the ultraluminous source NGC 4190 ULX1 using simultaneous NuSTAR and NICER observations to understand the nature of the accretion disk around the BH, to detect spectral signatures of outflows, and to search for possible pulsations. The temporal analysis shows that the source is in a quiescent state, with a slight decrease in the count rate toward the end of the observation. No pulsations are detected, although spectral markers such as flux ratios do not allow us to discard the pulsating nature of the compact object. The source shows typical ULX behavior and its spectrum can be well fitted with two thermal blackbody components plus a Comptonization tail at high energies. The luminosity in the thermal region is consistent with an inflated radiation-dominated disk with advection. This type of disk loses mass due to strong winds. The wind is opaque, so the disk emission is only visible when the system is viewed nearly face-on, through the funnel above the BH. The Comptonization tail found in the NuSTAR data indicates the presence in this funnel of a population of electrons capable of upscattering softer photons from the inner disk region. We were able to model the data assuming a BH of 10 M⊙ and an accretion rate of ∼10 ṀEdd. The matter escaping from the funnel could form a jet. Future high-resolution radio observations may reveal synchrotron radiation associated with the jet, while the detection of Balmer and He lines may provide more information about the wind, in particular its velocity.
Acknowledgments
We are grateful to the anonymous reviewer for their insightful comments and suggestions, which have helped us to improve the clarity and quality of our manuscript. J.A.C., E.A.S., F.A.F., and F.G. acknowledge support by PIP 0113 (CONICET). F.A.F. is fellow of CONICET. J.A.C., G.E.R., and F.G. are CONICET researchers. J.A.C. is a María Zambrano researcher fellow funded by the European Union NextGenerationEU (UJAR02MZ). This work received financial support from PICT-2017-2865 (ANPCyT). This work was partly supported by the Centre National d’Etudes Spatiales (CNES), and based on observations obtained with MINE: the Multi-wavelength INTEGRAL NEtwork. J.A.C. was also supported by grant PID2019-105510GB-C32/AEI/10.13039/501100011033 from the Agencia Estatal de Investigación of the Spanish Ministerio de Ciencia, Innovación y Universidades, and by Consejería de Economía, Innovación, Ciencia y Empleo of Junta de Andalucía as research group FQM-322, as well as FEDER funds. GER acknowledges financial support from the State Agency for Research of the Spanish Ministry of Science and Innovation under grants PID2019-105510GB-C31AEI/10.13039/501100011033/ and PID2022-136828NB-C41/AEI/10.13039/501100011033, and by “ERDF A way of making Europe”, by the “European Union”, and through the “Unit of Excellence María de Maeztu 2020-2023” award to the Institute of Cosmos Sciences (CEX2019-000918-M). Additional support came from PIP 0554 (CONICET). F.G. acknowledges support from PIBAA 1275 (CONICET).
References
- Abaroa, L., & Romero, G. E. 2023, Rev. Mex. Astron., submitted [arXiv:2311.15050] [Google Scholar]
- Abaroa, L., Romero, G. E., & Sotomayor, P. 2023, A&A, 671, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Bachetti, M. 2018, Astrophysics Source Code Library [record ascl:1805.019] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [Google Scholar]
- Bordas, P., Yang, R., Kafexhiu, E., & Aharonian, F. 2015, ApJ, 807, L8 [CrossRef] [Google Scholar]
- Brightman, M., Harrison, F., Walton, D. J., et al. 2016, ApJ, 816, 60 [Google Scholar]
- Colbert, E. J. M., & Mushotzky, R. F. 1999, ApJ, 519, 89 [NASA ADS] [CrossRef] [Google Scholar]
- del Valle, M. V., de Gouveia Dal Pino, E. M., & Kowal, G. 2016, MNRAS, 463, 4331 [Google Scholar]
- Dotan, C., & Shaviv, N. J. 2011, MNRAS, 413, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrika, S. N., Atapin, K. E., Vinokurov, A. S., & Sholukhova, O. N. 2021, Astrophys. Bull., 76, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Fogantini, F. A., García, F., Combi, J. A., et al. 2023, A&A, 669, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fukue, J. 2004, PASJ, 56, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Fukue, J. 2005, PASJ, 57, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Gendreau, K. C., Arzoumanian, Z., Adkins, P. W., et al. 2016, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, eds. J. W. A. den Herder, T. Takahashi, & M. Bautz, SPIE Conf. Ser., 9905, 99051H [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, T., & Rana, V. 2021, MNRAS, 504, 974 [CrossRef] [Google Scholar]
- Gladstone, J. C., Roberts, T. P., & Done, C. 2009, MNRAS, 397, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Gladstone, J. C., Copperwheat, C., Heinke, C. O., et al. 2013, ApJS, 206, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Gúrpide, A., Godet, O., Vasilopoulos, G., Webb, N. A., & Olive, J. F. 2021a, A&A, 654, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gúrpide, A., Godet, O., Koliopanos, F., Webb, N., & Olive, J. F. 2021b, A&A, 649, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [Google Scholar]
- Huppenkothen, D., Bachetti, M., Stevens, A. L., et al. 2019, ApJ, 881, 39 [Google Scholar]
- Kaaret, P., Feng, H., Wong, D. S., & Tao, L. 2010, ApJ, 714, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kaastra, J. S., & Bleeker, J. A. M. 2016, A&A, 587, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, A. R. 2008, MNRAS, 385, L113 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., Lasota, J.-P., & Middleton, M. 2023, New Astron. Rev., 96, 101672 [CrossRef] [Google Scholar]
- Koliopanos, F., Vasilopoulos, G., Godet, O., et al. 2017, A&A, 608, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markoff, S., Nowak, M. A., & Wilms, J. 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
- Mineshige, S., Takeuchi, M., & Nishimori, H. 1994, ApJ, 435, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Mukherjee, E. S., Walton, D. J., Bachetti, M., et al. 2015, ApJ, 808, 64 [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Ingram, A. 2017, MNRAS, 467, 1202 [NASA ADS] [Google Scholar]
- Ogawa, T., Mineshige, S., Kawashima, T., Ohsuga, K., & Hashizume, K. 2017, PASJ, 69, 33 [Google Scholar]
- Ohsuga, K., Mineshige, S., & Watarai, K.-Y. 2003, ApJ, 596, 429 [CrossRef] [Google Scholar]
- Poutanen, J., Lipunova, G., Fabrika, S., Butkevich, A. G., & Abolmasov, P. 2007, MNRAS, 377, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Rana, V., Harrison, F. A., Bachetti, M., et al. 2015, ApJ, 799, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., Loewenstein, M., Steiner, J. F., et al. 2022, AJ, 163, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Saavedra, E. A., Fogantini, F. A., Combi, J. A., García, F., & Chaty, S. 2022, A&A, 659, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saavedra, E. A., García, F., Fogantini, F. A., et al. 2023, MNRAS, 522, 3367 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Steiner, J. F., Narayan, R., McClintock, J. E., & Ebisawa, K. 2009, PASP, 121, 1279 [Google Scholar]
- Stobbart, A. M., Roberts, T. P., & Wilms, J. 2006, MNRAS, 368, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Sutton, A. D., Roberts, T. P., & Middleton, M. J. 2013, MNRAS, 435, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [Google Scholar]
- Walton, D. J., Fuerst, F., Harrison, F., et al. 2013, ApJ, 779, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Harrison, F. A., Grefenstette, B. W., et al. 2014, ApJ, 793, 21 [Google Scholar]
- Walton, D. J., Fürst, F., Harrison, F. A., et al. 2017, ApJ, 839, 105 [Google Scholar]
- Walton, D. J., Fürst, F., Heida, M., et al. 2018a, ApJ, 856, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Fürst, F., Harrison, F. A., et al. 2018b, MNRAS, 473, 4360 [Google Scholar]
- Watarai, K.-Y., Fukue, J., Takeuchi, M., & Mineshige, S. 2000, PASJ, 52, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
Appendix A: Additional table
Table A.1 shows in detail all the parameters of the models fitted to the XMM-Newton dataset. Luminosities are estimated in the 0.3-30 keV energy range, using a distance of 2900 kpc. Only the normalizations of high energy components were left free to vary.
Best fit parameters and 90% level uncertainties derived from XMM-Newton average spectra.
All Tables
Best fit parameters and 90% level uncertainties derived from XMM-Newton average spectra.
All Figures
 |
Fig. 1. NICER (0.3−12 keV, top panel) and NuSTAR (3−79 keV, bottom panel) background subtracted light-curves of NGC 4190 ULX-1 with a time bin of 30 s and 120 s respectively. |
| In the text | |
 |
Fig. 2. NICER+NuSTAR unfolded spectrum and residuals from both tested models. The NICER background dominated above 9 keV, while the NuSTAR background dominated above 30 keV. Left panel: SIMPL model. Right panel: CUTOFFPL model. |
| In the text | |
 |
Fig. 3. Luminosity–temperature relationship derived from NICER+NuSTAR (diamond marker) and XMM-Newton (circle marker) spectral fits. Unabsorbed luminosity was calculated assuming a distance of 2.9 Mpc (Tully et al. 2013). Left panel: DISKBB component. Right panel: DISKPBB model. In both cases, T2 and T4 trends were added for reference. |
| In the text | |
 |
Fig. 4. Top: SED of the X-ray emission of NGC 4190 ULX-1 on a logarithmic scale. We plot the radiation from the innermost part of the disk that escapes through the funnel (blue line) and the radiation produced by Comptonization of the disk emission by nonthermal electrons in the funnel (orange line). The black line represents the total SED, while red dots correspond to energy-binned observations from NICER and NuSTAR. We also present, for comparison, the application of our model assuming an accretion rate of 1 ṀEdd (dashed lines) and of 15 ṀEdd (dash-dotted lines). Bottom: residuals of the best fit. The six spectral bins correspond to the data in the 0.4 − 20 keV energy range. |
| In the text | |
 |
Fig. 5. Alternative model: SED of the X-ray emission of NGC 4190 ULX-1 on a logarithmic scale for a different, less conservative, set of parameters. Here we fixed the BH mass to 5 M⊙, the viscosity parameter to 0.1, and the content of relativistic particles to 0.25. We also show for comparison the application of our model assuming an accretion rate of 1 ṀEdd (dashed lines) and of 15 ṀEdd (dash-dotted lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



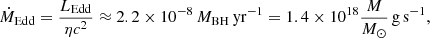
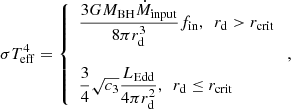
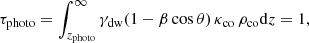
![$$ \begin{aligned} L_{\rm iso}\approx L_{\rm Edd}\left[1+ \frac{\ln {\dot{m}}}{b}\right], \end{aligned} $$](/articles/aa/full_html/2024/06/aa48895-23/aa48895-23-eq13.gif)