EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A188 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A188
Number of page(s) 12
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/202348755
Published online 13 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Stellar multiplicity is ubiquitous in the Galaxy, and even more so among pre-main sequence stars (Duchêne & Kraus 2013; Offner et al. 2023). Since the latter also host planet-forming disks, the influence of stellar companions on planet formation must be studied theoretically, numerically, and empirically. For instance, a long-established prediction is that the orbit of binary stars should severely truncate disks, leading to small circumstellar disks and/or large cavities interior to circumbinary disks (e.g., Artymowicz & Lubow 1994). A direct implication of the former is that circumstellar disks in close binaries should be rare, since small disks have a short (viscous) dissipation timescale, and compact in size. This has been extensively borne out by observations of young binary systems (e.g., Harris et al. 2012; Kraus et al. 2012; Akeson et al. 2019; Manara et al. 2019). Similarly, cavities carved out by central binaries have been observed in a number of systems (e.g., Dutrey et al. 1994; Monnier et al. 2019; Ragusa et al. 2021). Dynamical perturbations of disks by stellar companions have also been documented in multiple cases (e.g., Kurtovic et al. 2018; Cuello et al. 2023).

Among multiple systems, triple and higher-order systems are of particular interest. First of all, such high-order systems represent a sizable fraction of all systems: among field solar-type and low-mass stars, a quarter to a third of all non-single systems contain three or more stars (Hirsch et al. 2021; Reylé et al. 2021). Furthermore, the growing population of known exoplanets in triple and quadruple systems emphasizes the importance of understanding planet formation in this context (Cuntz et al. 2022). High-order systems are generally hierarchical in nature because these are inherently more stable (Tokovinin 2021, and references therein). Depending on the relative orientation of the inner and outer orbital planes, they can experience von Zeipel–Lidov–Kozai oscillations, through which orbital eccentricity and the relative alignment angle can vary over broad ranges on secular timescales (von Zeipel 1910; Lidov 1962; Kozai 1962). Most importantly, their dynamical influence on surrounding gas and dust is necessarily more complex than that of a binary system, potentially leading to different disk truncation thresholds, complex variability of accretion onto the individual stars, and multiple precession timescales and axes (e.g., Martin et al. 2022; Ceppi et al. 2022, 2023). GW Ori is a well-studied example of a triple-lined spectroscopic system that contains a circumtriple disk whose dynamics is strongly affected by its orbital configuration (Czekala et al. 2017; Bi et al. 2020; Kraus et al. 2020). In this study, we focus on wider, visual binaries, which also offer stable locations for individual, circumstellar disks.

GG Tau and UX Tau are two hierarchical high-order systems in the L1551 cloud in the Taurus star-forming region. Since they both host multiple disk components, they are ideal test-beds to assess the dynamical effects of multiple systems on their surrounding material. GG Tau is composed of a hierarchical triple system, GG Tau A, separated by 10″ from a binary system, GG Tau B (Leinert et al. 1993). The close binarity of GG Tau Ab was discovered by Di Folco et al. (2014) and its projected separation of ≈4 au suggested an orbital period of a few years. A massive gas and dust disk surrounds GGTauA (Guilloteau et al. 1999; Phuong et al. 2020) and several streamers of material connect it to small circumstellar disks associated with both GG Tau Aa and Ab (Roddier et al. 1996; Silber et al. 2000; Beck et al. 2012; Keppler et al. 2020). While it is expected that the orbital motion of the GG Tau Aa–Ab pair is responsible for carving the cavity inside of the massive disk, there remains some tension between the cavity size and binary orbit, and it is likely that the orbit and disk are not in a coplanar configuration (Beust & Dutrey 2006; Köhler 2011; Nelson & Marzari 2016; Aly et al. 2018; Keppler et al. 2020; Toci et al. 2024).

UX Tau is a quadruple system (Reipurth & Zinnecker 1993), with the close binarity of UX Tau B first reported by Duchêne (1999). Subsequent monitoring revealed significant orbital motion, although it remained insufficient for precise orbital fitting (Schaefer et al. 2014). While UX Tau B does not host circumstellar matter, UX Tau A harbors a well-studied transitional disk (e.g., Andrews et al. 2011; Akeson et al. 2019). UX Tau C represents a more complex case: despite a lack of near-infrared excess (White & Ghez 2001; McCabe et al. 2006), it was found to be associated with both gas and dust (Zapata et al. 2020; Ménard et al. 2020). Most strikingly, these studies identified tidal trails extending from the UX Tau A disk that suggest a direct dynamical interaction between the two components. Considering hydrodynamical simulations of different configurations, Ménard et al. (2020) concluded that the pair recently underwent an inclined prograde flyby, during which UX Tau C may have captured material from the UX Tau A disk.

In this paper, we present new high-resolution observations of the close GG Tau Ab and UX Tau B subsystems (Sect. 2), revealing (nearly) full orbital coverage and enabling precise orbital fits (Sect. 3.1). From these, we derive dynamical masses for the systems (Sect. 3.2) and constrain their geometry relative to the other components of the systems and to the various disks they host (Sect. 3.3). In Sect. 4, we discuss the implications of our findings on the stellar properties, the survival of compact circumstellar disks in close binaries, and the overall stability and dynamics of the systems.

2 Observations and detection of the companions

For both systems, our analysis combines published astrometry with new analysis of archival data. In this section, we describe how we processed the latter to determine the relative astrometry at new epochs.

2.1 GG Tau Ab

GG Tau has been imaged at 2 µm with the NIRC2 instrument behind the Keck II adaptive optics system at five epochs from 2010 to 2019 (PIs: A. Ghez, J.-L. Margot, J. Lu). In all cases, a number of short exposures were used to avoid saturation on the bright GG Tau A. We retrieved the pipeline-calibrated data, subtracted a global frame median to remove any residual background, and performed image alignment and median combination to produce “epoch average” frames. Because the separation of the GG Tau Aa–Ab pair is only ≈0″.25, much smaller than the atmospheric anisoplanetism angle, and assuming that it is a point source, we can consider GGTauAa as a perfectly matched PSF that can be used to test whether the Ab component is itself resolved as a close pair. In 2010, we do not see any evidence that GG Tau Ab is resolved, indicating that its separation and/or flux ratio was too small. In all other epochs, there is evidence for deviation from a single point source. The presence of the Ab2 component is most conspicuous in the 2019 data at a position angle of ≈250º but is also perceivable in the other epochs (see Fig. 1).

To estimate the relative astrometry of the system, we performed a non-linear least square fit using the Levenberg–Marquart algorithm as implemented in lmfit in which we modeled GG Tau Ab as the linear combination of two translated and scaled copies of GG Tau Aa. While the quality of the adaptive optics correction varies from epoch to epoch, and the fit is consequently sensitive to the initial guesses, we find that this approach is robust by performing the fit at the individual frame level (rather than on the epoch average frame) and use the standard deviation of the mean of these individual fits as an estimate of the random errors. Furthermore, we ran the binary fit with a range of initial parameters and used the range of resulting parameter values to evaluate the systematic uncertainties. In most cases, the latter dominate over the random uncertainties, and we consistently adopted the largest of the random and systematic uncertainties. This fitting process also yields the flux ratio of the system. In the case of a close asymmetric pair, however, the flux ratio and separation are generally correlated. This source of uncertainty is encapsulated in the methodology described above. As a consistency check, we also fitted the image of GG Tau Ab as a single star; the resulting residuals are shown in the last column of Fig. 1. As expected from fitting a binary system as a single star, they contain a strong positive-negative-positive pattern along the binary position angle, further confirming the binary nature of the system.

Interferometric H-band observations with PIONIER were obtained in 2013 and 2015 (PI: E. Di Folco) to follow up on the 2012 discovery observations. Two datasets were obtained in 2015, but only the 2015/12/21 was of sufficient quality. The data were reduced using the PIONIER pipeline, similar to the results presented in Di Folco et al. (2014). We then fitted a model consisting of two point sources to the calibrated visibilities and phases. The resulting χ2 maps are shown in Fig. 2. We note that the fits are imperfect in both epochs due to contamination from the nearby GG Tau Aa, but we consider that the relative astrometry of the close GGTauAb pair is well determined nonetheless. In both the published 2012 and the new 2013 observations, PIONIER was set in its broadband mode, resulting in a very sparse sampling of the (u, υ) plane and, consequently, in ambiguous results. Two possible solutions from the 2012 data were reported by Di Folco et al. (2014) and we find three plausible solutions in 2013. In 2012, we could resolve the ambiguity by comparison with the nearly contemporaneous (2 days difference) Keck observations. We find that the slightly less likely “second” solution matches very well with our Keck result whereas the most likely solution differs in position angle by 10º (see Fig. 4), a large enough deviation that we can confidently rule it out. In 2013, two of the three possible solutions have a separation of ≈0″.039 while the third has a separation of 0″.031. The latter is visually much more consistent with the orbital motion observed in the Keck images between 2012 and 20141. We therefore adopted the latter solution. In 2015, PIONIER was used in its spectrally dispersed mode, producing a significantly improved (u, υ) coverage and there is only one possible binary solution, which we adopt. We assigned the same astrometric uncertainties to both new PIONIER epochs, as systematic uncertainties are likely to dominate the error budget of such measurements. In principle, this analysis also yields an estimate of the binary flux ratio. Unfortunately, the presence of the nearby GG Tau Aa components introduces a systematic offset in the measured correlated fluxes, which translates to a large systematic error on flux ratio. We could not properly assess this effect without independent simultaneous measurement of the GG Tau Aa–Ab flux ratio and, therefore, could not reliably determine the flux ratio of GG Tau Ab itself from the PIONIER data.

thumbnail Fig. 1

Thumbnails of Keck/NIRC2 images in the GG Tau system. The first and second columns represent GG Tau Aa and GG Tau Ab, normalized to their peak values, respectively. The third column is the best-fit model of GG Tau Ab created by shifting and scaling two copies of GG Tau Aa, and the fourth column is the residuals from this model. Red and blue regions are negative and positive residuals, respectively, with the color map saturating at ±3% of the peak pixel in the image of GG Tau Ab. The fifth column shows the result of subtracting the model of GG Tau Ab 1 (centered on the black cross) from the image of GG Tau Ab, revealing GG Tau Ab2, which is scaled up by a factor of four for visual purposes. The last column shows the residuals of fitting GG Tau Ab as a single star instead; they are displayed with the same saturation levels as in the fourth column for direct comparison.
thumbnail Fig. 2

Reduced χ2 maps for the location of GG Tau Ab2 in the new PIONIER observations presented here. In the 2013 epoch, solution “a” is both the most likely from a pure likelihood perspective, and it is also the most plausible based on the motion observed between the 2012 and 2014 Keck observations (see Sect. 2.1). The second and third highest likelihood solutions (labelled “b” and “c”), located to the West-Southwest of the primary solution, are also illustrated in Fig. 4.
thumbnail Fig. 3

Thumbnails of HST/WFCP2, Gemini/NIRI and VLT/SPHERE images in the UX Tau system. The columns are similar to those in Fig. 1, except that no flux scaling is applied to UX Tau Bb in the last column.

2.2 UX Tau B

The projected separation of the UX Tau B pair was ≈0″.14 in its 1997 discovery epoch (Duchêne 1999), enabling multiple follow-up observations up to 2013 (Correia et al. 2006; Schaefer et al. 2014). We found two unpublished observations of the system in that same period in which the pair is clearly resolved, using HST/WFPC2 and Gemini/NIRI in 1997 and 2009, respectively (PIs: K. Stapelfeldt and P. Allen). We performed a similar analysis to the Keck/NIRC2 images of GG Tau discussed above to estimate the relative astrometry of the UX Tau B pair. Results are illustrated in the top two rows of Fig. 3. The HST/WFPC2 observations were obtained with two filters, which provide consistent estimates of the binary astrometry, but find that the flux ratio is wavelength-dependent: it rises from 0.5 to 0.64 between 0.6 and 0.8 µm.

More recently, UX Tau was observed at multiple epochs in 2015–2017 with the VLT/SPHERE adaptive optic systems using the IRDIS dual-channel mode (PIs: J.-L. Beuzit, M. Benisty). We discarded one epoch in which the quality of the observations were of insufficient quality and again performed a similar binary fit as above. In most SPHERE observations UX Tau A is either saturated or placed behind a coronagraphic mask and we therefore used UX Tau C as estimate of the contemporaneous PSF. As shown in Fig. 3, the model residuals in some epochs are not negligible and elongated. We interpret this as evidence that the distance between the UX Tau C and UX Tau B is sufficient for deviations in the PSF to be present. Indeed, the position angle of the B–C pair is ≈115°, roughly aligned with the PSF elongation. Another possibility is that the UX Tau C is marginally resolved due to scattering off its circumstellar dust, which was found to be elongated roughly along the North-South direction (Ménard et al. 2020). Either way, as UX Tau B is generally well-resolved, we trust that the binary astrometry is well determined with the systematic uncertainties that we estimated using the same method as for GG Tau Ab.

3 Results

3.1 Relative astrometry and orbital fits

All published and new astrometric results are represented in Table 1 and illustrated in Fig. 4. In both cases, the new observations presented here represent a significant improvement in the orbital coverage of both systems. For GG Tau Ab, not only do we present the first observation of orbital motion, but the system has nearly completed a full orbit between 2011 and 2019. Indeed, this ≈8 yr period further confirms the tentative “a posteriori detection” in 2003 discussed by Di Folco et al. (2014) if we adopt a position angle of ≈245° for that epoch. In the case of UX Tau B, while the position angle of the system had changed by ≈60° between 1998 and 2013, the new SPHERE observations represent a change of ≈270° in the subsequent 2 yr, and rapid year-by-year motion is evident between 2015 and 2017. These most recent observations lie at intermediate position between the 25 and 40 yr-period orbits presented by Schaefer et al. (2014). This improved coverage invites orbital fits, which we expect to be well constrained by existing observations.

To perform the orbital fit, we used the orbitize! package (Blunt et al. 2020) in combination with the parallel-tempered package ptemcee (Vousden et al. 2016). Given the tentative nature of the 2003 detection from Di Folco et al. (2014), and our lack of success in detecting GG Tau Ab2 in VLT/NaCo images at any epoch, we decided against using it in the fit. We nonetheless verified that, given its poor astrometric precision, including it would not significantly alter the fit. The free parameters used in orbitize! are the eccentricity (e), inclination (i), phase of periastron (τ0, measured relative to the earliest data point), position angle of the line of nodes (Ω), argument of periastron (ω), semi-major axis (a), and total system mass (Msys). During the fit, we fixed the parallax of the system to π = 6.91 mas (the median L1551 estimate from Galli et al. 2019, see Sect. 3.2) to convert from angular to physical separations, and we further converted Msys into the orbital period (P) and τ0 into the time of passage at periastron, T0. These three quantities are those readily constrained by the data. Uniform priors are used for e, ω, Ω and τ0, log-uniform and sine-uniform are used for a and i, respectively, and a Gaussian prior is used for Msys. In the absence of radial velocity measurements, solutions defined by (ω, Ω) and (ω + 180°, Ω + 180°) are degenerate; when extracting the MCMC chains, we solve the ambiguity by enforcing that 0° ≤ Ω < 180°. We applied broad priors on Msys that were informed by preliminary estimates of the semi-major axis and orbital period. Specifically, we used 1.0±0.5 M⊙ and 2±1 M⊙ for GG Tau Ab and UX Tau B, respectively. We performed each fit with ten temperatures and 100 walkers per temperature, and advanced the chains 40 000 steps past an initial 1000 steps of burn-in, and only kept every tenth walker position to remove correlations in the chains. Inspection of the chain evolution confirms that they have reached convergence. The resulting cornerplots are presented in Appendix A and 68-percentile for all parameters are listed in Table 2. We note that the large orbital coverage is such that there is no strong correlation between orbital parameters, with the exception of Ω and ω. The location of the periastron is nonetheless well constrained in both cases (see Fig. 5). Finally, we note that we have adopted the astrometric solution with i ≤ 90° instead of the solution with i > 90°, as justified in Sect. 3.3, even though the data at hand do not allow to solve that ambiguity.

The orbital fits for both systems are reasonable but, as indicated in Fig. 5, neither of the best orbital fit reaches min 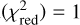, suggesting some underestimates of the astrometric uncertainties and/or the presence of outliers. We inspected the fit residuals and determined that the 2014 measurement of GG Tau Ab and the 1997, 1998 and 2015 measurements of UX Tau B were the most discrepant (at the ≈2.5–3σ level). We therefore repeated the orbital fit with “trimmed” datasets, namely excluding the 2014 measurement of GG Tau Ab, and the 19982 and 2015 measurements of UX Tau B. In both cases, the fits to the “trimmed” dataset produces a much better fit, with min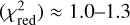. The confidence intervals for the “complete” and “trimmed” dataset overlap at the 1σ level, confirming that no datapoint biases the fit significantly. In most cases, the resulting uncertainties on orbital parameters are comparable for both fits, with the main exception being the semi-major axis and, consequently, system mass for GG Tau Ab. We conservatively adopt the “trimmed” dataset fit for the subsequent analysis.

Table 1

Astrometry of the GG Tau Ab and UX Tau B systems.

thumbnail Fig. 4

Relative orbit of the GG Tau Ab and UX Tau B binaries. In both panels, orange symbols represent published astrometric datapoints whereas blue symbols indicate new adaptive optics or HST observations that are presented here for the first time. In 2012 and 2013 (orange and red symbols, respectively), the PIONIER observations of GG Tau Ab allowed two and three possible solutions, respectively. Based on the Keck observations, solutions “a” in both epochs are the most plausible ones.
Table 2

Orbital parameters of the GG Tau Ab and UX Tau B systems.

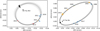thumbnail Fig. 5

Random set of 100 orbital solutions selected form the converged part of the MCMC chain for the GG Tau Ab and UX Tau B binaries (considering the “trimmed” dataset, see Sect. 3.1). Black + symbols indicate the periastron of each plotted orbit.

3.2 Dynamical masses

We then proceeded to convert the orbital solutions in terms of angular scale to physical scale, which requires determining the distance to the two systems. Specifically, Msys = a3 P−2 D3 M⊙, where a, P and D are expressed in arcsec, yr and pc, respectively. GG Tau A is included in the Gaia DR3 catalog (Gaia Collaboration 2016, 2023) but with a very poor RUWE parameter, most likely because of the internal orbital motion of the Aa–Ab pair. GG Tau Ba and GG Tau Bb are in the Gaia DR3 catalog with good RUWE parameters, however. Their parallaxes are 6.87±0.04 and 6.75±0.15 mas, respectively. Similarly, UX Tau B has a bad RUWE parameter and its Gaia DR3 parallax cannot be trusted but UX Tau A and C have good measurements, with parallaxes of 7.03±0.03 and 6.92±0.07 mas, respectively. In both cases the available measurements are marginally consistent with each other. We also note that both GG Tau and UX Tau are part of the L1551 group, for which the mean parallax and associated dispersion is 6.91 ±0.16 mas (Galli et al. 2019). Since the latter is consistent with all individual estimates and is more conservative, we adopted the L1551 parallax to determine the dynamical mass of both systems and consider that its associated uncertainty represents a systematic uncertainty, which we carry separately in Table 2 and illustrate in Fig. 6. For both systems, the systematic uncertainty is commensurate with, but smaller than, the random uncertainty.

Table 3

Angles defining key planes in the GG Tau and UX Tau systems.

thumbnail Fig. 6

Posterior distribution for the dynamical mass of the GG Tau Ab and UX Tau B systems. In both cases, dashed and solid histograms represent the distributions using “complete” and “trimmed” astrometric datasets, respectively. The black horizontal bars represent the systematic error introduced by the uncertainty on the distance to each system.

3.3 System architectures

Since the orbit properties of both systems are well constrained, we can compare the relative orientation of their orbital plane with other relevant planes in each system (see Table 3 and Fig. 7), as this is relevant to the stability and dynamical evolution of multiple systems and their associated disks. We computed the angle between two (orbital or disk) angular momentum vectors, ∆θ, following Eq. (1) in Czekala et al. (2019), using Monte Carlo method to sample the input posterior distributions. We note that for visual orbits, there is an inclination ambiguity whereby orbits with i and 180° −i inclinations (and, conjointly, ω and 360° −ω argument of periastron) are indistinguishable in the plane of the sky. When comparing with other planes, we must therefore consider two alternative deprojection solutions. In the case of GG Tau, we note that with inclinations of ≈35–40°, adopting the alternative inclination leads to orbits that are nearly perpendicular to each other. Similarly, the wider GG Tau Aa–Ab orbit is either close to coplanar or nearly perpendicular to the outer ring. While circumbinary disk in a polar configuration and highly misaligned hierarchical triple systems exist (e.g., Tokovinin 2017; Czekala et al. 2019), we focus here on the configurations that are close to coplanar. We also note that the relative orientation of the tighter orbit with respect to the circumtriple disk does not significantly affect the evolution of the system (Ceppi et al. 2023).

In the GG Tau A system, we can compare the Abl–Ab2 orbital solution we have obtained to the updated Aa–Ab orbit presented in Toci et al. (2024). Because the latter is only modestly constrained, the resulting misalignment angle is only loosely constrained. The most plausible value is ~12°, suggesting only a modest degree of misalignment between the two orbits. It is worth noting that the Aa–Ab pair has a distribution of periastron distances (a(1 − e)) of 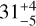au, which is about five times larger than the apoastron distance of the Ab1–Ab2 pair. This ratio is relevant in the context of the dynamical stability of the system (see Sect. 4.3). Another well-characterized plane in the GG Tau A system is that of the massive dust ring that surrounds it. Excluding the near polar configurations, we find that both orbits have low relative inclinations to the ring, with peaks in the posteriors of ∆θ ≈ 7° and 20° for the Aa–Ab and Ab1–Ab2 orbits, respectively.

Prior to this study, no orbit had been estimated in the UX Tau system due to the long orbital period associated with the large projected separations, and correspondingly long orbital periods, of the A–C and A–B pairs. It has not even been demonstrated whether they are physically bound, although it is statistically likely (e.g., Leinert et al. 1993). The apoastron distance of the Ba-Bb pair we find, ≈20 au, is ≈40 times smaller than the A–B projected separations. Regarding the orbital plane, the only other plane that is well determined in the system is that of the UX Tau A disk (Francis & van der Marel 2020; Zapata et al. 2020; Ménard et al. 2020). Considering the two ambiguous solutions, we find that the UX Tau Ba–Bb orbit is either mildly misaligned (∆θ ≲ 25° with a peak in the posterior at ∆θ ≈ 10°) with, or highly tilted (∆θ = 115 ± 25°) relative to the UX Tau A disk.

thumbnail Fig. 7

Angle between the orbital and ring angular momentum vectors in the GG Tausystem. In all cases, we solve the orbital inclination ambiguity by assuming that the planes are close to coplanar.
thumbnail Fig. 8

Orbital properties of T Tauri visual binaries. In both panels, black diamonds and green crosses represent ≲3 Myr-old systems with and without circumstellar material, respectively, while yellow crosses are ~ 10–20 Myr-old disk-free systems in Upper Scorpius and the TW Hya association. The two red stars mark the systems studied here. Left: comparison of orbital period and eccentricity based on literature results listed in Appendix B. Right: comparison of periastron distances and dynamical masses for the same systems.

4 Discussion

4.1 Stellar properties

The dynamical masses derived in this study must be interpreted in light of past studies of both systems. Here we consider how our results modify our understanding of the stellar properties in these systems.

GG Tau is among the best-studied T Tauri multiple systems, in large part because of the massive dust ring and gaseous disk that surrounds GG Tau A. Its gas dynamics has allowed for precise estimates of the total dynamical mass of GG Tau A (e.g., Guilloteau et al. 1999). Most recently, Phuong et al. (2020) derived a total system mass of 1.41 ±0.08 M⊙ (scaled to a distance of 145pc adopted here). Combined with our GG Tau Ab dynamical mass, this implies that the mass of GG Tau Aa is 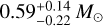, with the GG Tau Ab subsystem being at least as massive as, and up to ~ 60% more massive than, GG Tau Aa. The spectral types for GG Tau Aa and Ab have been estimated at K7–M0 and M0.5–M2, respectively (White et al. 1999; Hartigan & Kenyon 2003). Based on the observed range of dynamical masses for single stars in Taurus (Simon et al. 2019; Braun et al. 2021; Flores et al. 2022), we estimate that GG Tau Aa is most consistent with a ≈0.6 M⊙ mass. Similarly, we propose that GG Tau Ab1 and Ab2 have masses of ≈0.5–0.6 M⊙ and ≈0.2–0.3 M⊙, respectively. The observed K band flux ratio of the Ab1–Ab2 pair, if interpreted as representative of the stellar photospheres, would be most consistent a 1:3 mass ratio based on the BT-Set11 models (Allard et al. 2012), but we caution that the presence of continuum emission from circumstellar material precludes reaching a definitive conclusion without spatially resolved spectroscopy.

In the absence of a circumstellar disk whose Keplerian motion could be used (e.g., Akeson et al. 2019), the dynamical mass estimate we obtained for UX Tau B is the first for this component. Spectroscopic observations have led to a spectral type estimate of M1–M2 (Hartigan et al. 1994; White & Ghez 2001; Luhman 2018). Based on the compilation of Taurus dynamical masses mentioned above, this would suggest a 0.5–0.7 M⊙ mass for the individual masses, somewhat in tension with the dynamical mass of ≈1.5 M⊙ that we obtain. The systematic uncertainty introduced by the distance to the system does not appear large enough to account for this mismatch. We note, however, that the mass ratio of the close pair appears close to unity based on flux ratio measurements (Duchêne 1999; Correia et al. 2006; Schaefer et al. 2014) and it is possible that a slightly earlier spectral type (≈M 0.5) for both stars would be consistent with the derived dynamical mass.

4.2 Orbital properties and circumstellar matter

We now consider the implications of the orbital properties we have inferred for the two systems. We first note that, while GG Tau Ab has a moderate eccentricity, UX Tau B is among the highest eccentricity systems known among pre-main sequence visual binaries (see Fig. 8). Among main sequence binary systems, such a high eccentricity is also close to the maximum observed for this range of orbital periods (Raghavan et al. 2010). This limit is set by the onset of (partial) tidal circularization over the lifetime of the system. Therefore, the system could survive if its current configuration as far as interactions between individual stars are concerned.

The complete orbital solutions we have found place stringent constraints on where gas and dust can be maintained in a stable configuration. In particular, the similar ≈1.6 au periastron distances for both systems imply that circumstellar disks around each star can be no larger than <1 au. No infrared excess is detected in UX Tau B but there is one in GG Tau Ab, which is also found to be accreting (White & Ghez 2001; McCabe et al. 2006). Irrespective of which of the two components hosts this material, this proves that it is possible for extremely compact disks to survive in close binaries, despite the general tendency against it (Cieza et al. 2009; Kraus et al. 2012, see also Fig. 8) or the expectation of a very short viscous timescale (≲0.05 Myr, Cieza et al. 2009). Indeed, there is at least one system with an even smaller periastron distance, similar eccentricity, and confirmed infrared excess (ROXs 47, Rizzuto et al. 2016). The presence of streamers from the massive outer ring onto both GG Tau Aa and Ab (Keppler et al. 2020) confirms that continuous feeding of (small) circumstellar disks is likely ongoing, providing a possible explanation to the disk survival and ongoing accretion. We speculate that the lack of circumstellar material around either component of UX Tau B is due to a lack of outer reservoir that can feed the system, possibly compounded by its high eccentricity. Indeed, the higher binary eccentricity leads to regions of stable orbits around either component that are simply too small to sustain long-lived disks.

We find that the two orbital planes in the GG Tau system have a modest degree of misalignment (∆θ ~ 5–20°) with each other and with the circumtriple ring, in line with a scenario in which the entire system formed from a single core undergoing collapse and fragmentation (Offner et al. 2023). It is worth pointing out that the naive expectation would be for the circumtriple ring to be coplanar with the invariable plane of the triple system, which is distinct from the two orbital plane themselves, especially so since the Ab subsystem is somewhat more massive than the Aa component. We also stress that without radial velocity measurements or additional dynamical considerations (size of the circumtriple ring, three-body stability), we cannot exclude the orbital solutions in which the ring is on a roughly polar orbit around the Aa–Ab system.

4.3 System stability and dynamics

Hierarchical triple systems are prone to disruptive instability if their orbital properties are such that all three star-star separations become commensurable at some point along the orbits. In order to remain stable, it is therefore necessary that the tightest pair be much more compact than the separation to the outer third component. This has been extensively empirically verified for main sequence systems (e.g., Tokovinin 2014, 2021). Furthermore, numerical studies have explored this boundary, taking into account orbital eccentricity and deviation from coplanarity and over a broad range of mass ratios (Eggleton & Kiseleva 1995; Mardling & Aarseth 2001; He & Petrovich 2018). With its large projected separation relative to the semi-major axis of the close binary, the UX Tau A–B system is comfortably in a stable configuration. The case of GG Tau A is not as extreme, yet both its ratio of orbital periods (≳25) and the ratio of periastron of the outer orbit to periastron of the inner orbit (see Sect. 3.3) place it in the stable regime (He & Petrovich 2018) and among “typical” systems (Tokovinin 2021). We note, however, that this assessment assumes that the evolution of the system is driven exclusively by N-body dynamics, whereas continued accretion of gas and the interaction with the massive outer ring could further modify either orbits. Therefore, the long-term stability of the system cannot be definitively confirmed yet.

Beyond the simple ratio of orbital periods, the stability of the system could be affected by the interplay of von Zeipel–Lidov–Kozai oscillations in the triple system with the presence and dynamics of circumstellar disks. In order for these oscillations to take place, the misalignment angle between the two orbital planes must be ∆θ ≳ 40°. One of the two possible deprojection solutions has a modest misalignment angle (∆θ ≈ 15°), lower than the threshold for the von Zeipel–Lidov–Kozai mechanism to be triggered. This solution is broadly consistent with the statement that triple systems are generally mildly misaligned when the outer orbit is wider than ≈50 au (Tokovinin 2017). We also note that in this situation, the ratio of ~25–100 between the inner and outer orbital periods favors a low-to-moderate eccentricity for the outer GG Tau Aa–Ab system (Sterzik & Tokovinin 2002), which is independently more plausible to account for the inner radius of the circumtriple ring (Toci et al. 2024). In the alternative deprojection solution, however, von Zeipel–Lidov–Kozai mechanism would be triggered and both the misalignment angles and the orbital eccentricities should go through large oscillations. Given an orbital period of a few centuries and a moderate eccentricity for the GG Tau Aa–Ab orbit (Köhler 2011; Toci et al. 2024), the timescale of these oscillations should be ≲105 yr (Hamers 2021), significantly shorter than the age of the system but still much longer than the current orbital coverage.

Finally, we note that we have so far mostly considered UX Tau as a triple system containing the A and B components. As noted by Zapata et al. (2020) and Ménard et al. (2020), the morphology of extended spiral arms in the UX Tau A disk and the presence of circumstellar dust and gas associated with UX Tau C point to the strong dynamical influence of the latter. However, considering that UX Tau B system is an order of magnitude more massive than UX Tau C (Kraus & Hillenbrand 2009), it is possible that the close binary could also have a significant dynamical influence on the UX Tau A disk. Conversely, it is also possible that UX Tau C will alter the orbit of UX Tau B in case a reasonably close fly-by. The relative astrometry between the two components is not currently known sufficiently well to explore this possibility at this stage, however.

5 Conclusion

We have presented new adaptive optics and interferometric observations of the close binary systems GG Tau Ab and UX Tau B, which are both part of higher order multiple pre-main sequence systems. In both cases, the observations provide sufficient orbital coverage (≈60–100%) to tightly constrain the Keplerian orbits, with orbital periods of ≈8 and 32 yr for GG Tau Ab and UX Tau B, respectively.

Deriving dynamical masses for both systems, we find that GG Tau Aa and the combined Ab subsystem have similar masses, ≈0.6–0.8 M⊙, consistent with the known spectral types of the two components and the near-infrared flux ratio of the Ab subsystem. In the case of UX Tau B, we find its dynamical mass of 1.5 M⊙ to be somewhat higher than expected but could be reconciled if the two components are of equal mass and of slightly earlier spectral type than reported in the literature.

The orbital solution we obtain for both systems are eccentric, but markedly more so for UX Tau B (e ≈ 0.87). Along with the lack of outer reservoir that could feed the system, this high eccentricity could explain the lack of circumstellar dust in the subsystem, as stable orbits are confined to ≲1 au or ≳50 au.

While the orbit of the outer components of the system are moderately constrained (GG Tau Aa–Ab) or completely unconstrained (UX Tau A–B), we find it likely that the triple systems are stable on the long term and, thus, that they could contribute to the growing population of exoplanets in multiple systems observed in the field. The most important caveats to this assessment are in the GG Tau system, where 1) ongoing accretion could further alter the orbits, and 2) one of the possible deprojection solution implies a near-polar configuration for the triple system in which large von Zeipel–Lidov–Kozai oscillations would play a major role.

In both systems, new, dedicated hydrodynamical simulations are warranted to further explore the dynamics of both the stars and the gas+dust components in both systems. Planet formation in multiple system is an increasingly central topic is modern astronomy and these systems not only represent arguably typical systems but their properties are now known with high precision. Establishing with precision the orbital arrangement of young stars with discs will be pivotal to understand the long term evolution of discs in multiple stellar systems. This aspect is crucial to eventually pinpoint the locations at which planet(esimals) could form in such multiples.

Acknowledgements

We are grateful to an anonymous referee whose comments helped improve this manuscript. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon Europe research and innovation program (grant agreement no. 101053020, project Dust2Planets; grant agreement no. 101042275, project Stellar-MADE). This research has made use of the Keck Observatory Archive (KOA), which is operated by the W.M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST) at the Space Telescope Science Institute. Some of the data presented in this paper were obtained as part of ESO programs 096.C-0241, 097.C-0865, 198.C-0209, and 0100.C-0452, and retrieved from the ESO archive. M. Langlois acknowledges funding from the French National research agency (grant DDISK, ANR-21-CE31-0015-01). The reduced and calibrated PIONIER data presented here will be made available in the Optical Interferometry DataBase (Haubois et al. 2014), hosted by the Jean-Marie Mariotti Center (http://oidb.jmmc.fr/index.html).

Appendix A Cornerplots for the orbital fits

In Figures A.1 and A.2, we present the MCMC cornerplot resulting from the orbital fits to the GG Tau Ab and UX Tau B systems, respectively. The 180º ambiguity on ω and Ω is inherent to visual orbits and the two families are collapsed when computing the confidence intervals on all orbital parameters. We also note that the line of nodes is not defined for i = 0º, which explains the wide spread of solutions for ω and Ω at the lowest inclinations for the UX Tau B system.

thumbnail Fig. A.1

MCMC cornerplot resulting from the orbital fit to the GG Tau Ab orbit. While orbitize! converged on the solution with i > 90º, we adopt the equivalent supplementary angle, which match the convention of the circumtriple ring.
thumbnail Fig. A.2

MCMC cornerplot resulting from the orbital fit to the UX Tau B orbit.

Appendix B Orbits of pre-main sequence visual binaries form the literature

Here we compile the visual pre-main sequence binaries with published orbital solutions. When multiple solutions have been published, we adopted the most recent solution. Only systems with orbital periods P < 50 yr are considered here to ensure good orbital coverage, commensurable with that we obtained for GG Tau Ab and UX Tau B. We excluded HBC 351 from the sample as it is most likely to be a member of the 120Myr-old Plieades open cluster (Luhman et al. 2009).

Table B.1

Orbital solutions for visual pre-main sequence binaries. Systems marked with a † symbols are members of the Upper Scorpius or TW Hydra association, whose age (~ 10–20 Myr) is such that the absence of a disk may no longer be a consequence of multiplicity.

References

  1. Akeson, R. L., Jensen, E. L. N., Carpenter, J., et al. 2019, ApJ, 872, 158 [Google Scholar]
  2. Allard, F., Homeier, D., & Freytag, B. 2012, Philos. Trans. Roy. Soc. Lond. Ser. A, 370, 2765 [NASA ADS] [Google Scholar]
  3. Aly, H., Lodato, G., & Cazzoletti, P. 2018, MNRAS, 480, 4738 [NASA ADS] [Google Scholar]
  4. Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [Google Scholar]
  5. Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [Google Scholar]
  6. Beck, T. L., Bary, J. S., Dutrey, A., et al. 2012, ApJ, 754, 72 [NASA ADS] [CrossRef] [Google Scholar]
  7. Belinski, A., Burlak, M., Dodin, A., et al. 2022, MNRAS, 515, 796 [NASA ADS] [CrossRef] [Google Scholar]
  8. Beust, H., & Dutrey, A. 2006, A&A, 446, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bi, J., van der Marel, N., Dong, R., et al. 2020, ApJ, 895, L18 [Google Scholar]
  10. Blunt, S., Wang, J. J., Angelo, I., et al. 2020, AJ, 159, 89 [NASA ADS] [CrossRef] [Google Scholar]
  11. Boden, A. F., Torres, G., Duchêne, G., et al. 2012, ApJ, 747, 17 [NASA ADS] [CrossRef] [Google Scholar]
  12. Braun, T. A. M., Yen, H.-W., Koch, P. M., et al. 2021, ApJ, 908, 46 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ceppi, S., Cuello, N., Lodato, G., et al. 2022, MNRAS, 514, 906 [CrossRef] [Google Scholar]
  14. Ceppi, S., Longarini, C., Lodato, G., et al. 2023, MNRAS, 520, 5817 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cieza, L. A., Padgett, D. L., Allen, L. E., et al. 2009, ApJ, 696, L84 [NASA ADS] [CrossRef] [Google Scholar]
  16. Correia, S., Zinnecker, H., Ratzka, T., et al. 2006, A&A, 459, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cuello, N., Ménard, F., & Price, D. J. 2023, Eur. Phys. J. Plus, 138, 11 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cuntz, M., Luke, G. E., Millard, M. J., et al. 2022, ApJS, 263, 33 [NASA ADS] [CrossRef] [Google Scholar]
  19. Czekala, I., Andrews, S. M., Torres, G., et al. 2017, ApJ, 851, 132 [NASA ADS] [CrossRef] [Google Scholar]
  20. Czekala, I., Chiang, E., Andrews, S. M., et al. 2019, ApJ, 883, 22 [NASA ADS] [CrossRef] [Google Scholar]
  21. Di Folco, E., Dutrey, A., Le Bouquin, J.-B., et al. 2014, A&A, 565, A2 [Google Scholar]
  22. Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
  23. Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
  24. Duchêne, G., Ghez, A. M., McCabe, C., et al. 2003, ApJ, 592, 288 [CrossRef] [Google Scholar]
  25. Dutrey, A., Guilloteau, S., & Simon, M. 1994, A&A, 286, 149 [NASA ADS] [Google Scholar]
  26. Eggleton, P., & Kiseleva, L. 1995, ApJ, 455, 640 [NASA ADS] [CrossRef] [Google Scholar]
  27. Flores, C., Connelley, M. S., Reipurth, B., et al. 2022, ApJ, 925, 21 [NASA ADS] [CrossRef] [Google Scholar]
  28. Francis, L., & van der Marel, N. 2020, ApJ, 892, 111 [Google Scholar]
  29. Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Galli, P. A. B., Loinard, L., Ortiz-Léon, G. N., et al. 2018, ApJ, 859, 33 [Google Scholar]
  32. Galli, P. A. B., Loinard, L., Bouy, H., et al. 2019, A&A, 630, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Guilloteau, S., Dutrey, A., & Simon, M. 1999, A&A, 348, 570 [NASA ADS] [Google Scholar]
  34. Hamers, A. S. 2021, MNRAS, 500, 3481 [Google Scholar]
  35. Harris, R. J., Andrews, S. M., Wilner, D. J., et al. 2012, ApJ, 751, 115 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hartigan, P., & Kenyon, S. J. 2003, ApJ, 583, 334 [Google Scholar]
  37. Hartigan, P., Strom, K. M., & Strom, S. E. 1994, ApJ, 427, 961 [NASA ADS] [CrossRef] [Google Scholar]
  38. Haubois, X., Bernaud, P., Mella, G., et al. 2014, Proc. SPIE, 9146, 91460O [NASA ADS] [CrossRef] [Google Scholar]
  39. He, M. Y., & Petrovich, C. 2018, MNRAS, 474, 20 [NASA ADS] [CrossRef] [Google Scholar]
  40. Hirsch, L. A., Rosenthal, L., Fulton, B. J., et al. 2021, AJ, 161, 134 [NASA ADS] [CrossRef] [Google Scholar]
  41. Keppler, M., Penzlin, A., Benisty, M., et al. 2020, A&A, 639, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Köhler, R. 2011, A&A, 530, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Konopacky, Q. M., Ghez, A. M., Duchêne, G., et al. 2007, AJ, 133, 2008 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  45. Kraus, A. L., & Hillenbrand, L. A. 2009, ApJ, 704, 531 [Google Scholar]
  46. Kraus, A. L., Ireland, M. J., Hillenbrand, L. A., et al. 2012, ApJ, 745, 19 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kraus, S., Kreplin, A., Young, A. K., et al. 2020, Science, 369, 1233 [NASA ADS] [CrossRef] [Google Scholar]
  48. Kurtovic, N. T., Pérez, L. M., Benisty, M., et al. 2018, ApJ, 869, A44 [Google Scholar]
  49. Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
  50. Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
  51. Luhman, K. L. 2018, AJ, 156, 271 [Google Scholar]
  52. Luhman, K. L., Mamajek, E. E., Allen, P. R., et al. 2009, ApJ, 703, 399 [NASA ADS] [CrossRef] [Google Scholar]
  53. Manara, C. F., Tazzari, M., Long, F., et al. 2019, A&A, 628, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Mardling, R. A., & Aarseth, S. J. 2001, MNRAS, 321, 398 [NASA ADS] [CrossRef] [Google Scholar]
  55. Martin, R. G., Lepp, S., Lubow, S. H., et al. 2022, ApJ, 927, L26 [NASA ADS] [CrossRef] [Google Scholar]
  56. McCabe, C., Ghez, A. M., Prato, L., et al. 2006, ApJ, 636, 932 [CrossRef] [Google Scholar]
  57. Ménard, F., Cuello, N., Ginski, C., et al. 2020, A&A, 639, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Monnier, J. D., Harries, T. J., Bae, J., et al. 2019, ApJ, 872, 122 [Google Scholar]
  59. Nelson, A. F., & Marzari, F. 2016, ApJ, 827, 93 [Google Scholar]
  60. Offner, S. S. R., Moe, M., Kratter, K. M., et al. 2023, Protostars and Planets VII, 534, 275 [NASA ADS] [Google Scholar]
  61. Phuong, N. T., Dutrey, A., Diep, P. N., et al. 2020, A&A, 635, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [Google Scholar]
  63. Ragusa, E., Fasano, D., Toci, C., et al. 2021, MNRAS, 507, 1157 [NASA ADS] [CrossRef] [Google Scholar]
  64. Reipurth, B., & Zinnecker, H. 1993, A&A, 278, 81 [NASA ADS] [Google Scholar]
  65. Reylé, C., Jardine, K., Fouqué, P., et al. 2021, A&A, 650, A201 [Google Scholar]
  66. Riviere-Marichalar, P., Pinte, C., Barrado, D., et al. 2013, A&A, 555, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Rizzuto, A. C., Ireland, M. J., Dupuy, T. J., et al. 2016, ApJ, 817, 164 [NASA ADS] [CrossRef] [Google Scholar]
  68. Rizzuto, A. C., Dupuy, T. J., Ireland, M. J., et al. 2020, ApJ, 889, 175 [NASA ADS] [CrossRef] [Google Scholar]
  69. Roddier, C., Roddier, F., Northcott, M. J., et al. 1996, ApJ, 463, 326 [NASA ADS] [CrossRef] [Google Scholar]
  70. Schaefer, G. H., Prato, L., Simon, M., et al. 2014, AJ, 147, 157 [CrossRef] [Google Scholar]
  71. Schaefer, G. H., Beck, T. L., Prato, L., et al. 2020, AJ, 160, 35 [NASA ADS] [CrossRef] [Google Scholar]
  72. Silber, J., Gledhill, T., Duchêne, G., et al. 2000, ApJ, 536, L89 [NASA ADS] [CrossRef] [Google Scholar]
  73. Simon, M., Guilloteau, S., Beck, T. L., et al. 2019, ApJ, 884, 42 [NASA ADS] [CrossRef] [Google Scholar]
  74. Steffen, A. T., Mathieu, R. D., Lattanzi, M. G., et al. 2001, AJ, 122, 997 [NASA ADS] [CrossRef] [Google Scholar]
  75. Sterzik, M. F., & Tokovinin, A. A. 2002, A&A, 384, 1030 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Sullivan, K., & Kraus, A. L. 2022, ApJ, 928, 134 [NASA ADS] [CrossRef] [Google Scholar]
  77. Tang, S.-Y., Stahl, A. G., Prato, L., et al. 2023, ApJ, 950, 92 [CrossRef] [Google Scholar]
  78. Toci, C., Ceppi, S., Cuello, N., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348470 [Google Scholar]
  79. Tokovinin, A. 2014, AJ, 147, 87 [CrossRef] [Google Scholar]
  80. Tokovinin, A. 2017, ApJ, 844, 103 [NASA ADS] [CrossRef] [Google Scholar]
  81. Tokovinin, A. 2021, Universe, 7, 352 [NASA ADS] [CrossRef] [Google Scholar]
  82. von Zeipel, H. 1910, Astron. Nachr., 183, 345 [Google Scholar]
  83. Vousden, W. D., Farr, W. M., & Mandel, I. 2016, MNRAS, 455, 1919 [NASA ADS] [CrossRef] [Google Scholar]
  84. White, R. J., & Ghez, A. M. 2001, ApJ, 556, 265 [Google Scholar]
  85. White, R. J., Ghez, A. M., Reid, I. N., et al. 1999, ApJ, 520, 811 [NASA ADS] [CrossRef] [Google Scholar]
  86. Zapata, L. A., Rodríguez, L. F., Fernández-López, M., et al. 2020, ApJ, 896, 132 [Google Scholar]
1

Both of the alternative solutions are also readily excluded by orbit fits that includes either of them instead of the nominal solution that we adopt here (see Sect. 3.1).

2

We consider the 1997 HST datapoint more robust than the discovery 1998 CFHT measurement from Duchêne (1999) as precise astrometry was not a priority in that study.

All Tables

Table 1

Astrometry of the GG Tau Ab and UX Tau B systems.

In the text
Table 2

Orbital parameters of the GG Tau Ab and UX Tau B systems.

In the text
Table 3

Angles defining key planes in the GG Tau and UX Tau systems.

In the text
Table B.1

Orbital solutions for visual pre-main sequence binaries. Systems marked with a † symbols are members of the Upper Scorpius or TW Hydra association, whose age (~ 10–20 Myr) is such that the absence of a disk may no longer be a consequence of multiplicity.

In the text

All Figures

thumbnail Fig. 1

Thumbnails of Keck/NIRC2 images in the GG Tau system. The first and second columns represent GG Tau Aa and GG Tau Ab, normalized to their peak values, respectively. The third column is the best-fit model of GG Tau Ab created by shifting and scaling two copies of GG Tau Aa, and the fourth column is the residuals from this model. Red and blue regions are negative and positive residuals, respectively, with the color map saturating at ±3% of the peak pixel in the image of GG Tau Ab. The fifth column shows the result of subtracting the model of GG Tau Ab 1 (centered on the black cross) from the image of GG Tau Ab, revealing GG Tau Ab2, which is scaled up by a factor of four for visual purposes. The last column shows the residuals of fitting GG Tau Ab as a single star instead; they are displayed with the same saturation levels as in the fourth column for direct comparison.
In the text
thumbnail Fig. 2

Reduced χ2 maps for the location of GG Tau Ab2 in the new PIONIER observations presented here. In the 2013 epoch, solution “a” is both the most likely from a pure likelihood perspective, and it is also the most plausible based on the motion observed between the 2012 and 2014 Keck observations (see Sect. 2.1). The second and third highest likelihood solutions (labelled “b” and “c”), located to the West-Southwest of the primary solution, are also illustrated in Fig. 4.
In the text
thumbnail Fig. 3

Thumbnails of HST/WFCP2, Gemini/NIRI and VLT/SPHERE images in the UX Tau system. The columns are similar to those in Fig. 1, except that no flux scaling is applied to UX Tau Bb in the last column.
In the text
thumbnail Fig. 4

Relative orbit of the GG Tau Ab and UX Tau B binaries. In both panels, orange symbols represent published astrometric datapoints whereas blue symbols indicate new adaptive optics or HST observations that are presented here for the first time. In 2012 and 2013 (orange and red symbols, respectively), the PIONIER observations of GG Tau Ab allowed two and three possible solutions, respectively. Based on the Keck observations, solutions “a” in both epochs are the most plausible ones.
In the text
thumbnail Fig. 5

Random set of 100 orbital solutions selected form the converged part of the MCMC chain for the GG Tau Ab and UX Tau B binaries (considering the “trimmed” dataset, see Sect. 3.1). Black + symbols indicate the periastron of each plotted orbit.
In the text
thumbnail Fig. 6

Posterior distribution for the dynamical mass of the GG Tau Ab and UX Tau B systems. In both cases, dashed and solid histograms represent the distributions using “complete” and “trimmed” astrometric datasets, respectively. The black horizontal bars represent the systematic error introduced by the uncertainty on the distance to each system.
In the text
thumbnail Fig. 7

Angle between the orbital and ring angular momentum vectors in the GG Tausystem. In all cases, we solve the orbital inclination ambiguity by assuming that the planes are close to coplanar.
In the text
thumbnail Fig. 8

Orbital properties of T Tauri visual binaries. In both panels, black diamonds and green crosses represent ≲3 Myr-old systems with and without circumstellar material, respectively, while yellow crosses are ~ 10–20 Myr-old disk-free systems in Upper Scorpius and the TW Hya association. The two red stars mark the systems studied here. Left: comparison of orbital period and eccentricity based on literature results listed in Appendix B. Right: comparison of periastron distances and dynamical masses for the same systems.
In the text
thumbnail Fig. A.1

MCMC cornerplot resulting from the orbital fit to the GG Tau Ab orbit. While orbitize! converged on the solution with i > 90º, we adopt the equivalent supplementary angle, which match the convention of the circumtriple ring.
In the text
thumbnail Fig. A.2

MCMC cornerplot resulting from the orbital fit to the UX Tau B orbit.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.