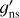| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | C1 | |
| Number of page(s) | 4 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202449899e | |
| Published online | 03 May 2024 | |
Impact of nonconvergence and various approximations of the partition function on the molecular column densities in the interstellar medium★ (Corrigendum)
1
Dept. Ciencias Integradas, Facultad de Ciencias Experimentales, Centro de Estudios Avanzados en Física, Matemática y Computación, Unidad Asociada GIFMAN, CSIC-UHU, Universidad de Huelva, Spain, Instituto Universitario “Carlos I” de Física Teórica y Computacional, Universidad de Granada,
Granada,
Spain
e-mail: miguel.carvajal@dfa.uhu.es
2
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
Firenze
50125,
Italy
3
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
4
Laboratoire Interuniversitaire des Systèmes Atmosphériques (LISA), UMR CNRS 7583, Université Paris-Est Créteil, Université de Paris, Institut Pierre Simon Laplace (IPSL),
Créteil,
France
5
Dept. of Astronomy, University of Michigan,
311 West Hall, 1085 South University Avenue,
Ann Arbor,
MI
48109,
USA
Key words: techniques: spectroscopic / ISM: abundances / radio lines: ISM / errata, addenda
The corrected Table D.2 is available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/685/C1
In the original version of this paper, the calculated values of the internal partition function of methyl cyanide (CH3CN) have some errors. This miscalculation came from using different values of the nuclear spin statistical weights for CH3CN at different stages of the work. In this erratum, we specify the values of the nuclear spin statistical weights considered in the original work and by different authors that gave rise to the miscalculations. However, using incorrect values for the internal partition function of CH3CN did not affect our conclusions. Here, we provide some clarifying details and enumerate the corrections carried out.
The rovibrational partition function of CH3CN, Q(T), defined as a direct sum of exponential terms, is approximated as a product of the rotational contribution, Qrot(T), and the vibrational one, Qvib(T) (Herzberg 1991; Carvajal et al. 2019):
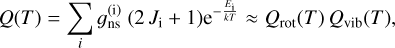 (1)
(1)
where 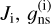 Ei, and T are the rotational angular momentum, the nuclear spin degeneracy of energy level i, the rovibrational energy levels (in this case with respect to the ground vibrational state), and the temperature of the environment, respectively.
Ei, and T are the rotational angular momentum, the nuclear spin degeneracy of energy level i, the rovibrational energy levels (in this case with respect to the ground vibrational state), and the temperature of the environment, respectively.
The vibrational contribution to the internal partition function, Qvib(T), was computed using the harmonic approximation (Herzberg 1991; Carvajal et al. 2019). This was proven to be a good approximation for computing the vibrational partition function within the typical interstellar medium temperatures (Carvajal et al. 2019). The rotational partition function, Qrot(T) (e.g., Herzberg 1991; Groner et al. 2007; Carvajal et al. 2019), can be computed as a direct sum:
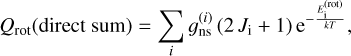 (2)
(2)
where 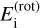 represents the energy for the i-th rotational state. The degeneracy
represents the energy for the i-th rotational state. The degeneracy 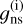 is included in the definition of the rotational contribution of the partition function (Eq. (2)) because, in general, the value of
is included in the definition of the rotational contribution of the partition function (Eq. (2)) because, in general, the value of 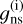 is associated with the quantum numbers, K, for a symmetric top (or Ka and Kc for an asymmetric top).
is associated with the quantum numbers, K, for a symmetric top (or Ka and Kc for an asymmetric top).
In addition, the rotational partition function (Eq. (2)) can be obtained with the approximated expression for symmetric tops (McDowell 1990) considering the rotational constants:
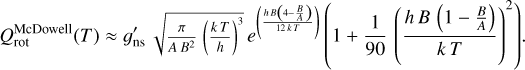 (3)
(3)
We note that the nuclear spin statistical weight in Eq. (3), 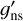 , takes different values than the nuclear spin statistical weight in Eq. (2),
, takes different values than the nuclear spin statistical weight in Eq. (2), 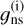 .
.
The following are the corrections we made to the internal partition function of methyl cyanide given in the original paper:
- 1.
The values from Tables 2 and 3 of the original paper concerning CH3CN were recomputed according to the nuclear spin statistical weights defined here, and are presented in Tables 1 and 2;
- 2.
The nuclear spin statistical weights reported in the literature and given in Table A.1 of the original paper needed extra clarification because they use different values,
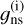 or
or 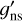 , according to the mathematical expression of the rotational partition function considered (i.e., Eq. (2) or (3), respectively);
, according to the mathematical expression of the rotational partition function considered (i.e., Eq. (2) or (3), respectively); - 3.
According to the first two corrections, the values of the polynomial coefficients fitted to the rovibrational partition function values, given in Table B.2 of the original paper, were also corrected and are presented in Table 5;
- 4.
The corrected values of the internal partition function of CH3CN at the excitation temperature deduced for this molecule in NGC 7538 (T = 350 K) and the column density estimates for CH3 CN given in Table 7 of the original paper are reported in Table 6.
Rotational partition function for CH3CN.
In Table 1 of this erratum, the classical approximation of the rotational partition function (Eq. (3)) for CH3CN is compared to the direct sum expression for the rotational partition function (Eq. (2)). The nuclear spin weight of Eq. (2) of this erratum was omitted as in the original paper and, therefore, considered to be gns = 1. The classical approximation (Eq. (3)) was computed using the rotational constants from Müller et al. (2015) considering 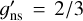 . The direct sum was computed for all the rotational energy levels up to J = 99 (Müller et al. 2009). This set of rotational energies is enough to make Qrot(direct sum) reach convergence for temperatures up to T = 500 K (for more details, see Carvajal et al. 2019). In addition, the classical approximation for the rotational partition function contribution is not accurate enough for temperatures below 18.75 K. If the estimate of the molecular column density of CH3CN for a cold interstellar medium region with a temperature around 10 K were carried out with the classical approximation (Eq. (3)), the molecular column density would be around 10% smaller than the estimate obtained with Qrot(direct sum).
. The direct sum was computed for all the rotational energy levels up to J = 99 (Müller et al. 2009). This set of rotational energies is enough to make Qrot(direct sum) reach convergence for temperatures up to T = 500 K (for more details, see Carvajal et al. 2019). In addition, the classical approximation for the rotational partition function contribution is not accurate enough for temperatures below 18.75 K. If the estimate of the molecular column density of CH3CN for a cold interstellar medium region with a temperature around 10 K were carried out with the classical approximation (Eq. (3)), the molecular column density would be around 10% smaller than the estimate obtained with Qrot(direct sum).
In Table 2 of this erratum, the values and their uncertainties of the rovibrational partition function (Eq. (1)), calculated as the product of the direct sum of the rotational contribution and the harmonic vibrational approximation, are given from 2.725 to 500 K (Col. 3). These values are compared with those of the rovibrational partition function provided by the CDMS catalog (our Col. 4; see also Endres et al. 2016). To allow for a comparison, the nuclear spin statistical weight has been reduced in both contributions and considered to be gns = 1. The values computed in this work and the CDMS ones disagree at temperatures higher than 300 K. The uncertainties of the internal partition function are rather small despite being estimated upward, considering the high rotational energy uncertainties of 100 MHz and uncertainties of 1 cm−1 for the vibrational fundamentals. In fact, the rovibrational partition function of CH3CN at T = 500 K is 32 358. and has an uncertainty of 72.; in other words, even with an upward estimate of the uncertainties, the relative uncertainty for the partition function at T = 500 K is around 0.2%.
Vibrational and rotational-vibrational partition function for CH3CN.
In Table D.2 (available at the CDS) of this erratum, the rotational, vibrational, and rovibrational partition function calculated in the present work for CH3CN are provided in intervals of 1 K up to T = 500 K. In addition, the values for the temperatures 2.725, 5, 9.375, 18.75, 37.5, 75, 150, 225, 300, and 500 K are also provided (without any truncation or rounding). In Table 2, these values for the rovibrational partition function are truncated and rounded off according to their uncertainties.
As previously noted, the value of the nuclear spin statistical weight in Eq. (3), 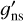 , is different than the nuclear spin statistical weight in Eq. (2),
, is different than the nuclear spin statistical weight in Eq. (2), 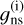 . The values of
. The values of 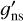 and
and 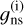 used in this work are given in Table 3 and are compared with others from the literature (Gordy & Cook 1984; Blake et al. 1987; Bunker & Jensen 1989; Turner 1991; Pickett et al. 1998; Rinsland et al. 2008; Mangum & Shirley 2015; Endres et al. 2016). In Table 3, the nuclear spin statistical weight in Eq. (2) for CH3CN is given as
used in this work are given in Table 3 and are compared with others from the literature (Gordy & Cook 1984; Blake et al. 1987; Bunker & Jensen 1989; Turner 1991; Pickett et al. 1998; Rinsland et al. 2008; Mangum & Shirley 2015; Endres et al. 2016). In Table 3, the nuclear spin statistical weight in Eq. (2) for CH3CN is given as 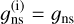 because it has the same value for the three possible symmetries of the rotational states, A1, A2, and E (see our Table 4 and Bunker & Jensen 1989). In this erratum we use gns = 1, which, when applying the temperature diagram method, should be substituted in Eq. (2) of the original paper to compute the degeneracy of the upper level before including it in the intensity expressions (Eqs. (3) and (4) of the original paper). Nevertheless, the values of gns for the rotational states with quantum number K = 0 or K ≠ 3n (n is an integer) are taken as half the value of the K = 3n states because the two K = 3n rotational states of CH3CN (with A1 and A2 symmetries) are considered to be a degenerate K doublet (see Table 4 and Loren & Mundy 1984; Turner 1991). Hence, in this erratum, the nuclear spin weight of K = 3n states is taken to be 2, whereas it is 1 for the rotational states with K = 0 or K ≠ 3n. Therefore, the rotational partition function calculated as a direct sum is Qrot(direct sum) = 5059.15 at T =300 K assuming gns = 1 (see Table 1), whereas the one published by the JPL and in the CDMS catalog is around 10118 (2 Qrot(direct sum)) and the one calculated by Rinsland et al. (2008) is about 60709 (12 Qrot(direct sum)). These three values agree with one another, differing only by a normalization factor that is due to the different nuclear spin statistical weights considered (see Table 3).
because it has the same value for the three possible symmetries of the rotational states, A1, A2, and E (see our Table 4 and Bunker & Jensen 1989). In this erratum we use gns = 1, which, when applying the temperature diagram method, should be substituted in Eq. (2) of the original paper to compute the degeneracy of the upper level before including it in the intensity expressions (Eqs. (3) and (4) of the original paper). Nevertheless, the values of gns for the rotational states with quantum number K = 0 or K ≠ 3n (n is an integer) are taken as half the value of the K = 3n states because the two K = 3n rotational states of CH3CN (with A1 and A2 symmetries) are considered to be a degenerate K doublet (see Table 4 and Loren & Mundy 1984; Turner 1991). Hence, in this erratum, the nuclear spin weight of K = 3n states is taken to be 2, whereas it is 1 for the rotational states with K = 0 or K ≠ 3n. Therefore, the rotational partition function calculated as a direct sum is Qrot(direct sum) = 5059.15 at T =300 K assuming gns = 1 (see Table 1), whereas the one published by the JPL and in the CDMS catalog is around 10118 (2 Qrot(direct sum)) and the one calculated by Rinsland et al. (2008) is about 60709 (12 Qrot(direct sum)). These three values agree with one another, differing only by a normalization factor that is due to the different nuclear spin statistical weights considered (see Table 3).
Symmetry of the rotational states (Γrot) for a C3v(M) molecule obtained according to the rotational quantum numbers (J,K) (Bunker & Jensen 1989).
It is worth mentioning that the internal partition function values obtained in this erratum are in general comparable with those provided in HITRAN2020 (Gamache et al. 2021). Gamache et al. (2021) computed the internal partition function as the product of the classical approximation for the rotational partition function (Eq. (3)), with a nuclear spin degeneracy 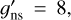 , and the harmonic approximation for the vibrational partition function. To compare our results with those from HITRAN2020, we reduced the HITRAN2020 nuclear spin statistical weight by dividing their values by 12. Below 3 K, the HITRAN2020 result is smaller than ours, with a relative difference of 2.8% at T = 3 K, 9.2% at T = 2 K, and 26.7% at T = 1 K. Above 4 K, HITRAN2020 provides practically the same result as this work, with relative differences of less than 1%. In fact, at T=500 K, the partition function of HITRAN2020 is 32363.33, essentially the same as our value of 32358.34 (i.e., a relative difference of 0.02%). This comparison with HITRAN2020 corroborates what was confirmed in the original paper: (a) the classical expression of the rotational partition function for symmetric tops (Eq. (3)) is a good approximation for higher temperatures and, (b) it is preferable to calculate the vibrational partition function with the harmonic approximation, considering all the fundamental vibrational energies, rather than using the direct sum for the vibrational energies when the available vibrational energy term values are limited to the lower energies.
, and the harmonic approximation for the vibrational partition function. To compare our results with those from HITRAN2020, we reduced the HITRAN2020 nuclear spin statistical weight by dividing their values by 12. Below 3 K, the HITRAN2020 result is smaller than ours, with a relative difference of 2.8% at T = 3 K, 9.2% at T = 2 K, and 26.7% at T = 1 K. Above 4 K, HITRAN2020 provides practically the same result as this work, with relative differences of less than 1%. In fact, at T=500 K, the partition function of HITRAN2020 is 32363.33, essentially the same as our value of 32358.34 (i.e., a relative difference of 0.02%). This comparison with HITRAN2020 corroborates what was confirmed in the original paper: (a) the classical expression of the rotational partition function for symmetric tops (Eq. (3)) is a good approximation for higher temperatures and, (b) it is preferable to calculate the vibrational partition function with the harmonic approximation, considering all the fundamental vibrational energies, rather than using the direct sum for the vibrational energies when the available vibrational energy term values are limited to the lower energies.
Polynomial coefficients fitted to the rovibrational partition function values of the present work for CH3CN.
The rovibrational partition function has been tabulated to a nonlinear sixth-order power expansion in terms of the temperature and a nonlinear sixth-order power expansion of log10(Q) in terms of the log10(T). The polynomial coefficients have been fitted to the rovibrational partition function values obtained in the present work (see Table 2). Table 5 provides the polynomial coefficients derived from the fitting as well as the corresponding relative differences between the fitted polynomial expansions and the rovibrational partition function values computed for this erratum. The sixth-order expansion is in good agreement for temperatures above 5 K, and the logarithm polynomial is generally in reasonable agreement with Qrv (present work) from T = 2.725 K up to T = 500 K. Because of the small relative differences between these two power expansions and the internal partition function values computed for CH3CN in this erratum (see Table 5), both power expansions can be used to interpolate the rovibrational partition function at any temperature from 2.725 to 500 K. Nevertheless, in the present work, the fitted polynomial expansion has a better agreement at higher temperatures than the nonlinear fit of the logarithm polynomial expansion.
Column density estimates of CH3CN in the NGC 7538 survey according to the partition function computed in the present work (rovibra-tional partition functions are computed as the product of the rotational contribution, given as a direct sum, and the harmonic approximation of the vibrational partition function) and in the CDMS and JPL databases.
Therefore, we decided to use the former to interpolate the partition function at the excitation temperature of the NGC 7538 survey to estimate the molecular column density.
The results of the different approximations of the rovibra-tional partition function used to derive the total beam-averaged column density for CH3CN are given in Table 6 at the specific temperature of T = 350.33 K from the NGC 7538 survey. The more reliable estimate of the total column density is given in Col. 8 of Table 6; it was obtained with the partition function computed in the present work at T = 350 K and reported in Table D.2 (available at the CDS) of this erratum. The result obtained in the present work with the rotational-vibrational partition function for CH3CN is compared with the results obtained with the partition function values reported in the JPL or CDMS catalogs and considering the linear and nonlinear interpolation approximations at T = 350 K. For the nonlinear interpolation at T = 350 K, we used the fitted sixth-order polynomial expansion of Qrv in terms of the temperature. The coefficients of Qrv (present work) can be found in Col. 2 of Table 5. The nonlinear interpolation of the partition function given in this erratum (Col. 5 of Table 6) provides practically the same result for the total column density as that obtained with the partition function values of Table D.2, available at the CDS (Col. 8 of Table 6). The linear interpolation at T = 350 K was carried out using the values of Qrv at T = 300 K and 500 K. In the present work, the values of Qrv(present work) at T = 300 K and 500 K can be found in Table 2. The relative differences between the column densities estimated with the different methods are also given in Table 6. The relative difference between the column densities estimated using the partition function of this work (Col. 8 in Table 6) and that of the CDMS and JPL databases obtained with a nonlinear interpolation (Col. 6 in Table 6) is 9%. The relative differences for the cases of the linear and nonlinear interpolations between the partition function values of this work and those obtained from the CDMS and JPL databases for CH3CN are 18% and 8%, respectively. The new and corrected values of Table 6 are practically two-thirds the values given in Carvajal et al. (2019) for both the partition function values and the column densities.
Acknowledgements
We acknowledge the comments and useful discussions with Dr. Edgar Mendoza. This work has received funding from the European Union’s Horizon 2020 research and innovation program under Marie Sklodowska-Curie grant agreement No. 872081 and grant PID2022-136228NB-C21 funded by MICIU/AEI/10.13039/501100011033 and, as appropriate, by “ERDF A way of making Europe”, by “ERDF/EU”, by the “European Union” or by the “European Union NextGenerationEU/PRTR”.
References
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [Google Scholar]
- Bunker, P. R., & Jensen, P. 1989, Molecular Symmetry and Spectroscopy (Ottawa: NRC Research Press) [Google Scholar]
- Carvajal, M., Favre, C., Kleiner, I., et al. 2019, Ottawa A&A, 627, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Gamache, R., Vispoel, B., Rey, M., et al. 2021, JQSRT, 271, 107713 [NASA ADS] [CrossRef] [Google Scholar]
- Gordy, W., & Cook, R. L. 1984, Microwave Molecular Spectra (New York: Wiley-Interscience) [Google Scholar]
- Groner, P., Winnewisser, M., Medvedev, I. R., et al. 2007, ApJS, 169, 28 [CrossRef] [Google Scholar]
- Herzberg, G. 1991, Spectra and Molecular Structure: II. Infrared and Raman Spectra of Polyatomic Molecules (Malabar, Florida: Krieger Pub. Co.) [Google Scholar]
- Loren, R., & Mundy, L. G. 1984, ApJ, 286, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
- McDowell, R. S. 1990, J. Chem. Phys., 93, 2801 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Drouin, B. J., & Pearson, J. C. 2009, A&A, 506, 1487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Brown, L. R., Drouin, B. J., et al. 2015, J. Mol. Spectr., 312, 22 [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
- Rinsland, C. P., Devi, V. M., Benner, D. C., et al. 2008, J. Quant. Spec. Radiat. Transf., 109, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B. E. 1991, ApJS, 76, 617 [NASA ADS] [CrossRef] [Google Scholar]
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
All Tables
Symmetry of the rotational states (Γrot) for a C3v(M) molecule obtained according to the rotational quantum numbers (J,K) (Bunker & Jensen 1989).
Polynomial coefficients fitted to the rovibrational partition function values of the present work for CH3CN.
Column density estimates of CH3CN in the NGC 7538 survey according to the partition function computed in the present work (rovibra-tional partition functions are computed as the product of the rotational contribution, given as a direct sum, and the harmonic approximation of the vibrational partition function) and in the CDMS and JPL databases.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.