| Issue |
A&A
Volume 661, May 2022
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 27 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202142869 | |
| Published online | 26 May 2022 | |
Accurate Einstein coefficients for electric dipole transitions in the first negative band of N2+
1
Groupe de Spectrométrie Moléculaire et Atmosphérique, GSMA, UMR CNRS 7331, U.F.R. Sciences Exactes et Naturelles, University of Reims Champagne-Ardenne,
51100
Reims,
France
e-mail: olfa.ferchichi@univ-reims.fr; alexander.alijah@univ-reims.fr
2
Laboratoire de Spectroscopie Atomique, Moléculaire et Applications, LSAMA, Departement of Physics, Faculty of Sciences, University of Tunis – El Manar,
1060
Tunis,
Tunisia
e-mail: najoua.derbel@gmail.com
3
Institut UTINAM, UMR 6213 CNRS-Univ. Bourgogne Franche-Comté, OSU THETA,
BP 1615,
25010
Besançon Cedex,
France
Received:
8
December
2021
Accepted:
14
February
2022
Context. The N2+ fluorescence spectrum of comet C/2016 R2 is modelled in a companion paper. That work relies on accurate Einstein coefficients for electric dipole transitions between the B2∑u+ and X2∑g+ electronic states of N2+.
Aims. These coefficients are provided in the present paper.
Methods. The potential energy curves and transition dipole moments were computed at a high level of ab initio theory and include relativistic corrections. Rovibrational wavefunctions were then obtained without assuming separability of vibrational and rotational motions.
Results. Vibrationally and rotationally resolved Einstein coefficients are presented in a convenient three-parameter functional form for three isotopologues. A possible explanation is given for the large variation in the experimental radiative lifetimes.
Key words: radiative transfer / comets: general / molecular data / planets and satellites: atmospheres
© O. Ferchichi et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The emission spectra of the first negative,  , and Meinel,
, and Meinel,  , bands of
, bands of  are well studied due to their importance for airglow and planetary entry physics (Qin et al. 2017).
are well studied due to their importance for airglow and planetary entry physics (Qin et al. 2017).  has also been detected recently in a few comets, especially in comet C/2016 R2, which presented unusual bright emission lines due to
has also been detected recently in a few comets, especially in comet C/2016 R2, which presented unusual bright emission lines due to  (Biver et al. 2018; Cochran & McKay 2018b,a; Opitom et al. 2019; Venkataramani et al. 2020). The focus of many experimental and theoretical works has been the accurate determination of vibrational energy levels and rotational constants from which rovibrational energy levels and hence transition frequencies can easily be computed. The electronic dipole moment functions and Einstein coefficients are less well investigated. There are two compilations of Einstein coefficients, one by Lofthus & Krupenie (1977) and a more recent one by Gilmore et al. (1992). Lofthus and Krupenie reported data that were originally obtained by Jain & Sahni (1967), who employed the experimental RKR potential determined by Singh & Rai (1966). The integral over the transition dipole moment was approximated by the R-centroid method, that is, it was replaced by a single value of the dipole moment, at R = Rcentroid. Ten years later, Langhoff, Bauschlicher, and Partrige (Langhoff et al. 1987; Langhoff & Bauschlicher 1988) published the results of their thorough ab initio investigations of the potential energy curves of the four lowest electronic states and transition dipole moments. For the
(Biver et al. 2018; Cochran & McKay 2018b,a; Opitom et al. 2019; Venkataramani et al. 2020). The focus of many experimental and theoretical works has been the accurate determination of vibrational energy levels and rotational constants from which rovibrational energy levels and hence transition frequencies can easily be computed. The electronic dipole moment functions and Einstein coefficients are less well investigated. There are two compilations of Einstein coefficients, one by Lofthus & Krupenie (1977) and a more recent one by Gilmore et al. (1992). Lofthus and Krupenie reported data that were originally obtained by Jain & Sahni (1967), who employed the experimental RKR potential determined by Singh & Rai (1966). The integral over the transition dipole moment was approximated by the R-centroid method, that is, it was replaced by a single value of the dipole moment, at R = Rcentroid. Ten years later, Langhoff, Bauschlicher, and Partrige (Langhoff et al. 1987; Langhoff & Bauschlicher 1988) published the results of their thorough ab initio investigations of the potential energy curves of the four lowest electronic states and transition dipole moments. For the  transitions, which are the ject of the present investigation, they found that the computed transition dipole moment is ignificantly different from the dipole moments used before. Gilmore et al. (1992) then re-evaluated the Einstein coefficients. Just as before (Lofthus & Krupenie 1977), experimental RKR potential energy curves were applied, but the integrals over the transition dipole moments were evaluated numerically using a second-order fit in R of the ab initio transition dipole moments in Langhoff & Bauschlicher (1988). The fit was made with the intention to provide A coefficients for a wide range of transitions. Unfortunately, it washes out some features of the ab initio curve.
transitions, which are the ject of the present investigation, they found that the computed transition dipole moment is ignificantly different from the dipole moments used before. Gilmore et al. (1992) then re-evaluated the Einstein coefficients. Just as before (Lofthus & Krupenie 1977), experimental RKR potential energy curves were applied, but the integrals over the transition dipole moments were evaluated numerically using a second-order fit in R of the ab initio transition dipole moments in Langhoff & Bauschlicher (1988). The fit was made with the intention to provide A coefficients for a wide range of transitions. Unfortunately, it washes out some features of the ab initio curve.
In the present work, we have recomputed the potential energy curves and transition dipole moment function at a very high level of ab initio theory: explicitly correlated multi-reference configuration interaction (MRCI-F12b) with the large aug-cc-pCVQZ-F12 basis. Moreover, all electrons were correlated, and relativistic corrections were applied. Rovibrational transition dipole moments were computed without assuming separation of vibrational and rotational motions. The rotational dependence of these matrix elements is represented in a functional form. For the complete determination of the Einstein A coefficients, our functions need still to be multiplied by the rotational line intensity factors, or Hönl-London factors. These must satisfy certain sum rules, and we note in passing that Hansson and Watson corrected some errors in the expressions for perpendicular singlet (Hansson & Watson 2005) and perpendicular multiplet dipole transitions (Watson 2008). The Hönl-London factors for the  system of
system of  , which are parallel transitions, were first derived by Mulliken (1931). To summarise, we provide in the present work Einstein A coefficients for the first negative band of
, which are parallel transitions, were first derived by Mulliken (1931). To summarise, we provide in the present work Einstein A coefficients for the first negative band of  with much higher precision than reported before. These data were used in the companion publication to analyse the fluorescence spectrum of comet C/2016 R2 (Rousselot et al. 2022).
with much higher precision than reported before. These data were used in the companion publication to analyse the fluorescence spectrum of comet C/2016 R2 (Rousselot et al. 2022).
Experimentally derived vs. computed energies of the v = 0 vibrational states of  , and relative energies.
, and relative energies.
 : computed vibrational energies, rotational constants, and their comparison with experiment.
: computed vibrational energies, rotational constants, and their comparison with experiment.
 |
Fig. 1 Potential energy curves of the four lowest electronic doublet states, |
2 Computational and theoretical approach
2.1 Lowest electronic states of  and transition dipole moments
and transition dipole moments
Electronic structure calculations for  are not trivial due to many curve crossings, as shown in Fig. 1 for the four lowest doublet states or in Fig. 1 of Cartwright & Dunning (1975) for full appreciation. Multi-reference approaches are therefore necessary. The potential energy and transition dipole moment curves for the three lowest doublet states of
are not trivial due to many curve crossings, as shown in Fig. 1 for the four lowest doublet states or in Fig. 1 of Cartwright & Dunning (1975) for full appreciation. Multi-reference approaches are therefore necessary. The potential energy and transition dipole moment curves for the three lowest doublet states of  were computed from first principles with the Molpro package (Werner et al. 2021) using the explicitly correlated MRCI-F12b method with Davidson correction and the large aug-cc-pCVQZ-F12 basis. Moreover, all electrons were correlated, including atomic 1s electrons, and scalar relativistic corrections were applied using the eighth-order Douglas-Kroll-Hess Hamiltonian. Our approach goes beyond the level of theory reported before (see e.g. Cartwright & Dunning 1975; Langhoff & Bauschlicher 1988; Spelsberg & Meyer 2001; Polák & Fišer 2003; Bruna & Grein 2004; Shi et al. 2011; Liu et al. 2014; Ayari et al. 2020 and references therein). The accuracy obtained here is demonstrated in Table 1, where the energy values corresponding to the minima of the potential curves including the vibrational zero-point energy are presented and compared with data derived from experiments. The error is about 5 cm−1. The rovibrational calculations of the lowest vibrational states on the X and B potential energy curves, which are of interest to the present work, are also more accurate than reported before, as can be inferred from Tables 2 and 3.
were computed from first principles with the Molpro package (Werner et al. 2021) using the explicitly correlated MRCI-F12b method with Davidson correction and the large aug-cc-pCVQZ-F12 basis. Moreover, all electrons were correlated, including atomic 1s electrons, and scalar relativistic corrections were applied using the eighth-order Douglas-Kroll-Hess Hamiltonian. Our approach goes beyond the level of theory reported before (see e.g. Cartwright & Dunning 1975; Langhoff & Bauschlicher 1988; Spelsberg & Meyer 2001; Polák & Fišer 2003; Bruna & Grein 2004; Shi et al. 2011; Liu et al. 2014; Ayari et al. 2020 and references therein). The accuracy obtained here is demonstrated in Table 1, where the energy values corresponding to the minima of the potential curves including the vibrational zero-point energy are presented and compared with data derived from experiments. The error is about 5 cm−1. The rovibrational calculations of the lowest vibrational states on the X and B potential energy curves, which are of interest to the present work, are also more accurate than reported before, as can be inferred from Tables 2 and 3.
The potential energy curves V(R) were computed in D2h symmetry between 1.3 a0 ≤ R ≤ 10 a0 on a very fine grid with spacing ΔR = 0.01 a0. MRCI transition dipole matrix elements were computed in Cs symmetry with a somewhat larger spacing ΔR = 0.05 a0.
The rovibrational energies and wavefunctions were computed with our own Numerov code by numerical integration of the rovibrational Schrödinger equation
 (1)
(1)
where N = J − S is the total angular momentum minus the spin, a good quantum number for Hund’s case b molecules. Each rovibrational level EvN is weakly split into two components denoted as F1 and F2, which correspond to J = N + 1/2 and J = N − 1/2, respectively. The energy splitting is ΔE = E(F1) − E(F2) = γ(N + 1/2), where γ is the spin-rotation constant. Gottscho et al. (1979) reported numerical values for the spin-rotation constant of the order of 10−2 cm−1. Although corrections could have been applied to the potential V(R), this has not been done as the splitting is too small to be resolved within the present theoretical approach. It can be accounted for by stituting experimental transition frequencies in the expressions for the Einstein coefficients. Rotational constants were obtained as
 (2)
(2)
and then expanded in powers of N(N + 1) as
![${B_{\upsilon N}}N(N + 1) = {B_\upsilon }N(N + 1) - {D_\upsilon }{[N(N + 1)]^2} + \cdots $](/articles/aa/full_html/2022/05/aa42869-21/aa42869-21-eq29.png) (3)
(3)
 : computed vibrational energies, rotational constants, and their comparison with experiment.
: computed vibrational energies, rotational constants, and their comparison with experiment.
Hönl-London factors for 2Σ – 2Σ transitions expressed in terms of N = N″(third column) or J = J″ (fourth column).
2.2 Electric dipole transitions
Electric dipole transitions (E1 transitions) between two 2Σ electronic states (Λ = 0) must satisfy the selection rules ΔN = ±1 and ΔJ = 0, ±1. Transitions with ΔJ = ΔN occur between F1 or F2 spin components, while transitions with ΔN = ±1 and Δ J = 0 require a spin flip. The Einstein coefficients read
 (4)
(4)
 (5)
(5)
In the above equations, v is the transition frequency, ϵ0 is the vacuum permittivity, h is the Planck constant, and c is the vacuum speed of light. S (Λ′, J′, Λ″, J″) or S (Λ′, N′, Λ″, N″) are the Hönl-London factors, first derived by Mulliken (1931). They are presented in Table 4 in terms of N and of J. As demonstrated in the table, they are normalised as
according to the standard convention (Whiting et al. 1980). The sum rule is satisfied for both J = J′ and J = J″, and the same is true for N. Schadee (1964) reported these factors using a normalisation that does not include the electronic spin term. His factors must be multiplied by two to normalise them according to Eq. (6). The expression for the Einstein coefficients can be written explicitly as
 (8)
(8)
to indicate the normalisation, with an analogous expression using J instead of N. In the remainder of the text, we mostly suppress the labels for Λ in the expressions for the Einstein coefficients and the Hönl-London factors.
The radiative lifetime τ of a rovibrational state (v′, J′) is given by
 (9)
(9)
To obtain the intensity of the emission from a rovibrational state (v′, J'), the Einstein coefficients must be multiplied with Nv′ J′, the number of molecules in that state,
 (10)
(10)
where Q denotes the partition function. Nv′,J′ is proportional to the statistical weight g' of the state. g' = g'ns × (2n′ + 1), if the levels with Σ = ± 1/2 are counted separately. If this is not the case, as intensities are additive, there is an additional factor of two. g′ns is the degeneracy of the nuclear spin state.
Allowed combinations of Ψvib, Ψel, Ψrot, and Ψns as well as the statistical weights, gns, of the corresponding states.
2.3 Symmetry considerations
To make this paper self-contained, we briefly state the well-known symmetry properties. The total wavefunction can be written as a product of vibrational, rotational, electronic, and
 (12)
(12)
Physically allowed functions for homonuclear  must be either symmetric or anti-symmetric with respect to nuclear permutation, depending on the nitrogen isotope. The principal isotope of nitrogen is 14N, which is a boson with nuclear spin i = 1. The second stable isotope, far less abundant, is 15N, a fermion with i = 1/2. The nuclear spin states of
must be either symmetric or anti-symmetric with respect to nuclear permutation, depending on the nitrogen isotope. The principal isotope of nitrogen is 14N, which is a boson with nuclear spin i = 1. The second stable isotope, far less abundant, is 15N, a fermion with i = 1/2. The nuclear spin states of  are I = 2,1,0. States with I = 2 and I = 0 are symmetric with respect to a permutation of the two nuclei, while I = 1 is anti-symmetric. The nuclear spin states of
are I = 2,1,0. States with I = 2 and I = 0 are symmetric with respect to a permutation of the two nuclei, while I = 1 is anti-symmetric. The nuclear spin states of  are I = 1,0. States with I = 1 are symmetric, and the state with I = 0 is anti-symmetric. The behaviour of the electronic wavefunctions with respect to nuclear permutation is indicated by the g/u label. Hence
are I = 1,0. States with I = 1 are symmetric, and the state with I = 0 is anti-symmetric. The behaviour of the electronic wavefunctions with respect to nuclear permutation is indicated by the g/u label. Hence  is symmetric and
is symmetric and  is anti-symmetric. The vibrational function is symmetric. The rotational functions are symmetric for even N and anti-symmetric for odd N. The allowed combinations and degeneracy factors are presented in Table 5. For a 2Σ electronic state, there is no electronic spin degeneracy because the two components have different energy. The statistical weights gns of the rovibrational functions in the electronic
is anti-symmetric. The vibrational function is symmetric. The rotational functions are symmetric for even N and anti-symmetric for odd N. The allowed combinations and degeneracy factors are presented in Table 5. For a 2Σ electronic state, there is no electronic spin degeneracy because the two components have different energy. The statistical weights gns of the rovibrational functions in the electronic  state enter into Eq. (11) as g′ns. For the mixed isotopologue, 14N15N+, no restrictions occur. The statistical weight is gns = 6 for all rovibronic states.
state enter into Eq. (11) as g′ns. For the mixed isotopologue, 14N15N+, no restrictions occur. The statistical weight is gns = 6 for all rovibronic states.
3 Results
Rousselot et al. (2022) compiled a list of accurate rovibronic frequencies for transitions between the three lowest vibrational levels of the B state and the eight lowest vibrational levels of the X state from the references cited in that paper. These bands were investigated in the present work. The Einstein coefficients were obtained numerically for angular momenta N = 0,…50 and are represented in terms of two sets of analytical expressions: In the first set, the square of the rovibrational transition dipole moment was fitted to a polynomial in N,
 (13)
(13)
where N is the smaller of N′ and N″. The Einstein coefficient then becomes
 (14)
(14)
In the above equations, the transition dipole moment is expressed in atomic units. v* is the (experimental) transition frequency measured in cm−1. A is obtained in s−1. The coefficients of the two fits, for ΔN = ±1, are collected in Tables B.3 and B.4.
In the second set of fits, Tables B.1 and B.2, the complete radial part in Eq. (5) including the v3 factor was represented by a polynomial in N,
 (15)
(15)
 (16)
(16)
so that the Einstein coefficients can conveniently be evaluated through
 (17)
(17)
We have verified explicitly through sample calculations at N = 100 that the expansions are stable, allowing extrapolation. The fits may be used to compute Einstein coefficients for transitions without spin-flip, ΔN = ΔJ = ± 1, that is, the F1 or F2 branches, and for those with spin-flip, ΔN = ± 1 with ΔJ = 0, since electronic spin effects are not resolved in the present theoretical approach. The form of the expansion in Eq. (16) was chosen such that the parameter Ã, if desired, can be replaced by an experimental value. Figures 2 and 3 present examples of the fits for v′ = 0 and v″ = 0,1,2,3. Transitions from v′ = 0 to higher vibrational levels of the X electronic state, v″ > 4, have very small Franck-Condon factors and the N-expansions are not meaningful. To the best of our knowledge, these angular momentum-dependent transition dipole moments have never before been reported in the literature.
The Einstein coefficients presented by Lofthus & Krupenie (1977) and by Gilmore et al. (1992) are somewhat different, as mentioned in the introduction. Lofthus and Krupenie reported the original data from Jain & Sahni (1967), who used RKR potentials and applied the R centroid method to estimate the transition dipole moments. The Einstein coefficients reported by Gilmore et al. (1992) are equally based on the experimental RKR potential energy curves, but the integrals over the transition dipole moments were evaluated numerically using RKR wavefunctions and a second-order fit in R of the ab initio transition dipole moments in Langhoff & Bauschlicher (1988). These dipole moments are more accurate than those used by previous works. The fit, however, does not reproduce some features of the ab initio curve faithfully, such as the curvature near R = 2.7 a0, which, as Langhoff & Bauschlicher (1988) wrote, is probably caused by the interaction between the B and C states. The two potential curves cross there, as shown in Fig. 1. Figure 4 demonstrates the limitations of the fit. It also shows that the present transition dipole moments and those computed by Langhoff and Bauschlicher are similar.
A comparison of purely vibrational A coefficients is provided in Table A.1. A (LB) and A (LB fit) were obtained using our ab initio potential energy curve and the transition moment based on the original data of Langhoff and Bauschlicher or based on Gilmore’s fit, respectively. In A (exp) the experimental transition frequencies provided by Rousselot et al. (2022) were used together with the present ab initio data. A (Gilmore) and A (Jain) are taken from the respective publications. It can be seen that A (Gilmore) and A (LB fit) are very similar, but different from A (Jain). A (LB) and A (this work) are comparable. They are close to the RKR data reported in Table VII of Langhoff & Bauschlicher (1988), which are for v′ ≤ 3. The present A values are thus more accurate than those presented in the compilations by Lofthus & Krupenie (1977) or by Gilmore et al. (1992), and they are more complete than the data by Langhoff and Bauschlicher.
Tables B.1 and B.2 list the fit parameters from which very accurate rovibrational Einstein A coefficients can be computed according to Eqs. (16) and (17). No separation of vibrational and rotational motions was made. For transitions with very weak vibrational Franck-Condon factors, (<0.002), a fit is not meaningful, and a constant value of A should be used for all N.
Radiative lifetimes were computed according to Eq. (9). The vibrational lifetimes are collected in Table 6 for three iso-topologues. As expected, they do not vary much upon isotopic stitution. A number of experiments were conducted quite some time ago to measure the lifetime of the v′ = 0 vibra-tional state. The most recent data seem to be those by Scholl et al. (1995) and by Schmoranzer et al. (1989), who reported τ = 61.8 ± 0.5 ns and τ = 61.35 ± 0.29 ns, respectively. They are slightly higher than our ab initio value. Johnson & Fowler (1970) reported τ = 59.1 ± 1.4 ns for v′ = 0 and τ = 58.5 ± 1.4 ns for v′ = 1 , which are close to the present values. However, as shown in the literature review by Johnson and Fowler or Schmoranzer et al., the experimental lifetimes vary considerable, between τ = 40 ± 20 ns and τ = 80 ± 20 ns.
It is instructive to analyse the radiative lifetimes with rotational resolution. These lifetimes were computed according to Eq. (9) for the F1 and F2 upper levels, and the three possible routes denoted I1 and I2 in Table 4 were accounted for each of them. They are presented graphically in Figs. 5 and 6. Considerable deviations from the vibrational lifetimes presented in Table 6 can be found for low values of N. The F1 rovibra-tional lifetimes approach the vibrational lifetimes from below as N increases, while the F2 rovibrational lifetimes approach them from above. This behaviour is real and follows from the numerical values of the Hönl-London factors. If the spin-splitting is neglected, that is, if the two spin-components are treated as a single rovibrational state, the lifetimes, computed as 1/τ = 1/τ(F1) + 1/τ(F2), yield average values that vary very little with the rotational quantum number N. This is demonstrated in Fig. 7 for the vibrational ground state v′ = 0. In these calculations, the degree of degeneracy in Eqs. (4) and (5) must be set to 2(2J′ + 1). This large variation of τ for low values of N might perhaps explain the spread in the experimental lifetimes.
 |
Fig. 2
|
 |
Fig. 3
|
 |
Fig. 4 Comparison of transition dipole moment functions. LB refers to Langhoff & Bauschlicher (1988), and LB-fit to a fit of their data by Gilmore et al. (1992). See main text for details. The dipole moment is expressed in atomic units: 1 a.u. = ea0 = 8.478353 … 10−30 Cm = 2.54175 Debye. |
Radiative B → X lifetimes, in ns, of the lowest vibrational states of the three isotopologues  ,
,  , and 14N15N+.
, and 14N15N+.
 |
Fig. 5 Radiative rovibrational lifetimes, in ns, for B rovibrational states with Σ = 1/2(F1). |
 |
Fig. 6 Radiative rovibrational lifetimes, in ns, for B rovibrational states with Σ = −1/2 (F2). |
 |
Fig. 7 Radiative lifetimes, in ns, for B rovibrational levels belonging to v′ = 0 and the F1 and F2 spin components. The average value is also shown. |
4 Conclusions
Very accurate rovibronic Einstein A coefficients for transitions between the  and
and  electronic states of
electronic states of  were computed for N up to 50 and represented in a compact form. Rovibrational wavefunctions were used for the two electronic states, that is, no separation of vibration and rotation was assumed. Data for the principal isotopologue
were computed for N up to 50 and represented in a compact form. Rovibrational wavefunctions were used for the two electronic states, that is, no separation of vibration and rotation was assumed. Data for the principal isotopologue  as well as those for 14N15N+ and the rare
as well as those for 14N15N+ and the rare  are collected in the appendix. These coefficients were used in the companion paper on comet spectra, Rousselot et al. (2022). That work is based on unique observational data obtained for comet C/2016 R2 in February 2018 with the 8 m Very large Telescope (VLT) of the European Southern Observatory equipped with a highresolution spectrograph (spectral resolution of about 0.06 Å). These spectra clearly show tens of emission lines with a good signal-to-noise ratio belonging to the (0,0) and (1,1) band of the
are collected in the appendix. These coefficients were used in the companion paper on comet spectra, Rousselot et al. (2022). That work is based on unique observational data obtained for comet C/2016 R2 in February 2018 with the 8 m Very large Telescope (VLT) of the European Southern Observatory equipped with a highresolution spectrograph (spectral resolution of about 0.06 Å). These spectra clearly show tens of emission lines with a good signal-to-noise ratio belonging to the (0,0) and (1,1) band of the  transition. These spectra reveal differences between the near-nucleus region, corresponding to “young”
transition. These spectra reveal differences between the near-nucleus region, corresponding to “young”  ions that are freshly created by photoionisation of N2, and spectra at the extremities of the slit, corresponding to a projected distance of about 6000 km from the nucleus, that is, at least a few thousand seconds of travel time from it. This difference is interpreted in terms of time necessary to reach a fluorescence equilibrium (because pure rotational transitions are forbidden), and the spectra obtained at the end of the slit can be satisfactorily explained by a Monte Carlo simulation based on the transition probabilities computed in this work. Some fluorescence efficiencies (the number of photons s−1 ion−1 , which depends on the solar radiation density received by the comet) were also computed, allowing a quantitative study of the N2 production rate in this comet and in future comets with a significant amount of this species. These fluorescence efficiencies diverge by about 30% from the previous estimates (Lutz et al. 1993) and predict a correct ratio of the (1,1) and (0,0) bands (in contrast to the previous estimate of these factors). Given the importance of N2 in comets, these improved transition probabilities will be very useful for tracing the physical properties during their formation process.
ions that are freshly created by photoionisation of N2, and spectra at the extremities of the slit, corresponding to a projected distance of about 6000 km from the nucleus, that is, at least a few thousand seconds of travel time from it. This difference is interpreted in terms of time necessary to reach a fluorescence equilibrium (because pure rotational transitions are forbidden), and the spectra obtained at the end of the slit can be satisfactorily explained by a Monte Carlo simulation based on the transition probabilities computed in this work. Some fluorescence efficiencies (the number of photons s−1 ion−1 , which depends on the solar radiation density received by the comet) were also computed, allowing a quantitative study of the N2 production rate in this comet and in future comets with a significant amount of this species. These fluorescence efficiencies diverge by about 30% from the previous estimates (Lutz et al. 1993) and predict a correct ratio of the (1,1) and (0,0) bands (in contrast to the previous estimate of these factors). Given the importance of N2 in comets, these improved transition probabilities will be very useful for tracing the physical properties during their formation process.
Acknowledgements
The authors gratefully acknowledge financial support from the “PHC Utique” programme of the French Ministry of Foreign Affairs and Ministry of Higher Education and Research and the Tunisian Ministry of Higher Education and Scientific Research, project number 18G1302, and computer time provided by the ROMEO HPC Center at the University of Reims Champagne-Ardenne and by CRIANN (Centre des Ressources Informatiques et Applications Numériques de Normandie).
Appendix A Vibrational Einstein coefficients for the  isotopologue
isotopologue
Vibrational transition dipole moments (µ, in atomic units), Franck-Condon factors (FC), R-centroids (in Angstroem) and a comparison of vibrational Einstein A coefficients in (s−1 ) for electronic dipole transitions between the electronic states  and
and  .v′ and v′" denote the vibrational quantum numbers of the B and X electronic states, using standard spectroscopic notation.
.v′ and v′" denote the vibrational quantum numbers of the B and X electronic states, using standard spectroscopic notation.
Appendix B Expansion parameters for the  isotopologue
isotopologue
Isotopologue 14N14N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= 1 electronic dipole transitions between the electronic states  and
and 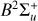
Isotopologue 14N14N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N14N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Isotopologue 14N14N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N"″= –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  , should be used.
, should be used.
Appendix C Expansion parameters for the 14N15N+ isotopologue
Isotopologue 14N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= 1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N15N+: Parameters for the evaluation of the squares of transition dipole moments for AN = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  , should be used.
, should be used.
Isotopologue 14N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ - N″ = –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Appendix D Expansion parameters for the 15n15n+ isotopologue
Isotopologue 15N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 15N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 15N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Isotopologue 15N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
References
- Ayari, T., Desouter-Lecomte, M., Linguerri, R., et al. 2020, Adv. Phys.: X, 5, 1831955 [NASA ADS] [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Paubert, G., et al. 2018, A&A, 619, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruna, P.J., & Grein, F. 2004, J. Mol. Spectr., 227, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Cartwright, D.C., & Dunning, T.H. 1975, J. Phys. B: At. Mol. Phys., 8, L100 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, A.L., & McKay, A.J. 2018a, ApJ, 856, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, A.L., & McKay, A.J. 2018b, ApJ, 854, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, F.R., Laher, R.R., & Espy, P.J. 1992, J. Phys. Chem. Ref. Data, 21, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Gottscho, R.A., Field, R.W., Dick, K., & Benesch, W. 1979, J. Mol. Spectro., 74, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hansson, A., & Watson, J.K. 2005, J. Mol. Spectro., 233, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Jain, D.C., & Sahni, R.C. 1967, Int. J. Quant. Chem., 1, 721 [CrossRef] [Google Scholar]
- Johnson, A.W., & Fowler, R.G. 1970, J. Chem. Phys., 53, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Klynning, L., & Pagès, P. 1982, Physica Scripta, 25, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Langhoff, S.R., & Bauschlicher, C.W. 1988, J. Chem. Phys., 88, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Langhoff, S.R., Bauschlicher, C.W., & Partridge, H. 1987, J. Chem. Phys., 87, 4716 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H., Shi, D., Wang, S., Sun, J., & Zhu, Z. 2014, J. Quant. Spectr. Rad. Transf., 147, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Lofthus, A., & Krupenie, P.H. 1977, J. Phys. Chem. Ref. Data, 6, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, B.L., Womack, M., & Wagner, R.M. 1993, Astrophys. J., 407, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Mulliken, R.S. 1931, Rev. Mod. Phys., 3, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Opitom, C., Hutsemékers, D., Jehin, E., et al. 2019, A&A, 624, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polák, R., & Fiser, J. 2003, Chem. Phys., 290, 177 [CrossRef] [Google Scholar]
- Qin, Z., Zhao, J., & Liu, L. 2017, J. Quant. Spectr. Rad. Transf., 202, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Rousselot, P., Anderson, S.E., Alijah, A., et al. 2022, A&A, 661, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schadee, A. 1964, Bull. Astron. Inst. Netherlands, 17, 311 [NASA ADS] [Google Scholar]
- Schmoranzer, H., Hartmetz, P., Marger, D., & Dudda, J. 1989, J. Phys. B: At. Mol. Opt. Phys., 22, 1761 [NASA ADS] [CrossRef] [Google Scholar]
- Scholl, T.J., Cameron, R., Rosner, S.D., & Holt, R.A. 1995, Phys. Rev. A, 51, 2014 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, D., Xing, W., Sun, J., Zhu, Z., & Liu, Y. 2011, Comput. Theor. Chem., 966, 44 [CrossRef] [Google Scholar]
- Singh, R.B., & Rai, D. 1966, J. Mol. Spectr., 19, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Spelsberg, D., & Meyer, W. 2001, J. Chem. Phys., 115, 6438 [NASA ADS] [CrossRef] [Google Scholar]
- Venkataramani, K., Ganesh, S., & Baliyan, K.S. 2020, MNRAS, 495, 3559 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, J.K. 2008, J. Mol. Spectr., 252, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P.J., Knizia, G., et al. 2021, MOLPRO, version 2021.1, a package of ab initio programs, see http://www.molpro.net [Google Scholar]
- Whiting, E.E., Schadee, A., Tatum, J.B., Hougen, J.T., & Nicholls, R.W. 1980, J. Mol. Spectr., 80, 249 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Experimentally derived vs. computed energies of the v = 0 vibrational states of  , and relative energies.
, and relative energies.
 : computed vibrational energies, rotational constants, and their comparison with experiment.
: computed vibrational energies, rotational constants, and their comparison with experiment.
 : computed vibrational energies, rotational constants, and their comparison with experiment.
: computed vibrational energies, rotational constants, and their comparison with experiment.
Hönl-London factors for 2Σ – 2Σ transitions expressed in terms of N = N″(third column) or J = J″ (fourth column).
Allowed combinations of Ψvib, Ψel, Ψrot, and Ψns as well as the statistical weights, gns, of the corresponding states.
Radiative B → X lifetimes, in ns, of the lowest vibrational states of the three isotopologues  ,
,  , and 14N15N+.
, and 14N15N+.
Vibrational transition dipole moments (µ, in atomic units), Franck-Condon factors (FC), R-centroids (in Angstroem) and a comparison of vibrational Einstein A coefficients in (s−1 ) for electronic dipole transitions between the electronic states  and
and  .v′ and v′" denote the vibrational quantum numbers of the B and X electronic states, using standard spectroscopic notation.
.v′ and v′" denote the vibrational quantum numbers of the B and X electronic states, using standard spectroscopic notation.
Isotopologue 14N14N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= 1 electronic dipole transitions between the electronic states  and
and 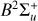
Isotopologue 14N14N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N14N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Isotopologue 14N14N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N"″= –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  , should be used.
, should be used.
Isotopologue 14N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″= 1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 14N15N+: Parameters for the evaluation of the squares of transition dipole moments for AN = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  , should be used.
, should be used.
Isotopologue 14N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ - N″ = –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Isotopologue 15N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 15N15N+: Franck-Condon factors (FC) and parameters for the evaluation of rovibrational Einstein A coefficients for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and 
Isotopologue 15N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = 1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
Isotopologue 15N15N+: Parameters for the evaluation of the squares of transition dipole moments for ∆N = N′ – N″ = –1 electronic dipole transitions between the electronic states  and
and  For transitions with very weak Franck-Condon factors, a constant value,
For transitions with very weak Franck-Condon factors, a constant value,  should be used.
should be used.
All Figures
 |
Fig. 1 Potential energy curves of the four lowest electronic doublet states, |
| In the text | |
 |
Fig. 2
|
| In the text | |
 |
Fig. 3
|
| In the text | |
 |
Fig. 4 Comparison of transition dipole moment functions. LB refers to Langhoff & Bauschlicher (1988), and LB-fit to a fit of their data by Gilmore et al. (1992). See main text for details. The dipole moment is expressed in atomic units: 1 a.u. = ea0 = 8.478353 … 10−30 Cm = 2.54175 Debye. |
| In the text | |
 |
Fig. 5 Radiative rovibrational lifetimes, in ns, for B rovibrational states with Σ = 1/2(F1). |
| In the text | |
 |
Fig. 6 Radiative rovibrational lifetimes, in ns, for B rovibrational states with Σ = −1/2 (F2). |
| In the text | |
 |
Fig. 7 Radiative lifetimes, in ns, for B rovibrational levels belonging to v′ = 0 and the F1 and F2 spin components. The average value is also shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.











