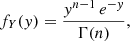| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | L10 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202449165 | |
| Published online | 10 April 2024 | |
Letter to the Editor
The dispersion of the Ep, i–Liso correlation of long gamma-ray bursts is partially due to assembling different sources
1
Department of Physics and Earth Science, University of Ferrara, Via Saragat 1, 44122 Ferrara, Italy
e-mail: mstmnl@unife.it
2
INFN – Sezione di Ferrara, Via Saragat 1, 44122 Ferrara, Italy
3
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Piero Gobetti 101, 40129 Bologna, Italy
Received:
5
January
2024
Accepted:
16
March
2024
Context. Long gamma-ray burst (GRB) prompt emission shows a correlation between the intrinsic peak energy, Ep, i, of the time-average νFν spectrum and the isotropic-equivalent peak gamma-ray luminosity, Lp, iso, as well as the total released energy, Eiso. The same correlation is found within individual bursts, when time-resolved Ep, i and Liso are considered. These correlations are characterised by an intrinsic dispersion, whose origin is still unknown. Discovering the origin of the correlation and of its dispersion would shed light on the still poorly understood prompt emission and would propel GRBs to powerful standard candles.
Aims. We studied the dispersion of both isotropic-equivalent and collimation-corrected time-resolved correlations. We also investigated whether the intrinsic dispersion computed within individual GRBs is different from that obtained including different bursts into a unique sample. We then searched for correlations between key features, such as the Lorentz factor and jet opening angle, and intrinsic dispersion, when the latter is treated as one of the characterising properties.
Methods. We performed a time-resolved spectral analysis of 20 long type-II or collapsar-candidate GRBs detected by the Fermi Gamma-ray Burst Monitor with a known redshift and estimates of the jet opening angle and/or the Lorentz factor. Time intervals were determined using Bayesian blocks. Then we carried out a statistical analysis starting from distributions of simulated values of the intrinsic dispersion of each burst in the sample.
Results. The collimation-corrected correlation appears to be no less dispersed than the isotropic-equivalent one. Also, individual GRBs are significantly less dispersed than the whole sample. We excluded (at a 4.2σ confidence level) the difference in samples’ sizes as the possible reason, thus confirming that individual GRBs are intrinsically less dispersed than the whole sample. No correlation was found between intrinsic dispersion and other key properties for the few GRBs with available information.
Conclusions. The contribution to the dispersion by the jet opening angle is not relevant. Moreover, our results prove that the intrinsic dispersion that affects the Ep, i − Liso correlation is partially, though not entirely, due to assembling different GRBs. We therefore conclude that the presence of different GRBs significantly contributes to the observed dispersion of both time-average Ep, i − Lp, iso and Ep, i − Eiso correlations.
Key words: methods: data analysis / methods: statistical / gamma-ray burst: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Despite the prompt emission of gamma-ray bursts (GRBs) that was discovered more than 50 years ago, several aspects are still poorly understood. One of them concerns some correlations that emerge when considering time-integrated spectra of type-II or collapsar GRBs with a known redshift. Specifically, it was found that the intrinsic (that is, redshift-corrected) peak energy, Ep, i, of the νFν spectrum correlates with the isotropic-equivalent gamma-ray radiated energy, Eiso (Amati et al. 2002), with peak luminosity, Lp, iso (Yonetoku et al. 2004), and with collimation-corrected energy, Eγ (Ghirlanda et al. 2004). These correlations have extensively been investigated over the last two decades mainly for two reasons: (1) they are key to gain clues on the radiative process(es) and on the dissipation mechanism at play (see Kumar & Zhang 2015 for a review); and (2) they can be exploited to use GRBs as probes of the cosmological parameters (see Moresco et al. 2022 for a review).
In this work, we focus on the time-resolved Ep, i − Liso correlation, which can be modelled as a power law (PL),
where m and q are the PL index and normalisation, respectively. The correlation is also characterised by an intrinsic dispersion, σint, whose origin is still unknown.
Even if this correlation was discovered starting from time-average spectra of different GRBs, several authors (Ghirlanda et al. 2010; Frontera et al. 2012; Lu et al. 2012; Basak & Rao 2013) found that it holds within individual GRBs as well, with a slope and normalisation consistent with the time-integrated values. The fact that the dispersion does not vanish within individual bursts is evidence that its origin cannot be entirely ascribed to properties that differ for each GRB, such as the jet opening angle, as originally suggested by Ghirlanda et al. (2004). Yet, the question remains as to which extent the dispersion must be ascribed to the dissipation mechanism operating within individual bursts and what is, instead, due to assembling different sources. To gain clues, we decided to compare the values of the dispersion of individual bursts with the dispersion of a whole sample of bursts.
Recently, Camisasca et al. (2023a) confirmed that the minimum variability timescale (MVT) of type-II GRBs correlates with peak luminosity and the Lorentz factor and they found evidence that it may also correlate with the jet opening angle. A possible interpretation builds on 3D general-relativity-magneto-hydrodynamic state-of-the-art simulations of a structured, relativistic jet propagating through stellar envelopes and possibly wobbling around the line of sight (Gottlieb et al. 2022). Motivated by these results, we tested the possibility that the intrinsic dispersion of individual bursts might be due to the putative wobbling of the jet: in fact, in that case, a correlation between σint, the jet angle, and/or the Lorentz factor could be expected, in principle.
As a matter of fact, type-I or binary merger candidate GRBs were initially found to be outliers from the Ep, i − Liso correlation of type-II GRBs. However, it was later found that these GRBs also obey a similar correlation, which is just shifted upwards in the Ep, i − Liso plane (see Minaev & Pozanenko 2020 and references therein). The different location of type-I GRBs in this plane offers an independent clue to classify GRBs, which can be particularly useful when the light curve (LC) alone is ambiguous (see Rossi et al. 2022; Rastinejad et al. 2022; Troja et al. 2022; Yang et al. 2022; Camisasca et al. 2023b).
In this work, we present a time-resolved spectral analysis of a sample of 20 type-II GRBs with a known redshift, which were detected by the Gamma-ray Burst Monitor (GBM; Meegan et al. 2009) aboard the Fermi satellite. In Sect. 2 we describe the sample selection and how the analysis was performed. Results and conclusions are reported in Sects. 3 and 4, respectively. The same ΛCDM cosmology as in Planck Collaboration VI (2020) was assumed.
2. Sample selection and data analysis
We used a sample of 20 type-II GRBs detected by Fermi-GBM for which estimates of the redshift z, the jet half-opening angle θj – both in the homogeneous interstellar medium (ISM) and wind profile (W) –, and/or the Lorentz factor Γ0 were available from the literature. In particular, we took z and θj from Zhao et al. (2020), while Γ0 from Ghirlanda et al. (2018). Exceptions were made for 171010A and 221010A. For the former, the uncertainties on θj reported by Zhao et al. (2020) were larger than the estimate of the angle itself; therefore, we used the value derived by Chand et al. (2019). For 221010A, we took z and θj from Zhu et al. (2023). We found no estimate of Γ0. The selected bursts are reported in Table 1. Hereafter this is referred to as the 𝒮 sample. The subsets of GRBs with estimates of  and
and  are referred to as the 𝒮(ISM) and 𝒮(W) samples, respectively. The number of bursts in each sample is reported in Table 2.
are referred to as the 𝒮(ISM) and 𝒮(W) samples, respectively. The number of bursts in each sample is reported in Table 2.
Sample of GRBs with redshift z, jet half-opening angle θj – both in the homogeneous interstellar medium (ISM) and wind profile (W) –, the Lorentz factor Γ0, and the minimum variability timescale (MVT).
Best-fit parameters of the Ep, i − L correlation (90% confidence) for the overall sample 𝒮 and for the sub-samples 𝒮(ISM) and 𝒮(W) of time-resolved spectra of GRBs with available information on  and on
and on  , respectively.
, respectively.
2.1. Time-resolved spectral analysis
The time-resolved spectral analysis of each burst in the sample 𝒮 was carried out with the GBM Data Tools1 as follows. We used the Time-Tagged Event (TTE) data of the two most illuminated NaI detectors. LCs were binned with a common bin time Δt, which ranged from a minimum of 64 ms to a maximum of 1024 ms according to the formula Δt = 64 × 2n ms, with n = 0, …, 4. The bin time was chosen so as to achieve the highest signal-to-noise ratio (S/N), with a maximum of 1024 ms to preserve the genuine structures in the LCs as much as possible. Then, we summed them to further increase the S/N. This required a preliminary background subtraction from both of the LCs, which had been done by interpolating the background with a polynomial function up to third order. The total LC, which we obtained from the procedure described above, was the starting point of our work.
Time intervals were determined adopting the scheme given by Bayesian blocks (BBs; Scargle et al. 2013) as implemented in the astropy.stats Python library. The choice of BBs was driven by the need to resolve spectrally different temporal structures in the burst LC in an unbiased way (Burgess 2014). At the same time, to ensure enough statistics, we adopted the following rule of thumb: ≥1000 counts had to be contained in each final interval, starting from the scheme given by BBs. Consequently, BBs were either taken as standalone intervals, or grouped so as to match our requirement on the minimum number of counts. The number of intervals, N, in which the LC of each GRB has been split is reported in Table 1.
Energy spectra in each selected final interval were fitted with a Band function (Band et al. 1993), also to ensure homogeneity where we fixed β = −2.3, since in most cases the high-energy tail of the 8−1000 keV spectrum was poorly constrained (see also the Fermi spectral catalogue by Poolakkil et al. 2021). We were therefore able to constrain the following: the low-energy index, α, the peak energy, Ep, and the average energy flux, F. Uncertainties on α and Ep were computed with GBM tools. For what concerns F, uncertainties were computed as follows. We approximated the posterior probability distribution function (PDF) of the model parameters around its maximum with a multi-dimensional normal distribution, whose mean and covariance matrix corresponded to the model parameter vector and covariance matrix derived from the fit, respectively. We then generated a random sample of model parameter vectors, Vi with i = 1, …, 1000, drawn from the multi-dimensional normal distribution. For each Vi, we computed the energy flux, Fi, with the GBM tools. We computed the standard deviation of the Fi sample and then converted it to 90% confidence level uncertainties.
The last step was moving from the observer-frame quantities Ep and F to the corresponding intrinsic quantities, namely Ep, i and Liso, exploiting the knowledge of the redshift. The isotropic-equivalent luminosity was computed in the GRB-rest-frame standard energy band 1 − 104 keV. We obtained a total of 793 time-resolved spectra for 𝒮, 421 for 𝒮(ISM), and 390 for 𝒮(W).
2.2. Modelling the time-resolved Ep, i–Liso correlation
For each burst we modelled the Ep, i − Liso correlation within a Bayesian context, adopting the D’Agostini likelihood (D’Agostini 2005), which self-consistently treats the intrinsic dispersion of the correlation as one of the model parameters. A uniform prior was assumed for the model parameters m, q, and σint. Parameter uncertainties were computed at a 90% confidence level by sampling the joint posterior PDF with a Python implementation of the affine-invariant ensemble sampler for Markov chain Monte Carlo (MCMC; Goodman & Weare 2010), using Python package emcee (Foreman-Mackey et al. 2013). Analogously, the value of dispersion, σint, t, relative to the overall sample 𝒮, was estimated merging the time-resolved pairs (Ep, i and Liso) of every burst into a unique sample and analysed as if it were a single GRB (see the top panel of Fig. 1).
 |
Fig. 1. Top panel: time-resolved Ep, i − Liso relation for the overall sample 𝒮. Bottom panel: collimation-corrected Ep, i − Lcoll relation for the subset 𝒮(ISM) of GRBs with available information on |
2.3. Simulated distributions of the intrinsic dispersion of individual bursts
To investigate to which extent assembling different GRBs affects the dispersion of the time-resolved Ep, i − Liso correlation, we assume that the latter is equally dispersed over the same region for all GRBs in the sample 𝒮 (hereafter H0 hypothesis). Under this assumption, points in the Ep, i − Liso plane belonging to any given GRB should be indistinguishable from random samplings of the overall sample. We exploited this predicted property to test H0.
Let (Ep, i, Liso)i, j be the pair of values of the ith interval of the jth burst, with i = 1, …, Nj and j = 1, …, 20, where Nj denotes the number of intervals in which the LC of the jth burst has been split. The total sample 𝒮 includes  observed pairs (Ep, i, Liso). For each round of simulations, we shuffled 𝒮 and split it into the 20 subsets with the same corresponding numbers of elements, Nj (j = 1, …, 20), as the real GRBs. For each shuffled subset of Nj pairs of (Ep, i, Liso) and the corresponding uncertainties, we modelled the correlation following the procedure described in Sect. 2.2. Eventually, we stored the values of the simulated intrinsic dispersion of each burst into an array R = (σ1, …, σ20).
observed pairs (Ep, i, Liso). For each round of simulations, we shuffled 𝒮 and split it into the 20 subsets with the same corresponding numbers of elements, Nj (j = 1, …, 20), as the real GRBs. For each shuffled subset of Nj pairs of (Ep, i, Liso) and the corresponding uncertainties, we modelled the correlation following the procedure described in Sect. 2.2. Eventually, we stored the values of the simulated intrinsic dispersion of each burst into an array R = (σ1, …, σ20).
The entire procedure described above was repeated 104 times. By assembling the Ri arrays together with i = 1, …, 104, we built a 104 × 20 matrix whose jth column contained 104 simulated values of the intrinsic dispersion of the jth burst in the sample (j = 1, …, 20). The distribution of the values of column j therefore represents the PDF of σj under H0, hereafter denoted as fj(σj). Furthermore, σj and σint, j denote the random variable and the measured value from real data, respectively, for the jth burst. We then determined the corresponding cumulative density function (CDF)  and calculated the probability Pj = Fj(σint, ul, j), where σint, ul, j is the upper limit on σint, j. We opted for a conservative approach, so the upper limit was taken instead of the corresponding value. Therefore, Pj is the probability that, under H0, Nj points randomly sampled in the Ep, i − Liso plane from the whole set of all GRBs are no more dispersed (within uncertainties) than the Nj measured points of the jth GRB.
and calculated the probability Pj = Fj(σint, ul, j), where σint, ul, j is the upper limit on σint, j. We opted for a conservative approach, so the upper limit was taken instead of the corresponding value. Therefore, Pj is the probability that, under H0, Nj points randomly sampled in the Ep, i − Liso plane from the whole set of all GRBs are no more dispersed (within uncertainties) than the Nj measured points of the jth GRB.
3. Results
Table 1 reports the parameters of the Ep, i − Liso correlation for individual bursts. The analogous values computed for the total sample 𝒮 are  ,
, 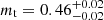 , and qt = −21.4 ± 0.9. The slope lies within the range of values reported by other authors on different data sets (0.36 ± 0.05 for Ghirlanda et al. 2010; 0.621 ± 0.003 for Lu et al. 2012; and
, and qt = −21.4 ± 0.9. The slope lies within the range of values reported by other authors on different data sets (0.36 ± 0.05 for Ghirlanda et al. 2010; 0.621 ± 0.003 for Lu et al. 2012; and  for Frontera et al. 2012), whereas the dispersion is instead compatible with that found by Lu et al. (2012) (σint, t = 0.256). The discrepancy between the values of the slope presented in the literature likely reflects the heterogeneity of approaches and data sets.
for Frontera et al. 2012), whereas the dispersion is instead compatible with that found by Lu et al. (2012) (σint, t = 0.256). The discrepancy between the values of the slope presented in the literature likely reflects the heterogeneity of approaches and data sets.
For both of the subsets 𝒮(ISM) and 𝒮(W), we computed the parameters mcoll, qcoll, and σcoll of the Ep, i − Lcoll correlation, where Lcoll = Liso(1 − cos θj) is the collimation-corrected luminosity (see the bottom panel of Fig. 1). The values are reported in Table 2. Both  and
and  are not smaller than σint, t (computed on either 𝒮(ISM) or 𝒮(W)), suggesting that the jet opening angle cannot be considered as the main source of dispersion in the Ep, i − Liso correlation, unless one admits the possibility that the way jet opening angles are routinely estimated from the afterglow modelling is not reliable.
are not smaller than σint, t (computed on either 𝒮(ISM) or 𝒮(W)), suggesting that the jet opening angle cannot be considered as the main source of dispersion in the Ep, i − Liso correlation, unless one admits the possibility that the way jet opening angles are routinely estimated from the afterglow modelling is not reliable.
3.1. Dispersion of individual bursts
Almost all of the dispersion values of individual bursts are smaller, or at most equal to the dispersion σint, t of the overall sample. This is the case for the former with respect to the slope and normalisation of each of them, which are generally different from those computed for the entire sample. This result apparently clashes with the hypothesis H0 (Sect. 2.3). Yet, as long as we consider the jth (j = 1, …, 20) GRB alone, its value of Pj is not small enough to reject H0 for that GRB. However, the simultaneous occurrence of 20 independent and relatively unlikely events demands a precise calculation, which correctly accounts for the multi-trial aspect.
To this aim, we defined the variable 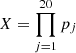 , where pj = Fj(σj). Using the values of pj = Pj derived in Sect. 2.3 on the real sample, we obtained X0 = 1.50 × 10−19. We note that X measures the relative probability of obtaining, under H0, a sample {σj}. To establish how unlikely X0 is, we have to determine its CDF, FX(x) = P(X ≤ x). Hence, the final significance that was looked for is Pt = FX(X0). In fact, we conveniently used
, where pj = Fj(σj). Using the values of pj = Pj derived in Sect. 2.3 on the real sample, we obtained X0 = 1.50 × 10−19. We note that X measures the relative probability of obtaining, under H0, a sample {σj}. To establish how unlikely X0 is, we have to determine its CDF, FX(x) = P(X ≤ x). Hence, the final significance that was looked for is Pt = FX(X0). In fact, we conveniently used  . Under H0, each burst can be thought of as an independent realisation of the same phenomenon, so the variables pj are identically and uniformly distributed in [0, 1]. Consequently, −ln pj is exponentially distributed. Given that Y is defined as the sum of n = 20 independent, identically, and exponentially distributed variables, its PDF, fY(y), is a Gamma distribution
. Under H0, each burst can be thought of as an independent realisation of the same phenomenon, so the variables pj are identically and uniformly distributed in [0, 1]. Consequently, −ln pj is exponentially distributed. Given that Y is defined as the sum of n = 20 independent, identically, and exponentially distributed variables, its PDF, fY(y), is a Gamma distribution
where Γ() is the Gamma function. Because of the minus sign, it is P(X ≤ X0) = P(Y ≥ Y0), where Y0 = −lnX0. Consequently, it is  , which corresponds to a confidence level of 4.2σ (Gaussian). We therefore reject H0 at this confidence level and conclude that GRBs are less dispersed when considered individually rather than collectively.
, which corresponds to a confidence level of 4.2σ (Gaussian). We therefore reject H0 at this confidence level and conclude that GRBs are less dispersed when considered individually rather than collectively.
3.2. Searching for a correlation between dispersion and other key observables
Motivated by the possibility that the dispersion intrinsic to the Ep, i − Liso correlation could be related to a structured, relativistic jet that wobbles around the line of sight, following the approach proposed by Camisasca et al. (2023a), we searched for correlations between σint and some key observables, namely θj, the Γ0, and the MVT. For the latter, we used the same values computed by Camisasca et al. (2023a), which are reported in Table 1. The only exception was 221010A, which was not in that sample. No evident correlation emerged. We also investigated whether σint is, to some extent, affected by the different number of spectra of each GRB, finding no evidence for it. For completeness, we repeated the same analysis replacing σint with the PL index m, and found nothing worth mentioning.
Given that type-I GRBs are shifted upwards in the Ep, i − Liso plane with respect to type-II GRBs, we investigated whether more dispersed bursts might be located closer to the former rather than the latter. To this aim, we searched for a relationship between dispersion and burst position in the intrinsic plane, where the latter was characterised as follows. For each GRB, both quantities were centred by subtracting the corresponding average values: log Ep, i − ⟨log Ep, i⟩ and log Liso − ⟨log Liso⟩. Using the centred values, we computed the parameters mc, j, qc, j, and σint, c, j as described in Sect. 2.2. We then calculated a representative value for the peak energy of any given jth GRB, which was evaluated at a common luminosity given by the average of the total sample, ⟨log Liso⟩t, and defined as (log Ep, i)c, j = ⟨log Ep, i⟩j + mc, j(⟨log Liso⟩t − ⟨log Liso⟩j)+qc, j (Ep, i and Liso are meant to be expressed in keV and 1052 erg s−1, respectively). The values of (log Ep, i)c are reported in Table 1. We found no correlation between σint and (log Ep, i)c.
3.3. On the robustness of the results
As discussed by Burgess (2014), the BB method alone does not ensure enough statistical quality for spectral modelling in each interval, as is instead the case when the source is more intense than the underlying background. In our analysis this was not always the case for bursts with a low S/N. Therefore, we tested the impact of our choice on the correlation parameters, as follows. We considered 090102, which had the lowest S/N that still allowed us to match the above prescription (i.e. source counts > background counts). We grouped different adjacent BBs at the same time, making sure that there were enough intervals and corresponding points in the Ep, i − Liso plane to compute the correlation parameters as in Sect. 2.2. We obtained the following values: mB = 0.9 ± 0.2, qB = −44 ± 12, and  , which are compatible within uncertainties with those in Table 1. This suggests that our choice of > 1000 counts in each selected interval does not affect the correlation modelling even when the above prescription of a dominant source over background is not fulfilled. Other GRBs with a better average S/N for the different time intervals are less affected by this potential bias, whose impact can therefore be neglected a fortiori.
, which are compatible within uncertainties with those in Table 1. This suggests that our choice of > 1000 counts in each selected interval does not affect the correlation modelling even when the above prescription of a dominant source over background is not fulfilled. Other GRBs with a better average S/N for the different time intervals are less affected by this potential bias, whose impact can therefore be neglected a fortiori.
With reference to Sect. 2.1, we explored the alternative approach of constraining the high-energy index of the Band function, by also using the data from the BGO detector with the more favourable viewing angle. We evaluated the impact on the correlation parameters of the three GRBs with the highest S/N and a high BGO signal, which are 160625B, 171010A, and 180720A. Whenever β could not be constrained through spectral analysis, we kept fixing it to −2.3. The results are reported in Table 3. We called NBGO and Nβ the number of selected intervals and the number of intervals with an estimated β, respectively. All parameters are compatible within uncertainties, suggesting that having neglected BGO data does not impact the modelling of the Ep, i − Liso correlation appreciably. In addition, all distributions of the estimated β peak around −2.3, which justifies our approach.
Best-fit parameters of the Ep, i − Liso correlation (90% confidence) of the GRBs with the highest S/N obtained including BGO data with a better viewing angle (mBGO, qBGO, and σint, BGO using the Band function; mCPL, qCPL, and σint, CPL using the CPL model) and NaI alone (m, q, and σint).
Given that only a fraction of GRBs is preferentially fitted by the Band function, following Sects. 2.1 and 2.2, we replicated the analysis (inclusive of BGO data) choosing the alternative cutoff power law (CPL), and we investigated the impact on the parameters of GRB 160625B, 171010A, and 180720A, for the same reason mentioned above. The results are presented in Table 3. Even in this case, all parameters are compatible with each other. We thus conclude that the model choice, such as Band versus CPL, does not seem to impact the correlation modelling significantly. The goodness of the best-fit modelling was computed with GBM tools for every interval using Profile Gaussian likelihood (PGSTAT), according to which neither the Band function nor the CPL model could be rejected.
4. Discussion and conclusions
Through a time-resolved spectral analysis of a sample of 20 type-II GRBs detected by Fermi-GBM with available estimates of z, θj, and/or Γ0, we proved that the intrinsic dispersion of the Ep, i − Liso correlation within individual GRBs is smaller than that of the sample including all of them (4.2σ confidence). This result is not an artefact of the different number of time-resolved intervals considered and it propels the dispersion of the correlation as an intrinsic property of each GRB, whose origin is not yet fully understood. It also confirms that the origin of the dispersion in the sibling time-average correlations, Ep, i − Eiso and Ep, i − Lp, iso, is to be partially ascribed to assembling different sources together. In addition, we searched for correlations between σint and some key properties, such as the jet half-opening angle, the Lorentz factor, and the MVT, that could bring signatures of a randomly wobbling jet, as suggested by recent state-of-the-art simulations, finding no evidence.
When the time-resolved isotropic-equivalent luminosity is replaced by the corresponding collimation-corrected estimates, either assuming an ISM or a wind environment, the dispersion of the Ep, i − Lcoll correlation does not decrease at all. This proves that the jet opening angle cannot be considered as a significant source of dispersion, unless the estimates for the angles obtained in the literature from the afterglow modelling are, for some unknown reason, unreliable. Instead, the viewing angle could be a relevant source of scattering, given that the correlation itself could also be interpreted as a viewing angle effect for a variety of jet models (see Salafia et al. 2015 and references therein). However, estimating the viewing angle from afterglow modelling is presently more challenging.
We also investigated whether bursts lying closer to type-I GRBs in the Ep, i − Liso plane, and therefore potentially misidentified compact binary merger candidates, exhibit a significantly different dispersion from the bulk of collapsar candidates, but no evidence for it was found. Yet, our search was significantly hampered by the low statistical sensitivity due to the small number of GRBs with available information. Only a larger sample of GRBs with estimates of the properties mentioned above will allow us to explore with the required sensitivity. In this respect, a major breakthrough will be achieved thanks to upcoming missions such as SVOM (Atteia et al. 2022), possibly followed by THESEUS (Amati et al. 2021), which has recently been selected by ESA for a Phase-A study within the M7 mission context. These missions will cover the entire spectrum of the prompt emission, thus constraining the spectral parameters of soft events and extending the dynamic range in the Ep, i − Liso plane. In parallel, the followup segments will contribute to increase the sample of GRBs with estimates of the above key properties. Ultimately, this will turn into a systematic and more accurate characterisation of the Ep, i − Liso correlation that will constrain the dissipation mechanism and the radiative processes that shape GRB prompt emission.
Acknowledgments
The constructive feedback from the anonymous reviewer is gratefully acknowledged. M.M. and R.M. acknowledge the University of Ferrara for the financial support of their PhD scholarships.
References
- Amati, L., Frontera, F., Tavani, M., et al. 2002, A&A, 390, 81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amati, L., O’Brien, P. T., Götz, D., et al. 2021, Exp. Astron., 52, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Atteia, J. L., Cordier, B., & Wei, J. 2022, Int. J. Mod. Phys. D, 31, 2230008 [NASA ADS] [CrossRef] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [Google Scholar]
- Basak, R., & Rao, A. R. 2013, MNRAS, 436, 3082 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, J. M. 2014, MNRAS, 445, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Camisasca, A. E., Guidorzi, C., Amati, L., et al. 2023a, A&A, 671, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camisasca, A. E., Guidorzi, C., Bulla, M., et al. 2023b, GRB Coordinates Network, 33577 [Google Scholar]
- Chand, V., Chattopadhyay, T., Oganesyan, G., et al. 2019, ApJ, 874, 70 [Google Scholar]
- D’Agostini, G. 2005, arXiv e-prints [arXiv:physics/0511182] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Frontera, F., Amati, L., Guidorzi, C., Landi, R., & in’t Zand, J. 2012, ApJ, 754, 138 [Google Scholar]
- Ghirlanda, G., Ghisellini, G., & Lazzati, D. 2004, ApJ, 616, 331 [Google Scholar]
- Ghirlanda, G., Nava, L., & Ghisellini, G. 2010, A&A, 511, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghirlanda, G., Nappo, F., Ghisellini, G., et al. 2018, A&A, 609, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Gottlieb, O., Liska, M., Tchekhovskoy, A., et al. 2022, ApJ, 933, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kumar, P., & Zhang, B. 2015, Phys. Rep., 561, 1 [Google Scholar]
- Lu, R.-J., Wei, J.-J., Liang, E.-W., et al. 2012, ApJ, 756, 112 [Google Scholar]
- Meegan, C., Lichti, G., Bhat, P. N., et al. 2009, ApJ, 702, 791 [Google Scholar]
- Minaev, P. Y., & Pozanenko, A. S. 2020, MNRAS, 492, 1919 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Amati, L., Amendola, L., et al. 2022, Liv. Rev. Relat., 25, 6 [NASA ADS] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poolakkil, S., Preece, R., Fletcher, C., et al. 2021, ApJ, 913, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, Nature, 612, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Rossi, A., Rothberg, B., Palazzi, E., et al. 2022, ApJ, 932, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Salafia, O. S., Ghisellini, G., Pescalli, A., Ghirlanda, G., & Nappo, F. 2015, MNRAS, 450, 3549 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D., Norris, J. P., Jackson, B., & Chiang, J. 2013, arXiv e-prints [arXiv:1304.2818] [Google Scholar]
- Troja, E., Fryer, C. L., O’Connor, B., et al. 2022, Nature, 612, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, J., Ai, S., Zhang, B.-B., et al. 2022, Nature, 612, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Yonetoku, D., Murakami, T., Nakamura, T., et al. 2004, ApJ, 609, 935 [Google Scholar]
- Zhao, W., Zhang, J.-C., Zhang, Q.-X., et al. 2020, ApJ, 900, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z.-P., Lei, W.-H., Malesani, D. B., et al. 2023, ApJ, 959, 118 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Sample of GRBs with redshift z, jet half-opening angle θj – both in the homogeneous interstellar medium (ISM) and wind profile (W) –, the Lorentz factor Γ0, and the minimum variability timescale (MVT).
Best-fit parameters of the Ep, i − L correlation (90% confidence) for the overall sample 𝒮 and for the sub-samples 𝒮(ISM) and 𝒮(W) of time-resolved spectra of GRBs with available information on  and on
and on  , respectively.
, respectively.
Best-fit parameters of the Ep, i − Liso correlation (90% confidence) of the GRBs with the highest S/N obtained including BGO data with a better viewing angle (mBGO, qBGO, and σint, BGO using the Band function; mCPL, qCPL, and σint, CPL using the CPL model) and NaI alone (m, q, and σint).
All Figures
 |
Fig. 1. Top panel: time-resolved Ep, i − Liso relation for the overall sample 𝒮. Bottom panel: collimation-corrected Ep, i − Lcoll relation for the subset 𝒮(ISM) of GRBs with available information on |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.