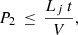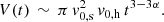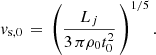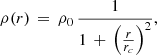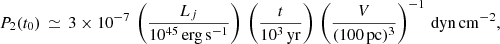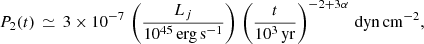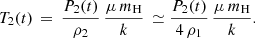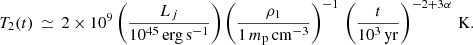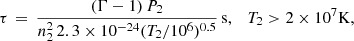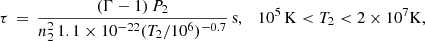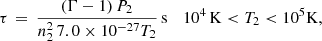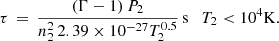| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202348624 | |
| Published online | 29 March 2024 | |
Shocks, clouds, and atomic outflows in active galactic nuclei hosting relativistic jets
1
Departament d’Astronomia i Astrofísica, Universitat de València, C/ Dr. Moliner, 50, 46100 Burjassot, València, Spain
e-mail: manel.perucho@valencia.edu
2
Observatori Astronòmic, Universitat de València, C/ Catedràtic José Beltrán 2, 46980 Paterna, València, Spain
Received:
15
November
2023
Accepted:
25
January
2024
Context. A number of observations have revealed atomic and/or molecular lines in active galaxies hosting jets and outflows. Line widths indicate outward motions of hundreds to a few thousands of kilometers per second. They appear to be associated with the presence of radio emission in Gigahert-peaked spectrum (GPS) and/or compact steep spectrum (CSS) sources, with linear sizes of ≤10 kpc. Numerical simulations have shown that the bow shocks triggered by relativistic jets in their host galaxies drive ionization and turbulence in the interstellar medium (ISM). However, the presence of atomic lines requires rapid recombination of ionized gas, which appears challenging to explain from the physical conditions revealed thus far based on numerical simulations of powerful jets.
Aims. The aim of this paper is to provide a global framework to explain the presence of lines in terms of jet and shock evolution and to fix the parameter space where the atomic and molecular outflows might occur.
Methods. This parameter space is inspired by numerical simulations and basic analytical models of jet evolution as a background.
Results. Our results show that a plausible general explanation involves momentum transfer and heating to the interstellar medium gas by jet triggered shocks within the inner kiloparsecs. The presence of post-shock atomic gas is possible in the case of shocks interacting with dense clouds that remain relatively stable after the shock passage.
Conclusions. According to our results, current numerical simulations cannot reproduce the physical conditions to explain the presence of atomic and molecular outflows in young radio sources. However, I show that these outflows might occur in low-power jets at all scales and I predict a trend towards powerful jets showing lines at CSS scales, when clouds have cooled to recombination temperatures.
Key words: galaxies: active / galaxies: ISM / galaxies: jets
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Relativistic jets in AGN are produced in the environment of central black holes. Our current understanding explains their formation in terms of magneto-hydrodynamical processes via the extraction of rotational energy either from a Kerr black-hole (Blandford & Znajek 1977) or from the inner accretion disk (Blandford & Payne 1982). The jets are launched as sub-Alfvénic Poynting-flux dominated and accelerated by magnetic fields (Vlahakis & Königl 2004; Komissarov et al. 2007; Komissarov 2012) and internal energy (Perucho & Martí 2007; Ricci et al. 2024) up to relativistic, superfast-magnetosonic speeds. It has been shown that the jets not only contribute to feedback at large scales and may participate in regulating star formation within their host galaxies (see, e.g., Shabala & Alexander 2009; Raouf et al. 2019), but also may play a significant role in driving atomic and molecular outflows within the inner kiloparsecs from the AGN (e.g., Morganti & Oosterloo 2018; Santoro et al. 2020; Morganti et al. 2021; Tadhunter et al. 2021; Kukreti et al. 2023).
Very long baseine interferometry (VLBI) observations of compact, young radio sources have revealed advance velocities of ∼0.2 c (e.g., Owsianik & Conway 1998; Polatidis & Conway 2003. Such velocities probably correspond to powerful jets. Numerical simulations of jet propagation within the inner kiloparsec of active galaxies have shown that they do expand at supersonic velocities and trigger strong shocks in the interstellar medium (see, e.g., Wagner & Bicknell 2011; Wagner et al. 2012; Mukherjee et al. 2016, 2018; Bicknell et al. 2018; Perucho et al. 2021; Meenakshi et al. 2022). Simulations also show that lateral expansion is slower by a factor of 3–5, as derived from aspect ratios, so the radial expansion velocity can be ≃0.04 − 0.06 c. Such strong shocks increase the temperature of the gas to values high enough to completely ionize hydrogen atoms. Post-shock temperatures of 108 − 1010 K can be easily achieved in this region, as we also justify in this work. In contrast, simulations of low-power jets (Lj ≃ 1042 erg s−1) present advance velocities of ≤10−3 c and the temperature jumps ≤2 (Perucho et al. 2014a) to values ∼107 K (in the hot ISM component).
However, radio observations of atomic lines show the presence of HI outflows in compact radio sources, namely, Gigahertz-peaked spectrum (GPS) sources (Holt et al. 2011), with linear sizes ≤1 kpc and compact steep spectrum (CSS) sources that are ≤10 kpc in size (see, e.g. O’Dea et al. 2002; Labiano et al. 2005; Shih et al. 2013; Reynaldi & Feinstein 2016; Morganti et al. 2016; Zovaro et al. 2019; Schulz et al. 2021, and Morganti & Oosterloo 2018 for a review). The presence of HI requires gas temperatures ≤1.5 × 105 K in the case of collisional equilibrium or even smaller in the case of thermodynamical equilibrium, that is, at least four orders of magnitude below the shocked gas temperature in powerful jets (e.g., Perucho et al. 2021). The inferred velocities range from several hundreds to few thousands of km s−1. In Holt et al. (2011), the authors point out that the line widths reveal larger velocities in two observed GPS galaxies than in CSSs and that they are compatible with an in situ shock-cloud collision. This has also been reported by Couto et al. (2020) for detected OIII lines. However, this is not obvious in all sources.
Although the aforementioned numerical simulations have tackled the problem of jet evolution inside the host galaxy, the authors have been forced to focus either on the inner kiloparsec (GPS region) or beyond (CSS region) by computational limitations, so the transition has barely been discussed in terms of heating and cooling of the ISM gas. Furthermore, none of the simulations had the required resolution to study the evolution of shocked clouds (also see Mandal et al., in prep.).
Bicknell et al. (1997, 2003) presented a model based on Begelman (1996) that successfully explained a number of properties of GPS sources. The authors show that radiative shocks can create an ionized shocked ISM that free-free absorbs low frequency radiation and explain the evolution of the peak frequency with size in these young radio-galaxies (Fanti et al. 1990; O’Dea & Baum 1997; Stanghellini et al. 1998). Those theoretical papers focus on high power jets (1045 − 46 erg s−1).
This paper takes a simple analytical approach to tackle the discrepancy between physical conditions derived from numerical simulations and those required for the presence of HI outflows in host galaxies (see, e.g., Snow & Hillier 2021a,b, and references therein for a detailed study of the physics of two-fluid shocked plasmas). The model presented here is motivated by results from numerical simulations of relativistic outflows (see, e.g. Hardcastle 2018; Turner et al. 2023, for other analytical models also driven by simulations and Turner & Shabala 2023 for a review) and focuses on the role of shocks on the environment, extending the study to low power radio-galaxies. The shocks are shown to be non radiative in the case of powerful jets, but to become radiative at a few kpc for low power jets. The model shows that atomic outflows are compatible with conditions produced by low power jets at all scales, but require further propagation time and cloud stability to allow for gas cooling in the case of powerful sources.
These results would point towards more powerful radio-sources showing atomic lines when they have propagated longer distances, but low power radio-sources presenting them at all scales, including smaller linear sizes. Altogether, this conclusion sets a plausible general scenario to explain observations of atomic outflows at all scales, depending on the jet power, either within or beyond the inner kiloparsec.
The paper is structured as follows. In Sect. 2, I present the physical arguments that could explain the presence of atomic lines in active galaxies based on shock-heating and estimated cooling times. In Sect. 3, I discuss the implications for both low and high power radio-galaxies, the caveats of the simple analytic approach and the implications for our understanding of jet physics and feedback at larger scales. Finally, in Sect. 4, I summarize the main conclusions of this paper.
2. Shocks: Heating and cooling
2.1. The heating
We focus here on the lateral expansion of jet-triggered shocks (i.e., misaligned with the jet direction), which affects a large volume of the ISM. The shock propagates into the two-phase ISM, with a hotter, dilute medium with temperatures ∼106 − 107 K and number densities ∼0.1 − 1 cm−3, and a colder, denser component in clouds, with temperatures ∼10 − 1000 K and densities ∼102 − 103 cm−3. The shocked ISM medium surrounds the shocked jet gas (or cocoon), with very high temperatures and lower densities (see, e.g., Wagner & Bicknell 2011; Mukherjee et al. 2016, 2018; Perucho et al. 2021). Nevertheless, our interest is focused on the shocked ISM-ISM interaction region (see Krause & Alexander 2007; Krause 2008, for the case of a cloud entering and interacting with the jet cocoon).
The following expressions (jump conditions in the shock reference frame) give the post-shock pressures and temperatures:
with subscripts 1 and 2 standing for pre and post-shock states of the interstellar medium (ISM), respectively, and where P represents pressure, ρ the gas rest-mass density, v the velocity in the shock propagation direction, and Γ the adiabatic exponent of an ideal gas.
In the reference frame of the shocked ISM, v1 = vs, the shock velocity. For an assumed ideal gas, we also have P/ρ = k T/μmH, where k is the Boltzmann constant, μ is the mean molecular weight, and mH is the atomic hydrogen mass. The previous expressions allow us to derive the shock advance velocity by imposing the ambient density and both pre and post-shock pressures.
2.1.1. The hot phase
In the case of AGN bow-shocks, the post-shock pressure is rapidly homogenized in the shocked hot phase because of the large sound speed achieved by the gas, as it has been shown by numerical simulations. Perucho et al. (2017) also showed that the following expression gives an order-of-magnitude estimate of post-shock pressure in relativistic jets:
where Lj is the jet power, and V is the shocked volume1. The ISM pressure can be taken to be the usually estimated value P1 ≃ 10−10 dyn cm−2. Therefore, if we are able to estimate the shocked volume with time, we can get an approximate value for the pressure jump. We can do this in a very raw way, taking the shocked volume to be a cylinder, with a radius, rs, and length, ls (a usual approximation used in analytical models, e.g., Begelman & Cioffi 1989): 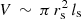 . Considering the mean head advance velocity at small evolution times (within the host galaxy), we can write rs ∼ vs t and ls ∼ vh t, where vs is the lateral shock velocity (the one we are interested in here) and vh is the head advance velocity. As stated above, vs is smaller than vh. Self-similarity appears as a result of keeping the ratio vh/vs constant. Kaiser & Alexander (1997) showed that this is a consequence of adiabatic expansion of jet-inflated cocoons. This is supported by observed lobe/hot-spot−distance evolution throughout the inner kpc (Perucho & Martí 2002; Polatidis & Conway 2003; Kawakatu et al. 2008) in the case of compact symmetric objects (CSOs). With this information, we can write the expression for the volume as a function of time:
. Considering the mean head advance velocity at small evolution times (within the host galaxy), we can write rs ∼ vs t and ls ∼ vh t, where vs is the lateral shock velocity (the one we are interested in here) and vh is the head advance velocity. As stated above, vs is smaller than vh. Self-similarity appears as a result of keeping the ratio vh/vs constant. Kaiser & Alexander (1997) showed that this is a consequence of adiabatic expansion of jet-inflated cocoons. This is supported by observed lobe/hot-spot−distance evolution throughout the inner kpc (Perucho & Martí 2002; Polatidis & Conway 2003; Kawakatu et al. 2008) in the case of compact symmetric objects (CSOs). With this information, we can write the expression for the volume as a function of time:
For the first time step, we can safely assume strong shock conditions 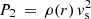 (where ρ(r) is the ambient density). With this, we obtain
(where ρ(r) is the ambient density). With this, we obtain
Finally, we assume a typical ambient medium density profile
and ρ0 = 1.67 × 10−24 g cm−3.
We can provide a general expression to estimate post-shock gas temperature by starting from Eq. (4). Taking an initial volume of ∼100 pc3 as a reference at t ∼ 103 yr, we get:
namely, a factor 103 over the ISM pressure (validating the strong shock hypothesis at t0). The evolution of pressure with time can then be written from the previous expression and the time-dependency obtained for the volume (see Eq. (5)):
where the constants in Eq. (5) have been absorbed in the initial volume taken to estimate P2(t0).
Post-shock temperature can be estimated from (for a strong, non-relativistic shock):
Taking ρ1 = ρ0 ≃ 1 mp cm−3 as a reference value for the unperturbed ISM, we obtain:
The equation shows that the post-shock temperature is linearly dependent on the jet power and inversely proportional to ISM gas density. The dependence on time is controlled by exponent α for velocity evolution. Plausible values range from α = 0, which is a consequence of a very steep density profile (ρ(r)∝r−2) or a buoyantly propagating bubble with constant velocity, and α ≤ 1 for low-power and or mass-loaded jets (Perucho et al. 2011, 2014a). Self-similarity implies α ∼ 0.4 (Scheuer 1974; Kaiser & Alexander 1997), so post-shock temperature would fall with time as t−0.8. The sensitivity of T2 to source age would be damped for α ≃ 0.5 − 0.6. On the contrary, it would be stronger if velocity is constant (α = 0 would make T2 ∝ t−2, owing to a fast pressure decrease) or if it fell rapidly (α ≃ 1 would make post-shock pressure become proportional to t, due to the increase in pressure if the advance is slowed down). For moderate values of α as that given by self-similarity, post-shock temperature might fall approximately as t−1 when propagating through an ambient medium with constant density, namely, the galactic core.
Therefore, beyond this initial set of values, we could impose self-similar expansion and strong-shock conditions all along the studied evolution. In this case, α = 2/5 and the evolution is determined by the previous equations. However, as we go on to show, the latter assumption could be not fulfilled for low power jets. In order to avoid this problem, we can proceed in a different way: the shock advance velocity in the radial direction at time ti, vs(ti), can be estimated from Eq. (3); namely, by skipping the strong-shock assumption. Once vs(ti) is derived (for time ti), we can obtain V(ti + 1) assuming constant expansion velocity for a sufficiently small time-step.
However, Eq. (5) requires not only vs but also vh to be known. We have seen that self-similarity can be a good assumption through the inner region and, in addition, the lobe length-to-radius ratio is ≤5, so we can assume a constant relation between both expansion velocities, for instance, vh ≃ 3vs. Although this assumption is probably weaker later on, when the ratio can decrease due to jet head deceleration, vh/vs must be always larger than 1, so we can impose the same velocity ratio along the whole studied distance range. Detailed analytical modelling by Turner et al. (2018) showed that in realistic environments, the ratio of jet head to transverse expansion velocity only increases moderately (factor 1.5 on scales of 100 s of kpc; see Figs. 8 and 9 in Turner et al. 2018). As shown in that paper, these analytical results are consistent with numerical simulations, and also observations of lobed 3C radio sources. Furthermore, this estimate cannot introduce significantly larger errors than the case of a cylindrical volume for the shocked region, for instance.
Finally, once the value of V(ti + 1) is obtained, we can find P2(ti + 1) from Eq. (4) and then proceed to compute vs(ti + 1). In this way, it is possible to avoid the dependency on α for the expansion velocity.
Figure 1 shows the evolution of shock position and velocity along the jet propagation direction (left panel) and post-shock temperatures (right panel) for different jet powers. The right panel also displays post-shock temperatures for media with constant number density 103 cm−3 (and pressure P1) in order to show the values attained inside clouds shocked at different locations within the host galaxy (see Sect. 2.1.2). We have set t0 = 103 yr and have used constant ambient pressure P1 = 10−10 dyn cm−2.
 |
Fig. 1. Left panel: radial shock velocity (vs, violet) and axial position (black) for jet powers 1046 (solid lines), 1044 (dashed), and 1042 erg s−1 (dotted). The thin, dark red lines indicate the ISM sound speed at the axial position. Right panel: post-shock temperatures for same jet powers as the left panel in the case of a medium density following Eq. (7) (black lines), i.e., a hot, diffuse ISM, and a medium with constant number density 103 cm−3, i.e., cold clouds. Horizontal lines indicate hydrogen ionization temperatures in local thermodynamical equilibrium, 3500 K (solid), and collisional equilibrium, 1.58 × 105 K (dashed). In these clouds, the sound speed is 3 km s−1. The temperatures have been derived for ionized hydrogen in Eq. (10). |
The right panel in Fig. 1 shows that post-shock temperatures reached by the hot, dilute ISM agree with those obtained for powerful radio-galaxies from numerical simulations. The ratios P2/P1 for pressure jumps across the shocks (see Fig. 2) indicate that overpressure goes below a factor of 10 only in the case of the low-power radio galaxies after 500 kyr, when the jet head is at ≃1 kpc, and reach values ≃7 at 1Myr (D ≃ 1.2 kpc). Therefore, the strong shock approximation would remain valid throughout most of the shown profiles for powerful jets, but low-power radio galaxies may transit to weaker (and radiative, see Sect. 2.2) shocks within the inner 2 kpc of propagation.
 |
Fig. 2. Lobe overpressure for jet powers 1046 (solid lines), 1044 (dashed), and 1042 erg s−1. The black lines for the hot, diffuse ISM, and red lines correspond to cold, dense clouds with a number density of 103 cm−3 are overlapped. |
2.1.2. The cold phase
The red lines in the right panel of Figs. 1 and 2 show the estimated values of temperature and overpressure for shock-cloud interactions, assuming n = 103 cm−3 for the three considered jet powers.
We have assumed v1, c ∼ (ρ1/ρ1, c)1/2v1 (subscript c stands for clouds, and no subscript for the values derived for the hot phase in the previous section). Taking P1, c = P1 and Γ = 5/3 for a cold, monoatomic gas (hydrogen), we can derive v2, c by rearranging the jump Eqs. (1)–(3), and then P2, c.
Assuming collisional ionization, which is expected to be a valid approximation for diffuse, astrophysical plasmas (Dopita & Sutherland 2003), hydrogen ionising temperatures are ∼105 K. Figure 1 shows that, for Lj = 1046 erg s−1 temperatures ≃105 K are reached in shocked clouds up to ≃100 kyr (D ≃ 2 kpc). In the case of Lj = 1044 erg s−1, this happens before 50 kyr (D ≃ 300 pc). Finally, low power jets may barely reach ionising post-shock temperatures in dense clouds within the inner tens of parsecs.
Although local thermodynamical equilibrium (LTE), in which the ionized states follow Boltzmann’s law (Dopita & Sutherland 2003), is probably not fulfilled in diffuse astrophysical plasmas, we can explore this possibility, too, for the case of clouds. Using the post-shock values derived for clouds and Saha equation, we can derive the degree of ionization in shocked clouds. In this case, ionising temperatures are ≃3000 K. The results are shown in Fig. 3 for Lj = 1042, 1043 and 1044 erg s−1. Low-power jets would be unable to ionize hydrogen in cold, dense clouds, beyond a few hundred parsecs, whereas the first traces of HI in shocked clouds would appear after D ≃ 3 kpc in 1044 erg s−1 jets. Post-shock temperatures are incompatible with the presence of non-ionized HI in shocked clouds in LTE for higher powers. Therefore, higher power jets would require efficient cooling to explain the presence of atomic outflows within the inner kiloparsecs of propagation, if LTE is assumed.
 |
Fig. 3. HI fraction in shocked clouds in LTE for jets with powers 1044 (dashed), and 1042 erg s−1 (dotted). The intermediate case of 1043 erg s−1 (dash-dot line) has been also included in this plot. |
These values are only a basic approximation because shocks in clouds are probably radiative (see Sect. 2.2), allowing for fast cooling. As an opposing, heating mechanism, the development of instabilities and mixing with the hotter environment could change this picture, as we discuss below.
2.2. The cooling
As we state in the introduction, outflows of atomic gas have been observed both in GPS (ls ≤ 1 kpc) and CSS sources (ls ≤ 10 kpc). The values obtained for temperature described in the previous section (see Eq. (11)) and drawn from numerical simulations of powerful jets certainly prohibit the presence of atomic hydrogen when the radio-galaxy extends over the inner hundreds of parsecs. Efficient cooling must take place to explain the presence of atomic outflows correlated with the presence of more powerful (Lj ≥ 1043 erg s−1) relativistic jets.
Dense clouds are expected to be located within the inner kiloparsec of the host galaxy. In the case of powerful jets that ionize most of the shocked ISM, we then expect the observed atomic outflows to be formed by the recombination of those ionized atoms, once the radio-source has evolved to larger scales.
According to cooling theory (see, e.g., Myasnikov et al. 1998; Dopita & Sutherland 2003; Draine 2011) the cooling function, Λ/nHne can be approximated to 1.1 × 10−22 (T/106)−0.7 erg cm3 s−1 for gas temperatures between 105 K and 2 × 107 K (taking number density of nH = 1 cm−3), beyond which it is dominated by Bremsstrahlung (2.3 × 10−24 (T/106)1/2erg cm3 s−1). At lower temperatures (between 104 and 105 K), it becomes 7 × 10−27 Terg cm3 s−1. Below 104 K, we use the cooling function for recombination of hydrogen atoms (2.39 × 10−27 T1/2erg cm3 s−1, see Vaidya et al. 2015). Using the values for post-shock densities and temperatures obtained in Sect. 2.1, we can compute the cooling times of the shocked gas.
The cooling times are computed as follows:
The results are shown in Fig. 4, where we observe that low-power jets present cooling times for the shocked hot, diluted ISM of the order or less than evolution times after 105 yr, when they become radiative. The cooling times derived for cold, dense clouds are shorter than 1 kyr and are thus not shown. This means that cooling in the clouds is basically instantaneous in relative terms. Therefore, although fast jet expansion and high post-shock temperatures would make it difficult to find atomic hydrogen within the inner kiloparsec in powerful jets, such short cooling times could make recombination plausible in shocked clouds even before a linear size of 2 kpc is reached.
 |
Fig. 4. Cooling times for the same cases given in Fig. 1 (left panel) and relative values with respect to the evolution times (right panel). Solid lines represent the powerful, 1046 erg s−1 case, dashed lines the 1044 erg s−1 case, and dotted lines the 1042 erg s−1. Calculations are shown for the shocked hot, dilute ISM described by Eq. (7). |
3. Discussion
3.1. Low-power radio galaxies
We see that the bow shock can weaken and cease to be “strong” beyond a few kpc for jet powers Lj < 1043 erg s−1 (see Figs. 1 and 2). Even though post-shock temperatures are high for the hot, diluted ISM phase, cooling times become similar to source age when the tip of the bow shock is still located within the inner kpc and keep decreasing further. In the case of cold, dense clouds, however, the post-shock temperatures are always ≤105 K. This means that 1) it is possible that part of the atomic gas is not ionized by the shock and 2) cooling times are basically instantaneous compared to the evolution time-scales.
As the shock weakens, post-shock temperature and velocity become smaller for the hot, dilute gas surrounding the clouds. Because the difference in conditions inside and outside shocked clouds would thus be alleviated, shocked clouds could be more stable within this environment than in that generated by stronger shocks. In addition, even if mixing occurred, the lower surrounding temperatures would still allow for rapid cooling. However, this must be studied via dedicated numerical simulations. Nevertheless, the simple analytical approach that we have used already indicates that the presence of atomic gas with outward motions in shocked regions within radio galaxies could be relatively easily explained.
3.2. Powerful radio galaxies
In Sect. 2.2 we see that despite the high temperatures achieved by the ISM after the passage of shocks, high-density regions could allow for fast enough cooling and, therefore, the presence of atomic (and molecular) gas within the inner kiloparsec(s) from the active nucleus. In addition, this gas has an outward momentum that can be aligned with the jet propagation direction or be perpendicular to it because the bow shocks propagate in all directions, in accordance with observations. The observed lines reveal radial velocities of hundreds up to few thousand km s−1 and these velocity fields are indeed reproduced in numerical simulations (Perucho et al. 2021; Meenakshi et al. 2022; Murthy et al. 2022).
The higher temperatures achieved by the shocked gas in powerful radio-sources and thus longer cooling times could lead us to expect a bias in the detection of atomic outflows towards larger distances to the nucleus in this case. Furthermore, (shocked) cloud stability has to be taken into account: disruption and mixing with the hotter environment would significantly delay cooling times and distances. An a fortiori argument favouring cloud stability conditions is given by the observations. Clouds must retain a certain degree of coherence after shock passage if atomic and molecular lines are observed within shock affected regions in radio-galaxies. Otherwise, this would be difficult to explain for relatively powerful radio-galaxies.
In a recent paper, Snow & Hillier (2021a) explore the physics of shock propagation through partially ionized plasmas and show that post-shock equilibrium in such systems can lead to rapid cooling and lower post-shock than pre-shock temperatures. If this scenario is confirmed and generalized in the context of AGN shocks and clouds, it could provide an easy explanation to the presence of atomic lines associated with young radio-galaxies.
Unstable processes evolve on timescales of ∼R/cs, where R is the cloud radius and cs its sound speed. The relatively low temperatures kept by cloud material (both unshocked and shocked) ensures relatively low sound speeds. For a cloud size of 10 pc and a sound speed (after shock passage) of 102 − 103 km s−1 dynamical times become ∼104 − 105 yr. This is on the order of typical evolution times shown in Fig. 1 and certainly longer than cooling times. This indicates that there could be time for cooling and recombination prior to eventual disruptive processes. So, even if mixing would induce further ionization, there could be a long enough time interval between shock passage and disruption when atomic lines could be observed. Another physical mechanism to be taken into account is enhanced clumping induced by self-gravity could also contribute to further cooling and stability (Mandal et al., in prep.).
As stated above, the development of instabilities would favour mixing with the hotter, shocked surrounding gas, acting against cooling and recombination in the region. Numerical simulations of radio source evolution (see, e.g., Mukherjee et al. 2016; Perucho et al. 2021) do not show any hints of post-shock gas colder than 108 K, although the densest clouds in set-ups do have densities ≥100 cm−3. The reason is numerical: the clouds in such simulations do not involve many cells (≤20 cells, in general), favouring rapid mixing by numerical diffusion. We therefore need devoted numerical simulations of shock-cloud interactions (evolved versions of the one presented here) to study this process in detail. It would be of particular interest to study the dependence of cloud stability on the properties of the surrounding shocked gas, which shows very different thermodynamic properties for different jet powers (see, e.g., Figs. 2 and 4). These runs are, however, costly owing to the relatively small shock propagation velocity in clouds and out of the scope of this theoretical approach.
3.3. Implications for large-scale feedback
The presence of atomic outflows with large mass fluxes has been interpreted sometimes in the literature as jets being cold, strongly mass-loaded and slow at large scales. This conclusion has been applied to study jet feedback at large scales (beyond the host galaxy; Vernaleo & Reynolds 2006; Cattaneo & Teyssier 2007; Sternberg & Soker 2008; Gaspari et al. 2011), even for powerful outflows (Lj ∼ 1046 erg s−1). In contrast, numerical simulations of powerful, relativistic jets show that it is very difficult to affect the global dynamics of powerful jets by stellar wind mass-load (Perucho et al. 2014a; Anglés-Castillo et al. 2021). In addition, observational studies have shown that such powerful jets must be mildly relativistic at large scales, on the basis of jet-to-counter-jet brightness ratios (e.g., Arshakian & Longair 2004).
Furthermore, the scenario we propose in this paper, which is based on results obtained from numerical simulations and is compatible with the physical scales of the problem, provides a reasonable frame that indicates that cold, massive outflows observed in active galaxies are produced as a result of the development of relativistic jets, but do not represent the nature of jets as it was assumed by a number of works (see, e.g., the references above) for studying jet feedback at hundreds of kiloparsecs. The same conclusion has also been derived from observational results (see, e.g. Dasyra et al. 2014, who show that massive outflows can be explained from a small fraction of the total jet power or Laing & Bridle 2002 for the case of the FRI radio-galaxy 3C 31). Altogether, the possibility that massive, cold outflows with powers of ∼1046 erg s−1 are not only not playing a role in large-scale feedback, but also not existing at all in the Universe, would have to be taken into serious consideration in cosmological or large-scale feedback simulations. In contrast, low power sources can be efficiently mass-loaded (Bowman et al. 1996; Perucho et al. 2014a; Anglés-Castillo et al. 2021), losing collimation and decelerating. However, the resulting outflows are not expected to reach hundreds of kiloparsecs as classical radio-galaxies do.
4. Summary
In this work, I present a general physical scenario to explain the presence of atomic gas outflows in GPS and CSS radio-sources. I have based the model in basic knowledge obtained from both numerical simulations and analytical models that have been systematically applied to analyse them (radio-galaxy evolution, e.g., Perucho & Martí 2007; Perucho et al. 2014b, 2019).
The model predicts that atomic outflows could easily be detected in the GPS regime (ls ≤ 1 kpc) for low-power jets (Lj ≤ 1043 erg s−1), as post-shock temperatures in clouds could easily fall below 104 K. In addition, the cooling times of the shocked hot phase can be shorter than the evolution time-scales.
On the contrary, the post-shock temperatures reached in the case of powerful jets could ionize a large percentage of the existing atomic gas at these scales. Thus, the presence of atomic gas in powerful radio-galaxies at those scales requires rapid cooling in shocked clouds. This relies on cloud stability for sufficiently long periods of time, which seems to be granted by the low sound speeds expected for post-shock temperatures of 104 − 105 K (see Fig. 1). In this case, the cooling times that would allow recombination to take place are compatible with the dynamical times required by jets to reach the CSS scales (≥2 kpc). In conclusion, a positive correlation between linear size and jet power should be expected in radio-galaxies showing atomic outflows.
Devoted numerical simulations of shock-cloud interaction must be run in order to study the stability and evolution of shocked cloud gas, also including the role of magnetic fields on the stability of the system (see, e.g., Snow & Hillier 2021a, for a recent work on the physics of shocked plasmas that could be relevant in this context). It has actually been shown that magnetic fields can be relevant to damp instability growth even if they are energetically irrelevant (López-Miralles et al. 2022) for a recent work on the physics of shocked plasmas that could be relevant in this context). If shocked clouds retain at least partly coherence, these regions can cool faster because of their larger densities and lower post-shock temperatures; in contrast, if instabilities and turbulent are mixing with the shocked hotter ISM component, the resulting temperature of the mixture could delay cooling and put constraints to the validity of this simple model. Nevertheless, observational evidence appears to require that shocked clouds remain fairly stable.
The expression implicitly assumes that all injected power is converted into internal energy driving the lobe expansion, which is valid for relativistic (hot and fast) outflows. Thus, this represents an upper limit for pressure, which propagates as an upper limit for the derived post-shock temperatures.
Acknowledgments
The author acknowledges support by the Spanish Ministry of Science through Grants PID2019- 105510GB-C31/AEI/10.13039/501100011033 and PID2022-136828NB-C43, from the Generalitat Valenciana through grant CIPROM/2022/49, and from the Astrophysics and High Energy Physics programme supported by MCIN and Generalitat Valenciana with funding from European Union NextGenerationEU (PRTR-C17.I1) through grant ASFAE/2022/005. The author also acknowledges the referee of this paper, Stas Shabala for his constructive criticism, which has improved the resulting text, and Pau Beltran-Palau for critical reading of the paper.
References
- Anglés-Castillo, A., Perucho, M., Martí, J. M., & Laing, R. A. 2021, MNRAS, 500, 1512 [Google Scholar]
- Arshakian, T. G., & Longair, M. S. 2004, MNRAS, 351, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C. 1996, in Cygnus A - Studay of a Radio Galaxy, eds. C. L. Carilli, & D. E. Harris, 209 [Google Scholar]
- Begelman, M. C., & Cioffi, D. F. 1989, ApJ, 345, L21 [CrossRef] [Google Scholar]
- Bicknell, G. V., Dopita, M. A., & O’Dea, C. P. O. 1997, ApJ, 485, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., Saxton, C. J., & Sutherland, R. S. 2003, PASA, 20, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., Mukherjee, D., Wagner, A. Y., Sutherland, R. S., & Nesvadba, N. P. H. 2018, MNRAS, 475, 3493 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, M., Leahy, J. P., & Komissarov, S. S. 1996, MNRAS, 279, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., & Teyssier, R. 2007, MNRAS, 376, 1547 [NASA ADS] [CrossRef] [Google Scholar]
- Couto, G. S., Storchi-Bergmann, T., Siemiginowska, A., Riffel, R. A., & Morganti, R. 2020, MNRAS, 497, 5103 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., Combes, F., Novak, G. S., et al. 2014, A&A, 565, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 2003, Astrophysics of the Diffuse Universe (New York: Springer) [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Fanti, R., Fanti, C., Schilizzi, R. T., et al. 1990, A&A, 231, 333 [NASA ADS] [Google Scholar]
- Gaspari, M., Brighenti, F., D’Ercole, A., & Melioli, C. 2011, MNRAS, 415, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J. 2018, MNRAS, 475, 2768 [Google Scholar]
- Holt, J., Tadhunter, C. N., Morganti, R., & Emonts, B. H. C. 2011, MNRAS, 410, 1527 [NASA ADS] [Google Scholar]
- Kaiser, C. R., & Alexander, P. 1997, MNRAS, 286, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Kawakatu, N., Nagai, H., & Kino, M. 2008, ApJ, 687, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. 2012, Relativistic Jets from Active Galactic Nuclei, 81 (Berlin: Wiley) [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Königl, A. 2007, MNRAS, 380, 51 [Google Scholar]
- Krause, M. G. H. 2008, Mem. Soc. Astron. Ital., 79, 1162 [Google Scholar]
- Krause, M., & Alexander, P. 2007, MNRAS, 376, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Kukreti, P., Morganti, R., Tadhunter, C., & Santoro, F. 2023, A&A, 674, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labiano, A., O’Dea, C. P., Gelderman, R., et al. 2005, A&A, 436, 493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laing, R. A., & Bridle, A. H. 2002, MNRAS, 336, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- López-Miralles, J., Perucho, M., Martí, J. M., Migliari, S., & Bosch-Ramon, V. 2022, A&A, 661, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meenakshi, M., Mukherjee, D., Wagner, A. Y., et al. 2022, MNRAS, 511, 1622 [NASA ADS] [CrossRef] [Google Scholar]
- Morganti, R., & Oosterloo, T. 2018, A&ARv, 26, 4 [Google Scholar]
- Morganti, R., Veilleux, S., Oosterloo, T., Teng, S. H., & Rupke, D. 2016, A&A, 593, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Oosterloo, T., Murthy, S., & Tadhunter, C. 2021, Astron. Nachr., 342, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, D., Bicknell, G. V., Sutherland, R., & Wagner, A. 2016, MNRAS, 461, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Mukherjee, D., Bicknell, G. V., Wagner, A. Y., Sutherland, R. S., & Silk, J. 2018, MNRAS, 479, 5544 [NASA ADS] [CrossRef] [Google Scholar]
- Murthy, S., Morganti, R., Wagner, A. Y., et al. 2022, Nat. Astron., 6, 488 [CrossRef] [Google Scholar]
- Myasnikov, A. V., Zhekov, S. A., & Belov, N. A. 1998, MNRAS, 298, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P., & Baum, S. A. 1997, AJ, 113, 148 [CrossRef] [Google Scholar]
- O’Dea, C. P., de Vries, W. H., Koekemoer, A. M., et al. 2002, AJ, 123, 2333 [CrossRef] [Google Scholar]
- Owsianik, I., & Conway, J. E. 1998, A&A, 337, 69 [NASA ADS] [Google Scholar]
- Perucho, M., & Martí, J. M. 2002, ApJ, 568, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., & Martí, J. M. 2007, MNRAS, 382, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Quilis, V., & Martí, J.-M. 2011, ApJ, 743, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Martí, J. M., Laing, R. A., & Hardee, P. E. 2014a, MNRAS, 441, 1488 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Martí, J.-M., Quilis, V., & Ricciardelli, E. 2014b, MNRAS, 445, 1462 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Martí, J.-M., Quilis, V., & Borja-Lloret, M. 2017, MNRAS, 471, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., Martí, J.-M., & Quilis, V. 2019, MNRAS, 482, 3718 [NASA ADS] [CrossRef] [Google Scholar]
- Perucho, M., López-Miralles, J., Reynaldi, V., & Labiano, Á. 2021, Astron. Nachr., 342, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Polatidis, A. G., & Conway, J. E. 2003, PASA, 20, 69 [Google Scholar]
- Raouf, M., Silk, J., Shabala, S. S., et al. 2019, MNRAS, 486, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Reynaldi, V., & Feinstein, C. 2016, MNRAS, 455, 2242 [CrossRef] [Google Scholar]
- Ricci, L., Perucho, M., López-Miralles, J., Martí, J. M., & Boccardi, B. 2024, A&A, 683, A235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santoro, F., Tadhunter, C., Baron, D., Morganti, R., & Holt, J. 2020, A&A, 644, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scheuer, P. A. G. 1974, MNRAS, 166, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Morganti, R., Nyland, K., et al. 2021, A&A, 647, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shabala, S., & Alexander, P. 2009, ApJ, 699, 525 [CrossRef] [Google Scholar]
- Shih, H.-Y., Stockton, A., & Kewley, L. 2013, ApJ, 772, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, B., & Hillier, A. 2021a, A&A, 645, A81 [EDP Sciences] [Google Scholar]
- Snow, B., & Hillier, A. 2021b, MNRAS, 506, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Stanghellini, C., O’Dea, C. P., Dallacasa, D., et al. 1998, A&AS, 131, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Soker, N. 2008, MNRAS, 384, 1327 [CrossRef] [Google Scholar]
- Tadhunter, C., Morganti, R., Santoro, F., & Bernhard, E. 2021, Astron. Nachr., 342, 1200 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., & Shabala, S. S. 2023, Galaxies, 11, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., Shabala, S. S., & Krause, M. G. H. 2018, MNRAS, 474, 3361 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, R. J., Yates-Jones, P. M., Shabala, S. S., Quici, B., & Stewart, G. S. C. 2023, MNRAS, 518, 945 [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., & Massaglia, S. 2015, A&A, 580, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernaleo, J. C., & Reynolds, C. S. 2006, ApJ, 645, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Vlahakis, N., & Königl, A. 2004, ApJ, 605, 656 [Google Scholar]
- Wagner, A. Y., & Bicknell, G. V. 2011, ApJ, 728, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, A. Y., Bicknell, G. V., & Umemura, M. 2012, ApJ, 757, 136 [CrossRef] [Google Scholar]
- Zovaro, H. R. M., Nesvadba, N. P. H., Sharp, R., et al. 2019, MNRAS, 489, 4944 [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Left panel: radial shock velocity (vs, violet) and axial position (black) for jet powers 1046 (solid lines), 1044 (dashed), and 1042 erg s−1 (dotted). The thin, dark red lines indicate the ISM sound speed at the axial position. Right panel: post-shock temperatures for same jet powers as the left panel in the case of a medium density following Eq. (7) (black lines), i.e., a hot, diffuse ISM, and a medium with constant number density 103 cm−3, i.e., cold clouds. Horizontal lines indicate hydrogen ionization temperatures in local thermodynamical equilibrium, 3500 K (solid), and collisional equilibrium, 1.58 × 105 K (dashed). In these clouds, the sound speed is 3 km s−1. The temperatures have been derived for ionized hydrogen in Eq. (10). |
| In the text | |
 |
Fig. 2. Lobe overpressure for jet powers 1046 (solid lines), 1044 (dashed), and 1042 erg s−1. The black lines for the hot, diffuse ISM, and red lines correspond to cold, dense clouds with a number density of 103 cm−3 are overlapped. |
| In the text | |
 |
Fig. 3. HI fraction in shocked clouds in LTE for jets with powers 1044 (dashed), and 1042 erg s−1 (dotted). The intermediate case of 1043 erg s−1 (dash-dot line) has been also included in this plot. |
| In the text | |
 |
Fig. 4. Cooling times for the same cases given in Fig. 1 (left panel) and relative values with respect to the evolution times (right panel). Solid lines represent the powerful, 1046 erg s−1 case, dashed lines the 1044 erg s−1 case, and dotted lines the 1042 erg s−1. Calculations are shown for the shocked hot, dilute ISM described by Eq. (7). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



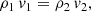
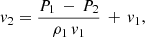
![$$ \begin{aligned} v_1^2&= \frac{1}{2\,\rho _1}\left[ (\Gamma +1)\,P_2+(\Gamma -1)\, P_1 \right] ,\end{aligned} $$](/articles/aa/full_html/2024/04/aa48624-23/aa48624-23-eq3.gif)