| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202348792 | |
| Published online | 06 March 2024 | |
Testing pulsation diagnostics in the rapidly oscillating magnetic Ap star γ Equ using near-infrared CRIRES+ observations
1
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail: sjarvinen@aip.de
2
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748
Garching,
Germany
3
Centre for Space Physics, North-West University,
Mahikeng
2735,
South Africa
4
Jeremiah Horrocks Institute, University of Central Lancashire,
Preston
PR1 2HE,
UK
5
European Southern Observatory,
Alonso de Cordova
3107,
Vitacura,
Santiago,
Chile
6
NASA Ames Research Center,
Moffett Field,
CA
94035,
USA
Received:
30
November
2023
Accepted:
16
January
2024
Context. Pulsations of rapidly oscillating Ap stars and their interaction with the stellar magnetic field have not been studied in the near-infrared (near-IR) region despite the benefits these observations offer compared to visual wavelengths. The main advantage of the near-IR is the quadratic dependence of the Zeeman effect on the wavelength, as opposed to the linear dependence of the Doppler effect.
Aims. To test pulsation diagnostics of roAp stars in the near-IR, we aim to investigate the pulsation behaviour of one of the brightest magnetic roAp stars, γ Equ, which possesses a strong surface magnetic field of the order of several kilogauss and exhibits magnetically split spectral lines in its spectra.
Methods. Two magnetically split spectral lines belonging to different elements, the triplet Fe I at 1563.63 nm and the pseudo-doublet Ce III at 1629.2 nm, were recorded with CRIRES+ over about one hour in the H band with the aim of understanding the character of the line profile variability and the pulsation behaviour of the magnetic field modulus.
Results. The profile shapes of both studied magnetically split spectral lines vary in a rather complex manner probably due to a significant decrease in the strength of the longitudinal field component and an increase in the strength of the transverse field components over the last decade. A mean magnetic field modulus of 3.9 kG was determined for the Zeeman triplet Fe I at 1563.63 nm, whereas for the pseudo-doublet Ce III at 1629.2 nm we observe a much lower value of only about 2.9 kG. For comparison, a mean field modulus of 3.4kG was determined using the Zeeman doublet Fe II at 6249.25 in optical PEPSI spectra recorded just about two weeks before the CRIRES+ observations. Different effects that may lead to the differences in the field modulus values are discussed. Our measurements of the mean magnetic field modulus using the line profiles recorded in different pulsational phase bins suggest a field modulus variability of 32 G for the Zeeman triplet Fe I at 1563.63 nm and 102 G for the pseudo-doublet Ce III at 1629.2 nm.
Key words: techniques: spectroscopic / stars: individual: γ Equ / stars: magnetic field
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The rapidly oscillating Ap (roAp) main-sequence stars belong to a sub-group of H-core-burning SrCrEu peculiar A stars with Teff in the range of about 6600–8500 K. They are usually strongly magnetic and pulsate in high-overtone, low-degree, non-radial p-modes with periods in the range of about 5–24 min. They have been observed intensively photometrically since their discovery by Kurtz (1978), who detected a 12 min pulsation period in Przybylski’s star (HD 101065) using ground-based photometric observations. Frequency analyses of the light curves of the roAp stars have yielded rich asteroseismic information on the degrees of the pulsation modes, the distortion of the modes from normal modes, the magnetic geometries, and the interaction of the pulsation with the magnetic field. Whereas several thousands of Ap stars are currently known (e.g. Renson & Manfroid 2009), the number of identified roAp stars is just over 100 (e.g. Smalley et al. 2015; Holdsworth et al. 2021, 2024).
The main property of roAp stars is that they are oblique pulsators, and the strength and geometry of their global magnetic fields constrain the pulsation modes. Kurtz (1982) suggested that the pulsation mode axis is aligned with the magnetic axis, which is itself inclined to the rotation axis so that the observer sees the pulsation modes from an aspect that varies with rotation. The roAp stars show not only photometric variability, but also rapid radial velocity (RV) variations with the same mode frequencies as those obtained from photometry. The detected pulsation amplitudes of radial velocities depend on the element used: the lines of rare earth elements (REEs) and the Hα core show the highest amplitudes, whereas iron-peak elements with the higher formation depth in the atmosphere usually show low RV variations (e.g. Kurtz et al. 2003, and references therein). This is an indication that the pulsation amplitudes are a function of atmospheric depth.
Assuming that the pulsations of roAp stars are governed by their magnetic fields, several authors obtained spectral time series in circular polarised light in a visual spectral region to study magnetic field variations over the pulsation cycle in a number of stars. Hubrig et al. (2004) measured the magnetic field variability over the pulsation cycles in six roAp stars using low-resolution FOcal Reducer low dispersion Spectrograph (FORS 1; Appenzeller et al. 1998) spectral time series; however, only one roAp star, Przybylski’s star (HD 101065), showed a signal for magnetic variability with a frequency of 1.365 mHz and an amplitude of 39 ± 12 G. Leone & Kurtz (2003) used high-resolution circular polarisation observations of individual lines in the spectra of the ultra-slowly rotating roAp star γ Equ (HD 201601) and reported a clear detection of the mean longitudinal field variability of up to 240 ± 37 G in the Nd III line at 5845.07 Å over the pulsation cycle. This discovery was, however, questioned by Kochukhov et al. (2004), who obtained an upper limit of 40–60 G using 13 Nd III lines.
Mathys et al. (2005, 2007) studied the pulsational behaviour of the individual π and σ components using the Eu II line at 6437 Å in the spectroscopic time series of the strongly magnetic roAp star HD 166473, which exhibits radial velocity variations due to pulsation with three frequencies: 1.833, 1.886, and 1.928 mHz (Kurtz et al. 2003). The results of these studies hinted at the occurrence of variations of the mean magnetic field modulus with the pulsation frequency 1.928 mHz and an amplitude of 21 ± 5 G.
Importantly, more recent studies of the oblique pulsator model showed that the mode geometries in roAp stars are complex and should be considered as a function of atmospheric height. Using high-resolution time-series spectroscopy, it became possible to identify the pulsation geometry not only over the stellar surface but also vertically in the stellar atmosphere. As an example, high-speed spectroscopy of the roAp star HD 99563 to study the pulsation amplitude and phase behaviour of elements in its stratified atmosphere over the 2.91-d rotation cycle was carried out by Freyhammer et al. (2009). The authors identified spectral features related to patches in the surface distribution of chemical elements and studied the pulsation amplitudes and phases as the patches moved across the stellar disc. The detected variability had been consistent with a distorted non-radial-dipole pulsation mode.
Hubrig et al. (2021) took a step further in the analysis of pulsations of roAp stars and investigated the usefulness of linear polarisation as an enhanced pulsation diagnostic. While the circular polarisation depends upon the magnetic vector projection on to the line of sight, the linear polarisation depends upon the magnetic vector projected on to the plane perpendicular to the line of sight. The authors reported on a possible detection of pulsational variability of the transversal field component in Fe, Nd, and Eu lines. The detected variability had been considered as due to the impact of pulsations on the transverse magnetic field, causing changes in the obliquity angles of magnetic force lines.
To better understand the interaction between the pulsation and the stellar magnetic field and to test the diagnostic potential of near-IR observations, we recently carried out high-resolution spectroscopical time series of one of the brightest roAp stars, γ Equ (mv = 4.7), over about one hour in the H band using the upgraded CRyogenic InfraRed Echelle Spectrograph (CRIRES+; Dorn et al. 2023). As of today, pulsations of roAp stars and their interaction with the stellar magnetic field have not been studied in the near-IR region despite the numerous advantages such observations offer compared to visual wavelengths. The main advantage of the near-IR is the quadratic wavelength dependence of the Zeeman effect, as opposed to the linear dependence of the Doppler effect. This opens the possibility, at a given magnetic field strength, of observing resolved lines in faster rotating stars (e.g. Chojnowski et al. 2019) or, conversely, at a given projected equatorial velocity, of resolving Zeeman split comments in more weakly magnetic stars. Furthermore, performing a near-IR study permits the exploration of a different range of photospheric depths, thus providing more insight into the depth dependence of pulsation. As the detection of the variation of the magnetic field modulus over the pulsation period is yet to be confirmed by independent observations, high-resolution spectroscopic time series obtained in the near-IR allowing the analysis of the pulsational behaviour of the individual π and σ components is especially important.
γ Equ is distinguished among the roAp stars by very sharp lines caused by the extremely slow rotation, a rather strong mean longitudinal magnetic field varying from about 630 G to –1180 G (e.g. Savanov et al. 2018), and a magnetic field modulus of 4 kG measured using magnetically split spectral lines resolved in the visible (e.g. Mathys 2017). The most recent estimate of the rotation period for this star gives a lower limit of 95 yr (Bychkov et al. 2016; Savanov et al. 2018). Furthermore, γ Equ exhibits a rather high amplitude of pulsational line profile radial velocities in the visual exceeding 1000 m s−1 in individual REE spectral lines and has well-studied pulsation characteristics, with the highest amplitude frequency corresponding to a period of about 12 min.
In the following we discuss the available observational material and the analysis of the pulsational behaviour of the π and σ components observed in the selected magnetically split spectral lines in the high-resolution spectroscopic CRIRES+ time series, and we discuss the potential usefulness of multi-wavelength observations for the improvement of our understanding of the pulsational properties of roAp stars.
2 Spectroscopic and photometric observations
To study the pulsation and its interaction with the magnetic field in the roAp star γ Equ, we obtained, on 2022 September 28, high-resolution spectroscopic CRIRES+ time series over 56 min in the H band (from 1438 to 1765 nm), sampling several lines belonging to iron-peak and rare-earth elements. The line identification in the H band was previously carried out by Chojnowski et al. (2019). Using the nodding cycle ABBA, we obtained 35 spectra with the narrowest available slit of 0.2″, resulting in a spectral resolution of about 100 000. Within the ABBA nodding cadence, the first exposure is recorded at the position A; then, it is followed by two exposures at the position B, and the fourth exposure is obtained moving back to the position A1. The purpose of nodding -moving the telescope to the positions A and B along the direction of the slit- is to remove sky emission, detector dark current and glow, and some ghosts. With the exposure time of individual frames of 10 s between the nodding and the full individual sequence, ABBA accounted for about 1.5 min. The data were reduced using the CR2RES pipeline recipes. As both ABBA and AB/BA nodding cycles are available, the reduction was carried out for both cycles. For the AB/BA nodding cycles, we obtained 70 spectra with the individual AB/BA cycle length of about 50 s. The typical signal-to-noise ratio (S/N) for the spectra obtained with the ABBA cycle is 212, whereas the S/N for the individual AB/BA cycles is 153.
Previous studies of Ap stars revealed that their magnetic fields cover the whole stellar surface and have a large-scale structure often resembling a single dipole whose axis is inclined with respect to the stellar rotation axis. Because the measured magnetic field strength depends on the viewing angle of the observer, that is, on the rotation phase of the star, it is important for our analysis that we know the strength of the mean longitudinal magnetic field and the mean magnetic field modulus at the time of observations. According to Hubrig et al. (2021), the mean longitudinal magnetic field was gradually decreasing from –922 G in 2011 to –572 G in 2020, and the mean magnetic field modulus was gradually decreasing from 3.80 kG in 2011 to 3.58 kG in 2017. Our most recent observations2 of γ Equ with the Potsdam Echelle Polarimetric and Spectroscopic Instrument (PEPSI; Strassmeier et al. 2015) installed at the 2 × 8.4 m Large Binocular Telescope (LBT) were obtained on 2022 September 15, just thirteen days before the CRIRES+ observations. They show an even lower field modulus of 3.36 kG, confirming the decreasing trend for the field strength. In Fig. 1, we present magnetically split components of the Zeeman doublet Fe π at 6149.25 Å used for the measurements of the mean magnetic field modulus in different years using different instruments. The PEPSI observations were made using the cross-dispersers CD II, covering 4236–4770 Å, and CD IV, covering 5391-6289 Å with a spectral resolution of R ~ 130 000 corresponding to 0.06 at 7600 Å. For more details on observations with PEPSI and data reduction, we refer the reader to Strassmeier et al. (2023) and Hubrig et al. (2021).
Since mean longitudinal magnetic field measurements of γ Equ after 2020 are not available in the literature, we relied on the work of Savanov et al. (2018), for example, who discussed the variability of the longitudinal field phase curve using a periodogram analysis. According to this work, the strength of the field had to be in the range of –200 to –300 G at the time of the CRIRES+ observations.
To be able to study the magnetic field variability over the pulsational cycle, we need to assign the pulsational phase to each of our spectra. Because γ Equ is known to have multiple pulsation periods near 12 min (Kurtz 1983; Libbrecht 1988; Martinez et al. 1996; Gruberbauer et al. 2008), we used more recent Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2015) observations to identify the frequency with the highest amplitude at a time closest to the spectroscopic observations.
γ Equ was observed by TESS in Sector 55 from 2022 August 5 to 2022 September 1. The analysis of these data is illustrated in Fig. 2, showing three main frequencies. The highest peak with an amplitude of 0.315 mmag is at 115.5654 + 0.0001 d−1 (l.3386 mHz; or Ρ = 747.0404s = 12.45067 min). The other two peaks with amplitudes of 0.127 mmag and 0.042 mmag are at 118.0236 d−1 (l.3660 mHz) and 113.2873 d−1 (1.3112 mHz), respectively.
These three frequencies are in complete agreement with the frequencies derived independently by Holdsworth et al. (2024). As those authors noted, we also see the harmonic of the highest amplitude peak and one combination frequency. However, it is notable that the frequencies previously derived for γ Equ in other studies (Kurtz 1983; Libbrecht 1988; Martinez et al. 1996; Gruberbauer et al. 2008) range from 113 to 123 d−1 and in general do not coincide with the frequencies derived from the TESS data. Possible explanations are that the star shows mode changes, that different modes are detected at different atmospheric depths (since the studies were both spectroscopic and photometric with different filters), or that there have been problems with aliasing in the ground-based data, which present significant time gaps. Importantly, the frequencies derived from the TESS data do not suffer significant aliasing, and the pulsation amplitude is stable over the 27-d time span of the Sector 55 data. Since the spectroscopic data were taken only a month after the TESS data, we assume that this mode stability continued over this short time span. Because of the possibility of some pulsation amplitude change, however, we cannot directly relate the photometric pulsation amplitude to the amplitude of the magnetic variations over the pulsation cycle. That requires simultaneous observations.
The frequency separations of the three peaks seen in Fig. 2 are 27 µHz, which is plausibly half the large separation; hence, we suggest that the observed modes are ℓ = 2, 1, 2 alternating-degree modes. We note that the modulation timescale for the outer mode frequencies to beat with the main mode frequency is about 10 hr; hence, these frequencies are not resolved in the 56 min of the CRIRES+ time series presented in this paper.
 |
Fig. 1 Zeeman doublet Fe II at 6149.25Å with a Landé factor geff = 1.35 used for measuring the mean magnetic field modulus in observations obtained in different years using different instruments. The corresponding Zeeman pattern is displayed above the line profiles, with the π components shown above the horizontal line and the σ components below. The lengths of the vertical bars are proportional to their relative strength. |
 |
Fig. 2 Frequency spectrum of γ Equ based on Sector 55 TESS photometry. |
3 Analysis of CRIRES+ spectroscopic time series
In the recorded CRIRES+ spectroscopic time series, two almost blend-free magnetically split lines, the Zeeman triplet Fe I at 1563.63 nm and the pseudo-doublet line Ce III at 1629.20 nm, appear to be most suitable to study the pulsational variability of the mean magnetic field modulus. Their identification is based on the work of Chojnowski et al. (2019). Zeeman patterns for both lines and the corresponding effective Landé factors are presented in Fig. 3.
While the spectral region around the Fe I 1563.63 nm line is perfectly clean and is not affected by telluric lines, the Ce III 1629.2 nm line shows a small telluric contribution on the red side of the line profile. It was removed using the ESO Sky-Calc based on the Cerro Paranal Sky Model (Noll et al. 2012; Jones et al. 2013). The original and the mean Ce III 1629.2nm corrected for the telluric contribution profiles for both sequences ABBA and AB/BA are presented in Fig. 4.
Individual line profiles’ time series obtained over 56min using the ABBA sequence are presented in Fig. 5. Surprisingly, in contrast to the high-resolution CRIRES (Kaeufl et al. 2003) and CRIRES + observations of the Fe I 1563.63 nm line obtained in previous years, the line profile shape recorded in our observations in 2022 shows a significant change, displaying rather flat σ components and not very clear separation between them and the π component. While the presence of the σ component on the red side of the line profile can still be perceived, the position of the blue-side σ component is not clearly defined. In Fig. 6 we present very different shapes of the line profiles of the Zeeman triplet Fe I 1563.63 nm observed in different years using CRIRES and CRIRES+. Observations on 2011 May 19 and 2011 June 16 were obtained with an exposure time of 450 s. For the observations on 2021 Oct 29, four frames with 20 s of exposure time each were obtained using one nodding cycle. It is possible that the ‘filling’ between the π and σ components that appeared in 2021–2022, while not present in 2011, is due to blending with a line of another element whose wavelength coincides with that of the Fe I 1563.63nm line. The ~10 yr elapsed from 2011 to 2021 may represent about one tenth of the rotation period, which may be enough for an overabundance spot of some element to have appeared on the visible stellar hemisphere as a result of stellar rotation. However, the measured equivalent width of this line is the same in 2021–2022 as it was in 2011.
As discussed in Sect. 2, the magnetic field strength in γ Equ is gradually decreasing and will probably approach the rotation phase of the best visibility of the magnetic equator in a few years, where the longitudinal magnetic field component is expected to be weaker and the transverse field component becomes the strongest. For a transverse field, the π components become, to the first order, twice as strong as the σ+ and the σ− components. Interestingly, in contrast with the observations in the near-IR, the profiles of the Zeeman triplet lines recorded by us in the visual wavelength region in 2020 and 2022 using PEPSI show much clearer σ components, which can be more easily used for the measurement of the magnetic field modulus. The different appearance of the triplets can probably be explained by different iron vertical stratification between the visual and near-IR regions. There may also be a significant difference in the optical depth from which the continuum is issued between the visible and the IR, and, as a consequence, there could be different (de)saturations of the split line components between the two wavelength regions. This alone may potentially result in differently looking triplets. In Fig. 7, we present line profiles of two Zeeman triplets and one Zeeman pseudo-triplet observed with PEPSI in the visual spectral region.
As shown in Fig. 5, several absorption bumps appear from time to time not only on both sides of the π component in the line profile of Fe I 1563.63nm, but also in the core of the Ce III 1629.2 nm line. Since the S/N of the individual spectrum is rather low, it is not clear whether the observed variability is intrinsic or is caused by the noise. To investigate the nature of these bumps in more detail, we determined, for each individual spectrum calculated in the ABBA sequence, the corresponding pulsation phase assuming the pulsational period of 12.45067 min as determined from the TESS observations. To increase the S/N, the spectra have been binned with the phase bin of 0.1. The number of individual spectra in each bin varies from two to five, allowing us to increase the S/N by a factor of 1.4–2.2, respectively. The plots for the mean spectra obtained within each bin are displayed in Fig. 8 together with the information on the number of spectra included in each bin. While no radial velocity variability is detected in the overplotted line profiles, we observe that the depth of the π component of the Fe I 1563.63nm line is slightly variable; moreover, the fractions of the profile around the π component show variable absorption bumps. A comparison of the variability of the profiles that have the largest numbers of individual spectra per bin and therefore a higher S/N (phases 0.0–0.1, 0.1–0.2, 0.2–0.3, 0.3–0.4, 0.7–0.8) shows that absorption bumps become stronger in the red part of the profile in the phase bins 0.0–0.1, 0.2–0.3, and 0.7–0.8. In the case of the Ce III line, the separation between the split components becomes much more clear in several phase bins, the clearest case being the phase bin 0.4–0.5.
To delve deeper into the character of the line profile variability, in Figs. 9–11 we present dynamical spectra for the observed profiles of Fe I 1563.63 nm and the Ce III 1629.2nm lines phased with the pulsation period and using both the ABBA and the AB/BA sequences. The blue-green colour in Fig. 9 constructed for the Fe I 1563.63 nm line clearly shows the variability of the σ component on the red side; it changes intensity and becomes significantly broader in some phases. The σ component on the blue side almost disappears in some phases, that is, between the phases 0.0–0.3. This behaviour is confirmed in the dynamical spectra presented in Fig. 10, where we mask out the π component to achieve a better contrast. Interestingly, absorption bumps discovered in the flat blue part of the profile appear shifted and stronger close to the pulsation phase 0.20, whereas the absorption bump on the red side becomes strongest in the pulsation phase around 0.7–0.8. In the plot corresponding to the AB/BA sequence, a sort of arc appears in the phases 0.80–0.90. The inspection of the dynamical spectra in Fig. 11 calculated for the Ce III 1629.2nm line shows that this line is also variable where the depth of the right component of the split profile almost disappears in the pulsation phases between 0.25–0.30 and 0.85–0.90.
 |
Fig. 3 Zeeman patterns of Fe I triplet and Ce III pseudo-doublet with corresponding Landé factors 𝑔eff. Each Zeeman component is represented by a vertical bar whose length is proportional to its relative strength. The π components are presented above the horizontal wavelength axis, and the σ± components are shown below it. The unit length of the wavelength axis is ∆λB, defined as the wavelength shift from the line centre of the σ components in a normal Zeeman triplet with a Landé factor of 𝑔eff= 1.· |
 |
Fig. 4 Mean Ce III 1629.2 nm line profiles in their original shape (left) and corrected for telluric contributions (right), calculated for both sequences ABBA and AB/BA. |
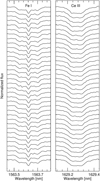 |
Fig. 5 Individual line profiles for Fe I 1563.63 nm (left) and for Ce in 1629.2 nm (right) after telluric correction. The time increases from bottom to top. |
 |
Fig. 6 Comparison of line profiles of Zeeman triplet Fe I 1563.63 nm between 2011 May, 2011 June, 2021 October, and 2022 September. The two spectra from 2011 were recorded with CRIRES, whereas for the observations in 2021 and 2022 CRIRES+ was used. The overplotted profiles are presented at the top. |
 |
Fig. 7 Line profiles of two Zeeman triplets and one pseudo-triplet observed with PEPSI in the visual spectral region in 2020 and 2022. The shape of the line profiles and the separation between the π and σ components are completely different compared to the appearance of the Zeeman triplet Fei I 563.63nm observed on 2022 September 28 with CRIRES+. Zeeman patterns for the spectral lines are presented at the top of each panel. |
 |
Fig. 8 Phase-binned mean line profiles of Fe I line (left) and Ce III line (right) calculated using the ABBA sequence. For each bin, profiles are plotted with different colours and shifted upward for better visibility. The number of spectra within each bin is indicated close to each profile. At the top, we show the overplotted profiles and the corresponding error bars. |
 |
Fig. 9 Dynamical spectrum of whole Fe I 1563.63 nm line. The bluest colour is for the deepest absorption at the π component, whereas red is at the continuum level. Left: profiles reduced using the ABBA sequence. Right: profiles reduced using the AB/BA sequence. |
4 Discussion
Our study of the pulsation behaviour of the magnetic roAp star γ Equ in the near-IR using CRIRES+ time series over 56 min reveals a distinct variability of the magnetically split lines Fe I 1563.63 nm and Ce III 1629.2nm. The character of this variability appears, however, rather complex, probably due to a significant decrease in the strength of the longitudinal field component and an increase in the strength of the transverse field component over the last decade. The reason for the observed absorption bumps around the π component in the Zeeman triplet Fe I 1563.63 nm is not clear. We simply speculate that they are possibly related to the near-surface convection in the presence of the stratification of iron.
In contrast to the older high-resolution CRIRES (Kaeufl et al. 2003) observations, the line profile shape of the Zeeman triplet Fe I 1563.63 nm recorded in our observations in 2022 displays rather flat σ components with unclear separation between them and the π component. Assuming that the outer absorption dips on both sides of the π component in the line profile of the Zeeman triplet Fe I 1563.63 nm present the σ components, we tried to measure the mean magnetic field modulus using the line profiles recorded in the pulsational phase bins 0.3–0.4 and 0.7– 0.8. The results of our measurements with a triple-Gaussian fit are presented in Fig. 12. Interestingly, the measured modulus strengths of 3.929 kG in the phase bin 0.3–0.4 and 3.897 kG in the phase bin 0.7–0.8 are not identical, implying that the mean magnetic field modulus probably varies over the pulsation period with an amplitude of 32 ± 7 G. On the other hand, the much stronger magnetic field modulus measured in the optical region contradicts the one reported for the IR (see Sect. 2 and Fig. 1). We measured a much lower field modulus of 3.36 kG on 2022 September 15 using the Zeeman doublet Fe IJ at 6149.25 Å. Such a difference is not unexpected, for various reasons. First, the mean magnetic field modulus is the average of the field modulus over the visible stellar hemisphere, averaged by the local emergent line intensity. Because the limb darkening is not the same in the visible and in the IR, the line intensity distribution over the stellar disk is different between the two wavelength regions, which leads to a different weighting of the contributions of the various parts of the stellar surface in the magnetic field averaging process. Furthermore, the continuum optical depth of the line-forming layer is not the same in the IR as in the visible. Accordingly, the saturation degree of the individual π and σ components of lines with anomalous Zeeman patterns may be different, which affects the interpretation of the observed line profiles in terms of magnetic field strength. Finally, while vertical gradients of the magnetic field strength may not be required to justify the difference in the field modulus values derived from the consideration of diagnostic lines in different wavelength ranges, their existence and their potential effect on the magnetic field measurements are plausible.
Much lower magnetic field modulus values are determined using the Zeeman pseudo-doublet Ce III 1629.2 nm. In the 0.3– 0.4 phase bin, we measure 2.954 kG, whereas the value 2.852 kG is determined for the spectra in the 0.5–0.6 phase bin. These results presented in Fig. 13 imply that the mean magnetic field modulus probably varies over the pulsation period with the amplitude of 102 ± 14 G. Since iron is reported to be gravitation-ally settled in the stellar atmospheres of roAp stars compared to the rare earth elements that are usually concentrated in the upper atmospheric layers (e.g. Nesvacil et al. 2013), it is expected that the lines of different elements trace the magnetic field strength and the pulsation amplitudes differently. However, because of the extremely abnormal chemical composition of the atmospheres of magnetic roAp stars, the calculation of the vertical element abundance distribution is a very complex process requiring the fitting of spectroscopic, photometric, and magnetic data using realistic self-consistent atmospheric models. There is also a number of previous studies indicating the possible presence of vertical magnetic field gradients in roAp stars (e.g. Nesvacil et al. 2004; Hubrig et al. 2018), with the mean magnetic field and longitudinal field strengths changing with atmospheric depth. The significant increase of the magnetic field in the deeper atmospheric layers would explain the difference in our measurements of the magnetic field modulus using the iron Zeeman triplet and the Ce Zeeman pseudo-doublet.
Even though the combination of a vertical gradient of the magnetic field and of stratification can plausibly contribute to the observed difference between the magnetic field strengths derived from consideration of the Fe I and Ce III lines, there is also another effect that must definitely play a role. Because the Zeeman pattern of the Fe I line at 1563.63 nm is a pure triplet, the determination of the mean magnetic field modulus from the separation of the split components is almost approximation-free. In particular, it does not depend on radiative transfer effects. By contrast, to determine ⟨B⟩ from the splitting of the line Ce III 1629.2 nm, whose Zeeman pattern is a pseudo-doublet, one must use the weak-line approximation. By doing so, one ignores saturation effects. The outer π components have a much higher relative strength than their inner counterparts. Therefore, the outer π components will saturate first. As a result of radiative transfer, the ratio of the depths of the inner-to-outer π components will become greater than the ratio of their strengths. As a result, the wavelength separation of the blue and red line components will be less than it would be for the Fe I line, for which radiative transfer effects are negligible. Thus, a smaller value of the mean magnetic field modulus will be derived. The effect is similar to what we observe. One way to achieve a better assessment of the importance of this effect (which definitely must be present) would be to observe a diagnostic line with a pseudo-doublet (or pseudo-triplet) pattern for which the radiative transfer effects should lead to an increase in the derived value of ⟨B⟩. Unfortunately, no suitable line in the wavelength range covered by our spectra was observed.
On the other hand, another effect that may also lead to differences in the values of ⟨B⟩ derived from lines of different ions are horizontal inhomogeneities, which may lead to the different sampling of the local magnetic field strength. Currently, we do not have enough information to assess the significance of this effect, but its potential contribution is still worth mentioning.
The results of our observations suggest that near-IR observations present an important diagnostic potential in the studies of pulsations in magnetic roAp stars using spectral lines with different formation heights. Future near-IR studies of roAp stars with strong mean longitudinal magnetic fields (observed close to the best visibility of their magnetic poles) in the near-IR using long, high-resolution spectroscopic time series and combined with detailed modelling will be worthwhile in the improvement of our understanding of the concerned physics.
 |
Fig. 10 As Fig. 9, but π component has been masked out in order to show the σ components better. Left: profiles reduced using ABBA sequence. Right: profiles reduced using AB/BA sequence. |
 |
Fig. 11 Dynamical spectrum of line core of Ce III 1629.2 nm. The bluest colour is for the deepest absorption, whereas red is for the shallower absorption. Black is used for phases not covered by the observations. Left: profiles reduced using ABBA sequence. Right: profiles reduced using AB/BA sequence. |
 |
Fig. 12 Zeeman triplet Fe I 1563.63 nm observed in phases 0.3–0.4 and 0.7–0.8. The black lines present the observed profiles and the red lines are used to show the triple-Gaussian fits. |
 |
Fig. 13 Zeeman pseudo-doublet Ce III 1629.2 nm observed in phases 0.3–0.4 and 0.5–0.6. The black lines present the observed profiles and the red lines are used to show the double-Gaussian fits. |
Acknowledgements
We thank the anonymous referee for their useful comments. This work is based on observations made with ESO telescopes at the La Silla Paranal Observatory under programme IDs 087.C-0124(A), 0108.D-0659(A), and 0109.D-0659(A) publicly available via ESO Archive. This work is partially based on observations carried out with the PEPSI spectropolarimeter. PEPSI was made possible by funding through the State of Brandenburg (MWFK) and the German Federal Ministry of Education and Research (BMBF) through their Verbundforschung grants 05AL2BA1/3 and 05A08BAC. LBT Corporation partners are the University of Arizona on behalf of the Arizona university system; Istituto Nazionale di Astrofisica, Italy; LBT Beteiligungsgesellschaft, Germany, representing the Max-Planck Society, the Leibniz-Institute for Astrophysics Potsdam (AIP), and Heidelberg University; the Ohio State University; and the Research Corporation, on behalf of the University of Notre Dame, the University of Minnesota, and the University of Virginia. This paper includes data collected by the TESS mission. Funding for the TESS mission is provided by the NASA Science Mission Directorate.
References
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Bychkov, V. D., Bychkova, L. V., & Madej, J. 2016, MNRAS, 455, 2567 [NASA ADS] [CrossRef] [Google Scholar]
- Chojnowski, S. D., Hubrig, S., Hasselquist, S., et al. 2019, ApJ, 873, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, R. J., Bristow, P., Smoker, J. V., et al. 2023, A&A, 671, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freyhammer, L. M., Kurtz, D. W., Elkin, V. G., et al. 2009, MNRAS, 396, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Gruberbauer, M., Saio, H., Huber, D., et al. 2008, A&A, 480, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holdsworth, D. L., Cunha, M. S., Kurtz, D. W., et al. 2021, MNRAS, 506, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Holdsworth, D. L., Cunha, M. S., Lares-Martiz, M., et al. 2024, MNRAS, 527, 9548 [Google Scholar]
- Hubrig, S., Kurtz, D. W., Bagnulo, S., et al. 2004, A&A, 415, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Järvinen, S. P., Madej, J., et al. 2018, MNRAS, 477, 3791 [NASA ADS] [Google Scholar]
- Hubrig, S., Järvinen, S. P., Ilyin, I., Strassmeier, K. G., & Schöller, M. 2021, MNRAS, 508, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A., Noll, S., Kausch, W., Szyszka, C., & Kimeswenger, S. 2013, A&A, 560, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaeufl, H.-U., Moorwood, A. F. M., & Pirard, J.-F. 2003, SPIE Conf. Ser., 4843, 223 [NASA ADS] [Google Scholar]
- Kochukhov, O., Ryabchikova, T., & Piskunov, N. 2004, A&A, 415, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, D. W. 1978, Inform. Bull. Variab. Stars, 1436, 1 [NASA ADS] [Google Scholar]
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W. 1983, MNRAS, 202, 1 [NASA ADS] [Google Scholar]
- Kurtz, D. W., Elkin, V. G., & Mathys, G. 2003, MNRAS, 343, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Leone, F., & Kurtz, D. W. 2003, A&A, 407, L67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Libbrecht, K. G. 1988, ApJ, 330, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Weiss, W. W., Nelson, M. J., et al. 1996, MNRAS, 282, 243 [NASA ADS] [Google Scholar]
- Mathys, G. 2017, A&A, 601, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., Kurtz, D. W., & Elkin, V. G. 2005, EAS Pub. Ser., 17, 113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., Kurtz, D. W., & Elkin, V. G. 2007, MNRAS, 380, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvacil, N., Hubrig, S., & Jehin, E. 2004, A&A, 422, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvacil, N., Shulyak, D., Ryabchikova, T. A., et al. 2013, A&A, 552, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., Kausch, W., Barden, M., et al. 2012, A&A, 543, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renson, P., & Manfroid, J. 2009, A&A, 498, 961 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
- Savanov, I. S., Romanyuk, I. I., & Dmitrienko, E. S. 2018, Astrophys. Bull., 73, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Smalley, B., Niemczura, E., Murphy, S. J., et al. 2015, MNRAS, 452, 3334 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., Järvinen, A., et al. 2015, Astron. Nachr., 336, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Carroll, T. A., & Ilyin, I. V. 2023, A&A, 674, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Zeeman doublet Fe II at 6149.25Å with a Landé factor geff = 1.35 used for measuring the mean magnetic field modulus in observations obtained in different years using different instruments. The corresponding Zeeman pattern is displayed above the line profiles, with the π components shown above the horizontal line and the σ components below. The lengths of the vertical bars are proportional to their relative strength. |
| In the text | |
 |
Fig. 2 Frequency spectrum of γ Equ based on Sector 55 TESS photometry. |
| In the text | |
 |
Fig. 3 Zeeman patterns of Fe I triplet and Ce III pseudo-doublet with corresponding Landé factors 𝑔eff. Each Zeeman component is represented by a vertical bar whose length is proportional to its relative strength. The π components are presented above the horizontal wavelength axis, and the σ± components are shown below it. The unit length of the wavelength axis is ∆λB, defined as the wavelength shift from the line centre of the σ components in a normal Zeeman triplet with a Landé factor of 𝑔eff= 1.· |
| In the text | |
 |
Fig. 4 Mean Ce III 1629.2 nm line profiles in their original shape (left) and corrected for telluric contributions (right), calculated for both sequences ABBA and AB/BA. |
| In the text | |
 |
Fig. 5 Individual line profiles for Fe I 1563.63 nm (left) and for Ce in 1629.2 nm (right) after telluric correction. The time increases from bottom to top. |
| In the text | |
 |
Fig. 6 Comparison of line profiles of Zeeman triplet Fe I 1563.63 nm between 2011 May, 2011 June, 2021 October, and 2022 September. The two spectra from 2011 were recorded with CRIRES, whereas for the observations in 2021 and 2022 CRIRES+ was used. The overplotted profiles are presented at the top. |
| In the text | |
 |
Fig. 7 Line profiles of two Zeeman triplets and one pseudo-triplet observed with PEPSI in the visual spectral region in 2020 and 2022. The shape of the line profiles and the separation between the π and σ components are completely different compared to the appearance of the Zeeman triplet Fei I 563.63nm observed on 2022 September 28 with CRIRES+. Zeeman patterns for the spectral lines are presented at the top of each panel. |
| In the text | |
 |
Fig. 8 Phase-binned mean line profiles of Fe I line (left) and Ce III line (right) calculated using the ABBA sequence. For each bin, profiles are plotted with different colours and shifted upward for better visibility. The number of spectra within each bin is indicated close to each profile. At the top, we show the overplotted profiles and the corresponding error bars. |
| In the text | |
 |
Fig. 9 Dynamical spectrum of whole Fe I 1563.63 nm line. The bluest colour is for the deepest absorption at the π component, whereas red is at the continuum level. Left: profiles reduced using the ABBA sequence. Right: profiles reduced using the AB/BA sequence. |
| In the text | |
 |
Fig. 10 As Fig. 9, but π component has been masked out in order to show the σ components better. Left: profiles reduced using ABBA sequence. Right: profiles reduced using AB/BA sequence. |
| In the text | |
 |
Fig. 11 Dynamical spectrum of line core of Ce III 1629.2 nm. The bluest colour is for the deepest absorption, whereas red is for the shallower absorption. Black is used for phases not covered by the observations. Left: profiles reduced using ABBA sequence. Right: profiles reduced using AB/BA sequence. |
| In the text | |
 |
Fig. 12 Zeeman triplet Fe I 1563.63 nm observed in phases 0.3–0.4 and 0.7–0.8. The black lines present the observed profiles and the red lines are used to show the triple-Gaussian fits. |
| In the text | |
 |
Fig. 13 Zeeman pseudo-doublet Ce III 1629.2 nm observed in phases 0.3–0.4 and 0.5–0.6. The black lines present the observed profiles and the red lines are used to show the double-Gaussian fits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


