| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202348717 | |
| Published online | 05 March 2024 | |
Collisional excitation of propyne (CH3CCH) by He atoms
KU Leuven, Department of Chemistry, Celestijnenlaan 200F, 3001 Leuven, Belgium
e-mail: malek.benkhalifa@kuleuven.be
Received:
23
November
2023
Accepted:
8
December
2023
Context. A detailed interpretation of the detected emission lines of environments where propyne (or methyl acetylene, CH3CCH) is observed requires access to its collisional rate coefficients with the most abundant species in the interstellar medium, namely, helium (He) or molecular hydrogen (H2).
Aims. We present the first three-dimensional potential energy surface (3D PES) for the CH3CCH-He molecular complex. We study the dynamics of the collision and report the first set of rate coefficients for temperatures up to 100 K for the collisional excitation of the lowest 60 ortho rotational levels and 60 para rotational levels of CH3CCH by He atoms.
Methods. We computed the 3D PES with the explicitly correlated coupled-cluster with a single-, double-, and perturbative triple-excitation method in conjunction with the augmented correlation-consistent triple zeta basis set (CCSD(T)-F12a/aug-cc-pVTZ). The 3D PES was then fitted to an analytical function and scattering computations of pure rotational (de-)excitation of CH3CCH by collision with He atoms were performed. State-to-state cross-sections were computed using the close coupling method for total energies up to 100 cm−1 and with the coupled states approximation at higher energies for both the ortho- and para- symmetries of CH3CCH.
Results. The PES we obtained is characterised by a large anisotropy and a potential well depth of 51.04 cm−1. By thermally averaging the collisional cross-sections, we determined the quenching rate coefficients for kinetic temperatures up to 100 K. A strong and even Δj propensity rule at almost all collision energies is present for CH3CCH-He complex. To evaluate the impact of rate coefficients on the analysis of observations, we carried out non-local thermodynamic equilibrium radiative transfer computations of the excitation temperatures and we demonstrate that local thermodynamic equilibrium conditions are not typically fulfilled for the propyne molecule.
Key words: astrochemistry / molecular data / radiative transfer / scattering / ISM: abundances / ISM: molecules
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
In recent decades, methyl acetylene (or propyne, CH3CCH) has received significant attention from the astrophysical and astrochemistry communities due to the part it plays in astrochemical processes (Mebel et al. 2017; Herbst 2017), such as its role as a precursor in the formation of several polycyclic aromatic hydrocarbons (PAHs, Parker & Kaiser 2017).
The earliest tentative detection of propyne in the interstellar medium (ISM) was reported toward the Sgr B2 molecular cloud by Buhl & Snyder (1973). Subsequently, propyne was observed by Lovas et al. (1976) towards Orion A and Sagittarius B2 via the 50 → 40 rotational line at 85 GHz. In later years, CH3CCH was identified in various astronomical environments: low-mass starforming regions (van Dishoeck et al. 1995), photodissociation regions throughout the Horsehead nebula with fractional abundances of 10−9 with respect to molecular hydrogen (Gratier et al. 2013; Guzmán et al. 2014; Hickson et al. 2016), massive young stellar objects (Fayolle et al. 2015), circumstellar envelopes of evolved stars (Agúndez et al. 2008), and even toward extagalactic sources such as M 82, NGC 253, and NGC 1068 (Mauersberger et al. 1991; Qiu et al. 2020). It has also been detected in cold and dense cores (Vastel et al. 2014; Gratier et al. 2016) and even toward a planetary nebula, as recently reported by Schmidt & Ziurys (2019). As a matter of fact, the widespread detection of propyne even extends to planetary atmospheres: in our solar system, CH3CCH has also been detected on Jupiter, Saturn, and Uranus as well as in the atmosphere of Titan (Fouchet et al. 2000; De Graauw et al. 1997; Burgdorf et al. 2006; Teanby et al. 2009).
The formation pathways of propyne in the gas phase have been widely studied and it has been demonstrated that there are no efficient synthetic pathways in gas-phase available to reproduce the abundances of CH3CCH in the cold molecular clouds (Hickson et al. 2016). It was proposed that the principal source of propyne in the gas phase is via ion-molecule reactions with 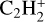 as a precursor (Schiff & Bohme 1979) and neutral-neutral reactions such as CCH + CH4 → CH3CCH + H (Turner et al. 1999), as well as dissociative recombination reactions involving larger hydrocarbons (Calcutt et al. 2019).
as a precursor (Schiff & Bohme 1979) and neutral-neutral reactions such as CCH + CH4 → CH3CCH + H (Turner et al. 1999), as well as dissociative recombination reactions involving larger hydrocarbons (Calcutt et al. 2019).
Those pathways have not been shown to be capable of reproducing the observed abundance of CH3CCH in astrophysical media. For this reason, surface reactions occurring on interstellar grains have been studied as well (Hickson et al. 2016; Guzmán et al. 2018). Propyne molecules are believed to adhere to the cold dust grains and then undergo hydrogenation at cold molecular cloud temperature of about 10 K. Additionally, CH3CCH was shown to form through the hydrogenation of C3 radicals, which could be further hydrogenated to propene. Nevertheless, models that include grain surface and gas phase reactions have not been able to reproduce the observed methyl acetylene abundance by more than an order of magnitude. This failure to reproduce the abundance of propyne demonstrates that more crucial formation pathways are still unknown at low temperatures (Hickson et al. 2016; Guzmán et al. 2014; Öberg et al. 2013).
The symmetric top molecule CH3CCH is among the most efficient thermometers available. The rotational levels jk associated to propyne depend on two quantum number j and k (where j is the total angular momentum of CH3CCH and k is the projection of j on the C3 rotational axis). These rotational levels are split into several levels with different k quantum numbers. Consequently, for each rotational transition, there are multiple transitions with different k quantum numbers that cover a wide energy range above the ground state, but are closely spaced in frequency and can therefore all be observed in the same bandwidth; for instance, many transitions can be observed simultaneously using the same antenna settings and sensitivities that reduce the calibration uncertainties. The dipole moment of propyne is parallel to the C3 axis, hence, radiative transitions with ∆k ≠ 0 are forbidden; different k–components are connected only via collisional processes, making their relative population sensitive to the kinetic temperature.
The interstellar medium where propyne generally resides is characterised by a very low density; therefore, the populations of its rotational states are typically not in local thermodynamic equilibrium (LTE). Therefore, the analysis of intensities of spectroscopic lines of CH3CCH requires the application of a radiative transfer model. Such a model requires spectroscopic data for radiative transfer rates, which are usually available, as well as collisional rate coefficients for rotational transitions induced by collisions with the dominant interstellar species, usually He or H2, which are often not available. Consequently, these collisional rates must be calculated in quantum scattering computations using a precise potential energy surface (PES) for the interaction of the molecule with He or H2.
To the best of our knowledge, no collisional state-to-state rate coefficients are available in the literature and the present set of collisional rate coefficients is the first one obtained by fully quantum methods.
In the present paper, we study the collisional excitation of the rigid symmetric top molecule CH3CCH with He atoms for temperature up to 100 K. The overall structure of this paper is as follows. Section 2 describes the ab-initio computation of the three-dimensional (3D) CH3CCH-He intermolecular potential, the analytical representation of the interaction potential is defined and the potential is illustrated. In Sect. 3 we describe the study of the dynamics, where we illustrate inelastic cross-sections in CH3CCH-He collisions. We discuss rate coefficients for CH3CCH-He collisions in Sect. 4. We analyse the impact of our rate coefficients by performing a radiative transfer calculation for typical interstellar conditions in Sect. 5. Our conclusions and future outlook are presented in Sect. 6.
2 Potential energy surface
In this section, our aim is to compute the first accurate potential energy surface between a symmetric top molecule, CH3CCH (X1A1), with a structureless helium atom (1S) in their respective electronic ground states.
The 3D PES was computed as a function of three Jacobi coordinates (R, θ, ϕ). The origin of the coordinate system is the centre of mass of CH3CCH molecule and the Ζ axis lies along its C3 symmetry axis. Here, R denotes the intermolecular separation between the center of mass of CH3CCH and He atom and θ and ϕ define the orientation of the He atom. The coordinates defining the geometry of the CH3CCH-He system are presented in Fig. 1. For ϕ = 0°, the He atom is in the plane formed by the axis of molecule and one of the C-H bonds, while for ϕ = 60°, the He atom is situated at equal distance between two hydrogen atoms.
The propyne molecule was assumed to be rigid in the computation of the interaction potential of CH3CCH-He, where the internal coordinates of CH3CCH were frozen to the average geometry of the ν = 0 vibrational state as follows: r(H− C) = 1.061 Å, r(C≡C) = 1.215 Å, r(C–C) = 1.458 Å, r(C– H) = 1.089 Å, and ∠(HCC) = 110.7° (El Idrissi et al. 2001).
We performed explicitly correlated coupled cluster computations, with the inclusion of single, double, and perturbatively triple excitations [CCSD(T)-F12a] (Knizia et al. 2009) in conjunction with the augmented correlation consistent polarised valence triple zeta (aug-cc-pVTZ) basis sets of Dunning (Dunning Jr 1989) to calculate ab initio points on the CH3CCH-He interaction potential. The MOLPRO code (Werner et al. 2015) was used to perform these computations in the C1 symmetry group.
The performance of such an approach was already tested for CH3CΝ-He, CH3ΝC-He (Ben Khalifa et al. 2022) as well as SiH3CΝ-He (Naouai et al. 2021). It was proven that CCSD(Τ)-F12 method, supplemented by the aVTZ basis set, offers an excellent accuracy for interactions involving rare gases.
A counterpoise correction of Boys & Bernardi (1970) was considered to correct for the basis set superposition error (BSSE) according to the following expression:
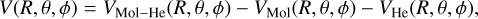 (1)
(1)
where VMol–He is the global electronic energy of the CH3CCH-He system and the last two terms are the energies of the two fragments, all performed using the full basis set of the total system.
The ranges of variation used to compute the PES was constructed as follows. For the angle θ, the grid is made up of 19 values from 0° to 180°, while for the angle ϕ, we used seven values from 0° to 60° uniformly distributed by steps of 10°. All other geometries are obtained by symmetry. Finally, for the intermolecular distance, R, we used a grid of 60 points (4 ≤ R ≤ 50 a0). We used a spacing of 0.2 a0 in the short-range; whereas in the long-range, the spacing is increased progressively. These parameters lead to a set of 7980 energy points.
We took into consideration the size-inconsistency when using the CCSD(T)-F12a method; thus, the PES computed with this approach was shifted by subtracting the asymptotic value of the PES at R = 50 a0, which is equal to –5.3 cm−1.
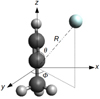 |
Fig. 1 Jacobi coordinates defining the geometry of the CH3CCH-He van der Waals complex. The origin of the reference frame is at the CH3CCH center-of-mass. The angles are defined so that for θ = 0°, He approaches along the C-H end of the molecule and for ϕ = 60°, the He atom lies in the plane defined by CHCH atoms on the side of the H atom. |
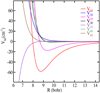 |
Fig. 2 Dependence on R of the first Vlm(R) components for CH3CCH-He with 0 ≤ l ≤ 4. |
2.1 Analytical fit
It is useful for the computation of the matrix elements of the interaction between scattering basis functions in time-independent quantum method to use the functional form presented below:
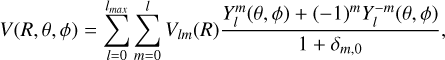 (2)
(2)
where Vlm(R) and 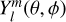 are the radial coefficients to be computed and the normalised spherical harmonics, respectively, and δm,0 is the Kronecker delta symbol. Due to the C3v symmetry of the propyne molecule, the values of m are restricted to terms for which m is multiple of 3 (m = 3n, n integer) in the expansion.
are the radial coefficients to be computed and the normalised spherical harmonics, respectively, and δm,0 is the Kronecker delta symbol. Due to the C3v symmetry of the propyne molecule, the values of m are restricted to terms for which m is multiple of 3 (m = 3n, n integer) in the expansion.
From a PES grid containing (19,7) values of (θ, φ), we could include radial coefficients up to lmax = 18 and m = 18. The total number of expansion coefficients is equal to 70, with a final accuracy better than 1 cm−1 for R ≥ 5 bohr. Finally, a least-squares interpolation was used over the entire range of intermolecular distances to supply continuous expansion coefficients suitable for scattering computations. For R ≥ 30 bohr, we extrapolated the long-range potential using an inverse exponent expansion implemented in the MOLSCAT (Hutson & Green 1995) computer code.
In Fig. 2, we present the dependence on R of the radial coefficients up to l = 4. Here, V00 represents the isotropic potential, responsible for elastic collisions, while terms with l ≥ 1 describe the anisotropic part of the PES responsible for inelastic collisions. As we can see, the largest (in magnitude) of the anisotropic terms (l ≥ 0) is associated to l = 2, a term that is responsible for transitions with Δ j = 2. This should have an effect on the propensity rules in the rotational excitation, as discussed in more detail below.
2.2 Analysis of the PES
The global minimum of the PES, which describes the main interaction of CH3CCH-He, is located at the equilibrium inter-molecular separation Re = 6.3 bohr with a well depth of De = 51.04 cm−1. The configuration of the global minimum is defined by the angles ϕ = 60° and θ = 104°, while a local minimum of 37.6 cm−1 is located at R = 8.6 bohr and θ = 180°. The global and local minima are separated by a barrier of −27.07 cm−1 that is located at θ = 137° and R = 8.35 bohr.
The internal rotation along the ϕ coordinate is almost free: the energy of the minimum increases between ϕ = 0° and ϕ = 30° (from −46.8 cm−1 at θ = 94° to −46.6 cm−1 at θ = 98°) and then decreases between ϕ = 30° and ϕ = 60° (from −46.6 cm−1 at θ = 98° to −51.04 cm−1 at θ = 104°). This behaviour was already observed for other systems with C3v symmetry such as CH3CN-He and CH3NC-He (Ben Khalifa et al. 2022) and is due to the elongated shape of the propyne molecule.
We note that the PES for CH3CCH-He share the same qualitative behaviour that was previously observed for molecules with a threefold symmetry axis interacting with rare gas atoms (Gubbels et al. 2012; Loreau et al. 2014; Loreau & Van der Avoird 2015; Ben Khalifa et al. 2022; Naouai et al. 2021), where the global minimum occurs at ϕ = 60°, that is, with the helium atom located between two hydrogen atoms. Because of the C3v symmetry of the CH3CCH molecule, there are two more symmetry equivalent orientations for the global minimum, at ϕ = 180° and ϕ = 300°. We illustrate in Fig. 3 (left panel), the 2D cut of the interaction potential as a function of two Jacobi coordinates (R and θ), while the ϕ angle is held fixed at its equilibrium value corresponding to the CH3CCH-He minimum. The variation in this cut shows a strong anisotropy of the interaction potential of CH3CCH-He along the θ coordinate. For a better appreciation of the topography of the PES, we also present a 2D cut of the 3D PES as a function of θ and ϕ for R = 6.6 bohr (Fig. 3, right panel). This type of plot offers a unique overview as it includes all minima and the barriers between them.
3 Scattering calculations
3.1 Spectroscopy
The prolate symmetric top molecule CH3CCH belongs to the C3v point group, with a dipole moment of 0.7829 Debye (Wlodarczak et al. 1988). The relevant rotational Hamiltonian associated with CH3CCH is expressed as follow:
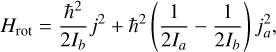 (3)
(3)
where j2 is the square of the angular momentum that satisfies the relation 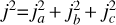 and Ia and Ib are the principal moments of inertia. The wave functions, | jkm〉, of a symmetric top molecule are defined by three quantum numbers, where k denotes the projection of j along the C3v axis of the body-fixed reference and m is its projection on the z-axis of the space-fixed frame of reference. The energies of the rotational levels are given by:
and Ia and Ib are the principal moments of inertia. The wave functions, | jkm〉, of a symmetric top molecule are defined by three quantum numbers, where k denotes the projection of j along the C3v axis of the body-fixed reference and m is its projection on the z-axis of the space-fixed frame of reference. The energies of the rotational levels are given by:
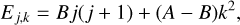 (4)
(4)
where B and A are the rotational constants which are equal to 0.2850 cm−1 and 5.3083 cm−1 (El Idrissi et al. 2001), respectively. Due to the identical nuclear spin of hydrogen atoms, we can distinguish two independent forms of propyne: ortho-CH3CCH (or, A–) and para-CH3CCH (or, The rotational levels associated to the propyne molecule are characterised by k = 3n ± 1 for para-CH3CCH and k = 3n for ortho-CH3CCH (n being integer).
It is important to note that the ortho-to-para transitions are strictly forbidden in such non-reactive collisions. Therefore, the scattering computations can be carried out separately for each nuclear spin species. The small values of the rotational constants A and B lead to a complex rotational structure with a high density of rotational levels. In the ISM, CH3CCH is usually detected via transitions between highly excited states, for instance, 21k to 20k, k = 0,…,7 (Calcutt et al. 2019). This implies that cross-sections of CH3CCH-He need to be carried out using a large rotational basis set, which limit the possibility of employing a full quantum-mechanical dynamics methods for scattering calculations.
 |
Fig. 3 2D contour plots of the interaction potential of the CH3CCH-He van der Waals complex. The left panel depicts the 3D PES as a function of θ and R at ϕ = 60°, while the right panel shows the PES as a function of ϕ and θ at R = 6.6a0. For each panel, the blue (red) contours represent the positive (negative) parts of the potential (in unit of cm−1). |
3.2 Cross-sections
The main focus of this paper is the study of the collisional (de-)excitation of CH3CCH by He atoms. Cross-sections for rotationally inelastic transitions of para- and ortho-CH3CCH-He were carried out using the time-independent close-coupling (CC) method up to Etot ≤ 100 cm−1 and the coupled state (CS) approximation for total energies ranging from 100 ≤ Etot ≤ 600 cm−1. The scattering calculations were carried out using the Manolopoulos (1986) propagator to solve the coupled differential equations implemented in the MOLSCAT computer code.
To keep the computational time under control, we start by testing the integrator parameters, STEPS and the size of the rotational basis set, Nlev, which were adjusted to ensure convergence of the rotational cross-sections over the entire energy range. Hence, the integration limits of the scattering computations were fixed at rmin = 3.5a0 and Rmax = 50a0. The STEPS parameter is set to 100 for Etot ≤ 50 cm−1, 70 for Etot ∈ [50,100] cm−1, 50 for 100 ≤ Etot ≤ 200 cm−1, and 30 for Etot ∈ [200,600] cm−1. All these propagator parameters were fixed by carrying out convergence tests. Furthermore, the size of the rotational basis set was optimised in order to include in the scattering computations all open channels along with a few closed channels. For ortho-CH3CCH, the number of rotational levels Nlev considered for our calculations was taken as: Nlev = 55 (up to jk = 243 with an energy of 216.24 cm−1) for total energies Etot ≤ 50 cm−1, Nlev = 80 (up to jk = 313 with an energy of 327.98 cm−1) for total energies 50 cm−1 ≤ Etot ≤ 100 cm−1, and Nlev = 155 (up to jk = 490 with an energy of 698.39 cm−1) for 102 cm−1 ≤ Etot ≤ 600 cm−1. For para-CH3CCH, we take Nlev = 105 (up to jk = 117 with an energy of 283.79 cm−1) for total energies Etot ≤ 100 cm−1, Nlev = 160 (up to jk = 372 with an energy of 420.88 cm−1) for total energies 100 ≤ Etot ≤ 200 cm−1, Nlev = 185 (up to jk = 384 with an energy of 502.83 cm−1) for total energies 202 ≤ Etot ≤ 300 cm−1 and Nlev = 215 (up to jk = 1910 with an energy of 610.65 cm−1) for total energies 305 ≤ Etot ≤ 600 cm−1.
We attribute a value of 0.05 Å2 to the off-diagonal tolerance, which determines the maximum value of the total angular momentum (J) that needs to be taken into account. Finally, given that the total angular momentum, J, is a quantity preserved, the integral cross-section was obtaining by summing partial wave contributions.
We calculated rotational cross-sections for total energy ranging from 0.1 to 600 cm−1. To do so, the energy grid was tuned to describe all the resonances in the cross-sections and to cover the entire energy range required to compute collisional rates accurately up to 100 K. We used an energy step dE of 0.2 cm−1 for energies below 50 cm−1, 0.5 cm−1 for energies between 50 and 100 cm−1, 2 cm−1 for energies between 100 cm−1 and 200 cm−1, 5 cm−1 for energies between 200 and 400 cm−1, and 10 cm−1 for energies between 400 and 600 cm−1.
For kinetic energies where the resonances become negligible (Ec ≥ 100 cm−1), the calculations using CC method, in the fully converged limit, turned out to be impractical and would require an inordinate amount of computing time; thus, we explored using the CS approximation to save time calculation. The CS approximation is indeed expected to be reliable at high kinetic energies (Phillips et al. 1996). We examined the accuracy of CS computations by direct comparison to CC ones as presented in Table 1 at a total energy of 100 cm−1. As can be seen in Table 1, the relative error between CC and CS cross-sections for selected transitions does not exceed 10% for Etot = 100 cm−1 with a disk occupancy and CPU time for the CC calculations that are several times larger than CS ones. We conclude that for CH3CCH-He collisions, the CS method can be used for total energies larger than 100 cm−1.
Figure 4 shows examples of the kinetic energy dependence of collisional cross-sections for the rotational excitation of para-CH3CCH-He (right panel) and ortho-CH3CCH-He (left panel) for some dipolar (Δj = 1) and quadrupolar (Δj = 2) transitions with Δk = 0. These figures underline the importance of using a sufficiently fine energy grid to correctly describe the resonances, especially for Ec ≤ 50 cm−1. The cross-sections for these transitions increase above the threshold at which these transitions open, until achieving a maximum, and they then decrease as the collision energies increase. The cross-sections exhibit many Feshbach and shape resonances at kinetic energies below 50 cm−1. This is due to the formation of quasi-bound states into the potential well depth before the dissociation of the collisional complex.
Figure 4 reveals the existence of a strong even Δ j propensity rule at almost all collision energies for CH3CCH-He. The largest cross-sections (in magnitude) are found for transitions with Δj = 2 that is, 10-30,20-40, and 30-50 for ortho-CH3CCH-He and for the transitions 11-31, 21-41, and 31-51 for para-CH3CCH-He. These propensity rules can be explained by exploring the shape of the PES, as the symmetry of the interaction potential will promote transitions with even |Δj|. Furthermore, this propensity rule can be understood by examining the radial terms Vlm(R) described in Fig. 2. Cross-sections with |Δ j| = 2 are mainly caused by the V20 term, which is the dominant anisotropic term for CH3CCH-He, hence, the magnitude of cross-sections corresponding to transitions with |Δ j| = 2 are larger than the results for other transitions.
Propensity rules that favor even values of |Δj| were already observed for the excitation of other symmetric top molecules with C3v symmetry by He atoms, such as CH3CN (Ben Khalifa et al. 2022) and SiH3CN(Naouai et al. 2021). Figure 4 only illustrates cross-sections for para- and ortho-CH3 CCH-He and for transitions with Δ j = 0, the same behaviour is also observed for other values of Δk.
 |
Fig. 4 Kinetic energy dependence of the rotational excitation cross-sections jk → j′k′ of ortho-CH3CCH-He (left panel) and para-CH3CCH-He (right panel) in collision with He for Δj = 1 and Δj = 2 transitions while Δk = 0. |
Comparison between CC and CS cross-sections (in Å2) for the excitation of para CH3CCH by He for total energies Etot = 100 cm−1 with Nlev = 80.
4 Rate coefficients
Calculated state-to-state rotational cross-sections were used to compute the corresponding rate coefficients for the collisions of ortho- and para- type levels of methyl acetylene with He atoms by averaging over the collision energy (Ec), as follows:
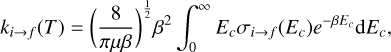 (5)
(5)
where β = 1/kBT and kB, T and µ = 3.638773549 au are the Boltzmann constant, the kinetic temperature, and the collision reduced mass, respectively.
In this work, the state-to-state cross-sections calculated for total energy up to 600 cm−1 can be used to compute rate coefficients for transitions among the first 60 ortho levels (up to jk = 136, Erot = 232.554 cm−1) and 60 para levels (up to jk = 105, Erot = 156.862 cm−1) for kinetic temperature between 5 and 100 K. This complete set of (de-)excitation rate coefficients will be made available online on the EMAA12 and BASECOL (Dubernet et al. 2013) databases for line radiative transfer studies.
Figure 5 displays plots of the quenching rate coefficients of CH3 CCH-He as a function of the kinetic temperature for selected Δj = 2 transitions, accompanied by Δk = 0, 1, and 3. These plots show that the order of magnitude of rate coefficients associated to transitions with ∆k = 0, is larger than those with ∆k > 0. The largest rate coefficients are found for the transitions: 53-33, 63-43, and 73-53 for ortho-CH3CCH-He and 42-22, 52-32, and 62-42 for para-CH3CCH-He. The rate coefficients for ∆j = 2 transitions are seen to vary only weakly with temperature in the range investigated here. However, for ∆j = 1 transitions (not shown), a stronger variation is observed with a decrease of the rate coefficients from 5 K to about 30 K and a slow increase at higher temperatures. To conclude, transitions with even |Δj| and |Δk| = 0 are more favorable compared to those with |Δj| and |Δk| ≠ 0. These results correspond to those already observed at the level of the cross-sections (see Fig. 4).
To the best of our knowledge, no collisional rates for the excitation of CH3CCH were available in literature and the rate coefficients for CH3CN were sometimes used in radiative transfer models to approximate the excitation of propyne in astrophysical media (Mauersberger et al. 1991). To assess the validity of such an approach in the collisional studies, we performed a comparison of CH3CCH-He and CH3CN-He collisional rate coefficients, computed recently by Ben Khalifa et al. (2023), with the same level of theory for both the construction of the PES as well as for the scattering dynamics. We present this comparison in Fig. 6 for transitions between the first 50 ortho levels and 50 para levels of CH3CCH and CH3CN at a temperature of T = 100 K. We can see that collisional rate coefficients for the dominant transitions (k > 10−11 cm3 s−1, corresponding to |Δk| = 0 transitions) of both species agree within a factor of 2; however, we observe important differences for the smaller collisional rates with relative differences that reach a factor of 5. These differences show that independent calculations have to be performed for each molecule, as the rate coefficients cannot be assumed to be equal.
The collisional rate coefficients obtained for the CH3CCH-He and CH3CN-He species allow us to predict that their excitation in the astrophysical environments is different. Therefore, a radiative transfer study must be carried out for CH3CCH, using its respective set of collisional rate coefficients to obtain an accurate abundance of propyne.
It is important to emphasise that this comparison is only for collisional excitation by He atoms, while the dominant collider in the ISM is H2 molecule. At present, no collisional data are available for either CH3CCHH2 or CH3CNH2. In this case, one usually scales all rate coefficients for excitation by He atoms by a single factor to account for the mass difference between He and H2, but the accuracy of such an approach is known to be limited.
 |
Fig. 5 Temperature dependence of the rotational excitation rate coefficients, jk → j′k′, of ortho-CH3CCH-He (left panel) and para-CH3CCH-He (right panel) in collision with He atom for ∆j = 2 and ∆k = 0,1, and 3. |
 |
Fig. 6 Comparison between ortho and para CH3CCH-He and CH3CN-He rate coefficients at T = 100 K. The diagonal line corresponds to equal rate coefficients and the dashed line to the difference of a factor of 5. |
5 Application
In the interstellar medium, the intensities of the emission lines are proportional to the population of the energy levels of the molecule. The evolution of these populations is based on collisional and radiative processes that are governed by collisional rate coefficients and radiative Einstein coefficients, respectively. The knowledge of these two sets of data allows one to perform a radiative transfer computation for the propyne molecule using the Radex (Van der Tak et al. 2007) computer code.
Non-LTE radiative transfer computations were performed using the escape probability approximation. Our collisional rate coefficients (from 5 to 100 K) were combined with spectroscopic data from the Cologne Data base for Molecular Spectroscopy portal (Müller et al. 2005). In practice, we have computed the excitation (Tex) and brightness (TB) temperatures for transitions jk = 6→4, with k = 0,1,2 and 3 at 102.5 GHz which are usually detected in astrophysical clouds (Andron et al. 2018). To do so, we scaled the CH3CCH-He rates by a factor of 1.39 to approximate the rate coefficients that para-H2(j = 0) would induce and we fixed the cosmic microwave background, the line width, and the column density of propyne at 2.73 K, 2.1 kms−1 (Andron et al. 2018) and 10−14 cm−2, respectively. Finally, we varied the volume density of the molecular hydrogen from 102 cm−3 to 108 cm−3 to examine the behaviour of the excitation of CH3CCH under and out of LTE conditions.
We display in Fig. 7 the variation of the excitation temperature of CH3CCH for selected kinetic temperatures of 20, 50, and 100 K. We observe a supra-thermal effect at T = 50 and 100 K for H2 densities between 104 and 106 cm−3, where the excitation temperature is higher than the kinetic temperature. At low H2 density ( cm−3), the medium is dilute and the excitation temperature is given by the cosmic background temperature (Tex = TCMB = 2.73 K), while at high density (
cm−3), the medium is dilute and the excitation temperature is given by the cosmic background temperature (Tex = TCMB = 2.73 K), while at high density ( cm−3) when the collisional excitation processes becomes more important, the Tex tends asymptotically to the kinetic temperature where LTE conditions are reached. From these plots, we observe that the LTE is reached for volume densities above 106 cm−3.
cm−3) when the collisional excitation processes becomes more important, the Tex tends asymptotically to the kinetic temperature where LTE conditions are reached. From these plots, we observe that the LTE is reached for volume densities above 106 cm−3.
 |
Fig. 7 Excitation temperature of CH3CCH for transitions jk → j′k′, with j = 6, j′ = 5, and k = k′ = 0 or 2 (para-CH3CCH) and k = k′ = 0 or 3 (ortho-CH3CCH) as a function of the H2 density for three kinetic temperature (20, 50 and 100 K) and a column density of 1014 cm−2. |
6 Conclusion
In this work, we computed the first 3D PES for the interaction between CH3CCH and He atoms using the explicitly correlated coupled cluster theory [CCSD(T)-F12a] and the aug-cc-pVTZ basis set. The global minimum was found to correspond to a potential well depth of 51.04 cm−1 and an equilibrium inter-molecular separation of 6.3 bohr. This interaction potential was used to compute rotationally-inelastic cross-sections for transitions between the first 60 ortho- and 60 para- levels of CH3CCH in collision with He atoms in time-independent close-coupled and coupled states quantum scattering computations. The rotational cross-sections were calculated as a function of the total energy up to 600 cm−1.
By thermally averaging the cross-sections over the collision energy, collisional rates were computed for temperatures relevant to interstellar conditions, from 5 to 100 K.
We have compared the new set of collisional rates of CH3CCH-He with those for CH3CN-He. This comparison shows that collisional rate coefficients are different by up to a factor of 5. Consequently, we must use the appropriate collisional rates of CH3CCH to study the excitation of propyne in the interstellar medium. We therefore recommend the use of this set of collisional rates in non-LTE models of CH3CCH excitation.
We have also used the new set of rate coefficients in a simple radiative transfer model to assess their impact on four observed transitions. This study shows that the propyne lines are not thermalised and non-LTE models should be employed to analyse its emission spectra.
Acknowledgements
We thank H. da Silva, Jr for help with HPC computing. M.B.K. acknowledges support from the FWO. J.L. acknowledges support from KU Leuven through grant no. C14/22/082. The scattering calculations presented in this work were performed on the VSC clusters (Flemish Supercomputer Center), funded by the Research Foundation-Flanders (FWO) and the Flemish Government.
References
- Agúndez, M., Fonfría, J. P., Cernicharo, J., Pardo, J. R., & Guélin, M. 2008, A&A, 479, 493 [Google Scholar]
- Andron, I., Gratier, P., Majumdar, L., et al. 2018, MNRAS, 481, 5651 [NASA ADS] [CrossRef] [Google Scholar]
- Ben Khalifa, M., Dagdigian, P. J., & Loreau, J. 2022, J. Phys. Chem. A, 126, 9658 [NASA ADS] [CrossRef] [Google Scholar]
- Ben Khalifa, M., Dagdigian, P., & Loreau, J. 2023, MNRAS, 523, 2577 [NASA ADS] [CrossRef] [Google Scholar]
- Boys, S. F., & Bernardi, F. 1970, Mol. Phys., 19, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Buhl, D., & Snyder, L. E. 1973, in Molecules in the Galactic Environment (Hoboken: John Wiley & Sons) [Google Scholar]
- Burgdorf, M., Orton, G., van Cleve, J., Meadows, V., & Houck, J. 2006, Icarus, 184, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Calcutt, H., Willis, E., Jørgensen, J., et al. 2019, A&A, 631, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Graauw, T., Feuchtgruber, H., Bezard, B., et al. 1997, A&A, 321, L13 [NASA ADS] [Google Scholar]
- Dubernet, M. L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunning Jr, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- El Idrissi, M., Liévin, J., Herman, M., Campargue, A., & Graner, G. 2001, Chem. Phys., 265, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Fayolle, E. C., Öberg, K. I., Garrod, R. T., van Dishoeck, E. F., & Bisschop, S. E. 2015, A&A, 576, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fouchet, T., Lellouch, E., Bézard, B., et al. 2000, arXiv e-prints [arXiv:0002273] [Google Scholar]
- Gratier, P., Pety, J., Guzmán, V., et al. 2013, A&A, 557, A101 [CrossRef] [EDP Sciences] [Google Scholar]
- Gratier, P., Majumdar, L., Ohishi, M., et al. 2016, ApJ, 225, 25 [NASA ADS] [Google Scholar]
- Gubbels, K. B., van de Meerakker, S. Y. T., Groenenboom, G. C., Meijer, G., & van der Avoird, A. 2012, J. Chem. Phys., 136, 074301 [NASA ADS] [CrossRef] [Google Scholar]
- Guzmán, V. V., Pety, J., Gratier, P., et al. 2014, Faraday Discuss., 168, 103 [Google Scholar]
- Guzmán, A. E., Guzmán, V. V., Garay, G., Bronfman, L., & Hechenleitner, F. 2018, ApJS, 236, 45 [CrossRef] [Google Scholar]
- Herbst, E. 2017, Int. Rev. Phys. Chem., 36, 287 [Google Scholar]
- Hickson, K. M., Wakelam, V., & Loison, J.-C. 2016, Mol. Astrophys., 3, 1 [CrossRef] [Google Scholar]
- Hutson, J. M., & Green, S. 1995, MOLSCAT computer code, version 14, Distributed by Collaborative Computational Project 6, Warington, UK: Daresbury Laboratory [Google Scholar]
- Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [Google Scholar]
- Loreau, J., Liévin, J., Scribano, Y., & van der Avoird, A. 2014, J. Chem. Phys., 141, 224303 [NASA ADS] [CrossRef] [Google Scholar]
- Loreau, J., & Van der Avoird, A. 2015, J. Chem. Phys., 143, 184303 [NASA ADS] [CrossRef] [Google Scholar]
- Lovas, F. J., Johnson, D. R., Buhl, D., & Snyder, L. E. 1976, ApJ, 209, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Manolopoulos, D. 1986, J. Chem. Phys., 85, 6425 [NASA ADS] [CrossRef] [Google Scholar]
- Mauersberger, R., Henkel, C., Walmsley, C., Sage, L., & Wiklind, T. 1991, A&A, 247, 307 [NASA ADS] [Google Scholar]
- Mebel, A. M., Landera, A., & Kaiser, R. I. 2017, J. Phys. Chem. A, 121, 901 [Google Scholar]
- Müller, H. S., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struc., 742, 215 [CrossRef] [Google Scholar]
- Naouai, M., Jrad, A., Badri, A., & Najar, F. 2021, MNRAS, 507, 5264 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boamah, M. D., Fayolle, E. C., et al. 2013, ApJ, 771, 95 [CrossRef] [Google Scholar]
- Parker, D. S., & Kaiser, R. I. 2017, Chem. Soc. Rev., 46, 452 [CrossRef] [Google Scholar]
- Phillips, T. R., Maluendes, S., & Green, S. 1996, ApJ, 107, 467 [NASA ADS] [Google Scholar]
- Qiu, J., Zhang, J., Zhang, Y., Jia, L., & Tang, X. 2020, A&A, 634, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schiff, H., & Bohme, D. K. 1979, ApJ, 232, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, D., & Ziurys, L. 2019, ApJ, 881, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Teanby, N., Irwin, P., de Kok, R., et al. 2009, Icarus, 202, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, B., Terzieva, R., & Herbst, E. 1999, ApJ, 518, 699 [Google Scholar]
- Van der Tak, F., Black, J. H., Schöier, F., Jansen, D., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Jansen, D. J., & Groesbeck, T. 1995, ApJ, 447, 760 [NASA ADS] [CrossRef] [Google Scholar]
- Vastel, C., Ceccarelli, C., Lefloch, B., & Bachiller, R. 2014, ApJ, 795, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2015, MOLPRO, version 2015.1, a package of ab initio programs, http://www.molpro.net [Google Scholar]
- Wlodarczak, G., Bocquet, R., Bauer, A., & Demaison, J. 1988, J. Mol. Spectr., 129, 371 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between CC and CS cross-sections (in Å2) for the excitation of para CH3CCH by He for total energies Etot = 100 cm−1 with Nlev = 80.
All Figures
 |
Fig. 1 Jacobi coordinates defining the geometry of the CH3CCH-He van der Waals complex. The origin of the reference frame is at the CH3CCH center-of-mass. The angles are defined so that for θ = 0°, He approaches along the C-H end of the molecule and for ϕ = 60°, the He atom lies in the plane defined by CHCH atoms on the side of the H atom. |
| In the text | |
 |
Fig. 2 Dependence on R of the first Vlm(R) components for CH3CCH-He with 0 ≤ l ≤ 4. |
| In the text | |
 |
Fig. 3 2D contour plots of the interaction potential of the CH3CCH-He van der Waals complex. The left panel depicts the 3D PES as a function of θ and R at ϕ = 60°, while the right panel shows the PES as a function of ϕ and θ at R = 6.6a0. For each panel, the blue (red) contours represent the positive (negative) parts of the potential (in unit of cm−1). |
| In the text | |
 |
Fig. 4 Kinetic energy dependence of the rotational excitation cross-sections jk → j′k′ of ortho-CH3CCH-He (left panel) and para-CH3CCH-He (right panel) in collision with He for Δj = 1 and Δj = 2 transitions while Δk = 0. |
| In the text | |
 |
Fig. 5 Temperature dependence of the rotational excitation rate coefficients, jk → j′k′, of ortho-CH3CCH-He (left panel) and para-CH3CCH-He (right panel) in collision with He atom for ∆j = 2 and ∆k = 0,1, and 3. |
| In the text | |
 |
Fig. 6 Comparison between ortho and para CH3CCH-He and CH3CN-He rate coefficients at T = 100 K. The diagonal line corresponds to equal rate coefficients and the dashed line to the difference of a factor of 5. |
| In the text | |
 |
Fig. 7 Excitation temperature of CH3CCH for transitions jk → j′k′, with j = 6, j′ = 5, and k = k′ = 0 or 2 (para-CH3CCH) and k = k′ = 0 or 3 (ortho-CH3CCH) as a function of the H2 density for three kinetic temperature (20, 50 and 100 K) and a column density of 1014 cm−2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


