| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/202347978 | |
| Published online | 08 March 2024 | |
Hot subdwarf wind models with accurate abundances
II. Helium-dominated merger products CD–46 8926 and CD–51 11879★
1
Ústav teoretické fyziky a astrofyziky, Masarykova univerzita,
Kotlářská 2,
611 37
Brno,
Czech Republic
e-mail: krticka@physics.muni.cz
2
Astronomický ústav, Akademie věd České republiky,
Fričova 298,
251 65
Ondřejov,
Czech Republic
3
Astroserver.org,
Fő tér 1,
8533
Malomsok,
Hungary
4
Instituto de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaiso,
Gran Bretaña 1111,
Playa Ancha,
2360102
Valparaíso,
Chile
Received:
15
September
2023
Accepted:
14
December
2023
Context. Helium-dominated subdwarfs are core helium burning stars stripped of their envelope. The nuclear evolution of these stars alters surface abundances. Modified abundances impact the strength of the stellar wind.
Aims. We aim to understand the influence of modified surface abundances on the strength of the stellar wind in the helium-dominated subdwarfs CD–46 8926 and CD–51 11879. A modified wind strength could resolve the problem with the X-ray emission of these stars, as the expected X-ray luminosity of both stars is significantly higher than the upper limit determined from observations.
Methods. We used our own optical spectroscopy combined with archival ultraviolet spectroscopy and photometry to derive basic parameters and surface abundances of selected subdwarfs. The resulting parameterst served as input for the METUJE stellar wind code, which predicts the wind structure of these stars. We compared the derived wind parameters with the predictions derived for solar abundances.
Results. The optical analysis showed that both subdwarfs have effective temperatures in excess of 60 kK and a strong overabundance of carbon in the case of CD–46 8926 and nitrogen in the case of CD–51 11879. We interpret the abundance patterns as being a result of enrichment by the products of nuclear reactions. The modified abundances reduce the wind mass-loss rate by tens of percent. The reduction improves the predicted wind line profiles in comparison to observations. The change in helium abundance does not have a strong effect on the wind parameters. As a result of a lower estimated bolometric luminosity and mass-loss rate and a larger distance, the expected X-ray luminosities become lower and agree with observational upper limits.
Conclusions. The nucleosynthesis does not significantly alter the strength of the wind of hot subdwarfs, but the inclusion of proper stellar parameters improves the agreement with observational wind characteristics. Our analysis indicates that subdwarfs overabundant in helium are typically able to launch wind. This conclusion is supported by data gathered for thousands of subdwarfs from the literature, which shows that subdwarfs overabundant in helium avoid the region in the Kiel diagram where the winds are predicted to be absent. This can be interpreted in terms of the gravitational settling of helium, which is suppressed by the winds.
Key words: stars: winds, outflows / stars: mass-loss / stars: early-type / stars: abundances / subdwarfs
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The stellar wind of hot stars is accelerated by the absorption of radiation in line transitions of heavy elements such as carbon, silicon, and iron (Lucy & Solomon 1970; Castor et al. 1975). As a result of this, the amount of mass lost by the wind per unit of time, that is, the wind mass-loss rate, varies as a function of the atmospheric metal content. Consequently, for a given set of stellar parameters, the mass-loss rate ranges from zero for a pristine hydrogen-helium composition of Population III stars (Krtička & Kubát 2006, 2009) to values by a factor of few higher than the solar-metallicity rates in a metal-rich environment (Puls 2008).
The variation of the stellar wind mass-loss rate with metal-licity is typically expressed as a function of only one parameter, which is the mass fraction of heavy elements (Vink & Cassisi 2002; Gormaz-Matamala et al. 2019; Björklund et al. 2023). This approach provides reasonable results not only for the Magellanic Clouds (Brands et al. 2022; Marcolino et al. 2022) but also for many other galaxies of the Local Group. However, simple metallicity scaling may break down once the chemical composition markedly differs from scaled solar chemical composition. This may happen particularly in later evolutionary phases, when products of nuclear burning appear on the stellar surface.
Hot subdwarfs belong to stars in such a later evolutionary phase, where the products of nuclear reactions can appear on their surfaces or where the effect of diffusion can significantly alter the surface chemical composition (see Heber 2016, for a review). Hot subdwarfs are typically core helium burning objects (Guo 2018) that appear below the main sequence in the Hertzsprung–Russel diagram. There are several evolutionary channels that typically involve binaries that can lead to hot sub-luminous objects. A star can be stripped on the red giant branch due to interaction with a low-mass companion and ejection of the common envelope (Xiong et al. 2017; Kramer et al. 2020) or due to a stable Roche-lobe overflow (Han et al. 2002). Signatures of such previous interactions can be found in a population of hot subdwarfs (Pelisoli et al. 2020). A merger of two helium white dwarfs (or even a white dwarf and a main-sequence star, Zhang et al. 2017) can also lead to a hot subdwarf, and there is an observational indication that such objects are helium dominated (Geier et al. 2022). Finally, a late helium flash can also produce hot subdwarfs (Brown et al. 2001; Lanz et al. 2004). The detection of subdwarfs in binaries that may have interacted in the past, for instance in classical Be stars (Božić et al. 1995; Peters et al. 2008; Koubský et al. 2014; Klement et al. 2022), also points to a binary origin of some subdwarfs (Pols et al. 1991; Shao & Li 2021).
The chemical composition of hot subdwarfs can vary considerably from star to star. Apart from the abundance of heavy elements, which can be affected by previous nucleosynthesis and elemental diffusion (Dorsch et al. 2019), even the fraction of the two most abundant elements, hydrogen and helium, may significantly differ from solar values. The range of possible helium abundances is truly enormous, from the helium abundance being lower than the solar value by a few orders of magnitude (Latour et al. 2018) up to a helium-dominated chemical composition (Luo et al. 2019; Naslim et al. 2019; Werner et al. 2022). Low helium abundance is likely caused by helium gravitational settling (Byrne & Jeffery 2018), while there are indications that helium overabundance reflects different evolutionary channels that are perhaps connected with mergers (Geier et al. 2022). But even merger products of helium white dwarfs may retain some hydrogen on their surfaces, which leads to the formation of hydrogen-rich subdwarfs (Hall & Jeffery 2016).
Abundance variations influence the wind mass-loss rate, which has several observational implications. The mass-loss rate is expected to determine the strength of the X-ray emission, which originates in wind shocks (Feldmeier et al. 1997; Owocki et al. 2013). This may be relevant for hot subdwarfs, some of which show X-ray emission that is supposed to originate in wind shocks (La Palombara et al. 2014; Mereghetti & La Palombara 2016). Subdwarfs show peculiarities as the result of atmospheric diffusion (Unglaub & Bues 2001; Michaud et al. 2011), which becomes inhibited in the presence of a stronger wind (Vauclair 1975).
Despite non-monotonic abundance variations for individual elements, stellar wind models of subdwarfs are typically calculated either for solar or scaled solar chemical composition (Vink & Cassisi 2002; Krtička et al. 2016). To understand the influence of individual chemical compositions on the wind strength of hot subdwarfs, we initiated an observational and theoretical program aimed at predicting mass-loss rates for individual sub-dwarfs regarding their actual chemical composition. We started with hydrogen-rich subdwarfs where we have tested the influence of the wind strength on the X-ray emission and elemental diffusion (Krtička et al. 2019). In this second paper, we continue our effort by studying two helium-dominated subdwarfs. Both objects have parameters for which a line-driven wind is expected (Krtička et al. 2016) but still do not show any X-ray emission (La Palombara et al. 2014).
Spectra used for the analysis.
2 Spectroscopy and photometry
The spectral analysis of our selected helium-dominated sub-dwarfs is based on optical spectroscopy obtained by us and through archival UV spectra. Such a combination of optical and UV spectroscopy can provide reliable stellar parameters of hot evolved objects (e.g., Latour et al. 2018; Schindewolf et al. 2018). We obtained the optical spectra using the high-resolution spectrograph UVES (R = 80 000) mounted at the Nasmyth B focus of VLT-UT2 (Kueyen) within our ESO proposal 097.D-0540(A). Both spectra were taken on 16 July 2016 with a total exposure time of 1500s in the case of CD–46 8926 and 1260s in the case of CD–51 11879. The spectra were reduced using standard IRAF1 routines (bias, flat, and wavelength calibration). The optical spectra cover the spectral region of 3752–4980 Å.
We supplemented the optical data with UV spectra derived using the Far Ultraviolet Spectroscopic Explorer (FUSE) and the International Ultraviolet Explorer (IUE, SWP and LWR cameras2, high-dispersion data) satellites. We downloaded the processed UV spectra from the MAST archive3. The list of all used spectroscopical observations is given in Table 1.
The photometry for the analysis of the spectral energy distribution was downloaded using the Virtual Observatory SED Analyzer4 web tool (VOSA; Bayo et al. 2008). The photometry was based on ubvy magnitudes of Paunzen (2015) and data from Tycho survey (Høg et al. 2000), the Carlsberg Meridian Telescope CCD drift scan survey (Evans et al. 2002), the Sloan Digital Sky Survey (SDSS; Alam et al. 2015), Gaia DR3 data (Gaia Collaboration 2023), the DENIS survey (Epchtein et al. 1999), the Panoramic Survey Telescope and Rapid Response System 1 survey (Pan-STARRS1; Chambers et al. 2016), the Two Micron All Sky Survey (2MASS Skrutskie et al. 2006), the Visible and Infrared Survey Telescope for Astronomy survey (VISTA; Cross et al. 2012), and Wide-field Infrared Survey Explorer data (WISE; Wright et al. 2010). We adopted the Cardelli et al. (1989) extinction law to correct the photometric data for interstellar extinction.
3 Spectral analysis
The analysis of available spectra was based on the stationary plane-parallel model atmosphere code TLUSTY (Hubeny 1988, version 200). For stars with weak winds, which are expected in subdwarfs, even the hydrostatic model atmospheres provide reliable stellar parameters (Bouret et al. 2003; Heap et al. 2006). The models allow for departures from the local thermodynam-ical equilibrium (also abbreviated as NLTE approach), which is crucial in hot subdwarfs. The atomic data, which are mostly based on the Opacity and Iron Projects (Seaton et al. 1992; Hummer et al. 1993), were adopted from Lanz & Hubeny (2003). We used the SYNSPEC code (Hubeny & Lanz 2011, version 49) to calculate synthetic spectra. The spectra were corrected for the Doppler effect by means of radial velocity determined from a cross-correlation with theoretical spectrum as a template (Zverko et al. 2007).
The atmospheric parameters, that is, the effective temperatures Teff, surface gravities log g, and elemental abundances εel, were determined by the χ2 minimization of the difference between observed and predicted spectra using the simplex method (Krtička & Štefl 1999). In this work, we give the abundances as number density ratios relative to helium, that is, εel = Nel/NHe. For elements not included in the minimization, we assumed solar (Asplund et al. 2009) density ratio melNel/ (mHNH + mHeNHe). To overcome the problems with atmosphere model convergence, we separated the determination into two steps. First, we calculated a grid of model atmospheres and a synthetic spectra in Teff and log g with fixed abundances. We minimized the difference between the observed spectrum and the predicted spectrum, which was interpolated from the grid, and we derived Teff and log g. We used only optical spectra in this step. As a second step, we calculated a model atmosphere with parameters determined in the previous step. Based on this model, we minimized the differences between the observed spectrum and the predicted spectrum calculated for actual abundances. In this step we used both optical and UV spectra. These steps were repeated until convergence.
4 Wind modeling
We used the stellar parameters determined from the spectro-scopic analysis to predict wind structure. For this purpose we applied the global wind code METUJE (Krtička & Kubát 2017). The code solves the structural equations from the hydrostatic photosphere to the supersonically expanding radiatively driven stellar wind. This approach provides so-called global (unified) models (Gabler et al. 1989; Gräfener & Hamann 2008; Sander et al. 2017; Sundqvist et al. 2019). The models are consistently derived from the solution of hydrodynamical equations in which the radiative force and the radiative heating terms are determined using the co-moving frame (CMF) radiative transfer equation. The thermodynamic state of the wind is given by the solution of the NLTE equations. The atomic data used for the wind modeling are the same as described in Krtička et al. (2020). Most of the data is based on the Opacity and Iron Project calculations (Seaton et al. 1992; Hummer et al. 1993) and the data obtained from the databases of NIST (Kramida et al. 2015), VALD (Piskunov et al. 1995, Kupka et al. 1999), and the Kurucz website5. The code assumes a stationary and spherically symmetric wind. We assumed a smooth wind and neglected wind inhomogeneities (clumping).
We used the METUJE code to understand the role of the specific chemical composition of subdwarfs in the driving of the wind. We mainly focused on the wind parameters that can be tested against observations, that is, the mass-loss rates Ṁ and the terminal velocities υ∞. For this purpose, we calculated three sets of wind models with the same stellar parameters (Teff, R, and M) but with different abundances. One set was calculated for a derived stellar chemical composition (yielding Ṁ and υ∞), a second set was calculated for the same composition of heavy elements but with helium replaced by a solar mixture of hydrogen and helium (at the same mass fraction, providing ṀH and 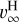 ), and a third set was calculated for a solar (Asplund et al. 2009) chemical composition (denoted as Ṁ⊙ and
), and a third set was calculated for a solar (Asplund et al. 2009) chemical composition (denoted as Ṁ⊙ and 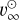 ). We assumed solar abundance per baryon for the elements whose abundances were not constrained from spectroscopy.
). We assumed solar abundance per baryon for the elements whose abundances were not constrained from spectroscopy.
Wavelengths of the strongest lines (in Å) used for abundance determination in CD–46 8926.
5 CD–46 8926
The helium-rich subdwarf CD–46 8926 (LSE 153, CPD-46 6542) is considered to be single based on an absence of photometric and radial velocity variations (Drilling 1983; Drilling & Heber 1986). A detailed optical NLTE spectral analysis was presented by Husfeld et al. (1989). From the determined luminosity, the scaling of Nazé (2009) for O stars predicts the X-ray luminosity of 9.9 × 1030 erg s−1, which is more than a factor of two higher than the upper limit from Chandra observations 3.8 × 1030 erg s−1 (La Palombara et al. 2014, corrected for Gaia distance). Spectropolarimetry has not revealed any magnetic field strong enough to be detected (Bagnulo et al. 2015).
5.1 Determination of stellar parameters
The effective temperature and surface gravity were determined from the fit of optical lines, while we also used FUSE and IUE spectra to derive abundances. Table 2 lists lines used for abundance determination. Neither the fit of optical and UV lines was fully satisfactory (see Figs. 1 and 2), which may possibly reflect missing line opacity in UV. The optical lines of heavy elements are sensitive to the stellar effective temperature, and it was not possible to select a single temperature that would fit all the lines. Most of the derived parameters given in Table 3 reasonably agree with the values determined by Husfeld et al. (1989), with the exception of surface gravity, which is slightly higher here. The derived abundances roughly correspond to rescaled solar abundances, with exception of enhanced carbon and nitrogen and depleted oxygen. Enhanced carbon and nitrogen abundance is typical among hot subdwarfs (Hirsch 2009).
We estimated the radius of CD–46 8926 together with the interstellar reddening E(B − V) by fitting of the spectral energy distribution (Fig. 3). This gave a radius of R = 0.37 R⊙ ± 0.04 R⊙ and E(B − V) = 0.07 mag, which is slightly lower than estimated by Schönberner & Drilling (1984). With spectroscopic surface gravity, the radius gives the mass as Μ = 0.47 ± 0.15 M⊙.
The radial velocity shift derived from FUSE spectra differs by about 20 km s−1 from the shift determined using optical spectroscopy. This is higher by more than a factor of two than the residual wavelength errors described in the FUSE Archival Data Handbook6. This may indicate the presence of a low-mass companion on the orbit with a period on the order of a year. We also note that an extremely low radial velocity of −128.7 ± 1.6km s−1 determined from the GALAH+ survey (Buder et al. 2021) is most likely wrong because it is based on the fit of solar abundance spectra.
Helium stars may form via CO+He and He+He white dwarf merger (Han et al. 2003; Justham et al. 2011; Miller Bertolami et al. 2022) or by the very late thermal pulse channel. Carbon overabundance (Table 3) indicates a weak contamination by a 3α reaction following the CNO cycle. The contamination would likely be much stronger for CO+He white dwarf merger products, which perhaps points to a hybrid CO–He+He white dwarf merger origin (Justham et al. 2011). Within this scenario, an sdB subdwarf evolves into a CO–He white dwarf and reignites helium in a shell after merger with a helium white dwarf. The parameters of CD–46 8926 (Table 3) correspond to such merger products (Fig. 2 in Justham et al. 2011), and the abundances (except Ne) are similar to R CrB stars and extreme helium stars (Zhang & Jeffery 2012a). Alternatively, the star could have been formed from a binary composed of two helium white dwarfs via a composite merger, which combines a fast merger featuring a hot corona and slow accretion of the disk (Zhang & Jeffery 2012b). The detected chemical composition may also result from a delayed helium core flash (Brown et al. 2001; Lanz et al. 2004).
Notes. X-ray luminosities Lx given in erg s−1 are upper limits from La Palombara et al. (2014). Distances were determined from Gaia DR3 data (Gaia Collaboration 2016, 2018, 2023). Solar abundances log ε⊙ were taken from Asplund et al. (2009). They were rescaled assuming that all hydrogen was converted into helium. The abundances in parentheses give the value of [X] defined by Jeffery et al. (2011). Blank items denote values that were not determined. The radial velocities were derived from the UVES spectrum. Mass-loss rates (introduced in Sect. 4) are given in M⊙ yr−1 and terminal and radial velocities in km s−1. The abundance of Ne in CD–51 11879 is a mean value determined from abundances of heavy elements (see Sect. 6.2).
 |
Fig. 1 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and UVES spectra (black line) of CD–46 8926 in the visual region. We plot the normalized spectrum as a function of wavelength. |
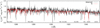 |
Fig. 2 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and IUE spectra (black line) of CD–46 8926 in the UV region. |
Derived parameters of studied stars.
5.2 Prediction of wind parameters
The stellar wind modeling with the determined parameters and abundances predicted a wind mass-loss rate of 2.5 × 10−9 M⊙ yr−1 (Table 3). This value is slightly lower than what was predicted by Krtička et al. (2016) due to a smaller stellar radius. As a result of the reduced radius, the X-ray luminosity 4.1 × 1030 erg s−1 expected for the derived value of bolomet-ric luminosity (Fig. 4) is close to the observational upper limit of X-ray luminosity 3.8 × 1030 erg s−1 (La Palombara et al. 2014; Fig. 4). Therefore, with improved stellar parameters and distance, the models agree much better with X-ray observations.
The mass-loss rate is not strongly affected by the relative abundance of hydrogen and helium (Table 3). These elements do not significantly contribute to the radiative force, and consequently, they influence the mass-loss rate only indirectly, for example, by a change in the number density of free electrons or by modification of radiative flux. In our case, a higher helium abundance leads to a slightly stronger emergent flux at the flux maximum at about 6 × 1015 s−1 and at higher frequencies, where many resonance lines are located, therefore leading to a slightly higher radiative force and mass-loss rate. This explains the small difference between Ṁ and ṀH in Table 3. The effect is opposite to that found by Sander et al. (2023) in Wolf-Rayet stars. These stars have large Eddington factors, and therefore, replacing hydrogen by helium leads to weaker radiative force due to free electrons and weaker winds.
The difference between the mass-loss rate Ṁ predicted for the chemical composition of CD–46 8926 and the solar chemical composition Ṁ⊙ is caused by the change in the abundance of individual elements, particularly iron. On average, the abundance of heavy elements was reduced with respect to the solar value by log ε − log ε⊙ = −0.2. This abundance reduction can reproduce the decreased mass-loss rate with the help of Eq. (1) of Krtička et al. (2016). But the spectral analysis determined the abundances of only a few of the elements that drive the wind because one-third of the line force comes from Na and Mg, whose abundances were not estimated within our analysis. Modified abundances can also explain lower terminal velocities because some elements that accelerate wind at large speeds, such as O, Ne, and Fe, have lower abundances.
When comparing the predicted wind N V 1239 Å and 1243 Å line profiles with that observed with the IUE satellite (Fig. 5), the line profiles predicted for CD–46 8926 chemical composition are weaker and agree better with observed spectra than the line profiles predicted for solar chemical composition. The relative weakness of nitrogen line profiles is caused by stronger far-UV ionizing radiation coming from helium-dominated atmospheres that depopulate N V ion in favor of N VI. However, the predicted O VI 1032 Å and 1038 Å lines show strong P Cygni line profiles, while these lines are nearly absent in the FUSE spectra. This could be an indication of lower oxygen abundance than has been estimated from spectroscopy or the influence of wind structure on emergent line profiles (Sundqvist et al. 2010; Šurlan et al. 2012).
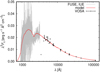 |
Fig. 3 Comparison of the predicted spectral energy distribution of CD–46 8926 from the TLUSTY code smoothed by a Gaussian filter with a dispersion of 50 Å (solid red line) and observational data derived using VOSA utility (Bayo et al. 2008) and from FUSE and IUE observations. |
 |
Fig. 4 Relation between observed X-ray luminosity and the bolometric luminosity for subdwarfs (adopted from Krtička et al. 2016). Blue symbols denote individual subdwarfs with X-ray detections (circles) and upper limits to X-ray luminosities (triangles). Filled symbols refer to subdwarfs in binaries, while empty symbols correspond to single stars. Black arrows with stellar identifications indicate the shift of the stellar parameters with respect to previous determinations. The solid red line extrapolates the mean observed relation for O stars (Nazé 2009). |
 |
Fig. 5 Comparison of observed IUE spectrum of CD–46 8926 (solid black line) with emergent flux from wind models METUJE in the region of the N V doublet. We plot the emergent fluxes for mass-loss rate predicted for solar chemical composition (dashed red line) and mass-loss rate predicted for determined abundances (solid red line). |
6 CD–51 11879
The hot helium subdwarf CD–51 11879 (LSE 263, ALS 19042) was discovered by Drilling (1983). It was soon recognized that it has a very high effective temperature (Schönberner & Drilling 1984), which was further supported by optical NLTE spectral analysis of Husfeld et al. (1989). The star was studied within the low-resolution optical survey of Németh et al. (2012). Neither the search for X-ray emission nor a magnetic field were successful, with a respective upper limit of 3.6 × 1030 erg s−1 (La Palombara et al. 2014, corrected for Gaia distance) and a mean longitudinal magnetic field strength of 〈Bz〉 = 360 ± 250 G (Bagnulo et al. 2015). However, the observational upper limit of the X-ray luminosity is lower than the estimate of 5.9 × 1030 erg s−1 based on the scaling of Nazé (2009).
Wavelengths of the strongest lines (in Å) used for abundance determination in CD–51 11879.
6.1 Determination of stellar parameters
We determined the effective temperature and surface gravity from the fit of optical helium lines. Notably, the lines of He I 4471 Å and 4713 Å turned out to be relatively sensitive temperature indicators. To determine the abundances, we supplemented optical spectra with UV spectra derived by the FUSE and IUE satellites. The list of lines used for the abundance analysis of CD–51 11879 is given in Table 4. The final derived parameters listed in Table 3 agree with the values determined by Husfeld et al. (1989).
A comparison of observed and fitted spectra in the optical region (Fig. 6) showed that while some lines are nicely fitted, the other lines slightly disagree. This is perhaps connected with several lines that appear in the observed UV spectrum but are absent in the predicted spectrum (Fig. 7). Enhanced cooling in the outer parts of the atmosphere could also lead to the disappearance of some emission lines that appear in the synthetic spectrum but are missing in the observed spectrum (Fig. 6). Moreover, some lines originate from levels approximated by superlevels in the model atom. This could lead to an incorrect estimate of level populations.
Gaia DR3 data (Gaia Collaboration 2016, 2018, 2021) provide a distance of 719 ± 60 pc. Our fit of the observed spectral energy distribution (Fig. 8) gave a stellar radius of R = 0.29 R⊙ ± 0.05 R⊙ and an interstellar reddening of E(B − V) = 0.06 mag, which is somewhat lower than estimated by Schönberner & Drilling (1984). Together with the spectroscopic surface gravity, the radius gives a mass of 0.52 ± 0.31 M⊙.
The RUWE value of 2.4 from the Gaia data indicates a possible binarity. Indeed, the spectral energy distribution in Fig. 8 reveals the presence of a cooler companion. We combined the subdwarf spectral energy distribution with solar-metallicity fluxes with log g = 4 calculated by Allard et al. (2012) and downloaded from the POLLUX database (Palacios et al. 2010). We note that the spectral energy distribution of the cool companion does not significantly depend on a particular value of surface gravity. A model with Teff = 2500 Κ assuming a radius of 2.2 R⊙ provides a reasonable fit of the data (Fig. 8). This could correspond to a young low-mass star. Given the absence of radial velocity variations, the companion might not have affected the evolution of the subdwarf. Moreover, as a result of its low effective temperature, the companion does not contribute to the optical spectrum in Fig. 6.
The star shows a helium-dominated chemical composition with an enhanced abundance of nitrogen and an underabundance of the remaining heavy elements (Table 3). Figure 9 shows a comparison of the chemical composition of CD–51 11879 with the solar chemical composition derived when assuming that all hydrogen was turned into helium. The CD–51 11879 abundances could correspond to the CNO processed material, which was suggested to appear on the surface of a merger product of two helium white dwarfs (Saio & Jeffery 2000). To test this, we plotted the typical CNO cycle abundances (Maeder 2009, Table 25.3) corrected for the mean CD–51 11879 composition determined using elements from Mg to Fe in Fig. 9. The reasonable agreement with observational values that we found supports the CNO cycle origin of the CD–51 11879 abundances.
 |
Fig. 6 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and UVES spectra (black line) of CD–51 11879 in the visual region. We plot the normalized spectrum as a function of wavelength. |
 |
Fig. 7 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and IUE spectra (black line) of CD–51 11879 in the UV region. |
 |
Fig. 8 Same as Fig. 3 but for CD-51 11879 and featuring distributions of hot and cool components (dashed lines) and combined distribution (solid line). |
 |
Fig. 9 Chemical composition of CD–51 11879 relative to the solar abundances from Table 3. We plot the relative abundances as a function of atomic number and compare them to the CNO equilibrium chemical composition. |
6.2 Prediction of wind parameters
The calculation of the wind models revealed that more than half of the acceleration comes from neon, whose abundance was not determined from spectroscopy. To alleviate this problem, we adopted a mean determined abundance (with respect to the solar value) of elements from magnesium to iron as the neon abundance. This value is given in Table 3.
Table 3 shows that the wind parameters predicted using CD–51 11879 abundances and solar abundances do not differ significantly. A large fraction of the acceleration is connected with optically thick lines that remain optically thick even at slightly lower abundances, and therefore, the metallicity does not affect the mass-loss rate significantly. Most of the difference comes from the lower neon abundance. Also in this case Eq. (1) of Krtička et al. (2016) provides a reasonable estimate of the reduction of the mass-loss rate due to decreased abundances. Hydrogen and helium do not significantly contribute to the radiative force. Consequently, the predicted mass-loss rate with the solar mixture of these elements remain nearly unchanged when hydrogen is replaced by helium (Table 3). A similar result was found by Vink & de Koter (2002) for luminous blue variables.
The analysis revealed a slightly lower luminosity of the star than determined previously. As a result, the expected wind X-ray luminosity (1.6 × 1030 erg s−1, Fig. 4) is below the observational upper limit 3.6 × 1030 erg s−1 (La Palombara et al. 2014). Therefore, the improved stellar parameters lead to results that agree with X-ray observations also in the case of this star.
The inspection of emergent spectra showed that the predicted wind line profiles, for instance of O VI 1032 Å and 1038 Å lines, are still too strong when compared with observations. However, the reduced mass-loss rate improves the agreement between the observed and the predicted spectra in the region of the 1371 Å O V line.
 |
Fig. 10 Parameters of helium overabundant (blue plus symbols) and helium underabundant (black crosses) subdwarſs (Geier 2020) in comparison with the domain where no wind exists (red area, Krtička et al. 2016). Overplotted are the evolutionary tracks of Dorman et al. (1993). |
7 Subdwarfs overabundant in helium in Teff versus log g diagrams
The inclusion of the two additional objects from Krtička et al. (2019) showed that while subdwarfs overabundant in helium have winds, subdwarfs with underabundant helium do not show winds. This indicates that the existence of the stellar wind is a necessary condition for appearance of helium overabundance. To further test this conclusion, we selected subdwarfs with known effective temperatures, surface gravities, and helium abundances and with estimated uncertainties from the catalog of Geier (2020). We plotted these parameters in the Teff versus log g (Kiel) diagram (Fig. 10) in comparison with the region where no wind is predicted (Krtička et al. 2016). We distinguished subdwarfs that have a higher abundance of helium than the Sun (Asplund et al. 2009) from helium underabundant subdwarfs.
The comparison in Fig. 10 shows that while helium under-abundant subdwarfs appear on both sides of the wind limit, helium overabundant subdwarfs mostly avoid the region where no wind is predicted. This difference can be explained in terms of radiative diffusion (Michaud et al. 2011; Alecian & Stift 2021). In hydrodynamically quiet atmospheres without winds, helium sinks due to gravitational settling. This deprives the surface layers of helium and exposes hydrogen and radiatively supported heavy elements in the atmosphere. In contrast, strong winds avoid gravitational settling and leave helium in the atmosphere (Vauclair 1975; Vauclair et al. 1991).
The appearance of a small group of helium overabundant subdwarfs in the region where the wind is not expected could be connected with the influence of other parameters, such as mass or metallicity, on the wind limit. Moreover, some stars could have been deprived of all hydrogen during their previous evolution.
8 Conclusions
We used our own optical spectroscopy together with archival UV spectroscopy and photometry to determine the stellar parameters and surface abundances of two helium dominated subdwarfs CD–16 8926 and CD–51 11879. Both subdwarfs have an effective temperature higher than 60 kK and an overabundance of either carbon or nitrogen. There are indications that both stars are binaries.
We computed wind models of both stars from observational stellar parameters. Both stars are predicted to have relatively weak line-driven wind with mass-loss rates on the order of 10−10−10−9 M⊙ yr−1. The deviation of the chemical composition from the solar values does not lead to significant changes in the wind mass-loss rate, not even in the case of helium. These variations in mass-loss rates induced by modified abundances can be reasonably well estimated using relations from the literature featuring a mean metallicity. Modified abundances also lead to lower wind terminal velocities. Wind models with more realistic abundances predict spectra that better agree with observations. Moreover, a downward revision of the luminosity shifts the estimated X-ray luminosity below the observed upper limits. To a considerable extent, this was also achieved thanks to a revision of the observational upper limits based on new Gaia distances. As a result, the updated stellar parameters give a predicted X-ray luminosity that is not in conflict with observations.
Although the chemical compositions of these two stars differ significantly despite their very similar effective temperatures and surface gravities, it is unlikely that the surface composition is affected by diffusion (as is typical for cooler subdwarfs, Michaud et al. 2011). Moreover, the wind seen in both stars would likely wipe out any peculiarities connected with diffusion. Consequently, the abundances most likely reflect slightly different levels of internal mixing or the distinct evolutionary paths of each star.
Acknowledgements
We thank Dr. Sandro Mereghetti for valuable comments on the manuscript and Prof. V. Štefl for the discussion of the cool companion. Computational resources were provided by the e-INFRA CZ project (ID:90254), supported by the Ministry of Education, Youth and Sports of the Czech Republic. P.N. acknowledges support from the Grant Agency of the Czech Republic (GAČR 22-34467S). The Astronomical Institute Ondřejov is supported by the project RVO:67985815. This publication makes use of VOSA, developed under the Spanish Virtual Observatory project supported from the Spanish MINECO through grant AyA2017-84089.
References
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
- Alecian, G., & Stift, M. J. 2021, MNRAS, 504, 1370 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, Philos. Trans. Roy. Soc. Lond. Ser. A, 370, 2765 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Fossati, L., Landstreet, J. D., & Izzo, C. 2015, A&A, 583, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Björklund, R., Sundqvist, J. O., Singh, S. M., Puls, J., & Najarro, F. 2023, A&A, 676, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Božic, H., Harmanec, P., Horn, J., et al. 1995, A&A, 304, 235 [Google Scholar]
- Brands, S. A., de Koter, A., Bestenlehner, J. M., et al. 2022, A&A, 663, A36 [Google Scholar]
- Brown, T. M., Sweigart, A. V., Lanz, T., Landsman, W. B., & Hubeny, I. 2001, ApJ, 562, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Byrne, C. M., & Jeffery, C. S. 2018, MNRAS, 481, 3810 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [Google Scholar]
- Chambers, K. C., Magnier, E. A., Metcalfe, N., et al. 2016, arXiv e-prints [arXiv: 1612.05560] [Google Scholar]
- Cross, N. J. G., Collins, R. S., Mann, R. G., et al. 2012, A&A, 548, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Dorsch, M., Latour, M., & Heber, U. 2019, A&A, 630, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drilling, J. S. 1983, ApJ, 270, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Drilling, J. S., & Heber, U. 1986, in IAU Colloq. 87: Hydrogen Deficient Stars and Related Objects, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Epchtein, N., Deul, E., Derriere, S., et al. 1999, A&A, 349, 236 [NASA ADS] [Google Scholar]
- Evans, D. W., Irwin, M. J., & Helmer, L. 2002, A&A, 395, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Gabler, R., Gabler, A., Kudritzki, R. P., Puls, J., & Pauldrach, A. 1989, A&A, 226, 162 [NASA ADS] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S. 2020, A&A, 635, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., Dorsch, M., Pelisoli, I., et al. 2022, A&A, 661, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gormaz-Matamala, A. C., Curé, M., Cidale, L. S., & Venero, R. O. J. 2019, ApJ, 873, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, J.-J. 2018, ApJ, 866, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, P. D., & Jeffery, C. S. 2016, MNRAS, 463, 2756 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [Google Scholar]
- Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [Google Scholar]
- Heber, U. 2016, PASP, 128, 082001 [Google Scholar]
- Hirsch, H. A. 2009, PhD thesis, Friedrich Alexander University of Erlangen-Nuremberg, Germany [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, A27 [NASA ADS] [Google Scholar]
- Hubeny, I. 1988, Comput. Phys. Commun., 52, 103 [Google Scholar]
- Hubeny, I., & Lanz, T. 2011, Astrophysics Source Code Library [record ascl:1109.022] [Google Scholar]
- Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Husfeld, D., Butler, K., Heber, U., & Drilling, J. S. 1989, A&A, 222, 150 [NASA ADS] [Google Scholar]
- Jeffery, C. S., Karakas, A. I., & Saio, H. 2011, MNRAS, 414, 3599 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Podsiadlowski, P., & Han, Z. 2011, MNRAS, 410, 984 [CrossRef] [Google Scholar]
- Klement, R., Schaefer, G. H., Gies, D. R., et al. 2022, ApJ, 926, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Koubský, P., Kotková, L., Kraus, M., et al. 2014, A&A, 567, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramer, M., Schneider, F. R. N., Ohlmann, S. T., et al. 2020, A&A, 642, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2015, NIST Atomic Spectra Database, https://www.nist.gov/pml/atomic-spectra-database [Google Scholar]
- Krticka, J., & Kubát, J. 2006, A&A, 446, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., & Kubát, J. 2009, A&A, 493, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., & Štefl, V. 1999, A&AS, 138, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., Kubát, J., & Krticková, I. 2016, A&A, 593, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., Janík, J., Krticková, I., et al. 2019, A&A, 631, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krticka, J., Kubát, J., & Krticková, I. 2020, A&A, 635, A173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., Brown, T. M., Sweigart, A. V., Hubeny, I., & Landsman, W. B. 2004, ApJ, 602, 342 [CrossRef] [Google Scholar]
- La Palombara, N., Esposito, P., Mereghetti, S., & Tiengo, A. 2014, A&A, 566, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Latour, M., Chayer, P., Green, E. M., Irrgang, A., & Fontaine, G. 2018, A&A, 609, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [Google Scholar]
- Luo, Y., Németh, P., Deng, L., & Han, Z. 2019, ApJ, 881, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars, (Astronomy & Astrophysics Librairy- Springer) [Google Scholar]
- Marcolino, W. L. F., Bouret, J. C., Rocha-Pinto, H. J., Bernini-Peron, M., & Vink, J. S. 2022, MNRAS, 511, 5104 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., & La Palombara, N. 2016, Adv. Space Res., 58, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Michaud, G., Richer, J., & Richard, O. 2011, A&A, 529, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Battich, T., Córsico, A. H., Althaus, L. G., & Wachlin, F. C. 2022, MNRAS, 511, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Naslim, N., Jeffery, C. S., & Woolf, V. M. 2019, MNRAS, 491, 874 [NASA ADS] [Google Scholar]
- Nazé, Y. 2009, A&A, 506, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Németh, P., Kawka, A., & Vennes, S. 2012, MNRAS, 427, 2180 [Google Scholar]
- Owocki, S. P., Sundqvist, J. O., Cohen, D. H., & Gayley, K. G. 2013, MNRAS, 429, 3379 [NASA ADS] [CrossRef] [Google Scholar]
- Palacios, A., Gebran, M., Josselin, E., et al. 2010, A&A, 516, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E. 2015, A&A, 580, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelisoli, I., Vos, J., Geier, S., Schaffenroth, V., & Baran, A. S. 2020, A&A, 642, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, G. J., Gies, D. R., Grundstrom, E. D., & McSwain, M. V. 2008, ApJ, 686, 1280 [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [Google Scholar]
- Pols, O. R., Cote, J., Waters, L. B. F. M., & Heise, J. 1991, A&A, 241, 419 [NASA ADS] [Google Scholar]
- Puls, J. 2008, in The Metal-Rich Universe, ed. G. Israelian, & G. Meynet, 295 [CrossRef] [Google Scholar]
- Saio, H., & Jeffery, C. S. 2000, MNRAS, 313, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Sander, A. A. C., Hamann, W.-R., Todt, H., Hainich, R., & Shenar, T. 2017, A&A, 603, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sander, A. A. C., Lefever, R. R., Poniatowski, L. G., et al. 2023, A&A, 670, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindewolf, M., Németh, P., Heber, U., et al. 2018, A&A, 620, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schönberner, D., & Drilling, J. S. 1984, ApJ, 278, 702 [CrossRef] [Google Scholar]
- Seaton, M. J., Zeippen, C. J., Tully, J. A., et al. 1992, Rev. Mex. Astron. Astrofis., 23 [Google Scholar]
- Shao, Y., & Li, X.-D. 2021, ApJ, 908, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Feldmeier, A. 2010, A&A, 510, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Björklund, R., Puls, J., & Najarro, F. 2019, A&A, 632, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Kubát, J., Oskinova, L. M., & Feldmeier, A. 2012, A&A, 541, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unglaub, K., & Bues, I. 2001, A&A, 374, 570 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vauclair, S. 1975, A&A, 45, 233 [NASA ADS] [Google Scholar]
- Vauclair, S., Dolez, N., & Gough, D. O. 1991, A&A, 252, 618 [NASA ADS] [Google Scholar]
- Vink, J. S., & Cassisi, S. 2002, A&A, 392, 553 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., & de Koter, A. 2002, A&A, 393, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., Reindl, N., Geier, S., & Pritzkuleit, M. 2022, MNRAS, 511, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Xiong, H., Chen, X., Podsiadlowski, P., Li, Y., & Han, Z. 2017, A&A, 599, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, X., & Jeffery, C. S. 2012a, MNRAS, 426, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., & Jeffery, C. S. 2012b, MNRAS, 419, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., Hall, P. D., Jeffery, C. S., & Bi, S. 2017, ApJ, 835, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Zverko, J., Žižnovský, J., Mikulášek, Z., & Iliev, I. K. 2007, Contrib. Astron. Observatory Skalnate Pleso, 37, 49 [NASA ADS] [Google Scholar]
Mikulski Archive for Space Telescopes: http://archive.stsci.edu
All Tables
Wavelengths of the strongest lines (in Å) used for abundance determination in CD–46 8926.
Wavelengths of the strongest lines (in Å) used for abundance determination in CD–51 11879.
All Figures
 |
Fig. 1 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and UVES spectra (black line) of CD–46 8926 in the visual region. We plot the normalized spectrum as a function of wavelength. |
| In the text | |
 |
Fig. 2 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and IUE spectra (black line) of CD–46 8926 in the UV region. |
| In the text | |
 |
Fig. 3 Comparison of the predicted spectral energy distribution of CD–46 8926 from the TLUSTY code smoothed by a Gaussian filter with a dispersion of 50 Å (solid red line) and observational data derived using VOSA utility (Bayo et al. 2008) and from FUSE and IUE observations. |
| In the text | |
 |
Fig. 4 Relation between observed X-ray luminosity and the bolometric luminosity for subdwarfs (adopted from Krtička et al. 2016). Blue symbols denote individual subdwarfs with X-ray detections (circles) and upper limits to X-ray luminosities (triangles). Filled symbols refer to subdwarfs in binaries, while empty symbols correspond to single stars. Black arrows with stellar identifications indicate the shift of the stellar parameters with respect to previous determinations. The solid red line extrapolates the mean observed relation for O stars (Nazé 2009). |
| In the text | |
 |
Fig. 5 Comparison of observed IUE spectrum of CD–46 8926 (solid black line) with emergent flux from wind models METUJE in the region of the N V doublet. We plot the emergent fluxes for mass-loss rate predicted for solar chemical composition (dashed red line) and mass-loss rate predicted for determined abundances (solid red line). |
| In the text | |
 |
Fig. 6 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and UVES spectra (black line) of CD–51 11879 in the visual region. We plot the normalized spectrum as a function of wavelength. |
| In the text | |
 |
Fig. 7 Comparison of the best-fit synthetic spectra from SYNSPEC (red line) and IUE spectra (black line) of CD–51 11879 in the UV region. |
| In the text | |
 |
Fig. 8 Same as Fig. 3 but for CD-51 11879 and featuring distributions of hot and cool components (dashed lines) and combined distribution (solid line). |
| In the text | |
 |
Fig. 9 Chemical composition of CD–51 11879 relative to the solar abundances from Table 3. We plot the relative abundances as a function of atomic number and compare them to the CNO equilibrium chemical composition. |
| In the text | |
 |
Fig. 10 Parameters of helium overabundant (blue plus symbols) and helium underabundant (black crosses) subdwarſs (Geier 2020) in comparison with the domain where no wind exists (red area, Krtička et al. 2016). Overplotted are the evolutionary tracks of Dorman et al. (1993). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


