| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347898 | |
| Published online | 06 March 2024 | |
Dynamical study of Geminid formation assuming a rotational instability scenario
1
Department of Physics and Astronomy, Seoul National University,
1 Gwanak-ro, Gwanak-gu,
Seoul
08826,
Republic of Korea
2
SNU Astronomy Research Center, Department of Physics and Astronomy, Seoul National University,
1 Gwanak-ro, Gwanak-gu,
Seoul
08826,
Republic of Korea
e-mail: hangbin9@snu.ac.kr; ishiguro@snu.ac.kr
Received:
7
September
2023
Accepted:
26
December
2023
Context. Various ideas have been proposed to explain the formation of the Geminid meteoroid stream from the asteroid (3200) Phaethon. However, little has been studied regarding whether the Geminid formation could be the result of mass ejection via rotational instability of this asteroid.
Aims. In this work, we present the first dynamical study of the Geminid formation taking into account low-velocity mass ejection caused by Phaethon’s rotational instability.
Methods. We conducted numerical simulations for 1-mm and 1-cm particles ejected in a wide range of ejection epochs (103–105 yr ago). We computed the minimum orbital intersecting distance (MOID) of the dust particles as the realistic condition, that is, the Earth’s radius and the Earth–Moon distance to be observed as the Geminid meteoroid stream.
Results. We found that the low-velocity ejection model produced the Geminid-like meteoroid stream when the dust particles were ejected more than ~2000 yr ago. In this case, close encounters with terrestrial planets would transport some dust particles from the Phaethon orbit (the current MOID is as large as ~460 Earth radii) to the Earth-intersecting orbits. The optimal ejection epoch and the estimated mass were 18 000 yr ago and ~1010–1014 g (<0.1% of the Phaethon mass).
Conclusions. Our results suggest that the JAXA DESTINY+ mission has the potential to find evidence of recent rotational instability recorded on the surface of Phaethon.
Key words: radiation: dynamics / interplanetary medium / meteorites, meteors, meteoroids / zodiacal dust / minor planets, asteroids: individual: (3200) Phaethon
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The interplanetary space of the Solar System is populated by interplanetary dust particles (IDPs). Despite being the smallest constituents, these particles are important subjects for investigating the evolution of the Solar System’s small bodies. Although a significant fraction of these dust particles are linked to cometary origins (Nesvorný et al. 2010), the question remains open regarding the source and evolution of other dust particles that are unseen due to bias and observational limitations (Lasue et al. 2020).
A near-Earth asteroid, (3200) Phaethon, is the target asteroid of JAXA’s DESTINY+ mission (Arai et al. 2018). It is an interesting specimen for several reasons. Phaethon has a highly eccentric orbit (e = 0.89) and a small perihelion distance (q = 0.14 au). Although near-Earth object population models predict that more asteroids should share similar orbital traits, the lack of them raises the possibility that additional mechanisms have degraded objects that get too close to the Sun. It is therefore important to investigate the Geminid meteor stream, which is thought to be fragments of Phaethon and could contain clues about the nature of the aforementioned degrading mechanism. Ever since the connection between Phaethon and the Geminids was made (Hughes 1983; Whipple 1983), there has been extensive research on how Phaethon produced this dust stream. Jewitt & Li (2010), Li & Jewitt (2013), Jewitt et al. (2013), Hui & Li (2017) observed dust activity on Phaethon near its perihelion, but they all commonly found the particles to be of a micron-scale size, and the dust production rate was deemed too low to fuel the Geminid stream. Moreover, recent studies suggest that this present-day activity is predominantly sodium volatilization, while dust production is minimal (Masiero et al. 2021; Zhang et al. 2023). In comparison, observations of the Geminid shower revealed the presence of millimeter- and centimeter-sized dust particles (Borovička et al. 2010; Blaauw 2017).
So far, it is still a mystery as to how Phaethon produced a dust stream whose mass could be comparable to Phaethon itself (Ryabova 2017) and how its present-day activity is related to the birth of the Geminids. Several dust ejection mechanisms have been proposed as the cause of the Geminids, with the earliest one being comet-like ice sublimation (Gustafson 1989). However, thermal modeling has suggested that there would not be enough ice in Phaethon for such activity to occur (Jewitt & Li 2010; Jewitt 2012). On the contrary, Yu et al. (2019) found that Phaethon could have retained a small amount of ice in its core. Even in this case, the resulting sublimation would be too weak to cause a spontaneous, large-scale ejection event. Asteroidal dust ejection by thermal fracture is also a viable scenario based on its possible contribution to the particle ejection event on the asteroid (101955) Bennu observed by OSIRIS-REx (Origins, Spectral Interpretation, Resource Identification, and Security–Regolith Explorer; Lauretta et al. 2019; Molaro et al. 2020), and it has been suggested as the ejection mechanism for Phaethon by Jewitt & Li (2010) and Jewitt (2012). However, questions remain as to whether thermal fracture can cause massive mass ejection and why such a phenomenon has not been observed in modern times. The feasibility of other mechanisms, such as electrostatic lofting (Kimura et al. 2022) and thermal radiation pressure (Bach & Ishiguro 2021), have also been proposed for small-sized dust ejection. However, none are suitable explanations for the larger-sized dust populating the Geminids. Lastly, Nakano & Hirabayashi (2020) hypothesized that YORP (Yarkovsky–O’Keefe–Radzievskii-Paddack effect)-induced rotational instability may have formed the Geminids. Indeed, in recent years asteroid activity by rotational instability has been discovered in cases such as (6478) Gault (Luu et al. 2021) and 311P/Gibbs (Jewitt et al. 2021). A recent observation has indicated that Phaethon’s rotation accelerates by 2.1 × 10−6 º day−1 (Marshall et al. 2022). If a similar acceleration happened in the past, rotational instability could be the key to the formation of the Geminids. Nonetheless, the cause of the Geminid formation and its relation to the current activity on Phaethon is still under debate and not fully understood. To investigate Phaethon and its dust environment in detail, the mission Demonstration and Experiment of Space Technology for INterplanetary voYage, Phaethon fLyby and dUst Science Phaethon fLyby with reUSable probe (DESTINY+) is planned to perform a flyby mission (Arai et al. 2018) that will provide us with more observational constraints.
In addition to these observational studies of Phaethon, theoretical approaches have been conducted to trace back the history of the Geminid stream. The initial dust ejection velocities, the most critical assumption for dust evolution, are based on the above-mentioned dust ejection models. In particular, Whipple’s formula (Whipple 1951) is the most widely applied to derive the ejection velocity by assuming a comet-like mechanism. This model yields up to an ejection velocity of several hundreds of meters per second (Fox et al. 1982, 1983; Hunt et al. 1986; Jones & Hawkes 1986; Williams & Wu 1993; Ryabova 2007, 2008, 2013, 2016, 2017). Although not an example of Whipple’s formula, despite the similar velocity regime, it is worth mentioning that Jakubík & Neslušan (2015) simulated sequential ejections of particles from 103 to 105 yr with 1/1000 of the orbital velocity at perihelion as the initial velocity (~200 m s−1). Thermal fatigue was addressed by Ryabova (2012, 2018) by using the upper limit ejection velocity of 30 m s−1 (Jewitt & Li 2010), but neither could successfully re-create the Geminid stream. In the case of lower ejection velocities, Ye et al. (2018) tested the gravitational escape speed as the initial velocity in order to investigate the possibility of whether Phaethon fragments released within three centuries can come into a close encounter with Earth. However, they did not consider the Geminid formation with a realistic criterion, as they addressed whether large fragments would be observable via telescopic observations by applying an enormously large criterion of ≤0.02 au from Earth (about ten times further than the Earth-Moon distance). Meanwhile, Ryabova (2012) used a wide range of ejection velocities extending from an escape velocity to 100 ms−1. However, the author found no particles reaching less than 0.01 au from Earth (~230 Earth radii). Similarly, Cukier & Szalay (2023) explored a velocity range from zero to scales of up to several kilometers per second, assuming that the ejection happened 2000 yr ago. Although this study is close to the timescale and velocity regime of our interest, it was done with a relatively small number of particles, leading to the use of a loose distance limit of 0.03 au to determine the particles’ interaction with Earth. Despite numerous dynamical studies on the Geminid stream, there is no research on the Geminid formation based on the assumption that Phaethon’s rotational instability generated the Geminid meteoroid stream.
Motivated by a more realistic dust ejection study in Nakano & Hirabayashi (2020) and other associated observations of top-shape asteroids, such as (162173) Ryugu and (101955) Bennu, we conducted a dynamical simulation where millimeter- and centimeter-sized meteoroid particles are ejected from Phaethon with low velocity via rotational instability. We emphasize that our dynamical study is more rigorous and comprehensive than many previous studies in setting a strict condition for the minimum orbital intersecting distance (MOID) and investigating a wide range of ejection epochs (103 to 105 yr). Based on our numerical results, we discuss the detailed formation mechanism of the Geminids and describe the expectation of the JAXA DESTINY+ mission.
2 Method
We conducted our dynamical simulations using the Mercury6 N-body integrator (Chambers 1999) with the following additional equations:
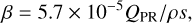 (1)
(1)
![${F_{{\rm{rad}}}} = {F_{\rm{g}}}\beta \left\{ {\left[ {1 - 2(1 + \xi ){{{\bf{v}} \cdot {\bf{r}}} \over {cr}}} \right]\hat r - (1 + \xi ){{\bf{v}} \over c}} \right\},$](/articles/aa/full_html/2024/03/aa47898-23/aa47898-23-eq2.png) (2)
and
(2)
and
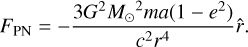 (3)
(3)
Equation (1) defines β, the ratio of radiation pressure force Frad to the Newtonian gravitational force Fg. In Eq. (1), QPR, ρ, and s denote the radiation pressure coefficient, particle mass density, and radius, respectively (Burns et al. 1979). Equation (2) characterizes the radiation pressure and Poynting–Robertson (PR) drag exerted on a particle at the heliocentric position r and velocity v, while c is the light speed (Burns et al. 1979; Liou et al. 1995; Klačka et al. 2012). For the solar wind coefficient ξ, we assumed 0.3 (Gustafson 1994). Equation (3) is the post-Newtonian correction formula (Thornton & Marion 2004; Stewart 2005), where a, e, and m denote the semi-major axis, eccentricity, and mass of the Solar System object. We used Mercury6 for two purposes: (i) to find the position and velocity of Phaethon in the past when dust particles were ejected and (ii) to trace the orbital evolution of ejected dust particles until the present day. We chose the Bulirsch-Stoer algorithm (Stoer & Bulirsch 1980) with an initial time step of one day for all simulations of our study.
Backward integration of Phaethon is essential in order to obtain accurate orbital positions and velocities of the dust source at the dust ejection epoch. Mercury6 offers a built-in backward integration feature. The feature works in two steps: backward integration to the user-defined initial epoch and subsequent forward integration to the final epoch, during which the particle dynamics are recorded. In other words, Mercury6 performs a duplicate integration of the same path backward and forward for the sake of output recording. In the case of Phaethon, which is subject to gravitational perturbation of terrestrial planets, we find that this process amplifies the chaotic nature of Phaethon’s orbital history. Therefore, we chose not to use this feature for this process. Instead, the backward integration was realized by forward integrating with reversed velocities.
The initial positions of the eight planets and Phaethon were obtained based on the JPL DE43l ephemerides at JD 2459000.5, provided by JPL Horizons1. Using the osculating orbital elements (see Tables 1 and A.1), we created 100 clones from the multivariate normal distribution generated by the covariance matrix of the orbital elements. We integrated the dust trajectories for about 105 yr with an output interval of one day and created an “archive” of the orbital evolution of Phaethon and its clones from which we could extract the orbital position and velocity of Phaethon at any given day within the past 105 yr.
The age of the Geminids has been estimated by various studies with varying methods, such as backward integration of meteoroids (Gustafson 1989), a spin-up timescale to observed flickering of fireballs (Beech 2002), and analysis of meteoroid orbital separation (Ryabova 1999). Most of these works indicate that the Geminid age is on the order of 103 yr. Therefore, we selected ejection epochs between ~103 and ~104 yr ago with 103-yr intervals. Specifically, we started with the ejection epoch at about 2000 yr ago, JD 1740898.5 (April 25, 54), when Phaethon’s perihelion distance was smallest. We then selected eight more epochs in the past with an interval of 365 000 days. For a more thorough investigation of the ~104-yr-old regime, we also conducted additional simulations for ejection epochs of approximately 15, 18, 20, 25, 30, and 100000 yr ago. Again, we used the interval of 365 000 days starting from JD 1740898.5 when selecting the ejection epochs. We only relied on the ejection epoch as our initial setting, resulting in the asteroid’s initial position in the orbit effectively being random rather than fixed at perihelion or aphelion.
The forward integration from the ejection epoch to the present day requires the β value and the velocity of the particles and the initial position of the dust source. We set the β value of the dust particles in Eq. (1), assuming that Qpr is unity and mass density is 2.9 g cm−3. We chose particle radii of 1 mm and 1 cm.
The ejection of a particle can be described by its position and velocity vector (r, θ, ϕ, vr, vθ, vϕ), each corresponding to the radial distance, polar angle, and azimuthal angle, respectively, in the Phaethon-centric frame. Ejection velocity by rotational instability is usually assumed to be near the escape speed of the parent body, but depending on its cohesive strength, the actual ejection velocity can be higher (Hirabayashi et al. 2014). Notably, P/2013 R3 is thought to have been broken up by rotational instability, and its fragments have the velocity dispersion of 0.33 ± 0.03 ms−1, which is more than 50% higher than the assumed escape speed, ~0.2 ms−1, of the progenitor (Jewitt et al. 2017). Taking this into account, we assumed vr = 1 m s−1 and took r as the Hill radius of Phaethon at perihelion:
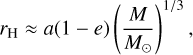 (4)
(4)
where Phaethon’s mass M = 1.16 × 1017 g is calculated assuming a spherical body with its mass density and diameter reported in Hanuš et al. (2018). With this initial setting, we assumed that the particle had an initial surface velocity that was about 1.4 times higher than the escape velocity but had lost most of its kinetic energy when the particle reached the Hill radius (see Fig. 1).
Focusing on rotational instability as the cause of the dust ejection, we further assumed that the particles are ejected in the lower latitude region of Phaethon and follow its rotational direction. As such, we binned the remaining vector components (θ, ϕ, vθ, vϕ) with 20 bins in [−π/18,π/18], [0,2π], [−π/18,π/18], [0,π/2] respectively, resulting in 320 000 particles per simulation. The vectors were then rotated to match Phaethon’s current rotational axis (Hanuš et al. 2016). This initialization process is visualized in Fig. 1. We then combined the position and velocity vectors of the dust particles with the orbital vectors of Phaethon at the ejection epoch. All particles are considered massless in the simulation and are therefore subject to external gravity and radiation forces, but they do not exert gravity itself. The particles were then forward integrated until the present day (JD 2459000.5) along with the eight planets and Phaethon (to take into account the initial gravitational influence from the parent body) with an output interval of 500 days.
Orbital elements of Phaethon (JD 2459000.5).
 |
Fig. 1 Schematic illustration of dust ejection in our model. In the figure, the gray sphere corresponds to the Hill radius of Phaethon (r = 78 km from Phaethon’s center of mass at present-day orbit). The dust particles have small outward terminal velocities (blue arrows) on the Hill sphere (vr = 1 m s−1). |
 |
Fig. 2 Orbital history of 100 Phaethon clones from backward integration. The colored lines are clones we used for the dust sources. |
3 Results
In this section, we first scrutinize the simulation results under the MOID condition. After this, we then compare the results with the Geminid observations in terms of solar longitude.
3.1 Stream location based on minimum orbital intersecting distance
Figure 2 shows the orbital history of Phaethon from backward integration. It is important to note that the deviation between the orbital elements of nominal Phaethon and its clones noticeably increased ~4000 yr ago, triggered by planetary perturbations (Hanuš et al. 2016). To eliminate this uncertainty in Phaethon’s orbital history, we selected two “extreme” clones that correspond to the maximum and minimum semi-major axis after the first 10 000 yr of backward integration. We then randomly chose two additional clones. The initial orbital elements of these clones are given in Table A.2, and their backward integration results are also marked with colored lines in Fig. 2.
To determine the existence of particles that interact with Earth, we employed the minimum orbit intersecting distance (MOID). The idea is that each simulation particle represents numerous dust particles sharing the same orbital elements but a random mean anomaly. Therefore, even if the simulation particle does not directly contact Earth, if its MOID is small enough, then there will be a corresponding dust particle in reality that collides with Earth. Similar approaches to identify interactions between Earth and meteors have been used in studies such as Melikyan et al. (2021) and Ryabova (2021). We set two MOID criteria, namely, Earth’s radius (~4.26 × 10−5 au) and the semi-major axis of the lunar orbit (~2.57 × 10−3 au), because the meteor observations have been conducted either from Earth’s surface or the lunar orbit. We calculated the MOΓDs of the particles using the code by Wiźniowski & Rickman (2013). For example, in Fig. 3a, we found particle MOIDs smaller than the lunar orbit and even Earth’s radius, indicating the presence of particles interacting with the Moon and Earth in this case. It is worth noting that the stream’s core locates at ~0.0l au from Earth at its closest encounter distance, implying that Earth is merely grazing the stream. This evidence implies that if a distance condition at a scale of 0.01 au is used, one risks overrepresenting particles from the stream core. In other words, using lenient distance conditions of ≥0.0l au does not accurately represent Geminid meteoroids. In the right column of Fig. 3, we show examples of the MOID distribution of the particles from our dynamical simulation. However, while MOID is a strong indicator of how close the dust approaches Earth, where the dust crosses is also another important condition that should be considered.
Figures 4 and 5 summarize the number of interacting particles from each ejection epoch for 1-mm and 1-cm particles. We found that the number of interacting particles became significantly reduced if the particles were ejected after 4000 yr ago. This can be explained by the fact that Phaethon’s current orbit is far from the Earth, and apart from occasional weak gravitational perturbations of terrestrial planets, there is not enough external force that can transport the particles from Phaethon’s orbit to an Earth-interacting orbit in time. Further back in time, we found Phaethon’s orbital uncertainty increases, resulting in larger variations in the number of interacting particles between the nominal and clone cases. We also point out that the number of 1-mm particles is much smaller than that of 1-cm particles. Nonetheless, for all ejection epochs, our simulation produced Earth-dust interactions from the initial Phaethon ejections in both the nominal and clone cases.
 |
Fig. 3 Examples of the dust simulation result from nominal Phaethon ejection. The ejection epoch is labeled at the top in Julian date format (and its corresponding year is in brackets). The left plots show random samples of particle orbits on the ecliptic plane at the present day (JD 2459000.5). The right plots are the histograms of the MOID of particles to Earth, and the Earth radius and Earth-Moon distance marked by dotted lines. |
 |
Fig. 4 Number of 1-mm particles satisfying the MOID criteria from each ejection epoch with different ranges of ejection epoch (top: 10 000–30 000 yr ago, bottom: 2000–10000 yr ago). Different colors respectively represent the MOID criteria of Earth radius (darker color) and Earth-Moon distance (lighter color). The dotted line shows the mean-averaged values of the number of particles with MOIDs within Earth’s radius from nominal and clone parent bodies. The solid line is the equivalent of the dotted line for the Earth-Moon distance criterion. Simulation results with no particles within the MOID criteria are not present, but they were included when calculating the mean average. |
3.2 Stream location based on solar longitude
Although the MOID criterion is one of the strong indicators of the stream–Earth interaction, it does not necessarily mean that the simulation results exactly reproduce the spatial distribution of the Geminids. For example, Fig. 3b shows a stream from an ejection 100 000 yr ago, and one can visibly note that the stream has shifted considerably from Phaethon’s orbit at present day. Indeed, although a large number of particles in this stream interact with Earth, the intersection is too far off compared to observed Geminid locations. As a result, we can henceforth completely reject the models from 100 000 yr ago. For stream models from other ejection epochs, this intersection discrepancy can be less obvious. Thus, it is essential to introduce an additional criterion to select a suitable Geminid-like model stream.
Most well-observed Geminid showers have their peaks at the solar longitude of ~262º (Rendtel 2004, 2019; Arlt & Rendtel 2006; Zigo et al. 2009). More specifically, Rendtel (2004) reported a maximum activity plateau at 261.5º–262.4º that is consistent for 60 yr of observations. Figure 6 shows the mode solar longitude, in other words, the solar longitude corresponding to the peak activity of 1-cm particles from each model. As mentioned in Sect. 3.1, due to the lack of 1-mm particles relative to 1-cm particles within the MOID criteria, extracting the mode solar longitude from 1-mm particles is statistically unreliable and was thus ignored (we address this issue in Sect. 4.1). We found that several models at ejection epochs of 3000, 18 000, and 20 000 yr ago are marginally in the range of the maximum activity plateau, although most of our simulation results have a systematical offset of ~1º for the solar longitude, as noticed in previous studies (Ryabova 2007, 2016). We discuss these cases in depth in Sect. 4.3.
4 Discussion
4.1 Replenishment of millimeter-sized particles from collisional cascading
As mentioned in Sect. 3.2, the simulation result shows a relative shortage of 1-mm particles within the MOID criteria. Figure 4 indicates that the paucity of 1-mm particles becomes more severe in older epochs. Over a timescale of >104 yr, 1-mm particles deviate significantly from the orbital trend of 1-cm particles and even Phaethon due to a complex interplay of the Poynting-Robertson drag (Burns et al. 1979), Kozai–Lidov mechanism (Lidov 1962; Kozai 1962), and perihelion precession. The Poynting–Robertson drag reduces the semi-major axis and eccentricity of the particles, thereby affecting the gravitational influence of the planets in the three-body relation with the Sun and a test particle as well as the resulting Kozai–Lidov oscillation and perihelion precession. Thus, particles smaller than ~1-mm should be excluded from the Geminid stream.
Our simulation results would be inconsistent with observations because particles as large as 1 mm have been observed as Geminids meteor showers. Such small particles (~1 mm) may have been supplied at a different epoch from the larger particle ejection. However, this hypothesis is unlikely because particles ejected recently (within the past 2000 yr; see Fig. 4) have no dynamical path to reach the near-Earth region due to weak gravitational perturbations by the terrestrial planets.
Another potential solution is that the millimeter-sized particles were produced through the collisional cascading of larger particles. Early calculations such as Tokhtas’ev (1982), Steel & Elford (1986) estimated the lifetime of the Geminids based on the collision probability with interplanetary particles, assuming various zodiacal cloud distribution models, and derived a range of ~105 yr for 1-cm particles. On the other hand, the recent Interplanetary Meteoroid Environment Model 2 (IMEM2, Soja et al. 2019), which is an interplanetary dust cloud model derived from dust ejected by Jupiter-family comets, Halley-type comets, and main-belt asteroids, showed that in the centimeter regime, the collisional lifetime of a dust particle moving along Phaethon’s orbit can range from ~103–105 yr. Meanwhile, the lifetime of millimeter-sized particles does not exceed 103 yr. Therefore, a significant portion of <1-mm particles in the current Geminids was likely produced through the collisional cascading of >1-cm particles in ~104 yr. In this case, we can assume that the more recently created millimeter-sized particles would closely follow the orbits of centimeter-sized particles, and thus, the results from centimeter-sized particles are applicable to the millimeter scale as well. However, it is worth noting that the observational traits of sporadic meteors do not agree with the various dynamical models of the zodiacal cloud, including IMEM2. In order to compensate for this discrepancy, it was found that particles of >0.1 mm should have a longer lifetime than calculated in the dynamical models (Nesvorný et al. 2011; Pokorný et al. 2014). As a result, it is not uncommon to use an artificial factor, denoted as Fcoll in Pokorný et al. (2014) and Soja et al. (2019), to increase the lifetime of larger particles in the zodiacal cloud by one order of magnitude or more. Then, one might question if the above-mentioned lifetimes of millimeter- and centimeter-sized Geminid particles are greatly underestimated and thus whether their collisional effects are negligible. However, since Phaethon, a near-Earth object, is not part of the dust source considered in IMEM2, we suggest that the Geminids are not subject to the artificial factor, which only accounts for the collisions between the dust cloud inhabitants.
 |
Fig. 6 Mode solar longitude of 1-cm particles within the lunar distance MOID criterion. If there was more than one maximum peak, we registered the mean solar longitude of the peaks as the corresponding data point. The blue line is the mean of the data points. The shaded area indicates the maximum activity plateau (261.5–262.4°) reported by Rendtel (2004). |
4.2 Estimate of the Geminid stream mass
Although we have demonstrated that particles ejected with low velocity can form a meteoroid stream, it is important to investigate the validity of the number of Earth-interacting particles. This analysis makes two assumptions: (1) the interacting particles represent the Geminid mass influx on Earth and (2) the stream comprises particles originating from the ejection epoch under consideration. Based on these assumptions, we estimated the total mass of the stream and compared the mass with known estimates.
Our mass estimation process is as follows. In general, the mass distribution of a dust cloud can be given by
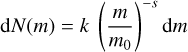 (5)
(5)
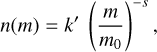 (6)
(6)
where N(m) is the cumulative mass distribution of the infalling Geminids with mass larger than m. We converted this to n(m), which is the number of dust particles with mass m. We note that N(m) and n(m) do not characterize the entire Geminid stream but only a portion that interacts with the Earth’s orbit. The terms k and k′ are constants that characterize the stream mass for reference mass m0, which we arbitrarily chose to be 1 g.
Because the dust population in our simulation is not continuous in mass, we modified Eq. (6) as shown:
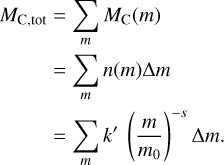 (7)
(7)
m was derived by assuming that the dust particles are spherical particles of 2.9 g cm−3 with radii of 0.1 mm, 1 mm, 1 cm, and 10 cm, which roughly corresponds to the mass range used in Blaauw (2017) to estimate MC,tot. The term Δm represents logarithmically equally spaced intervals centered around 0.1 mm, 1 mm, 1 cm, and 10 cm. The differential mass distribution power index from the meteor and lunar impact monitoring was reported to be s = 1.68 ± 0.04, while the observed mass influx was MC,tot 1.5 × 108 g in Blaauw (2017). However, our simulation indicates a total stream width, or shower duration, of only three days, which is much shorter than the 14-day activity profile derived in Blaauw (2017). Therefore, we only considered the activity of three days around the peak. We calculated that this portion of the profile represented 0.49 of the total area, resulting in MC,tot = 7.35 × 107 g. Finally, we then calculated the constant k′ and consequently computed the observed mass influx for particles of mass m, MC(m). We note that the power index s used in this calculation characterizes the dust population that falls into Earth but not necessarily the entire Geminid stream. Nonetheless, we point out that the use of this s-value in this section is only for the purposes of calculating k′ by retracing the original calculations of Blaauw (2017).
We utilized a variation of the mass estimation formula proposed by Hughes & McBride (1989). The original equation assumes a circular cross section for the meteoroid stream and a uniform meteoroid flux throughout this cross section, with the flux equivalent to the maximum shower activity. Under these conditions, the authors defined MF as the meteoroid flux integrated over the cross section, deriving it with the following relation:
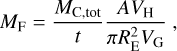 (8)
(8)
where t is the shower duration, which is the time it takes for Earth to pass through the stream. The terms VH and VG are the heliocentric and geocentric stream velocities, respectively, and A is the cross section area of the stream, while RE and VE represent the Earth’s radius and orbital velocity. The factor, 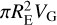 , can be interpreted as the volume of the tube formed by Earth’s movement relative to the stream during t. Similarly, AVH is the total volume that the stream passes through during t. Thus, the rightmost fraction in Eq. (8) is the ratio between the volume of the stream passing through a perpendicular plane and the volume created by the passing of the Earth within the stream as they intersect each other. Following their initial assumptions, Hughes & McBride (1989) equated this ratio of volumes to the ratio of meteoroid numbers and subsequently managed to extrapolate observed Geminid mass influx into the total Geminid stream mass. In this work, we are able to count the number of particles that interact with Earth and the number of those that do not, removing the need for such assumptions. Therefore, Eq. (8) can be changed to
, can be interpreted as the volume of the tube formed by Earth’s movement relative to the stream during t. Similarly, AVH is the total volume that the stream passes through during t. Thus, the rightmost fraction in Eq. (8) is the ratio between the volume of the stream passing through a perpendicular plane and the volume created by the passing of the Earth within the stream as they intersect each other. Following their initial assumptions, Hughes & McBride (1989) equated this ratio of volumes to the ratio of meteoroid numbers and subsequently managed to extrapolate observed Geminid mass influx into the total Geminid stream mass. In this work, we are able to count the number of particles that interact with Earth and the number of those that do not, removing the need for such assumptions. Therefore, Eq. (8) can be changed to
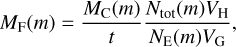 (9)
(9)
where NE(m) is the number of simulation particles interacting with Earth (in other words, the number of simulation particles satisfying the MOID criteria) and Ntot(m) is the total number of simulation particles of mass m. We used t = 3 days, which is the approximate duration of the shower based on our simulation. Using the mean orbital period P of the simulation particles, the total stream mass can then be calculated as
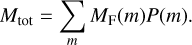 (10)
(10)
Although the original MC value was derived assuming a mass range of 0.1 mm–10 cm, we were computationally limited to performing simulations for the entire mass range. The Poynting-Robertson timescale for 1-cm and 10-cm particles are ~1–10 Myr. Given that our simulation timescale spans ~ 10 000 yr or less, the radiative effects on the orbital motion of these particles are negligible. Hence, it is reasonable to extrapolate the simulation results of 1-cm particles to those of 10-cm particles. However, the same cannot be assumed for 0.1 mm, whose Poynting-Robertson timescale is ~10 000 yr. To overcome this, we relied on the mass population distribution power-law index to derive the mass of 0.1-mm particles from our more statistically reliable 1-cm particle population. The mass index s used in Eqs. (5)–(7) describes the infalling Geminid population but not necessarily the entire Geminid population, as the vast majority of the Geminid stream does not interact with Earth.
In the scenario of rotational instability, it is reasonable to hypothesize that the resulting dust population would retain the mass distribution index of its regolith phase. With this in mind, we employed two mass indices obtained by the Hayabusa2 mission on the asteroid Ryugu. The first index is the global boulder cumulative size distribution index of 2.65 (Michikami et al. 2019). The second is the cumulative power-law index of 3.88 for the cumulative size distribution of Ryugu regolith samples (Yada et al. 2021). It is worth noting that the larger size index of the returned regolith sample is attributed to the fragmentation caused by the impact experiment. If we convert the cumulative size distribution index to the differential mass distribution index, the values are 1.88 and 2.29, respectively. In comparison, this value is slightly higher than the observed index found by Blaauw (2017) (1.68 ± 0.04) and close to the index used by Ryabova (2017) (2.17–2.438). With this considered, the 0.1-mm particles will have approximately 103.76 or 101.3 times the total mass of the 1-cm particles, depending on the index. In several models, we had models with no 1-mm particles satisfying the MOID criteria, leading to a divided-by-zero problem in Eq. (9). As such, if no 1-mm particles were present within the MOID criteria, we approximated the mass of 1-mm particles as 101.88 or 100.65 times that of 1-cm particles, similar to our approach with 0.1-mm particles.
Figures 7 and 8 illustrate the estimated mass of the dust streams from all models. Our calculation of the total stream mass yielded a range of ~1010–1014 g. Compared to Phaethon’s mass, which is currently estimated at around 1017 g (Hanuš et al. 2018), the upper bound corresponds to about 0.1%, or 42 cm, of its surface layer. Interestingly, this range overlaps with the mass range of the Phaethon dust trail, ~ 1013–1015 g, found by the Wide-field Imager on the Parker Solar Probe under the assumption that the trail consists of 0.5-mm particles (Battams et al. 2022).
Past estimations of the Geminid stream mass range widely depending on the author and methodology, for example, 1.6 × 1016 g (Hughes & McBride 1989; Blaauw 2017); (1.4 ± 0.5) × 1015 g (Jenniskens 1994); and 5.0 × 1015−4.3 × 1017 g (Ryabova 2017). Our model does not replicate the total width of the Geminid activity profile (we discuss this more in Sect. 4.6), and therefore, the derived mass estimate could be underestimated by a factor of three to five. Nonetheless, the difference in orders of magnitudes between our result and the estimates from previous studies should be addressed. In the following paragraphs, we provide an explanation for this disparity.
In the cases of Hughes & McBride (1989), Jenniskens (1994), Blaauw (2017), the calculation is based on Eq. (8), which assumes the stream structure to be a uniform cylindrical tube whose density is determined from the maximum shower activity, and the cross sectional area to the ecliptic plane is derived from the shower duration. Consequently, this dust tube model generates an activity profile that looks like a boxcar function, with the peak corresponding to the maximum activity. Moreover, an additional multiplication factor f was introduced as well to account for the more realistic situation where Earth does not traverse the stream’s center. For the Geminids, this factor is often chosen as ten. With all of these conditions combined, it is natural that estimates derived from this method would tend to yield larger values for the total Geminid stream mass.
The idea behind Ryabova (2017) is akin to our mass estimation method, but the crucial difference lies with the selected dust mass range. As mentioned earlier, we chose the particle size range of 0.1 mm–10 cm to maintain consistency with the measurements of Blaauw (2017), and almost all Geminid mass estimations do not set a lower limit smaller than 0.1 mm. On the other hand, Ryabova (2017) is an exception, and in that case, the lower mass limit was set to 10−12 g, which is roughly equivalent to a particle size of 0.001 mm. Notably, considering that the total mass of particles with radius r is proportional to r3 × r−3s−1, expanding the mass range to 0.001 mm would increase the total stream mass by at least seven orders of magnitude. In other words, the discrepancy between our mass estimate and that of Ryabova (2017) largely arises from our use of a narrower mass range.
This difference stems from how one defines the Geminid stream. In the case of Ryabova (2017), the entire dust population released by Phaethon during the formation event is considered to be the Geminid stream. Indeed, particles of ≥0.001 mm in size can survive being blown away by radiation pressure after being ejected from Phaethon (Moorhead 2021), but the PR lifetime of particles of 0.01 mm or less is ≲ 10 000 yr (Whipple & Wyatt 1949), which is comparable to the timescale of our simulations. In other words, at the timescale of this study, particles smaller than 0.1 mm ejected directly from Phaethon have deviated significantly from the Geminid shower particles and no longer contribute to the meteor shower. Unlike the observed Geminid meteors, this subset of Phaethon-born dust particles is not constrained by observation, and its boundary between the background sporadic complex is vague (Moorhead 2021). On the other hand, our idea of the Geminid stream in this study is the dust complex that is in the vicinity of Earth’s orbit and is directly connected to the Geminid shower. As we have shown from our results, the stream of millimeter- and centimeter-sized particles match this description, and therefore, we define the Geminid stream to be the dust stream consisting of these particles and their products of collisional cascading. Nevertheless, we find both definitions used by Ryabova (2017) and our study to be valid, but we also note that the impact of using different definitions is significant for stream mass estimation.
 |
Fig. 7 Mass estimate of the Geminid stream for all the simulations performed in this study. The index by Yada et al. (2021) was assumed. The top panel displays data points ranging from ~ 15–30 kyr ago, while the bottom panel shows the values from ~2–10 kyr ago. The letters A and B mark the optimal models chosen in Sect. 4.3. |
 |
Fig. 8 Same as Fig. 7 but for the index by Michikami et al. (2019). |
4.3 Activity profile
In Sect. 3.2, we found several noteworthy models whose peak solar longitude is very close to the known maximum activity plateau. We searched for models with (1) a peak solar longitude lower than 262.45° and (2) with more than ten particles constituting the peak. We set (1) to match the Geminid observation, while (2) was set to ensure statistical reliability. These criteria left us with two models: Clone 50 18 000 yr ago and nominal Phaethon 18 000 yr ago. Henceforth, we call them Models A and B. Their present-day orbits and MOID distributions are shown in Fig. 9. Using the Earth-Moon distance criterion, the mass of Models A and B are 1.7 × 1013 g and 2.5 × 1012 g, respectively, in Fig. 7.
Figure 10 presents the number density of 1-cm particles divided into 0.05° bins of solar longitude. This distribution can be interpreted as the activity profile of the model Geminids observed from Earth. Both Model A and B exhibit a peak at 262.425°. Notably, these locations are near the upper boundary of the maximum activity plateau, 262.4 + 0.05° (Rendtel 2004), and imply that larger particles are concentrated at the descending side of the profile, which is in agreement with radio observation data (Zigo et al. 2009). In short, our investigation has led us to create a Geminid stream model that closely approximates the observed peak activity location, despite employing stringent distance conditions to evaluate meteoroid interaction with Earth. However, while our activity profile demonstrates promising aspects, it is not without its limitations, which we address in Sect. 4.6.
Figure 11 provides a visual representation of the cross section of the stream. The core of the stream is ~0.01 au away from Earth’s orbit, and compared to the interacting particles, it is skewed to a lower solar longitude. Thus, as we pointed out earlier in Sect. 3.1, using ≳0.01 au as the distance condition to determine the particle intersection with Earth overrepresents stream core particles, which can result in a misleading statistical analysis.
 |
Fig. 10 Number density of the points in Fig. 11 by solar longitude (J2000.0) for Models A (top) and B (bottom). The histogram was binned with an interval of 0.05°. The shadowed area represents the maximum activity plateau by Rendtel (2004). |
4.4 The dynamics of the Geminid meteoroids
In this section, we aim to identify the differences between particles that interact with Earth and those that do not. Figure 12 summarizes the orbital histories of the interacting 1-cm particles from Model B. We also added randomly selected non-interacting 1-cm particles to Fig. 12 for comparison. The distinction between the two particle categories becomes visibly evident in the panel showing the semi-major axis. Here, we observed two notable divergences separating the interacting and non-interacting particles. These divergences occurred ~ 18 000 and ~4000 yr ago, coinciding with the close encounter of Venus and Earth. In the case of ~4000 yr ago, the particles encountered both major terrestrial planets almost at the same time. Such encounters likely increased the chaotic behavior in the stream’s orbit, causing a portion of the stream to migrate to larger semi-major axes. Subsequently, this migration would eventually have led to a section of the stream directly crossing Earth in the present day. Looking back at Fig. 2, one can notice hints of these planetary encounters in the backward integration of Phaethon as well.
Table 2 compares the orbital elements of the Earth-interacting particles with those found with video observations of the Geminid meteoroids (Hajduková et al. 2017). While all five orbital elements fall within the range of the standard deviation of the observed data, it is important to acknowledge that this is partially attributable to the standard deviation being relatively wide (we discuss this further in Sect. 4.6).
The first reports of the modern Geminid shower date back to the 19th century, with observational records from the 1880s or even as early as the 1830s in literary accounts (Connolly & Hoffleit 1991; Jakubík & Neslušan 2015). Furthermore, Ryabova & Rendtel (2018) showed that the Geminid activity level increased based on numerical simulation and visual observations. We performed a similar analysis in Fig. 13 and found that our model activity had also grown over the past two centuries. In particular, the increase in activity from the 1980s to the present day is similar to the fit by Ryabova & Rendtel (2018), albeit slightly shallower.
 |
Fig. 11 MOID points of the particle orbits with MOID < Earth–Moon distance projected on the ecliptic plane. The reference frame is the Cartesian J2000.0 ecliptic coordinate system, the Earth’s orbit is drawn with a solid black line, and solar longitudes labeled with diamonds. |
 |
Fig. 12 Orbital evolution of Earth-interacting particles (blue) and randomly selected non-interacting particles (gray). The top row displays close encounter distances (≤3 Hill radius) of the particles with Mercury, Venus, and Earth throughout the simulation. From middle to bottom row, from left to right, are the present-day orbits of the particles and the time plot of the semi-major axis, inclination, eccentricity, argument of perihelion, and longitude of ascending node. |
 |
Fig. 13 Relative number of interacting particles from Model B in 1780-2019 with a 50-yr cadence. The solid red line is the linear fit to the observed activity of 1985–2016 analyzed in Ryabova & Rendtel (2018) and is extended by the dotted line for visual reference. All y-axis values were normalized to the value in 2019. |
4.5 Reflecting on the age of the Geminid meteoroids
Traditionally, the age of the Geminid stream was estimated to be ~1000–~10000 yr, according to the works of Jones (1978, 1985), Williams & Wu (1993), Ryabova (1999), Beech (2002), Jakubík & Neslušan (2015). More recent studies have tended to favor an age of ~2000 yr (Ryabova 2007, 2016, 2017). In this context, our work suggests that the Geminid age might be older by several factors or even an entire order of magnitude than the recent estimate. Nonetheless, we argue that the widely known age estimate should be approached with caution.
Studies such as Williams & Wu (1993) backward integrated observed Geminid meteoroids or their mean orbital elements, sometimes without applying the Poynting-Robertson effect. Jones (1985) also utilized backward integration and arrived at the age of 6000 yr by matching their result with the observed bimodality. Another approach involves using the secular variation in the meteoroids’ orbital elements, assuming that this variation is the combined product of the Poynting-Robertson effect and corpuscular drag (Belkovich 1986; Ryabova 1999). Yet, as Ryabova (1999) pointed out, these methods are highly sensitive to uncertainties in the initial parameters and should be interpreted carefully.
Another factor that was often underestimated in previous studies was the planetary perturbation of terrestrial planets, especially Venus and Earth. Ryabova (2007) employed the semi-analytical, nested polynomial method to create a model Geminid stream with a presumed age of 2000 yr with only Jupiter’s perturbation included. Although this method may be valid for 2000 yr, as described in Sect. 4.4, the gravitational influences exerted by Venus and Earth become non-negligible when extending the analysis to epochs older than 4000 yr. Subsequent numerical simulations, such as those of Ryabova (2016), started incorporating these effects as well, but they still did not venture beyond the 2000-yr mark.
We found Jakubík & Neslušan (2015) and Ryabova (2018) to be the only studies that probed ejection epochs further than 4000 yr ago while accounting for planetary perturbations and the Poynting-Robertson effect. In the case of Jakubík & Neslušan (2015), they ejected particles of various ß values in a sequence of ejection events spanning 103–105 yr and compared the orbital elements of their model to the observed meteoroids. Their analysis, based on the longitude of ascending node distribution, indicated that particles with β = 0.009 launched 1000 yr ago fit well with observed meteoroid orbits. However, one should note that the ßvalue is at least one order of magnitude larger than that used in our study. For other epochs, only the orbital elements for the combined stream of all simulated ßvalues were provided, rather than detailed results for each specific β value, thereby limiting comparison with our findings. Furthermore, the selected distance criterion was 0.05 au, which we demonstrated in Sect. 4.3 to be too lenient.
Regarding Ryabova (2018), the author only used 100 1-mm-sized particles and ejection epochs of 500–5000 yr ago with an initial velocity of 30 ms−1 and a distance criterion of 0.03 au. The author concluded that such ejection did not produce a meteor shower at present day. However, it is possible that this finding is likely due to the small number of particles in the simulation. As demonstrated in Figs. 4 and 5, our study finds multiple particles satisfying the MOID criteria at a similar age range after using 320000 particles, albeit with a different ejection velocity. As only a minority of 1-mm particles interacted with Earth in our simulations, we propose that a significant portion of the present-day millimeter-sized Geminid meteors were generated through collisional cascading of larger particles within this timescale, as discussed in Sect. 4.1.
Apart from dynamical simulations, Beech (2002) theorized that the flickering of Geminid fireballs was caused by their rotation, and by assuming that the age of the fireballs is the time it took for solar radiation scattering to spin them up, he derived an age range of 1000–4000 yr. This idea was challenged by Babadzhanov & Konovalova (2004), who instead suggested that the flickering was due to an autofluctuation mechanism of meteoroid ablation.
In short, the Geminid age range that has become widely referred to should be dealt with caution given that it originates from studies constrained by computational limitations or potentially unreliable methodologies. In addition, this age range has not been properly tested since the initial dynamical studies. However, while we acknowledge that even our age estimate of 18 000 yr is not far off this range, we also encourage future research to engage in numerical simulations of the Geminids in order to thoroughly delve into various epochs.
Orbital elements of Earth-interacting particles (JD 2459000.5).
4.6 Limitations and future work
Based on the stream location, our models have shown a remarkable resemblance to the observed Geminid meteoroids. Nonetheless, there are several limitations of our models that warrant being addressed. A prominent Geminid activity feature is the bimodality, or double peak. Geminid bimodality with a ~1º gap has been predicted by Ryabova (1989) and has been consistently observed throughout decades of observations. The observed gap between the two peaks varies from year to year but is generally around 0.1º (Rendtel 2004). Although Models A and B both display some minor peaks near the main peak, their magnitudes are insufficient to be interpreted as part of a double peak. However, it is important to note that direct comparison with observation in terms of bimodality can be challenging, as the number, location, spacing, and strength of Geminid activity peaks can vary widely depending on the year of observation (Rendtel 2004; Zigo et al. 2009).
Another feature that we could not replicate is stream width. The widths of the models’ profiles are much narrower than observed activity profiles, which can span up to ~10º. This discrepancy is reflected in the standard deviations of the orbital elements in Table 2, where the observed data clearly shows greater dispersion. Previous simulations, even with significantly higher initial velocities of ~100 m s−1, also could not reproduce a stream width larger than 3º (Ryabova 2007, 2016). Therefore, we propose that the initial dispersion during dust ejection is not likely to be the sole contributor to the stream width. Instead, it is crucial to bear in mind that our activity profiles were constructed under the assumption that the entire Geminid stream was created by a single ejection event. However, if the stream was born from multiple ejection events within <~1000 yr, the combined infall of the ejected particles can look more similar to the multi-peak, widely dispersed activity of the Geminids. For example, one could imagine a scenario where rotational instability is the initial major mass ejection event and that it subsequently triggers the exposure and volatilization of subsurface sodium sources, which in turn lead to secondary ejection events (Zhang et al. 2023). Taking into account that Phaethon’s current rotational acceleration is faster than that predicted by the YORP effect (Marshall et al. 2022), one could also conjecture that it could have reached its critical spin period multiple times through a spin up-down-up sequence that occurs more frequently than predicted by the YORP timescale. We also note that the stream width problem was addressed by previous studies such as Ryabova (2016), where it was proposed that the observed width could be caused by Phaethon’s orbit being altered during the Geminid formation event. While this idea is plausible for directional ejections, such as comet-like activity, since mass ejection by rotational instability would theoretically be axisymmetric, we consider the orbital change caused by the ejection to be negligible.
Although this work shows the viability of low-velocity dust ejection as the initial dynamical condition of Geminid meteoroids, we leave it to future works to probe whether rotational instability on Phaethon can eject the estimated mass of our models. Furthermore, we anticipate that the upcoming DESTINY+ mission will greatly contribute to our understanding of the rotation and activity of Phaethon. As Hayabusa2 and OSIRIS-REx demonstrated from their in situ observations of Ryugu and Bennu, insights could potentially be derived from assessments of the space weathering effect, boulder arrangement, or crater distribution (Sugita et al. 2019; DellaGiustina et al. 2020; Jawin et al. 2020).
5 Summary and conclusions
We have presented the first thorough investigation of dust ejection from the asteroid Phaethon via rotational instability. We conducted numerical simulations of millimeter- and centimeter-sized dust ejection ~2–100 kyr ago, assuming a low initial velocity induced by rotational instability. Using strict and realistic MOID criteria, we found particles crossing Earth at present day from multiple ejection epochs. By deriving the location of the peak activity of our models, we found two models that are close to the observed peak solar longitude. We estimated the mass of the model streams to be ~1012 g, or ~10-5 Phaethon mass. The models are ~18 000 yr old, which is more than 10 kyr older than the previously assumed Geminid age. We analyzed the orbital evolution and the simulation particles and identified close encounters with Venus and Earth to be the key events that caused some of the ejected dust to migrate to Earth-intersecting orbits in the present day. However, our models are not perfect, as we could not replicate the width and bimodality of the Geminid stream.
To summarize, this work demonstrates that Geminid formation by rotational instability is dynamically possible. Further investigation is required to verify that rotational instability can sufficiently supply the estimated mass of our models. We also expect that future observations by the DESTINY+ mission will give us valuable insight into the nature of Phaethon’s activity and the birth of the Geminids.
Acknowledgements
This research at SNU was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MEST) (No. 2023R1A2C1006180). This research utilized the computational facility gmunu and we thank Prof. Hyung Mok Lee, Prof. Woong-Tae Kim, Gain Lee and Da-jung Jang for generously sharing it with us, as well as Dr. Hee-il Kim for kindly providing us with technical support. The authors thank Yoonsoo Bach, Sunho Jin and Jooyeon Geem for their helpful comments and discussions as well. We would also like to thank G.O. Ryabova for the insightful review as well.
Appendix A Clone generation parameters
The covariance matrix of the orbital elements of Phaethon that we used is shown in Table A.1. The rows and columns of the matrix are in the following order: e, perihelion distance (au), perihelion epoch (JD), Ω, ω, i, A2. As mentioned in Sect. 2, we generated 100 clones from this matrix. The semi-major axis and mean anomaly, which are needed for Mercury6, were derived from the given orbital elements. Table A.2 shows the orbital elements of the clones selected for use in this study.
Covariance matrix of the orbital elements of Phaethon at JD 2459000.5.
Orbital elements of Phaethon clones used in this work (JD 2459000.5).
References
- Arai, T., Kobayashi, M., Ishibashi, K., et al. 2018, in Lunar Planet. Sci. Conf., 2570 [Google Scholar]
- Arlt, R., & Rendtel, J. 2006, MNRAS, 367, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Babadzhanov, P. B., & Konovalova, N. A. 2004, A&A, 428, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bach, Y. P., & Ishiguro, M. 2021, A&A, 654, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battams, K., Gutarra-Leon, A. J., Gallagher, B. M., et al. 2022, ApJ, 936, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M. 2002, MNRAS, 336, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Belkovich, O. I. 1986, Astron. Vestnik, 20, 142 [NASA ADS] [Google Scholar]
- Blaauw, R. C. 2017, Planet. Space Sci., 143, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J., Koten, P., Spurný, P., et al. 2010, in Icy Bodies of the Solar System, 263, eds. J. A. Fernandez, D. Lazzaro, D. Prialnik, & R. Schulz, 218 [Google Scholar]
- Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [Google Scholar]
- Connolly, L. P., & Hoffleit, D. 1991, in Bull. Am. Astron. Soc., 23, 941 [Google Scholar]
- Cukier, W. Z., & Szalay, J. R. 2023, Planet. Sci. J., 4, 109 [NASA ADS] [CrossRef] [Google Scholar]
- DellaGiustina, D. N., Burke, K. N., Walsh, K. J., et al. 2020, Science, 370, eabc3660 [Google Scholar]
- Fox, K., Williams, I. P., & Hughes, D. W. 1982, MNRAS, 200, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, K., Williams, I. P., & Hughes, D. W. 1983, MNRAS, 205, 1155 [NASA ADS] [Google Scholar]
- Gustafson, B. A. S. 1989, A&A, 225, 533 [NASA ADS] [Google Scholar]
- Gustafson, B. A. S. 1994, Annu. Rev. Earth Planet. Sci., 22, 553 [CrossRef] [Google Scholar]
- Hajduková, Mária, J., Koten, P., Kornoš, L., & Tóth, J. 2017, Planet. Space Sci., 143, 89 [CrossRef] [Google Scholar]
- Hanuš, J., Delbo’, M., Vokrouhlický, D., et al. 2016, A&A, 592, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Vokrouhlický, D., Delbo’, M., et al. 2018, A&A, 620, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirabayashi, M., Scheeres, D. J., Sánchez, D. P., & Gabriel, T. 2014, ApJ, 789, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, D. W. 1983, Nature, 306, 116 [Google Scholar]
- Hughes, D. W., & McBride, N. 1989, MNRAS, 240, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, M.-T., & Li, J. 2017, AJ, 153, 23 [NASA ADS] [Google Scholar]
- Hunt, J., Fox, K., & Williams, I. P. 1986, in Asteroids, Comets, Meteors II, eds. C. I. Lagerkvist, H. Rickman, B. A. Lindblad, & H. Lundstedt, 549 [Google Scholar]
- Jakubík, M., & Neslušan, L. 2015, MNRAS, 453, 1186 [CrossRef] [Google Scholar]
- Jawin, E. R., Walsh, K. J., Barnouin, O. S., et al. 2020, J. Geophys. Res. Planets, 125, e06475 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P. 1994, A&A, 287, 990 [NASA ADS] [Google Scholar]
- Jewitt, D. 2012, AJ, 143, 66 [CrossRef] [Google Scholar]
- Jewitt, D., & Li, J. 2010, AJ, 140, 1519 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D., Li, J., & Agarwal, J. 2013, ApJ, 771, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D., Agarwal, J., Li, J., et al. 2017, AJ, 153, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D., Li, J., & Kim, Y. 2021, AJ, 162, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J. 1978, MNRAS, 183, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J. 1985, MNRAS, 217, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, J., & Hawkes, R. L. 1986, MNRAS, 223, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., Ohtsuka, K., Kikuchi, S., et al. 2022, Icarus, 382, 115022 [NASA ADS] [CrossRef] [Google Scholar]
- Klačka, J., Petržala, J., Pástor, P., & Kómar, L. 2012, MNRAS, 421, 943 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Lasue, J., Levasseur-Regourd, A.-C., & Renard, J.-B. 2020, Planet. Space Sci., 190, 104973 [NASA ADS] [CrossRef] [Google Scholar]
- Lauretta, D. S., Hergenrother, C. W., Chesley, S. R., et al. 2019, Science, 366, 3544 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., & Jewitt, D. 2013, AJ, 145, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet. Space Sci., 9, 719 [Google Scholar]
- Liou, J.-C., Zook, H. A., & Jackson, A. A. 1995, Icarus, 116, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Luu, J. X., Jewitt, D. C., Mutchler, M., et al. 2021, ApJ, 910, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, S., Devogele, M., Taylor, P., et al. 2022, in AAS/Division for Planetary Sciences Meeting Abstracts, 54, 514.07 [NASA ADS] [Google Scholar]
- Masiero, J. R., Davidsson, B. J. R., Liu, Y., Moore, K., & Tuite, M. 2021, Planet. Sci. J., 2, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Melikyan, R. E., Clark, B. E., Hergenrother, C. W., et al. 2021, J. Geophys. Res. Planets, 126, e06817 [NASA ADS] [CrossRef] [Google Scholar]
- Michikami, T., Honda, C., Miyamoto, H., et al. 2019, Icarus, 331, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Molaro, J. L., Hergenrother, C. W., Chesley, S. R., et al. 2020, J. Geophys. Res. Planets, 125, e06325 [NASA ADS] [CrossRef] [Google Scholar]
- Moorhead, A. V. 2021, Icarus, 354, 113949 [NASA ADS] [CrossRef] [Google Scholar]
- Nakano, R., & Hirabayashi, M. 2020, ApJ, 892, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Jenniskens, P., Levison, H. F., et al. 2010, ApJ, 713, 816 [CrossRef] [Google Scholar]
- Nesvorný, D., Janches, D., Vokrouhlický, D., et al. 2011, ApJ, 743, 129 [CrossRef] [Google Scholar]
- Pokorný, P., Vokrouhlický, D., Nesvorný, D., Campbell-Brown, M., & Brown, P. 2014, ApJ, 789, 25 [CrossRef] [Google Scholar]
- Rendtel, J. 2004, Earth Moon Planets, 95, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Rendtel, J. 2019, WGN, J. Int. Meteor Organ., 47, 180 [NASA ADS] [Google Scholar]
- Ryabova, G. O. 1989, WGN, J. Int. Meteor Organ., 17, 240 [NASA ADS] [Google Scholar]
- Ryabova, G. O. 1999, Solar Syst. Res., 33, 224 [NASA ADS] [Google Scholar]
- Ryabova, G. O. 2007, MNRAS, 375, 1371 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2008, Earth Moon Planets, 102, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2012, MNRAS, 423, 2254 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2013, Solar Syst. Res., 47, 219 [CrossRef] [Google Scholar]
- Ryabova, G. O. 2016, MNRAS, 456, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2017, Planet. Space Sci., 143, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2018, MNRAS, 479, 1017 [NASA ADS] [Google Scholar]
- Ryabova, G. O. 2021, MNRAS, 507, 4481 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O., & Rendtel, J. 2018, MNRAS, 475, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Soja, R. H., Grün, E., Strub, P., et al. 2019, A&A, 628, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steel, D. I., & Elford, W. G. 1986, MNRAS, 218, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, M. G. 2005, Am. J. Phys., 73, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Stoer, J., & Bulirsch, R. 1980, Introduction to Numerical Analysis (New York: Springer) [CrossRef] [Google Scholar]
- Sugita, S., Honda, R., Morota, T., et al. 2019, Science, 364, eaaw0422 [Google Scholar]
- Thornton, S., & Marion, J. 2004, Classical Dynamics of Particles and Systems (Brooks/Cole) [Google Scholar]
- Tokhtas’ev, V. S. 1982, in Meteor Matter in the Interplanetary Space, 184 [Google Scholar]
- Whipple, F. L. 1951, ApJ, 113, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1983, IAU Circ., 3881, 1 [NASA ADS] [Google Scholar]
- Whipple, F. L., & Wyatt, Stanley P., J. 1949, AJ, 54, R138 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, I. P., & Wu, Z. 1993, MNRAS, 262, 231 [NASA ADS] [Google Scholar]
- Wiźniowski, T., & Rickman, H. 2013, Acta Astron., 63, 293 [NASA ADS] [Google Scholar]
- Yada, T., Abe, M., Okada, T., et al. 2021, Nat. Astron., 6, 214 [Google Scholar]
- Ye, Q., Wiegert, P. A., & Hui, M.-T. 2018, ApJ, 864, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, L. L., Ip, W. H., & Spohn, T. 2019, MNRAS, 482, 4243 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q., Battams, K., Ye, Q., Knight, M. M., & Schmidt, C. A. 2023, Planet. Sci. J., 4, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Zigo, P., Porubcan, V., Cevolani, G., & Pupillo, G. 2009, Contrib. Astron. Observatory Skalnate Pleso, 39, 5 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Schematic illustration of dust ejection in our model. In the figure, the gray sphere corresponds to the Hill radius of Phaethon (r = 78 km from Phaethon’s center of mass at present-day orbit). The dust particles have small outward terminal velocities (blue arrows) on the Hill sphere (vr = 1 m s−1). |
| In the text | |
 |
Fig. 2 Orbital history of 100 Phaethon clones from backward integration. The colored lines are clones we used for the dust sources. |
| In the text | |
 |
Fig. 3 Examples of the dust simulation result from nominal Phaethon ejection. The ejection epoch is labeled at the top in Julian date format (and its corresponding year is in brackets). The left plots show random samples of particle orbits on the ecliptic plane at the present day (JD 2459000.5). The right plots are the histograms of the MOID of particles to Earth, and the Earth radius and Earth-Moon distance marked by dotted lines. |
| In the text | |
 |
Fig. 4 Number of 1-mm particles satisfying the MOID criteria from each ejection epoch with different ranges of ejection epoch (top: 10 000–30 000 yr ago, bottom: 2000–10000 yr ago). Different colors respectively represent the MOID criteria of Earth radius (darker color) and Earth-Moon distance (lighter color). The dotted line shows the mean-averaged values of the number of particles with MOIDs within Earth’s radius from nominal and clone parent bodies. The solid line is the equivalent of the dotted line for the Earth-Moon distance criterion. Simulation results with no particles within the MOID criteria are not present, but they were included when calculating the mean average. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 but for 1-cm particles |
| In the text | |
 |
Fig. 6 Mode solar longitude of 1-cm particles within the lunar distance MOID criterion. If there was more than one maximum peak, we registered the mean solar longitude of the peaks as the corresponding data point. The blue line is the mean of the data points. The shaded area indicates the maximum activity plateau (261.5–262.4°) reported by Rendtel (2004). |
| In the text | |
 |
Fig. 7 Mass estimate of the Geminid stream for all the simulations performed in this study. The index by Yada et al. (2021) was assumed. The top panel displays data points ranging from ~ 15–30 kyr ago, while the bottom panel shows the values from ~2–10 kyr ago. The letters A and B mark the optimal models chosen in Sect. 4.3. |
| In the text | |
 |
Fig. 8 Same as Fig. 7 but for the index by Michikami et al. (2019). |
| In the text | |
 |
Fig. 9 Same as Fig. 3 but for Model A (top) and B (bottom). |
| In the text | |
 |
Fig. 10 Number density of the points in Fig. 11 by solar longitude (J2000.0) for Models A (top) and B (bottom). The histogram was binned with an interval of 0.05°. The shadowed area represents the maximum activity plateau by Rendtel (2004). |
| In the text | |
 |
Fig. 11 MOID points of the particle orbits with MOID < Earth–Moon distance projected on the ecliptic plane. The reference frame is the Cartesian J2000.0 ecliptic coordinate system, the Earth’s orbit is drawn with a solid black line, and solar longitudes labeled with diamonds. |
| In the text | |
 |
Fig. 12 Orbital evolution of Earth-interacting particles (blue) and randomly selected non-interacting particles (gray). The top row displays close encounter distances (≤3 Hill radius) of the particles with Mercury, Venus, and Earth throughout the simulation. From middle to bottom row, from left to right, are the present-day orbits of the particles and the time plot of the semi-major axis, inclination, eccentricity, argument of perihelion, and longitude of ascending node. |
| In the text | |
 |
Fig. 13 Relative number of interacting particles from Model B in 1780-2019 with a 50-yr cadence. The solid red line is the linear fit to the observed activity of 1985–2016 analyzed in Ryabova & Rendtel (2018) and is extended by the dotted line for visual reference. All y-axis values were normalized to the value in 2019. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


