| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A173 | |
| Number of page(s) | 12 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202346080 | |
| Published online | 18 March 2024 | |
Collisional effects in modeling solar polarized lines
Astronomy and Space Science Department, Faculty of Science, King Abdulaziz University, PO Box 80203 Jeddah 21589, Saudi Arabia
e-mail: derouichmoncef@gmail.com, aldarwish@kau.edu.sa
Received:
4
February
2023
Accepted:
10
December
2023
Context. Rigorous implementation of the effects of collisions in modeling the formation of the polarized solar lines is of utmost importance in order to realistically analyze the available, highly sensitive solar spectropolarimetric observations. Indeed, even when an observation seems to fit well with theory, one can misinterpret results if important effects due to collisions are not correctly implemented in the modeling process.
Aims. We point out inconsistencies in the models adopted to implement the Paschen Back effect together with collisional effects on the solar linear polarization formed by scattering of anisotropic radiation. Because the significance of these inconsistencies increases as polarization becomes increasingly responsive to collisions, we investigate the range of hydrogen densities nH to which the polarization is sensitive.
Methods. We used the density matrix formalism in the tensorial irreducible basis, which was developed within the theory of atom-radiation interaction and of atomic collisions. We solved the statistical equilibrium equations for multi-level atoms with hyperfine structure (HFS) in order to evaluate the collisional depolarization of levels of the D1-D2 lines of the K I atom.
Results. We find that collisions play a prominent role, particularly at hydrogen densities of between 1013 and 1016 cm−3.
Conclusions. So far, analyses of polarized lines formed in the presence of solar magnetic field have incorporated, if at all, collisional rates calculated assuming zero magnetic field. This could be a good approximation in the Hanle regime but not in the Paschen Back regime. For typical quiet Sun magnetic fields, the latter regime could be reached, and level-crossing takes place in several atomic systems. Therefore, one must be careful when using collisional rates calculated in the zero-field case to interpret linear polarization formed in magnetized media.
Key words: atomic processes / line: formation / line: profiles / magnetic fields / polarization / Sun: photosphere
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the solar photosphere, atoms and molecules that emit polarized light are exposed to collisions with neutral hydrogen atoms. The effects of these collisions must be correctly incorporated into the model of the line formation in order to properly interpret the observed polarized lines. The internal states of the perturbed atom can be described by the density matrix components expressed in the tensorial basis, 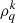 . We adopt the usual notations, where k denotes the tensorial rank (order) and q quantifies the coherence between the levels. Calculating the polarization of spectral lines requires the determination of the elements
. We adopt the usual notations, where k denotes the tensorial rank (order) and q quantifies the coherence between the levels. Calculating the polarization of spectral lines requires the determination of the elements 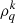 . Theoretically, collisions produce distinct but correlated effects on the
. Theoretically, collisions produce distinct but correlated effects on the 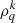 values and consequently lead to variation of the polarization of the emitted light. In this context, the following factors must be taken into account:
values and consequently lead to variation of the polarization of the emitted light. In this context, the following factors must be taken into account:
– Isotropic collisions produce gain terms due to transfer rates and loss terms due to relaxation rates. Collisional rates must be calculated in the tensorial basis to quantify the contribution of these collisions to the statistical equilibrium equations (SEEs) giving the variation of 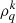 values (e.g., Derouich et al. 2003; Sahal-Bréchot et al. 2007; Derouich 2020).
values (e.g., Derouich et al. 2003; Sahal-Bréchot et al. 2007; Derouich 2020).
– For a given radiative transition, collisions cause perturbation to the energies of the levels participating in the transition, which results in broadening of the corresponding line; the rate of this broadening is denoted w. The value of w depends on the density of the perturbers and the Hamiltonian of the system, as well as the dynamics of the collisions (e.g., Derouich et al. 2015). We note that 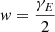 , where γE is the rate of elastic collisions, which usually enters the branching ratios of the redistribution matrices (more details about w and γE are available in Derouich et al. 2015).
, where γE is the rate of elastic collisions, which usually enters the branching ratios of the redistribution matrices (more details about w and γE are available in Derouich et al. 2015).
– Modeling the polarization profiles, particularly if partial frequency redistribution (PRD) effects must be considered, requires the correct evaluation of the role of collisions (e.g., Nagendra et al. 2020).
More details about collisions and their effects on polarized lines can be found in our previous work published over the last 20 years (see Derouich 2020 and references therein).
In the solar conditions, collisional rate calculations available in the literature are performed for a Hamiltonian H0, which completely neglects the impact of a magnetic field during the collisions. In such calculations, the basis used consists of the vectors |αJMJ⟩, which are the eigenvectors of H0; the total angular momentum, J, is considered to be well defined and to constitute a good quantum number (here MJ is the projection of J along the quantization axis and α summarizes the electronic configuration quantum numbers). Similarly, if the problem necessitates the inclusion of HFS, the total angular momentum F is taken to be a good quantum number and the basis {|βFMF⟩} becomes the eigenbasis of H0 (here MF represents the projection of F and β denotes the other quantum numbers associated to the level). In our investigation, we take into account the coherence between the different F-levels within a given J-level.
2. Challenges of modeling polarized lines in strong magnetic fields and collisions
Strictly speaking, one cannot use elastic collisional broadening rates w and depolarization rates Dk calculated in a zero-magnetic field case to model polarized line formation in the presence of a nonzero magnetic field. This strict condition might be supplemented with a looser one stating that zero-field collisional rates can be adopted in modeling cases where the magnetic field is sufficiently weak, specifically within the Hanle regime, where the angular momenta F and J are good (well-defined) quantum numbers.
Both collisional line broadening and collisional depolarization share similar approximations, and for a given level they are calculated using the same scattering collisional matrix S (Derouich et al. 2003, 2015; Kerkeni et al. 2004; Sahal-Bréchot & Bommier 2014, 2019). The main distinction is that Dk pertains to a single state, whereas w involves two states. However, this does not alter the fact that the elastic collision contribution to line broadening (w) and (de)polarization (Dk rates) of the lower and upper levels are expressed in terms of the same S-matrix elements derived from calculating the interaction potential and solving the Schrödinger equation. The scattering collisional matrix S strongly depends on the Hamiltonian of the system and its eigenbasis. As a result, both Dk and w depend on the presence of a magnetic field.
The similarities between Dk and w have been well documented and are firmly established. For instance, Derouich et al. (2003) used the Anstee-O’Mara-Barklem (ABO) theory (as described by Barklem & O’Mara 1998) to calculate w, and subsequently employed the same interaction potential and solved the same Schrödinger equation to determine the depolarization rates Dk. It is important to emphasize that the broadening w, as well as Dk, are known to be dependent on the J-level (in cases involving only fine structure) or F-level (when considering hyperfine structure) (see, e.g., Nienhuis 1976; Omont 1977; Green 1988; Belli et al. 2000; Kerkeni et al. 2004; Buffa & Tarrini 2011; Sahal-Bréchot & Bommier 2014, 2019; Derouich 2020).
A sufficiently strong magnetic field (as in the case of the incomplete Paschen-Back (PB) regime) greatly modifies the structure of the energy levels and induces level crossings and anti-crossings. Therefore, quantum numbers such as J and F, which are good quantum numbers in the absence of a magnetic field, lose their physical sense in the PB regime. Consequently, zero-field elastic collisional rates, such as the broadening w(JF) and the depolarization rate Dk(JF), lose their physical sense. Diagonalization of the Hamiltonian is necessary, and an eigenbasis and eigenvalues with new good quantum numbers must be obtained for each magnetic field strength. In this sense, previous and ongoing works including the effects of collisions in the presence of arbitrary magnetic fields appear to be inconsistent (see, e.g., Kerkeni & Bommier 2002; Bommier 2017, 2018; Nagendra et al. 2020; Alsina Ballester et al. 2021; Alsina Ballester 2022).
Kerkeni & Bommier (2002) investigated the ffects of mixing zero-field depolarization collisional rates with arbitrary (strong) magnetic field in the case of the Na I D1 and D2 lines where the PB effect (also called the Back-Goudsmit effect) is reached. In addition to the depolarization rates, these authors included the collisional broadening rates calculated in the zero-field case. As shown in Fig. 1, the PB effect induces crossings among the hyperfine sublevels of the 2P3/2 state of Na I at a magnetic field strength of approximately 15 Gauss. This value can be reached in the lower chromosphere where the D-Na I lines are formed. For instance, collision effects at a density of 1016 cm−3 are mixed together in the same model with magnetic field going from 0.1 to 100 Gauss, which severely influences their conclusions (see Fig. 8 of Kerkeni & Bommier 2002). In this sense, these latter authors pointed out that the loops visible in their polarization–magnetic fields diagrams (Figs 5–7 of Kerkeni & Bommier 2002) appear and disappear due to strong magnetic and collisional effects. This implies that these authors, in their interpretation, inconsistently take into account both effects happening in a strong magnetic field (incomplete PB regime) and collisional effects calculated in a zero-magnetic-field case. It is worth mentioning that the PB regime is reached in the case of the D2 upper level 2P3/2 for lower magnetic field values than those needed to reach the PB regime in the D1 upper level 2P1/2. However, the atomic polarization degrees of the HFS levels within the 2P1/2 state are inaccurately and inconsistently determined in the PB regime, because they are strongly coupled to those within the 2P3/2 state by the SEE.
 |
Fig. 1. Crossings between the hyperfine sublevels of the state 2P3/2 of Na I due to magnetic-field-strength effects (this figure is taken from Landi Degl’Innocenti & Landolfi 2004). |
The redistribution function obtained by Bommier 2017, 2018) incorporates the zero-field collisional broadening rate w (denoted ΓE in Bommier 2017) within the PB regime. Bommier (2017, 2018) did not acknowledge the inherent inconsistency of including elastic collisional effects calculated in a zero-field scenario within the framework of the PB regime1. Consequently, works that based their calculations on the methodology presented by Bommier (2017, 2018) exhibit inconsistencies. As can be seen in Alsina Ballester (2022), the inconsistency should be encountered in the case of the K I atom, because the incomplete PB regime is reached at a magnetic field of B ∼ 5 Gauss. Furthermore, interpretation of the polarization of the K I lines for magnetic fields with B > 5 Gauss faces a serious problem because of collisional effects, which are not known in the incomplete PB regime. Sowmya et al. (2015, 2019) examined Li I D1 and D2 lines within a collisionless model and encountered the incomplete PB regime at magnetic fields of as low as around 2 Gauss. If one were to consider the Li atoms in the incomplete PB regime and use zero-field collision rates, a similar inconsistency would be encountered.
There are two essential steps in the computation of the collisional depolarization or broadening rates:
-
Determination of the Hamiltonian of the system. We note that, in the PB regime, the magnetic Hamiltonian cannot be safely neglected when one calculates the total Hamiltonian of the system.
-
Treatment of the collision dynamics which needs to be performed in a suitable eigenbasis of the Hamiltonian determined for each value of the magnetic field.
Usually, one determines the collisional rates as a function of the temperature after averaging the cross-sections over the velocity distribution function and multiplying by nH (e.g., Derouich et al. 2003). Typically, collisional rates vary with temperature as ∼T0.4. However, in the future, significant effort should be devoted to the determination of the rates as a two-variable function Dk(T, B) and w(T, B), which is a challenging problem.
3. Collisional effects in a multilevel atom with hyperfine structure
As explained above, the inclusion of collision rates calculated in a zero-magnetic-field case in modeling the formation of polarization in the PB regime is conceptually wrong. The severity of the effects of this error depends on how much the polarization is sensitive to collisions.
To evaluate the (de)polarizing effect of isotropic collisions, at first glance, one might compare the depolarization rates Dk to the appropriate radiative rates associated with the transitions between the HFS levels. However, a more precise approach is to solve the SEE for the case of a multilevel atom with hyperfine structure.
We adopt the case of the multilevel atom with hyperfine structure detailed in Landi Degl’Innocenti & Landolfi (2004) by incorporating the influence of coherences between distinct F-levels within a given J-level. We include zero-field collisional rates in our analysis, focusing solely on the effects of collisions and radiative rates, while disregarding the magnetic field. We solved the SEE for the HFS levels involved in modeling the formation of the D1 and D2 lines of the K I atom.
We developed a numerical code that takes data describing HFS quantum levels as input, together with the number of photons per mode 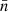 and the corresponding anisotropy factor wa. Einstein coefficients required in the SEE are extracted from the NIST database and, using the results of Manso Sainz & Landi Degl’Innocenti (2002), we determined that
and the corresponding anisotropy factor wa. Einstein coefficients required in the SEE are extracted from the NIST database and, using the results of Manso Sainz & Landi Degl’Innocenti (2002), we determined that 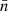 (D1) = 0.001906, wa(D1) = 0.08365,
(D1) = 0.001906, wa(D1) = 0.08365, 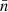 (D2) = 0.001875, and wa(D2) = 0.0842. In addition to the expressions of the radiative rates taken from Landi Degl’Innocenti & Landolfi (2004), the numerical code incorporates collisional data as input to compute the evolution of the atomic density matrix. Its evolution is affected by the gain terms, which are called collisional polarization transfer rates and are denoted Dk(J′FF′→JFF′), and by the loss terms associated with relaxation or depolarization rates, denoted Dk(JFF′). The Dk(JFF′) and Dk(JFF′→J′FF′) rates are obtained through a methodology first proposed by Nienhuis (1976) and Omont (1977), where Dk(JFF′) and Dk(J′FF′→JFF′) are represented as linear combinations of the Dk(J) and Dk(J′→J) rates, with these latter taken from Derouich (2012; see also Derouich 2020). To conveniently investigate the effect of collisions on polarization, it is essential to simultaneously take into account gain and loss collisional effects. We recognize that our current implementation in the SEE does not encompass all possible collisional rates governing coherence gain or loss. Nevertheless, our present inclusion of these aspects is novel and adequately conveys the core message of our paper. The incorporation of all possible rates poses a numerical challenge that we plan to address in the future.
(D2) = 0.001875, and wa(D2) = 0.0842. In addition to the expressions of the radiative rates taken from Landi Degl’Innocenti & Landolfi (2004), the numerical code incorporates collisional data as input to compute the evolution of the atomic density matrix. Its evolution is affected by the gain terms, which are called collisional polarization transfer rates and are denoted Dk(J′FF′→JFF′), and by the loss terms associated with relaxation or depolarization rates, denoted Dk(JFF′). The Dk(JFF′) and Dk(JFF′→J′FF′) rates are obtained through a methodology first proposed by Nienhuis (1976) and Omont (1977), where Dk(JFF′) and Dk(J′FF′→JFF′) are represented as linear combinations of the Dk(J) and Dk(J′→J) rates, with these latter taken from Derouich (2012; see also Derouich 2020). To conveniently investigate the effect of collisions on polarization, it is essential to simultaneously take into account gain and loss collisional effects. We recognize that our current implementation in the SEE does not encompass all possible collisional rates governing coherence gain or loss. Nevertheless, our present inclusion of these aspects is novel and adequately conveys the core message of our paper. The incorporation of all possible rates poses a numerical challenge that we plan to address in the future.
We consider a slab in the solar atmosphere containing K I atoms and illuminated anisotropically by photospheric unpolarized radiation field. Assuming that the incident radiation has cylindrical symmetry around the local solar vertical, at a frequency ν only the radiation matrix elements 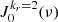 with kr = 0 and kr = 2 are needed to describe the incident radiation where
with kr = 0 and kr = 2 are needed to describe the incident radiation where 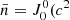 /2hν3) and
/2hν3) and 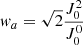 (see, e.g., Trujillo Bueno 2001; Landi Degl’Innocenti & Landolfi 2004; Derouich 2008).
(see, e.g., Trujillo Bueno 2001; Landi Degl’Innocenti & Landolfi 2004; Derouich 2008).
In these conditions, due to the cylindrical symmetry of the problem, only the linear polarization is formed by scattering.
The D1 and D2 K I lines result from the atomic transitions 2S1/2–2P1/2 and 2S1/2–2P3/2, respectively. The K I atom has nuclear spin I = 3/2. Therefore, each of the levels 2SJ = 1/2 and 2PJ = 1/2 splits into two HFS levels F = 1 and F = 2. The D2 upper level 2P3/2 has J = 3/2 and therefore splits into four HFS levels, F= 0, 1, 2, and 3. Therefore, eight HFS levels are involved in the atomic model considered to simulate the formation of the K I D lines. By taking into account only the even k-orders, with q = 0 give that the coherence is neglected, the SEE have 36 unknowns representing the density matrix elements 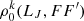 with even k values. We note that the tensorial order k varies from |F − F′| to F + F′, implying that, for example, the maximum value of k is kmax = 6 for F = F′ = 3. In our calculation, we take into account all orders k. We recall that Dk rates are q-independent because the collisions are considered to be isotropic.
with even k values. We note that the tensorial order k varies from |F − F′| to F + F′, implying that, for example, the maximum value of k is kmax = 6 for F = F′ = 3. In our calculation, we take into account all orders k. We recall that Dk rates are q-independent because the collisions are considered to be isotropic.
We compute the density matrix elements of all F-levels for the case of a tangential observation in a slab in the solar atmosphere. Our code provides all values of density matrix elements associated to the K I HFS levels as output. Analytical expressions of the SEE are given in the Appendix A to ensure that they are easily accessible to all readers.
According to Bruls et al. (1992) and Alsina Ballester (2022), the line-core profile of the K I D lines should be formed at photospheric heights corresponding to hydrogen densities nH ranging between ∼1014 and 1016 cm−3. In the present work, we conduct a comprehensive analysis by scanning a range of hydrogen densities nH going from 1012 cm−3 to 1018 cm−3 in order to fully investigate the possible role of collisions in the formation of the K I D lines. We adopt a photospheric temperature of T = 5780 K. Figure 2 shows the ratio 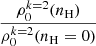 , which gives the variation of the alignment as a function of nH. It can be seen that collisions begin to influence the alignment of the HFS levels associated to the 2S1/2 for nH ∼ 1013 − 1014 cm−3. The ground-level 2S1/2 is almost completely depolarized for nH > 1015 cm−3. The density matrix element
, which gives the variation of the alignment as a function of nH. It can be seen that collisions begin to influence the alignment of the HFS levels associated to the 2S1/2 for nH ∼ 1013 − 1014 cm−3. The ground-level 2S1/2 is almost completely depolarized for nH > 1015 cm−3. The density matrix element 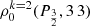 , which reflects the alignment of hyperfine level F = 3 within 2P3/2, has two remarkable features. First, it exhibits a wide range of variation covering four orders of magnitude from 1013 to 1017 cm−3. Second, it is noteworthy that this effect becomes evident at relatively low values, commencing at just 1013 cm−3.
, which reflects the alignment of hyperfine level F = 3 within 2P3/2, has two remarkable features. First, it exhibits a wide range of variation covering four orders of magnitude from 1013 to 1017 cm−3. Second, it is noteworthy that this effect becomes evident at relatively low values, commencing at just 1013 cm−3.
 |
Fig. 2. Emergent alignment for different HFS KI levels as a function of the density of neutral hydrogen nH. |
To understand this behavior, in the absence of collisions, we determined an analytical expression giving the density matrix elements 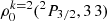 and we find that it is expressed as a function of the density matrix elements
and we find that it is expressed as a function of the density matrix elements 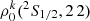 :
:
where B and A refer to the Einstein coefficients associated with the 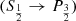 transition. Equation (1) can be written numerically as:
transition. Equation (1) can be written numerically as:
Equations (1) and (2) show that the alignment of level (2P3/2, 3 3) is connected only to the density matrix elements of level (2S1/2, 2 2).
We find that the values of ρk = 2, 4(2S1/2, 2 2) begin to exhibit a noticeable decrease when the hydrogen density nH is approximately 1013 cm−3, and they become zero at around nH ≈ 1015 cm−3. Therefore, for nH > 1015 cm−3, the only remaining density matrix element capable of providing alignment to the level (2P3/2, 3 3) is the population ρk = 0(2S1/2, 2 2). The continued existence of ρk = 0(2S1/2, 2 2), and therefore the survival of ρk = 2(2P3/2, 3 3), relies on the gain in population from (2S1/2, 1 1) by collisional transfer rates, which results in a population increase counterbalancing the relaxation process. If we neglect the transfer rates and focus on the relaxation rates, the population ρk = 0(2S1/2, 2 2), and therefore ρk = 2(2P3/2, 3 3), would be completely eliminated at around nH = 1015 cm−3. Conversely, when we take population transfer (gain) into account, although ρk = 2(2P3/2, 3 3) begins to decrease at nH ≈ 1013 cm−3 due to the decrease in ρk = 2, 4(2S1/2, 2 2), it keeps decreasing but does not reach zero until nH = 1017 cm−3, as illustrated in Fig. 2.
On the other hand, an analogous analysis of the SEE can provide insight into the behavior of other F-states within the P-state. Specifically, it elucidates the similar decrease in both 2P1/2 and 2S1/2 as the hydrogen density nH increases, spanning a range from 1013 to 1015 cm−3. It is worth mentioning that, similarly, Trujillo Bueno et al. (2002) noted an equal sensitivity of the 2P1/2 and 2S1/2 HFS levels to the depolarizing influence of a magnetic field. That being said, it should be noted that the alignments of F-levels related to S-state are definitively destroyed by collisions only when nH exceeds 1015 cm−3. However, the alignments of F-levels associated to the 2P1/2 are clearly destroyed by collisions only for nH > 1017 cm−3. We also note that, for the F-levels of the 2P1/2 state, a minor increase occurs at approximately nH ≃ 1016 cm−3 (see Fig. 2). It is noteworthy that the enhancement of alignment by isotropic collisions within a specific range of hydrogen density is not a novel result. This effect was observed by Derouich et al. (2007), even when HFS was entirely disregarded (see Derouich et al. 2007). By analogy, in a specific range of magnetic values, a localized enhancement of the alignment of the 2P3/2 (F = 1 and F = 2) levels has also been found; see Trujillo Bueno et al. (2002). By taking into account collisional effects on all HFS levels, we conclude that the polarization of the K I D lines is sensitive to the presence of isotropic collisions for a large range of nH, going from ∼1013 cm−3 to ∼1017 cm−3.2
D1- and D2-type lines of alkali atoms have the same atomic model and their collisional rates with atomic hydrogen (see Derouich 2012) –as well as their Einstein coefficients– are of the same order of magnitude as those of the K I atomic system. Therefore, like the K I D lines, other alkali atoms should be very sensitive to collisions for photospheric hydrogen densities, which complicates their interpretation, especially in the PB regime.
4. Important remark
We note that, in addition to the inconsistency arising from the use of zero-magnetic rates in conditions where polarization is generated in the presence of a strong magnetic field, there is also a misapplication of collision rates in the absence of a magnetic field. To model the collisional effect on the Q/I profiles of K I D lines, Alsina Ballester (2022) used the destruction of the orientation rates Dk = 1, obtained according to the formulae given in Sect. 7.13 of Landi Degl’Innocenti & Landolfi (2004). However, it is important to note that Dk = 1 rates are only relevant in studies where the scattering circular polarization exists and is coupled to linear polarization3. In this sense, the inclusion of Dk = 1 rates by Alsina Ballester (2022) in the zero-field case does not seem to be appropriate. On the other hand, the rates due to elastic collisions γE should also be of importance and can be found by applying the analytical expressions provided by Derouich et al. (2015), where a numerical model unifying γE (or broadening w) and collisional depolarization rates is obtained by using accurate genetic programming (GP) numerical methods. We note that several works (e.g., Stenflo 1994; Faurobert-Scholl et al. 1995; Berdyugina & Fluri 2004; Smitha et al. 2014; Alsina Ballester 2022), in the framework of the solar application, assume simple relations between broadening and depolarizing rates, which is difficult to justify either theoretically or numerically. For instance, for atomic and molecular collisions, there is no justification for the widely used relation 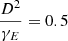 (or 0.38 or 0.1) (e.g., Faurobert-Scholl et al. 1995; Berdyugina & Fluri 2004; Smitha et al. 2014).
(or 0.38 or 0.1) (e.g., Faurobert-Scholl et al. 1995; Berdyugina & Fluri 2004; Smitha et al. 2014).
5. Conclusions
Current collisional data dedicated to solar applications are calculated in the absence of external magnetic field. Such data are useful only for polarimetric diagnostics in unmagnetized plasmas or in media with sufficiently weak magnetic fields, such as in the Hanle effect regime. Incorporating collision rates derived in a zero magnetic field context into models for polarization formation within the incomplete or complete PB regime is conceptually incorrect. The impact of this conceptual error depends on the degree to which polarization is sensitive to collisions. For instance, in regions of the Sun where the hydrogen density nH is low enough to imply that collision effects are negligible, this conceptual error becomes irrelevant.
Collisions have various effects on the polarized lines, including broadening, depolarization, and the partial redistribution of frequencies. In our investigation, we focused on one specific aspect, which is the depolarization caused by collisions. By solving the SEE for K I, which is modeled as a multilevel atom with HFS, we show the role that collisions can play in the modeling of polarization formation. Therefore, one must be careful when using collisional rates calculated in the zero-field case to interpret atomic polarization of HFS levels in magnetized media. In the cases where level crossings take place, such as in solar alkali atoms, close coupling treatments of atomic collisions including magnetic fields are necessary in order to properly decipher the information encoded in the polarized radiation.
Increasing the strength of the external magnetic field not only induces the mixing of states with different total angular momenta but also exerts an influence on collisional rates through modification of the value of the total Hamiltonian of the system (e.g., Volpi & Bohn 2002; Krems & Dalgarno 2004; Bivona et al. 2005). To ensure the unicity and reliability of the solution of the problems concerned with the formation of polarization in spectral lines originating from alkaline atoms, such as K I, all major processes must be included in the modeling. Proper treatment of the collisions in the conditions of the (incomplete) PB regime might lead to novel interpretations and could allow confirmation of the findings of previous works or rectify their shortcomings.
The omission of Dk in Bommier (2017, 2018) does not indicate that she recognized the inconsistency of utilizing zero-field rates in the presence of strong magnetic fields. Instead, she excluded these rates because of difficulties related to factorization problems, which prevent an analytical solution of the SEE for any B ≠ 0 (we refer readers to the last paragraph of Sect. 2.2.1 of Bommier 2017).
We note that the behavior of the 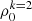 when depolarizing collisions are increased via increasing nH is similar to that obtained when the depolarizing effect of a magnetic field is increased. However, when the magnetic field is increased, the alignment is not completely destroyed and a residual remains, but when collisions increase (nH ≥ 1017) the alignment becomes zero (there is no saturation regime for collisions).
when depolarizing collisions are increased via increasing nH is similar to that obtained when the depolarizing effect of a magnetic field is increased. However, when the magnetic field is increased, the alignment is not completely destroyed and a residual remains, but when collisions increase (nH ≥ 1017) the alignment becomes zero (there is no saturation regime for collisions).
Circular polarization can be produced, for example, by illuminating the atom with circularly polarized radiation, or by the alignment-to-orientation conversion mechanism, which can be triggered by the PB effect (see, e.g., Landi Degl’Innocenti & Landolfi 2004).
Acknowledgments
This research work was funded by Institutional Fund Projects under grant no. (IFPIP:230-130-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
References
- Alsina Ballester, E. 2022, A&A, 666, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo, Bueno J. 2021, Phys. Rev. Lett., 127, 081101 [NASA ADS] [CrossRef] [Google Scholar]
- Alsina Ballester, E., Belluzzi, L., & Trujillo, Bueno J. 2022, A&A, 664, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asensio Ramos, A., & Trujillo Bueno, J. 2006, ApJ, 636, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Belli, S., Buffa, G., Di Lieto, A., et al. 2000, J. Mol. Spectrosc., 201, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Fluri, D. M. 2004, A&A, 417, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Braun, P. A., Fluri, D. M., & Solanki, S. K. 2005, A&A, 444, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bivona, S., Burlon, R., Ferrante, G., & Leone, C. 2005, J. Phys. B: At. Mol. Opt. Phys., 38, S131 [NASA ADS] [CrossRef] [Google Scholar]
- Bommier, V. 2017, A&A, 607, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bommier, V. 2018, A&A, 619, C1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 [NASA ADS] [Google Scholar]
- Buffa, G., & Tarrini, O. 2011, J. Chem. Phys., 134, 174310 [NASA ADS] [CrossRef] [Google Scholar]
- Derouich, M. 2004, PhD Thesis, Paris VII-Denis Diderot University, Paris, France, https://tel.archives-ouvertes.fr/tel-00331859 [Google Scholar]
- Derouich, M. 2008, A&A, 481, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M. 2012, A&A, 545, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M. 2020, ApJS, 247, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Derouich, M., Sahal-Bréchot, S., & Barklem, P. S. 2003, A&A, 409, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Trujillo Bueno, J., & Manso Sainz, R. 2007, A&A, 472, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Radi, A., & Barklem, P. S. 2015, A&A, 584, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faurobert-Scholl, M., Feautrier, N., Machefert, F., Petrovay, K., & Spielfiedel, A. 1995, A&A, 298, 289 [NASA ADS] [Google Scholar]
- Green, S. 1988, J. Chem. Phys., 88, 7331 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, E. L. 1929, Phys. Rev., 34, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Kerkeni, B., & Bommier, V. 2002, A&A, 394, 707 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerkeni, B., Spielfiedel, A., & Feautrier, N. 2000, A&A, 358, 373 [NASA ADS] [Google Scholar]
- Kerkeni, B., Barklem, P. S., Spielfiedel, A., & Feautrier, N. 2004, J. Phys. B, 37, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Krems, R., & Dalgarno, A. 2004, in Fundamental World of Quantum Chemistry, eds. E. J. Brändas, & E. S. Kryachko (Kluwer), 3, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) [Google Scholar]
- Manso Sainz, R., & Landi Degl’Innocenti, E. 2002, A&A, 394, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nagendra, K. N., Sowmya, K., Sampoorna, M., Stenflo, J. O., & Anusha, L. S. 2020, ApJ, 898, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Nienhuis, G. 1976, J. Phys. B: Atom. Molec. Phys., 9, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 1977, Prog. Quantum Electronics, 5, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., & Bommier, V. 2014, Adv. Space Res., 54, 1164 [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., & Bommier, V. 2019, ASP Conf. Ser., 526, 35 [Google Scholar]
- Sahal-Bréchot, S., Derouich, M., Bommier, V., & Barklem, P. S. 2007, A&A, 465, 66 [Google Scholar]
- Schadee, A. 1978, J. Quant. Spec. Radiat. Transf., 19, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, A. I., Fluri, D. M., Berdyugina, S. V., Bianda, M., & Ramelli, R. 2011, A&A, 529, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smitha, H. N., Nagendra, K. N., Stenflo, J. O., Bianda, M., & Ramelli, R. 2014, ApJ, 794, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., Trujillo Bueno, J., & Landi Degl’Innocenti, E. 2005, ApJS, 160, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Sowmya, K., Nagendra, K. N., Sampoorna, M., & Stenflo, J. O. 2015, ApJ, 814, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Sowmya, K., Nagendra, K. N., Sampoorna, M., & Stenflo, J. O. 2019, ASP Conf. Ser., 526, 43 [Google Scholar]
- Stenflo, J. O. 1994, Solar Magnetic Fields: Polarized Radiation Diagnostics, Astrophys. Space Sci. Lib., (Dordrecht: Kluwer Academic Publishers), 189 [Google Scholar]
- Trujillo Bueno, J. 2001, ASP Conf. Ser., 236, 161 [Google Scholar]
- Trujillo Bueno, J., Casini, R., Landolfi, M., & Landi Degl’Innocenti, E. 2002, ApJ, 566, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Tscherbul, T. V., & Dalgarno, A. 2010, J. Chem. Phys., 133, 184104 [NASA ADS] [CrossRef] [Google Scholar]
- van Vleck, J. H. 1926, Phys. Rev., 28, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Volpi, A., & Bohn, J. L. 2002, Phys. Rev. A, 65, 052712 [CrossRef] [Google Scholar]
Appendix A: The statistical Equilibrium equations
In the system of equations below, 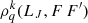 denote the atomic density matrix elements describing the hyperfine structure levels F and F′ for the level with orbital angular momentum L, electronic angular momentum J and nuclear spin I. The total angular momentum F takes values between |J − I| and J + I; k denotes the tensorial order of the atomic density matrix element.
denote the atomic density matrix elements describing the hyperfine structure levels F and F′ for the level with orbital angular momentum L, electronic angular momentum J and nuclear spin I. The total angular momentum F takes values between |J − I| and J + I; k denotes the tensorial order of the atomic density matrix element. 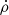 represents the variation in ρ with time.
represents the variation in ρ with time. 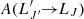 and
and 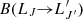 denote Einstein’s coefficients for spontaneous emission and absorption, respectively.
denote Einstein’s coefficients for spontaneous emission and absorption, respectively. 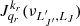 indicates the value of the radiation field tensor of order kr at the frequency
indicates the value of the radiation field tensor of order kr at the frequency 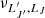 . Dk(LJ, F F′) and
. Dk(LJ, F F′) and 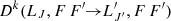 respectively denote the collisional relaxation and the collisional transfer rates affecting the matrix element. In order to calculate the
respectively denote the collisional relaxation and the collisional transfer rates affecting the matrix element. In order to calculate the 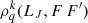 unknowns, we have assumed statistical equilibrium, i.e.,
unknowns, we have assumed statistical equilibrium, i.e., 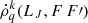 = 0. It is important to note that since the resulting system of equations is not linearly independent, one of the equations associated with the population of the sublevels, typically
= 0. It is important to note that since the resulting system of equations is not linearly independent, one of the equations associated with the population of the sublevels, typically 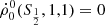 , which corresponds to the ground sublevel population, must be replaced by the trace equation
, which corresponds to the ground sublevel population, must be replaced by the trace equation 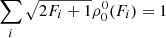 .
.
All Figures
 |
Fig. 1. Crossings between the hyperfine sublevels of the state 2P3/2 of Na I due to magnetic-field-strength effects (this figure is taken from Landi Degl’Innocenti & Landolfi 2004). |
| In the text | |
 |
Fig. 2. Emergent alignment for different HFS KI levels as a function of the density of neutral hydrogen nH. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



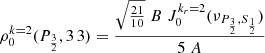
![$$ \begin{aligned}&\qquad \qquad \quad \times {\ {\rho _0}}^{ {k}= {0}} ( {S}_\frac{ {1}}{ {2}}, 2 \, 2) + \bigg {[ } \frac{\sqrt{6}\ \; B \; J_0^{k_r=0}(\nu _{{P_\frac{3}{2},S_\frac{1}{2}}})}{5 \; A } \nonumber \\&\qquad \qquad \qquad +\frac{2\sqrt{3}\ B \; J_0^{k_r=2}(\nu _{{P_\frac{3}{2},S_\frac{1}{2}}})}{35 \; A }\bigg {] } \times {\rho }^{ {k}= {2}} ({S}_\frac{ {1}}{ {2}}, 2 \, 2) \nonumber \\&\qquad \qquad \quad + \frac{\sqrt{\frac{3}{5}} \; B \; J_0^{k_r=2}(\nu _{{P_\frac{3}{2},S_\frac{1}{2}}})}{35 \; A } \times {\rho }^{{k}={4}}({S}_\frac{1}{2}, 2 \, 2)\nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq18.gif)
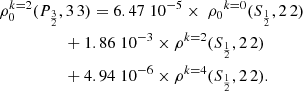
![$$ \begin{aligned} \dot{\rho }^0_0 (S_{\frac{1}{2}},1\,1) \!\!\!&= \!\!\! -\Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J^{0}_{0}(\nu _{{P_{\frac{1}{2}},S_{\frac{1}{2}}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J^{0}_{0}(\nu _{{P_{\frac{3}{2}},S_{\frac{1}{2}}}}) + D^0(S_{\frac{1}{2}},1\, 1) \Big ] \rho ^0_0(S_{\frac{1}{2}},1\, 1) \\&\!\!\! +\frac{1}{6} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{1}{2}},1\, 1) + D^0(S_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! S_{\frac{1}{2}},1\, 1) \rho ^0_0(S_{\frac{1}{2}},2\, 2) +\frac{1}{2} \sqrt{\frac{5}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{1}{2}},2\, 2) \nonumber \\&\!\!\! +\frac{1}{\sqrt{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},0\, 0) +\frac{5}{6} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},1\, 1) +\frac{1}{2} \sqrt{\frac{5}{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},2\, 2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq34.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(S_{\frac{1}{2}},1\, 1) \!\!\!&= \!\!\! -\Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J^{0}_{0}(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J^{0}_{0}(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^2(S_{\frac{1}{2}},1\,1) \Big ] \rho ^2_0(S_{\frac{1}{2}},1\, 1) \\&\!\!\! -\frac{1}{12} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,1)+D^2(S_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! S_{\frac{1}{2}},1\,1) \rho ^2_0(S_{\frac{1}{2}},2\,2) +\frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,2) \nonumber \\&\!\!\! -\frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,1)+\frac{1}{4}\sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,2) +\frac{1}{\sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},0\,2) \nonumber \\&\!\!\! -\frac{5}{12} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,1)+\frac{\sqrt{5}}{4} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,2) +\frac{1}{\sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,0) \nonumber \\&\!\!\! -\frac{\sqrt{5}}{4} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,1)+\frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq35.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(S_{\frac{1}{2}},1\,2) \!\!\!&= \!\!\! -\Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J^{0}_{0}(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J^{0}_{0}(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^2(S_{\frac{1}{2}},1\,2) \Big ] \rho ^2_0(S_{\frac{1}{2}},1\,2) \\&\!\!\!\! +\frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,1) -\frac{1}{12} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,2) -\frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,1) \nonumber \\&\!\!\!\! +\frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,2)+\frac{1}{\sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},0\,2) -\frac{1}{4} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\!\! +\frac{\sqrt{5}}{12} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,2)+\frac{1}{3} \sqrt{\frac{7}{2}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,3) +\frac{1}{4 \sqrt{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,1) \nonumber \\&\!\!\!\! -\frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,2)+\sqrt{\frac{7}{15}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq36.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(S_{\frac{1}{2}},2\,1) \!\!\!&= \!\!\! - \Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^2(S_{\frac{1}{2}},2\,1) \Big ] \rho ^2_0(S_{\frac{1}{2}},2\,1) \\&\!\!\! - \frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,1)- \frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,2) - \frac{1}{12} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,1) \nonumber \\&\!\!\! - \frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,2)+ \frac{1}{4} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,1) + \frac{1}{4 \sqrt{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,2) \nonumber \\&\!\!\! - \frac{1}{\sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,0)+ \frac{\sqrt{5}}{12} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,2) \nonumber \\&\!\!\! - \frac{1}{3} \sqrt{\frac{7}{2}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},3\,1)+ \sqrt{\frac{7}{15}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},3\,2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq37.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(S_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^0(S_{\frac{1}{2}},2\,2) \Big ] \rho ^0_0(S_{\frac{1}{2}},2\,2) \\&\!\!\! + \frac{1}{2} \sqrt{\frac{5}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{1}{2}},1\,1)+ \frac{1}{2} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{1}{2}},2\,2) + \frac{1}{2 \sqrt{15}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\! + \frac{1}{2} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},2\,2)+ \sqrt{\frac{7}{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^0_0(P_{\frac{3}{2}},3\,3) + D^0(S_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! S_{\frac{1}{2}},2\,2) \rho ^0_0(S_{\frac{1}{2}},1\,1) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq38.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(S_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^2(S_{\frac{1}{2}},2\,2) \Big ] \rho ^2_0(S_{\frac{1}{2}},2\,2) \\&\!\!\! + \frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,1)+ \frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},1\,2) - \frac{1}{4} \sqrt{\frac{7}{3}} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,1) \nonumber \\&\!\!\! + \frac{1}{4} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{1}{2}},2\,2)+ \frac{1}{20} \sqrt{\frac{7}{3}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,1) + \frac{1}{4} \sqrt{\frac{7}{15}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,2) \nonumber \\&\!\!\! + \frac{1}{5 \sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},1\,3)- \frac{1}{4} \sqrt{\frac{7}{15}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,1) + \frac{1}{4} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,2) \nonumber \\&\!\!\! + \frac{1}{\sqrt{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},2\,3)+ \frac{1}{5\sqrt{6}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},3\,1) - \frac{1}{\sqrt{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},3\,2) \nonumber \\&\!\!\! +\frac{2\sqrt{6}}{5} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^2_0(P_{\frac{3}{2}},3\,3)+ D^2(S_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! S_{\frac{1}{2}},2\,2) \rho ^2_0(S_{\frac{1}{2}},1\,1) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq39.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(S_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) + D^4(S_{\frac{1}{2}},2\,2) \Big ] \rho ^4_0(S_{\frac{1}{2}},2\,2) \\&\!\!\! - \frac{1}{3} A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{1}{2}},2\,2)+ \frac{1}{\sqrt{10}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},1\,3) - \frac{1}{3} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},2\,2) \nonumber \\&\!\!\! + \frac{1}{3} \sqrt{\frac{5}{2}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},2\,3)+ \frac{1}{\sqrt{10}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},3\,1) - \frac{1}{3} \sqrt{\frac{5}{2}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},3\,2) \nonumber \\&+ \frac{1}{3} \sqrt{\frac{11}{5}} A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) \rho ^4_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq40.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{1}{2}},1\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \Big ] \rho ^0_0(P_{\frac{1}{2}},1\,1) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{6} \rho ^0_0(S_{\frac{1}{2}},1\,1) + \frac{1}{2} \sqrt{\frac{5}{3}} \rho ^0_0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{1}{12} \rho ^2_0(S_{\frac{1}{2}},1\,1) - \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},1\,2) + \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^0_0(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{3}{2}},0\,0 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^0_0(P_{\frac{3}{2}},0\,0) + D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^0_0(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\! + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^0_0(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^0_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq41.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{1}{2}},1\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \Big ] \rho ^2_0(P_{\frac{1}{2}},1\,1) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \\&\!\!\! \times \!\left\{ \! - \frac{1}{12} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},1\,2) - \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,2) - \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \!\right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \!\left\{ \! \!-\! \frac{1}{12} \rho ^0_0(S_{\frac{1}{2}},1\,1) \!-\! \frac{1}{6 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},1\,1) \!+\! \frac{1}{4 \sqrt{15}} \rho ^0_0(S_{\frac{1}{2}},2\,2) \!+\! \frac{1}{2 \sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \!+\! 3 \sqrt{\frac{3}{70}} \rho ^4_0(S_{\frac{1}{2}},2\,2) \!\right\} \! \!\Bigg ]\! \nonumber \\&\!\!\! + D^2(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^2_0(P_{\frac{1}{2}},2\,2) + D^2(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^2_0(P_{\frac{3}{2}},1\,1) + D^2(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^2_0(P_{\frac{3}{2}},2\,2) \nonumber \\&\!\!\! + D^2(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \rho ^2_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq42.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{1}{2}},1\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{1}{2}},1\,2) + D^0(P_{\frac{1}{2}},1\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,2) \Big ] \rho ^2_0(P_{\frac{1}{2}},1\,2) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \times \\&\!\!\! \Bigg [ J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},1\,1) - \frac{1}{12} \rho ^2_0(S_{\frac{1}{2}},1\,2) - \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{1}{4} \rho ^0_0(S_{\frac{1}{2}},1\,1) + \frac{1}{4} \sqrt{\frac{3}{5}} \rho ^0_0(S_{\frac{1}{2}},2\,2) + \frac{1}{6 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},1\,2) \right. \nonumber \\&\!\!\! \left. + \frac{1}{2 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{\sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},2\,2) - \sqrt{\frac{3}{70}} \rho ^4_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq43.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{1}{2}},2\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{1}{2}},2\,1) + D^0(P_{\frac{1}{2}},2\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,1) \Big ] \rho ^2_0(P_{\frac{1}{2}},2\,1) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ - J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},1\,2) + \frac{1}{12} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \rho ^0_0(S_{\frac{1}{2}},1\,1) - \frac{1}{4} \sqrt{\frac{3}{5}} \rho ^0_0(S_{\frac{1}{2}},2\,2) + \frac{1}{2 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},1\,2) \right. \nonumber \\&\!\!\! \left. + \frac{1}{6 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},2\,1) - \frac{1}{\sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},2\,2) + \sqrt{\frac{3}{70}} \rho ^4_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq44.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \Big ] \rho ^0_0(P_{\frac{1}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{5}{3}} \rho ^0(S_{\frac{1}{2}},1\,1) + \frac{1}{2} \rho ^0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4 \sqrt{15}} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{4} \sqrt{\frac{3}{5}} \rho ^2_0(S_{\frac{1}{2}},1\,2) - \frac{1}{4} \sqrt{\frac{3}{5}} \rho ^2_0(S_{\frac{1}{2}},2\,1) - \frac{1}{4} \sqrt{\frac{7}{5}} \rho ^2_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^0(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^0_0(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{3}{2}},0\,0 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^0_0(P_{\frac{3}{2}},0\,0) + D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^0_0(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\! + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^0_0(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^0_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq45.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \Big ] \rho ^2_0(P_{\frac{1}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \sqrt{\frac{7}{3}} \rho _0^2 (S_{\frac{1}{2}},1\,1) + \frac{1}{4} \sqrt{\frac{7}{3}} \rho _2^2 (S_{\frac{1}{2}},1\,2) - \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^2_0(S_{\frac{1}{2}},2\,1) + \frac{1}{4} \rho ^2_0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \sqrt{\frac{7}{3}} \rho ^0_0(S_{\frac{1}{2}},1\,1) - \frac{1}{4} \sqrt{\frac{7}{5}} \rho ^0_0(S_{\frac{1}{2}},2\,2) + \frac{1}{2 \sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{\sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},1\,2) \right. \nonumber \\&\!\!\! \left. - \frac{1}{\sqrt{42}} \rho ^2_0(S_{\frac{1}{2}},2\,1) - \frac{5}{14 \sqrt{2}} \rho ^2_0(S_{\frac{1}{2}},2\,2) - \frac{3}{7\sqrt{10}} \rho ^4_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^2(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^2_0(P_{\frac{1}{2}},1\,1) + D^2(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^2_0(P_{\frac{3}{2}},1\,1) + D^2(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^2_0(P_{\frac{3}{2}},2\,2) \nonumber \\&\!\!\! + D^2(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^2_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq46.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{1}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{1}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \Big ] \rho ^4_0(P_{\frac{1}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{1}{2}}) \Bigg [ - \frac{1}{3} J_0^0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \rho ^4_0(S_{\frac{1}{2}},2\,2) + J^2_0(\nu _{P_{\frac{1}{2}},S_{\frac{1}{2}}}) \times \nonumber \\&\!\!\! \left\{ 3 \sqrt{\frac{3}{70}} \rho ^2_0(S_{\frac{1}{2}},1\,1) - \sqrt{\frac{3}{70}} \rho ^2_0(S_{\frac{1}{2}},1\,2) + \sqrt{\frac{3}{70}} \rho ^2_0(S_{\frac{1}{2}},2\,1) - \frac{3}{7 \sqrt{10}} \rho ^2_0(S_{\frac{1}{2}},2\,2) - \frac{5\sqrt{2}}{21} \rho ^4_0(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^4(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^4_0(P_{\frac{3}{2}},2\,2) + D^4(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \rho ^4_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq47.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{3}{2}},0\,0) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{3}{2}},0\,0) \Big ] \rho ^0_0(P_{\frac{3}{2}},0\,0) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Big [ \frac{1}{2\sqrt{3}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho ^0_0(S_{\frac{1}{2}},1\,1) \\&\!\!\! +\frac{1}{2\sqrt{3}} J^2_0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho ^2_0(S_{\frac{1}{2}},1\,1) \Big ] +D^0(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},0\,0) \rho ^0_0(P_{\frac{1}{2}},1\,1) +D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},0\,0) \rho ^0_0(P_{\frac{1}{2}},2\,2) \nonumber \\&\!\!\! +D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},0\,0) \rho ^0_0(P_{\frac{3}{2}},1\,1) +D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},0\,0) \rho ^0_0(P_{\frac{3}{2}},2\,2) +D^0(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},0\,0) \rho ^0_0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq48.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},0\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},0\,2) \Big ] \rho ^2_0(P_{\frac{3}{2}},0\,2) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2\sqrt{6}} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{2\sqrt{6}} \rho ^2_0(S_{\frac{1}{2}},1\,2) \right\} \nonumber \\&\!\!\! + J^2_0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2\sqrt{6}} \rho ^0_0(S_{\frac{1}{2}},1\,1) - \frac{1}{4\sqrt{3}} \rho ^2_0(S_{\frac{1}{2}},1\,1) + \frac{1}{4\sqrt{3}} \rho ^2_0(S_{\frac{1}{2}},1\,2) \right\} \Bigg ] \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq49.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{3}{2}},1\,1) \!\!\!&= \!\!\! -\Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{3}{2}},1\,1) + D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \Big ] \rho _0^0(P_{\frac{3}{2}},1\,1) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{5}{12} \rho _0^0(S_{\frac{1}{2}},1\,1) + \frac{1}{4 \sqrt{15}} \rho _0^0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! +J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{5}{24} \rho _0^2(S_{\frac{1}{2}},1\,1) + \frac{1}{8} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{1}{8} \rho _0^2(S_{\frac{1}{2}},2\,1) + \frac{1}{40} \sqrt{\frac{7}{3}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^0(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^0(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^0(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{3}{2}} 0\,0 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^0(P_{\frac{3}{2}},0\,0) \nonumber \\&\!\!\! + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^0(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq50.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},1\,1) \!\!\!&= \!\!\! -\Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},1\,1) + D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,1) \Big ] \rho _0^2(P_{\frac{3}{2}},1\,1) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{5}{24} \rho _0^2(S_{\frac{1}{2}},1\,1) - \frac{1}{8} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{1}{8} \rho _0^2(S_{\frac{1}{2}},2\,1) + \frac{1}{40} \sqrt{\frac{7}{3}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{5}{24} \rho _0^0(S_{\frac{1}{2}},1\,1) + \frac{1}{40 \sqrt{15}} \rho _0^0(S_{\frac{1}{2}},2\,2) - \frac{5}{12 \sqrt{2}} \rho _0^2(S_{\frac{1}{2}},1\,1) + \frac{1}{20 \sqrt{42}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right. \nonumber \\&\!\!\! \left. + \frac{3}{10} \sqrt{\frac{3}{70}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] + D^2(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^2(P_{\frac{1}{2}},1\,1) + D^2(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^2(P_{\frac{1}{2}},2\,2) \nonumber \\&\!\!\! + D^2(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^2(P_{\frac{3}{2}},2\,2) + D^2(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},1\,1) \rho _0^2(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq51.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},1\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},1\,2) + D^0(P_{\frac{3}{2}},1\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},1\,2) \Big ] \rho _0^2(P_{\frac{3}{2}},1\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{\sqrt{5}}{8} \rho _2^2(S_{\frac{1}{2}},1\,1) + \frac{\sqrt{5}}{24} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{1}{8\sqrt{5}} \rho _0^2(S_{\frac{1}{2}},2\,1) + \frac{1}{8} \sqrt{\frac{7}{15}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{\sqrt{5}}{8} \rho _0^0(S_{\frac{1}{2}},1\,1) + \frac{ \sqrt{3}}{40} \rho _0^0(S_{\frac{1}{2}},2\,2) - \frac{1}{12} \sqrt{\frac{5}{2}} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{1}{4 \sqrt{10}} \rho _0^2(S_{\frac{1}{2}},2\,1) \right. \nonumber \\&\!\!\! \left. + \frac{1}{2 \sqrt{210}} \rho _0^2(S_{\frac{1}{2}},2\,2) - \frac{1}{10} \sqrt{\frac{3}{14}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq52.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},1\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},1\,3) \Big ] \rho _0^2(P_{\frac{3}{2}},1\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{6} \sqrt{\frac{7}{2}} \rho _0^2(S_{\frac{1}{2}},1\,2) \right. \\&\!\!\! \left. + \frac{1}{10 \sqrt{6}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{10} \sqrt{\frac{21}{10}} \rho _0^0(S_{\frac{1}{2}},2\,2) - \frac{5}{12\sqrt{7}} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{23}{140 \sqrt{3}} \rho _0^2(S_{\frac{1}{2}},2\,2) + \frac{1}{70}\sqrt{\frac{3}{5}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq53.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},1\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},1\,3) \Big ] \rho _0^4(P_{\frac{3}{2}},1\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{1}{2 \sqrt{10}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{1}{2} \sqrt{\frac{3}{7}} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{3}{70} \rho _0^2(S_{\frac{1}{2}},2\,2) - \frac{\sqrt{5}}{28} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq54.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},2\,0) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},2\,0) \Big ] \rho _0^2(P_{\frac{3}{2}},2\,0) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2\sqrt{6}} \rho _0^2(S_{\frac{1}{2}},1\,1) \right. \\&\!\!\! \left. - \frac{1}{2\sqrt{6}} \rho _0^2(S_{\frac{1}{2}},2\,1) \right\} + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2\sqrt{6}} \rho _0^0(S_{\frac{1}{2}},1\,1) -\frac{1}{4\sqrt{3}} \rho _0^2(S_{\frac{1}{2}},1\,1) -\frac{1}{4\sqrt{3}} \rho _0^2(S_{\frac{1}{2}},2\,1) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq55.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},2\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},2\,1) + D^0(P_{\frac{3}{2}},2\,1 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,1) \Big ] \rho _0^2(P_{\frac{3}{2}},2\,1) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{\sqrt{5}}{8} \rho _0^2(S_{\frac{1}{2}},1\,1) + \frac{1}{8\sqrt{5}} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{\sqrt{5}}{24} \rho _0^2(S_{\frac{1}{2}},2\,1) - \frac{1}{8} \sqrt{\frac{7}{15}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{\sqrt{5}}{8} \rho _0^0(S_{\frac{1}{2}},1\,1) - \frac{\sqrt{3}}{40} \rho _0^0(S_{\frac{1}{2}},2\,2) - \frac{1}{4 \sqrt{10}} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{1}{12} \sqrt{\frac{5}{2}} \rho _0^2(S_{\frac{1}{2}},2\,1) . \right. \nonumber \\&\!\!\! \left. - \frac{1}{2 \sqrt{210}} \rho _0^2(S_{\frac{1}{2}},2\,2) + \frac{1}{10} \sqrt{\frac{3}{14}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq56.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{3}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \Big ] \rho _0^0(P_{\frac{3}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{4} \sqrt{\frac{5}{3}} \rho _0^0(S_{\frac{1}{2}},1\,1) +\frac{1}{4} \rho _0^0(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{8 \sqrt{15}} \rho _0^2(S_{\frac{1}{2}},1\,1) - \frac{1}{8} \sqrt{\frac{3}{5}} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{1}{8} \sqrt{\frac{3}{5}} \rho _0^2(S_{\frac{1}{2}},2\,1) - \frac{1}{8} \sqrt{\frac{7}{5}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^0(P_{\frac{1}{2}},1\,1,P_{\frac{3}{2}},2\,2) \rho _0^0(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2)\rho _0^0(P_{\frac{1}{2}},2\,2) + D^0(P_{\frac{3}{2}},0\,0 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2)\rho _0^0(P_{\frac{3}{2}},0\,0) \nonumber \\&\!\!\! + D^0(P_{\frac{3}{2}},1 1 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^0(P_{\frac{3}{2}},1\,1) + D^0(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^0(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq57.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \Big ] \rho _0^2(P_{\frac{3}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{8} \sqrt{\frac{7}{3}} \rho _0^2(S_{\frac{1}{2}},1\,1) - \frac{1}{8} \sqrt{\frac{7}{3}} \rho _0^2(S_{\frac{1}{2}},1\,2) + \frac{1}{8} \sqrt{\frac{7}{3}} \rho _0^2(S_{\frac{1}{2}},2\,1) + \frac{1}{8} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{8} \sqrt{\frac{7}{3}} \rho _0^0(S_{\frac{1}{2}},1\,1) - \frac{1}{8} \sqrt{\frac{7}{5}} \rho _0^0(S_{\frac{1}{2}},2\,2) + \frac{1}{4 \sqrt{42}} \rho _0^2(S_{\frac{1}{2}},1\,1) - \frac{1}{2 \sqrt{42}} \rho _0^2(S_{\frac{1}{2}},1\,2) \right. \nonumber \\&\!\!\! \left. + \frac{1}{2 \sqrt{42}} \rho _0^2(S_{\frac{1}{2}},2\,1) - \frac{5}{28 \sqrt{2}} \rho _0^2(S_{\frac{1}{2}},2\,2) - \frac{3}{14\sqrt{10}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^2(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^2(P_{\frac{1}{2}},1\,1) + D^2(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^2(P_{\frac{1}{2}},2\,2) + D^2(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^2(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\! + D^2(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^2(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq58.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},2\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},2\,2) + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{1}{2}},2\,2) \Big ] \rho _0^4(P_{\frac{3}{2}},2\,2) \\&\!\!\! + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ - \frac{1}{6} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{3}{2} \sqrt{\frac{3}{70}} \rho _0^2(S_{\frac{1}{2}},1\,1) + \frac{1}{2} \sqrt{\frac{3}{70}} \rho _0^2(S_{\frac{1}{2}},1\,2) \right. \nonumber \\&\!\!\! \left. - \frac{1}{2} \sqrt{\frac{3}{70}} \rho _0^2(S_{\frac{1}{2}},2\,1) - \frac{3}{14 \sqrt{10}} \rho _0^2(S_{\frac{1}{2}},2\,2) - \frac{5}{21\sqrt{2}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \\&\!\!\! + D^4(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^4(P_{\frac{1}{2}},2\,2) + D^4(P_{\frac{3}{2}},3\,3 \!\!\rightarrow \!\! P_{\frac{3}{2}},2\,2) \rho _0^4(P_{\frac{3}{2}},3\,3) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq59.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},2\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},2\,3) \Big ] \rho _0^2(P_{\frac{3}{2}},2\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{7}{15}} \rho _0^2(S_{\frac{1}{2}},1\,2) \right. \\&\!\!\! \left. + \frac{1}{2\sqrt{5}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ - \frac{1}{10} \sqrt{7} \rho _0^0(S_{\frac{1}{2}},2\,2) + \frac{1}{2\sqrt{210}} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{1}{14 \sqrt{10}} \rho _0^2(S_{\frac{1}{2}},2\,2) + \frac{3}{70\sqrt{2}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq60.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},2\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},2\,3) \Big ] \rho _0^4(P_{\frac{3}{2}},2\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{1}{6} \sqrt{\frac{5}{2}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{3}{7}} \rho _0^2(S_{\frac{1}{2}},1\,2) - \frac{3}{14} \rho _0^2(S_{\frac{1}{2}},2\,2) + \frac{\sqrt{5}}{84} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq61.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},3\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},3\,1) \Big ] \rho _0^2(P_{\frac{3}{2}},3\,1) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ -\frac{1}{6} \sqrt{\frac{7}{2}} \rho _0^2(S_{\frac{1}{2}},2\,1) \right. \\&\!\!\! \left. +\frac{1}{10 \sqrt{6}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{10} \sqrt{\frac{21}{10}} \rho _0^0(S_{\frac{1}{2}},2\,2) +\frac{5}{12\sqrt{7}} \rho _0^2(S_{\frac{1}{2}},2\,1) -\frac{23}{140 \sqrt{3}} \rho _0^2(S_{\frac{1}{2}},2\,2) +\frac{1}{70} \sqrt{\frac{3}{5}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq62.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},3\,1) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},3\,1) \Big ] \rho _0^4(P_{\frac{3}{2}},3\,1) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{1}{2 \sqrt{10}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{3}{7}} \rho _0^2(S_{\frac{1}{2}},2\,1) +\frac{3}{70} \rho _0^2(S_{\frac{1}{2}},2\,2) -\frac{1}{28} \sqrt{5} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq63.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},3\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},3\,2) \Big ] \rho _0^2(P_{\frac{3}{2}},3\,2) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{7}{15}} \rho _0^2(S_{\frac{1}{2}},2\,1) \right. \\&\!\!\! \left. -\frac{1}{2\sqrt{5}} \rho _0^2(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2\sqrt{210}} \rho _0^2(S_{\frac{1}{2}},2\,1) +\frac{1}{10} \sqrt{7} \rho _0^0(S_{\frac{1}{2}},2\,2) +\frac{1}{14 \sqrt{10}} \rho _0^2(S_{\frac{1}{2}},2\,2) -\frac{3}{70\sqrt{2}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq64.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},3\,2) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},3\,2) \Big ] \rho _0^4(P_{\frac{3}{2}},3\,2) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ - \frac{1}{6} \sqrt{\frac{5}{2}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{2} \sqrt{\frac{3}{7}} \rho _0^2(S_{\frac{1}{2}},2\,1) +\frac{3}{14} \rho _0^2(S_{\frac{1}{2}},2\,2) -\frac{\sqrt{5}}{84} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq65.gif)
![$$ \begin{aligned} \dot{\rho }^0_0(P_{\frac{3}{2}},3\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^0(P_{\frac{3}{2}},3\,3) \Big ] \rho _0^0(P_{\frac{3}{2}},3\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{1}{2} \sqrt{\frac{7}{5}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^0(S_{\frac{1}{2}},2\,2) \\&\!\!\! + \frac{1}{10} J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^2(S_{\frac{1}{2}},2\,2) \Bigg ] + D^0(P_{\frac{1}{2}},1\,1,P_{\frac{3}{2}},3\,3) \rho _0^0(P_{\frac{1}{2}},1\,1) + D^0(P_{\frac{1}{2}},2\,2,P_{\frac{3}{2}},3\,3) \rho _0^0(P_{\frac{1}{2}},2\,2) \nonumber \\&\!\!\! + D^0(P_{\frac{3}{2}},0\,0 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^0(P_{\frac{3}{2}},0\,0) + D^0(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^0(P_{\frac{3}{2}},1\,1) + D^0(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^0(P_{\frac{3}{2}},2\,2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq66.gif)
![$$ \begin{aligned} \dot{\rho }^2_0(P_{\frac{3}{2}},3\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^2(P_{\frac{3}{2}},3\,3) \Big ] \rho _0^2(P_{\frac{3}{2}},3\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{\sqrt{6}}{5} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^2(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{1}{5} \sqrt{\frac{21}{10}} \rho _0^0(S_{\frac{1}{2}},2\,2) +\frac{2\sqrt{3}}{35} \rho _0^2(S_{\frac{1}{2}},2\,2) +\frac{1}{35} \sqrt{\frac{3}{5}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \nonumber \\&\!\!\! + D^2(P_{\frac{1}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^2(P_{\frac{1}{2}},1\,1) + D^2(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^2(P_{\frac{1}{2}},2\,2) + D^2(P_{\frac{3}{2}},1\,1 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^2(P_{\frac{3}{2}},1\,1) \nonumber \\&\!\!\! +D^2(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^2(P_{\frac{3}{2}},2\,2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq67.gif)
![$$ \begin{aligned} \dot{\rho }^4_0(P_{\frac{3}{2}},3\,3) \!\!\!&= \!\!\! - \Big [ A(P_{\frac{3}{2}} \!\!\rightarrow \!\! S_{\frac{1}{2}}) + D^4(P_{\frac{3}{2}},3\,3) \Big ] \rho _0^4(P_{\frac{3}{2}},3\,3) + B(S_{\frac{1}{2}} \!\!\rightarrow \!\! P_{\frac{3}{2}}) \Bigg [ \frac{1}{6} \sqrt{\frac{11}{5}} J_0^0(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho _0^4(S_{\frac{1}{2}},2\,2) \\&\!\!\! + J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \left\{ \frac{3\sqrt{22}}{35} \rho _0^2(S_{\frac{1}{2}},2\,2) + \frac{1}{21} \sqrt{\frac{10}{11}} \rho _0^4(S_{\frac{1}{2}},2\,2) \right\} \Bigg ] + D^4(P_{\frac{1}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^4(P_{\frac{1}{2}},2\,2) \nonumber \\&\!\!\! + D^4(P_{\frac{3}{2}},2\,2 \!\!\rightarrow \!\! P_{\frac{3}{2}},3\,3) \rho _0^4(P_{\frac{3}{2}},2\,2) \nonumber \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq68.gif)
![$$ \begin{aligned} \dot{\rho }^6_0(P_{\frac{3}{2}},3\,3)&= - \Big [ A(P_{\frac{3}{2}} \rightarrow S_{\frac{1}{2}}) + D^6(P_{\frac{3}{2}},3\,3) \Big ] \rho ^6_0(P_{\frac{3}{2}},3\,3) + \frac{1}{2} \sqrt{\frac{15}{11}} B(S_{\frac{1}{2}} \rightarrow P_{\frac{3}{2}}) J_0^2(\nu _{P_{\frac{3}{2}},S_{\frac{1}{2}}}) \rho ^4_0(S_{\frac{1}{2}},2\,2) \end{aligned} $$](/articles/aa/full_html/2024/03/aa46080-23/aa46080-23-eq69.gif)