| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 8 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202348495 | |
| Published online | 11 December 2023 | |
Letter to the Editor
Detection of vibrationally excited C6H in the cold prestellar core TMC-1 with the QUIJOTE line survey⋆
1
Dept. de Astrofísica Molecular, Instituto de Física Fundamental (IFF-CSIC), C/ Serrano 121, 28006 Madrid, Spain
e-mail: jose.cernicharo@csic.ese-mail: r.fuentetaja@csic.es
2
Observatorio Astronómico Nacional (OAN, IGN), C/ Alfonso XII, 3 28014 Madrid, Spain
3
Centro de Desarrollos Tecnológicos, Observatorio de Yebes (IGN), 19141 Yebes, Guadalajara, Spain
Received:
5
November
2023
Accepted:
17
November
2023
In this work, we present the detection of twelve doublets with quantum numbers of N = 12–11 to N = 17–16 of the ν11(μ2Σ) vibrationally excited state of C6H towards TMC-1. This marks the first time that an excited vibrational state of a molecule has been detected in a cold starless core. The data are part of the QUIJOTE line survey gathered with the Yebes 40m radio telescope. The line intensities have been aptly reproduced with a rotational temperature of 6.2 ± 0.4 K and a column density of (1.2 ± 0.2)×1011 cm−2. We also analysed the ground state transitions of C6H, detecting fourteen lines with quantum numbers of J = 23/2–21/2 to J = 35/2 for each of the two 2Π3/2 and 2Π1/2 ladders. It is not possible to model the intensities of all the transitions of the ground state simultaneously using a single column density. We considered the two ladders as two different species and found that the rotational temperature is the same for both ladders, Trot(2Π3/2)=Trot(2Π1/2)=6.2 ± 0.2, achieving a result that is comparable to that of the ν11(2μΣ) state. The derived column densities are N(2Π3/2) = (6.2 ± 0.3)×1012 cm−2 and N(2Π1/2) = (8.0 ± 0.4)×1010 cm−2. The fraction of C6H molecules in its 2Π3/2, 2Π1/2, and ν11(μ2Σ) states is 96.8%, 1.3%, and 1.9%, respectively. Finally, we report that this vibrational mode has also been detected towards the cold cores Lupus-1A and L1495B, as well as the low-mass star forming cores L1527 and L483, with fractions of C6H molecules in this mode of 3.8%, 4.1%, 14.8%, and 6%, respectively.
Key words: astrochemistry / line: identification / molecular data / ISM: molecules / ISM: individual objects: TMC-1
© ESO 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The first detection of C6H in space has been achieved towards TMC-1 (Suzuki et al. 1986; Cernicharo et al. 1987) and in the direction of the carbon rich star IRC+10216 (Guélin et al. 1987a). The identification was based on ab initio calculations of the structure and electronic state of the molecule, which indicate that the ground state could be a 2Π state (Murakami et al. 1988), contrary to CCH and C4H, which have a 2Σ+ ground state. The detection in space of two series of harmonically lines with half-integer quantum numbers (lines from the 2Π3/2 and the 2Π1/2 ladders, Suzuki et al. 1986; Guélin et al. 1987a; Cernicharo et al. 1987) clearly supported the identification. Nevertheless, the assignment of the observed lines to this species was confirmed by the generation of the radical and the observation of its rotational spectrum in the laboratory (Pearson et al. 1988). The spin orbit constant, ASO, is −15.04 cm−1 (Linnartz et al. 1999). Hence, the energy of the 2Π1/2 ladder is ∼22 K above the 2Π3/2 one.
C6H has six stretching modes, ν1 − ν6, and five bending modes, ν7 − ν11 (Brown et al. 1999). The ν11 mode is the bending with the lowest energy, which has been estimated to be between 120 and 134 cm−1 (Brown et al. 1999; Cao & Peyerimhoff 2001). This bending mode produces a 2Δ and two 2Σ vibronic modes. One of the 2Σ states, labelled as μ2Σ by Zhao et al. (2011), and the 2Δ one have been identified in IRC+10216 during a search for C5N− (Cernicharo et al. 2008). The assignment was subsequently confirmed by extensive laboratory spectroscopy of C6H in its ν11 vibrationally excited state (Gottlieb et al. 2010).
The ν11 vibrational mode is affected by a strong Renner-Teller interaction resulting from the coupling of the degenerate bending vibration with the orbital angular momentum of an unpaired electron (Zhao et al. 2011). This coupling produces a considerably lowering of the energy of the μ2Σ vibronic mode. This energy has been estimated to be 20 ± 10 K (Gottlieb et al. 2010). In a detailed study involving the electronic transition B2Π–X2Π, this energy has been determined to be 11.0 ± 0.8 cm−1 (Zhao et al. 2011), namely, around 15.8 K. This value is below the energy the 2Π1/2 ladder of the ground electronic state. Hence, this vibronic mode of the ν11 vibrational state could be detected in sensitive line surveys of cold sources.
TMC-1 is a cold starless core located in Taurus at a distance of 140 pc (Cernicharo & Guélin 1987). Its kinetic temperature is 10 K and, so far, all observed lines correspond to rotational transitions of a large variety of molecular species in their ground vibrational state. Using the sensitive QUIJOTE1 line survey (Cernicharo et al. 2021a), we report the detection in TMC-1 of 12 lines of the ν11(μ2Σ) vibrational mode of C6H, and of 28 lines of the 2Π3/2 and 2Π1/2 ladders of its ground electronic state. It is the first time that emission from a vibrationally excited state has been detected in a cold astrophysical environment.
2. Observations
The observational data used in this work are part of QUIJOTE (Cernicharo et al. 2021a), a spectral line survey of TMC-1 in the Q-band carried out with the Yebes 40m telescope at the position 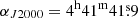 and
and 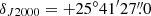 , corresponding to the cyanopolyyne peak (CP) in TMC-1. The receiver was built within the Nanocosmos project2 and consists of two cold high-electron mobility transistor amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarisations. Receiver temperatures achieved in the 2019 and 2020 runs vary from 22 K at 32 GHz to 42 K at 50 GHz. Some power adaptation in the down-conversion chains have reduced the receiver temperatures over the course of 2021 to 16 K at 32 GHz and 30 K at 50 GHz. The backends are 2 × 8 × 2.5 GHz fast Fourier transform (FFT) spectrometers with a spectral resolution of 38 kHz, providing the whole coverage of the Q-band in both polarisations. A more detailed description of the system is given by Tercero et al. (2021).
, corresponding to the cyanopolyyne peak (CP) in TMC-1. The receiver was built within the Nanocosmos project2 and consists of two cold high-electron mobility transistor amplifiers covering the 31.0–50.3 GHz band with horizontal and vertical polarisations. Receiver temperatures achieved in the 2019 and 2020 runs vary from 22 K at 32 GHz to 42 K at 50 GHz. Some power adaptation in the down-conversion chains have reduced the receiver temperatures over the course of 2021 to 16 K at 32 GHz and 30 K at 50 GHz. The backends are 2 × 8 × 2.5 GHz fast Fourier transform (FFT) spectrometers with a spectral resolution of 38 kHz, providing the whole coverage of the Q-band in both polarisations. A more detailed description of the system is given by Tercero et al. (2021).
The data of the QUIJOTE line survey presented here were gathered in several observing runs between November 2019 and July 2023. All observations were performed using frequency-switching observing mode with a frequency throw of 8 and 10 MHz. The total observing time on the source for data taken with frequency throws of 8 MHz and 10 MHz is 465 and 737 h, respectively. Hence, the total observing time on source is 1202 h. The measured sensitivity varies between 0.08 mK at 32 GHz and 0.2 mK at 49.5 GHz. The sensitivity of QUIJOTE is around 50 times better than that of previous line surveys in the Q band of TMC-1 (Kaifu et al. 2004). For each frequency throw, different local oscillator frequencies were used in order to remove possible side band effects in the down conversion chain. A detailed description of the QUIJOTE line survey is provided in Cernicharo et al. (2021a). The data analysis procedure has been described in Cernicharo et al. (2022). The main beam efficiency measured during our observations in 2022 varies from 0.66 at 32.4 GHz to 0.50 at 48.4 GHz (Tercero et al. 2021) and can be given across the Q-band by Beff = 0.797 exp[−(ν(GHz)/71.1)2]. The forward telescope efficiency is 0.97. The telescope beam size at half power intensity is 54.4″ at 32.4 GHz and 36.4″ at 48.4 GHz.
The intensity scale utilised in this study is the antenna temperature (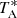 ). Calibration was performed using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985); Pardo2001. The absolute calibration uncertainty is 10%. However, the relative calibration between lines within the QUIJOTE survey is probably better because all the spectral features have common pointing and calibration errors. The data were analysed with the GILDAS package3.
). Calibration was performed using two absorbers at different temperatures and the atmospheric transmission model ATM (Cernicharo 1985); Pardo2001. The absolute calibration uncertainty is 10%. However, the relative calibration between lines within the QUIJOTE survey is probably better because all the spectral features have common pointing and calibration errors. The data were analysed with the GILDAS package3.
3. Results
The line identification in this work was performed using the MADEX code (Cernicharo 2012) and the CDMS catalogue (Müller et al. 2005). The spectroscopy of C6H in the ground electronic state is directly adopted from the CDMS catalogue. C6H has been previously observed in its ground electronic state in TMC-1 (Suzuki et al. 1986; Cernicharo et al. 1987). The ν11(μ2Σ) state is highly perturbed and high distortion constants are needed to reproduce the laboratory frequencies (Gottlieb et al. 2010). We fit all laboratory frequencies with distortion constants D, H, L, and M for the rotation, as well as D and H for the fine structure. The results have been implemented into the MADEX code to predict the frequencies of its rotational and fine structure transitions (see Appendix A). The adopted dipole moment of the molecule is 5.54 D (Woon 1995). We have asumed that it is the same for the ν11(μ2Σ) vibrationally excited state. However, the dipole moment for the rovibrational transitions ν11(μ2Σ) → X2Π is unknown. Moreover, the corresponding frequencies would lie in the millimeter and submillimeter frequency domains.
We detected a total of 40 lines of C6H within the QUIJOTE line survey. Their intensities range from 148 mK to ∼1 mK. The derived line parameters are given in Table B.1. Among these lines, we detected 12 transitions of the ν11(μ2Σ) vibrationally excited state. They involve quantum numbers from N = 12–11 to N = 17–16. For each rotational transition, two fine structure components were detected (J = N + 1/2 and J = N − 1/2; denoted as a and b in Tables B.1 and B.2). The lines are shown in Fig. 1. The hyperfine splitting of the lines of ν11(μ2Σ) state is smaller than that of the lines in the ground state and does not affect the line widths. Fourteen of the detected lines correspond to the 2Π3/2 ladder of the ground electronic state. They are the strongest transitions of C6H and their quantum numbers range from J = 23/2–21/2 to J = 35/2–33/2. For the 2Π1/2 ladder, we also detected 14 lines involving the same quantum numbers. They are are the weakest lines of C6H, that is, even weaker than those of the ν11(2Σ) state. The two ladders of the ground electronic state show two Lambda-type doubling components for each rotational transition (denoted as e and f in Table B.1 and in Fig. 2). The observed lines of the ground state are shown in Fig. 2. These lines are slightly broadened due to the hyperfine structure of each line (∼60 and 40 kHz for the 2Π3/2 and 2Π1/2 ladders, respectively). All the observed frequencies of the ground state are within 5 kHz of the predicted center frequencies for each transition. For the ν11(μ2Σ) mode we have merged the observed frequencies with the laboratory data of Gottlieb et al. (2010) to get an improved set of rotational, fine structure, and distortion constants (see Appendix A).
 |
Fig. 1. Selected transitions for the excited state of C6H in TMC-1. Left and right panels correspond to the J = N + 1/2 and J = N − 1/2 components of each transition, respectively. The abscissa corresponds to the local standard of rest (LSR) velocity. The derived line parameters are given in Table B.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in mK. Blanked channels correspond to negative features produced when folding the frequency-switched data. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectra for this species for Trot = 6.2 K and a column density of 1.2 × 1011 cm−2. |
 |
Fig. 2. Observed transitions in TMC-1 of the 2Π3/2 (two left columns) and 2Π1/2 (two right columns) states of C6H. The labels e and f correspond to the Lambda-type doubling components of each transition. The abscissa corresponds to the LSR velocity. The derived line parameters are given in Table B.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in mK. Blanked channels correspond to negative features produced when folding the frequency-switched data. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectra for this species (see Sect. 3). |
To estimate the column densities and rotational temperatures, we assumed that the source has a diameter of 80″ and that it has an uniform brightness distribution for all observed lines (Fossé et al. 2001, Fuentetaja et al., in prep.). The adopted intrinsic linewidth is 0.6 km s−1. The ν11(μ2Σ) mode is radiatively connected to the 2Π3/2 and 2Π1/2 ladders of the ground state. All the levels should be treated simultaneously to solve the statistical equilibrium equations.
Although collisional rates are available for C6H in its ground electronic state (Walker et al. 2018), no such rates are available for the ν11(μ2Σ) mode. The energy of the levels involved in the transitions observed for this state, without adding the energy difference between it and the ground state, varies between 10.4 (Nu = 12) and 20.5 K (Nu = 17). Consequently, Trot should be well constrained by the data. To obtain the column density and rotational temperature, we used a model line fitting procedure, adopting a LTE approach (all transitions with identical rotational temperature) in which both parameters are optimised (see e.g. Cernicharo et al. 2021b). We obtain Trot = 6.2 ± 0.4 K and N(ν11(μ2Σ)) = (1.2 ± 0.2) × 1011 cm−2. Using a standard rotational diagram, we obtained similar results. The column density for the ν11(μ2Σ) state is similar to that of C6H− (McCarthy et al. 2006) and to that of many other molecules of the CnHm, CnH, CnH−, and CnH+ families previously analysed with QUIJOTE (Table A.1 of Cernicharo et al. 2022).
For the ground electronic state, we tried to use the collisional rates of C6H, with He calculated by Walker et al. (2018) and including the two ladders. However, no satisfactory solutions have been found (see discussion on this point in Agúndez et al. 2023). To roughly reproduce the intensities of the 2Π3/2 ladder, we have to use a value for n(H2) that is uncommon for TMC-1, ∼106 cm−3, without having still a reasonable fit to the lines of the 2Π1/2 ladder. Rotational temperatures for these high densities are around 6 K and the column density needed to reproduce the 2Π3/2 ladder is ∼5 × 1012 cm−2. However, the predicted lines of the 2Π1/2 ladder are a factor of two stronger than what is observed. Using the line fitting procedure, with the assumption of a common rotational temperature for all levels, we found the same problem if both ladders are treated simultaneously. In both cases, LVG or LTE, the column density that fits the 2Π3/2 ladder has to be divided by a factor of two to reproduce the intensities of the 2Π1/2 one. This indicates that the rotational and interladder temperatures are different, and/or that the 2Π1/2 ladder is sharing a fraction of its population with the ν11(μ2Σ) vibrational mode.
To obtain reasonable values for the column densities in the two ladders of the ground vibrational state, we considered each ladder separately. We derived Trot(2Π3/2) = 6.2 ± 0.2 K, Trot(2Π1/2) = 6.2 ± 0.4 K, N(2Π3/2) = (6.2 ± 0.2) × 1012 cm−2, and N(2Π1/2) = (8.0 ± 0.3) × 1010 cm−2. The calculated synthetic spectra are shown in Fig. 2 and they fit the observed lines of the two ladders remarkably well. From the derived column densities and the energy difference of 22 K between the ladders, it is possible to derive an interladder temperature of 5.1 ± 0.3 K (which neglects the contribution of the ν11(μ2Σ) mode). The total column density of C6H has to take into account the contribution of the two ladders and of the ν11(μ2Σ) vibrational state. Hence, N(C6H)=(6.4 ± 0.2) × 1012 cm−2. This value of N(C6H) is consistent (within 10%) with that derived previously (see Table A.1 of Cernicharo et al. 2022). The fraction of C6H molecules in the 2Π3/2, 2Π1/2, and ν11 states is 96.8%, 1.3%, and 1.9%, respectively. Adopting the energy of 15.8 K for the ν11(μ2Σ) level (Zhao et al. 2011), then the interladder temperature between the ground 2Π3/2 state and this vibrational level is 4.0 ± 0.3 K.
Our failure to reproduce the intensity of the lines when considering the two ladders simultaneously is due to the fact that the rotational levels of the ν11(μ2Σ) state have to be merged with those of 2Π ground state. The partition function of C6H has to take into account all levels. Taking into account that this vibrational mode is slightly below in energy than the 2Π1/2 ladder (15.8 versus 22 K), a significant fraction of the level population in this ladder is transfered to the vibrational mode. Consequently, for future analyses of C6H, it will be necessary to consider that the molecule has three ladders: the two spin components of the ground and the low-lying vibrational mode ν11(μ2Σ).
 |
Fig. 3. Selected transitions of C6H ν11(μ2Σ) observed in Lupus-1A, L1527, L1495B, and L483 with the Yebes 40m telescope. Abcisa is the LSR velocity in km s−1. The ordinate is the antenna temperature corrected for telescope and atmospheric losses. Line parameters for all observed lines are given in Table B.2. |
Detections in other sources. We also detected C6H in the ν11(μ2Σ) vibrational state in four additional cold dense clouds, namely Lupus-1A, L1527, L1495B, and L483. These sources were observed with the Yebes 40m telescope in the Q band, selected because they exhibit strong emission in the lines of cyanopolyynes and radicals, and they serve as a comparative benchmark with TMC-1. Details of these observations can be found in Agúndez et al. (2023). The coordinates of these sources are given in Table B.2. A selection of the detected lines of C6H ν11(μ2Σ) is shown in Fig. 3, while the line parameters for all observed transitions are listed in Table B.2. We derived the column densities of C6H in the ν11(μ2Σ) state towards Lupus-1A and L1527 through rotational diagrams, assuming that the source fills the beam of the telescope. In the case of Lupus-1A and L1527, there are enough lines to derive a rotational temperature, while for L1495B and L483, there is only a low number of lines; therefore, we fixed the rotational temperature to the values determined for C6H in the ground vibrational state (Agúndez et al. 2023). In Lupus-1A, we derived Trot = 10.5 ± 2.1 K and N(C6H, ν11(μ2Σ)) = (1.4 ± 0.5) × 1011 cm−2; while in L1527, we obtained Trot = 30.8 ± 17.1 K and N(C6H, ν11(μ2Σ)) = (1.3 ± 0.4) × 1011 cm−2. For Lupus-1A, the rotational temperature derived is consistent with the value of 10.7 ± 0.7 K derived for C6H by Agúndez et al. (2023); while in the case of L1527, the rotational temperature is somewhat higher, although it is consistent within the uncertainty, with the value of 19.6 ± 3.4 K derived for C6H by Agúndez et al. (2023). For L1495B and L483, we adopted rotational temperatures of 7.0 K and 8.3 K, respectively, and we derived column densities for C6H ν11(μ2Σ) of 6.1 × 1010 cm−2 and 4.5 × 1010 cm−2, respectively.
The column density ratios between the ν11(μ2Σ) state and the ground vibrational state of C6H are 3.8%, 14.8%, 4.1%, and 6.0% for Lupus-1A, L1527, L1495B, and L483, respectively. These population fractions correspond to interladder temperatures of 4.8, 8.3, 5.0, and 5.6 K, respectively. The vibronic state ν11(μ2Σ) is therefore more populated in these four clouds than in TMC-1, especially in the case of L1527. This latter cloud is known to be significantly warmer than the others (Sakai et al. 2008; Agúndez et al. 2023). It thus seems that the fraction of C6H in the vibronic state is correlated with the gas kinetic temperature and the volume density, which suggests that the rotational levels within this vibrationally excited state are mainly populated through collisions. That is to say, the warmer and denser the source, the larger the fractional population of the vibrationally excited state. However, the exact way in which these levels are excited is likely the result of a complex interplay of collisional and radiative processes involving the 2Π3/2, 2Π1/2, and ν11(μ2Σ) ladders.
4. Discussion and conclusions
We report the first detection of an excited vibrational state in cold starless cores. This opens up the possibility that other low-lying vibrationally excited states of abundant species are detected in these types of sources. We also searched for the lines of the 2Δ vibronic state, observed towards IRC+10216 (Cernicharo et al. 2008). However, as expected from its energy of ∼60 K (Zhao et al. 2011), these lines have not been detected in TMC-1 or in any of the other sources. IRC+10216 represents a warmer environment and infrared radiative pumping plays an important role in the population of the vibrational states of abundant molecules (Cernicharo et al. 2008, 2013, 2014; Pardo et al. 2018). Thermal emission from vibrationally excited states of HC3N is often found in warm and hot molecular clouds (de Vicente et al. 2000; Peng et al. 2017; Taniguchi et al. 2022). However, its lowest bending mode is at ∼222 cm−1 (Bizzocchi et al. 2017). Hence, we do not expect emission from this vibrational level in cold sources.
The detection of lines from the ν11(μ2Σ) vibrational mode of C6H in cold dark clouds indicates that the low energy vibrational levels of abundant molecules have to be considered in the analysis of sensitive line surveys. Lines arising from low-lying vibrationally excited bending states of CnH and CnN radicals are potential candidates. Some of these species have a low-lying electronic state close to their ground state that could induce important effects in the energy of their bending vibrational modes (see, e.g. Botschwina et al. 1997). Other molecules have such Renner-Teller interactions lowering the energies of their bending modes. Among the ones that have been fully characterised in the laboratory, we have the ν4 mode of C3H (Yamamoto et al. 1990) and the ν7 mode of C4H (Yamamoto et al. 1987; Guélin et al. 1987b; Cooksy et al. 2015). The latter has been observed in IRC+10216 (Guélin et al. 1987b; Cernicharo et al. 2000). However, the rotational transitions arising from these vibrational modes involve energy levels above 30 K and, thus, they were not detected in the sources observed in this work.
We have found that the available collisional rates for C6H (Walker et al. 2018) require very high volumne densities (n(H2)≥106 cm−3) to reproduce the observed intensities and the rotational temperatures derived in our analysis. Refined quantum chemical calculations of these rates are needed, including the ν11 state, in order to obtain reasonable values for the volume density from the observation of the C6H radical in interstellar clouds.
Acknowledgments
We thank Ministerio de Ciencia e Innovación of Spain (MICIU) for funding support through projects PID2019-106110GB-I00, PID2019-107115GB-C21/AEI/10.13039/501100011033, and PID2019-106235GB-I00. We also thank ERC for funding through grant ERC-2013-Syg-610256-NANOCOSMOS. We would like to thank our referee, Prof. S. Yamamoto, for usefull comments and suggestions.
References
- Agúndez, M., Marcelino, N., Tercero, B., et al. 2023, A&A, 677, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bizzocchi, L., Tamassia, F., Lass, J., et al. 2017, ApJ, 233, 11 [NASA ADS] [Google Scholar]
- Botschwina, P., Horn, M., Markey, K., & Oswald, R. 1997, Mol. Phys., 92, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, S. T., Rienstra-Kiracofe, R., & Schaefer, H. F., III 1999, J. Phys. Chem. A, 103, 4065 [CrossRef] [Google Scholar]
- Cao, Z., & Peyerimhoff, S. D. 2001, Phys. Chem. Chem. Phys., 3, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012, in ECLA 2011: Proc. of the European Conference on Laboratory Astrophysics, eds. C. Stehl\’{e}, C. Joblin, & L. d’Hendecourt (Cambridge: Cambridge Univ. Press), EAS Publ. Ser., 58, 251 [NASA ADS] [Google Scholar]
- Cernicharo, J., & Guélin, M. 1987, A&A, 176, 299 [Google Scholar]
- Cernicharo, J., Guélin, M., Menten, K., & Walmsley, C. M. 1987, A&A, 181, L1 [NASA ADS] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Guélin, M., Agúndez, M., et al. 2008, ApJ, 688, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Daniel, F., Castro-Carrizo, A., et al. 2013, ApJ, 778, L25 [CrossRef] [Google Scholar]
- Cernicharo, J., Teyssier, D., Quintana-Lacaci, G., et al. 2014, ApJ, 796, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Agúndez, M., Kaiser, R., et al. 2021a, A&A, 652, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Cabezas, C., Endo, Y., et al. 2021b, A&A, 646, L3 [EDP Sciences] [Google Scholar]
- Cernicharo, J., Fuentetaja, R., Agúndez, M., et al. 2022, A&A, 663, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooksy, A. L., Gottlieb, C. A., Killian, T. C., et al. 2015, ApJS, 216, 30 [NASA ADS] [CrossRef] [Google Scholar]
- de Vicente, P., Martín-Pintado, J., & Colom, P. 2000, A&A, 361, 1058 [NASA ADS] [Google Scholar]
- Fossé, D., Cernicharo, J., Gerin, M., & Cox, P. 2001, ApJ, 552, 168 [Google Scholar]
- Gottlieb, C. A., McCarthy, M. C., & Thaddeus, P. 2010, ApJS, 189, 261 [CrossRef] [Google Scholar]
- Guélin, M., Cernicharo, J., Kahane, C., et al. 1987a, A&A, 175, L5 [Google Scholar]
- Guélin, M., Cernicharo, J., Navarro, S., et al. 1987b, A&A, 182, L37 [NASA ADS] [Google Scholar]
- Kaifu, N., Ohishi, M., Kawaguchi, K., et al. 2004, PASJ, 56, 69 [Google Scholar]
- Linnartz, H., Motylewski, T., Vaizert, O., et al. 1999, J. Mol. Spectrosc., 197, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, M. C., Gottlieb, C. A., Gupta, H., et al. 2006, ApJ, 652, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Murakami, A., Kawaguchi, K., & Saito, S. 1988, PASJ, 39, 189 [NASA ADS] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antennas Propag., 49, 12 [Google Scholar]
- Pardo, J. R., Cernicharo, J., Velilla-Prieto, L., et al. 2018, A&A, 615, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, J. C., Gottlieb, C. A., Woodward, D. R., & Thaddeus, P. 1988, A&A, 189, L3 [NASA ADS] [Google Scholar]
- Peng, Y., Qin, S. L., Schilke, P., et al. 2017, ApJ, 837, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [Google Scholar]
- Suzuki, H., Ohishi, M., Kaifu, N., et al. 1986, PASJ, 38, 911 [NASA ADS] [Google Scholar]
- Taniguchi, K., Tanak, K. E. I., Zhang, Y., et al. 2022, ApJ, 931, 99 [CrossRef] [Google Scholar]
- Tercero, F., López-Pérez, J. A., Gallego, J. D., et al. 2021, A&A, 645, A37 [EDP Sciences] [Google Scholar]
- Walker, K. M., Lique, F., & Dawes, R. 2018, MNRAS, 473, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Woon, D. E. 1995, Chem. Phys. Lett., 244, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, S., Shuji, S., Guélin, M., et al. 1987, ApJ, 323, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamoto, S., Shuji, S., Suzuki, H., et al. 1990, ApJ, 348, 363 [CrossRef] [Google Scholar]
- Zhao, D., Haddad, M. A., Linnartz, H., et al. 2011, J. Chem. Phys., 135, 044307 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Improved rotational constants for C6H ν11(2Σ)
The ν11(μ2Σ) state is highly perturbed and high distortion constants (D, H, L) are needed to reproduce the laboratory frequencies (Gottlieb et al. 2010). Although the predicted frequencies for the lines of this state within the QUIJOTE line survey fit the observed ones reasonably well, we have included them in a merged fit to all laboratory and space lines. The distortion constants D, H, L, and M for the rotation, and D and H for the fine structure have been included. The results are given in Table A.1 and correspond to the recommended constants to predict the frequencies of the ν11(2Σ) state. The table also gives the constants derived by Gottlieb et al. (2010) and those derived from the same set of measurements but including the distortion constant, M.
Rotational and distortion constants C6H ν11(2Σ).
Appendix B: Line parameters
Line parameters for all observed transitions were derived by fitting a Gaussian line profile to them using the GILDAS package. A velocity range of ±20 km s−1 around each feature was considered for the fit after a polynomial baseline was removed. Negative features produced in the folding of the frequency switching data were blanked before baseline removal. The derived line parameters for TMC-1 are given in Table B.1 and in Table B.2 for the other sources.
Observed line parameters for C6H in the ν11(μ2Σ) excited and ground states in TMC-1.
Observed line parameters for C6H ν11(μ2Σ) in Lupus-1A, L1527, L1495B, and L483.
All Tables
Observed line parameters for C6H in the ν11(μ2Σ) excited and ground states in TMC-1.
Observed line parameters for C6H ν11(μ2Σ) in Lupus-1A, L1527, L1495B, and L483.
All Figures
 |
Fig. 1. Selected transitions for the excited state of C6H in TMC-1. Left and right panels correspond to the J = N + 1/2 and J = N − 1/2 components of each transition, respectively. The abscissa corresponds to the local standard of rest (LSR) velocity. The derived line parameters are given in Table B.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in mK. Blanked channels correspond to negative features produced when folding the frequency-switched data. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectra for this species for Trot = 6.2 K and a column density of 1.2 × 1011 cm−2. |
| In the text | |
 |
Fig. 2. Observed transitions in TMC-1 of the 2Π3/2 (two left columns) and 2Π1/2 (two right columns) states of C6H. The labels e and f correspond to the Lambda-type doubling components of each transition. The abscissa corresponds to the LSR velocity. The derived line parameters are given in Table B.1. The ordinate is the antenna temperature, corrected for atmospheric and telescope losses, in mK. Blanked channels correspond to negative features produced when folding the frequency-switched data. The quantum numbers of each transition are indicated in the corresponding panel. The red line shows the computed synthetic spectra for this species (see Sect. 3). |
| In the text | |
 |
Fig. 3. Selected transitions of C6H ν11(μ2Σ) observed in Lupus-1A, L1527, L1495B, and L483 with the Yebes 40m telescope. Abcisa is the LSR velocity in km s−1. The ordinate is the antenna temperature corrected for telescope and atmospheric losses. Line parameters for all observed lines are given in Table B.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


