| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202347289 | |
| Published online | 05 December 2023 | |
Cluster Ages to Reconstruct the Milky Way Assembly (CARMA)
I. The final word on the origin of NGC 6388 and NGC 6441
1
INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: davide.massari@inaf.it
2
atlanTTic, Universidade de Vigo, Escola de Enxeñaría de Telecomunicación, 36310 Vigo, Spain
3
Universidad de La Laguna, Avda. Astrofísico Fco. Sánchez, 38205 La Laguna, Tenerife, Spain
4
Instituto de Astrofísica de Canarias, Calle Vía Láctea s/n, 38206 La Laguna, Tenerife, Spain
5
INAF – Osservatorio Astronomico di Roma, Via Frascati 33, 00078 Monte Porzio Catone, Roma, Italy
6
INAF – Osservatorio Astronomico di Abruzzo, Via M. Maggini, 64100 Teramo, Italy
7
INFN – Sezione di Pisa, Universitá di Pisa, Largo Pontecorvo 3, 56127 Pisa, Italy
8
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
9
Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
10
Universidad de Granada, Departamento de Física Teórica y del Cosmos, Campus Fuente Nueva, Edificio Mecenas, 18071 Granada, Spain
11
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, Via Piero Gobetti 93/2, 40129 Bologna, Italy
12
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
Received:
26
June
2023
Accepted:
27
September
2023
We present CARMA, the Cluster Ages to Reconstruct the Milky Way Assembly project, the aim of which is to determine precise and accurate age measurements for the entire system of known Galactic globular clusters (GCs) and to use them to trace the most significant merger events experienced by the Milky Way. The strength of CARMA relies on the use of homogeneous photometry, theoretical isochrones, and statistical methods, which will enable us to define a systematic uncertainty-free chronological scale for the complete sample of Milky Way GCs. In this paper, we describe the CARMA framework in detail, and present a first application on a sample of six metal-rich GCs, with the aim being to unequivocally elucidate the debated origin of NGC 6388 and NGC 6441. Our results demonstrate that this pair of clusters is coeval with another four systems that have a clear in situ origin. Moreover, their location in the age–metallicity plane matches that occupied by in situ field stars. The accurate age comparison enabled by the CARMA methodology rules out the possibility that NGC 6388 and NGC 6441 were accreted as part of a past merger event.
Key words: Galaxy: evolution / globular clusters: general / techniques: photometric / Galaxy: structure
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The precise six-dimensional phase space information provided by the ESA-Gaia space mission (Gaia Collaboration 2021, 2023) in terms of position, parallax, proper motion, and line-of-sight velocity measurements has revolutionised our view of the early history of the Milky Way (see Helmi 2020, for a review). In combination with chemical abundances provided by large spectroscopic surveys such as APOGEE (Majewski et al. 2017), GALAH (De Silva et al. 2015), the Gaia ESO Survey (Gilmore et al. 2012), H3 (Conroy et al. 2019), RAVE (Steinmetz et al. 2006), SEGUE (Yanny et al. 2009), and LAMOST (Cui et al. 2012), this groundbreaking wealth of information has enabled the disentanglement of the contribution of several past merger events in building up the halo of our Galaxy.
Analyses conducted on this unprecedented data set have identified the debris of the Gaia-Enceladus-Sausage (GES) dwarf galaxy as the main component of the local halo (Helmi et al. 2018; Belokurov et al. 2018). GES is unambiguously recognised as the latest significant merger event experienced by the Milky Way, and is also recognised as being responsible for dynamically heating the Galactic proto-disc that was already in place at the time of GES accretion (e.g., Di Matteo et al. 2019; Gallart et al. 2019; Belokurov et al. 2020). Other than GES, and in addition to the obvious contribution by the Sagittarius dwarf Galaxy (Ibata et al. 1994), other prominent substructures have been discovered as over-densities showing some degree of coherency in the chemo-dynamical space populated by halo stars and globular clusters (GCs), such as the Helmi streams (Helmi et al. 1999; Koppelman et al. 2019b), Sequoia (Myeong et al. 2019), Thamnos (Koppelman et al. 2019a), and Kraken (Kruijssen et al. 2019; Massari et al. 2019). A first merger tree of the Milky Way based on the properties of these progenitors was presented by Kruijssen et al. (2020).
With the constant improvement of the quality and completeness of the available data, this early picture has become more and more complex. Many new substructures in the dynamical space have been discovered (see e.g., Yuan et al. 2020; Naidu et al. 2020; Necib et al. 2020; Aguado et al. 2021; Horta et al. 2021; Re Fiorentin et al. 2021; Mardini et al. 2022; Malhan et al. 2022; Myeong et al. 2022; Oria et al. 2022; Tenachi et al. 2022; Ruiz-Lara et al. 2022b; Dodd et al. 2023; Mikkola et al. 2023). Nevertheless, their interpretation as independent merger events rather than overdensities from already known progenitors or even in situ structures originating from the Milky Way disc is challenged by the fact that (i) these structures often dynamically overlap, and (ii) the distribution in energy of the debris of progenitors that sink rapidly shows multiple bumps and wrinkles, which originate from each stripping event (Amarante & Debattista 2022; Khoperskov & Gerhard 2022). In these cases, the addition of chemical information is crucial, and yet sometimes is not sufficient to unambiguously solve the most controversial cases (e.g., Monty et al. 2020, 2023; Feuillet et al. 2021; Malhan et al. 2022; Horta et al. 2023). Additional information is therefore required, and one key ingredient could be provided by stellar ages.
Despite their importance, estimating accurate stellar ages remains a challenging task in astrophysics (Soderblom 2010). Many of the current limitations stem from our poor understanding of some of the physical processes involved in stellar evolution and the difficulty in controlling systematic effects on the observational measurements (Lebreton et al. 2014a,b). Most age-dating methods rely on measurements of stellar properties such as luminosity, chemical composition, and surface temperature (which can be affected by various factors such as stellar activity or atmospheric dynamics), and on their comparison with the predictions of stellar evolution models. Uncertainties in our knowledge of the underlying physics and assumptions made in the models (both stellar evolution models and synthetic spectra) also translate to uncertainties in the age estimates. Nevertheless, age measurements for individual stars in the old regime are becoming more and more precise. On the one hand, this is thanks to the availability of homogeneous photometric and spectroscopic data for large samples of stars, which help in overcoming some of the systematic effects (see e.g., Gallart et al. 2019; Xiang & Rix 2022). On the other hand, the development of asteroseismology has led to age measurement precisions of ∼10% (see e.g., Montalbán et al. 2021). The asteroseismic age-dating technique, which does not require a large sample of stars to achieve high precision and depends more weakly on the estimate of stellar photospheric properties, is particularly promising in this respect (see e.g., Verma et al. 2022; Tailo et al. 2022), but further refinement and testing are still required.
Among the tracers of the Milky Way assembly history, those for which age can be measured in the most precise and accurate way are GCs. When considering relative ages, the current best measurements can achieve a precision of the order of ∼500 Myr (VandenBerg et al. 2013). With these precise measurements, the age–metallicity relation (AMR) of Milky Way GCs has proven to be a powerful tool to assess the origin of GCs as in situ or accreted stellar systems (see e.g., Forbes & Bridges 2010; Leaman et al. 2013; Kruijssen et al. 2019; Massari et al. 2019; Callingham et al. 2022). Even more precise measurements might allow us to distinguish between the different progenitors of the accreted ones, and in turn to precisely characterise their accretion time (Kruijssen et al. 2020). Unfortunately, precise GC age measurements are limited to relatively small samples. Different age indicators, photometric catalogues, assumptions on distance and reddening, and theoretical models are examples of the many sources of systematic uncertainties that affect different compilations of GC ages. By comparing the results from Forbes & Bridges (2010) and VandenBerg et al. (2013), Massari et al. (2019) demonstrated that these systematic errors can add up to differences of 2 Gyr or more, and that properly taking them into account and correcting for them is not trivial, as they might depend on the GC age itself as well as on the GC metallicity.
The objective of CARMA (Cluster Ages to Reconstruct the Milky-way Assembly) is to overcome this limitation by building up the first complete and homogeneous catalogue of Milky Way GC ages. In combination with the dynamical and chemical properties of the GCs, this will enable a complete characterisation of the accreted and in situ population of Milky Way GCs by solving the cases for which the origin remains ambiguous (see e.g., Minelli et al. 2021; Carretta & Bragaglia 2022). At the same time, this approach will allow us to characterise the progenitors of the past merger events in terms of accretion time thanks to analysis of their AMRs, and from analysis of the colour–magnitude diagrams (CMDs) of the progenitor systems through CMD-fitting (e.g., Gallart et al. 2019; Ruiz-Lara et al. 2022a), whenever possible.
In this first paper of the series, we present the method that CARMA will employ to determine the GCs ages, and we describe its first application: the unequivocal determination of the origin of two GCs, namely NGC 6388 and NGC 6441, whose in situ or accreted nature cannot be unambiguously determined using either dynamical information or their chemical properties. To this end, we derive homogeneous ages for these two GCs and for four additional GCs of similar metallicity ([Fe/H] ≃ −0.5) for which there is agreement in the literature about their in situ origin based on dynamical (see Massari et al. 2019; Forbes 2020; Bajkova et al. 2020; Callingham et al. 2022) and chemical (Minelli et al. 2021) evidence. As additional evidence, we also compare the ages and metallicities of these clusters with the two age–metallicity sequences of the Milky Way kinematic halo (one associated to GES, the other to the heated early disc) derived using Gaia Data Release 3 (DR3) data and updated methodology with respect to Gallart et al. (2019).
The paper is organised as follows. Section 2 presents the method adopted by CARMA to determine GC ages, including a description of the theoretical models and of the isochrone-fitting algorithm employed for this goal. In Sect. 3, we discuss the proof-of-concept scientific case concerning the origin of the pair of GCs NGC 6388 and NGC 6441 together with the data used in the analysis. We present the results of our investigation of these two GCs in Sect. 4, and outline our final conclusions as to their origin in Sect. 5.
2. The method
In this section, we present the method employed to determine the age of each GC, which is based on the isochrone fitting code presented in Saracino et al. (2019), here refined and updated. We also present a brief summary of the CMD-fitting technique applied here to derive the age–metallicity relation of Milky Way halo field stars, highlighting the differences with respect to the original work by Gallart et al. (2019).
2.1. Stellar evolution framework
CARMA relies on the adoption of the stellar theoretical models provided within the latest release of the Bag of Stellar Tracks and Isochrones (BaSTI) database (Hidalgo et al. 2018; Pietrinferni et al. 2021). More specifically, for the present analysis, we adopt the model sets accounting for the occurrence of diffusive processes (we refer to Hidalgo et al. 2018, for a detailed discussion on the adopted input physics and physical assumptions). For the sake of the aim of our project, which is to ensure the highest possible degree of accuracy in terms of age determination, we decided to only use solar-scaled models. This prescription and use of the global metallicity [M/H] rather than the iron content [Fe/H] as input for the code allow us to avoid making any assumption on the α-element abundance of each GC, which would otherwise be based on heterogeneous measurements coming from many different sources. Salaris et al. (1993) demonstrated that the impact of different [α/Fe] mixtures on theoretical models for population II stars can simply be treated as an additional term on the global metallicity [M/H], according to the relation1
This is especially true when working in the optical–infrared colour combinations adopted in this work, as in these bands the effect of the specific α-elements distribution on the bolometric corrections becomes negligible (Cassisi et al. 2004). Estimates of [α/Fe] for the target GCs are only used a posteriori to perform a direct comparison of our best-fit metallicity with existing (possibly high-resolution) spectroscopic measurements.
The whole sets of isochrones adopted in the present work were transferred from the theoretical Hertzsprung-Russell diagram to the various relevant photometric planes by adopting self-consistent color–temperature (Teff) relations and bolometric corrections (for more details, we refer to Hidalgo et al. 2018).
The ratio between the extinction in a given photometric band Aλ and AV depends on the flux distribution of the stellar source, and is in principle dependent on parameters such as Teff, surface gravity (log g), and the chemical composition (see e.g., Bedin et al. 2005, for a discussion on this issue). When AV is small, this effect is also small and a single value of Aλ/AV can be safely applied along the whole isochrone. However, for those clusters affected by large extinction (typically for values larger than E(B − V) = 0.10), it is necessary to consider the variation of Aλ/AV along the isochrones in the fit to the observed CMD. Such an effect is increasingly significant towards bluer photometric passbands.
To properly take into account this effect in the procedure of isochrone fitting to the CMD of those clusters affected by large extinction, we applied Teff-dependent reddening corrections to the magnitudes of the theoretical isochrones. The Teff-dependent corrections were evaluated by adopting the web interface2 that implements the prescriptions by Girardi et al. (2008) in order to determine the extinctions in the various photometric passbands, covering a wide range of Teff and values of interstellar extinction. Figure 1 shows how the total extinction in the two filters used in this work, namely AF606W and AF814W, varies as a function of Teff and E(B − V).
 |
Fig. 1. Behaviour of the total extinction in the two filters used in this work, AF606W (left-hand panel) and AF814W (right-hand panel), as a function of Teff and colour-coded based on E(B − V). |
2.2. The isochrone-fitting code
The isochrone fitting algorithm developed within CARMA is a series of procedures that provide age, metallicity, distance, and reddening best-fit values within a Markov Chain Monte Carlo (MCMC) statistical framework, thus further associating robust uncertainty estimates to all of the output parameters. The steps followed by the algorithm are described in detail, as follows:
1. The first step of the algorithm consists in the construction of the best CMD to be fit. This includes the application of photometric quality cuts; the selection of GC member stars via kinematic information (whenever available) or via a selection based on the distance from the cluster centre; the correction of differential reddening effects; and the exclusion of obvious photometric binaries along the CMD main sequence. The details of this step applied to the case under study are described in Sect. 3.1.
2. A grid of BaSTI (Hidalgo et al. 2018) theoretical isochrones in the appropriate photometric bands is created with a very fine sampling of the age–metallicity space. The adopted step in [M/H] is of 0.01 dex, whereas the step in age is of 100 Myr, but a linear interpolation algorithm3 enables us to sample the parameter space even more finely. As explained in Sect. 2.1, the adopted models have a solar-scaled [α/Fe] mixture, include diffusion effects as well as mass loss, and are corrected for Teff-dependent reddening effects. Finally, the models are converted to the observational plane by applying the cluster distance modulus and extinction, by assuming the reddening law by Cardelli et al. (1989).
3. At this point a fitting function is defined, which measures the goodness-of-fit between the isochrones and the observed CMD. The portion of the isochrones that is fit to the CMD goes from the bottom of the main sequence to the tip of the red giant branch. Building upon the method presented in Saracino et al. (2019), our proposed function is the sum of two terms. The first term (ℒpriors) is the likelihood that evaluates the consistency of the inferred parameters with the initial priors on [M/H], distance, and E(B − V); it has a Gaussian form and, when expressed in natural logarithm, can be written as:
where each individual term is in turn expressed as the natural logarithm of a Gaussian function:
with x = [E(B − V), DM, [M/H]], and xprior and xstd being the adopted values of the priors and their associated uncertainties, respectively. The second term (ℒfit) is the likelihood associated to the fit of the i individual points of the CMD, and is computed as
where N is the total number of stars in the CMD, min(dist) is the minimum distance between data and model, and σ is the photometric error. After some testing, we realised that in a few cases the fitting algorithm prefers local solutions that are significantly different from (by more than 0.5 dex) the spectroscopic measurements of [M/H] used as prior. Given that the spectroscopic metallicity is an independent and very robust prior, we decided to help the algorithm to avoid these local solutions – which are clearly offset even by visual inspection – by assigning greater importance to the first term, with a weight of 1. Conversely, the second term, which measures the disparity between the CMD and the isochrone, is assigned a lower weight, but not so low as to force the solution on the priors. Rather, we want the MCMC chains to still sample a wide range of parameters that can deviate from the values of the priors while still providing visually good fits. After some tests, we find that the best weight to assign to the second term in this sense is 0.3, so that
4. The algorithm then looks for the best-fitting isochrone – meaning the model that minimizes ℒtot – by exploring the parameter space (age, [M/H], distance, and reddening) by means of the emcee (Foreman-Mackey et al. 2019) Python package that provides an efficient implementation of the affine-invariant MCMC ensemble planner.
5. Finally, the algorithm provides the best solution in terms of age, [M/H], distance, and E(B − V), together with the associated uncertainties (corresponding to the 16th and the 84th percentiles of the posterior distributions) and their correlation parameter.
The results coming from the application of this algorithm to the GCs under study are shown in Appendix A.
2.3. The CMD-fitting methodology
The star formation history (SFH) and the distribution of ages and metallicities of the stars in a complex stellar system can be quantitatively retrieved from the comparison of its observed CMD – reaching the oldest main sequence turnoff – with theoretical CMDs derived from stellar evolution models, that is, after observational effects are properly taken into account (e.g., Gallart et al. 1999; Dolphin 2002; Cignoni & Tosi 2010; Monelli et al. 2010). The application of this technique to Gaia DR2 data by members of our team is discussed in Gallart et al. (2019) and Ruiz-Lara et al. (2020), while updated procedures, which we call CMDft.Gaia are introduced in Ruiz-Lara et al. (2022a) and in more detail in Gallart et al. (in prep). We refer to these works for a detailed description of the methodology, while a brief summary is presented here.
CMDft.Gaia is a suite of procedures that includes (i) the computation of synthetic CMDs in the Gaia bands, adopting a given set of stellar evolution models, IMF, and a parameterization of the binary star population; (ii) the simulation in the synthetic CMDs of the observational errors and completeness affecting the observed CMD after quality and reddening cuts; and (iii) the derivation of the SFH with DirSFH, which finds the combination of simple stellar populations (SSPs) that best fits the observed CMD. A distinctive feature of DirSFH is that it defines the SSPs with a Dirichlet tesselation (Green & Sibson 1978) of the synthetic CMD from a grid of seed points within the available range of ages and metallicities. The final SFH is derived as the weighted average of a large number (of the order of 100) of individual solutions obtained by slightly modifying the grid of age and metallicity seed points.
3. Application: The origin of NGC 6388 and NGC 6441
Using a combination of dynamical properties and AMR data, Massari et al. (2019) associated the 151 GCs with Gaia DR2 proper motions to their most likely galaxy progenitor, which is either the Milky Way or one of the past accretion events described in Sect. 1. Some of these associations are naturally uncertain, as for example the location of a GC in the (E, Lz) integrals of motion space is sometimes at the boundary between regions associated with different progenitors. Among these uncertain associations, those concerning the pair NGC 6388-NGC 6441 have attracted particular attention in the literature. According to Massari et al. (2019), NGC 6388 is an in situ GC associated with the bulge of our Galaxy, while NGC 6441 was accreted during the merger event involving the Kraken dwarf galaxy4. These associations did not take into account any age estimate, as the authors demonstrated that for [Fe/H] ≳ −0.5 (as is the case for these two GCs) the systematic uncertainties among different compilations of age measurements can reach up to more than 2 Gyr; they are therefore purely based on orbital properties computed using the distances provided by the Harris catalogue (Harris 1996). When adopting the distances provided by Baumgardt & Vasiliev (2021) instead, the orbital apocentre of NGC 6388 increases from 3.4 kpc to 4.2 kpc, and the cluster enters the region occupied by Kraken’s GCs. Vice versa, the vertical angular momentum of NGC 6441 increases from Lz = 268 km s−1 kpc to Lz = 519 km s−1 kpc, so that the cluster moves from the Kraken to an in situ association with the Milky Way disc. According to Forbes (2020) and Callingham et al. (2022), both clusters are in situ.
A solution was not found for this dynamical ambiguity when including information on the chemistry of the cluster. By performing a direct relative comparison among the abundances of [Zn/Fe], [Sc/Fe], and [V/Fe] of these two GCs and a sample of undoubtedly in situ GCs, Minelli et al. (2021) found that NGC 6388 and NGC 6441 show systematically lower abundances, and therefore recognised both clusters as accreted. By investigating the same chemical elements for NGC 6388, Carretta & Bragaglia (2022) instead reached the opposite conclusion, associating the cluster to the Milky Way. Finally, by analysing APOGEE α-element abundance, Horta et al. (2020) suggested a possible accreted origin for NGC 6388.
NGC 6388 and NGC 6441 are therefore perfect test cases for CARMA, allowing us to demonstrate the importance of accurate and precise age measurements in unravelling the origin of the entire system of Milky Way GCs, and in turn to contribute to the reconstruction of our Galaxy assembly history. In particular, we propose to determine accurate relative ages for a sample that includes these two GCs of ambiguous origin as well as four clusters in the same metallicity range ([Fe/H] ∼ −0.5) whose origin is unambiguously in situ according to all the indicators (dynamics and chemistry) and to the different studies in the literature (Massari et al. 2019; Forbes 2020; Bajkova et al. 2020; Callingham et al. 2022). These four clusters are NGC 5927, NGC 6304, NGC 6352, and NGC 6496. If NGC 6388 and NGC 6441 are of accreted origin, according to the behaviour of the AMR observed in dwarf galaxies (Kruijssen et al. 2019) they should be about 2 Gyr younger than the sample of in situ clusters.
3.1. The globular cluster data set
In order to ensure the highest possible accuracy on our differential age comparison for all six GCs, we used Hubble Space Telescope photometry taken with the Wide Field Channel of the Advanced Camera for Survey (ACS/WFC) in the F606W and F814W filters. The catalogues produced with the KS2 code (Bellini et al. 2017) were made public by the HUGS survey (Piotto et al. 2015; Nardiello et al. 2018), and the photometry comes from observations of the ACS Survey of Galactic Globular Clusters (GO-10775, PI: A. Sarajedini, see Sarajedini et al. 2007). By following the prescriptions in Bellini et al. (2017), Nardiello et al. (2018), we adopted the photometry acquired using KS2 method-2, as it is best suited for faint stars and crowded environments.
Before running the isochrone-fitting code on the photometric catalogues, we took some other actions to perform our age estimates on the best possible photometry. First of all, the HUGS survey provides proper-motions-based probability memberships for all the sources in the catalogues. We therefore restricted our analysis to stars with a probability membership of > 90%, which is particularly crucial in the regions that are highly contaminated by field stars, such as those populated by NGC 6388 and NGC 6441.
After the membership selection, we performed a differential reddening correction for each cluster using the method described by Milone et al. (2012). Briefly, we used main sequence stars down to four magnitudes below the turnoff as the reference sample, and paid particular attention to the removal of the equal-mass binary sequence from it. Main sequence stars are preferred over red giants as they are more numerous and thus ensure higher resolution in the determination of the reddening spatial variation. Then, for each individual cluster member, we estimated the differential reddening value d[E(B − V)] as the median offset from the mean ridge line along the reddening vector, computed among the 60 closest reference neighbours. We adopted an RV = AV/E(B − V) of 3.1 and the reddening law by Cardelli et al. (1989). This process was repeated iteratively – typically two or three times depending on the GC – until the residual d[E(B − V)] values matched the typical photometric error. An example of the resulting correction on the CMD can be found in Fig. 2. The associated reddening map is instead shown in Fig. 3.
 |
Fig. 2. Example of differential reddening correction in the case of NGC 6352. The original CMD is shown on the left and the corrected one on the right. |
 |
Fig. 3. Example of a differential reddening map for NGC 6352. Each of the stars used to compute the differential reddening correction is plotted in sky coordinates and coloured according to its value of dE(B − V). |
The differential-reddening-corrected, membership-selected catalogues were then further cut by excluding the innermost regions of each cluster, with a distance cut that ranged between a projected radius of R = 20 arcsec and R = 60 arcsec depending on each GC density and core radius size. Such a cut confers a double advantage. On the one hand, it excludes sources in the most crowded regions, where the photometry is affected by poor-quality measurements. On the other hand, given that we are solely interested in the age measurement, we do not want the complexity of GC stellar populations (the so-called multiple-population phenomenon; see Gratton et al. 2019, for a review) to affect our estimates. With only a few exceptions (see e.g., Leitinger et al. 2023), all the observational results agree over the finding that, regardless of the kind of complexity involved (from the iron spread, to the helium variation, and the (anti-)correlation affecting lighter elements; see e.g., Pancino et al. 2003; Piotto et al. 2007; Massari et al. 2014; Milone et al. 2017), the first primordial population of GCs is less centrally concentrated than any other peculiar one. The choice of colour–magnitude diagrams (CMDs) in the F606W and F814W filters already ensures that only possible iron- and helium spreads should affect the CMD by broadening the evolutionary sequences and thus altering the age estimates. The radial distance cut further reduces this possibility by preferentially excluding peculiar populations (see e.g., Sbordone et al. 2011; Cassisi et al. 2013; Cassisi & Salaris 2020).
Nonetheless, NGC 6388 and NGC 6441 are known to be extremely peculiar GCs. Indeed, Bellini et al. (2013) demonstrated that the two clusters share a similar helium spread, which reaches values of ΔY ≃ 0.07 (see also Caloi & D’Antona 2007; Busso et al. 2007), but despite their similar metallicity and helium content, their CMDs in the optical and ultra-violet bands display differences that can likely be ascribed to peculiar C, N, O abundances. For what concerns this study, these complex stellar populations manifest as split subgiant branches (SGBs) and broad red giant branches in the optical CMD of the clusters, and most importantly, these photometric features are not entirely erased by the radial distance cut. This is why we followed the prescriptions by Milone et al. (2017; see also Milone et al. 2015) and the HUGS photometry in the required bands to create a chromosome map for each of the two clusters and to select only stars belonging to the primordial populations. Figure 4 shows an example of how such a selection works in the region of the (mF814W, mF606W − mF814W) CMD around the SGB, which is the most peculiar sequence of these two clusters in the optical CMD. Stars excluded from the analysis are those shown in cyan, which, moreover, tend to occupy a region that is redder and fainter than the primordial population (black symbols), and would therefore affect the isochrone fitting.
 |
Fig. 4. Zoom-in around the region of the SGB for the (mF814W, mF606W − mF814W) CMDs of NGC 6388 (left-hand panel) and NGC 6441 (right-hand panel). Stars highlighted in cyan are those selected via chromosome maps as belonging to chemically peculiar populations, and are therefore excluded from the analysis. Black symbols are instead stars belonging to the primordial population. |
3.2. The halo field dataset and its SFH derivation
From Gaia DR3 (Gaia Collaboration 2023), we selected stars belonging to the Milky Way halo within a cylinder of heliocentric radius 1 kpc and distance from the plane |Z|< 3.5 kpc, by adopting a cut in tangential velocities VT > 200 km s−1 (as defined from proper motions in Gaia Collaboration 2018). This CMD presents the typical double sequence of stars indicating the presence of an in situ population and an accreted one (Helmi et al. 2018; Gallart et al. 2019). We only consider stars with a small relative parallax error (parallaxovererror > 5) in order to derive their distances directly by inversion of the parallax (after applying the global zero-point indicated in Lindegren et al. 2021), and we corrected their colours and magnitudes for extinction using the 3D extinction maps by Green et al. (2019) with the recipes presented in Gaia Collaboration (2018).
We calculated the synthetic CMD used to derive the SFH and associated age–metallicity relations with the BaSTI solar-scaled models (see Sect. 2.1), assuming a Kroupa initial mass fraction (IMF; Kroupa 2001), a fraction of unresolved binaries (β) of 30%, and a minimum mass ratio for binaries (q) of 0.1.
As a consistency check, we also derived alternative SFHs by (i) correcting the reddening of the observed stars with the 3D extinction map by Lallement et al. (2018); and (ii) adopting a fraction of unresolved binaries of 50%. The resulting age–metallicity relations are similar, with small differences that do not affect the conclusions of this work.
4. Results
The result of the isochrone fitting for each of the six GCs under analysis is shown in Figs. A.1–A.6. We ran the isochrone fitting code using Gaussian priors on the input paramaters, centred on the metallicity (assuming solar-scaled [α/Fe] mixture), colour-excess, and distance modulus values provided in Harris (1996), and with dispersions of σ[M/H] = 0.1, σE(B − V) = 0.05, and σ[DM] = 0.1, respectively. Finally, we ran the code twice per GC, once on the (mF814W, mF606W − mF814W) CMD and once on the (mF606W, mF606W − mF814W) CMD. The results we present here are the average value of the two, while the overall uncertainties are computed so as to encompass the upper and lower limits of both runs combined (all the uncertainties of < 0.01 were conservatively rounded up to that value). Table 1 summarises these results.
Results of the isochrone fitting.
As a first sanity check, we compare the output metallicity, E(B − V), and DM with existing estimates from the literature. For the metallicity, we adopt the catalogue by Harris (1996) as a reference. As explained in Sect. 2.1, the output of the isochrone fitting is [M/H], and corresponds to [Fe/H] only in case of solar-scaled α-element abundances (see Equation 1). We therefore determined the [α/Fe] value that minimises the average difference between our results and those from the literature, finding that [α/Fe] = 0.08 makes the difference null, as shown in Fig. 5. Given that these GCs are rather metal-rich, and the typical behaviour of the [α/Fe] abundance ratio shows a decrease towards solar values in the metal-rich regime (see e.g., Horta et al. 2020), [α/Fe] ≃ 0.1 appears to be a reasonable value. The scatter of the distribution (σ = 0.07) further guarantees that the adopted priors are not too stringent. Overall, the sanity check on the cluster metallicity is successful.
 |
Fig. 5. Difference between the output metallicities [Fe/H] computed assuming [α/Fe] = 0.08 and literature spectroscopic estimates for each GC, as provided by Harris (1996). The scatter around the mean value is 0.07 dex. Error bars are given by the sum in quadrature between our uncertainties and those by Harris (1996), and amount to ∼0.1 dex. |
The same sanity check performed on colour excess and distance modulus values from the literature provides good results as well. Figure 6 shows the difference between our findings and other E(B − V) and DM estimates coming from isochrone fitting methods (contrarily to the adopted priors, which come from multiple different techniques). In particular, the values for the four in situ GCs were taken from VandenBerg et al. (2013), while those for NGC 6388 were provided by Moretti et al. (2009) and those for NGC 6441 by Baumgardt & Vasiliev (2021). Concerning the colour excess (see the left-hand panel), the mean difference is only −0.006 mag, and the dispersion around the mean is 0.01 mag. In the plot, the error bars are computed as the sum in quadrature between the uncertainties estimated by our code and a 5% uncertainty, which is a typical value for literature estimates. As for DM values (see the right-hand panel of Fig. 6), the mean difference is zero, with a small dispersion of 0.02. In this case, the uncertainties shown in the plot are the sum in quadrature between ours and a typical literature value of 0.05 mag.
 |
Fig. 6. Difference between the absolute reddening value (left-hand panel) and distance modulus (right-hand panel) coming from our best-fit solution and literature ones. |
All these successful consistency checks demonstrate that the isochrone fitting has worked properly, converging to reasonable solutions. In the following, we focus on the age estimates, with the important caveat that, without an appropriate independent absolute zero-point (which is currently missing), these isochrone-fitting absolute ages have to be interpreted in a relative sense by focusing on age differences rather than on their absolute values.
Figure 7 shows the location of the six GCs analysed here in the age–metallicity plane, overplotted on the age–metallicity relation derived from the halo field population. The first immediate feature that stands out is that all of the six GCs have rather similar ages. The youngest is NGC 6388, but its age is perfectly consistent within a 1σ uncertainty with the age of at least two of the in situ GCs, namely NGC 5927 and NGC 6352. The other cluster with debated origin is NGC 6441, which is even older, and has an age that is consistent with those of NGC 6304 and NGC 6496. By looking at the nominal uncertainties, which take into account the interplay of all of the parameters involved in the fit, it might be tempting to distinguish the six GCs in two groups with strikingly similar age, one group (NGC 6441, NGC 6304 and NGC 6496) with a mean ⟨t⟩ = 13.10 Gyr (and a tiny dispersion of σt = 0.03 Gyr), and a second group (NGC 6388, NGC 5927 and NGC 6352) with ⟨t⟩ = 12.05 Gyr and σt = 0.25 Gyr. If this second group consists of the youngest among the in situ GCs, as CARMA will determine when the sample of GC ages becomes increasingly complete, they might precisely pin-point an important event in the Milky Way merger history that halted the in situ GC formation. Moreover, the quoted numbers are not dissimilar from the estimated accretion time of the Kraken (Kruijssen et al. 2020) or of the GES (Helmi et al. 2018; Gallart et al. 2019; Montalbán et al. 2021; Xiang & Rix 2022; Ciucă et al. 2023) merger events. For the moment though, given that we focus here on age differences, we prefer not to make strong claims, and to leave this possible evidence as an interesting feature to be more thoroughly investigated in the future.
 |
Fig. 7. Location of the six GCs under study in the age–metallicity plane, overplotted on the age–metallicity relation derived from the halo CMD. GCs with undoubted in situ origin are shown as black symbols, while NGC 6388 and NGC 6441 are marked in white. The location of GES (black dashed line) and of the Milky Way thick disc (black ellipse) are shown for comparison. |
In order to come to an unequivocal conclusion as to the origin of the two GCs NGC 6388 and NGC 6441, in Fig. 7 we compare their position on the age–metallicity plane with the age–metallicity relation for the halo field population, which clearly shows the signature of GES at low metallicity ([M/H] < −0.75) and that of the heated early disc in situ population at the highest metallicity end. GES stars show a clearly distinct age–metallicity relation with [M/H] ≃ −1.25 at 13 Gyr ago and [M/H] ≃ −0.8 at 12 Gyr ago, while the in situ disc remains ∼13 Gyr old up to [M/H] ≃ −0.7 and then becomes younger at higher metallicity. Very clearly, the six GCs studied here are all entirely consistent with the pattern expected for an in situ formation. In particular, to be located on the AMR of an accreted system like GES, NGC 6388 and NGC 6441 should be about 2 Gyr younger (or more) than the in situ GCs, which is excluded at levels of 2.5σ and 7σ, respectively. We can therefore conclude that both clusters were born in the Milky Way with a high statistical significance.
5. Summary and conclusions
In this first paper of a series, we present the CARMA project, highlighting its methods and objectives. We further demonstrate an immediate application of its results, and finally settle a longstanding debate over the origin of the pair of GCs, NGC 6388 and NGC 6441.
The aim of CARMA is to provide the first complete and homogeneous compilation of GC ages to date, targeting precision and accuracy of < 0.5 Gyr. To this end, we developed an isochrone fitting code that builds upon the work of Saracino et al. (2019) and provides age estimates and uncertainties in a statistically robust MCMC framework. Using differential-reddening-corrected and kinematically decontaminated photometry, which is then properly treated in order to exclude chemically peculiar stars and poor-quality measurements, CARMA code finds the best solution among a fine grid of BaSTI theoretical isochrones corrected for temperature-dependent extinction effects, and provides homogeneous estimates of [M/H], E(B − V), DM, and age.
As a proof-of-concept study, we applied our method to six Milky Way GCs. Four out of these six have a well-established in situ origin, while the other two, namely NGC 6388 and NGC 6441, have widely debated origins in the literature. Our results show that NGC 6388 and NGC 6441 are coeval with other in situ GCs, and a comparison between their location in the age–metallicity plane and that of the sequences derived for GES and the heated in situ early disc indicate – with high statistical significance – that they formed in situ as well. The youngest among these in situ GCs might pin-point the moment when GC formation in the Milky Way disc was suppressed (or when a second peak in GC formation was triggered) by the merger event with a large dwarf galaxy such as Kraken or Gaia-Enceladus-Sausage. However, further investigation in conjunction with independent absolute age calibrators (such as those that will be provided by the asteroseismic mission HAYDN, Miglio et al. 2021) is required to make more robust claims in this sense.
These findings demonstrate the power of precise and accurate GC age measurements in the context of reconstructing the Milky Way assembly history. Future investigations by CARMA will target GCs associated with different external progenitors – including the Milky Way itself – in order to disentangle uncertain associations and put precise constraints on the accretion time and mass of the related merger events.
The coefficients of this relation are slightly different from the ones provided by Salaris et al. (1993) in order to take into account the use of a different reference solar mixture between the BaSTI models, which are based on the heavy-element distribution provided by Caffau et al. (2011), whereas the models by Salaris et al. (1993) were based on the Ross & Aller (1976) mixture.
The interpolation is performed by means of the Python library scipy.interpolate.1d (Virtanen et al. 2020). Different choices of interpolation algorithms might introduce further small systematic errors on the age estimates, but CARMA avoids this source of inhomogeneity as well.
Kraken is referred to as Low-Energy group in the nomenclature by Massari et al. (2019).
Acknowledgments
We thank the anonymous referee for comments and suggestions that improved the quality of our paper. D.M. thanks the Fundactión Jesús Serra visiting programme and the Instituto de Astrofísica de Canarias for hospitality. D.M., S.C., E.P. and A.M. acknowledge financial support from PRIN-MIUR-22: CHRONOS: adjusting the clock(s) to unveil the CHRONO-chemo-dynamical Structure of the Galaxy” (PI: S. Cassisi). A.S. acknowledges support from the European Research Council Consolidator Grant funding scheme (project ASTEROCHRONOMETRY, G.A. n. 772293, http://www.asterochronometry.eu). Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement No. DNRF106). S.S. acknowledges funding from STFC under the grant no. R276234. C.G., E.F.A., T.R.L. and S.C. acknowledge support from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (AEI-MCINN) under grant “At the forefront of Galactic Archaeology: evolution of the luminous and dark matter components of the Milky Way and Local Group dwarf galaxies in the Gaia era” with reference PID2020-118778GB-I00/10.13039/501100011033. C.G. also acknowledges support from the Severo Ochoa program through CEX2019-000920-S. T.R.L. acknowledges support from Juan de la Cierva fellowship (IJC2020-043742-I), financed by MCIN/AEI/10.13039/501100011033. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 804240) for S.S. and Á.S. M.M. acknowledges support from the Agencia Estatal de Investigación del Ministerio de Ciencia e Innovación (MCIN/AEI) under the grant “RR Lyrae stars, a lighthouse to distant galaxies and early galaxy evolution” and the European Regional Development Fun (ERDF) with reference PID2021-127042OB-I00, and from the Spanish Ministry of Science and Innovation (MICINN) through the Spanish State Research Agency, under Severo Ochoa Programe 2020-2023 (CEX2019-000920-S). P.J. acknowledges support from the Swiss National Science Foundation.
References
- Aguado, D. S., Myeong, G. C., Belokurov, V., et al. 2021, MNRAS, 500, 889 [NASA ADS] [Google Scholar]
- Amarante, J. A. S., Debattista, V. P., Beraldo e Silva, L., Laporte, C. F. P., & Deg, N., 2022, ApJ, 937, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bajkova, A. T., Carraro, G., Korchagin, V. I., Budanova, N. O., & Bobylev, V. V. 2020, ApJ, 895, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Bedin, L. R., Cassisi, S., Castelli, F., et al. 2005, MNRAS, 357, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Piotto, G., Milone, A. P., et al. 2013, ApJ, 765, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Bellini, A., Anderson, J., Bedin, L. R., et al. 2017, ApJ, 842, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., Erkal, D., Evans, N. W., Koposov, S. E., & Deason, A. J. 2018, MNRAS, 478, 611 [Google Scholar]
- Belokurov, V., Sanders, J. L., Fattahi, A., et al. 2020, MNRAS, 494, 3880 [Google Scholar]
- Busso, G., Cassisi, S., Piotto, G., et al. 2007, A&A, 474, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caffau, E., Ludwig, H. G., Steffen, M., Freytag, B., & Bonifacio, P. 2011, Sol. Phys., 268, 255 [Google Scholar]
- Callingham, T. M., Cautun, M., Deason, A. J., et al. 2022, MNRAS, 513, 4107 [NASA ADS] [CrossRef] [Google Scholar]
- Caloi, V., & D’Antona, F. 2007, A&A, 463, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carretta, E., & Bragaglia, A. 2022, A&A, 660, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., & Salaris, M. 2020, A&ARv, 28, 5 [Google Scholar]
- Cassisi, S., Salaris, M., Castelli, F., & Pietrinferni, A. 2004, ApJ, 616, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Mucciarelli, A., Pietrinferni, A., Salaris, M., & Ferguson, J. 2013, A&A, 554, A19 [EDP Sciences] [Google Scholar]
- Cignoni, M., & Tosi, M. 2010, Adv. Astron., 2010, 158568 [CrossRef] [Google Scholar]
- Ciucă, I., Kawata, D., Ting, Y.-S., et al. 2023, MNRAS, in press, https://doi.org/10.1093/mnrasl/slad033 [Google Scholar]
- Conroy, C., Bonaca, A., Cargile, P., et al. 2019, ApJ, 883, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [Google Scholar]
- De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Haywood, M., Lehnert, M. D., et al. 2019, A&A, 632, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dodd, E., Callingham, T. M., Helmi, A., et al. 2023, A&A, 670, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolphin, A. E. 2002, MNRAS, 332, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Feuillet, D. K., Sahlholdt, C. L., Feltzing, S., & Casagrande, L. 2021, MNRAS, 508, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A. 2020, MNRAS, 493, 847 [Google Scholar]
- Forbes, D. A., & Bridges, T. 2010, MNRAS, 404, 1203 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Farr, W., Sinha, M., et al. 2019, J. Open Source Softw., 4, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallart, C., Freedman, W. L., Aparicio, A., Bertelli, G., & Chiosi, C. 1999, AJ, 118, 2245 [NASA ADS] [CrossRef] [Google Scholar]
- Gallart, C., Bernard, E. J., Brook, C. B., et al. 2019, Nat. Astron., 3, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Girardi, L., Dalcanton, J., Williams, B., et al. 2008, PASP, 120, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Gratton, R., Bragaglia, A., Carretta, E., et al. 2019, A&ARv, 27, 8 [Google Scholar]
- Green, P. J., & Sibson, R. 1978, Comput. J., 21, 168 [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
- Helmi, A., White, S. D. M., de Zeeuw, P. T., & Zhao, H. 1999, Nature, 402, 53 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Hidalgo, S. L., Pietrinferni, A., Cassisi, S., et al. 2018, ApJ, 856, 125 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2020, MNRAS, 493, 3363 [NASA ADS] [CrossRef] [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2021, MNRAS, 500, 1385 [Google Scholar]
- Horta, D., Schiavon, R. P., Mackereth, J. T., et al. 2023, MNRAS, 520, 5671 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [Google Scholar]
- Khoperskov, S., & Gerhard, O. 2022, A&A, 663, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Roelenga, S., & Bastian, U. 2019a, A&A, 625, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koppelman, H. H., Helmi, A., Massari, D., Price-Whelan, A. M., & Starkenburg, T. K. 2019b, A&A, 631, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Pfeffer, J. L., Reina-Campos, M., Crain, R. A., & Bastian, N. 2019, MNRAS, 486, 3180 [Google Scholar]
- Kruijssen, J. M. D., Pfeffer, J. L., Chevance, M., et al. 2020, MNRAS, 498, 2472 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Capitanio, L., Ruiz-Dern, L., et al. 2018, A&A, 616, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leaman, R., VandenBerg, D. A., & Mendel, J. T. 2013, MNRAS, 436, 122 [Google Scholar]
- Lebreton, Y., Goupil, M. J., & Montalbán, J. 2014a, EAS Pub. Ser., 65, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lebreton, Y., Goupil, M. J., & Montalbán, J. 2014b, EAS Pub. Ser., 65, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitinger, E., Baumgardt, H., Cabrera-Ziri, I., Hilker, M., & Pancino, E. 2023, MNRAS, 520, 1456 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Malhan, K., Ibata, R. A., Sharma, S., et al. 2022, ApJ, 926, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Mardini, M. K., Frebel, A., Chiti, A., et al. 2022, ApJ, 936, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Mucciarelli, A., Ferraro, F. R., et al. 2014, ApJ, 795, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miglio, A., Girardi, L., Grundahl, F., et al. 2021, Exp. Astron., 51, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Mikkola, D., McMillan, P. J., & Hobbs, D. 2023, MNRAS, 519, 1989 [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, A&A, 540, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Marino, A. F., Piotto, G., et al. 2015, MNRAS, 447, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Renzini, A., et al. 2017, MNRAS, 464, 3636 [Google Scholar]
- Minelli, A., Mucciarelli, A., Massari, D., et al. 2021, ApJ, 918, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Monelli, M., Gallart, C., Hidalgo, S. L., et al. 2010, ApJ, 722, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
- Monty, S., Venn, K. A., Lane, J. M. M., Lokhorst, D., & Yong, D. 2020, MNRAS, 497, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Monty, S., Yong, D., Marino, A. F., et al. 2023, MNRAS, 518, 965 [Google Scholar]
- Moretti, A., Piotto, G., Arcidiacono, C., et al. 2009, A&A, 493, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myeong, G. C., Vasiliev, E., Iorio, G., Evans, N. W., & Belokurov, V. 2019, MNRAS, 488, 1235 [Google Scholar]
- Myeong, G. C., Belokurov, V., Aguado, D. S., et al. 2022, ApJ, 938, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Naidu, R. P., Conroy, C., Bonaca, A., et al. 2020, ApJ, 901, 48 [Google Scholar]
- Nardiello, D., Libralato, M., Piotto, G., et al. 2018, MNRAS, 481, 3382 [NASA ADS] [CrossRef] [Google Scholar]
- Necib, L., Ostdiek, B., Lisanti, M., et al. 2020, Nat. Astron., 4, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Oria, P.-A., Tenachi, W., Ibata, R., et al. 2022, ApJ, 936, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Pancino, E., Seleznev, A., Ferraro, F. R., Bellazzini, M., & Piotto, G. 2003, MNRAS, 345, 683 [CrossRef] [Google Scholar]
- Pietrinferni, A., Hidalgo, S., Cassisi, S., et al. 2021, ApJ, 908, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Bedin, L. R., Anderson, J., et al. 2007, ApJ, 661, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., Milone, A. P., Bedin, L. R., et al. 2015, AJ, 149, 91 [Google Scholar]
- Re Fiorentin, P., Spagna, A., Lattanzi, M. G., & Cignoni, M. 2021, ApJ, 907, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, J. E., & Aller, L. H. 1976, Science, 191, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lara, T., Gallart, C., Bernard, E. J., & Cassisi, S. 2020, Nat. Astron., 4, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lara, T., Matsuno, T., Lövdal, S. S., et al. 2022a, A&A, 665, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz-Lara, T., Helmi, A., Gallart, C., Surot, F., & Cassisi, S. 2022b, A&A, 668, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Chieffi, A., & Straniero, O. 1993, ApJ, 414, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Saracino, S., Dalessandro, E., Ferraro, F. R., et al. 2019, ApJ, 874, 86 [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [Google Scholar]
- Sbordone, L., Salaris, M., Weiss, A., & Cassisi, S. 2011, A&A, 534, A9 [CrossRef] [EDP Sciences] [Google Scholar]
- Soderblom, D. R. 2010, ARA&A, 48, 581 [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [Google Scholar]
- Tailo, M., Corsaro, E., Miglio, A., et al. 2022, A&A, 662, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tenachi, W., Oria, P.-A., Ibata, R., et al. 2022, ApJ, 935, L22 [NASA ADS] [CrossRef] [Google Scholar]
- VandenBerg, D. A., Brogaard, K., Leaman, R., & Casagrande, L. 2013, ApJ, 775, 134 [Google Scholar]
- Verma, K., Rørsted, J. L., Serenelli, A. M., et al. 2022, MNRAS, 515, 1492 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Xiang, M., & Rix, H.-W. 2022, Nature, 603, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [Google Scholar]
- Yuan, Z., Myeong, G. C., Beers, T. C., et al. 2020, ApJ, 891, 39 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Isochrone fitting results
In this Appendix, we show the results of our isochrone fitting algorithm applied to the six GCs under study in this work. Each figure is made up of four panels. The lower ones show the posterior distribution of the parameters of the model, including their correlation, resulting from the fit of the (mF814W, mF606W-mF814W) CMD and of the (mF606W, mF606W-mF814W) CMD. The upper panels overplot the isochrone corresponding to the best-fitting solution to the observed CMDs, where the green symbols mark the stars that were actually used for the fit.
 |
Fig. A.1. Results for NGC 5927. Panel (a): Best-fit model in the (mF814W, mF606W-mF814W) CMD. Panel (b): Best-fit model in the (mF606W, mF606W-mF814W) CMD. Panel (c): Posterior distributions for the output parameters and the best-fit solution, quoted in the labels, in the (mF814W, mF606W-mF814W) CMD. Panel (d): Posterior distributions for the output parameters and the best-fit solution, quoted in the labels, in the (mF606W, mF606W-mF814W) CMD. |
 |
Fig. A.2. Results for NGC 6304. The contents of the different panels are the same as in Fig. A.1 |
 |
Fig. A.3. Results for NGC 6352. The contents of the different panels are the same as in Fig. A.1 |
 |
Fig. A.4. Results for NGC 6388. The contents of the different panels are the same as in Fig. A.1 |
 |
Fig. A.5. Results for NGC 6441. The contents of the different panels are the same as in Fig. A.1 |
 |
Fig. A.6. Results for NGC 6496. The contents of the different panels are the same as in Fig. A.1 |
All Tables
All Figures
 |
Fig. 1. Behaviour of the total extinction in the two filters used in this work, AF606W (left-hand panel) and AF814W (right-hand panel), as a function of Teff and colour-coded based on E(B − V). |
| In the text | |
 |
Fig. 2. Example of differential reddening correction in the case of NGC 6352. The original CMD is shown on the left and the corrected one on the right. |
| In the text | |
 |
Fig. 3. Example of a differential reddening map for NGC 6352. Each of the stars used to compute the differential reddening correction is plotted in sky coordinates and coloured according to its value of dE(B − V). |
| In the text | |
 |
Fig. 4. Zoom-in around the region of the SGB for the (mF814W, mF606W − mF814W) CMDs of NGC 6388 (left-hand panel) and NGC 6441 (right-hand panel). Stars highlighted in cyan are those selected via chromosome maps as belonging to chemically peculiar populations, and are therefore excluded from the analysis. Black symbols are instead stars belonging to the primordial population. |
| In the text | |
 |
Fig. 5. Difference between the output metallicities [Fe/H] computed assuming [α/Fe] = 0.08 and literature spectroscopic estimates for each GC, as provided by Harris (1996). The scatter around the mean value is 0.07 dex. Error bars are given by the sum in quadrature between our uncertainties and those by Harris (1996), and amount to ∼0.1 dex. |
| In the text | |
 |
Fig. 6. Difference between the absolute reddening value (left-hand panel) and distance modulus (right-hand panel) coming from our best-fit solution and literature ones. |
| In the text | |
 |
Fig. 7. Location of the six GCs under study in the age–metallicity plane, overplotted on the age–metallicity relation derived from the halo CMD. GCs with undoubted in situ origin are shown as black symbols, while NGC 6388 and NGC 6441 are marked in white. The location of GES (black dashed line) and of the Milky Way thick disc (black ellipse) are shown for comparison. |
| In the text | |
 |
Fig. A.1. Results for NGC 5927. Panel (a): Best-fit model in the (mF814W, mF606W-mF814W) CMD. Panel (b): Best-fit model in the (mF606W, mF606W-mF814W) CMD. Panel (c): Posterior distributions for the output parameters and the best-fit solution, quoted in the labels, in the (mF814W, mF606W-mF814W) CMD. Panel (d): Posterior distributions for the output parameters and the best-fit solution, quoted in the labels, in the (mF606W, mF606W-mF814W) CMD. |
| In the text | |
 |
Fig. A.2. Results for NGC 6304. The contents of the different panels are the same as in Fig. A.1 |
| In the text | |
 |
Fig. A.3. Results for NGC 6352. The contents of the different panels are the same as in Fig. A.1 |
| In the text | |
 |
Fig. A.4. Results for NGC 6388. The contents of the different panels are the same as in Fig. A.1 |
| In the text | |
 |
Fig. A.5. Results for NGC 6441. The contents of the different panels are the same as in Fig. A.1 |
| In the text | |
 |
Fig. A.6. Results for NGC 6496. The contents of the different panels are the same as in Fig. A.1 |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}{[\mathrm{M/H}]} = [\mathrm{Fe/H}]+\log (0.694\times 10^{[\alpha /\mathrm{Fe}]}+0.301). \end{aligned} $$](/articles/aa/full_html/2023/12/aa47289-23/aa47289-23-eq1.gif)
![$$ \begin{aligned} \mathcal{L} _{\rm priors}=\mathcal{L} _{E(B-V)}+\mathcal{L} _{\rm DM}+\mathcal{L} _{[\mathrm{M/H}]}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47289-23/aa47289-23-eq2.gif)
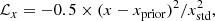
![$$ \begin{aligned} \mathcal{L} _{\rm fit} = \sum _{i=1}^{N}[\min (dist_{i})]^{2}/\sigma _{i}^{2}, \end{aligned} $$](/articles/aa/full_html/2023/12/aa47289-23/aa47289-23-eq4.gif)