EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 680 (December 2023) A&A, 680 (2023) A21 Full HTML
Open Access
Issue
A&A
Volume 680, December 2023
Article Number A21
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202347158
Published online 05 December 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Small bodies with satellites are a highly diverse population in the Solar System, spanning wide ranges of diameters, separations, and size ratios (see Fig. 1 and Margot et al. 2015, for a review). Some systems are made of large and similarly sized bodies. These double systems are thought to be primordial and are abundant in the Kuiper belt (Fraser et al. 2017). The largest small bodies (diameters above 100 km typically) can also have small satellites, believed to form from the reaccumulation of ejecta after impacts, and are found in both the asteroid and Kuiper belts (e.g., Ragozzine & Brown 2009; Berthier et al. 2014; Carry et al. 2019, 2021; Vachier et al. 2022). A significant fraction (about 15%; Margot et al. 2002; Pravec et al. 2006) of small asteroids (diameters less than 10 km) have close-in satellites, likely produced by fission due to YORP (Yarkovsky–O’Keefe–Radzievskii–Paddack) spin-up (Walsh et al. 2008; Walsh & Jacobson 2015; Zhang et al. 2022).

As of today, the least characterized population of small bodies in terms of multiplicity are the Jupiter Trojans. Only seven multiple systems have been discovered: (617) Patroclus by Gemini (Merline et al. 2001), (624) Hektor by W.M. Keck (Marchis et al. 2006), (3548) Eurybates with the Hubble Space Telescope (HST; Noll et al. 2020), (15094) Polymele via stellar occultation (Buie et al. 2022), (16974) Iphtime with the HST (Noll et al. 2016), and both (17365) Thymbraeus and (29314) Eurydamas from light curves (Mann et al. 2007). This low number of binary systems is most likely the result of observing biases. Radar observations efficient at discovering satellites are limited in range (Benner et al. 2015), and adaptive-optics observations require a bright source and have been mainly limited to large main-belt asteroids and the brightest Kuiper belt objects (KBOs; Merline et al. 1999; Marchis et al. 2005; Carry et al. 2011; Yang et al. 2020). While the HST does not require a bright source, most studies focused on KBOs (Noll et al. 2004; Brown et al. 2006; Grundy et al. 2011) until the approval of NASA’s Lucy mission (Levison et al. 2017). Finally, while the majority of binaries have been discovered via light curves (see Johnston 2018), often by amateur astronomers, the Jupiter Trojans are too faint for most amateur equipment (Mousis et al. 2014).

However, Jupiter Trojans are a unique population, related to the outer Solar System, and were trapped on the L4/L5 Lagrangian points of the Sun-Jupiter system during the phase of dynamical instability in the early Solar System (Morbidelli et al. 2005; Nesvorný et al. 2018). We focus here on the reported binary (17365) Thymbraeus1. We conducted an observing campaign spanning several oppositions to determine the physical properties of this object.

The article is organized as follows. In Sect. 2 we present the observations and data reduction. We describe how we determine the properties of Thymbraeus in Sect. 3, and discuss their implications in Sect. 4. We summarize our findings in Sect. 5.

thumbnail Fig. 1

Diversity among small-body binaries, with the seven known Jupiter Trojans (JTO) in black. The satellite diameters and semimajor axes are from Johnston (2018), and the diameters of the primary bodies are from the SsODNet service (Berthier et al. 2023).

2 Observations

We observed Thymbraeus in 2015 on seven dates with the 104 cm Omicron telescope of the Centre Pédagogique Planète et Univers (C2PU) facility (Bendjoya et al. 2012) located at the Calern observing site (Côte d’Azur Observatory, France, IAU code: 010). In 2021, we used three facilities. We collected 29 epochs with the 60 cm André Peyrot telescope mounted at Les Makes observatory (IAU code 181) on La Réunion island. We acquired 15 and 5 epochs with the TRAPPIST south and north telescopes, respectively (IAU code I40 and Z53; Jehin et al. 2011). For all these observations, standard reduction (dark subtraction and flat-fielding) and photometry procedures (plate solution, zero point, and aperture photometry) were carried out. We also retrieved the four light curves obtained in 2013 by Stephens et al. (2014) with a 40 cm telescope at the CS3-Trojan Station observatory (IAU code U81), available from ALCDEF2 (Warner 2016). The detailed logs of observations are provided in Table 1. Photometric uncertainties are estimated to about 0.03 mag from their scatter.

We complemented this data set with the observations from 2005 and 2006 reported by Mann et al. (2007), which we digitized. These last two light curves are only plotted in figures in Mann et al. (2007) and were not available in tabular format. Furthermore, they were reported as a function of the rotation phase and in reduced magnitude, not as observed (i.e., without the epoch and apparent magnitude). We thus did not use these two light curves for modeling but as a posteriori validation of the solution.

3 Analysis

3.1 Synodic period

We used the phase dispersion minimization (PDM) technique (Stellingwerf 1978) to search for the synodic rotation period within the photometric data (all epochs were light-time-corrected). We assumed that two maxima and minima occur per rotation.

The PDM technique works as follows: based on a trial period, it bins data according to the rotational phase. The average variance of these subsets is then compared to the overall variance of the full set of observations. It next defines the statistical parameter, θ. The best estimate of the period is the one that minimises θ. The method does not assume any sinusoidal variation in the light curve and is well suited for unevenly spaced observations. It finds all periodic components or subharmonics (aliases of the period).

We followed the approach used by Berthier et al. (2020) for (617) Patroclus: we first determined the synodic period with PDM for each epoch of observation: 2013, 2015, and 2021. We then searched for the fundamental synodic period by combining all epochs, and find Psyn = 12.671575 ± 0.000003 h.

Table 1

Log of observations.

thumbnail Fig. 2

Solution space for the pole of rotation for pairs 2013+2021 (left) and 2015+2021 (right). See the main text for more information. The black cross gives the solution intersection of the red and blue areas.

3.2 Spin-vector coordinates

From the change in the shape of the light curves collected in 2013, 2015, and 2021, we determined a set of two symmetric pole solutions. We therefore solved the system of equations shown below, which gives the position of the rotation pole from simple and relevant assumptions on the latitude of the sub-observer point (Descamps et al. 2007). The latitude of the sub-observer point (βSEP) and the north pole position angle (np) are related to the equatorial coordinates of the rotation pole (α0, δ0) and the equatorial coordinates of the asteroid (α, δ) for each epoch by the following equations: 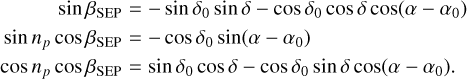(1)

Our search for possible solutions for the rotation pole of the asteroid was mainly based on assumptions concerning the latitude of the sub-observer point. They are constrained by the observed amplitudes of the light curves. The light curve observed in 2013 has the lowest amplitude, 0.76 mag, and that of 2015 the largest, 1.16 mag. The amplitude of the 2021 light curve, while lower than the 2015 one, remains significant. From these findings, we made the following assumptions: in 2013, |βSEP| > 14°; in 2015, |βSEP| < 4°; and in 2021, |βSEP| < 10°.

We considered two observation pairs: 2013+2021 and 2015+2021. For each pair, we searched graphically for the areas of the solution space for which the previous conditions on the latitude of the sub-observer point are satisfied. Each pair of sub-terrestrial latitude values for each epoch point was defined on a grid of values from −16° to +16° in steps of 0.5° (Fig. 2).

In order for the above conditions to be satisfied, it is necessary to select the solutions that are at the intersection of the red area for the 2013+2021 epoch (Fig. 2, left) and the blue area for the 2015+2021 epoch (Fig. 2, right). We could then infer two symmetrical pole solutions (direct and retrograde), which are shown in Fig. 2 as black crosses. The J2000 equatorial coordinates of the pole 1 are α0 = 92 ± 2° and δ0 = −77 ± 2°. The solution for pole 2 is given by α0 = 268 ± 2° and δ0 = +77 ± 2°.

3.3 Shape

High brightness variations (greater than 0.9 mag), U-shaped maxima, and V-shaped minima are highly suggestive of an elongated shape with two lobes at the ends separated by a narrower neck (Descamps 2015). In a previous study devoted to the Trojan asteroid Thymbraeus, Mann et al. (2007) sought to model their photometric light curves using two tightened and doubly synchronized equilibrium Roche ellipsoids. The aim was to determine how well the observations could be matched by theoretical light curves of a bilobated shape.

However, Gnat & Sari (2010) showed that equilibrium figures of tightly bound binaries are no longer triaxial ellipsoids and that departures from the pure ellipsoidal forms may amount to nearly 20%. They found that, at a mutual separation on the order of twice the sum of their mean radius, departures from ellipsoids given by the Roche binary approximation are negligible. On the other hand, Descamps (2015) show that two Roche ellipsoids only provide an approximation to the properties of a bilobated object, while dumbbell-shaped equilibrium figures provide a numerical solution without bias on the angular momentum. In a such case, the solution is entirely described by a single parameter, the normalized angular velocity, Ω, defined by the ratio between the angular frequency, ω, and the critical spin rate for a spherical body, ωc, which is the maximum spin rate that can be sustained by a rigid body: 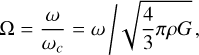(2)

where G is the gravitational constant, and ρ the bulk density.

Therefore, we investigated a more reliable shape solution belonging to the dumbbell equilibrium sequence. The objects of this sequence are symmetric with respect to one axis and rotate around a second axis perpendicular to the symmetry axis. The dumbbell sequence was first computed by Eriguchi et al. (1982) and more recently fully characterized by Descamps (2015). The synthetic light curves are produced taking into account the photometric effects induced by the scattering effects of sunlight by the surface of the object coupled to the phase angle. We present these light curves along with the observations in Fig. 3. The light curves agree well with observations (RMS residuals of 0.05, 0.12, and 0.6 mag for the three epochs) though do present some departures, likely due to surface features not represented by the dumbbell equilibrium figure. In addition, even at the small phase angles involved (8° in 2013, 6° in 2015, and 4° in 2021), it is necessary to take the significant effect of mutual shadowing into account. We adopted a scattering law that combines, through a weight factor k, a Lambertian icy-type law, suitable for high albedo surfaces, and a lunar-type reflection described by the Lommel-Seeliger law, appropriate for low albedo surfaces (Kaasalainen et al. 2001). We adopted k = 0.05. The best-fit solution was obtained simultaneously with the determination of the sidereal periods for each pole solution: Ω = 0.285 ± 0.01, Psid,1 = 12.671821 h, and Psid,2 = 12.672607 h. We determined a density of ρ = 830 ± 50 kg m−3 from the sidereal periods and the normalized angular velocity. This low density is similar to the density of 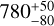kg m−3 originally reported by Mann et al. (2007), is typical of Trojans and similarly sized KBOs (e.g., Carry 2012; Scheeres et al. 2015), and suggests a porous interior characteristic of rubble piles.

The light curves present an asymmetry between the minima, noticeably apparent in 2013 with a magnitude differential of 0.05 mag. We thus applied a small perturbation to the hydrostatic equilibrium shape solution using a Gaussian random sphere (Muinonen 1998), which allowed us to take the substantial internal friction present in rubble pile objects into account (Descamps 2016). In doing so, we constructed a so-called near-equilibrium shape by combining the initial dumbbell shape model with a Gaussian random sphere, which approximates the departure from the real shape. Obviously, this does not mean that the resulting solution is the exact solution, just that the asymmetry between photometric minima can be interpreted by small shape deviations from a perfect fluid solution. We used a Gaussian random sphere generated by two parameters: the relative standard deviation of radial distance, σ = 0.05, and the input correlation angle of the Gaussian sphere, Γ = 180°. The resulting object has the following statistical properties according to the notations introduced in Muinonen (1998) and Muinonen & Lagerros (1998): 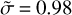, , 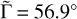, 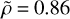and the standard deviation of shape angle .

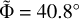The inferred estimated slope angle (assimilated to the angle of repose) is 2.5°. The angle of repose for a fluid body is, however, strictly zero. It is often pointed out that loosely consolidated piles of aggregated particles have slopes that are maintained at the angle of repose with respect to horizontal. We present in Fig. 4 the final shape solution obtained for Thymbraeus.

Our model faithfully reproduces the observed light curves without invoking two Roche ellipsoids with a significant secondary-to-primary mass ratio, which was done for the solution proposed by Mann et al. (2007). Our solution also reproduces the light curves observed in April 2005 and February 2006 and published in Mann et al. (2007, see our Fig. 5). The photometric ranges and the asymmetries between the minima are perfectly reproduced. Mann et al. (2007) assumed that the object was viewed equatorially in 2005 (aspect angle of 90° or βSEP = 0°), thus producing the larger photometric range of ~ 1 mag but at the cost of a differential drop between minima of nearly 0.1 mag. With the 2006 observations, they found that an aspect angle of 75°(βSEP = 15°) produced a better fit. Our solution gives βSEP = −6° in 2005 and βSEP = −10° in 2006. Furthermore, if we do not take the effects of cast shadows into account, we obtain an amplitude of 0.917 mag in 2005 instead of 0.971 mag and with a quasi-absence of asymmetry (Fig. 5). We also plot the synthetic light curves for different values of Ω. They show that the photometric range increases with Ω while the differential in magnitude decreases. This results from the fact that when Ω increases, the corresponding equilibrium figure of the dumbbell sequence elongates and its waist thickens. With the nominal solution Ω = 0.285, the magnitude differential is Δ = 0.034 mag, but for Ω = 0.300, Δ = 0.017 mag.

None of the light curves collected so far show unequal minima; this implies that the two lobes are of similar size. If this were not the case, we would observe a differential in magnitude whatever the orientation of the system. This proves that the magnitude differential arises from a significant mutual shadowing between the lobes under specific geometric configurations, which indicates that the two differ in terms of shape but not size. This underlines the importance of taking all photometric effects into account, including mutual shadowing, which must be combined simultaneously with a reliable pole solution, independently derived from any consideration on the shape model, and a realistic shape solution.

thumbnail Fig. 3

Observed light curves of Thymbraeus compared with the synthetic light curves with two spin solutions. The coordinates (α0, δ0) of the spin solutions are (92°,−77°) and (268°,−77°) for Spin 1 and 2. respectively (see text).
thumbnail Fig. 4

Shape model of Thymbraeus as seen from the equator (top) and the spin axis (bottom).
thumbnail Fig. 5

Effect of Ω on the light curve, compared to the observations from 2005 and 2006 by Mann et al. (2007). The solution marked with a star (★) does not account for self-shadowing.

4 Discussion

The dumbbell model had already been successfully applied to the asteroid (216) Kleopatra (Descamps 2015), which was known from radar imagery to have two lobes at its extremities (Ostro et al. 2000), earning it the nickname “dog bone”. However, the radar model could not satisfactorily account for the photometric observations, which required the effects of self-shadowing to be taken into account. Stellar occultation observations confirmed that the radar model was not sufficiently elongated and that its central waist was narrower (Descamps et al. 2011). More recently, new high resolution imaging made with the ESO VLT SPHERE/ZIMPOL camera confirmed that the shape of (216) Kleopatra is very close to an equilibrium dumbbell figure with two lobes, a slightly thicker waist (Marchis et al. 2021), and Ω = 0.334, which is only slightly higher than the value of 0.297 found by Descamps (2015). Consequently, the dumbbell equilibrium figure formalism seems to be a trustworthy approach, and our dumbbell model of Thymbraeus appears to be the best suited to explain the photometric light curves.

The presence of two large lobes, separated by a narrower central part, that are roughly identical in size but different in shape is supported by the importance of self-shadowing effects in photometric observations, without which it is impossible to account for the difference in magnitude drop between the minima of some light curves. Such a physical feature is rare and is key for understanding the origin and future of this striking shape. It now needs to be confirmed with new high resolution observations either by precision photometry or by stellar occultations. Precision photometry should also allow one to discriminate between the two pole solutions.

The shape solution found in this work is at the end of the dumbbell equilibrium sequence (Fig. 6). The angular momentum, H, is computed as 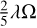, with λ the non-sphericity parameter (Descamps 2015), equal to 4.5932 for Thymbraeus. This sequence ends for the value Ω = 0.2815 and at this point joins the sequence of synchronous congruent binaries numerically investigated by Sharma (2009) and more completely by Gnat & Sari (2010). Furthermore, the bulk density derived from the model is very close to that determined for another Trojan asteroid, (617) Patroclus (Berthier et al. 2020), which is a doubly synchronous system. Should Thymbraeus’s rotation be accelerated, it would fission and produce a doubly synchronized system.

thumbnail Fig. 6

Angular velocity, Ω, against angular momentum, H, for Thymbraeus. The solid curves represent the Jacobi, dumbbell (Descamps 2015), and twin synchronous binary ellipsoid sequences (Gnat & Sari 2010). The Roche approximation is represented by the dashed curve. This figure is adapted from Descamps (2015).

5 Conclusions

We collected light curves of the Trojan (17365) Thymbraeus in 2015 and 2021 and retrieved observations from 2005, 2006, and 2013. These observations present periodic large-amplitude variations, hinting at a binarity nature for Thymbraeus. We analyzed these light curves with the formalism of dumbbell equilibrium figures. We determine Thymbraeus to be a bilobated asteroid, with two lobes of equal size but differing shapes. Its sidereal rotation is found to be 12.672 h, and two symmetric poles corresponding to the direct and prograde rotation are determined at J2000 equatorial coordinates (α0,δ0) of (92°, −77°) and (268°, +77°), respectively, with an uncertainty of 2°. The density of Thymbraeus is found to be 830 ± 50 kg m−3, confirming the original report by Mann et al. (2007), which is similar to that of other Jupiter Trojans and small KBOs. The rotation of Thymbraeus is close to the end of the dumbbell equilibrium sequence. A faster-rotating Thymbraeus would fission into an equal-size binary reminiscent of (617) Patroclus.

Acknowledgements

We thank the AGORA association which administrates the 60 cm telescope at Les Makes observatory, La Reunion island, under a financial agreement with Paris Observatory. Thanks to A. Peyrot, J.-P. Teng for local support, and A. Klotz for helping with the robotizing. TRAPPIST-South is funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, FNRS) under the grant PDR T.0120.21. TRAPPIST-North is a project funded by the University of Liège, and performed in collaboration with Cadi Ayyad University of Marrakesh. E. Jehin is a Belgian FNRS Senior Research Associate. The authors acknowledge the use of the Virtual Observatory tools Miriade (http://vo.imcce.fr/webservices/miriade/) (Berthier et al. 2008), SsODNet (https://ssp.imcce.fr/webservices/ssodnet/) (Berthier etal. 2023), and TOPCAT (http://www.star.bris.ac.uk/mbt/topcat/) and STILTS (http://www.star.bris.ac.uk/mbt/stilts/) (Taylor 2005). Thanks to the developers and maintainers.

References

  1. Bendjoya, P., Abe, L., Rivet, J. P., et al. 2012, in SF2A-2012: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. S. Boissier, P. de Laverny, N. Nardetto, et al., 643 [Google Scholar]
  2. Benner, L. A. M., Busch, M. W., Giorgini, J. D., Taylor, P. A., & Margot, J. L. 2015, Asteroids IV, Radar Observations of Near-Earth and Main-Belt Asteroids (Tucson: University Arizona Press), 165 [Google Scholar]
  3. Berthier, J., Hestroffer, D., Carry, B., et al. 2008, LPI Contrib., 1405, 8374 [Google Scholar]
  4. Berthier, J., Vachier, F., Marchis, F., Durech, J., & Carry, B. 2014, Icarus, 239, 118 [CrossRef] [Google Scholar]
  5. Berthier, J., Descamps, P., Vachier, F., et al. 2020, Icarus, 352, 113990 [CrossRef] [Google Scholar]
  6. Berthier, J., Carry, B., Mahlke, M., & Normand, J. 2023, A&A, 671, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Brown, M. E., van Dam, M. A., Bouchez, A. H., et al. 2006, ApJ, 639, 4346 [Google Scholar]
  8. Buie, M., Keeney, B., Levison, H., Olkin, C., & Lucy Occultations Team 2022, AAS/Div. Planet. Sci. Meeting Abstracts, 54, 512.03 [Google Scholar]
  9. Carry, B. 2012, Planet. Space Sci., 73, 98 [CrossRef] [Google Scholar]
  10. Carry, B., Hestroffer, D., DeMeo, F., et al. 2011, A&A, 534, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Carry, B., Vachier, F., Berthier, J., et al. 2019, A&A, 623, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carry, B., Vernazza, P., Vachier, F., et al. 2021, A&A, 650, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Descamps, P. 2015, Icarus, 245, 64 [CrossRef] [Google Scholar]
  14. Descamps, P. 2016, Icarus, 265, 29 [NASA ADS] [CrossRef] [Google Scholar]
  15. Descamps, P., Marchis, F., Michalowski, T., et al. 2007, Icarus, 187, 482 [NASA ADS] [CrossRef] [Google Scholar]
  16. Descamps, P., Marchis, F., Berthier, J., et al. 2011, Icarus, 211, 1022 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eriguchi, Y., Hachisu, I., & Sugimoto, D. 1982, Prog. Theor. Phys., 67, 1068 [CrossRef] [Google Scholar]
  18. Fraser, W. C., Bannister, M. T., Pike, R. E., et al. 2017, Nat. Astron., 1, 0088 [Google Scholar]
  19. Gnat, O., & Sari, R. 2010, ApJ, 719, 1602 [NASA ADS] [CrossRef] [Google Scholar]
  20. Grundy, W. M., Noll, K. S., Nimmo, F., et al. 2011, Icarus, 213, 678 [Google Scholar]
  21. Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
  22. Johnston, W. R. 2018, NASA Planetary Data System [Google Scholar]
  23. Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
  24. Levison, H. F., Olkin, C., Noll, K. S., Marchi, S., & Lucy Team 2017, Annual Lunar Planet. Sci. Conf. Lunar Planet. Sci. Conf., 48, 2025 [NASA ADS] [Google Scholar]
  25. Mann, R. K., Jewitt, D., & Lacerda, P. 2007, AJ, 134, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  26. Marchis, F., Descamps, P., Hestroffer, D., & Berthier, J. 2005, Nature, 436, 822 [CrossRef] [Google Scholar]
  27. Marchis, F., Wong, M. H., Berthier, J., et al. 2006, IAU Circ., 8732, 1 [NASA ADS] [Google Scholar]
  28. Marchis, F., Jorda, L., Vernazza, P., et al. 2021, A&A, 653, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Margot, J. L., Nolan, M. C., Benner, L. A. M., et al. 2002, Science, 296, 1445 [CrossRef] [Google Scholar]
  30. Margot, J.-L., Pravec, P., Taylor, P., Carry, B., & Jacobson, S. 2015, Asteroid Systems: Binaries, Triples, and Pairs, eds. P. Michel, F. DeMeo, & W. F. Bottke (University of Arizona Press), 355 [Google Scholar]
  31. Merline, W. J., Close, L. M., Dumas, C., et al. 1999, Nature, 401, 565 [NASA ADS] [CrossRef] [Google Scholar]
  32. Merline, W. J., Close, L. M., Siegler, N., et al. 2001, IAU Circ., 7741, 2 [NASA ADS] [Google Scholar]
  33. Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [Google Scholar]
  34. Mousis, O., Hueso, R., Beaulieu, J.-P., et al. 2014, Exp. Astron., 38, 91 [NASA ADS] [CrossRef] [Google Scholar]
  35. Muinonen, K. 1998, A&A, 332, 1087 [NASA ADS] [Google Scholar]
  36. Muinonen, K., & Lagerros, J. S. V. 1998, A&A, 333, 753 [NASA ADS] [Google Scholar]
  37. Nesvorný, D., Vokrouhlický, D., Bottke, W. F., & Levison, H. F. 2018, Nat. Astron., 2, 878 [Google Scholar]
  38. Noll, K. S., Stephens, D. C., Grundy, W. M., & Griffin, I. 2004, Icarus, 172, 402 [CrossRef] [Google Scholar]
  39. Noll, K. S., Grundy, W. M., Ryan, E. L., & Benecchi, S. D. 2016, Ann. Lunar Planet. Sci. Conf., 2632 [Google Scholar]
  40. Noll, K. S., Brown, M. E., Weaver, H. A., et al. 2020, PSJ, 1, 44 [NASA ADS] [Google Scholar]
  41. Ostro, S. J., Hudson, R. S., Nolan, M. C., et al. 2000, Science, 288, 836 [CrossRef] [Google Scholar]
  42. Pravec, P., Scheirich, P., Kušnirák, P., et al. 2006, Icarus, 181, 63 [NASA ADS] [CrossRef] [Google Scholar]
  43. Ragozzine, D., & Brown, M. E. 2009, AJ, 137, 4766 [NASA ADS] [CrossRef] [Google Scholar]
  44. Scheeres, D. J., Britt, D., Carry, B., & Holsapple, K. A. 2015, Asteroid Inte¬riors and Morphology, eds. P. Michel, F. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 745 [Google Scholar]
  45. Sharma, I. 2009, Icarus, 200, 636 [NASA ADS] [CrossRef] [Google Scholar]
  46. Stellingwerf, R. F. 1978, ApJ, 224, 953 [Google Scholar]
  47. Stephens, R. D., French, L. M., Davitt, C., & Coley, D. R. 2014, Minor Planet Bull., 41, 95 [NASA ADS] [Google Scholar]
  48. Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
  49. Vachier, F., Carry, B., & Berthier, J. 2022, Icarus, 382, 115013 [NASA ADS] [CrossRef] [Google Scholar]
  50. Walsh, K. J., & Jacobson, S. A. 2015, Asteroids 4, Formation and Evolution of Binary Asteroids, eds. P. Michel, F. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 375 [Google Scholar]
  51. Walsh, K. J., Richardson, D. C., & Michel, P. 2008, Nature, 454, 188 [Google Scholar]
  52. Warner, B. D. 2016, Minor Planet Bull., 43, 26 [NASA ADS] [Google Scholar]
  53. Yang, B., Hanuš, J., Carry, B., et al. 2020, A&A, 641, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Zhang, Y., Michel, P., Barnouin, O. S., et al. 2022, Nat. Commun., 13, 4589 [NASA ADS] [CrossRef] [Google Scholar]
1

Formerly 1978 VF11.

All Tables

Table 1

Log of observations.

In the text

All Figures

thumbnail Fig. 1

Diversity among small-body binaries, with the seven known Jupiter Trojans (JTO) in black. The satellite diameters and semimajor axes are from Johnston (2018), and the diameters of the primary bodies are from the SsODNet service (Berthier et al. 2023).
In the text
thumbnail Fig. 2

Solution space for the pole of rotation for pairs 2013+2021 (left) and 2015+2021 (right). See the main text for more information. The black cross gives the solution intersection of the red and blue areas.
In the text
thumbnail Fig. 3

Observed light curves of Thymbraeus compared with the synthetic light curves with two spin solutions. The coordinates (α0, δ0) of the spin solutions are (92°,−77°) and (268°,−77°) for Spin 1 and 2. respectively (see text).
In the text
thumbnail Fig. 4

Shape model of Thymbraeus as seen from the equator (top) and the spin axis (bottom).
In the text
thumbnail Fig. 5

Effect of Ω on the light curve, compared to the observations from 2005 and 2006 by Mann et al. (2007). The solution marked with a star (★) does not account for self-shadowing.
In the text
thumbnail Fig. 6

Angular velocity, Ω, against angular momentum, H, for Thymbraeus. The solid curves represent the Jacobi, dumbbell (Descamps 2015), and twin synchronous binary ellipsoid sequences (Gnat & Sari 2010). The Roche approximation is represented by the dashed curve. This figure is adapted from Descamps (2015).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.