| Issue |
A&A
Volume 650, June 2021
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202140342 | |
| Published online | 17 June 2021 | |
Evidence for differentiation of the most primitive small bodies★,★★
1
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS,
Laboratoire Lagrange,
France
e-mail: benoit.carry@oca.eu
2
Aix Marseille Univ, CNRS, LAM, Laboratoire d’Astrophysique de Marseille,
Marseille,
France
3
IMCCE, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Univ Paris 06, Univ. Lille,
France
4
University of Maryland College Park,
College Park,
MD 20742,
USA
5
NASA Goddard Space Flight Center,
Greenbelt,
MD 20771,
USA
6
Institute of Astronomy, Faculty of Mathematics and Physics, Charles University,
V Holešovičkách 2,
18000
Prague,
Czech Republic
7
Space sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août 17,
4000
Liège,
Belgium
8
Department of Earth, Atmospheric and Planetary Sciences, MIT,
77 Massachusetts Avenue,
Cambridge,
MA 02139,
USA
9
Mathematics and Statistics, Tampere University,
33014
Tampere,
Finland
10
Astronomical Observatory Institute, Faculty of Physics, Adam Mickiewicz University,
ul. Słoneczna 36,
60-286
Poznań,
Poland
11
Geneva Observatory,
1290
Sauverny,
Switzerland
12
Oukaimeden Observatory, High Energy Physics and Astrophysics Laboratory, Cadi Ayyad University,
Marrakech,
Morocco
13
Astronomical Institute of the Romanian Academy,
5 Cutitul de Argint,
040557
Bucharest,
Romania
14
Jet Propulsion Laboratory, California Institute of Technology,
4800 Oak Grove Drive,
Pasadena,
CA 91109,
USA
15
European Space Agency, ESTEC - Scientific Support Office,
Keplerlaan 1,
Noordwijk
2200 AG,
The Netherlands
16
Institut Polytechnique des Sciences Avancées IPSA,
63 bis Boulevard de Brandebourg,
94200
Ivry-sur-Seine,
France
17
Thirty-Meter-Telescope,
100 West Walnut St, Suite 300,
Pasadena,
CA 91124,
USA
18
Open University, School of Physical Sciences, The Open University,
MK7 6AA,
UK
19
Laboratoire Atmosphères, Milieux et Observations Spatiales, CNRS & Université de Versailles Saint-Quentin-en-Yvelines,
Guyancourt,
France
20
SETI Institute, Carl Sagan Center,
189 Bernado Avenue,
Mountain View,
CA 94043,
USA
21
Sección Física, Departamento de Ciencias, Pontificia Universidad Católica del Perú,
Apartado 1761,
Lima,
Peru
22
Institute of Physics, University of Szczecin,
Wielkopolska 15,
70-453
Szczecin,
Poland
23
Departamento de Física, Ingeniería de Sistemas y Teoría de la Señal, Universidad de Alicante, Alicante,
Spain
24
Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona (IEEC-UB),
Martí Franquès 1,
E08028
Barcelona,
Spain
25
Towson University,
Towson,
MD,
USA
26
Center for Solar System Studies,
446 Sycamore Ave.,
Eaton,
CO 80615,
USA
27
European Southern Observatory (ESO),
Alonso de Cordova 3107,
1900
Casilla Vitacura,
Santiago,
Chile
Received:
14
January
2021
Accepted:
5
March
2021
Context. Dynamical models of Solar System evolution have suggested that the so-called P- and D-type volatile-rich asteroids formed in the outer Solar System beyond Neptune’s orbit and may be genetically related to the Jupiter Trojans, comets, and small Kuiper belt objects (KBOs). Indeed, the spectral properties of P- and D-type asteroids resemble that of anhydrous cometary dust.
Aims. We aim to gain insights into the above classes of bodies by characterizing the internal structure of a large P- and D-type asteroid.
Methods. We report high-angular-resolution imaging observations of the P-type asteroid (87) Sylvia with the Very Large Telescope Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE) instrument. These images were used to reconstruct the 3D shape of Sylvia. Our images together with those obtained in the past with large ground-based telescopes were used to study the dynamics of its two satellites. We also modeled Sylvia’s thermal evolution.
Results. The shape of Sylvia appears flattened and elongated (a/b ~1.45; a/c ~1.84). We derive a volume-equivalent diameter of 271 ± 5 km and a low density of 1378 ± 45 kg m−3. The two satellites orbit Sylvia on circular, equatorial orbits. The oblateness of Sylvia should imply a detectable nodal precession which contrasts with the fully-Keplerian dynamics of its two satellites. This reveals an inhomogeneous internal structure, suggesting that Sylvia is differentiated.
Conclusions. Sylvia’s low density and differentiated interior can be explained by partial melting and mass redistribution through water percolation. The outer shell should be composed of material similar to interplanetary dust particles (IDPs) and the core should be similar to aqueously altered IDPs or carbonaceous chondrite meteorites such as the Tagish Lake meteorite. Numerical simulations of the thermal evolution of Sylvia show that for a body of such a size, partial melting was unavoidable due to the decay of long-lived radionuclides. In addition, we show that bodies as small as 130–150 km in diameter should have followed a similar thermal evolution, while smaller objects, such as comets and the KBO Arrokoth, must have remained pristine, which is in agreement with in situ observations of these bodies. NASA Lucy mission target (617) Patroclus (diameter ≈140 km) may, however, be differentiated.
Key words: minor planets, asteroids: general / Kuiper belt: general / minor planets, asteroids: individual: Sylvia
Tables A.1, B.1, C.1 and C.2 and the reduced and deconvolved SPHERE images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/650/A129
Based on observations made with ESO telescopes at the La Silla Paranal Observatory under program 073.C-0851 (PI Merline), 073.C-0062 (PI Marchis), 085.C-0480 (PI Nitschelm), 088.C-0528 (PI Rojo), 199.C-0074 (PI Vernazza).
© B. Carry et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The Cybele region at the outer rim of the asteroid belt (3.27–3.7 au) is essentially populated by P- and D-type asteroids and to a lesser extent by C-type bodies (DeMeo & Carry 2013, 2014). P- and D-type asteroids are thought to have formed in the outer Solar System (beyond 10 au), among the progenitors of the current Kuiper Belt, and to have been implanted in the inner Solar System (asteroid belt, Lagrangian Points of Jupiter) following giant planet migrations (see Levison et al. 2009; DeMeo et al. 2014; Vokrouhlický et al. 2016). This implies that the P- and D-type main belt asteroids and the Jupiter Trojans could be compositionally related to outer small bodies, such as Centaurs, short-period comets, and small (D ≤ 300 km) Kuiper belt objects (KBOs). This dynamical scenario is currently supported by the similarity in size distributions between the Jupiter Trojans and small KBOs (Fraser et al. 2014) as well as the similarity in terms of spectral properties between P- and D-type main belt asteroids, the Trojans of Jupiter and comets (Vernazza et al. 2015; Vernazza & Beck 2016).
Overall,the outer Solar System is of tremendous interest, as it is recognized as being the least processed since the dawn of the Solar System and thus the closest to the primordial materials from which the Solar System formed (e.g., McKinnon et al. 2020). This is currently supported by the analysis of the spectral properties of P- and D-type main belt asteroids, Jupiter Trojans, and comets that reveal a surface composition compatible with that of anhydrous chondritic porous interplanetary dust particles (CP IDP, see Vernazza et al. 2015). The CP IDPs are currently seen among the available extra-terrestrial materials as being the closest to the starting ones (Bradley 1999). In particular, based on its albedo and visible, near-, and mid-infrared spectrum, it is now well established (see Vernazza et al. 2013) that the aqueously altered Tagish Lake meteorite cannot be representative of the surface composition of D-type asteroids nor that of most P-type asteroids as suggested earlier (Hiroi et al. 2001). As such, CP IDPs are currently the most likely analogs of the refractory materials present at the surface of P- and D-type asteroids.
There are only four known large (diameter ≥100 km) P- and D-type asteroids with satellites: (87) Sylvia, (107) Camilla, (617) Patroclus, and (624) Hektor, with reported densities of 1400 ± 200 kg m−3 (e.g., Berthier et al. 2014), 1280 ± 130 kg m−3 (Pajuelo et al. 2018), 800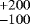 to 1080 ± 330 kg m−3 (Marchis et al. 2006; Mueller et al. 2010), and 1000 ± 300 kg m−3 (Marchis et al. 2014) respectively. Patroclus is a double asteroid with nearly equally-sized 150–100 km components (e.g., Buie et al. 2015; Hanuš et al. 2017; Berthier et al. 2020) and is therefore atypical among asteroids but further strengthens the common origin of P and D asteroids and small KBOs (Nesvorný et al. 2018), many of which likely formed as binaries (Fraser et al. 2017; Nesvorný et al. 2019; Robinson et al. 2020). Both Camilla and Sylvia are among the largest asteroids, with diameters above 250 and 280 km, respectively (Carry 2012). Their low density implies a bulk composition that cannot consist only of refractory materials but that must also comprise a large amount of volatiles (Pajuelo et al. 2018).
to 1080 ± 330 kg m−3 (Marchis et al. 2006; Mueller et al. 2010), and 1000 ± 300 kg m−3 (Marchis et al. 2014) respectively. Patroclus is a double asteroid with nearly equally-sized 150–100 km components (e.g., Buie et al. 2015; Hanuš et al. 2017; Berthier et al. 2020) and is therefore atypical among asteroids but further strengthens the common origin of P and D asteroids and small KBOs (Nesvorný et al. 2018), many of which likely formed as binaries (Fraser et al. 2017; Nesvorný et al. 2019; Robinson et al. 2020). Both Camilla and Sylvia are among the largest asteroids, with diameters above 250 and 280 km, respectively (Carry 2012). Their low density implies a bulk composition that cannot consist only of refractory materials but that must also comprise a large amount of volatiles (Pajuelo et al. 2018).
With an estimated diameter of nearly 280 km (Carry 2012, and reference therein), (87) Sylvia is the largest body in the Cybele region and more generally the largest P- and D-type asteroid in the inner (≤5.5 au) Solar System. Its surface composition is fully consistent with that of anhydrous chondritic porous IDPs (Vernazza et al. 2015; Usui et al. 2019). Furthermore, it is the first asteroid around which two satellites were discovered (Marchis et al. 2005). Because of its rather large angular size at opposition (≈ 0.14′′) and its two moons, Sylvia is an ideal target for high angular-resolution adaptive-optics (AO) observations as these allow an accurate characterization of its 3D shape and of the mass of the system, and hence of its bulk density. Furthermore, the two moons allow for one to probe the internal structure and in particular the harmonics of the gravity field (at least the lowest-order gravitational moment, the quadrupole J2). This information, in turn, probes the distribution of material inside Sylvia, that is to say whether its interior is homogeneous or differentiated.
Several authors have studied Sylvia’s dynamical system (Marchis et al. 2005; Winter et al. 2009; Frouard & Compère 2012; Fang et al. 2012; Beauvalet & Marchis 2014; Berthier et al. 2014; Drummond et al. 2016). While these studies agreed on the mass of Sylvia and its low density (around 1300 kg m−3), there is no consensus regarding its gravitational potential (of which only the quadrupole J2 has been studied, Table 1). The latter is, however, a direct consequence of the internal structure of Sylvia.
To constrain the bulk density of Sylvia and its internal structure, we observed it as part of our imaging survey of D ≥ 100 km main-belt asteroids (ID 199.C-0074, PI P. Vernazza, see Vernazza et al. 2018, 2020; Viikinkoski et al. 2018; Fétick et al. 2019; Carry et al. 2019; Hanuš et al. 2019, 2020; Marsset et al. 2020; Yang et al. 2020; Ferrais et al. 2020). We imaged Sylvia over two apparitions, separated by a year, throughout its rotation at high angular resolution with the Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE) extreme AO InfraRed Dual-band Imager and Spectrograph (IRDIS) and Zurich Imaging Polarimeter (ZIMPOL) cameras (Thalmann et al. 2008; Schmid et al. 2018; Beuzit et al. 2019) mounted on the European Southern Observatory (ESO) Very Large Telescope (VLT). Aside from contributing to our understanding of the formation and evolution of the Solar System’s most primitive bodies, the present study also provides the context for the future in situ exploration of primitive P- and D-type bodies by NASA’s Lucy mission to the Jupiter Trojans.
Mass, density, and quadrupole J2 of Sylvia, derived using either Romulus, Remus, or both satellites, from the literature compared with the present study.
2 Observations and data reduction
2.1 High-angular-resolution imaging
The data used in the present study to extract the position of the moons comprise all the high angular resolution images of Sylvia taken with the Hubble Space Telescope (HST) and ground-based telescopes equipped with AO cameras: Gemini North, ESO VLT, W. M. Keck, and SOR (Drummond et al. 2016). The data span 51 different epochs, with multiple images each, over 17 years from February 2001 to November 2018. For the reconstruction of Sylvia’s 3D shape, however, only the images with the highest resolution were used, that is, those acquired with VLT/SPHERE/ZIMPOL (Sect. 3).
The images from the HST were obtained with the second Wide Field and Planetary Camera (WFPC2, Holtzman et al. 1995). The images from the VLT were acquired with both the first generation instrument NACO (NAOS-CONICA, Lenzen et al. 2003; Rousset et al. 2003) and SPHERE (Fusco et al. 2006; Beuzit et al. 2019), the second generation extreme-AOinstrument designed for exoplanet detection and characterization. The images acquired with SPHERE were taken with both the IRDIS (Dohlen et al. 2008) and ZIMPOL (Schmid et al. 2018) subsystems. Images taken at Gemini North used the Near InfraRed Imager (NIRI) camera (Hodapp et al. 2003), fed by the ALTAIR AO system (Herriot et al. 2000). Finally, observations at Keck were acquired with the guiding camera of NIRSPEC in 2001 (McLean et al. 1998) and Near-InfraRed Camera 2 (NIRC2; van Dam et al. 2004; Wizinowich et al. 2000) later on.
To reduce the AO-imaging data, a standard data processing protocol (sky subtraction, bad-pixel identification and correction, and flat-field correction) was followed using in-house routines developed in Interactive Data Language (IDL) (see Carry et al. 2008). The images were then deconvolved with the Mistral algorithm (Fusco 2000; Mugnier et al. 2004) to restore their optimal angular resolution (see Fétick et al. 2019, for details). Separately, the reduced images were processed to subtract the bright halo surrounding Sylvia to enhance the detectability of the satellites (see Pajuelo et al. 2018; Carry et al. 2019, for details).
2.2 Optical lightcurves
We used the 40 lightcurves from Kaasalainen et al. (2002) to create a convex 3D shape model of Sylvia1, compiled from the Uppsala Asteroid Photometric Catalog (Lagerkvist & Magnusson 2011). We also compiled 11 lightcurves acquired by amateur astronomers within the Courbes de rotation d’astéroïdes et de comètes database (CdR2).
In addition to these data, we acquired 12 lightcurves using the 60 cm André Peyrot telescope mounted at Les Makes observatory on La Réunion Island, operated as a partnership among Les Makes Observatory and the IMCCE, Paris Observatory, and seven lightcurves with the 60 cm TRAPPIST telescopes located at La Silla Observatory in Chile and the Oukaïmeden observatory in Morocco (Jehin et al. 2011). Finally, we extracted 51 lightcurves from the data archive of the SuperWASP survey (Pollacco et al. 2006) for the period from 2006 to 2009 (Parley et al. 2005; Grice et al. 2017). In summary, a total of 121 lightcurves observed between 1978 and 2017 (Table A.1) were used in this work and are presented in Fig. A.1.
2.3 Stellar occultations
Nine stellar occultations by Sylvia have been recorded since 1984, mostly by amateur astronomers during the last decade (see Mousis et al. 2014; Dunham et al. 2016; Herald et al. 2020). We converted the timings of the disappearance and reappearance of the occulted stars3 into segments (called chords) on the plane of the sky, using the location of the observers on Earth and the apparent motion of Sylvia following the recipes listed in Berthier (1999). Only five stellar occultations had multiple chords that could be used to constrain the size and apparent shape of Sylvia (Fig. B.1). For the January 2013 and October 2019 occultations, several observers reported secondary events due to the occultation of the stars by either Romulus or Remus (Berthier et al. 2014; Vachier et al. 2019). We thus used the relative positions between Sylvia and its satellites at the time of the occultations to constrain their mutual orbits. We list the observers of the occultations in Table B.1.
3 Sylvia’s 3D shape
We fed the All-Data Asteroid Modeling (ADAM) algorithm with all SPHERE/ZIMPOL images, lightcurves, and stellar occultations to determine the spin and 3D shape of Sylvia (Viikinkoski et al. 2015a). Optical lightcurves are often required for ADAM to constrain the regions not imaged and to stabilize the shape optimization. The procedure is similar to that published in our previous studies with SPHERE, and we refer readers to these papers for more details (e.g., Viikinkoski et al. 2015b; Marsset et al. 2017; Vernazza et al. 2018). We used the sidereal rotation period and the spin-axis coordinates of Sylvia from the literature (Kaasalainen et al. 2002; Hanuš et al. 2013, 2017) as input values to ADAM.
We further modeled the shape by using the Multi-resolution PhotoClinometry by Deformation (MPCD) method (Jorda et al. 2016), following the procedure of our previous works (e.g., Ferrais et al. 2020). MPCD gradually deforms the vertices of a previous mesh (here ADAM model) to minimize the difference between the observed images and synthetic images of the model (Jorda et al. 2010). Both models only present marginal differences (Fig 1, Table 2), and in what follows, we report on the MPCD model.
The derived shape is, in essence, similar to that based on lower angular resolution images (Berthier et al. 2014; Hanuš et al. 2017). A striking feature of Sylvia is its remarkable elongated shape (Table 2, Fig. 2). To put its peculiar shape into context, we measured the tri-axial diameters of 103 asteroids larger than 100 km from their shape models4 and compiled their rotation periods from the Planetary Data System (Harris et al. 2017). Sylvia appears to be more elongated and to spin faster than most asteroids larger than 100 km (Fig. 2). In particular, the population of asteroids with satellites stands out from the population of singletons, with a median ratio of equatorial diameters a∕b of 1.37 (versus 1.16 for the background) and a median rotation period of 5.5 h (versus 7.9 h for the background). We compared the a∕b ratio and rotation period distributions of asteroids with and without satellites using the Kolmogorov-Smirnov test. The p-values for both are 5 × 10−4 and 7 × 10−5, respectively.We thus conclude that the distributions are different above the 99.5% confidence level. While asteroids with a diameter smaller than about 15 km are subject to YORP spin-up and surface re-arrangement (Walsh et al. 2008; Vokrouhlický et al. 2015), Sylvia is too large to have been affected. The origin of this difference is thus unclear. It may result from the impact at the origin of the satellite formation (Margot et al. 2015), or alternatively, satellites may be more stable around elongated bodies (see Winter et al. 2009).
4 Dynamics of the system
The two satellites orbit Sylvia on equatorial, circular, and prograde orbits (Table 3). The root mean square (RMS) residual between the observations and the computed positions is only 9.3 mas, in other words within the pixel size of most observations. The positive occultations by both satellites in October 2019 provide a practical estimate of the reliability of the orbital solution, as the two satellites were detected at only 5 mas from the positions we predicted (Vachier et al. 2019). It also highlights the importance of accurate ephemerides to prepare the observation of the occultation by placing observers on the path of the satellites.
The mass of Sylvia is constrained with an uncertainty of less than 1%: (1.44 ± 0.01) × 1019 kg, thanks to the long baseline of observations. Combined with our volume-equivalent diameter estimate (271 ± 5 km, see above), the density of Sylvia is found to be 1378 ± 45 kg m−3, which is reminiscent of that of other large asteroids with a surface composition consistent with that of IDPs (C, P, and D types, see Carry 2012; Vernazza et al. 2015). In Fig. 3, we present all the possible bulk compositions of Sylvia, considering a mixture of rocks and ices, with voids. We used a range of densities from 2200 to 3000 kg m−3 for the rock phase (from rocks with organics to the density of the silicate phase reported by the Stardust mission, Brownlee et al. 2006). The density of Sylvia implies the presence of both ices and macroporosity in its interior.
We estimate the masses of Romulus and Remus to be (1.4 ± 1.2) × 1015 kg and (7.8 ± 7.3) × 1014 kg (i.e., effectively upper limits), very close to the masses reported by Fang et al. (2012). Assuming a similar albedo for Sylvia and its two moons, their magnitude differences with Sylvia (Table 3) imply diameters of 15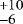 km and 10
km and 10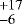 km for Romulusand Remus (consistent with occultation chords, Berthier et al. 2014), and hence densities of 790 ± 680 and 1480 ± 1400 kg m−3. The density of both satellites is loosely constrained and similar to that of Sylvia.
km for Romulusand Remus (consistent with occultation chords, Berthier et al. 2014), and hence densities of 790 ± 680 and 1480 ± 1400 kg m−3. The density of both satellites is loosely constrained and similar to that of Sylvia.
Finally, we note that the best orbital solutions are obtained for the smallest quadrupole J2 (Fig. 4), tending toward J2 = 0 (i.e., fully Keplerian orbits over the 19 years baseline). Although there are orbits fitting the data within 1 σ of the observations, their residuals are systematically larger.
 |
Fig. 1 Comparison of the SPHERE image (top row) with the MPCD (middle) and ADAM (bottom) models. |
Spin solution (coordinates in ecliptic and equatorial J2000 reference frames) and shape model parameters.
 |
Fig. 2 Distribution of the ratio of equatorial diameters (a∕b) and rotation period of 103 asteroids larger than 100 km in diameter. The difference between asteroids with and without satellites is striking. |
Orbital elements of the satellites of Sylvia, expressed in EQJ2000, obtained with Genoid.
 |
Fig. 3 Bulk composition of Sylvia, assuming three end members: rocks, ices (density of 920 kg m−3), and voids. The dashed and dotted lines represent the 1 and 2 σ boundaries, respectively. |
5 Implication for the internal structure
Under the assumption of a homogeneous density in the interior, the shape of Sylvia implies a J2 of 0.082 ± 0.005 (computed with SHTOOLS5, see Wieczorek & Meschede 2018). This value contrasts with the null J2 determined dynamically (Sect. 4). This discrepancy reveals an inhomogeneous density distribution inside Sylvia and hints ata more spherical mass concentration than suggested by Sylvia’s oblate and elongated 3D shape. This implies a denser, more spherical core, surrounded by a less dense envelope. Based on similar considerations, similar internal structures have recently been proposed for other large P-type asteroids such as the Cybele (107) Camilla (Pajuelo et al. 2018) and the Jupiter Trojan (624) Hektor (Marchis et al. 2014).
This differentiated structure is at odds with the IDP-like spectral properties, which provide evidence for an absence of both thermal metamorphism and aqueous alteration. This suggests that partial differentiation occurred and was limited by the insufficient amount of heat generated by radionuclides which did not propagate to the surface. Such structures have indeed been suggested for the parent bodies of CV carbonaceous chondrites (Elkins-Tanton et al. 2011), ordinary chondrites (Bryson et al. 2019), and mid-sized KBOs (Desch et al. 2009).
Building upon the work of Neveu & Vernazza (2019), we modeled the thermal and internal structure history of Sylvia. The evolution of internal temperatures and structure was computed numerically using a one-dimensional code (Desch et al. 2009). Sylvia is assumed to be made of rock (idealizing a mixture of refractory materials such as silicates, metals, and organic material), water ice, and voids (the macroporosity). The mass was distributed assuming spherical symmetry over 200 grid zones that were initially evenly spaced in radius. The internal energy in each grid zone was computed from the initial temperature using equations of state for rock and ice. Material is never hot enough in our simulations for rock-metal differentiation, which is neglected. Initial radionuclide abundances are provided in Table 1 of Neveu & Vernazza (2019). Simulations start once Sylvia is fully formed, neglecting the progressive accretion of material over time. Because of this and the near-absence of short-lived radionuclide heating given the assumed formation time, Sylvia’s simulated early evolution is cold. The implementation of instantaneous differentiation in the central regions that warm above 273 K rests on the assumption that sufficiently large rock grains settle via Stokes flow on timescales smaller than one time step.
Sylvia is assumed to accrete homogeneously at 60 K, 6 million years (My) after the formation of Ca-Al-rich inclusions (consistent with a surface without aqueous alteration; Neveu & Vernazza 2019). This is the equilibrium temperature for an albedo 0.05 at a distance of 17–18 au (i.e., the postulated accretion distance of KBOs, Morbidelli & Nesvornỳ 2020) from the Sun with 70% of the present-day luminosity. The surface temperature is instantaneously raised to 148 K (the present-day equilibrium temperature) at the time of heliocentric migration. We tested different timings, from a late planet migration (hundreds of millions of years) such as the one described by the Nice model (Tsiganis et al. 2005; Morbidelli et al. 2005; Gomes et al. 2005; Levison et al. 2009) to an early dynamical instability occurring a few million years after the dissipation of the gas disk (Nesvorný et al. 2018; Clement et al. 2019), and we find that the timing of implantation into the asteroid belt seldom affects its structure or peak temperature. In the results below, the time of migration was set to 6 My after formation (i.e., 12 My after Ca–Al-rich inclusions).
The thermal structure was determined by balancing conductive heat transfer with primarily radiogenic heating by 26Al, 40K, 232Th, 235U, and 238U, using a finite-difference method and a 50-yr time step, for 5 billion years (Gy). Thermal conductivities mainly depend on porosities (Fig. 6), but also on composition and temperature (Desch et al. 2009). Porosity is allowed to compact at rates determined from material viscosities as described in Neveu & Rhoden (2017). Sylvia’s bulk density constrains the void porosity and rock volume fractions to about 40–55% and 20–35%, respectively, mainly depending on the rock density (Fig. 3).
Convection is generally neglected as it is assumed that the postulated porous, rock-rich internal structure for Sylvia is not prone to fluid or ice advection. In the ice-rich case (Fig. 5, right panel), solid-state convection is allowed to occur but it does not because the critical Rayleigh number is never exceeded. Although this was not simulated, in the percolation case below we expect convection to be possible in the central region rich in liquid water, until this region refreezes. In all simulations, volume changes due to water melting or freezing are neglected.
The viscosity of ice-rock mixtures, used to compute the Rayleigh number and pore compaction, was calculated following Roberts (2015). Above a 30% ice volume, it is equated to the viscosity of ice. Below 30% ice volume fraction, as a first approximation, it was set to the geometric mean of the rock and ice viscosities at a given grain size, stress (equated with hydrostatic pressure), and temperature. Roberts (2015) note that this approximation tends to underestimate mixture viscosities relative to extrapolations of laboratory measurements. The ice and rock flow laws adopted in the model are the composite rheology of Goldsby & Kohlstedt (2001) and the dry diffusion creep flow law for olivine of Korenaga & Karato (2008), respectively.
The key factor governing thermal evolution in these simulations is porosity Φ, which decreases thermal conductivities k of rock-ice mixtures, of order 1 W m−1 K−1 (Desch et al. 2009, and references therein), by up to two orders of magnitude. The adopted thermal conductivity-porosity relationship (Shoshany et al. 2002) was derived from Monte-Carlo modeling of porous cometary ice: k was decreased with increasing Φ via multiplication by a factor (1 − Φ∕0.7)nΦ+0.22. This relationship is shown in Fig. 6. We adopted n = 4.1 (gray curve)for the canonical simulation with 52% porosity, following the discussion in Shoshany et al. (2002). We set n =3.5 (black curve) for the simulation with 60% porosity; choosing n = 4.1 would resultin more heating and compaction than shown in Fig. 5. There is a wide spread in the Monte Carlo results of Shoshany et al. (2002) in how Φ affects k, with some of their models suggesting a lesser effect of porosity. Conversely, independent measurements of porous silica aggregates (Krause et al. 2011) and extrapolated results from models of highly porous aggregates (Arakawa et al. 2017) both suggest similar or slightly higher decrease factors due to porosity (Fig. 6) than the relationships we have assumed. Thus, the assumedrelationships seem to adequately represent the state of understanding how porosities of a 50–60% volume decrease thermal conductivities.
In order for Sylvia’s observed anhydrous surface and low J2 despite an oblate shape to be compatible, it is crucial for time-evolution simulations with this model constrain the volume fraction of water to be low, less than a 40% volume relative to rock or a 15% volume overall. For higher volume fractions, ice grains tend to become adjoined and control the mechanical properties of the interior. In that case, the material viscosity is assumed to be equal to that of water ice (Goldsby & Kohlstedt 2001), and any void porosity rapidly decreases as the interior warms due to radiogenic heating and porosity insulation. Instantaneous ice-rock differentiation happens first once the central (warmest) regions warm above 273 K. It then proceeds outward if the interior keeps warming. This yields a gravitationally unstable structure: the topmost undifferentiated layers are denser than underlying layers, which are poorer in rock. Once Sylvia is differentiated out to more than half its radius, differentiation is assumed to proceed by gravitational (Rayleigh-Taylor) instabilities: layers overturn if their viscosity is below a threshold that corresponds to T ≈ 150 K (Rubin et al. 2014). Since Sylvia’s post-migration surface temperature is warmer, 148 K, differentiation out to the surface is essentially inevitable. This ought to result in evidence of surface water, either as ice or as mineral hydration, as observed on asteroids linked to carbonaceous chondrites (Rivkin & Emery 2010; Campins et al. 2010). This is inconsistent with Sylvia’s anhydrous, IDP-like surface composition. Ice-rock differentiation can be prevented if ice dominates the volume fraction (Fig. 5, right column), since in that case the combination of low rock (i.e., radionuclide) content and low insulating void porosity results in a cold interior in which ice never melts. However, in such a homogeneous interior, the mass distribution should result in a higher J2 than observed given Sylvia’s oblate shape.
It follows that to retain a pristine anhydrous external envelope, Sylvia’s water volume fraction must be low (consistently with observations of the comet 67P nucleus by the Rosetta spacecraft; Pätzold et al. 2019; Choukroun et al. 2020) so that interior solids are less prone to deformation, inhibiting both porosity compaction and instability-driven differentiation. As a canonical case, we assumed an interior comprised of a 52% volume void porosity, 35% rock of density 3075 kg m−3, and 13% water (Fig. 5, central column). The void porosity decreases the interior’s thermal conductivity by a factor of ≈ 15 relative to a compact rock-ice mixture. This favors accumulation of radiogenic heat, melting ice in the central regions after ≈ 0.15–0.2 Gy. At such a low water volume fraction and high void porosity, it is sensible for liquid water to percolate downward in pores without significantly disturbing the remaining rock-void porosity structure, since rock grains already tend to be adjoined (see Figs. 3a,b of Neumann et al. 2020, for a pictorial description). This would result in a three-layer structure (Fig. 5, bottom central panel): a central region where the porosity has been filled with percolated water, surrounded by a porous layer free of water, and a primordial outer layer that remains too cold for ice to melt. Our thermal evolution simulations do not explicitly track percolation. The example interior structure of Fig. 5 (bottom central panel) was obtained by manually moving the mass of water that is liquid at 0.2 Gy to fill porosity at the center, and assuming that in the middle layer, the empty volume left behind by the displaced water is compacted (so that the void porosity remains 52% in this layer). This compaction leads to a volume-averaged diameter decrease from 283.4 km to 271.4 km, which is the observed value. The spherical central mass distribution in this three-layer model implies a J2 of 5 × 10−5 only, which is consistent with the observed dynamics of both satellites.
Although this is not a unique solution, assuming lower rock densities (Fig. 3) requires increasing the rock volume fraction at the expense of ice or void porosity so as to keep matching Sylvia’s bulk density. Neither the bulk ice volume fractions nor the bulk void porosity are likely to be much lower than assumed given the need to invoke the migration ofmelted ice, enabled by the insulating effect of porosity, to explain a more spherical mass distribution (low J2) than suggested by Sylvia’s oblate shape.
Another, less likely explanation for a spherical mass distribution inside Sylvia is the central compaction of the rock. Although we assumed a rather low viscosity for rock-ice mixtures, Sylvia’s relatively low gravity (lithostatic pressures) precludes compaction below 900 K. The required thermal insulation could be achieved with a bulk void porosity as low as 60% (Fig. 5; left column). However, such a hot evolution would result in advection and, likely, outward outgassing of water (Prialnik & Podolak 1999; Young et al. 2003), which are not captured in these simulations and would cool the interior.
We thus deem percolation of water in the deep interior as being the likelier explanation for Sylvia’s low J2 despite its oblate shape. This implies that, unlike the pristine outer layers comparable to the CP IDPs, the innermost region may insteadbe analogous to hydrated material exemplified by chondritic smooth IDPs or perhaps the Tagish Lake meteorite (Fujiya et al. 2019). The minimum body diameter for such percolation to take place (holding all other quantities constant) is between 130 and 150 km, implying that even objects as small as Patroclus (diameter ≈ 140 km, see Hanuš et al. 2017), which is a target of NASA’s Lucy mission, may have experienced a low degree of central liquid water percolation.
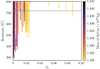 |
Fig. 4 Orbital residuals (χ2) as a functionof the dynamical quadrupole J2. The horizontal gray line corresponds to the χ2 providing a fit at 1 σ of the observations. |
 |
Fig. 5 Long-term evolution of the internal structure of Sylvia. The baseline scenario is presented in the central column, while the left and right columns present extreme cases in which the structure is dictated by rock-compaction and water ice rheology,respectively. |
 |
Fig. 6 Effect of porosity Φ on the thermal conductivity k. The orange and teal curves show relationships that were only validated in the regimes where the curves are solid. The orange curve is a thermal conductivity in W m−1 K−1 (rather thana decrease factor). Data points of a given color are from the same source as the fit curve of that color. |
6 Conclusions
We used newly acquired high-angular resolution imaging observations of (87) Sylvia with the SPHERE instrument on the ESO VLT, along with archival images, lightcurves, and stellar occultations to reconstruct its 3D shape and to constrain the orbital properties of its two moons. We find that Sylvia possesses a low density of 1378 ± 45 kg m−3, similar to that of other large C, P, and D asteroids whose surface composition is mostly consistent with that of anhydrous interplanetary dust particles. Sylvia spins quickly and is oblate and elongated, a property shared by most 100+ km multiple asteroids, as opposed to the physical properties of large asteroids without satellites.
The orbits of the two satellites is in apparent contradiction with the oblate shape of Sylvia: The two orbits do not show the nodal precession expected from the shape. We interpret it as evidence for a central spherical mass concentration due to water percolation over millions of years triggered by long-lived radionuclides. This long lasting heating episode allowed for partial differentiation, the outer shell of Sylvia remaining pristine. It follows that even the most primitive small bodies with diameters larger than 150 km did not avoid thermal processing, leaving only their outermost layers intact.
Acknowledgements
Some of the work presented here is based on observations collected at the European Organisation for Astronomical Research in the Southern Hemisphere under ESO programs 073.C-0851 (PI Merline), 073.C-0062 (PI Marchis), 085.C-0480 (PI Nitschelm), 088.C-0528 (PI Rojo), 199.C-0074 (PI Vernazza). Some of the data presented herein were obtained at the W.M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W.M. Keck Foundation. This research has made use of the Keck Observatory Archive (KOA), which is operated by the W.M. Keck Observatory and the NASA Exoplanet Science Institute (NExScI), under contract with the National Aeronautics and Space Administration. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Mauna Kea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. We thank the AGORA association which administrates the 60 cm telescope at Les Makes observatory, La Reunion island, under a financial agreement with Paris Observatory. Thanks to A. Peyrot, J.-P. Teng for local support, and A. Klotz for helping with the robotizing. B. Carry, P. Vernazza, A. Drouard, and J. Grice were supported by CNRS/INSU/PNP. This work has been supported by the Czech Science Foundation through grants 20-08218S (J. Hanuš, J. Ďurech) and by the Charles University Research program No. UNCE/SCI/023. The work of TSR was carried out through grant APOSTD/2019/046 by Generalitat Valenciana (Spain). This work was supported by the MINECO (Spanish Ministry of Economy) through grant RTI2018-095076-B-C21 (MINECO/FEDER, UE). This material is partially based upon work supported by the National Science Foundation under Grant No. 1743015. Our colleague and co-author M. Kaasalainen passed away while this work was carried out. Mikko’s influence in asteroid 3D shape modeling has been enormous. This study is dedicated to his memory. This paper makes use of data from the DR1 of the WASP data (Butters et al. 2010) as provided by the WASP consortium, and the computing and storage facilities at the CERIT Scientific Cloud, reg. no. CZ.1.05/3.2.00/08.0144 which is operated by Masaryk University, Czech Republic. TRAPPIST-South is funded by the Belgian Fund for Scientific Research (Fond National de la Recherche Scientifique, FNRS) under the grant PDR T.0120.21, with the participation of the Swiss FNS. TRAPPIST-North is a project funded by the University of Liège, and performed in collaboration with Cadi Ayyad University of Marrakesh. E. Jehin is a Belgian FNRS Senior Research Associate. Thanks to all the amateurs worldwide who regularly observe asteroid lightcurves and stellar occultations. The great majority of observers have made these observations at their own expense, including occasions when they have travelled significant distances. Most of those observers are affiliated with one or more of (i) European Asteroidal Occultation Network (EAON), (ii) International Occultation Timing Association (IOTA), (iii) International Occultation Timing Association – European Section (IOTA–ES), (iv) Japanese Occultation Information Network (JOIN), (v) Trans Tasman Occultation Alliance (TTOA). The authors acknowledge the use of the Virtual Observatory tools Miriade (http://vo.imcce.fr/webservices/miriade/) (Berthier et al. 2008), TOPCAT (http://www.star.bris.ac.uk/~mbt/topcat/), and STILTS (http://www.star.bris.ac.uk/~mbt/stilts/) (Taylor 2005). This research used the SSOIS (http://www.cadc-ccda.hia-iha. nrc-cnrc.gc.ca/en/ssois) facility of the Canadian Astronomy Data Centre operated by the National Research Council of Canada with the support of the Canadian Space Agency (Gwyn et al. 2012). Thanks to the developers and maintainers.
Appendix A Lightcurve observations
 |
Fig. A.1 Optical lightcurves of Sylvia (gray dots), compared with the synthetic lightcurves generated with the ADAM and MPCD shape models (blue and orange lines). In each panel, the observing date, number of points, duration of the lightcurve (in hours), and RMS residuals between the observations and the synthetic lightcurves from the shape model are displayed. In many cases, measurement uncertainties are not provided by the observers but can be estimated from the scatter of measurements. |
Appendix B Stellar occultations
 |
Fig. B.1 Five stellar occultations by Sylvia used in this work, compared with the shape model projected on the plane of the sky for the times of the occultations. The dark gray lines represent the chords and the thick light gray lines illustrate their uncertainties. |
References
- Arakawa, S., Tanaka, H., Kataoka, A., & Nakamoto, T. 2017, A&A, 608, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beauvalet, L., & Marchis, F. 2014, Icarus, 241, 13 [CrossRef] [Google Scholar]
- Berthier, J. 1999, Notes scientifique et techniques du Bureau des longitudes, S064 [Google Scholar]
- Berthier, J., Hestroffer, D., Carry, B., et al. 2008, LPI Contrib., 1405, 8374 [Google Scholar]
- Berthier, J., Vachier, F., Marchis, F., Ďurech, J., & Carry, B. 2014, Icarus, 239, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Berthier, J., Descamps, P., Vachier, F., et al. 2020, Icarus, 352, 113990 [CrossRef] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanco, C., di Martino, M., Gonano, M., Jaumann, R., & Mottola, S. 1989, Mem. Soc. Astron. Italiana, 60, 195 [Google Scholar]
- Bradley, J. P. 1999, in NATO Advanced Science Institutes (ASI) Series C, 523, NATO Advanced Science Institutes (ASI) Series C, eds. J. M. Greenberg, & A. Li, 485 [Google Scholar]
- Brownlee, D., Tsou, P., Aléon, J., et al. 2006, Science, 314, 1711 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bryson, J. F. J., Weiss, B. P., Getzin, B., et al. 2019, J. Geophys. Res. (Planets), 124, 1880 [CrossRef] [Google Scholar]
- Buie, M. W., Olkin, C. B., Merline, W. J., et al. 2015, AJ, 149, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Butters, O. W., West, R. G., Anderson, D. R., et al. 2010, A&A, 520, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campins, H., Hargrove, K., Pinilla-Alonso, N., et al. 2010, Nature, 464, 1320 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Carry, B. 2012, Planet. Space Sci., 73, 98 [Google Scholar]
- Carry, B., Dumas, C., Fulchignoni, M., et al. 2008, A&A, 478, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carry, B., Vachier, F., Berthier, J., et al. 2019, A&A, 623, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choukroun, M., Altwegg, K., Kührt, E., et al. 2020, Space Sci. Rev., 216, 1 [CrossRef] [Google Scholar]
- Clement, M. S., Raymond, S. N., & Kaib, N. A. 2019, AJ, 157, 38 [CrossRef] [Google Scholar]
- DeMeo, F. E., & Carry, B. 2013, Icarus, 226, 723 [Google Scholar]
- DeMeo, F. E., & Carry, B. 2014, Nature, 505, 629 [Google Scholar]
- DeMeo, F., Binzel, R. P., Carry, B., Polishook, D., & Moskovitz, N. A. 2014, Icarus, 229, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Desch, S. J., Cook, J. C., Doggett, T. C., & Porter, S. B. 2009, Icarus, 202, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in SPIE, 7014, Ground-based and Airborne Instrumentation for Astronomy II, 70143L [Google Scholar]
- Drummond, J. D., Reynolds, O. R., & Buckman, M. D. 2016, Icarus, 276, 107 [CrossRef] [Google Scholar]
- Dunham, D., Herald, D., preston, S., et al. 2016, in Asteroids: New Observations, New Models, eds. S. R. Chesley, A. Morbidelli, R. Jedicke, & D. Farnocchia, 318th Symposium of the International Astronomical Union, 177 [Google Scholar]
- Dunham, D. W., Herald, D., Frappa, E., et al. 2017, Asteroid Occultations, NASA Planetary Data System, EAR-A-3-RDR-OCCULTATIONS-V15.0 [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elkins-Tanton, L. T., Weiss, B. P., & Zuber, M. T. 2011, Earth Planet. Sci. Lett., 305, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, J., Margot, J.-L., & Rojo, P. 2012, AJ, 144, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrais, M., Vernazza, P., Jorda, L., et al. 2020, A&A, 638, A15 [CrossRef] [EDP Sciences] [Google Scholar]
- Fétick, R. J., Jorda, L., Vernazza, P., et al. 2019, A&A, 623, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraser, W. C., Brown, M. E., Morbidelli, A., Parker, A., & Batygin, K. 2014, ApJ, 782, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, W. C., Bannister, M. T., Pike, R. E., et al. 2017, Nat. Astron., 1, 0088 [CrossRef] [Google Scholar]
- Frouard, J., & Compère, A. 2012, Icarus, 220, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiya, W., Hoppe, P., Ushikubo, T., et al. 2019, Nat. Astron., 3, 910 [CrossRef] [Google Scholar]
- Fusco, T. 2000, PhD thesis, Université de Nice Sophia-Antipolis, France [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Opt. Express, 14, 7515 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsby, D. L., & Kohlstedt, D. L. 2001, J. Geophys. Res.: Solid Earth, 106, 11017 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [Google Scholar]
- Grice, J., Snodgrass, C., Green, S., Parley, N., & Carry, B. 2017, Asteroids, Comets, and Meteors: ACM 2017 [Google Scholar]
- Gwyn, S. D. J., Hill, N., & Kavelaars, J. J. 2012, PASP, 124, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Marchis, F., & Ďurech J. 2013, Icarus, 226, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Ďurech, J., Oszkiewicz, D. A., et al. 2016, A&A, 586, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Viikinkoski, M., Marchis, F., et al. 2017, A&A, 601, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Marsset, M., Vernazza, P., et al. 2019, A&A, 624, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanuš, J., Vernazza, P., Viikinkoski, M., et al. 2020, A&A, 633, A65 [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., & Young, J. W. 1980, Icarus, 43, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Warner, B. D., & Pravec, P. 2017, NASA Planetary Data System [Google Scholar]
- Herald, D., Gault, D., Anderson, R., et al. 2020, MNRAS, 499, 4570 [Google Scholar]
- Herriot, G., Morris, S., Anthony, A., et al. 2000, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 4007, Adaptive Optical Systems Technology, ed. P. L. Wizinowich, 115 [Google Scholar]
- Hiroi, T., Zolensky, M. E., & Pieters, C. M. 2001, Science, 293, 2234 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hodapp, K. W., Jensen, J. B., Irwin, E. M., et al. 2003, PASP, 115, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Hester, J. J., Casertano, S., et al. 1995, PASP, 107, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Jorda, L., Spjuth, S., Keller, H. U., Lamy, P., & Llebaria, A. 2010, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 7533, Computational Imaging VIII, eds. C. A. Bouman, I. Pollak, & P. J. Wolfe, 753311 [Google Scholar]
- Jorda, L., Gaskell, R., Capanna, C., et al. 2016, Icarus, 277, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Piironen, J. 2002, Icarus, 159, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Korenaga, J., & Karato, S.-I. 2008, J. Geophys. Res.: Solid Earth, 113 [Google Scholar]
- Krause, M., Blum, J., Skorov, Y. V., & Trieloff, M. 2011, Icarus, 214, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I., & Magnusson, P. 2011, Asteroid Photometric Catalog V1.1. EAR-A-3-DDR-APC-LIGHTCURVE-V1.1, NASA Planetary Data System [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, SPIE, 4841, 944 [Google Scholar]
- Levison, H. F., Bottke, W. F., Gounelle, M., et al. 2009, Nature, 460, 364 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marchis, F., Descamps, P., Hestroffer, D., & Berthier, J. 2005, Nature, 436, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Marchis, F., Hestroffer, D., Descamps, P., et al. 2006, Nature, 439, 565 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marchis, F., Durech, J., Castillo-Rogez, J., et al. 2014, ApJ, 783, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Margot, J.-L., Pravec, P., Taylor, P., Carry, B., & Jacobson, S. 2015, Asteroid Systems: Binaries, Triples, and Pairs, eds. P. Michel, F. DeMeo, & W. F. Bottke (Univ. Arizona Press), 355–374 [Google Scholar]
- Marsset, M., Carry, B., Dumas, C., et al. 2017, A&A, 604, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsset, M., Brož, M., Vernazza, P., et al. 2020, Nat. Astron., 4, 569 [CrossRef] [Google Scholar]
- McKinnon, W. B., Richardson, D. C., Marohnic, J. C., et al. 2020, Science, 367, aay6620 [CrossRef] [Google Scholar]
- McLean, I. S., Becklin, E. E., Bendiksen, O., et al. 1998, in Proc. SPIE, 3354, Infrared Astronomical Instrumentation, ed. A. M. Fowler, 566 [Google Scholar]
- Morbidelli, A.,& Nesvornỳ, D. 2020, in The Trans-Neptunian Solar System (Elsevier), 25–59 [CrossRef] [Google Scholar]
- Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [Google Scholar]
- Mousis, O., Hueso, R., Beaulieu, J.-P., et al. 2014, Exp. Astron., 38, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Mueller, M., Marchis, F., Emery, J. P., et al. 2010, Icarus, 205, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Mugnier, L. M., Fusco, T., & Conan, J.-M. 2004, J. Opt. Soc. Am. A, 21, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., Bottke, W. F., & Levison, H. F. 2018, Nat. Astron., 2, 878 [Google Scholar]
- Nesvorný, D., Li, R., Youdin, A. N., Simon, J. B., & Grundy, W. M. 2019, Nat. Astron., 3, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Neumann, W., Jaumann, R., Castillo-Rogez, J., Raymond, C. A., & Russell, C. T. 2020, A&A, 633, A117 [CrossRef] [EDP Sciences] [Google Scholar]
- Neveu, M., & Rhoden, A. R. 2017, Icarus, 296, 183 [CrossRef] [Google Scholar]
- Neveu, M., & Vernazza, P. 2019, ApJ, 875, 30 [Google Scholar]
- Pajuelo, M., Carry, B., Vachier, F., et al. 2018, Icarus, 309, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Parley, N. R., McBride, N., Green, S. F., et al. 2005, Earth Moon Planets, 97, 261 [CrossRef] [Google Scholar]
- Pätzold, M., Andert, T. P., Hahn, M., et al. 2019, MNRAS, 483, 2337 [NASA ADS] [CrossRef] [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Podolak, M. 1999, in Composition and Origin of Cometary Materials (Springer), 169–178 [CrossRef] [Google Scholar]
- Prokof’eva, V. V., & Demchik, M. I. 1992, Astronomicheskij Tsirkulyar, 1552, 27 [Google Scholar]
- Rivkin, A. S., & Emery, J. P. 2010, Nature, 464, 1322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Roberts, J. H. 2015, Icarus, 258, 54 [CrossRef] [Google Scholar]
- Robinson, J. E., Fraser, W. C., Fitzsimmons, A., & Lacerda, P. 2020, A&A, 643, A55 [EDP Sciences] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, SPIE, 4839, 140 [Google Scholar]
- Rubin, M. E., Desch, S. J., & Neveu, M. 2014, Icarus, 236, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M., Bazzon, A., Roelfsema, R., et al. 2018, A&A, 619, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schober, H. J., & Surdej, J. 1979, A&AS, 38, 269 [Google Scholar]
- Shoshany, Y., Prialnik, D., & Podolak, M. 2002, Icarus, 157, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in ASP Conf. Ser., 347, Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, 29 [Google Scholar]
- Thalmann, C., Schmid, H. M., Boccaletti, A., et al. 2008, in Proc. SPIE, 7014, Ground-based and Airborne Instrumentation for Astronomy II, 70143F [CrossRef] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [Google Scholar]
- Usui, F., Hasegawa, S., Ootsubo, T., & Onaka, T. 2019, PASJ, 71, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Vachier, F., Berthier, J., Carry, B., et al. 2019, CBET, 4703 [Google Scholar]
- van Dam, M. A., Le Mignant, D., & Macintosh, B. 2004, Appl. Opt., 43, 5458 [Google Scholar]
- Vernazza, P., & Beck, P. 2016, Planetesimals: Early Differentiation and Consequences for Planets, eds. L. T. Elkins-Tanton, & B. P. Weiss (Cambridge University Press) [Google Scholar]
- Vernazza, P., Fulvio, D., Brunetto, R., et al. 2013, Icarus, 225, 517 [Google Scholar]
- Vernazza, P., Marsset, M., Beck, P., et al. 2015, ApJ, 806, 204 [Google Scholar]
- Vernazza, P., Brož, M., Drouard, A., et al. 2018, A&A, 618, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernazza, P., Jorda, L., Ševeček, P., et al. 2020, Nat. Astron., 4, 136 [Google Scholar]
- Viikinkoski, M., Kaasalainen, M., & Durech, J. 2015a, A&A, 576, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viikinkoski, M., Kaasalainen, M., Ďurech, J., et al. 2015b, A&A, 581, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viikinkoski, M., Vernazza, P., Hanuš, J., et al. 2018, A&A, 619, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, The Yarkovsky and YORP Effects, eds. P. Michel, F. DeMeo, & W. F. Bottke, 509 [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., & Nesvorný, D. 2016, AJ, 152, 39 [Google Scholar]
- Walsh, K. J., Richardson, D. C., & Michel, P. 2008, Nature, 454, 188 [Google Scholar]
- Weidenschilling, S. J., Chapman, C. R., Davis, D. R., et al. 1987, Icarus, 70, 191 [Google Scholar]
- Weidenschilling, S. J., Chapman, C. R., Davis, D. R., Greenberg, R., & Levy, D. H. 1990, Icarus, 86, 402 [Google Scholar]
- Wieczorek, M. A., & Meschede, M. 2018, Geochem. Geophys. Geosyst., 19, 2574 [Google Scholar]
- Winter, O. C., Boldrin, L. A. G., Vieira Neto, E., et al. 2009, MNRAS, 395, 218 [Google Scholar]
- Wizinowich, P. L., Acton, D. S., Lai, O., et al. 2000, in Proc. SPIE, 4007, 2 [Google Scholar]
- Yang, B., Hanuš, J., Carry, B., et al. 2020, A&A, 641, A80 [CrossRef] [EDP Sciences] [Google Scholar]
- Young, E. D., Zhang, K. K., & Schubert, G. 2003, Earth Planet. Sci. Lett., 213, 249 [Google Scholar]
Available on DAMIT (Ďurech et al. 2010): https://astro.troja.mff.cuni.cz/projects/damit/
Compiled by Dunham et al. (2017) and publicly available on the Planetary Data System (PDS): http://sbn.psi.edu/pds/ resource/occ.html
Retrieved from DAMIT (Ďurech et al. 2010): https://astro.troja.mff.cuni.cz/projects/damit/
All Tables
Mass, density, and quadrupole J2 of Sylvia, derived using either Romulus, Remus, or both satellites, from the literature compared with the present study.
Spin solution (coordinates in ecliptic and equatorial J2000 reference frames) and shape model parameters.
Orbital elements of the satellites of Sylvia, expressed in EQJ2000, obtained with Genoid.
All Figures
 |
Fig. 1 Comparison of the SPHERE image (top row) with the MPCD (middle) and ADAM (bottom) models. |
| In the text | |
 |
Fig. 2 Distribution of the ratio of equatorial diameters (a∕b) and rotation period of 103 asteroids larger than 100 km in diameter. The difference between asteroids with and without satellites is striking. |
| In the text | |
 |
Fig. 3 Bulk composition of Sylvia, assuming three end members: rocks, ices (density of 920 kg m−3), and voids. The dashed and dotted lines represent the 1 and 2 σ boundaries, respectively. |
| In the text | |
 |
Fig. 4 Orbital residuals (χ2) as a functionof the dynamical quadrupole J2. The horizontal gray line corresponds to the χ2 providing a fit at 1 σ of the observations. |
| In the text | |
 |
Fig. 5 Long-term evolution of the internal structure of Sylvia. The baseline scenario is presented in the central column, while the left and right columns present extreme cases in which the structure is dictated by rock-compaction and water ice rheology,respectively. |
| In the text | |
 |
Fig. 6 Effect of porosity Φ on the thermal conductivity k. The orange and teal curves show relationships that were only validated in the regimes where the curves are solid. The orange curve is a thermal conductivity in W m−1 K−1 (rather thana decrease factor). Data points of a given color are from the same source as the fit curve of that color. |
| In the text | |
 |
Fig. A.1 Optical lightcurves of Sylvia (gray dots), compared with the synthetic lightcurves generated with the ADAM and MPCD shape models (blue and orange lines). In each panel, the observing date, number of points, duration of the lightcurve (in hours), and RMS residuals between the observations and the synthetic lightcurves from the shape model are displayed. In many cases, measurement uncertainties are not provided by the observers but can be estimated from the scatter of measurements. |
| In the text | |
 |
Fig. B.1 Five stellar occultations by Sylvia used in this work, compared with the shape model projected on the plane of the sky for the times of the occultations. The dark gray lines represent the chords and the thick light gray lines illustrate their uncertainties. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


