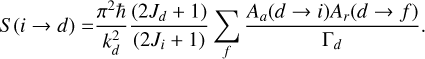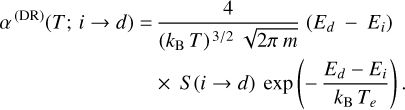EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A13 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A13
Number of page(s) 9
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202347456
Published online 31 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Dielectronic recombination (DR) can be described as a two-step process, involving an N-electron ion and a free electron. In the first step, the free electron is resonantly captured into an (N + 1)-electron resonance level embedded into the continuum of the initial ion. In the second step, the resonance level can either decay radiatively to some final states below the ionization threshold of the ion or re-autoionize back to the initial charge state.

The DR process dominates the electron-ion recombination dynamics in many astrophysical and laboratory plasmas (Beiersdorfer et al. 1992; Kallman & Palmeri 2007; Pütterich et al. 2008; Wu et al. 2015); thus, its knowledge is crucial for the investigation of plasma properties such as the level population and the ionization balance (Beiersdorfer 2003; Huang et al. 2018, Khan et al. 2018).

Experimental as well as theoretical studies have been systematically performed in support of the astronomical observations (see, for instance, Schippers et al. 2010), and repositories were created, in which the DR rate coefficients are tabulated for several electron temperatures (Summers 2003). DR rate coefficients can be retrieved from the cross sections measured at heavy-ion storage ring facilities (see, for instance, Badnell et al. 2003; Schuch and Böhm 2007, and Schippers 2009, 2015) or estimated theoretically by means of “ab initio” computations (see, for instance, Altun et al. 2006, 2007; Zatsarinny et al. 2006; Badnell et al. 2006; Abdel-Naby et al. 2012; Fritzsche 2021). Ab initio methods compute the DR rate coefficients by the additive inclusion of electron excitations. In turn, electron excitations are classified as the difference Δn = n′ – n, where n and n′ mark the principal quantum numbers of the excited bound electron in the initial state and resonance levels, respectively (see, for instance, Fritzsche 2021). In turn, each electron excitation encompasses all the possible dielectronic capture resonances nl → n′l′,n′′l′′, in which a bound electron is excited from an initial shell, nl, to a final shell, n′l′, with the simultaneous capture of a free electron into a Rydberg shell, n″l″. As any electron excitation contributes to the total DR, theoretical investigations focus only on the supposedly most important ones.

Iron ions have been thoroughly targeted for DR investigations, as iron is the most astronomically abundant heavy element. Moreover, spectral lines ascribed to these ions were detected by several X-ray observatories (Khan et al. 2018). In particular, strong X-ray lines associated with L-shell iron ions were observed in binary star systems such as Capella (Canizares et al. 2000) and II Pegasi (Huenemoerder et al 2001), and in the elliptical galaxy NGC 4636 (Xu et al. 2001). A broad unresolved transition array (UTA) occurring at 16-17 Å was detected in active galactic nuclei (AGN) in the vicinity of a supermassive black hole (Behar et al. 2001, 2003; Pounds et al. 2001; Pounds 2004; Kaspi et al. 2002; Kaspi 2004, Steenbrugge et al. 2003; Gallo et al. 2004; Netzer 2004; Krongold et al. 2005) and attributed mostly to M-shell Fe ions. These UTA lines were assigned to resonances involving 2l and 3l shells (Behar et al. 2001; Sako et al. 2001). In particular, the lines at 16 Å were attributed to 2p → 3d core electron excitations, while the lines in the 14–16 Å region were ascribed to 2p → 4d core electron excitations. The contribution of 2p → 4d and high-energy 3l → nl′ electron excitations to the equivalent width was predicted to become important for ionic column densities larger than 1017 cm−2 (Behar et al. 2001).

Such astronomical observations demand experimental as well as theoretical investigations into the DR of L- and M-shell iron ions. For the DR of L-shell Fe ions, both theory and measurements have focused on the 2l → 2l′ and 2l → 3l′ valence electron excitations (see Zatsarinny et al. 2003, 2004a, 2006; Altun et al. 2005). For a few ionic species even the 2l → 4l′ (see Zatsarinny et al. 2004b) and the inner-core 1s → 2l (see Chen 1991; Savin et al. 2006) electron excitations have been investigated.

The experimental investigations into the DR of M-shell Fe ions have mostly covered the free-electron energies due to the lowest lying resonances, corresponding to the 3l → 3l′ and 3l → 4l′ valence electron excitations (see Schippers et al. 2010 and references therein). As an exception to this approach, recent measurements of the DR of the Mg-like Fe14+ ions (Bernhardt et al. 2014) have focused on the free-electron energies due to the 2(s + p) → 3l core electron excitations. For the remaining M-shell Fe ions, the DR contributions due to these core electron excitations have only been determined theoretically (see, for instance, Badnell et al. 2006; Altun et al. 2006, 2007). Unlike the theoretical investigations of the L-shell Fe ions, the Δn = 2 electron excitations have never been included in the modeling of DR for M-shell Fe ions.

For this study, we assessed the importance of the Δn = 2 electron excitations in the DR process of M-shell Fe ions. Specifically, we modeled the DR of the Na-like Fe15+, Mg-like Fe14+ and Al-like Fe13+ ions upon additive inclusion of the core 2(s + p) → 4l and the valence 3l → 5l′ excitations alongside the Δn = 0 (i.e., 3l → 3l′) and Δn =1 (i.e., 2(s + p) → 3l and 3l → 4l′) electron excitations. The importance of such Δn = 2 electron excitations in the overall DR was then quantified by the computation of the related plasma DR rate coefficients.

Our work is organized as follows: in Sect. 2, we describe the theory of DR in plasmas and the computational strategy employed in the present calculations; Sect. 3 is devoted to discussing the plasma DR rate coefficients computed for Na-like, Mg-like, and Al-like Fe ions. Our findings and related perspectives are summarized as concluding remarks in Sect. 4.

2 Plasma dielectronic recombination rates in multiply charged ions

2.1 Theoretical background

The DR of an ion in a given charge state involves an initial state, i = (αi𝕁i), a resonance (doubly excited) level embedded within the continuum of the initial ion, d = (αd𝕁d), and a final state, f = (αf𝕁f), into which the recombined system may decay radiatively. Both states and levels are labeled in terms of their total angular momentum and parity, 𝕁 ≡ JP, while all further quantum numbers are referred to as α. In plasmas, electron-ion recombination is temperature-dependent, due to the Maxwellian distribution of the free electrons that are captured by the ions (Massey and Bates 1942). For a single ion per unit volume in the initial state, i, the explicit rate to recombine with a Maxwell-distributed electron at electron temperature, T, is called the DR plasma rate coefficient, α (DR)(T; i), and reads as (Fritzsche 202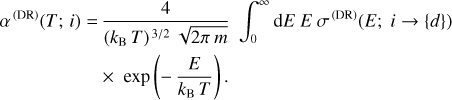1) (1)

Here, σ (DR)(E; i → {d}) stands for the total cross section associated with the capture of the colliding electron into a span of intermediate levels, {d}. This quantity can be written in terms of the resonance strength, S (i → d) (Griffin 1989; Tu et al. 2016), and the kinetic energy of the colliding electron, ɛd = Ed – Ei, thus yielding (Hahn 1985) 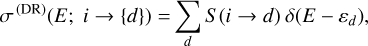(2)

with (3)

In Eq. (3) the resonance strength is expressed in terms of the Auger (Aa) and radiative (Ar) rates of the resonance level, d, as well as its half-width, Γd.

If we substitute Eq. (2) into (1), the total DR plasma rate coefficient can be expressed as a sum over the partial DR plasma rate coefficients, α(DR)(T; i → d). Each partial rate coefficient refers to a specific i → d dielectronic capture resonance, 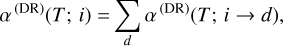(4)

with (5)

2.2 Computational strategy

We modeled the Hamiltonian of all the ions with the multi-configuration Dirac-Hartree-Fock (MCDHF) method in the intermediate coupling, as implemented in the Jena Atomic Calculator (JAC) toolbox (Fritzsche 2019; JACb 2023). Electron-electron correlations are described by means of a Dirac-Coulomb interaction term and only electric-dipole radiative decays are allowed. With this approach we first computed the partial DR plasma rate coefficients for the Δn = 0, 1, and 2 core and valence electron excitations and subsequently summed them to yield the total plasma DR rate coefficients, as described in Eq. (4). All the calculations were performed over a range of electron temperatures spanning from 104 up to 109 K in order to encompass both the photoionized (approximately 104 K ≤ T ≤ 105 K) and the collisionally ionized (approximately 106 K ≤ T ≤ 107 K) plasma temperatures (Mazzotta et al. 1998; Kallman and Bautista 2001).

The partial plasma rate coefficients associated with the low-energy Δn = 0 electron excitations need to be computed with reasonable accuracy, since they dominate the photoionized plasma region (Fritzsche 2021). This requirement led us to adopt two different computational strategies to calculate them: i) in the photoionized plasma region we included only the lowest-lying resonance levels in the calculations, but improved the modeling of the electron-electron correlations; ii) beyond the photoionized plasma region we computed the plasma rate coefficients with a dielectronic capture cascade computation. Such a cascade begins from the capture of the free electron into various nl shells and then models the subsequent electron and photon emission as a stepwise decay of the ion toward its ground configuration. The relevant configurations are either treated independently or combined into moderate groups of configurations. Indeed, this approach provides a relatively simplified modeling of the electron-electron correlations, but enables the inclusion of a larger number of resonance states compared to strategy i).

The remaining Δn =1,2 core and valence electron excitations were computed by the sole dielectronic cascade computation, as described in ii).

3 Results and discussion

3.1 Plasma rate coefficients of Na-like Fe

We chose the electronic ground state of Fe15+, 1s22s22p63s 2S1/2 as the initial state from which the DR process starts. We followed the approach of Altun et al. (2006) in the choice of the bound electron excitations, and thus, by Δn = 0, we mean the excitation of a 3s → 3(p + d) bound electron and the capture of a free electron into a high-lying nl shell. This reads as:

Δn = 1 includes those DR resonances in which the bound electron is excited either from the 3s orbital to the 4l shell or from the 2(s + p) orbitals to the 3l shell, while a free electron is captured into a high-lying nl′ shell:

Besides the above resonances, we added the Δn = 2 electron excitations:

The resonance energies associated with the Δn = 0 electron excitations were shifted by −0.228 eV, in order to match the strongest resonances measured by Linkemann et al. (1995).

In Fig. 1, we compare our plasma rate coefficients for the 3s → 3l, nl′ and 3s → 4l, nl′ DR resonances with the intermediate-coupling multi-configuration Breit-Pauli (MCBP) computations of Altun et al. (2006) and the experimentally derived results by Schippers et al. (2010). Our results compare favorably with the experimentally derived data in the photoionized plasma region: between 2 × 104 and 105 K the discrepancy between our computed plasma rate coefficients and the analogs by Schippers et al. amounts at most to a factor of 1.2. Similar deviations from the experimental benchmark affect the MCBP computations. The largest discrepancy in the photoionized plasma region occurs at around 104 K, where our plasma rate coefficients are 1.4 times larger than the experimentally derived analogs, in analogy with the results of Altun et al. For electron temperatures between 105 and 106 K our results align with the theoretical reference.

Our plasma rate coefficients at the collisionally ionized plasma temperatures lie between the experimental and theoretical references. At around 5 × 106 K our results attain the best agreement with the experimentally derived data. However, we interpret this good agreement as fortuitous. In fact, our plasma rate coefficient at this electron temperature is significantly smaller than both its analog at about 2 × 106 and 107 K. This feature suggests that a better account for electron-electron correlation would be necessary at such an electron temperature. Above the collisionally ionized plasma temperatures, our computed plasma rate coefficients overlap with the MCBP calculations.

We now compare our results for the Δn = 0, 1 electron excitations with the MCBP and MCDHF computations of Altun et al. and Gu (2004), respectively. This comparison is illustrated in Fig. 2. Our results are presented in two sets, with only the Δn = 0, 1 (thick orange line) and with the additional Δn = 2 (thick blue line) electron excitations. Let us focus on the electron temperatures beyond the photoionized plasma region, as there resonances for core electron excitations and excitations from the valence shells to shells with n > 4 become important. Our results align with the references between 105 and about 106 K. At higher electron temperatures our plasma rate coefficients are 1.25 times smaller than the references. This deviation may be attributed to the lower number of resonance levels included in our calculations compared to the reference. However, the comparison depicted in Fig. 1 also shows that the benchmark computations may be significantly overestimated with respect to the data retrieved experimentally. Therefore, we ascribe this reasonable discrepancy partly to the intrinsic limits of our computational approach and partly to the overestimating trend in the theoretical literature.

Let us now focus on the Δn = 2 electron excitations: the comparison of our two sets of results shows a significant increase in the plasma rate coefficients upon the inclusion of the 2(s + p) → 4l, nl′ and 3s → 5l, nl′ DR resonances. We evaluate the importance of such contributions in Fig. 3, which shows the partial plasma rate coefficients associated with each DR resonance, alongside the total plasma rate coefficients. A detailed insight into the contribution of each resonance is provided in Table 1, where the partial plasma rate coefficients are listed across a set of electron temperatures. These electron temperatures coincide with those reported in the ADAS (Summers 2003) repository for the DR of Na-like Fe ions. It can be observed from Fig. 3 that the photoionized plasma region is dominated by the 3s → 3l, nl′ and 3s → 4l, nl′ DR resonances. The resonances associated with the 2(s + p) → 3l core electron excitations and the Δn = 2 electron excitations contribute significantly in the collisionally ionized plasma region. Here, the 2(s + p) → 3l, nl′ DR resonances are dominant: their contribution accounts for 49% of the total DR at 4.5 × 106 K and steadily grows as the electron temperature increases, up to 62% at 109 K. The importance of these contributions to the total plasma rate coefficients at high electron temperatures was already reported by several authors, among them Linkemann et al. (1995); Altun et al. (2006), and Lestinsky et al. (2009). The contribution from the Δn = 2 electron excitations becomes significant at the end of the collisionally ionized plasma region (16% of the total DR plasma rate coefficients between 4.5 × 106 and 107 K) and grows alongside the electron temperature up to 20% at 109 K. The 3s → 5l, nl′ resonances always contribute more than the 2(s + p) → 4l, nl′, although the difference between the two contributions becomes smaller as the electron temperature increases.

thumbnail Fig. 1

Δn = 0, 1 plasma DR rate coefficients for initially sodium-like Fe15+ ions. The present results (thick blue line) are compared with the MCBP computations of Altun et al. (2006; dashed orange line) and the results experimentally derived by Schippers et al. (2010; dotted green line).
Table 1

Total and partial DR plasma rate coefficients of initially Fe15+ ions.

thumbnail Fig. 2

Total plasma DR rate coefficients for initially sodium-like Fe15+ ions. The present results include the Δn = 0, 1 (thick orange line) and 2 (thick blue line) core excitations and are compared to the MCBP computations of Altun et al. (2006; dotted purple line) and the MCDHF computations of Gu (2004; dotted green line).
thumbnail Fig. 3

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially sodium-like Fe15+ ions. Each partial rate coefficient is associated with a different resonance, respectively: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line), and 3s → 5l (dark green line). The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.

3.2 Plasma rate coefficients of Mg-like Fe

The DR process of Mg-like Fe ions starts from the electronic ground state, 1s22s22p63s2 1S0. The choice of the bound electron excitations follows the approach of Altun et al. (2007). Accordingly, the Δn = 0 electron excitations account for the 3s → 3l excitations of the bound electron, while a free electron is captured in a high-lying nl′ shell:

These resonances were computed together in both the atomic and the cascade calculations, in order to include further electron-electron correlations.

For Δn = 1 a core electron is excited from the 2(s + p) shell up to the 3l shell, while the free electron is captured in an nl′ shell with n ≥ 3. This reads as

These resonances were modeled together by means of a cascade computation.

We added the contributions due to the Δn = 2 electron excitations to the partial plasma rate coefficients thus computed. These electron excitations involve the 3s → 5l and 2(s + p) → 4l bound electron excitations and the free electron captured into an nl′ shell. This process can be summarized as

The most recent literature works available on Fe14+ include the above-mentioned MCBP computations of Altun et al. (2007) and the experimentally derived plasma rate coefficients of Bernhardt et al. (2014). The latter measured the DR contributions due to the Δn = 0, 1 electron excitations.

We first adjusted the 3s → 3l, nl′ resonance energies by −0.03 eV. In this way, the strongest low-lying resonances were put in good agreement with the measured analogs. In the second step, we compared our plasma rate coefficients with the theoretical and experimental benchmarks. This comparison is illustrated in Fig. 4, where our results are presented as two sets: the first set includes only the Δn = 0, 1 electron excitations (thick orange line), while the second set includes the Δn = 2 electron excitations (thick blue line).

Our plasma rate coefficients are smaller than the experimentally derived data in the photoionized plasma region. Similar underestimations also appears in the state-of-the-art MCBP computations of Altun et al.. Our discrepancy with the experimental reference lies between a factor of 1.6 at about 104 K and a factor of 1.3 at about 105 K. Our agreement with the data of Bernhardt et al. improves beyond the photoionized plasma region and aligns with the MCBP computations in the collisionally ionized region. There, both our results and the theoretical reference overlap with the experimentally derived plasma rate coefficients. The discrepancy with the references increases again at electron temperatures higher than 107 K. In this region our computed plasma rate coefficients are 1.5 times larger than the experimentally derived plasma rate coefficients of Bernhardt et al. and the MCBP computations. This discrepancy is explained as being likely due to the modeling of the highest-lying continuum orbitals included in the computations. In particular, the hydro-genic approximation used by Altun et al. (2007) to model the free-electron capture into the high Rydberg shells is likely more accurate than the approximation employed in our cascade calculations. Nonetheless, the good overall agreement of our results with the references suggests that this reasonable discrepancy does not compromise the reliability of our approach.

We notice a significant increase of the plasma rate coefficients upon including the Δn = 2 electron excitations. Figure 4 shows that this increase is particularly remarkable in the collisionally ionized plasma region, while Fig. 5 displays the partial plasma rate coefficients for each resonance together with the total plasma rate coefficients. For a quantitative evaluation of these partial contributions across the whole electron temperature range, they are listed in Table 2. The temperatures reported in the table are the same as those listed in the ADAS (Summers 2003) data tables for the DR of the Mg-like Fe ions.

The photoionized plasma region is dominated by the 3s → 3l, nl′ resonances, while the partial plasma rate coefficients for the Δn = 1 and 2 electron excitations become important in the collisionally ionized plasma region. The contributions from the 2(s + p) → 3l, nl′ resonances are significantly smaller than their counterparts in the DR of Fe15+ and account, at most, for 40% of the total DR. Another striking difference with respect to Fe15+ regards the importance of the Δn = 2 electron excitations: in the electron temperature region from the collisionally ionized plasma temperatures up to 109 K, these electron excitations provide the largest contribution to the total DR. The 3s → 5l, nl′ resonances always prevail over the 2(s + p) → 4l, nl′ ones, and their contribution reaches 40% of the total plasma rate coefficients in the collisionally ionized plasma region. This explains the substantial increase in the plasma rate coefficients in this electron temperature range. By contrast, the contribution due to the 2(s + p) → 4l, nl′ electron excitations is never larger than approximately 4%. Overall, the Δn = 2 electron excitations account for 40% of the total plasma rate coefficients in the electron temperature region between 107 and 109 K. This value is roughly twice the contribution of these electron excitations in the DR of Fe15+ ions and can be easily explained in terms of the electron configuration of Fe14+ : in fact, in the DR of this ion, two 3s electrons can be excited to the 5l shell. In summary, the contributions from the Δn = 2 electron excitations to the total DR plasma rate coefficients is much more important for Fe14+ than for Fe15+, due to the closed-shell electron configuration of the former.

thumbnail Fig. 4

Total plasma DR rate coefficients for initially magnesium-like Fe14+ ions. The present results include the 2(s + p) → 3l and 3s resonances (Δn = 1 core excitations, thick orange line) and the Δn = 2 (thick blue line) core excitations, and are compared to the MCBP computations of Altun et al. (2007; green dotted line) and the experimentally derived data of Bernhardt et al. (2014; purple dashed line).
Table 2

Total and partial DR plasma rate coefficients of initially Fe14+ ions.

thumbnail Fig. 5

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially magnesium-like Fe14+ ions. Each partial rate coefficient is associated with a different resonance: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line), and 3s → 5l (dark green line), respectively. The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.

3.3 Plasma rate coefficients of Al-like Fe

The DR process for Fe13+ begins from the electronic ground state, 1s22s22p63s23p 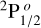. The modeling of the Δn = 0, 1 electron excitations follows the approach of Badnell et al. (2006). Thus, Δn = 0 includes the excitation of one valence electron from the 3s or 3p orbitals into the 3p or 3d orbitals. In summary,

Due to the strong configuration mixing within the 3l shell (see Badnell et al. 2006; Schmidt et al. 2006; Abdel-Naby et al. 2012), modeling these core excitations by means of one atomic calculation is hardly feasible. Therefore, we modeled the 3(s + p) → 3p, nl′ and 3(s + p) → 3d, nl′ resonances by two atomic computations and then summed them. By contrast, in the cascade computations these resonances were modeled together, due to the smaller cost of this approach compared to the correlated atomic computations.

The Δn = 1 electron excitations involve the 3(s + p) → 4l valence electron excitations and the 2(s + p) → 3l core electron excitations:

For the Δn = 2 bound electron excitations we considered the 3(s + p) → 5l valence electron excitation and the 2(s + p) → 4l core electron excitations, while a free electron was resonantly captured into a span of Rydberg shells:

We first assess our results for the partial plasma rate coefficients associated with the 3(s + p) → 3(p + d), nl and 3(s + p) → 4l, nl′ DR resonances. Our calculations are benchmarked with respect to the experimentally derived results of Schippers et al. (2010) and the MCBP computations of Abdel-Naby et al. (2012). We display our partial plasma rate coefficients alongside the experimentally derived and theoretical benchmarks in Fig. 6. Our plasma rate coefficients in the photoionized plasma temperature range are in excellent agreement with the experimentally derived data. The only exception to this trend occurs between 2 × 104 and 3.9 × 104 K: in this electron temperature range our results are 1.7 times smaller than the data of Schippers et al. Nevertheless, this discrepancy is comparable with the analogous deviation affecting the data of Abdel-Naby et al. (2012). The discrepancy with the experimentally derived data increases, starting from the collisionally ionized plasma temperatures: there, our plasma rate coefficients deviate from the experimental reference by a factor of 1.2 at most. This discrepancy increases up to a factor of 1.3 in the electron temperature range between 4 × 107 and 109 K. Such a deviation is reasonable, but should be ascribed to the different modeling of the high-lying resonance states in our approach compared to the approach of Abdel-Naby and coworkers. In their work, the authors modeled these resonance levels by means of a hydrogenic approximation, whereas our atomic cascade approach includes part of the configuration interaction for all the resonance levels computed. Their modeling is likely more accurate for high nl shells compared to ours.

The second step in the validation of our approach is illustrated in Fig. 7, where we compare our plasma rate coefficients for the Δn = 0, 1 electron excitations (thick orange line) with the MCBP computations of Badnell et al. (2006). In the figure we also show the total plasma rate coefficients computed for the Δn = 0, 1, 2 electron excitations (thick blue line). At the photoionized plasma temperatures our results lie up to 1.5 times higher than the MCBP reference. At these electron temperatures the plasma rate coefficients are dominated by the lowest-lying 3(s + p) → 3(p + d), nl DR resonances. The comparison of these resonances with the experimentally derived data of Schippers et al. (see Fig. 6) already validates the accuracy of our approach in the photoionized plasma region. Our results and the references are in very good agreement between 3.92 × 105 and 3.92 × 106 K, where the highest discrepancy amounts to a factor of 1.2. At higher electron temperatures the discrepancy increases and becomes significant beyond 3.92 × 107 K, where our results lie 1.7 times higher than the reference. Two factors may affect this substantial deviation. First, the modeling of the highest-lying resonance states. As for the plasma rate coefficients associated with the lowest-lying DR resonances (Fig. 6), the hydrogenic approximation may provide a better description of the most energetic DR resonances than our limited account of the configuration-interaction effects. As the second factor, we should also consider that Badnell’s results turned out to underestimate the experimentally derived plasma rate coefficients, at least at the photoionized plasma temperatures. Thus, it is also possible that some underestimation affects Badnell’s plasma rate coefficients. Upon accounting for this intrinsic underestimation, the inaccuracy of our results at high electron temperatures appears quite reasonable.

The inclusion of the 2(s + p) → 4l, nl′ and 3(s + p) → 5l, nl′ resonances into the DR process increases the total plasma rate coefficients. To estimate such a growth, we list the partial plasma rate coefficients for each resonance in Fig. 8, alongside the total DR plasma rate coefficients. We also list each partial plasma rate coefficient in Table 3, across a set of electron temperatures that coincide with those reported in the ADAS repository for this ionic species.

The lowest-lying 3(s + p) → 3(p + d), nl resonances are dominant at the photoionized plasma temperatures and the electron temperature interval between the photoionized and the collision-ally ionized plasma regions. The DR contributions due to the higher-lying 3(s + p) → 4l, nl′ resonances become comparable to the 3(s + p) → 3(p + d), nl analogs only at the collision-ally ionized plasma temperatures. There, they contribute at most 42% of the total DR. Beyond this electron temperature region the 2(s + p) → (3l + 4l), nl′ and 3(s + p) → 5l, nl′ resonances become non-negligible. The 2(s + p) → 3l, nl′ DR resonances provide the largest contribution to the total DR in this electron temperature interval, in analogy with the DR of Fe15+. These resonances contribute as much as 33% of the total DR at electron temperatures between 2 × 108 and 4 × 108 K, approximately. This contribution is slightly smaller than the analogous contribution to the DR of Mg-like Fe ions. The DR contributions due to the Δn = 2 core and valence electron excitations are less important than the 2(s + p) → 3l, nl′ resonance, but their contribution is anyway non-negligible and can reach up to 22% of the total DR at about 109 K. The importance of these electron excitations in the DR of Al-like Fe ions is comparable to the role of their counterparts in the Fe15+ DR. This analogy is explained if we consider that for both ions the valence orbital is occupied by one electron. Unlike the DR of Na-like iron ions, in the DR of the Al-like Fe the 2(s + p) → 4l, nl′ resonances contribute more than the 3(s + p) → 5l, nl′ ones between 108 and 109 K. In fact, in this electron temperature region the contribution of the 2(s + p) → 4l, nl′ resonances to the total plasma rate coefficients ranges from 12% (at about 108 K) up to 14% (at about 109 K), while the contribution of the 3(s + p) → 5l, nl′ resonances never exceeds 8.5%. We can tentatively explain this behavior in terms of the larger resonance level density of Fe13+ compared to Fe15+, but further investigations into the DR of Fe ions with 3d1 (K-like) and 4s1 (Mn-like) would be helpful to validate this hypothesis.

thumbnail Fig. 6

3(s + p) → 3(p + d) and 3(s + p) → 4l plasma DR rate coefficients for initially aluminum-like Fe13+ ions. The present results (thick blue line) are compared with state-of-the-art MCBP computations (Abdel-Naby et al. 2012; orange dotted line) and the heavy-ion storage ring measurements by Schippers et al. (2010; green dashed line).
thumbnail Fig. 7

Total plasma DR rate coefficients for initially aluminum-like Fe13+ ions. The present results include the Δn = 0, 1 (thick orange line) and 2 (thick blue line) core excitations and are compared to the MCBP computations of Badnell et al. (2006; green dotted line).
Table 3

Total and partial DR plasma rate coefficients of initially Fe13+ ions.

thumbnail Fig. 8

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially aluminum-like Fe13+ ions. Each partial rate coefficient is associated with a different resonance, respectively: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line) and 3s → 5l (dark green line). The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.

4 Concluding remarks

We investigated the importance of the high-energy 2(s + p) → 4l, nl′ and 3l → 5l′, nl″ resonances (Δn = 2 electron excitations) in the DR plasma rate coefficients of Fe15+, Fe14+, and Fe13+ across the electron temperature interval that encompasses both the photoionized and collisionally ionized plasma temperatures. Our results for the resonances involving the excitation of a valence electron to the 3l or 4l shells and of a core 2(s + p) electron to the 3l shell (Δn = 0, 1 electron excitations) show a reasonable overall agreement with the available experimentally derived data and the state-of-the-art atomic calculations. The favorable comparison of our Δn = 0, 1 plasma rate coefficients with the benchmarks validates our theoretical approach. The inclusion of the Δn = 2 electron excitations is found to raise the total plasma rate coefficients up to a non-negligible extent in the electron temperature interval between the collisionally ionized plasma temperatures and 109 K. We further estimate the 2(s + p) → 4l, nl′ and 3l → 5l′nl″ resonances to account, at most, for approximately 21%, 40%, and 22% of the total DR plasma rate coefficients of Fe15+, Fe14+, and Fe13+, respectively. The large contributions from these resonances in the DR of Mg-like Fe are explained in terms of the two 3s valence electrons that can be excited to the 5l shells. On the other hand, the similarity between the Δn = 2 contributions in the DR of Na- and Al-like Fe ions is ascribed to their similar electron configurations, which feature one electron in the outermost orbital. The slightly larger contribution of these resonances in the DR of Fe13+ compared to Fe15+ may be due to the two subvalence 3s electrons featuring the former’s electron configuration. However, we would need a systematic investigation into the DR of Fe ions with 3d and 4s singly occupied valence orbitals in order to confirm this explanation.

On this ground, we expect these highly energetic resonances to contribute to the plasma DR more and more remarkably as the valence 3l orbitals are filled, with the highest contributions to be attained for closed-shell iron ions. Thus, such resonances contribute substantially to the DR of M-shell iron ions and cannot be neglected in the modeling of this process at high electron temperatures. Furthermore, our results support the predictions of Sako et al. (2001) and Behar et al. (2001), that the high-energy 2(s + p) → 4l, nl′ and 3l → 5l′, nl″ resonances can significantly shape the UTA observed in active galactic nuclei at reasonably high temperatures.

Acknowledgements

G.V. would like to thank Dr. Anna Maiorova, Dr. L.-G. Jiao and Dr. Zh. Wu for the fruitful discussions on this topic.

References

  1. Abdel-Naby, Sh.A., Nikolic, D., Gorczyca, T.W., et al. 2012, A&A, 537, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Altun, Z., Yumak, A., Badnell, N. R., et al. 2005, A&A, 433, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Altun, Z., Yumak, A., Badnell, N. R., et al. 2006, A&A, 447, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Altun, Z., Yumak, A., Yavuz I., et al. 2007, A&A, 474, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Badnell, N. R. 2006, J. Phys. B: At. Mol. Opt. Phys., 39, 4825 [NASA ADS] [CrossRef] [Google Scholar]
  6. Badnell, N. R., O’Mullane, M.G., Summers, H.P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Behar, E., Sako, M., & Kahn, S. M. 2001, ApJ, 563, 497 [NASA ADS] [CrossRef] [Google Scholar]
  8. Behar, E., Rasmussen, A. P., Blustin, A. J., et al. 2003, ApJ, 598, 232 [Google Scholar]
  9. Beiersdorfer, P. 2003, ARA&A, 41, 343 [NASA ADS] [CrossRef] [Google Scholar]
  10. Beiersdorfer, P., Phillips, T. W., Wong, K. L., et al. 1992, Phys. Rev. A, 46, 7 [Google Scholar]
  11. Bernhardt, D., Becker, A., Grieser, M., et al. 2014, Phys. Rev. A, 90, 012702 [NASA ADS] [CrossRef] [Google Scholar]
  12. Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
  13. Canizares, C. R., et al. 2000, ApJ, 539, L41 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chen, M. H. 1991, Phys. Rev. A, 44, 7 [Google Scholar]
  15. Fritzsche, S. 2019, Comput. Phys. Commun. 240, 1 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fritzsche, S. 2021, A&A, 656, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Fritzsche, S., Palmeri, P., & Schippers, S. 2021, Symmetry, 13, 520 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fritzsche, S. 2020, JAC: User Guide, Compendium & Theoretical Background, unpublished, https://github.com/OpenJAC/JAC.jl [Google Scholar]
  19. Gallo, L. C., Boller, T., Brandt, W. N., Fabian, A. C., & Vaughan, S. 2004, A&A, 417, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Griffin, D. C. 1989, Phys. Scr., T28, 17 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gu, M. F. 2004, ApJS, 153, 389 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hahn, Y. 1985, Adv. At. Mol. Phys. 21, 123 [NASA ADS] [CrossRef] [Google Scholar]
  23. Huang, Z. K., Wen, W. Q., Xu, X., et al. 2018, ApJS, 235, 2 [NASA ADS] [CrossRef] [Google Scholar]
  24. Huenemoerder, D. P., Canizares, C. R., & Schulz, N. S. 2001, ApJ, 559, 1135 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kallman, T. R., & Bautista, M. B. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kallman, T. R., & Palmeri, P. 2007, Rev. Mod. Phys., 79, 1 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kaspi, S., Brandt, W. N., George, I. M., et al. 2002, ApJ, 574, 643 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kaspi, S., Netzer, H., Chelouche, D., et al. 2004, ApJ, 611, 68 [NASA ADS] [CrossRef] [Google Scholar]
  29. Khan, N., Huang, Z.-K., Wen, W.-Q. et al. 2018, Chinese Phys. C, 42, 6, 064001 [NASA ADS] [CrossRef] [Google Scholar]
  30. Krongold, Y., Nicastro, F., Elvis, M., et al. 2005, ApJ, 620, 165 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lestinsky, M., Badnell, N. R., Bernhardt, D., et al. 2009, ApJ, 698, 648 [NASA ADS] [CrossRef] [Google Scholar]
  32. Linkemann, J., Kenntner, J., Müller, A. et al. 1995, Nucl. Instr. and Meth. in Phys. Res. B, 98, 154 [CrossRef] [Google Scholar]
  33. Massey, H. S. W., & Bates, D. R. 1942, Rep. Prog. Phys. 9, 62 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Netzer, H. 2004, ApJ, 604, 551 [NASA ADS] [CrossRef] [Google Scholar]
  36. Pounds, K., Reeves, J., O’Brien, P., et al. 2001, ApJ, 559, 181 [NASA ADS] [CrossRef] [Google Scholar]
  37. Pounds, K., Reeves, J. N., King, A. R., & Page, K. L. 2004, MNRAS, 350, 10 [NASA ADS] [CrossRef] [Google Scholar]
  38. Pütterich, T., Neu, R., Whiteford, A. D., et al. 2008, Plasma Phys. Control. Fusion 50, 085016 [CrossRef] [Google Scholar]
  39. Sako, M., Kahn, S. M., Behar, E., et al. 2001, A&A, 365, L168 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Savin, D. W., Gwinner, G., Grieser, M. et al. 2006, ApJ, 642, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  41. Schippers, S. 2009 J. Phys. Conf. Ser., 163, 012001 [NASA ADS] [CrossRef] [Google Scholar]
  42. Schippers, S., Lestinsky, M., Müller, A., et al. 2010, Int. Rev. At. Mol. Phys., 1, 109 [Google Scholar]
  43. Schippers, S. 2015, NIMPB, 350, 61 [Google Scholar]
  44. Schmidt, E. W., Schippers, S., Müller, A. et al. 2006, ApJ, 641, L157 [NASA ADS] [CrossRef] [Google Scholar]
  45. Schuch, R., & Böhm, S. 2007, J. Phys. Conf. Ser., 88, 012002 [NASA ADS] [CrossRef] [Google Scholar]
  46. Steenbrugge, K. C., Kaastra, J. S., de Vries, C. P., & Edelson, R. 2003, A&A, 402, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Summers, H. P. 2003, ADAS User Manual, https://www.adas.ac.uk/manual.php [Google Scholar]
  48. Tu, B., Xiao, J., Shen, Y., et al. 2016, Phys. Plasmas, 23, 053301 [NASA ADS] [CrossRef] [Google Scholar]
  49. Wu, Z., Zhang, Y., Fu, Y., et al. 2015, Eur. Phys. J. D, 69: 140 [NASA ADS] [CrossRef] [Google Scholar]
  50. Xu, H., Kahn, S. M., Peterson, J. R., et al. 2001, in ASP Conf. Ser., 251, 424 [NASA ADS] [Google Scholar]
  51. Zatsarinny, O., Gorczyca, T. W., Korista, K. T., et al. 2003, A&A, 412, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Zatsarinny, O., Gorczyca, T. W., Korista, K. T., et al. 2004a, A&A, 417, 1153 [Google Scholar]
  53. Zatsarinny, O., Gorczyca, T. W., Korista, K. T., et al. 2004b, A&A, 426, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Zatsarinny, O., Gorczyca, T. W., Fu, J., et al. 2006, A&A, 447, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Total and partial DR plasma rate coefficients of initially Fe15+ ions.

In the text
Table 2

Total and partial DR plasma rate coefficients of initially Fe14+ ions.

In the text
Table 3

Total and partial DR plasma rate coefficients of initially Fe13+ ions.

In the text

All Figures

thumbnail Fig. 1

Δn = 0, 1 plasma DR rate coefficients for initially sodium-like Fe15+ ions. The present results (thick blue line) are compared with the MCBP computations of Altun et al. (2006; dashed orange line) and the results experimentally derived by Schippers et al. (2010; dotted green line).
In the text
thumbnail Fig. 2

Total plasma DR rate coefficients for initially sodium-like Fe15+ ions. The present results include the Δn = 0, 1 (thick orange line) and 2 (thick blue line) core excitations and are compared to the MCBP computations of Altun et al. (2006; dotted purple line) and the MCDHF computations of Gu (2004; dotted green line).
In the text
thumbnail Fig. 3

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially sodium-like Fe15+ ions. Each partial rate coefficient is associated with a different resonance, respectively: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line), and 3s → 5l (dark green line). The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.
In the text
thumbnail Fig. 4

Total plasma DR rate coefficients for initially magnesium-like Fe14+ ions. The present results include the 2(s + p) → 3l and 3s resonances (Δn = 1 core excitations, thick orange line) and the Δn = 2 (thick blue line) core excitations, and are compared to the MCBP computations of Altun et al. (2007; green dotted line) and the experimentally derived data of Bernhardt et al. (2014; purple dashed line).
In the text
thumbnail Fig. 5

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially magnesium-like Fe14+ ions. Each partial rate coefficient is associated with a different resonance: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line), and 3s → 5l (dark green line), respectively. The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.
In the text
thumbnail Fig. 6

3(s + p) → 3(p + d) and 3(s + p) → 4l plasma DR rate coefficients for initially aluminum-like Fe13+ ions. The present results (thick blue line) are compared with state-of-the-art MCBP computations (Abdel-Naby et al. 2012; orange dotted line) and the heavy-ion storage ring measurements by Schippers et al. (2010; green dashed line).
In the text
thumbnail Fig. 7

Total plasma DR rate coefficients for initially aluminum-like Fe13+ ions. The present results include the Δn = 0, 1 (thick orange line) and 2 (thick blue line) core excitations and are compared to the MCBP computations of Badnell et al. (2006; green dotted line).
In the text
thumbnail Fig. 8

Total (thick blue line) and partial (dashed lines) DR plasma rate coefficients for initially aluminum-like Fe13+ ions. Each partial rate coefficient is associated with a different resonance, respectively: 2(s + p) → 3l′ (orange line), 2(s + p) → 4l (light green line), 3s → 3l (purple line), 3s → 4l (golden line) and 3s → 5l (dark green line). The two dark areas between 104 and 105 K and between 106 and 107 K indicate the photoionized and collisionally ionized plasma regions, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.