| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202346830 | |
| Published online | 08 November 2023 | |
Bright-Moon sky as a wide-field linear Polarimetric flat source for calibration
1
Institute of Astrophysics, Foundation for Research and Technology - Hellas, Vasilika Vouton,
70013
Heraklion, Greece
e-mail: sidh345@gmail.com
2
Department of Physics, University of Crete,
Voutes University Campus,
70013
Heraklion, Greece
3
Inter-University Centre for Astronomy and Astrophysics,
Post Bag 4,
Ganeshkhind,
Pune -
411 007, India
4
South African Astronomical Observatory,
PO Box 9,
Observatory,
7935,
Cape Town, South Africa
e-mail: siddharth@saao.ac.za
5
Cahill Center for Astronomy and Astrophysics, California Institute of Technology,
1216 E California Blvd,
Pasadena, CA
91125, USA
6
Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029
Blindern,
NO-0315
Oslo, Norway
7
National Institute of Science Education and Research, An OCC of Homi Bhabha National Institute,
Jatni,
Bhubaneswar -
752050, India
8
Astrophysics Division, National Centre for Nuclear Research,
Pasteura 7,
Warsaw,
02093, Poland
9
Department of Space, Earth & Environment, Chalmers University of Technology,
412 93
Gothenburg, Sweden
10
Institute of Computer Science, Foundation for Research and Technology-Hellas,
Vasilika Vouton,
70013
Heraklion, Greece
11
Department of Computer Science, University of Crete,
Voutes,
70013
Heraklion, Greece
12
Department of Physics, University of Johannesburg,
PO Box 524,
Auckland Park
2006, South Africa
13
Owens Valley Radio Observatory, California Institute of Technology,
1200 E California Blvd,
Pasadena, CA
91125, USA
14
Steward Observatory, University of Arizona,
933 N Cherry Ave,
Tucson, Arizona,
85721, USA
15
Université Libre de Bruxelles, Science Faculty
CP230,
Av. Franklin Roosevelt 50,
1050
Brussels, Belgium
Received:
7
May
2023
Accepted:
30
August
2023
Context. Next-generation wide-field optical polarimeters such as Wide-Area Linear Optical Polarimeters (WALOPs) have a field of view (FoV) of tens of arcminutes. Wide-field polarimetric flat sources are essential to the efficient and accurate calibration of these instruments. However, no established wide-field polarimetric standard or flat sources exist at present.
Aims. This study tests the feasibility of using the polarized sky patches of the size of around 10 × 10 arcminutes2, at a distance of up to 20° from the Moon, on bright-Moon nights as a wide-field linear polarimetric flat source.
Methods. We observed 19 patches of the sky adjacent to the bright-Moon with the RoboPol instrument in the SDSS-r broadband filter. These patches were observed on five nights within two days of the full-Moon across two RoboPol observing seasons.
Results. We find that for 18 of the 19 patches, the uniformity in the measured normalized Stokes parameters q and u is within 0.2%, with 12 patches exhibiting uniformity within 0.07% or better for both q and u simultaneously, making them reliable and stable wide-field linear polarization flats.
Conclusions. We demonstrate that the sky on bright-Moon nights is an excellent wide-field linear polarization flat source. Various combinations of the normalized Stokes parameters q and u can be obtained by choosing suitable locations of the sky patch with respect to the Moon.
Key words: instrumentation: polarimeters / techniques: polarimetric / Moon / atmospheric effects
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Optical polarimetry is a powerful diagnostic tool that has been used by astronomers to probe many astrophysical objects, especially with respect to systems where asymmetry is present in the light emission and/or propagation. Some commonly studied objects through optical polarimeters include active galactic nuclei, novae and supernovae, and dust clouds in the interstellar medium (e.g., Hough 2006; Scarrott 1991; Trippe 2014). Polarimeters are often designed to achieve accuracies of p ≲ 0.1% or better with careful calibration observations to estimate the instrument-induced polarization. Most polarimeters built to date are optimized for observation of either point sources or very narrow fields of view (FoV) of a few arcminutes. The calibration of these polarimeters is done using measurements of polarimetric standard stars, as described in papers reporting the commissioning and performance of various instruments of the past (e.g., Ramaprakash et al. 1998, 2019; Kawabata et al. 2008; Potter et al. 2016; Tinyanont et al. 2018; Piirola et al. 2014; Clemens et al. 2007).
As with many other fields in astronomy, optical polarimetry is entering an era of large sky surveys with such programs as Polar-Areas Stellar Imaging in Polarization High-Accuracy Experiment (PASIPHAE, Tassis et al. 2018), SouthPol (Magalhães et al. 2012), and VSTpol (Covino et al. 2020), which are currently under development. All of these surveys will be equipped with polarimeters of an unprecedentedly large FoV (>0.25 square degrees) as their main workhorse instruments, with the aim to achieve polarimetric accuracy of p ≲ 0.1% to enable the tomographic reconstruction of the dusty magnetized interstellar medium (Pelgrims et al. 2023), among other science cases. Of these, PASIPHAE will be concurrently carried out from the northern and southern hemispheres using two Wide-Area Linear Optical Polarimeter (WALOP) instruments. The first of the two WALOPs, that is, WALOP-south will be mounted on the South African Astronomical Observatory’s 1 m telescope at the Sutherland Observatory and is scheduled for commissioning in 2023. Maharana et al. (2020, Maharana et al. 2021) have provided a detailed description of the optical and optomechanical design of the WALOP-South instrument.
The goal of the WALOP-South instrument is to achieve a polarimetric measurement accuracy of p ≲ 0.1% across a FoV of 35 × 35 arcminutes2. A complete modeling of the instrument’s polarization behavior, as well as the development of the on-sky calibration method, was achieved and presented in (Maharana et al. 2022; to be referred to as Paper I henceforth) and Anche et al. (2022). The calibration model for the WALOP-South instrument uses the following two ingredients: (a) an built-in calibration polarizer at the beginning of the instrument and (b) multiple on-sky linear polarimetric flat sources of size 10 × 10 arcminutes2 or more at various polarization angles (i.e., electric vector position angle, EVPA, θ); namely, the polarization values are spread across the q – u plane.
In the case of WALOP-South, instrumental polarization is expected in the following forms: (a) polarimetric efficiency and cross-talk and (b) polarimetric zero-offsets. An elaborate description of these effects in Mueller matrix formalism is presented in Sects. 2.2 and 2.3 of Paper I. The polarimetric efficiency and cross-talk captures the dependence of the measured Stokes parameters qm and um on intrinsic Stokes parameters q and u of the source. To measure and correct for these in WALOP-South, the built-in calibration polarizer at the beginning of the instrument will be deployed in the optical path to give, as its input, fully linearly polarized light at different EVPAs and measure the corresponding qm and um. The polarimetric zero-offset, which is the main instrumental polarization that most polarimeters suffer from, corresponds to the measured Stokes parameters when the input source is unpolarized. It is measured in small FoV polarimeters by observing unpolarized and polarized standard stars. The polarimetric flats, along with a small number of standard star measurements will be used to find and correct for the polarimetric zero-offsets in the WALOP-South. Polarimetric flats allow for the measurement of the relative polarimetric-offsets over a large field at once, which cannot be efficiently done with point sources (standard stars). In conjugation, using standard unpolarized and polarized star measurements at a few points in the field will enable absolute polarimetric zero-offset calibration over the wide field.
This presented methodology of using polarimetric flats for calibrations has been developed keeping in mind wide-field instruments (1 × 1 arcmin2 or more) such as WALOPs, where we expect a significant change in the instrumental polarization as a function of CCD and field position greater than the desired accuracy of the measurements (0.1% for most polarimeters). In general, for this method to be useful, the images of the ordinary and extraordinary rays must either: (a) fall on separate detectors such as WALOP or (b) fall on different and non-overlapping regions of the detectors such as the FOcal Reducer and low-dispersion Spectrograph 2 (FORS2) polarimeter (González-Gaitán et al. 2020) and inside the mask of the RoboPol polarimeter (Ramaprakash et al. 2019).
Currently, while there are multiple known polarized and unpolarized standard stars (Blinov et al. 2020), they are scattered across the sky and, alone, they are unsuitable for wide-field instrument calibration. While unpolarized wide-field regions can be predicted based on ISM extinction (Skalidis et al. 2018), finding uniformly polarized regions is harder as it requires long-term monitoring of hundreds of stars, which is unfeasible with currently available limited FoV polarimeters. As mentioned, for WALOP instruments, in particular, multiple wide-field polarized sources, spread over the q – u planes are needed. Standard polarized regions whose polarization values are known a priori would be ideal, but knowledge about the polarization value is not a critical requirement. Rather, linear polarimetrically flat regions, which have a constant polarization across the region, are sufficient for the calibration of wide-field instruments, as demonstrated in Paper I for WALOPs and by González-Gaitán et al. (2020) for the FORS2 polarimeter (described later in this work).
One promising candidate for a polarimetric flat field is the sky on bright-Moon nights (González-Gaitán et al. 2020). During such times, owing to the geometry of the Sun-Earth-Moon system, the light entering the atmosphere from the Moon is unpolarized on full-Moon nights or polarized up to a low level when within a few days of it.
While traversing the atmosphere, the polarization state of the light beam is modified primarily due to the scattering by small atmospheric molecules, described by Rayleigh scattering. Therefore, the observed polarization depends on the scattering geometry between the observer (telescope), the sky location, and the position of the Moon in the sky. Assuming that the atmosphere can be described by a single-layer scattering region, Rayleigh scattering predicts that, for unpolarized light on full-Moon nights, the polarization fraction, p, depends on the angular distance of the region, γ, from the Moon, as given by Eq. (1) (Gál et al. 2001; Wolstencroft & Bandermann 1973; Harrington et al. 2011; Strutt 1871; Smith 2007).
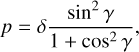 (1)
(1)
where δ is an empirical parameter whose value depends on the sky conditions and for clear cloudless nights, it is found to be around 0.8 (Gál et al. 2001).
As can be seen, the value of p increases as the (γ) is farther away from the Moon, with the maximum value at γ = π/2, whereas it is zero near the vicinity of the Moon. The expected EVPA, θ, is a function of the sky position of the Moon as well as the sky pointing. By choosing a suitable combination of these, desired EVPAs can be achieved. In this way, required combinations of p and θ (i.e., q and u) can be obtained depending on the calibration requirements.
This scattering model predicts that within an area of 10 × 10 arcminutes2 and sky positions of up to 15−20 degrees away from the Moon, p (and, q and u) will remain constant to a level of few hundredths of a percent (see Fig. 1). While deviations from this simple picture may arise due to several complicating factors, the polarization is still likely to remain constant within such a patch. Previously, assuming the sky on the full-Moon nights as a linear polarimetric flat source, González-Gaitán et al. (2020) calibrated the FORS2 polarimeter mounted at the Very Large Telescope (VLT), which has a FoV of 7 arcminutes, to an accuracy better than 0.05% in p. They assumed the instrumental polarization to be zero at the center of the FoV and used the measured linear polarization there as the polarization of the sky across the FoV.
While it would be ideal to have a polarimetric flat source of the size of WALOP-South FoV of 35 × 35 arcminutes2, based on the sky scattering models, we expect the variation in q and u across a 35 arcminutes FoV to be larger than 0.1%; thus, it cannot be used as a flat source in our case. Consequently, we tested the sky flatness for a field of size 10 × 10 arcminutes2. To calibrate the 35 × 35 arcminutes2 FoV, it must be divided into 25 boxes of size 7 × 7 arcminutes2, each of which are to be calibrated independently (Fig. 13, Paper I). While the Moon sky flats are of size 10 × 10 arcminutes2, the calibration boxes have been kept of size 7 × 7 arcminutes2 to have overlapping regions between flat patches of neighbouring boxes.
In this work, we carried out linear polarimetric observations of the extended sky greater than ten arcminutes in size to verify the suitability of the polarized sky as a wide-field polarimetric flat source. We used the RoboPol instrument to observe a total of 19 patches on five different nights within two days of the full-Moon in the Sloan Digital Sky Survey (SDSS)-r band filter. Section 2 presents the details of the observations carried out for this study. The data analysis is presented in Sect. 3, where we find that 12 of the 19 patches are simultaneously uniform in q and u to within 0.07%, while the other patches are uniform to within 0.3%. We discuss our results in Sect. 4 and provide our conclusions and an outlook for future works in Sect. 5.
 |
Fig. 1 Simulated polarization for a 10 × 10 arcminutes2 patch at a distance of 15.5° from the Moon based on a single-layer Rayleigh scattering model to describe the atmosphere. In this example, the coordinates of the Moon are (RA = 0°, Dec = 0°), while the patch is centered at (RA = 11.0°, Dec = 11.0°) in the geocentric celestial reference system (GCRS) coordinate system. |
2 Observations
All observations were performed in the SDSS-r filter with the RoboPol instrument mounted on the 130 cm Telescope of the Skinakas Observatory in Crete, Greece. The instrument is described in detail by Ramaprakash et al. (2019). It is a four-channel one-shot optical linear Polarimeter that measures q and u in a single exposure. The four channels are projected on the same CCD, as shown in Fig. 2. A central mask blocks light from neighboring regions of the observed target field, increasing the accuracy by reducing the sky background. We observed 19 patches of the sky at different separations from the Moon and during different Moon phases, as listed in Table 1. Each patch nominally covered an area of either 10 × 10 (patches 1−11) or 5 × 7.5 arcminutes2 (patches 12−19) in the GCRS based equatorial coordinates, as shown in Figs. 3a and 3b. The coordinates of the Moon and the sky presented in this work and used for calculations are in the GCRS as the motion of the Moon is bound by Earth’s gravity. Each patch was divided into a rectangular grid of points (coordinates), which were observed through RoboPol inside the mask. The observed patches were divided into a grid of 6 × 6 pointing during the first 3 nights (patches 1−11) and into a grid of 5 × 4 pointing for the remaining observations (patches 12−19).
The observation sequence of the grid points for a patch was chosen while keeping the following two effects into consideration: (1) While the observations of any patch are being carried out, the sky position of the Moon changes with respect to the patch due to its non-sidereal motion. So, the rectangular grid becomes distorted with respect to the Moon. (2) The overall accuracy of the telescope pointing is 2 arcminutes if the telescope slews (when the separation between consecutive grid points is greater than 8 arcminutes). However, if the separation is less than 8 arcminutes, the telescope moves through very precise and small offset motion with an accuracy of a few arcseconds, yielding high accuracy pointing.
Thus, the observation sequence for the grid points of a patch was decided so as to minimize the effect of the Moon’s motion on the patch size and morphology, while using only small offsets to move the telescope and obtain high accuracy pointing. Two different observation sequences were followed for different nights (Figs. 3a and b), leading to a different morphology of the grid points of the patches with respect to the Moon. For patches 1−11, the square grid becomes distorted with respect to the Moon, resembling a pattern as shown in Fig. 3c. Figure 3d shows the corresponding plot for patches 12−19. The patch size noted in Table 1 is the overall extent in the Right ascension (RA) and declination (Dec) coordinates for the patches. As can be seen, the grid points which were nominally spread over up to 10 × 10 arcminutes2 in form of a rectangular grid become distorted and spread over tens of arcminutes on the sky with respect to the Moon.
The exposure time per pointing ranged from 2.5 to 90 s and was chosen for each patch such that the uncertainty in measured fractional polarization from photon noise was 0.04−0.05% in the central masked region. The exposure time depends on the sky’s brightness, which itself is a function of the angular separation from the Moon as well as the Moon phase. Furthermore, patches for the observation of the sky were chosen using the following two criteria: (a) to sample various distances as well as orientations with respect to the Moon and (b) the patch should contain very few stars (and no bright stars). During the observations, it was ensured that no star fell inside the central masked region. Multiple standard stars, used to calibrate the RoboPol polarimeter, were observed during the observation nights. The instrumental zero polarization obtained from those measurements was consistent with the values reported in Table 2, obtained for the full observing seasons following the standard RoboPol pipeline (Blinov et al. 2020, 2023). This pipeline incorporates long-term and high-cadence measurements of the RoboPol instrumental polarization through observations of standard stars and takes into account effects such as minor variations in the RoboPol instrumental polarization due to the position of star within the mask.
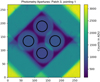 |
Fig. 2 central region of RoboPol used for making the measurements. Four images of the source, corresponding to 0°, 45°, 90° and 135° polarization are formed simultaneously at the CCD and differential photometry of the two pairs of images yields the Stokes parameters q and u. The apertures used for the photometry of the four channels are marked in black circles. The color bar indicates the counts in ADUs for the exposure. |
Details of observed sky patches.
3 Results
A dedicated data reduction pipeline was written in Python to analyze the raw data. Aperture photometry (without any background subtraction) was carried out using the Photutils package (Bradley et al. 2020) on the images to obtain the intensities of the four beams of the sky on the CCD (Fig. 2). Circular apertures of size 12 arcseconds were used. From these, the Stokes parameters were found using the normalized difference between corresponding intensities. The instrumental zero polarization was then subtracted from these measurements. Throughout the analysis, careful attention was given to the error estimation and propagation in each step.
To check for the polarimetric flatness of a patch, we calculated the mean and the standard deviation of the normalized Stokes parameters q and u for all the n grid points using the conventional formulae, as shown in Eqs. (2)−(5), shown below:
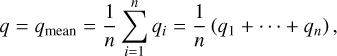 (2)
(2)
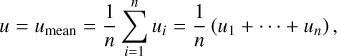 (3)
(3)
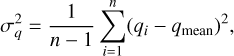 (4)
(4)
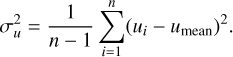 (5)
(5)
Figure 4 shows the measured polarizations in the q − u plane for patch 1. Corresponding plots for all the other patches are shown in Figs. A.1 and A.2. These measurements of polarimetric flatness for all the patches are listed in Table 3. In general, we find the patches to have a scatter in q and u under 0.07%. For 12 of the 19 patches, we found q and u both to be constant within 0.07%, with the maximum value reaching 0.30% for patch 16. We find a higher spread (> = 0.1%) in the measurement of either q and/or u in patches 13, 15, 16, 17, and 19.
We draw attention to the fact that the correction of the instrumental polarization on the measurements does not affect the estimates of the standard deviation in the patches and, thus, of the flatness of the sky polarization. The observational quantification of these dispersion is the main result of this paper, as it confirms that the sky polarization around the full Moon is a good flat-source candidate in sky regions of 10 × 10 arcminutes2 or more.
Instrumental zero polarization of RoboPol during the observation runs (Blinov et al. 2023).
 |
Fig. 3 Nominal pointing positions for patches 1−11 (panel a). The overall size of the patch is 10 × 10 arcminutes2. Nominal pointing positions for patches 12−19 (panel b). The overall size of the patch is 4.8 × 7.5 arcminutes2. Patches 1−11 and 12−19 were observed with RoboPol through a rectangular grid of either 6 × 6 or 5 × 4 pointing coordinates, respectively, in the sequence marked in the images. Due to the motion of the Moon in the sky, the shape of the grid with respect to the Moon is distorted, depending on the sequence of observations followed. For patch 10, the grid points are spread across a region of 21.8 × 4.3 arcminutes2 (panel c). Patches 1 to 11 have similar pattern, and their geometrical extant is noted in Table 1. For patch 18, the grid points are spread across a region of 19.5 × 11 arcminutes2 (panel d). Patches 12 to 19 have similar pattern, and their geometrical extents are noted in Table 1. |
 |
Fig. 4 Measured q and u values for all the pointing for patch 1 (yellow crosses) as well as the overall mean value and the measured standard deviation (black cross), whose values are mentioned in the top left legend. The median individual errors in the bottom left legend refer to the median of expected errors in the Stokes parameters owing to photon noise across the grid points. The value of the degree of linear polarization, p, is presented without any correction for polarimetric bias; p is calculated for each grid point and then their mean and variance are found, similar to q and u. |
4 Discussion
As shown in Table 3, the standard deviation within each patch is typically less than 0.07% in q and u and, consequently, these are also polarimetric flats in the degree and angle of linear polarization, p and θ as well. Several effects contribute to the observed scatter of measurements in individual patches: photon noise, variability in the instrumental polarization, the gradient in sky polarization as a function of distance, and (possibly) changes in sky polarization during the observations. As already noted, the exposure times during observations were adjusted for each patch such that the achieved photon noise contribution is around 0.05% for all our q and u measurements.
The stability of RoboPol is around 0.15% over an entire observation season from 2014 to 2022 (Blinov et al. 2020). However, for the observations presented in this work, we find that the instrumental polarization is non-variable to within 0.07% during the observations of each patch, on a timescale of half an hour to two hours. These low values indicate that the change in instrumental polarization is small for such exposure times and for small sky regions, thus mitigating any source of systematics from possible instrumental flexure and other sources of variable instrumental polarization.
Another contribution to the scatter is the fact that the polarization is expected to change depending on the position within the patch, according to Eq. (1) (and as shown in Fig. 1). Our results demonstrate that this effect is less than 0.1% levels for patches extending up to 20 arcminutes. We observe trends in the spatial spread of the data points in the q − u plots, as in patches 1, 2, and 5 (among others); this may be due to the above mentioned effect. In this work, we did attempt to model these effects, which promises to reduce the scatter further in sky polarimetric flats. Such efforts are currently underway with an expanded data-set and will be reported in future publications.
We must notice that the sky polarization may change during the observations due to fluctuations in atmospheric conditions. While it might be the dominant source of scatter in our measurements for patches 13, 15, 16, 17, and 19, our observations show that this source of scatter remains lower than 0.3% (in p) within the time scales needed to observe individual patches (half an hour to two hours). A wide-field polarimeter such as WALOP will observe an entire patch in a single exposure of a much shorter time than required with RoboPol. Therefore, we expect that the time variability of the sky polarization will not play a significant role.
The use of polarimetric flats will enable fast and reliable calibrations of wide-field polarimeters such as WALOPs. Unlike smaller FoV polarimeters, wide-field polarimeters have a large spatial variation in the instrumental polarization as a function of CCD/field position that goes above and beyond the desired accuracy of the measurements; thus, cannot be efficiently calibrated by standard stars alone. Please note that the sky polarimetric flats can be used to calibrate any polarimeter that satisfies the following requirement: the ordinary and extraordinary rays fall on non-overlapping regions of the detector(s). Consequently, these cannot be used to calibrate polarimeters which do not satisfy the above condition, such as the FoV of RoboPol outside the mask, as each point in the region receives in two ordinary and two extraordinary beams from nearby regions of the sky.
To carry out these calibration observations for WALOPs, we will allot a dedicated amount of time to these on bright nights. While we can, in principle, devise an observing strategy by which we schedule observations of science targets so that they fall in the vicinity of the bright Moon to simultaneously also serve as polarimetric flats – in practice, it would be impractical as the sky background would be too large to obtain the required photometric signal-to-noise ratio (S/N) to yield a 0.1% accuracy within a reasonable amount of time.
Mean and standard deviation of linear polarization properties in patches.
5 Conclusions
Currently, no known and established polarimetric flat sources exist for the calibration of wide-field optical polarimeters such as WALOPs. A critical ingredient in the on-sky calibration method of the WALOP polarimeters is the use of multiple partially polarized polarimetric flat sources whose polarization values are spread across the q − u plane.
In this paper, we demonstrate experimentally that the sky in the vicinity of the full Moon can be used as an extended linear polarimetric flat source for the relative calibration of wide-field linear polarimeters. The sky polarization indeed remains constant at the level of 0.1% or lower in sky regions of 10 to 20 arcminutes. Furthermore, different combinations of q − u can be achieved based on the relative sky positions of the Moon and the target patch.
While we have only demonstrated this in SDSS-r band and for the bright-Moon sky within two days of the full-Moon, it is expected to hold true for other filters in the optical wavelengths as the polarizing mechanism remains the same. In the near future, we plan to carry out similar measurements with RoboPol in other broadband filters to confirm this.
Acknowledgements
The PASIPHAE program is supported by grants from the European Research Council (ERC) under grant agreement No 771282 and No 772253, from the National Science Foundation, under grant number AST-1611547 and the National Research Foundation of South Africa under the National Equipment Programme. This project is also funded by an infrastructure development grant from the Stavros Niarchos Foundation and from the Infosys Foundation. V.P. acknowledges support by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the “First Call for H.F.R.I. Research Projects to support Faculty members and Researchers and the procurement of high-cost research equipment grant” (Project 1552 CIRCE), funding from a Marie Curie Action of the European Union (grant agreement No. 101107047), and from the Foundation of Research and Technology - Hellas Synergy Grants Program through project MagMASim, jointly implemented by the Institute of Astrophysics and the Institute of Applied and Computational Mathematics. K.T. acknowledges support from the Foundation of Research and Technology – Hellas Synergy Grants Program through project POLAR, jointly implemented by the Institute of Astrophysics and the Institute of Computer Science. This work was supported by NSF grant AST-2109127. S.M. would like to thank Anna Steiakaki for providing careful comments and corrections to the various drafts of the manuscript. This work utilized the open source software packages Astropy (Astropy Collaboration 2013, 2018), Numpy (Harris et al. 2020, Scipy (Virtanen et al. 2020), Matplotlib (Hunter 2007) and Jupyter notebook (Kluyver et al. 2016).
Appendix A Polarimetric measurement plots of all patches
Figures A.1 and A.2 show the measured polarizations and flatness in the q − u plane for patches 2 to 19.
 |
Fig. A.1 Polarimetric measurements for patches 2 to 10, with details similar to those in Fig. 4. Yellow crosses represent the q and u values for all the individual pointing for a patch. The overall mean value and the measured standard deviation (black cross) are noted in legend at the top-left. |
 |
Fig. A.2 Polarimetric measurements for patches 11 to 19, similar to Fig. 4. Yellow crosses represent the q and u values for all the individual pointing for a patch. The overall mean value and the measured standard deviation (black cross) are mentioned in the legend at the top left. |
References
- Anche, R. M., Maharana, S., Ramaprakash, A. N., et al. 2022, SPIE, 12188, 121882C [NASA ADS] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A & A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Blinov, D., Kiehlmann, S., Pavlidou, V., et al. 2020, MNRAS, 501, 3715 [Google Scholar]
- Blinov, D., Maharana, S., Bouzelou, F., et al. 2023, A & A, 677, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, L., Sipocz, B., Robitaille, T., et al. 2020, https://doi.org/10.5281/zenodo.4044744 [Google Scholar]
- Clemens, D. P., Sarcia, D., Grabau, A., et al. 2007, PASP, 119, 1385 [NASA ADS] [CrossRef] [Google Scholar]
- Covino, S., Smette, A., & Snik, F. 2020, https://doi.org/10.5281/zenodo.3906379 [Google Scholar]
- Gál, J., Horváth, G., Barta, A., & Wehner, R. 2001, J. Geophys. Res. Atmos., 106, 22647 [CrossRef] [Google Scholar]
- González-Gaitán, S., Mourão, A. M., Patat, F., et al. 2020, A & A, 634, A70 [CrossRef] [EDP Sciences] [Google Scholar]
- Harrington, D. M., Kuhn, J. R., & Hall, S. 2011, PASP, 123, 799 [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hough, J. 2006, Astron. Geophys., 47, 3.31 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kawabata, K. S., Nagae, O., Chiyonobu, S., et al. 2008, SPIE, 7014, 1585 [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Powerin Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Scmidt (Amsterdam: IOS Press), 87 [Google Scholar]
- Magalhães, A. M., de Oliveira, C. M., Carciofi, A., et al. 2012, AIP Conf. Proc., 1429, 244 [CrossRef] [Google Scholar]
- Maharana, S., Kypriotakis, J. A., Ramaprakash, A. N., et al. 2020, SPIE, 11447, 1135 [Google Scholar]
- Maharana, S., Kypriotakis, J. A., Ramaprakash, A. N., et al. 2021, J. Astron. Teles. Instrum. Syst., 7, 1 [CrossRef] [Google Scholar]
- Maharana, S., Anche, R. M., Ramaprakash, A. N., et al. 2022, J. Astron. Teles. Instrum. Syst., 8, 038004 [NASA ADS] [CrossRef] [Google Scholar]
- Pelgrims, V., Panopoulou, G. V., Tassis, K., et al. 2023, A & A, 670, A164 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piirola, V., Berdyugin, A., & Berdyugina, S. 2014, SPIE, 9147, 2719 [Google Scholar]
- Potter, S. B., Nordsieck, K., Romero-Colmenero, E., et al. 2016, SPIE, 9908, 810 [Google Scholar]
- Ramaprakash, A. N., Gupta, R., Sen, A. K., & Tandon, S. N. 1998, A & AS, 128, 369 [NASA ADS] [Google Scholar]
- Ramaprakash, A. N., Rajarshi, C. V., Das, H. K., et al. 2019, MNRAS, 485, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Scarrott, S. 1991, Vistas Astron., 34, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Skalidis, R., Panopoulou, G. V., Tassis, K., et al. 2018, A & A, 616, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, G. S. 2007, Am. J. Phys., 75, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Strutt, H. J. 1871, Lond. Edinb. Dublin Philos. Mag. J. Sci., 41, 107 [CrossRef] [Google Scholar]
- Tassis, K., Ramaprakash, A. N., Readhead, A. C. S., et al. 2018, ArXiv e-prints [arXiv:1810.05652] [Google Scholar]
- Tinyanont, S., Millar-Blanchaer, M. A., Nilsson, R., et al. 2018, PASP, 131, 025001 [Google Scholar]
- Trippe, S. 2014, J. Korean Astron. Soc., 47, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wolstencroft, R. D., & Bandermann, L. W. 1973, MNRAS, 163, 229 [CrossRef] [Google Scholar]
All Tables
Instrumental zero polarization of RoboPol during the observation runs (Blinov et al. 2023).
All Figures
 |
Fig. 1 Simulated polarization for a 10 × 10 arcminutes2 patch at a distance of 15.5° from the Moon based on a single-layer Rayleigh scattering model to describe the atmosphere. In this example, the coordinates of the Moon are (RA = 0°, Dec = 0°), while the patch is centered at (RA = 11.0°, Dec = 11.0°) in the geocentric celestial reference system (GCRS) coordinate system. |
| In the text | |
 |
Fig. 2 central region of RoboPol used for making the measurements. Four images of the source, corresponding to 0°, 45°, 90° and 135° polarization are formed simultaneously at the CCD and differential photometry of the two pairs of images yields the Stokes parameters q and u. The apertures used for the photometry of the four channels are marked in black circles. The color bar indicates the counts in ADUs for the exposure. |
| In the text | |
 |
Fig. 3 Nominal pointing positions for patches 1−11 (panel a). The overall size of the patch is 10 × 10 arcminutes2. Nominal pointing positions for patches 12−19 (panel b). The overall size of the patch is 4.8 × 7.5 arcminutes2. Patches 1−11 and 12−19 were observed with RoboPol through a rectangular grid of either 6 × 6 or 5 × 4 pointing coordinates, respectively, in the sequence marked in the images. Due to the motion of the Moon in the sky, the shape of the grid with respect to the Moon is distorted, depending on the sequence of observations followed. For patch 10, the grid points are spread across a region of 21.8 × 4.3 arcminutes2 (panel c). Patches 1 to 11 have similar pattern, and their geometrical extant is noted in Table 1. For patch 18, the grid points are spread across a region of 19.5 × 11 arcminutes2 (panel d). Patches 12 to 19 have similar pattern, and their geometrical extents are noted in Table 1. |
| In the text | |
 |
Fig. 4 Measured q and u values for all the pointing for patch 1 (yellow crosses) as well as the overall mean value and the measured standard deviation (black cross), whose values are mentioned in the top left legend. The median individual errors in the bottom left legend refer to the median of expected errors in the Stokes parameters owing to photon noise across the grid points. The value of the degree of linear polarization, p, is presented without any correction for polarimetric bias; p is calculated for each grid point and then their mean and variance are found, similar to q and u. |
| In the text | |
 |
Fig. A.1 Polarimetric measurements for patches 2 to 10, with details similar to those in Fig. 4. Yellow crosses represent the q and u values for all the individual pointing for a patch. The overall mean value and the measured standard deviation (black cross) are noted in legend at the top-left. |
| In the text | |
 |
Fig. A.2 Polarimetric measurements for patches 11 to 19, similar to Fig. 4. Yellow crosses represent the q and u values for all the individual pointing for a patch. The overall mean value and the measured standard deviation (black cross) are mentioned in the legend at the top left. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


