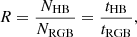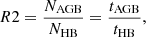| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202346382 | |
| Published online | 09 November 2023 | |
Impact of the uncertainties of 3α and 12C(α, γ)16O reactions on the He-burning phases of low- and intermediate-mass stars
1
Dipartimento di Fisica “Enrico Fermi”, Università di Pisa, Largo Pontecorvo 3, 56127 Pisa, Italy
e-mail: valle@df.unipi.it
2
INFN, Sezione di Pisa, Largo Pontecorvo 3, 56127 Pisa, Italy
Received:
11
March
2023
Accepted:
4
September
2023
Aims. We aim to estimate the impact on the stellar evolution of the uncertainties in the 3α and the 12C(α, γ)16O reaction rates, taking into account the recent improvements in their precision.
Methods. We calculated models of low- and intermediate-mass stars for different values of 3α and 12C(α, γ)16O reaction rates. The 3α reaction rate was varied up to ±24% around the reference value, while the 12C(α, γ)16O reaction rate was varied by up to ±35%, taking into account different recent values for these quantities available in the literature. The models were calculated with the FRANEC evolutionary code for two different initial chemical compositions, namely, Y = 0.246, Z = 0.0001, and Y = 0.28, Z = 0.015 to represent different stellar populations. A M = 0.67 M⊙ model was chosen as representative of the first class (halo ancient stars), while for the second composition (disk stars), the M = 1.5 M⊙ and M = 2.5 M⊙ models were considered. The impact of 3α and 12C(α, γ)16O reaction rates on the central He-burning lifetime and the asymptotic giant branch (AGB) lifetime, as well as the mass of the C/O core at the central He exhaustion and the internal C and O abundances, was investigated.
Results. A variation of the 12C(α, γ)16O reaction rates within its nominal error resulted in marginal differences in the analysed features among the three considered stellar masses, except for the C/O abundances. The central He-burning lifetime changed by less than 4%, while the AGB lifetime was affected only at the 1% level. The internal C and O abundances showed greater variation, with a change of about 15%. The uncertainty in the 3α reaction rate mainly influences the C and O central abundances (up to 10%) for all the models considered, and the AGB lifetime for intermediate mass stars (up to 5%). Most of the investigated features were affected by less than 2%.
Conclusions. The current uncertainty in the explored reaction rates has a negligible effect on the predicted evolutionary time scale with respect to other uncertainty sources. On the other hand, the variability in the chemical profile left at the end of the shell He-burning phase is still relevant. We also checked that there is no interaction between the effects of the two reaction rates, as would be expected in the case of small perturbations.
Key words: stars: evolution / stars: abundances / stars: fundamental parameters / methods: statistical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Nuclear reactions are the primary source of energy production in stars and determine the evolution of a star’s chemical composition. Since most nuclear reactions occur in stellar interiors at lower energies than those accessible in the laboratory, their cross-sections are generally extrapolated from the data obtained at higher energies. Thus, depending on the nuclear reaction and the characteristics of the involved nuclei, the rate can be affected by a non-negligible uncertainty, which influences the evolutionary features.
In advanced stellar evolutionary phases, starting from central He ignition throughout the central and shell He-burning phases, the 3α and 12C(α, γ)16O reactions compete for energy production. Therefore, they directly affect the evolutionary characteristics of stars, such as the central and shell He-burning lifetimes, the chemical profile of the star, and the CO core mass at central He exhaustion and at the end of the shell He-burning phase. Furthermore, for low- and intermediate-mass stars, a stellar chemical profile variation also alters the subsequent evolutionary characteristics, particularly with respect to the white dwarf (WD) cooling time (Prada Moroni & Straniero 2002, 2007; Straniero et al. 2003; Salaris et al. 2010; Althaus et al. 2010), as well as impacting WD g-mode pulsation periods (De Gerónimo et al. 2017; Chidester et al. 2022).
Due to their importance for He-burning and later stages, the 3α and 12C(α, γ)16O reactions have been studied throughout the years to obtain more precise estimates of their rates. The 3α reaction rate is dominated by the presence of an excited state with Jπ = 0+ at an energy of about 7.6 MeV, which increases the capture process by a factor of 10–100 million (Freer & Fynbo 2014). One of the most frequently used rates in evolutionary codes was calculated by the NACRE collaboration (Angulo 1999) with an uncertainty of about 25% at He-burning temperatures. More recently, the rate estimate was refined by Fynbo et al. (2005), with an error of about 12% at central He-burning temperature (≈108 K). This 3α value generally agrees with other estimates of the rate, although Kibédi et al. (2020) recently reported a value that differs from current estimates by about 34%.
On the other hand, determining the 12C(α, γ)16O rate is far more complex. Because of the compound structure of 16O, the astrophysical S factor is dominated by broad resonances which interfere with each other and with few narrow resonances superposed upon them (deBoer et al. 2017). Thus, the estimated cross-section for this reaction has always been characterised in the past by a great uncertainty, which, however, decreased during the years. The cross-section error decreased from a factor of 2 at the end of the 1990s (Caughlan et al. 1985; Caughlan & Fowler 1988) down to the 35% figure reported by Kunz et al. (2002), and then 30% by Hammer et al. (2005). A recent estimate of the 12C(α, γ)16O was proposed by deBoer et al. (2017), with an associated uncertainty of about 20% at central He-burning temperature.
A series of studies has provided a discussion of the impact of the uncertainties in the 3α and the 12C(α, γ)16O reaction rates on the stellar evolution over the years (e.g. Caughlan et al. 1985; Cassisi et al. 2001; Straniero et al. 2003; Weiss et al. 2005; Dotter & Paxton 2009; Valle et al. 2013; Fields et al. 2016; De Gerónimo et al. 2017; Pepper et al. 2022). The aim of the present paper is to investigate how the recent improvements in the precision of the reaction rates affect the results reported in the existing literature. The effects on the evolutionary characteristics of the 3α and the 12C(α, γ)16O reaction rate changes, within the current uncertainties, were analysed separately for each reaction. We also discuss a set of results obtained by varying simultaneously the two rates at their upper and lower boundaries to investigate the presence of interactions between the effects of the two reaction rates.
2. Methods
To analyse the effects of the present uncertainties on the studied reactions, models of low and intermediate mass stars were calculated for different values of 3α and 12C(α, γ)16O reaction rates.
As a reference, we adopted the 3α reaction rate by Fynbo et al. (2005) and the 12C(α, γ)16O reaction rate by deBoer et al. (2017). Additional models were computed with the analysed reaction rates varied within their errors. The 3α reaction rate was varied up to ±24%, which is about the double of the uncertainty by Fynbo et al. (2005) the Kibédi et al. (2020) +34% variation has also been taken into account. The 12C(α, γ)16O reaction rate was varied by up to ±35%, the uncertainty associated with the Kunz et al. (2002) estimate, which is widely used in the literature. This choice is dictated by the fact that the recent high precision data on the 12C(α, γ)16O cross-section by deBoer et al. (2017) are still somehow debated in the literature (see Smith et al. 2021 for more details). The values of the reaction rates were changed one by one since, for a small variation in the input physics, we do not expect correlation effects on the model results, as previously discussed in the literature (e.g. Valle et al. 2013). However, we explicitly tested this assumption by performing computations that simultaneously varied the two rates at their upper and lower boundaries. The results, presented in Appendix A, support this claim. Therefore, any combination of the joint impact of the two reaction rate uncertainties can be obtained by a simple sum of the effects of the individual rates.
The models were calculated with the FRANEC evolutionary code in the same configuration as in the paper by Dell’Omodarme et al. (2012), which includes a complete description of the adopted input physics. Here, we discuss only the input relevant to a comparison with recent results.
Models were computed without core overshooting, adopting the Schwarzschild criterion to define convective boundaries; furthermore, instantaneous mixing was assumed in convective regions. Semiconvection during the central He-burning phase was treated following the numerical scheme described in Castellani et al. (1985). Breathing pulses were suppressed (Cassisi et al. 2001; Constantino et al. 2017) following the procedure adopted in Dell’Omodarme et al. (2012).
H-burning reaction rates were obtained from the NACRE database (Angulo 1999) with the exception of the pp and the 14N(p, γ)15O reaction rates, which are from Marcucci et al. (2019) and the LUNA collaboration (Imbriani et al. 2005), respectively.
Models were calculated for two different initial chemical compositions. The first one (Y = 0.246 and Z = 0.0001) is typical of ancient low mass stars populating the halo of our Galaxy, while the other (Y = 0.28 and Z = 0.015) characterises stars in the Galactic disk. Different stellar ages and mass ranges were considered in the two scenarios. A star with M = 0.67 M⊙ during the He-burning phases, with a 0.8 M⊙ mass star as a progenitor, was chosen to represent ancient stars with a halo chemical composition. Regarding intermediate mass stars, M = 1.5 M⊙ and M = 2.5 M⊙ stars with disk chemical composition have been taken as reference. The 2.5 M⊙ star is assumed to be in the typical mass range of progenitors of 0.55 − 0.6 M⊙ white dwarfs, which are at the peak of the field WD mass distribution (Prada Moroni & Straniero 2007; Salaris & Cassisi 2008).
3. Effect of the 12C(α, γ)16O reaction rate uncertainties
The 12C(α, γ)16O reaction is fundamental for stellar nucleosynthesis and evolution during the He-burning phases; unlike the 3α-burning, the 12C(α, γ)16O reaction only affects the evolutionary characteristics after the central He ignition.
The analysis focuses on the following: the central He-burning lifetime (tHB), defined as the time from the onset of He-burning until when the central He abundance drops below 10−6; the asymptotic giant branch (AGB) lifetime (tAGB), defined as the time from the central He exhaustion and the first thermal pulse; the central C and O abundances at the central He exhaustion. Central carbon and oxygen abundances, which do not change during the AGB evolution, are particularly relevant because they also affect the white dwarf evolution, including their pulsation properties (De Gerónimo et al. 2017; Chidester et al. 2022). To explore the impact on the stellar evolution of such a variation, we also investigated the chemical profile at the first thermal pulse.
The results are shown in Table 1 for the three different masses discussed in Sect. 2. Overall, only marginal differences were detected in the relative impact of the reaction rate variations among the three considered stellar masses.
Impact of the uncertainty in the 12C(α, γ)16O reaction rate for the three considered stellar masses.
Regarding the He-burning lifetime, the increase in the 12C(α, γ)16O reaction rate enhances tHB by few percents. This is expected because 3α and 12C(α, γ)16O are the only reactions which contribute to the energy production in the core during the central He-burning phase. In fact, the total stellar energy production is fixed to balance the stellar radiative losses from the surface, so decreasing or increasing one of the two rates influences the relative efficiency of the two reactions. The 3α burns three He nuclei per reaction, while for each 12C(α, γ)16O reaction, only one α particle is consumed. At fixed stellar luminosity, an increase in the 12C(α, γ)16O cross-section enhances the relative contribution of the reaction to the energy production. This reduces the He consumption rate, while more carbon is burned as a result; thus, the central He-burning lifetime increases. Overall, the variation induced by the 12C(α, γ)16O uncertainty in tHB is quite negligible; namely, it s lower than other uncertainty sources, as we discuss in Sect. 5.
A change in the 12C(α, γ)16O reaction rate also impacts the chemical composition of the whole region inside the He shell and of the region affected by semi-convective mixing at central He exhaustion and at the first thermal pulse. At the central He exhaustion, the abundances of carbon and oxygen in the core and in the semi-convective region are significantly modified, while the remaining external parts of the previous He core remain unchanged. As expected, increasing (decreasing) the 12C(α, γ)16O reaction rate decreases (increases) the remaining 12C abundance. The greater the variation in the rate, the higher the change in the abundances. The carbon and oxygen central abundances are significantly affected by the changes in the 12C(α, γ)16O reaction rate, with a maximum variation between −22% and +34% in 12C and between +15% and −21% in 16O. Then the He-burning continues in shell during the AGB phase. The effect of different 12C(α, γ)16O rates on the chemical profile at the first thermal pulse can be seen in Fig. 1. This modification has a relevant impact on stellar nucleosynthesis and also mildly affects the AGB evolution. Moreover, the variation of the chemical composition influences the cooling time of the stars in the following white dwarf phase (see e.g. Prada Moroni & Straniero 2002, 2007; Straniero et al. 2003; Salaris et al. 2010, 2013, 2022); a precise knowledge of the chemical profile of the progenitor star is of fundamental importance to the understanding of the thermal capacity of the stellar matter and, thus, how cooling carries on. This has, in turn, consequences on the globular cluster or galactic disk and halo age determinations through the comparison between theory and observation for the white dwarf cooling sequence (Prada Moroni & Straniero 2002, 2007; Straniero et al. 2003; Salaris et al. 2010; Hansen et al. 2013; García-Berro et al. 2014; Kilic et al. 2019; Prišegen et al. 2021).
 |
Fig. 1. Profile of 4He, 12C and 16O abundances at the first thermal pulse as a function of mass fraction. Left: profile obtained by increasing (dashed lines) and decreasing (dot dashed lines) the 12C(α, γ)16O reaction rate by 20%. The continuous lines correspond to the data obtained with the standard rate. The green lines represent the abundance of 4He, the orange lines the one of 12C, and the purple lines the one of 16O. Right: same as in the left panel but for a rate variation of ±35%. |
Finally, tAGB is only mildly affected, at the level of few percents. As discussed in Bossini et al. (2015) and Cassisi (2014), an increase in the extension of the central He-burning convective region, and thus of the 12C/16O core mass at the central He exhaustion, reduces the AGB lifetime, since the He shell forms closer to the H shell. Increasing the 12C(α, γ)16O reaction rate enhances, even if very slightly, the 12C/16O core mass at the central He exhaustion and thus the AGB lifetime is slightly reduced. Other quantities such as the luminosity of the AGB clump or the 12C/16O core mass at the first thermal pulse are practically unaffected by a change within the present errors of the 12C(α, γ)16O reaction rate, with variations lower than 1%.
The effects of varying the 12C(α, γ)16O reaction rates have been extensively studied in the literature, mainly when the related uncertainty was quite large. As an example, the error of the 12C(α, γ)16O reaction rate was of a factor of 2 at the beginning of the 90s of the last century (Caughlan et al. 1985; Caughlan & Fowler 1988). From the results reported in Cassisi et al. (2001) and Imbriani et al. (2001), for stars of 0.75 − 0.8 M⊙, one can see that a change of this order of magnitude in the reaction rate produces a variation in tHB by about 10%, while the change in 12C and 16O abundances is about 60% and 40%, respectively, in agreement with our results. The data obtained for the 2.5 M⊙ are also consistent with the present literature. From the results obtained by Fields et al. (2016) and Straniero et al. (2003), it is apparent that our data follow the same trend with the 12C(α, γ)16O reaction rate, with comparable percentage variations. A relevant comparison is with the results recently reported by Pepper et al. (2022) who investigate the impact of different 12C(α, γ)16O reaction rates in several stellar evolutionary phases. Their analysis adopts MESA tracks, computed under different assumptions about diffusion, treatment of semi-convection, and suppression of breathing pulses with respect to those adopted in our tracks. Among the explored rates, Pepper et al. (2022) adopted NACRE values, assuming an uncertainty of 32%, very similar to the 35% adopted here. Their mass ranges overlap with our M = 1.5 M⊙ and M = 2.5 M⊙ models, allowing for a direct comparison. It is however important to consider that the models were computed assuming a different rate functional form, because we adopted deBoer et al. (2017) results as our reference; thus, at different metallicity, the impact of these differences cannot be correctly accounted for.
Regarding the C/O ratio at the central He exhaustion Pepper et al. (2022) report 0.520, varying in the range (0.310; 0.977), and 0.492 (0.289; 0.935) for M = 1.5 and 2.5 M⊙, respectively. For comparison, we obtained 0.625 (0.418; 1.06) and 0.551 (0.359; 0.941). While the results are quite similar for M = 2.5 M⊙, there is a non-negligible offset for the 1.5 M⊙ model. However, the spanned range is similar.
Pepper et al. (2022) also investigated on the difference in tHB reporting variations within the ranges of (−6.6; 3.8) Myr and (−6.5; 3.5) Myr for 1.5 and 2.5 M⊙, respectively. Our results for the two considered stellar masses are in the range (−4.2; 2.9) Myr and (−5.9; 4.3) Myr. Also, in this case, the results show a better agreement for the more massive star, the difference in the range width for the lightest one being about 50%.
A change in the 12C(α, γ)16O reaction rate also affects the theoretical estimate of two observational parameters, the R and R2 parameters. The former is defined as
where NHB is the number of stars in the horizontal branch and NRGB is the number of stars in the red giant branch (RGB) with a luminosity greater than the zero-age horizontal branch (ZAHB). As described in Cassisi et al. (2003), it is possible to estimate the R parameter via theoretical models, as in Eq. (1), where tHB is the He-burning lifetime from the ZAHB to central He exhaustion, while tRGB is the life time of the star during the RGB from the point in which the luminosity is higher than the ZAHB; for the ZAHB luminosity, we can assume the luminosity of its horizontal portion. The R parameter is the most important indirect indicator for the original He abundance in globular cluster stars; however to appropriately use this parameter, a precise evaluation of the associated uncertainty is mandatory.
The R2 parameter is defined as:
that is as the ratio between the number of stars in the AGB phase (NAGB) and in the horizontal branch phase (NHB). As described in Buonanno et al. (1985), the R2 parameter can be calculated in theoretical models with the ratio between the AGB lifetime and the HB lifetime. Thus, its theoretical estimate is affected by the changes in both tHB and tAGB.
A precise knowledge of the uncertainty related to this parameter is fundamental because it is particularly useful to obtain information on mixing processes during the central He-burning phase. For example, the study of the R2 parameter was used to determine if breathing pulses are numerical artifacts in evolutionary codes or a real process during stellar evolution(see also Buonanno et al. 1985; Cassisi et al. 2003).
Table 2 reports the theoretical values of the R and R2 parameters obtained for a 0.67 M⊙ for the selected 12C(α, γ)16O reaction rate values. The effect is only few percents, which is significantly lower than the current observational uncertainty that are affected by the errors in star counts (about 30%; for more details see Constantino et al. 2015 or Cassisi et al. 2003). Thus, at the present level of precision, the 12C(α, γ)16O reaction rate no longer constitutes a relevant error source for the theoretical estimation of R and R2 parameters.
R and R2 parameters for different 12C(α, γ)16O reaction rates.
4. Effect of the 3α reaction rate uncertainties
Stellar models were computed assuming 3α reaction rate variations of ±12% (the present uncertainty for the 3α reaction rate from Fynbo et al. 2005; Freer & Fynbo 2014), ±24% (2σ variation) and +34%. The latter is related to the data discussed in Kibédi et al. (2020).
Thus, in addition to the evolutionary characteristics investigated for the 12C(α, γ)16O reaction rate, we studied also the effect of the 3α on the He core mass, stellar age, and luminosity at the RGB tip, and the ZAHB characteristics. The results are reported in Table 3 for the three selected models.
At the end of the RGB evolutionary phase low mass stars ignite He in an electron degenerate core, at the RGB tip. The luminosity at He ignition is directly related to the He core mass, which depends on the temperature needed to activate the 3α reaction; thus, it depends on the 3α reaction rate itself. An increase (decrease) of 3α reaction rate corresponds to a slightly lower (greater) temperature required to activate the reaction and to a reduced (enhanced) He core mass at the RGB tip (see e.g. Valle et al. 2013).
As can be seen in Table 3 the change in MHe is quite negligible, with a maximum variation of between −0.5% and 0.4%. This produces a negligible change in the luminosity of the star at the RGB tip and at the ZAHB (see Fig. 2), with a maximum change below 0.3%. Furthermore, the stellar age at the RGB tip is unchanged, with a variation of about 0.001%, in agreement with the results by Valle et al. (2013).
 |
Fig. 2. Zero-age horizontal branch for different values of the 3α reaction rate. |
The effect on the central He-burning lifetime of the 3α reaction variation is quite small, with a maximum of about 1% for all the selected values, lower than the effect due to changes of the 12C(α, γ)16O rate. For the 0.67 M⊙ a variation of −12% in the rate reduces tHB more than a change of −24%; this is connected to the breathing pulses treatment. The start of breathing pulses is directly related to the He central abundance, therefore, changing the rate at which He is burned affects the time at which breathing pulses start, and their length. This change of about 1% in tHB is the typical variation associated with the 3α reaction rate in the literature (see e.g. Weiss et al. 2005).
The chemical profiles of the stars at the first thermal pulse are significantly affected by variations of 3α reaction rate, as shown in Fig. 3. As expected, a variation of the 3α reaction rate influences the carbon and oxygen abundances inside the 12C/16O core, in the region which experienced semi-convection and all the zones affected by the He-burning shell. Increasing (decreasing) the 3α reaction rate enhances (reduces) the 12C abundance while the 16O one lowers (grows). The change in 12C and 16O central abundances is generally smaller (about 60%) than the one that is due to the 12C(α, γ)16O rate variation.
 |
Fig. 3. Profiles of 4He, 12C, and 16O abundances at the first thermal pulse as a function of mass fraction. Left: profiles obtained increasing (dashed lines) and decreasing (dot-dashed lines) the 3α reaction rate by 12%. The continuous lines correspond to the data obtained with the standard rate. The green lines represent the abundance of 4He, the orange ones the abundance of 12C, and the purple lines the one of 16O. Right: same as in the left panel, but for a 3α reaction rate variation by ±24% and +34% (dotted lines). |
The 3α reaction rate also affects the evolutionary time during the AGB phase. Increasing the 3α reaction rate enhances tAGB because the 12C/16O core lowers in mass. The change in tAGB with the 3α reaction rate increases with the stellar mass, with a maximum variation of about 5% for the 2.5 M⊙ mass star. The 3α reaction rate also affects the evolutionary time at the first thermal pulse (tHB + tAGB) with a change similar to the central He-burning lifetime because tAGB is almost an order of magnitude lower than tHB. Lastly, the 12C/16O core mass and the luminosity of the AGB clump are marginally affected by a change in the 3α reaction rate, with a maximum variation lower than 1%.
The impact of a 3α reaction rate variation was analysed in the literature mainly when the uncertainties were higher. The results of Weiss et al. (2005) or Valle et al. (2013) show that for low mass stars, a variation of about 20% produces an almost negligible effect on the evolutionary characteristics at He ignition (Ltip, LZAHB) with respect to other uncertainty sources in evolutionary models (mainly the radiative opacity); furthermore, the obtained variations for the analysed quantities are comparable to the ones presented here.
As for the 12C(α, γ)16O reaction rate, the effect of changing the 3α reaction rate on the theoretical determination of the R and R2 parameters was assessed. As reported in Table 4, the variation in the two parameters is about ±2%, which is lower than both the effect due to the uncertainty of the 12C(α, γ)16O rate and the observational errors, making the effect quite negligible.
5. Conclusions
In this work, we analyse the effect on the evolutionary characteristics of He-burning stars of the present uncertainty on the 3α and 12C(α, γ)16O reaction rates. The 3α and 12C(α, γ)16O are competing reactions for central and shell He-burning; thus, they affect several stellar characteristics in these phases. Particularly, they are known to influence the He-burning lifetimes and, more significantly, the carbon and oxygen abundance profile, which, in turn, influences the subsequent WD evolution. Because the uncertainties in these two reaction rates have been considerably reduced over the years, it is important to quantitatively evaluate the present scenario.
We adopted as reference for the 12C(α, γ)16O reaction rate the value proposed by deBoer et al. (2017), with a quoted uncertainty of 20% at He-burning temperatures, and for the 3α the rate estimate by Fynbo et al. (2005), with a nominal 12% error. Stellar models were computed adopting a 3α reaction rate changed up to about ±2σ; we also considered a value of +34%, from the recent measurements by Kibédi et al. (2020). The 12C(α, γ)16O rate was modified up to ±35%, arising from the estimate by Kunz et al. (2002).
The two reaction rates were varied independently to study how they affect the evolution of three stellar models: a low mass star (0.67 M⊙, Y = 0.246, Z = 0.0001) with a 0.8 M⊙ as a progenitor, (representative of halo stars) and two intermediate mass models, 1.5 M⊙ and 2.5 M⊙ (Y = 0.28, Z = 0.015), with a chemical composition that is typical of disk stars. We also explicitly verified that the uncertainty related to the two reactions propagate independently of the stellar evolution.
Regarding the 12C(α, γ)16O reaction rate, the present uncertainties marginally affect most of the analysed evolutionary characteristics. The central He-burning lifetime changes by ∼2% for a rate variation of ±20%, and by ∼4% for a change of ±35%. The AGB lifetime is affected only at the order of 1%. This variation in the evolutionary times affects the theoretical estimate of two important observables for globular clusters, the R and R2 parameters, up to 3% and 4%, respectively, for a ±35% change of the reaction rate. On the other hand, the star’s chemical profile up to the first thermal pulse is still significantly affected. The 12C central abundance is modified between 13% and 18%, depending on the mass of the star, for a variation of the 12C(α, γ)16O reaction rate by ±1σ. Similarly, the 16O central abundance is affected at the order of 10% for the same 12C(α, γ)16O rate change (±20%).
The present uncertainty of the 3α reaction rate mainly influences the carbon and oxygen central abundances for all the considered models and the AGB lifetime, tAGB, for intermediate mass stars. For low-mass stars, the quantities at He ignition, namely, the He core mass, the luminosity of the RGB tip, and the luminosity of the ZAHB are all affected for less than 1%. In the case of the 0.67 M⊙ and 1.5 M⊙, the central He-burning lifetime and the AGB lifetime vary less than 1% and 2%, respectively, for a 1σ variation in the reaction rate; on the other hand a change in the 3α reaction rate produces a noticeable effect on the tAGB of the 2.5 M⊙. The carbon and oxygen central abundances at the first thermal pulse change between 5% and 6% for 12C, and between 3% and 4% for 16O, when the 3α is varied by 1σ. The extreme rate variation of +34% affects the central carbon abundance by +15% and the oxygen one by −9%.
It is worth noting that different methods of treating convective mixing during the central He-burning phase are adopted in the literature. They influence the evolutionary characteristics of stars, particularly the evolutionary times. As reported, for instance, by Constantino et al. (2015) and Straniero et al. (2003), depending on the mixing scheme the HB evolutionary time can change by about 4%, making the effect more significant than the one due to both the 3α and 12C(α, γ)16O reaction rate uncertainties, if the present errors are considered.
On the other hand, the uncertainty of the chemical profile related to the treatment of convection is still comparable with the one due to the errors of the two reaction rates. The chemical profile at the end of the shell He-burning phase influences the WD cooling sequence, particularly the cooling time, and WD g-modes pulsation periods (De Gerónimo et al. 2017; Chidester et al. 2022). As an example, a change in the 12C(α, γ)16O reaction rate of about ±35% can affect the WD cooling time between 7% and 3% depending on the numerical prescriptions adopted to calculate the evolution; this is an effect that is still relevant with respect to other uncertainty sources in this phase, (see e.g. Salaris et al. 2010). Further investigations are needed to analyse in detail the effects of the present uncertainties of the 3α and 12C(α, γ)16O rates on the WD evolution of low- and intermediate-mass stars.
Acknowledgments
G.V., P.G.P.M., and S.D. acknowledge INFN (Iniziativa specifica TAsP).
References
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C. 1999, in Experimental Nuclear Physics in europe: Facing the next millennium, AIP Conf. Ser., 495, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Bossini, D., Miglio, A., Salaris, M., et al. 2015, Eur. Phys. J. Web Conf., 101, 06012 [CrossRef] [EDP Sciences] [Google Scholar]
- Buonanno, R., Corsi, C. E., & Fusi Pecci, F. 1985, A&A, 145, 97 [NASA ADS] [Google Scholar]
- Cassisi, S. 2014, EAS Pub. Ser., 65, 17 [Google Scholar]
- Cassisi, S., Castellani, V., Degl’Innocenti, S., Piotto, G., & Salaris, M. 2001, A&A, 366, 578 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassisi, S., Salaris, M., & Irwin, A. W. 2003, ApJ, 588, 862 [Google Scholar]
- Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tables, 40, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Caughlan, G. R., Fowler, W. A., Harris, M. J., & Zimmerman, B. A. 1985, At. Data Nucl. Data Tables, 32, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Chidester, M. T., Farag, E., & Timmes, F. X. 2022, ApJ, 935, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [Google Scholar]
- Constantino, T., Campbell, S. W., & Lattanzio, J. C. 2017, MNRAS, 472, 4900 [NASA ADS] [CrossRef] [Google Scholar]
- De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2017, A&A, 599, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- deBoer, R. J., Görres, J., Wiescher, M., et al. 2017, Rev. Mod. Phys., 89, 035007 [NASA ADS] [CrossRef] [Google Scholar]
- Dell’Omodarme, M., Valle, G., Degl’Innocenti, S., & Prada Moroni, P. G. 2012, A&A, 540, A26 [CrossRef] [EDP Sciences] [Google Scholar]
- Dotter, A., & Paxton, B. 2009, A&A, 507, 1617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fields, C. E., Farmer, R., Petermann, I., Iliadis, C., & Timmes, F. X. 2016, ApJ, 823, 46 [CrossRef] [Google Scholar]
- Freer, M., & Fynbo, H. O. U. 2014, Prog. Part. and Nucl. Phys., 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, H. O. U., Diget, C. A., Bergmann, U. C., et al. 2005, Nature, 433, 136 [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., & Miller Bertolami, M. M. 2014, A&A, 571, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammer, J. W., Fey, M., Kunz, R., et al. 2005, Nucl. Phys., Sect. A, 752, 514 [CrossRef] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Limongi, M., Gialanella, L., et al. 2001, ApJ, 558, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [Google Scholar]
- Kibédi, T., Alshahrani, B., Stuchbery, A. E., et al. 2020, Phys. Rev. Lett., 125, 182701 [CrossRef] [PubMed] [Google Scholar]
- Kilic, M., Bergeron, P., Dame, K., et al. 2019, MNRAS, 482, 965 [Google Scholar]
- Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [CrossRef] [Google Scholar]
- Marcucci, L. E., Schiavilla, R., & Viviani, M. 2019, Phys. Rev. Lett., 123, 019901a [NASA ADS] [CrossRef] [Google Scholar]
- Pepper, B. T., Istrate, A. G., Romero, A. D., & Kepler, S. O. 2022, MNRAS, 513, 1499 [NASA ADS] [CrossRef] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [CrossRef] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2007, A&A, 466, 1043 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prišegen, M., Piecka, M., Faltová, N., Kajan, M., & Paunzen, E. 2021, A&A, 645, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., & Cassisi, S. 2008, Evolution Of Stars and Stellar Populations (Wiley), 49 [Google Scholar]
- Salaris, M., Cassisi, S., Pietrinferni, A., Kowalski, P. M., & Isern, J. 2010, ApJ, 716, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Cassisi, S., Pietrinferni, A., & Hidalgo, S. 2022, MNRAS, 509, 5197 [Google Scholar]
- Smith, R., Gai, M., Stern, S. R., Schweitzer, D. K., & Ahmed, M. W. 2021, Nat. Commun., 12, 5920 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O., Domínguez, I., Imbriani, G., & Piersanti, L. 2003, ApJ, 583, 878 [NASA ADS] [CrossRef] [Google Scholar]
- Valle, G., Dell’Omodarme, M., Prada Moroni, P. G., & Degl’Innocenti, S. 2013, A&A, 549, A50 [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., Serenelli, A., Kitsikis, A., Schlattl, H., & Christensen-Dalsgaard, J. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Joint effect of 3α and 12C(α, γ)16O reaction rates
This appendix presents some results obtained by varying simultaneously the two rates at their upper (label hh in Table A.1) and lower (label ll) boundary. Thus, hh corresponds to a 12C(α, γ)16O rate of +35% and 3α rate of +24%. From the results by Valle et al. (2013), we expect that in a small perturbation regime, there is no interaction between the different reaction rates. This is confirmed by the results shown in Table A.1, which presents the values tHB, tAGB as well as the abundances of C and O core at the central He exhaustion. The percent difference, d, with respect of the reference value and the expected value, dl, assuming that the effects of the two rates can be added linearly, are presented. It is apparent that the linearity assumption is justified.
Joint effect of the 3α and 12C(α, γ)16O reaction rates. The columns labelled ll correspond to computation performed with both rates at their lower boundary; those labelled hh to the rates at their upper boundary; d is the percent difference with respect to the reference value, dl is the effect computed by assuming indepen dence between the two rates.
All Tables
Impact of the uncertainty in the 12C(α, γ)16O reaction rate for the three considered stellar masses.
Joint effect of the 3α and 12C(α, γ)16O reaction rates. The columns labelled ll correspond to computation performed with both rates at their lower boundary; those labelled hh to the rates at their upper boundary; d is the percent difference with respect to the reference value, dl is the effect computed by assuming indepen dence between the two rates.
All Figures
 |
Fig. 1. Profile of 4He, 12C and 16O abundances at the first thermal pulse as a function of mass fraction. Left: profile obtained by increasing (dashed lines) and decreasing (dot dashed lines) the 12C(α, γ)16O reaction rate by 20%. The continuous lines correspond to the data obtained with the standard rate. The green lines represent the abundance of 4He, the orange lines the one of 12C, and the purple lines the one of 16O. Right: same as in the left panel but for a rate variation of ±35%. |
| In the text | |
 |
Fig. 2. Zero-age horizontal branch for different values of the 3α reaction rate. |
| In the text | |
 |
Fig. 3. Profiles of 4He, 12C, and 16O abundances at the first thermal pulse as a function of mass fraction. Left: profiles obtained increasing (dashed lines) and decreasing (dot-dashed lines) the 3α reaction rate by 12%. The continuous lines correspond to the data obtained with the standard rate. The green lines represent the abundance of 4He, the orange ones the abundance of 12C, and the purple lines the one of 16O. Right: same as in the left panel, but for a 3α reaction rate variation by ±24% and +34% (dotted lines). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.