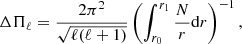EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 683 (March 2024) A&A, 683 (2024) A189 Full HTML
Open Access
Issue
A&A
Volume 683, March 2024
Article Number A189
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202348276
Published online 18 March 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Stars in the red clump (RC) are somewhat high-metallicity (higher than approximately −0.6 dex), low-mass (≲1.8 M⊙) stars that are in the process of fusing helium in their cores. Their key properties derive from the fact that their progenitors had a core made of degenerate matter when they were in the red giant branch (RGB) phase; this property results in helium core masses that are largely independent of the total mass. Consequently, the properties of the RC stars depend little on the stellar mass, which makes them targets of significant astrophysical importance. RC stars have been proposed as standard candles (because of their narrow luminosity range) and reddening indicators (Cannon 1970), as well as tracers of the chemical evolution of the Galaxy (e.g., Nidever et al. 2014). Because these stars are also the progenitors of later stages of stellar evolutions, it is key to improve their models to place better constraints on the structure of, for instance, white dwarf stars.

However, the modeling of several physical processes that occur within RC stars is still uncertain. The first main unknown is mixing at the boundary of the convective core, which we refer to as core boundary mixing (CBM). Schwarzschild & Härm (1969) found a semiconvective region around the core, whose properties have been studied by Castellani et al. (1971a,b). However, the need for semiconvection was questioned by Bressan et al. (1986), who showed that including a strong overshoot (over a distance of about a pressure scale height) allows us to reproduce the star counts of globular clusters without the need of a semiconvective region.

Other uncertainties in the modeling of RC stars are nuclear reactions rates, specifically, the rates of the helium-burning 3α and 12C(α, γ)16O reactions. The rate of the first reaction is somewhat well determined. However, the rate of the latter is notoriously ill-defined experimentally because the rates need to be extrapolated to low-energy stellar regimes, which is made more difficult by several interfering resonant states (Angulo et al. 1999; Kunz et al. 2002; deBoer et al. 2017).

The data from the space missions of the last decade, and especially Kepler (Borucki et al. 2010), have enabled us to retrieve the seismic properties of thousands of RC stars. RC stars are solar-like oscillators, whose modes are stochastically excited by the turbulence in the outer convective envelope of these stars. Notably, their nonradial modes have a mixed nature, acting as gravity modes in the core and as pressure modes in layers above. Therefore, the study of these modes allows us to constrain the properties of the deep layers of the star, and especially, the properties of the CBM. A striking result from the Kepler asteroseismic observables is that a large core extension is required to reproduce the observed seismic properties (e.g., Montalbán et al. 2013; Constantino et al. 2015; Bossini et al. 2015).

In this paper, we build on the works of Constantino et al. (2015, 2017), and Bossini et al. (2015, 2017) to investigate the combined effects of core boundary mixing, nuclear reaction rates, and composition on the period spacing of RC stars. We probe a wide parameter space in order to assess the changes in the period spacings. We review in Sect. 2 the seismic properties of RC stars and the structural features that are probed by the period spacing. In Sect. 3, after describing the physics of the models, we explain the properties of the different CBM schemes we used and their effect on the period spacing. In Sect. 4, we study the effect of varying the rates of 12C(α, γ)16O and 3α on the period spacing. In Sect. 5, we study the effect of the metallicity on the period spacing. Then, in Sect. 6, we examine the combined effects of CBM, nuclear reaction rates, and metallicity. We discuss our results and conclude in Sects. 7 and 8, respectively.

2. Seismic properties of RC stars

Nonradial modes of RC stars are mixed modes, which behave like gravity modes in the g-mode cavity and like pressure modes in the p-mode cavity. For a mode whose angular frequency is ω, the g-mode cavity is delimited by ω2 < N2, 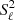S l 2 $ S^2_\ell $, N being the Brunt–Väisälä frequency and Sℓ the Lamb frequency for a mode with degree ℓ. Conversely, the p-mode cavity is defined by 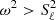ω 2 > S l 2 $ \omega^2 > S^2_\ell $, N2. In Fig. 1, we show these two cavities in an RC star. The g-mode cavity is located in the radiative region between the convective core and convective envelope, while the p-mode cavity is located in the outer layers of the star. The g-modes are therefore more sensitive to the inner part of the star, while the p-modes probe the envelope properties.

thumbnail Fig. 1.

Propagation diagram of an RC star. The Brunt–Väisälä frequency and ℓ = 1 Lamb frequencies are shown with blue and pink lines, respectively. They delimit the g-mode (light blue) and p-mode (light pink) cavities. Finally, the typical range of observed frequencies is shown in green.

Pure g-modes are asymptotically equally spaced in period (Shibahashi 1979). The periods of consecutive modes of degree ℓ are separated by a period spacing ΔΠℓ, which is defined as

Δ Π ℓ = 2 π 2 ℓ ( ℓ + 1 ) ( ∫ r 0 r 1 N r d r ) − 1 , $$ \begin{aligned} \Delta \Pi _\ell = \frac{2 \pi ^2}{\sqrt{\ell (\ell +1)}} \left(\int _{r_0}^{r_1} \frac{N}{r} \mathrm{d} r\right)^{-1}, \end{aligned} $$(1)

where r is the radial coordinate, and r0, r1 are the limits of the g-mode cavity. In the following, we only consider the period spacing of dipole modes because we only observe these modes; for simplicity, we call this ΔΠ. Through the integral of N/r in the g-mode cavity, ΔΠ is tightly related to the size of the convective core. A larger convective core would make the g-mode cavity smaller and accordingly increase ΔΠ. This makes the period spacing a very good probe of the properties near the convective core and a precise measure of the mass of the helium core (Montalbán et al. 2013). In this paper, we computed ΔΠ using Eq. (1). It is the main seismic observable of interest because we study the effect of helium-burning reactions, which occur in the core of the star.

The Kepler satellite data enable us to measure the period spacing for thousands of RC stars. The data cover a range of period spacings from approximately 230 to 340 s, largely independently of the mass (Vrard et al. 2016), as we can expect for low-mass stars with a degenerate core on the red giant branch.

3. Physics of the models

3.1. General properties

We computed models with MESA version r22.11.1 (Paxton et al. 2011, 2013, 2015, 2018, 2019; Jermyn et al. 2023). The equation of state is a mix of FreeEOS (Irwin 2012) in the envelope and Skye (Jermyn et al. 2021) in the core. The opacities came from the OPAL code (Iglesias & Rogers 1996), and we used the solar mixture of Grevesse & Sauval (1998). The convection regions were computed using the time-dependent local Kuhfuss (1986) model, adapted in such a way that it reduces to the Cox & Giuli (1968) mixing-length prescription at typical stellar evolutionary times. We set the mixing-length parameter αMLT to 1.8. The nuclear reaction rates were taken from the REACLIB database1 (Cyburt et al. 2010). Any modification in the nuclear reaction rates described in the text were made with respect to these rates.

3.2. Core boundary mixing

During the helium-burning phase, the core becomes enriched in carbon and oxygen, which increases the opacity and thus the radiative gradient, leading to a growing core. When the core reaches a certain size, the radiative gradient within it is no longer monotonic, and after a minimum, it increases with radius. This radiative temperature gradient is illustrated in Fig. 2. The core is then split in two regions: the fully mixed core (between the center and the minimum of ∇rad), and the partially mixed (PM) region, between the minimum of ∇rad and the radiative region. The properties of the PM region have a significant effect on the Brunt–Väisälä frequency profile, and therefore, on the asymptotic period spacing. Thus, we examine the effect of different partial mixing prescriptions in this work. As an illustration, we show in Fig. 3 the profile of different properties (temperature gradients, Brunt–Väisälä frequency, and composition) for the four different mixing prescriptions. We describe the prescriptions below.

thumbnail Fig. 2.

Central structure of a 1 M⊙ core helium-burning star in terms of radiative and adiabatic temperature gradients vs. the fractional mass. The radiative and adiabatic gradients are shown as solid blue and dashed black lines, respectively. We also show the convective core and partially mixed regions in pale pink and green.

Semiconvection. Schwarzschild & Härm (1969) found that the PM region is a semiconvective region that is buoyantly neutral (i.e., ∇rad = ∇ad). To achieve this, we used the convective premixing (CPM) scheme (Paxton et al. 2019). This scheme treats every convective boundary with an iterative approach (within an evolutionary time step) such that the Schwarzschild (or Ledoux) criterion is respected on the convective side of the boundary (in accordance with the recommendation from Gabriel et al. 2014). To explain the formation of a semiconvective region through the CPM scheme, we start from a situation similar to the one shown in Fig. 2. At the outer boundary of the partially PM region, ∇rad > ∇ad, which causes the boundary to move to a larger radius due to overshooting. This brings fresh unburned helium in the PM region that lowers the opacity in the PM region and therefore the radiative gradient. As a consequence, the inner PM region boundary, which was defined by the local minimum of the radiative gradient and was marginally unstable, moves to a larger radius, leaving a buoyantly neutral region in its wake. This process repeats, until the full PM region is buoyantly neutral. This mechanism of mixing through successive shrinking convective shells was described by Gabriel (1970) for massive star models, and it is similar to the Castellani et al. (1985) semiconvection scheme for core helium-burning (CHeB) stars. Semiconvection is sensitive to the core breathing pulses (CBP), which occur at the end of the core helium-burning phase. These pulses are sudden increases in the core size that are caused by the strong increase in the energy produced by the 3α triple alpha reaction when a small (in absolute sense) but high (in relative sense) quantity of helium is injected in the core. This unstable behavior impacts both ΔΠ and the duration of the core helium-burning phase. However, CBP seem to be ruled out by observations of globular clusters and asteroseismology (Caputo et al. 1989; Cassisi et al. 2001; Constantino et al. 2017). We therefore avoided the increase in the central helium abundance during the CHeB phase. This helped us to reduce the number of CBP without totally eliminating them. Finally, Constantino et al. (2015) observed that mode trapping may occur in the semiconvective region, which may impact the seismic properties of the star. We discuss this process in Sect. 7.1.

Maximal overshoot. This scheme was introduced by Constantino et al. (2015) to reconcile model predictions with seismic observations, and it results in a large asymptotic period spacing. It is defined by the following algorithm: When the local ∇rad minimum appears in the core, it extends the core such that the local minimum of the radiative gradient is equal to the adiabatic gradient. A core larger than this would decrease the radiative gradient, which would split the convective region into two and thus lower the period spacing. This scheme is ad hoc and quite nonphysical, notably because the Schwarzschild criterion is not respected on the convective side of the external boundary (see Fig. 3a). However, it leads to a behavior of the period spacing that is similar to the behavior that results from a potential mode trapping in the semiconvective region. We discuss this in Sect. 7.1.

thumbnail Fig. 3.

Properties around the core of 1 M⊙, solar metallicity models computed with the maximal overshoot (solid blue), overmixing (dashed pink), penetrative convection (dotted green), and semiconvection (dash-dotted yellow) core boundary mixing schemes. Panel a: radiative and adiabatic gradients. Panel b: temperature gradients (∇ = ∂lnT/∂lnP). Panel c: Brunt–Väisälä frequency profile. Panel d: helium composition profile.

Overmixing and penetrative convection. The core can be extended over a certain distance dov, defined by a free parameter αov such that dov = αovHp, with Hp the pressure scale height. The thermal stratification in the extension region can either be radiative (i.e., ∇ = ∇rad) or adiabatic (i.e., ∇ = ∇ad). The first case is known as overmixing, and the second case is known as penetrative convection. We note that at some point in the evolution, a convective shell appears at the outer boundary of the overshooting region. This shell becomes a semiconvective region in a convective premixing scheme. The overmixing and penetrative convection schemes used here are different from those used in Bossini et al. (2015, 2017) because of this semiconvective region. More details on the effect of αov and the core boundary scheme are given in Sect. 7.2.

Figure 4 shows the evolution of the asymptotic period spacing ΔΠ of 1.0 M⊙ models with solar metallicity and different core boundary mixing prescriptions. We used αov = 1.0 for overmixing and penetrative convection. As expected, every prescription yields significantly different ranges of ΔΠ. Notably, the maximum value of period spacing for models with semiconvection is approximately 290 s, which is significantly lower than the highest observational values of Vrard et al. (2016). Maximal overshoot and overmixing schemes both show a similar behavior, with a continuous growth of the core. Finally, the penetrative convection behaves similarly to the overmixing scheme, but is approximately 30 s higher.

thumbnail Fig. 4.

Evolution of ΔΠ of a 1 M⊙ model of solar metallicity for different core-boundary mixing prescriptions. The evolution is indicated with age (upper panel) and central helium abundance Yc (lower panel).

4. Effect of nuclear reaction rates on the seismic observables

4.1. Nuclear reactions in RC stars

Helium burning mainly occurs through two reactions. The first is the 3α process, which occurs in two steps: 4He+4He→7Be and 7Be+4He→12C + γ. This reaction dominates during the early part of the helium-burning phase. The second reaction is the 12C(α, γ)16O reaction (12C+4He→16O + γ), which dominates at the end of the helium-burning phase.

The formal uncertainties on the 3α reaction are relatively low, about 10% in the NACRE compilation (Angulo et al. 1999). For the 12C(α, γ)16O reaction, Table 1 summarizes the rate at 0.1 GK found in the literature. Notably, Kunz et al. (2002) considerably lowered the nominal rate compared to the NACRE compilation. Shen et al. (2023) also recently found a rate that was significantly higher than the values of Xu et al. (2013) and deBoer et al. (2017). The value of the 12C(α, γ)16O rate is therefore still uncertain.

Table 1.

Nuclear rate of the 12C(α, γ)16O reaction at 108 K from different literature sources.

In this work, the standard rate for the 3α and 12C(α, γ)16O reactions was assumed to be the rate from Fynbo et al. (2005) and Xu et al. (2013), respectively. The models described in this section are 1 M⊙ models with solar metallicity, and they were computed with the maximal overshoot scheme.

4.2. Effect of the nuclear reaction rates on the period spacing

4.2.1. 3α reaction

In Fig. 5 we show the evolution of ΔΠ during the core helium-burning phase for different factors by which the standard 3α reaction rate was changed. When the rate of the 3α process is increased, we obtain models with larger asymptotic period spacing during the whole helium-burning phase. For instance, multiplying the rate by 2 increases the period spacing by approximately 4 s, which is consistent with the results of Constantino et al. (2015).

thumbnail Fig. 5.

Evolution of ΔΠ during the CHeB phase for different 3α reaction rates.

This effect on the period spacing is due to two competing processes: (1) A higher 3α rate allows the He flash to start at lower temperature, that is, earlier in the RGB evolution. The inert He core is therefore less massive, and so is the convective core during the CHeB phase. This decreases the asymptotic period spacing. (2) Because of the higher rate, the same luminosity can be produced in a lower-density environment. This decreases the local gravity within the star and thus the Brunt–Väisälä frequency, eventually yielding a higher period spacing. The amplitude of the second process is slightly larger than the first amplitude, which explains the fact that period spacing is higher with an increased 3α rate.

4.2.2. 12C(α, γ)16O reaction

In Fig. 6 we show the evolution of ΔΠ for different rates of the 12C(α, γ)16O reaction. We find that at first, for a CHeB age younger than 0.4 × 108 years, the period spacing of the different models is identical. This is because initially the 12C(α, γ)16O produces a negligible part of the total luminosity of the star. The main effect of increasing the rate of ΔΠ is to extend the CHeB phase. The CHeB duration of models with a rate that is multiplied by 5 is approximately 20% longer.

thumbnail Fig. 6.

Same as Fig. 5, now for different 12C(α, γ)16O reaction rates.

The core expands during core helium burning, which continuously increases the period spacing. Therefore, by extending the CHeB phase, the models reach higher ΔΠ values. Thus, models with a rate multiplied by 2 cover a period spacing range of 89 s, that is, 10 s larger than the models with a standard rate. We note that Constantino et al. (2015) found the same order of magnitude, but surprisingly did not find that increasing the 12C(α, γ)16O rate lengthens the CHeB phase, in contrast to results presented in earlier literature (e.g., Salaris & Cassisi 2005).

To explain the increase in the duration of the CHeB phase, we show in Fig. 7 the share of the luminosity production between the different reactions for a model with a standard rate (left) and with a rate multiplied by 5 (right). The total luminosities of the two models are very similar, but the distribution of the energy production between the reactions differ. At a given Yc, 12C(α, γ)16O produces a larger fraction of the energy when its rate is multiplied by 5. However, one 12C(α, γ)16O reaction consumes one nucleus of helium while the 3α reaction consumes three for an approximately equal amount of energy production. Consequently, the helium consumption will be lowered when 12C(α, γ)16O dominates at a given total luminosity. This results in a longer core helium-burning phase, which in turn increases the range of ΔΠ during the CHeB phase. We note that similar results and explanations have recently been found by Tognini et al. (2023).

thumbnail Fig. 7.

Evolution of the distribution of the total luminosity of a 1 M⊙ CHeB star between the different nuclear reactions for a star with a normal rate and a rate multiplied by 5.

5. Effect of composition

Metallicity has a significant impact on the period spacing during the CHeB phase. A metal-poor star ignites helium at a more massive core, which in turn affects the size of the convective helium-burning core (see e.g., Sweigart & Gross 1976). Consequently, we expect a higher period spacing for metal-poor models, which is verified in our models, as shown in Fig. 8. In addition, decreasing the metallicity shortens the CHeB duration. Figure 8 shows the evolution of the period spacing for 1 M⊙ models, computed with a maximal overshoot scheme at different metallicities. We found that the period spacing for stars with a metallicity of 0.2 dex is roughly 25 s lower than a model with a metallicity of −0.5 dex during the whole CHeB phase. These results are consistent with the findings of Constantino et al. (2017) and Bossini et al. (2017).

thumbnail Fig. 8.

Evolution of ΔΠ for different metallicities at 1.0 M⊙. A model with Y0 = 0.25 and high metallicity is also shown.

In contrast with the metallicity, the models show that the initial helium Y0 has a small impact on the period spacing, except at the very beginning of the core helium-burning phase. In Fig. 8 we illustrate this with a model computed with 0.2 dex metallicity and Y0 = 0.25 instead of the original Y0 = 0.29 metallicity.

6. Combined effect of mixing, nuclear reaction rates, and metallicity

In this section, we study the combined effect of the core boundary mixing, nuclear reaction rates of 12C(α, γ)16O, and metallicity on the period spacing. Figure 9 shows the span of the period spacing for models with different mixing, metallicities, and 12C(α, γ)16O nuclear reaction rates. We chose metallicity values of −0.5 and 0.2 dex, which encompass the metallicities of the stars in the Kepler field. The values for the rates are half, double, and equal to the standard rate.

thumbnail Fig. 9.

ΔΠ range for models computed with a different mixing prescription, 12C(α, γ)16O nuclear reaction rates, and metallicities. Models with metallicities of −0.5, 0, and 0.2 dex are shown in shades of blue, orange, and green, respectively. The opacity of the bar scales with the time that the model spends at that given period spacing. The observations from Vrard et al. (2016) are shown in purple, and the opacity is related to the number of stars observed at that value of ΔΠ. The models with semiconvection, overmixing, and penetrative convection were computed with the CPM scheme.

From this figure, we find that on the one hand, the penetrative convection scenario, when computed with αov = 1.0, can reproduce the highest observed values of the period spacing, but not the lowest. On the other hand, the models computed with penetrative convection and αov = 0.1 can reproduce the lower values, but not the higher values. Thus, no value of αov seems to allow the penetrative convection to be compatible with the observations.

The asymptotic period spacing of the models computed with semiconvection and overmixing (for both αov = 1.0 and 0.1) cannot reproduce the full range of observed values, especially the highest values. However, maximal overshoot yields scenarios that are compatible with the observations.

We note that the effect of increasing the rate is stronger for models computed with maximal overshoot (increase in the maximum value of the period spacing of 10 s) compared to models computed with a semiconvective region (increase by 7 s). This effect also depends on the metallicity, if slightly, with a stronger effect for models with lower metallicity (the increase is 2 s longer for −0.5 dex).

Finally, it seems difficult to distinguish the different reaction rates because of the uncertainties on the core boundary mixing and the rather strong effect of metallicity.

7. Discussion

7.1. Mode trapping

In models with overmixing or semiconvection, the PM region is part of the g-mode cavity, and its outer boundary is delimited by a strong chemical discontinuity. For these reasons, as noted by Constantino et al. (2015), some modes may be trapped within the PM region, while the other modes are trapped in the rest of the g-mode cavity. Consequently, their frequencies behave as if the inner boundary of their cavity were the outer boundary of the PM region. For this reason, the observed period spacing, obtained with frequencies, may be significantly larger than the asymptotic period spacing as defined in Eq. (1) (Constantino et al. 2015; Pinçon & Takata 2022).

We did not explicitly account for this process in our work. However, the period spacing yielded by the maximal overshoot scheme is close to the observed period spacing that would result from mode trapping in a semiconvective region. The reason is that the extent of the maximal overshoot core is close to the extent of the core plus the semiconvection region. We can therefore consider that the results coming from the maximal overshoot scheme are, at least for ΔΠ, equivalent to the trapped-mode scenario in the case of semiconvection.

A thorough study of the mode-trapping phenomenon in RC stars is beyond the scope of this paper. We note, nevertheless, that we observed this trapping in a subset of our models with semiconvection and overmixing when we computed frequencies (with, e.g., GYRE Townsend & Teitler 2013). The development of trapped modes seems to depend on the physics of the models, however, especially on the inclusion of microscopic diffusion.

7.2. Effect of the core boundary scheme and αov in the overshoot models

In this section, we discuss the different ways in which the boundary of the convective region with overshoot can be handled, as well as the effect of αov.

The burning of helium in the core increases the opacity, which in turn increases the radiative gradient. Thus, the local maximum of ∇rad situated at the outer overshoot boundary (see panel a of Fig. 3) at some point in the evolution becomes larger than ∇ad, which causes the outer part of the overshoot region to become convective. This convective shell is stable in the basic convective boundary scheme, which can be questioned (see Sect. 7 of Gabriel et al. 2014). However, when we use the convective premixing scheme (CPM), as done in this work, the convective shell becomes semiconvective, which impacts the Brunt–Väisälä frequency profile and therefore the period spacing. Figures 10 and 11 illustrates this effect for overmixing and penetrative convection, respectively. Notably, the CPM clearly decreases the period spacing when the semiconvective region appears. Consequently, our models have period spacings with maximum values that are lower than those computed without a semiconvective region, such as in Bossini et al. (2015, 2017).

thumbnail Fig. 10.

Evolution of the asymptotic period spacing for overmixing models with αov = 0.1 (blue) and αov = 0.9 (pink), computed with the default core boundary scheme (dark colors) and the CPM scheme (light colors; see text for details). The arrows indicate the moment in the evolution at which a semiconvective region appears. Strong episodes of CBP are visible in the low-overshoot models for Yc < 0.15.

thumbnail Fig. 11.

Same as Fig. 10, now with penetrative convection (∇ = ∇ad in the overshoot region). Similarly to Fig. 10, several CBP events are present.

Another effect of the CPM scheme is to smoothen the evolution of the core boundary at low overshoot. As noted in Straniero et al. (2003), when a convective shell is present in the overshoot region, it intermittently merges with the convective core, which suddenly expands it. Then, there is a strong helium intake, and the core size is reduced. This erratic core behavior is visible in the evolution of the period spacing for models with low overshoot2, as shown in Figs. 10 and 11, while the evolution of the period spacing when computed with CPM appears to be smoother.

The effect of the αov parameter on the period spacing differs between the overmixing and penetrative convection cases. In the first case, it does not impact ΔΠ much because the overshoot region is part of the g-mode cavity, as shown in panel c of Fig. 3. Therefore, modifying the extent of the overshoot region does not directly impact the extent of the g-mode cavity, which limits the effect of the parameter on the period spacing. However, the smaller the αov the parameter, the sooner the semiconvective region appears (as noted by the arrows), which decreases the maximum value of the period spacing, as shown in Fig. 10.

For the penetrative convection case, the g-modes do not propagate in the overshoot region. Thus, increasing αov increases the period spacing, as we showed in Fig. 11. Similarly to the models with overmixing, the semiconvection region also appears sooner in the evolution for models with low αov. As a result of these two effects, αov has a considerable effect on ΔΠ for models with penetrative convection.

8. Conclusion

We have investigated the combined effects of the 3α and 12C(α, γ)16O reaction rates, core boundary mixing, and metallicity on the period spacing of RC stars. These stars exhibit mixed modes whose properties, and especially the period spacing ΔΠ, allow us to probe the properties of the region around the core. In accordance with the literature (Constantino et al. 2015, 2017; Bossini et al. 2015, 2017), we found that the core boundary mixing scheme is the main source of uncertainties on the period spacing of our models because the period spacing strongly depends on the size of the convective core, as well as on the temperature and composition stratification in the core boundary region. We confirm the findings of Constantino et al. (2015) that the maximal overshoot alone is able to reproduce the lowest and highest values of ΔΠ. Additionally, we found that even if the scheme itself is ad hoc, the resulting period spacings are similar to those that result from mode trapping in a semiconvective region. We also tested overmixing (∇ = ∇rad in the overshoot region) and penetrative convection (∇ = ∇ad in the overshoot region). We found that no single value of the overshoot parameter can reproduce both the highest and lowest observed values of ΔΠ. These results differ from those of Bossini et al. (2015, 2017). This difference is due to the use of the convective premixing scheme in this work, which causes a semiconvective region around the core. This decreases the value of the period spacing. This semiconvection region notably solves the issue of an unphysical core boundary, in which ∇rad > ∇ad at the inner side of the boundary.

We also investigated the effect of changing the rates of the 3α and 12C(α, γ)16O reactions. On the one hand, regarding the 3α reaction, a higher rate causes an earlier helium flash and a lower central density during the helium-burning phase. These effects decrease and increase the period spacing, respectively, such that the resulting effect is negligible. On the other hand, the effect of increasing the rate of the 12C(α, γ)16O reaction mainly is to increase the duration of the CHeB phase. This allows the cores to grow to a larger size, which eventually increases the maximum value of the period spacing. We find that doubling the rate increases the maximum period spacing value by 10 s for a model computed with maximal overshoot, and 7 s for a model computed with the convective premixing scheme without overshoot. The effect of increasing the rate is slightly stronger for models with lower metallicity, but with a negligible amplitude (2 s higher for a −0.5 dex model).

Mainly due to the uncertainties on the mixing3, it is currently not (yet) possible to perform an inverse analysis, that is, to constrain the 12C(α, γ)16O rate using the period spacing of the RC stars. However, with better constraints on the core boundary mixing, as well as with more data from the upcoming PLATO mission (Rauer et al. 2014), RC star seismology could provide astrophysical constraints on the 12C(α, γ)16O reaction rate.

1

During this work, it has been found that the above version of MESA has a faulty implementation of the reverse 3α reaction, which causes a depletion of carbon at the end of the core helium-burning phase. However, it does not affect us since we do not take this reaction into account in our nuclear network because its rate is extremely low at temperatures relevant to our study. We are therefore not concerned by this issue.

2

This erratic evolution of ΔΠ does not occur at high αov because as the overshoot region is larger, the convective shell is more distant from the core and thus never merges.

3

We note the recent work from Blouin et al. (2024), which through 3D simulations, explore the stability of the different core boundary mixing schemes used in this work, and find that a semiconvective region is quickly erased by overshooting mixing through overshooting from the convective core.

Acknowledgments

We thank the anonymous referee for comments that improved the clarity of this paper. A.N. and S.H. acknowledge funding from the ERC Consolidator Grant DipolarSound (grant agreement #10s1000296). S.B. acknowledges NSF grant AST-2205026.

References

  1. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [Google Scholar]
  2. Blouin, S., Herwig, F., Mao, H., Denissenkov, P., & Woodward, P. R. 2024, MNRAS, 527, 4847 [Google Scholar]
  3. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  4. Bossini, D., Miglio, A., Salaris, M., et al. 2015, MNRAS, 453, 2290 [Google Scholar]
  5. Bossini, D., Miglio, A., Salaris, M., et al. 2017, MNRAS, 469, 4718 [Google Scholar]
  6. Bressan, A., Bertelli, G., & Chiosi, C. 1986, Mem. Soc. Astron. It., 57, 411 [NASA ADS] [Google Scholar]
  7. Cannon, R. D. 1970, MNRAS, 150, 111 [NASA ADS] [CrossRef] [Google Scholar]
  8. Caputo, F., Castellani, V., Chieffi, A., Pulone, L., & Tornambe, A., Jr. 1989, ApJ, 340, 241 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cassisi, S., Castellani, V., Degl’Innocenti, S., Piotto, G., & Salaris, M. 2001, A&A, 366, 578 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Castellani, V., Giannone, P., & Renzini, A. 1971a, Ap&SS, 10, 340 [NASA ADS] [CrossRef] [Google Scholar]
  11. Castellani, V., Giannone, P., & Renzini, A. 1971b, Ap&SS, 10, 355 [NASA ADS] [CrossRef] [Google Scholar]
  12. Castellani, V., Chieffi, A., Tornambe, A., & Pulone, L. 1985, ApJ, 296, 204 [Google Scholar]
  13. Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [Google Scholar]
  14. Constantino, T., Campbell, S. W., & Lattanzio, J. C. 2017, MNRAS, 472, 4900 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cox, J. P., & Giuli, R. T. 1968, Principles of Stellar Structure (New York: Gordon and Breach) [Google Scholar]
  16. Cyburt, R. H., Amthor, A. M., Ferguson, R., et al. 2010, ApJS, 189, 240 [NASA ADS] [CrossRef] [Google Scholar]
  17. deBoer, R. J., Görres, J., Wiescher, M., et al. 2017, Rev. Mod. Phys., 89, 035007 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fynbo, H. O. U., Diget, C. A., Bergmann, U. C., et al. 2005, Nature, 433, 136 [Google Scholar]
  19. Gabriel, M. 1970, A&A, 6, 124 [NASA ADS] [Google Scholar]
  20. Gabriel, M., Noels, A., Montalbán, J., & Miglio, A. 2014, A&A, 569, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
  22. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  23. Irwin, A. W. 2012, Astrophysics Source Code Library [record ascl:1211.002] [Google Scholar]
  24. Jermyn, A. S., Schwab, J., Bauer, E., Timmes, F. X., & Potekhin, A. Y. 2021, ApJ, 913, 72 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jermyn, A. S., Bauer, E. B., Schwab, J., et al. 2023, ApJS, 265, 15 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kuhfuss, R. 1986, A&A, 160, 116 [NASA ADS] [Google Scholar]
  27. Kunz, R., Fey, M., Jaeger, M., et al. 2002, ApJ, 567, 643 [CrossRef] [Google Scholar]
  28. Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [Google Scholar]
  29. Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [Google Scholar]
  30. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  31. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  32. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  33. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  34. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  35. Pinçon, C., & Takata, M. 2022, A&A, 661, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [Google Scholar]
  37. Salaris, M., & Cassisi, S. 2005, Evolution of Stars and Stellar Populations (Wiley-VCH), 162 [Google Scholar]
  38. Schwarzschild, M., & Härm, R. 1969, BAAS, 1, 99 [Google Scholar]
  39. Shen, Y., Guo, B., deBoer, R. J., et al. 2023, ApJ, 945, 41 [NASA ADS] [CrossRef] [Google Scholar]
  40. Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
  41. Straniero, O., Domínguez, I., Imbriani, G., & Piersanti, L. 2003, ApJ, 583, 878 [NASA ADS] [CrossRef] [Google Scholar]
  42. Sweigart, A. V., & Gross, P. G. 1976, ApJS, 32, 367 [NASA ADS] [CrossRef] [Google Scholar]
  43. Tognini, F., Valle, G., Dell’Omodarme, M., Degl’Innocenti, S., & Prada Moroni, P. G. 2023, A&A, 679, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [Google Scholar]
  45. Vrard, M., Mosser, B., & Samadi, R. 2016, A&A, 588, A87 [CrossRef] [EDP Sciences] [Google Scholar]
  46. Xu, Y., Takahashi, K., Goriely, S., et al. 2013, Nucl. Phys. A, 918, 61 [Google Scholar]

All Tables

Table 1.

Nuclear rate of the 12C(α, γ)16O reaction at 108 K from different literature sources.

In the text

All Figures

thumbnail Fig. 1.

Propagation diagram of an RC star. The Brunt–Väisälä frequency and ℓ = 1 Lamb frequencies are shown with blue and pink lines, respectively. They delimit the g-mode (light blue) and p-mode (light pink) cavities. Finally, the typical range of observed frequencies is shown in green.
In the text
thumbnail Fig. 2.

Central structure of a 1 M⊙ core helium-burning star in terms of radiative and adiabatic temperature gradients vs. the fractional mass. The radiative and adiabatic gradients are shown as solid blue and dashed black lines, respectively. We also show the convective core and partially mixed regions in pale pink and green.
In the text
thumbnail Fig. 3.

Properties around the core of 1 M⊙, solar metallicity models computed with the maximal overshoot (solid blue), overmixing (dashed pink), penetrative convection (dotted green), and semiconvection (dash-dotted yellow) core boundary mixing schemes. Panel a: radiative and adiabatic gradients. Panel b: temperature gradients (∇ = ∂lnT/∂lnP). Panel c: Brunt–Väisälä frequency profile. Panel d: helium composition profile.
In the text
thumbnail Fig. 4.

Evolution of ΔΠ of a 1 M⊙ model of solar metallicity for different core-boundary mixing prescriptions. The evolution is indicated with age (upper panel) and central helium abundance Yc (lower panel).
In the text
thumbnail Fig. 5.

Evolution of ΔΠ during the CHeB phase for different 3α reaction rates.
In the text
thumbnail Fig. 6.

Same as Fig. 5, now for different 12C(α, γ)16O reaction rates.
In the text
thumbnail Fig. 7.

Evolution of the distribution of the total luminosity of a 1 M⊙ CHeB star between the different nuclear reactions for a star with a normal rate and a rate multiplied by 5.
In the text
thumbnail Fig. 8.

Evolution of ΔΠ for different metallicities at 1.0 M⊙. A model with Y0 = 0.25 and high metallicity is also shown.
In the text
thumbnail Fig. 9.

ΔΠ range for models computed with a different mixing prescription, 12C(α, γ)16O nuclear reaction rates, and metallicities. Models with metallicities of −0.5, 0, and 0.2 dex are shown in shades of blue, orange, and green, respectively. The opacity of the bar scales with the time that the model spends at that given period spacing. The observations from Vrard et al. (2016) are shown in purple, and the opacity is related to the number of stars observed at that value of ΔΠ. The models with semiconvection, overmixing, and penetrative convection were computed with the CPM scheme.
In the text
thumbnail Fig. 10.

Evolution of the asymptotic period spacing for overmixing models with αov = 0.1 (blue) and αov = 0.9 (pink), computed with the default core boundary scheme (dark colors) and the CPM scheme (light colors; see text for details). The arrows indicate the moment in the evolution at which a semiconvective region appears. Strong episodes of CBP are visible in the low-overshoot models for Yc < 0.15.
In the text
thumbnail Fig. 11.

Same as Fig. 10, now with penetrative convection (∇ = ∇ad in the overshoot region). Similarly to Fig. 10, several CBP events are present.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.