EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 678 (October 2023) A&A, 678 (2023) A53 Full HTML
Open Access
Issue
A&A
Volume 678, October 2023
Article Number A53
Number of page(s) 10
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202346958
Published online 05 October 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) are an essential and pervasive constituent of carbonaceous materials in space. It has been two decades since the PAH hypothesis was proposed to explain the association of unidentified IR bands (UIRs) with interstellar environments (ISM). Though 5–20% of ISM carbon is locked up in PAHs (Joblin & Tielens 2011), understanding the formation and evolution of such complex organic structures is still challenging for many astrophysical settings. PAHs still remain one of the most researched chemical species in different branches of science (e.g., astrophysics, chemistry, atmospheric science, etc.).

PAHs exist as an assortment of radicals, ions, and neutral entities in the ISM (Allamandola et al. 1999). They are expected to have a significant influence on the chemical and hydrodynamical evolution of protoplanetary disks as well as on the dynamics of atmospheric structures of newborn exoplanets (Ercolano et al. 2022; Gorti et al. 2009). They are essential for understanding the ionization equilibrium of the medium and, consequently, the evolution of gaseous atmospheres (Thi et al. 2019). Moreover, from an astrobiological standpoint, PAHs are considered to be associated with prebiotic chemistry and abiogenesis, constituting an essential step in the production of amino acids and nucleotides (Ehrenfreund et al. 2006, Ehrenfreund et al. 2007; Rapacioli et al. 2006; Ehrenfreund & Charnley 2000; Wakelam & Herbst 2008; Galliano et al. 2008; Kim et al. 2012; Sandstrom et al. 2011; Puzzarini et al. 2017).

Furthermore, PAHs show interesting photochemical properties and can act as photosensitizers and photoinitiators in numerous chemical reactions, such as polymerizations. This is highly interesting in the context of prebiotic chemistry, where PAHs can activate prebiotically formed photoredox organocat-alysts such as imidazolidine-4-thiones (Closs et al. 2020) and enable chemical transformations such as the alpha-alkylation of aldehydes, thus providing precursors of canonical amino acids. Such processes bridge the gap between the formation of small molecular building blocks, for example those obtained by meteorite catalysis, and the formation of more complex precursors for the assembly of amino acids and nucleosides. Such a system represents the first photochemical process, utilizing sunlight as an energy source for chemical energy. In addition, the first evolutionary steps in these photoredox organocatalysts can be initiated at the molecular level (Closs et al. 2022).

Unraveling the formation and subsequent growth history of complex organic molecules has become the central focus of the PAH community in recent times. The fundamental physicochemical mechanisms of the formation process of large PAHs remain obscure, especially with regard to the important step of chemical reactions between tiny organic components and interstellar dust (Hanine et al. 2020). Molecular dynamics, quantum chemistry, and laboratory experiments have suggested different chemical pathways leading to their synthesis in thermalized conditions from different precursor molecules (Hanine et al. 2020; Hirai 2021; He et al. 2023; Campisi 2021). Moreover, photochemistry and vertical mixing might also play an important role in determining their abundance in planetary atmospheres. However, their significance has not been robustly explored yet in any of the atmospheric models.

Ercolano et al. (2022) have shown the 3.3 μm feature (aromatic C-H stretching vibrational mode) to be a promising option for the detection of PAHs on planet atmospheres and also on protoplanetary disks. While PAHs have been detected substantially on Earth and on Saturn’s moon Titan (Dinelli et al. 2013; López-Puertas et al. 2013), the hunt for PAHs on exoplanets still remains elusive due to the limitation of ground and space-based telescopes: (a) the 3.3 μm atmospheric window on Earth is contaminated by other molecular fingerprints (Seok & Li 2017) and (b) previous space-based systems lacked the required wavelength coverage. The James Webb Space Telescope (JWST), specifically the NIRSpec PRISM mode (0.6-5.3 μm), presents a solution to these shortcomings. The upcoming space missions, Ariel (Tinetti et al. 2018, 2020) and Twinkle (Edwards et al. 2019), are also suitable for observing at 3.3 μm with high sensitivity (Ercolano et al. 2022).

In this paper, we aim to present a preliminary study of PAH formation under thermalized circumstances. Our main focus is to understand the influence of different parameters on PAH production. We self-consistently simulated a large grid of planetary atmospheres for some irradiated hot Jupiters and directly imaged planets and obtained synthetic spectra for different conditions. Our procedures and assumptions are outlined in Sect. 2. In the next section (i.e., Sect. 3), we present the results from our atmospheric models. Section 4 concludes with a concise summary of our findings.

2 Methods

We have produced a grid of self-consistent planetary atmospheres for irradiated and non-irradiated hot Jupiters with petitCODE (Mollière et al. 2015; Mollière 2017) to study the effect of different parameters on PAH formation under thermalized conditions. In the following sections, petitCODE is described along with the parameter space and models.

2.1 petitCODE

petitCODE is a 1D self-consistent model (Mollière et al. 2015, Mollière 2017) that solves the atmospheric structures for some physical input parameters and under the assumption of radiative-convective equilibrium (both absorption/emission and scattering are considered). After certain iterations of the atmospheric structure, the final solution of the model is obtained when chemical abundances, their opacities, and radiation fields are in equilibrium with the temperature-pressure structure (TP structure) of the atmosphere. Equilibrium chemical abundances are computed using petitCODE’s self-written Gibbs free energy minimizer. petitCODE uses the Feautrier method to obtain the radiative transfer solution and applies the Accelerated Lambda Iteration (Olson et al. 1986) and Ng acceleration (Ng 1974) method to speed up convergence.

The following physical parameters are used as inputs for the code: effective stellar temperature, stellar radius, star-planet distance or effective planetary temperature, planet mass and radius (or surface gravity), atomic elemental abundances, and preferred insolation treatment (day-side averaged, globally averaged, or angle of incidence for irradiation).

There are also options for cloud treatment inside the planet atmosphere: providing the lognormal particle distribution width (σg), the settling factor (fsed), and vertical mixing (Kzz) (following the Ackerman & Marley 2001 prescription); or by introducing the size of cloud particles and setting the maximum cloud mass fraction (see Mollière 2017). In our present investigation, we focus on irradiated and non-irradiated hot Jupiters under cloud-free conditions, thus excluding considerations of condensation processes in our models. Further dedicated studies will be needed to explore cloudy planet atmospheres.

Atomic species, their elemental abundances, and their product molecules (gaseous, condensate, and liquid species) are needed for the calculation (see Molaverdikhani et al. 2019 for details). Additionally, the inclusion or non-inclusion of collision induced absorption (CIA) species in the models needs to be specified.

2.2 Grid properties

We explore a grid of models with varying carbon to oxygen ratios, metallicities, planetary effective temperatures (see Sect. 2.3), and opacity species. We limit our study to the case of a G5 star (T* = 5660 K, R* = 1 R⊙, V = 9, and K = 7.5) and log(g) = 3 (Rp = 1 RJ, Mp = 1 MJ, where RJ and MJ are the radius and mass of Jupiter, respectively).

2.2.1 Carbon to oxygen ratio (C/O)

The C/O ratio can have a significant influence on the TP structure of the atmosphere and the distribution pattern of molecular abundances in atmospheric layers. Photochemical hazes are anticipated to be important for exoplanet atmospheres, especially those with higher C/O ratios or higher metallicities (He et al. 2023; Hörst et al. 2018). For this reason, we focused on supersolar C/O ratios, starting from solar value C/O = [0.55, 0.80, 1.00, 1.25, 1.50].

We varied the C/O ratio according to the recipe chosen by Madhusudhan (2012), Mollière et al. (2015), Woitke et al. (2018), and Molaverdikhani et al. (2019): by changing the oxygen elemental abundance while keeping the carbon elemental abundance constant. This captures the accumulation of variable water content on a young accreting planet through gases and planetesimals.

2.2.2 Metallicity [Fe/H]

As mentioned in Sect. 2.2.1, photochemical hazes may have a crucial impact on atmospheres in the presence of enhanced metallicity values. Gas and ice giants in our solar system show diversified bulk composition, ranging from 3× to 100× the solar metallicity value (Guillot et al. 2022). In this work, we choose to explore an extended range of metallicities in our thermochemical models, spanning from solar to 10 000× solar. While a metallicity of 10 000× solar is unrealistic for any gas or ice giant, it is useful to provide a limiting case for PAH formation.

Our metallicity grid spans the following values: [Fe/H] = [0, 1, 2, 3, 4]. Here, [Fe/H] stands for metallicity in the log scale. So, [Fe/H] = 1 signifies a ten times higher metal-rich atmosphere than our Sun. All elements except H and He are considered as “metal” here.

2.2.3 Reactant and opacity species

In this work, we employ petitCODE’s default chemical network, which includes atomic species and their products. The following gas opacity species are provided for the models: CH4, H2O, CO2, HCN, CO, H2S, NH3, C2H2, Na, K, TiO, and VO. CIA species (H2–H2 and H2–He) are also taken into account.

In the modeling of directly imaged planets, some condensate species (Mg2SiO4(c), MgAl2O4(c), and Fe2SiO4(c)) had to be removed from the network due to poor convergence of the models. This is a known problem, lying with the abundance matrix in Gibbs’s free energy minimizer (see Appendix A of Molaverdikhani et al. 2019 for more details).

2.3 0D models for organic chemical species

As predicted by molecular dynamics simulations (Hanine et al. 2020; Hirai 2021), PAH formation is favored at a critical temperature region. Lower temperatures are insufficient for PAHs to form thermally, and higher temperatures lead to the thermal cleavage of PAHs. To check the critical temperature inside the planet’s atmosphere, we ran a set of 0D models for 180 organic species (alkanes, alkenes, alkynes, and aromatic species, etc.) with the equilibrium chemistry solver of petitCODE for a C/O ratio of 1.25. NASA9 polynomial coefficients (for Gibbs free energy calculation) for all the molecules have been taken from the Elke Goos & Ruscic (2016) database.

We considered a wide range of temperatures (800 K, 1000 K, 1100 K, 1200 K, 1300 K, 1400 K, 1500 K, 1600 K, 1750 K, and 2000 K) and fixed the pressure at 10−2 bar for the calculation. The temperature grid was designed to encompass the full range of observed planetary effective temperatures (Teff), excluding an extremely irradiated hot Jupiter, which might have intrinsically different atmospheric chemistry (Molaverdikhani et al. 2019). The pressure layer was also chosen in terms of planetary photosphere context. The photosphere is the specific region inside a planet’s atmosphere (between 1 and 10−3 bar) that we probe for the transmission and emission spectra of a planet.

2.4 Modelling planets for PAH formation

2.4.1 1D self-consistent models for transiting planets

Based on the result from the 0D models (see Fig. 1), we calculated self-consistent forward models of planetary atmospheres with Teff = 1300 K and planet internal temperature (Tint) = 200 K, but with different metallicities and C/O ratios. We considered Tint ≪ Teff to satisfy the following condition for irradiated planets: Teqm ≪ Teff. This can easily be understood from a simple relation: 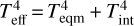Teff4=Teqm4+Tint4$T_{{\rm{eff}}}^4 = T_{{\rm{eqm}}}^4 + T_{{\mathop{\rm int}} }^4$, where Teqm is the planet’s equilibrium temperature.

For the sake of simplicity, we limited our study to a few selected PAH species: anthracene (C14H10), perylene (C20H12), coronene (C24H12), and ovalene (C32H14). These were selected because of their larger abundance predicted by thermochemical equilibrium models (see Sect. 3.1).

2.4.2 Extraplanetary origins of PAHs

PAHs are abundant species in the ISM, with a typical number density of 3 × 10−7 relative to H (Tielens 2008). In addition to the in situ formation of PAHs within a planetary atmosphere, there are several potential pathways through which a planet can accumulate PAHs at levels comparable to those found in the ISM. One significant mechanism involves the continuous influx of interplanetary dust via various astronomical processes, such as comet and asteroid impacts, among others. These events contribute to the enrichment of PAHs on the planet’s surface. We convert the ISM value for the number density of PAHs to a mass fraction as follows: 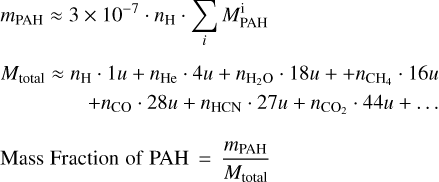mPAH≈3×10−7⋅nH⋅∑iMPAHiMtotal≈nH⋅1u+nHe⋅4u+nH2O⋅18u++nCH4⋅16u                        +nCO⋅28u+nHCN⋅27u+nCO2⋅44u+…Mass Fraction of PAH = mPAHMtotal$\matrix{ {{m_{{\rm{PAH}}}} \approx 3 \times {{10}^{ - 7}} \cdot {n_H} \cdot \sum\limits_i {M_{{\rm{PAH}}}^{\rm{i}}} } \hfill \cr {{M_{{\rm{total}}}} \approx {n_{\rm{H}}} \cdot 1u + {n_{{\rm{He}}}} \cdot 4u + {n_{{{\rm{H}}_2}{\rm{O}}}} \cdot 18u + + {n_{{\rm{C}}{{\rm{H}}_4}}} \cdot 16u} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {n_{{\rm{CO}}}} \cdot 28u + {n_{{\rm{HCN}}}} \cdot 27u + {n_{{\rm{C}}{{\rm{O}}_2}}} \cdot 44u + \ldots } \hfill \cr {{\rm{Mass}}\,{\rm{Fraction}}\,{\rm{of}}\,{\rm{PAH}}\,{\rm{ = }}\,{{{m_{{\rm{PAH}}}}} \over {{M_{{\rm{total}}}}}}} \hfill \cr }$(1)

where mPAH = net mass of all PAHs, 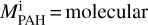MPAHi=molecular$M_{{\rm{PAH}}}^{\rm{i}} = {\rm{molecular}}$ mass of ith PAH species, Mtotal = total mass of molecules present in the atmosphere, and nk = number density of kth species in the atmosphere.

We kept the same planet parameters as listed in Sect. 2.4.1; however, we fixed the C/O ratio to the solar value (C/O = 0.55) and the [Fe/H] to 1, which is relevant to the question of whether PAH signatures are detectable on planets transiting Sun-like stars. Even though several attempts have been made in the past, measuring the C/O ratios of exoplanets remains a challenge due to the poor detectability of carbon-bearing species. While transiting planets and directly imaged planets exhibit a wide range of C/O ratios, the measured values are subject to enormous uncertainty (see Hoch et al. 2023). High-resolution data from JWST might be useful to constrain the C/O ratio of planets with greater precision in the near future.

2.4.3 1D self-consistent model for directly imaged planets

We further investigated if the imprints of PAHs could be visible in a carbon-rich atmosphere of a directly imaged planet. Directly imaged planets are young planets that have generally formed far away from their host stars. Irradiation from the central star is generally negligible and they are detected in the infrared thanks to their warm interiors. We modeled the planets with star-planet distance (d) = 10 au, Tint = 700 K, constant C/O = 1.2, and with varying metallicities.

We reduced the atmospheric pressure range to 10-10−3 bar and decreased the temperature step inside the petitCODE to make the convergence smoother.

2.5 Calculation of transmission and emission spectra from modeled atmospheres

Very little is known currently about PAHs in exoplanet atmospheres, partially due to the instrumental limitations. A dedicated search for the PAH signature in transmission and emission spectra using the atmospheric retrieval method has not been attempted yet. Here, we used our atmospheric models to produce synthetic spectra to determine whether such detection is within reach of current and future instrumentation. We coupled the outputs from petitCODE to the radiative transfer modeling and atmospheric retrieval code petitRADTRANS (Mollière et al. 2019, 2020) for the calculation of synthetic transmission (for transiting planets) and emission spectra (for directly imaged planets) at a resolution of λ/Δλ = 1000. We considered the line opacity species: H2O, CO (HITEMP; see Rothman et al. 2010), C2H2, CH4, and HCN (ExoMol; see Chubb et al. 2021); and the Rayleigh opacity species: H2, He; CIA species: H2-H2, H2-He (see Mollière et al. 2019 for further details).

We followed Ercolano et al. (2022) and calculated the PAH cross sections following Li & Draine (2001) and including updates from Draine & Li (2007) for circumcoronene PAHs consisting of 54 carbon and 18 hydrogen atoms for both neutral and ionized PAHs, as described by Woitke et al. (2016). This results in a PAH mass of 667 amu and a PAH radius of 4.87 Å (Weingartner & Draine 2001). These cross sections correspond to the optical properties of “astro-PAHs” and align well with astronomical observations in the ISM. These opacities are regularly employed in protoplanetary disk models including the hot irradiated atmospheres of the inner regions of disks.

thumbnail Fig. 1

0D modeling of 90 organic species (PAHs and other organic molecules) for P = 10−2 bar and over a wide temperature grid: the nth isomer for some species is displayed with the symbol ‘_n’ (n is an integer). Subfigures (a) and (b) showcase the PAHs and saturated/less unsaturated species, respectively. Entities with more unsaturation are separately shown in (e). (c) and (d) display a combination of different categories together.

3 Results

3.1 0D models: Optimum temperature for PAH formation and correlation with other organic species

3.1.1 Model for a large number of molecules as carbon-bearing species

We estimated the mass fractions of different organic species, including saturated (alkanes) and unsaturated (alkenes, alkynes, and PAHs) hydrocarbons as a function of temperature and at a pressure value consistent with the planetary photosphere regime (see Fig. 1). Structural isomers were also analyzed for a few species. For the sake of simplicity, we neglected charged species and oxygen or nitrogen-substituted species in particular.

We introduce a new parameter, β (β = nC/nH, where nC and nH refer to the number of carbon atoms and hydrogen atoms present in a molecule), that classifies the molecules into three different classes: (1) β ≥ 1 (species with more unsaturation), (2) β < 1 (saturated and less unsaturated species), and (3) β ≫ 1 (highly unsaturated hydrocarbon radicals i.e., with more carbon atoms and fewer hydrogen atoms).

The three classes show different correlations with temperature. Class 1 shows a peak at 1300 K and dips both ways. It implies that the formation of PAHs and other highly unsaturated species is favored at 1300 K in thermalized conditions. A similar trend was earlier found by Hirai (2021). The temperature dependency is derived from the dependency of the thermodynamical coefficients with temperature, resulting in different values of ΔG. Since the formation of a given molecular species requires that ΔG < 0 thermodynamically, for each species there exists a specific temperature range that favors the formation of that species. This temperature range lies in the neighborhood of 1300 K for highly unsaturated species.

Class 2 molecules exhibit a distinct behavior. At lower temperatures, they follow a positive correlation with temperature, but they undergo a dip at 1300 K. It manifests the contribution of saturated/less unsaturated species toward the formation of Class 1 species at the optimum temperature regime. However, it is also important to note that Class 2 hydrocarbons with nC > 11 fail to form (see N-undecane, N-dodecane from Fig. 1b, and C14H28, C14H30 from Fig. 1e). Carbon atoms seem to be entrapped in smaller compounds. This can be understood by looking at the relative mass fractions from Fig. 1b. β-factor too has a key role here. Mass fractions of Class 2 molecules decrease with a decrease in the β-factor. Even though both factors have a combined influence on the abundance of Class 2 species, the former is more significant in this instance.

Due to them being radical hydrocarbon entities, we neglected the role of Class 3 (Fig. 1d shows seven of them in two different subplots) in PAH formation for equilibrium models. But their presence is important for the disequilibrium models, which will be the focus of our future work.

3.1.2 Only PAHs as carbon-bearing species

It is difficult to estimate the exact magnitude of the PAH abundances in our models. The reason is that the absolute value strongly depends on how the available carbon is distributed among all carbon-bearing species.

An upper limit can, however, be obtained by making the assumption that all available carbon is locked into PAHs. This is shown in Fig. 2, which shows PAH abundances that are several orders of magnitude higher than in our previous calculation (see Fig. 1a).

3.2 Constraining the C/O ratio and [Fe/H] for the PAH signature in planetary spectra from 1D self-consistent models

3.2.1 Transiting planets

The C/O ratio and metallicity have very strong effects on the atmospheric characteristics of a planet. In our models, PAH formation also shows a strong dependency on the C/O ratio. We find that PAH production is low for solar or slightly higher than solar C/O ratios, as the results for C/O ≤ 0.80 are shown in Fig. 3. PAHs in planet atmospheres are more pronounced at lower pressures, primarily attributed to the TP structure. This correlation is shown in Fig. 4, wherein lower pressures correspond to temperatures that coincide with the optimal range for the formation of PAHs, as illustrated in Fig. 1. The contribution of PAH features to the planet’s spectra begins to be visible in models where C/O = 1, which we assume to be the lower limit for thermalized conditions (see Fig. 5). The 3.3 μm feature is not discernible in the transmission spectra due to the presence of the 3.4 μm feature of aliphatic hydrocarbon (e.g., CH4 for our model). It becomes noticeable however as the C/O ratio increases. The pronounced steep slope observed in the UV region (see Figs. 5c–e) results from the adopted PAH cross sections. This observation aligns with the likelihood that photochemical hazes play a significant role in generating super-Rayleigh slopes in the planet’s transmission spectra, as highlighted in the study by Ohno & Kawashima (2020). Figure 6 illustrates the contributions of various molecules (for a supersolar C/O ratio) to the overall planetary spectrum, where CH4 and C2H2 emerge as the primary constituents (the cutoff of CH4 and C2H2 opacity at ~0.8 and ~ 1 μm, respectively, is not real and is caused by the lack of data). While the absorption features between 6 and 12 μm, including the spectra slope at UV, appear more prominent, a more detailed investigation of atmospheric retrieval is needed to assess its detectability with current and future space facilities. This will be the focus of Paper II of this series (Grübel et al., in prep.).

The average temperature of the photosphere (between 1 and 10−3 bar pressure range) also allows a better understanding of the 0D models (see Fig. 4). An average photospheric temperature, Tphoto ~ 1300 K is obtained from different models. Here, we extended the C/O ratio to 2.0 to better understand the TP profile and to establish a connection between the C/O ratio and PAH formation. The increase in Tphoto of the planet with increasing the C/O ratio is not very significant, and hence the C/O ratio has a dominating role over the planetary effective temperature for the formation of PAHs.

We further investigated the sensitivity of the models to our assumed metallicity values. Figure 7 reflects the dependency on metallicity of planets bearing a supersolar C/O ratio (C/O = 1.0). Metallicity also impacts the formation of PAHs in a similar way as the C/O ratio does: enhanced metallicity favors PAH formation. However, for the solar C/O ratio, we find that the PAH abundance does not change significantly with the increase in the metallicity, leading us to the conclusion that the C/O ratio is the dominant parameter for the PAH abundance.

Our current models consider a cloud-free context. However, it is essential to note that the same scenario may not apply to cloudy atmospheres. Specifically, under supersolar C/O ratios or high metal-rich conditions, graphite condensation can exert a substantial influence on atmospheric chemical composition by extracting carbon from the gas phase (see Lodders & Fegley 1997; Moses et al. 2013). As a result, this process may lead to a reduced abundance of PAHs.

At lower C/O ratios, equilibrium models favor the formation of water over any carbon-bearing species (Molaverdikhani et al. 2019). Equilibrium models thus exclude the presence of PAHs at solar C/O. If a transiting planet bears the signature of PAH in its spectra, two possible scenarios can explain that case: (1) various astronomical pathways have led to the incorporation of PAHs into the planetary atmosphere (see Sect. 2.4.2), or (2) the PAHs were formed in situ, via a chemical pathway that has not been explored in this work. While this study addresses the ther-mochemical equilibrium scenarios, disequilibrium aspects for in situ formation will be the focus of future work.

Figure 8 shows the planetary transmission spectrum for the solar C/O ratio where the ISM abundance of PAH is considered. Due to the prominence of the H2O feature in the spectrum, PAH characteristics are not visible to the naked eye except for the slope. While the PAH features are hidden by the H2O features and are not easily discernible by visual inspection, these might be detectable by means of atmospheric retrieval.

thumbnail Fig. 2

0D model representing PAHs as the only carbon-bearing species. Other small and large hydrocarbons have been removed from the calculation to better constrain the order of mass fractions for PAHs with temperature.
thumbnail Fig. 3

Mass fraction of four different PAHs, H2O, CH4, HCN, CO, and C2H2, for transiting planet (Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0) for different C/O ratios.
thumbnail Fig. 4

Pressure-temperature profile for a modeled planet: Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0.
thumbnail Fig. 5

Transmission spectra for a modeled planet revolving around a G5 star (Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, log(g) = 3.0) with different C/O ratios: (a) C/O = 0.55 (solar), (b) C/O = 0.80, (c) C/O = 1.00, (d) C/O = 1.25, and (e) C/O = 1.50. The blue line indicates the PAH cross section for the abundance obtained from the models for four PAHs together. The red and green lines represent transmission spectra with and without considering PAHs, respectively, in the atmosphere. The gray zones cover the areas with the most important PAH features (represented with the dotted lines) at 3.3 μm and 6–12 μm.

3.2.2 Directly imaged planets

To better understand the influence of metallicity and C/O ratio on PAH formation, we extended our investigation to directly imaged planets. Similar to transiting planets, solar C/O was not able to form PAHs significantly, even with enhanced metallicity values. Therefore, the main investigation was executed for a fixed supersolar C/O ratio but for different metallicities.

Figure 9 shows the mass fractions of four different PAHs at different metallicity values. The [Fe/H] = 0 and 1 cases are less important in this regard as they could not produce PAHs significantly. Increasing metallicity boosts PAH formation by a few orders of magnitude, emphasizing the importance of metallicity on PAH formation for directly imaged planets. It is interesting to note that lower metallicities favor the formation of small PAHs, while the formation of larger PAHs is observed for higher metallicity values.

For directly imaged planets, molecular signatures are probed using the absorption features from the planetary emission spectrum. We simulated the planetary emission spectra for [Fe/H] = 2, and no PAH feature was observed from the spectra (see Fig. 10). Here, directly imaged planets pose a challenge in identifying the molecular signature of PAHs in emission spectra due to the presence of prominent CH4 and C2H2 absorption features, coupled with low PAH abundance at lower metallicity values. This scenario holds true for the range of expected metallicity values and only starts to break down when we reach unrealistically high metallicities (i.e., [Fe/H] = 4).

thumbnail Fig. 6

Transmission spectrum for the synthetic planet (Teff = 1300 K, Tint = 200 K, C/O =1.25, [Fe/H] = 1.0, and log(g) = 3.0) with key contributors to the atmospheric spectrum.
thumbnail Fig. 7

Mass fraction of four different PAHs for transiting planet (Teff = 1300 K, Tint = 200 K, C/O =1.0, and log(g) = 3.0) for different metallicity values. Top left: anthracene. Top right: perylene. Bottom left: coronene. Bottom right: ovalene. [Fe/H] = 0 yields PAH abundances less than 10−20 and hence is not significant for the planet’s atmosphere.
thumbnail Fig. 8

Transmission spectrum for a modeled planet containing ISM abundance for PAHs: Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0.
thumbnail Fig. 9

Mass fraction of four different PAHs for the directly imaged planet model (d =10 au, Tint = 700 K, C/O = 1.2, log(g) = 3.0) for different metallicities. Top left: anthracene. Top right: perylene. Bottom left: coronene. Bottom right: ovalene. Similar to Fig. 7, we kept a lower limit of 10−20 for molecular abundance. [Fe/H] = 0 and 1 cases produce an insignificant amount of PAHs in the atmosphere and hence are not shown here.

4 Conclusion

We simulated atmospheres self-consistently for transiting and directly imaged planets around a Sun-like star. We show the role of planetary effective temperature in PAH formation from the 0D model. Planets with an effective temperature of around 1300 K are the most promising targets for investigating PAHs. Additionally, higher C/O ratios and increased metallicity are crucial in facilitating PAH formation under thermalized conditions. Among the three parameters considered, the C/O ratio exhibits a dominant influence in this context.

The attainment of supersolar C/O ratios in planet atmospheres can be linked to planet formation pathways. In the absence of an efficient release of volatiles from the core or late enrichment through interactions with planetesimals, gas giants that accumulate a substantial portion of their atmospheres after reaching the pebble isolation mass tend to acquire envelopes characterized by substellar C/H and O/H ratios along with notably high C/O ratio compositions (C/O > 1.0) (see Bosman et al. 2021 for further details). Giant planet formation through core accretion, involving the accumulation of mm- or cm-sized pebbles without substantial core-envelope mixing, can also result in supersolar C/O ratios (Madhusudhan et al. 2017). Planet formation beyond the CO2 snowline, accompanied by disk-free migration, is associated with a C/O ratio of approximately one. Alternatively, for planets forming between the H2O and CO2 snowlines and subsequently undergoing migration through the protoplanetary disk, pebble drift can raise the C/O ratio from approximately 0.7 to about 1.0 (Booth et al. 2017). Moreover, the rainout of oxygen-rich refractory species in the atmosphere can further enhance the atmospheric C/O ratio when C/O < 1, potentially leading the atmosphere towards a C/O ≈ 1 scenario (Burrows & Sharp 1999). Recent studies have found many protoplanetary disks that exhibit C/O ≥ 1 (Bergin et al. 2016; Kama et al. 2016; Miotello et al. 2019). These disks could potentially serve as the molecular factory for the formation of PAH-rich worlds.

If a planet acquires an ex situ abundance of PAHs, atmospheric retrieval could lead to the detection of PAH features from planet spectra. To draw robust conclusions regarding detectability, a comprehensive investigation involving a substantial population of planets is necessary. This can be achieved by leveraging data from current and upcoming space missions, such as JWST, Twinkle, and Ariel, which will significantly enhance our understanding of planetary atmospheres.

We particularly focused on irradiated planets as they exhibit a more intricate interplay of equilibrium and disequilibrium chemistry across various regions of their atmospheres. However, this does not imply that non-irradiated planets do not show such processes. Understanding the formation and destruction processes of large PAHs is crucial to connect the presence of PAHs in temperate planets (like our Earth and Titan), which are potentially habitable worlds in the Universe. Although photochemistry, vertical mixing, and chemical kinetics are essential in this regard, there are caveats for the complex structures of these large molecules. We hope to address these challenges in our next work.

thumbnail Fig. 10

Emission spectrum for a synthetic directly imaged planet: d =10 au, Tint = 700 K, C/O =1.2, log(g) = 3.0, and [Fe/H] = 2. The orange line represents the blackbody spectrum for 700 K, which is the Teff of the planet.

Acknowledgements

This research was supported by the Excellence Cluster ORIGINS, which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC-2094 – 390783311 (http://www.universe-cluster.de/). Softwares: Our Python scripts are dependent on the following libraries: numpy (Harris et al. 2020), matplotlib (Hunter 2007), jupyter (Kluyver et al. 2016), dill (McKerns et al. 2011), and seaborn (Waskom 2021).

References

  1. Ackerman, A. S., & Marley, M. S. 2001, ApJ, 556, 872 [Google Scholar]
  2. Allamandola, L., Hudgins, D., & Sandford, S. 1999, ApJ, 511, L115 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bergin, E. A., Du, F., Cleeves, L. I., et al. 2016, ApJ, 831, 101 [Google Scholar]
  4. Booth, R. A., Clarke, C. J., Madhusudhan, N., & Ilee, J. D. 2017, MNRAS, 469, 3994 [Google Scholar]
  5. Bosman, A. D., Alarcón, F., Bergin, E. A., et al. 2021, ApJS, 257, 7 [NASA ADS] [CrossRef] [Google Scholar]
  6. Burrows, A., & Sharp, C. M. 1999, ApJ, 512, 843 [NASA ADS] [CrossRef] [Google Scholar]
  7. Campisi, D. 2021, PhD thesis, Leiden University, The Netherlands [Google Scholar]
  8. Chubb, K. L., Rocchetto, M., Yurchenko, S. N., et al. 2021, A & A, 646, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Closs, A. C., Fuks, E., Bechtel, M., & Trapp, O. 2020, Chemistry, 26, 10702 [CrossRef] [Google Scholar]
  10. Closs, A. C., Bechtel, M., & Trapp, O. 2022, Angew. Chem. Int. Ed., 61, e202112563 [CrossRef] [Google Scholar]
  11. Dinelli, B. M., López-Puertas, M., Adriani, A., et al. 2013, Geophys. Res. Lett., 40, 1489 [NASA ADS] [CrossRef] [Google Scholar]
  12. Draine, B., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  13. Edwards, B., Rice, M., Zingales, T., et al. 2019, Exp. Astron., 47, 29 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ehrenfreund, P., & Charnley, S. B. 2000, ARA & A, 38, 427 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ehrenfreund, P., Rasmussen, S., Cleaves, J., & Chen, L. 2006, Astrobiology, 6, 490 [NASA ADS] [CrossRef] [Google Scholar]
  16. Ehrenfreund, P., Ruiterkamp, R., Peeters, Z., et al. 2007, Planet. Space Sci., 55, 383 [NASA ADS] [CrossRef] [Google Scholar]
  17. Elke Goos, A. B., & Ruscic, B. 2016, New NASA Thermodynamic Polynomials Database With Active Thermochemical Tables Updates, https://www.dlr.de/vt/desktopdefault.aspx/tabid-7603/12862_read-32379/ [Google Scholar]
  18. Ercolano, B., Rab, C., Molaverdikhani, K., et al. 2022, MNRAS, 512, 430 [NASA ADS] [CrossRef] [Google Scholar]
  19. Galliano, F., Dwek, E., & Chanial, P. 2008, ApJ, 672, 214 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gorti, U., Dullemond, C. P., & Hollenbach, D. 2009, ApJ, 705, 1237 [Google Scholar]
  21. Guillot, T., Fletcher, L. N., Helled, R., et al. 2022, arXiv e-prints [arXiv: 2205.04100] [Google Scholar]
  22. Hanine, M., Meng, Z., Lu, S., et al. 2020, ApJ, 900, 188 [NASA ADS] [CrossRef] [Google Scholar]
  23. Harris, C. R., Millman, K. J., Van Der Walt, S. J., et al. 2020 z, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
  24. He, C., Radke, M., Moran, S. E., et al. 2023, arXiv e-prints [arXiv:2301.02745] [Google Scholar]
  25. Hirai, H. 2021, Chem. Phys., 548, 111225 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hoch, K. K. W., Konopacky, Q. M., Theissen, C. A., et al. 2023, AJ, 166, 85 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hörst, S. M., He, C., Lewis, N. K., et al. 2018, Nat. Astron., 2, 303 [Google Scholar]
  28. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  29. Joblin, C., & Tielens, A.G. G. M. 2011, PAHs and the Universe: A Symposium to Celebrate the 25th Anniversary of the PAH Hypothesis, in EAS Publications Series, 46 [Google Scholar]
  30. Kama, M., Bruderer, S., Van Dishoeck, E., et al. 2016, A & A, 592, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kim, J. H., Im, M., Lee, H. M., et al. 2012, ApJ, 760, 120 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Scmidt (IOS Press), 87 [Google Scholar]
  33. Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
  34. Lodders, K., & Fegley, B. 1997, Astrophysical implications of the laboratory study of presolar materials, eds. T. J. Bernatowicz, & E. Zinner, American Institute of Physics Conference Series, 402, 391 [NASA ADS] [CrossRef] [Google Scholar]
  35. López-Puertas, M., Dinelli, B. M., Adriani, A., et al. 2013, ApJ, 770, 132 [CrossRef] [Google Scholar]
  36. Madhusudhan, N. 2012, ApJ, 758, 36 [NASA ADS] [CrossRef] [Google Scholar]
  37. Madhusudhan, N., Bitsch, B., Johansen, A., & Eriksson, L. 2017, MNRAS, 469, 4102 [NASA ADS] [CrossRef] [Google Scholar]
  38. McKerns, M. M., Strand, L., Sullivan, T., Fang, A., & Aivazis, M. A. G. 2011, in Proceedings of the 10th Python in Science Conference, eds. S. van der Walt, & J. Millman, 76 [CrossRef] [Google Scholar]
  39. Miotello, A., Facchini, S., Van Dishoeck, E., et al. 2019, A & A, 631, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Molaverdikhani, K., Henning, T., & Mollière, P. 2019, ApJ, 873, 32 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mollière, P. M. 2017, PhD thesis, Ruprecht-Karls-Universität Heidelberg, Germany [Google Scholar]
  42. Mollière, P., van Boekel, R., Dullemond, C., Henning, T., & Mordasini, C. 2015, ApJ, 813, 47 [Google Scholar]
  43. Mollière, P., Wardenier, J. P., van Boekel, R., et al. 2019, A & A, 627, A67 [CrossRef] [EDP Sciences] [Google Scholar]
  44. Mollière, P., Stolker, T., Lacour, S., et al. 2020, A & A, 640, A131 [CrossRef] [EDP Sciences] [Google Scholar]
  45. Moses, J. I., Line, M. R., Visscher, C., et al. 2013, ApJ, 777, 34 [Google Scholar]
  46. Ng, K. 1974, J. Chem. Phys., 61, 2680 [NASA ADS] [CrossRef] [Google Scholar]
  47. Ohno, K., & Kawashima, Y. 2020, ApJ, 895, L47 [NASA ADS] [CrossRef] [Google Scholar]
  48. Olson, G. L., Auer, L., & Buchler, J. R. 1986, J. Quant. Spectr. Rad. Transf., 35, 431 [NASA ADS] [CrossRef] [Google Scholar]
  49. Puzzarini, C., Baiardi, A., Bloino, J., et al. 2017, AJ, 154, 82 [NASA ADS] [CrossRef] [Google Scholar]
  50. Rapacioli, M., Calvo, F., Joblin, C., et al. 2006, A & A, 460, 519 [CrossRef] [EDP Sciences] [Google Scholar]
  51. Rothman, L., Gordon, I., Barber, R., et al. 2010, JQSRT, 111, 2139 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sandstrom, K. M., Bolatto, A. D., Bot, C., et al. 2011, ApJ, 744, 20 [Google Scholar]
  53. Seok, J. Y., & Li, A. 2017, ApJ, 835, 291 [Google Scholar]
  54. Thi, W. F., Lesur, G., Woitke, P., et al. 2019, A & A, 632, A44 [CrossRef] [EDP Sciences] [Google Scholar]
  55. Tielens, A. G. 2008, Annu. Rev. Astron. Astrophys., 46, 289 [CrossRef] [Google Scholar]
  56. Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
  57. Tinetti, G., Eccleston, P., Haswell, C., et al. 2020, Ariel: Enabling Planetary Science Across Light-years (European Space Agency), report number: ESA/SCI(2020)1 [Google Scholar]
  58. Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
  59. Waskom, M. L. 2021, J. Open Source Softw., 6, 3021 [CrossRef] [Google Scholar]
  60. Weingartner, J. C., & Draine, B. T. 2001, ApJS, 134, 263 [CrossRef] [Google Scholar]
  61. Woitke, P., Min, M., Pinte, C., et al. 2016, A & A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Woitke, P., Helling, C., Hunter, G. H., et al. 2018, A & A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

0D modeling of 90 organic species (PAHs and other organic molecules) for P = 10−2 bar and over a wide temperature grid: the nth isomer for some species is displayed with the symbol ‘_n’ (n is an integer). Subfigures (a) and (b) showcase the PAHs and saturated/less unsaturated species, respectively. Entities with more unsaturation are separately shown in (e). (c) and (d) display a combination of different categories together.
In the text
thumbnail Fig. 2

0D model representing PAHs as the only carbon-bearing species. Other small and large hydrocarbons have been removed from the calculation to better constrain the order of mass fractions for PAHs with temperature.
In the text
thumbnail Fig. 3

Mass fraction of four different PAHs, H2O, CH4, HCN, CO, and C2H2, for transiting planet (Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0) for different C/O ratios.
In the text
thumbnail Fig. 4

Pressure-temperature profile for a modeled planet: Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0.
In the text
thumbnail Fig. 5

Transmission spectra for a modeled planet revolving around a G5 star (Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, log(g) = 3.0) with different C/O ratios: (a) C/O = 0.55 (solar), (b) C/O = 0.80, (c) C/O = 1.00, (d) C/O = 1.25, and (e) C/O = 1.50. The blue line indicates the PAH cross section for the abundance obtained from the models for four PAHs together. The red and green lines represent transmission spectra with and without considering PAHs, respectively, in the atmosphere. The gray zones cover the areas with the most important PAH features (represented with the dotted lines) at 3.3 μm and 6–12 μm.
In the text
thumbnail Fig. 6

Transmission spectrum for the synthetic planet (Teff = 1300 K, Tint = 200 K, C/O =1.25, [Fe/H] = 1.0, and log(g) = 3.0) with key contributors to the atmospheric spectrum.
In the text
thumbnail Fig. 7

Mass fraction of four different PAHs for transiting planet (Teff = 1300 K, Tint = 200 K, C/O =1.0, and log(g) = 3.0) for different metallicity values. Top left: anthracene. Top right: perylene. Bottom left: coronene. Bottom right: ovalene. [Fe/H] = 0 yields PAH abundances less than 10−20 and hence is not significant for the planet’s atmosphere.
In the text
thumbnail Fig. 8

Transmission spectrum for a modeled planet containing ISM abundance for PAHs: Teff = 1300 K, Tint = 200 K, [Fe/H] = 1.0, and log(g) = 3.0.
In the text
thumbnail Fig. 9

Mass fraction of four different PAHs for the directly imaged planet model (d =10 au, Tint = 700 K, C/O = 1.2, log(g) = 3.0) for different metallicities. Top left: anthracene. Top right: perylene. Bottom left: coronene. Bottom right: ovalene. Similar to Fig. 7, we kept a lower limit of 10−20 for molecular abundance. [Fe/H] = 0 and 1 cases produce an insignificant amount of PAHs in the atmosphere and hence are not shown here.
In the text
thumbnail Fig. 10

Emission spectrum for a synthetic directly imaged planet: d =10 au, Tint = 700 K, C/O =1.2, log(g) = 3.0, and [Fe/H] = 2. The orange line represents the blackbody spectrum for 700 K, which is the Teff of the planet.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.